Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

5.1 Introduction

The thermodynamics of strong interactions under a strong magnetic background has proven to be a very rich and subtle subject. Recent developments were initially motivated by the utility of magnetic fields in separating charge in space, which would render the possible formation of sphaleron-induced CP-odd domains in the plasma created in high-energy heavy ion collisions, in the so-called chiral magnetic effect [1–7], measurable. In fact, the magnetic fields created in non-central collisions in heavy ion experiments at RHIC-BNL and the LHC-CERN are possibly the highest since the epoch of the electroweak phase transition, reaching values such as B∼1019 Gauss (\(eB \sim6 m_{\pi}^{2}\)) for peripheral collisions at RHIC [8, 9] and even much higher at the LHC due to the fluctuations in the distribution of protons inside the nuclei [10, 11].

From the theoretical point of view, the non-trivial role played by magnetic fields in the nature of phase transitions has been known for a long time [12]. Modifications in the vacuum of QED and QCD have also been investigated within different frameworks, mainly using effective models [13–27], especially the NJL model [28], and chiral perturbation theory [29–31], but also resorting to the quark model [32] and certain limits of QCD [33]. Interesting phases in dense systems [34–41], as well as effects on the dynamical quark mass [42] were also considered. Nevertheless, the mapping of the new T–eB phase diagram is still an open problem. There are clear indications that sufficiently large magnetic fields could significantly modify the behavior of the chiral and the deconfinement phase transition lines [43–69], or even transform the vacuum into a superconducting medium via ρ-meson condensation [70–73]. Although most of the analyses so far relied on effective models, lattice QCD has definitely entered the field and has been producing its first results for the phase diagram [74–81].

From the first results obtained within effective models for the deconfining [43] and chiral [44, 45] transition lines, one would expect the phase diagram structure illustrated in Fig. 5.1, as discussed in Ref. [48]. Indeed, after the prediction of a splitting between the chiral and deconfining transition lines, with the appearance of a new phase, in Ref. [48], several model descriptions produced the same effect [52–58, 67]. However, until 2011, all model studies have yielded either a monotonically increasing or an essentially flat functional form for the deconfinement critical line as B increases to very large values.Footnote 1 Pioneering lattice simulations [77, 78] also found an essentially flat behavior for both critical lines, that seemed to increase together at a very low rate. Nevertheless, since the pion mass used in these simulations was still very high, this could be an indication that one would probably need huge magnetic fields in the simulations in order to be able to compare to effective model predictions.

Fig. 5.1
figure 1

Originally expected magnetic field–temperature phase diagram of strong interactions. The thick lines indicate first-order transitions, the filled circles are the (second-order) endpoints of these lines, and the thin dashed lines stand for the corresponding crossovers. A new phase with broken chiral symmetry and deconfinement appears at high magnetic fields. Extracted from Ref. [48]

Full size image

This was the scenario, rather coherent in terms of expectations for the behavior of the critical lines for the chiral and deconfining transitions in the presence of a magnetic background, until lattice simulations of magnetic QCD with physical masses and fine grids were performed [80] and showed that both critical temperatures actually go down for increasing B, saturating for very large fields, very differently from what has been predicted by all previous effective model calculations and found in previous lattice simulations.

Soon after the appearance of the new lattice results, the behavior of the critical temperature for deconfinement in the presence of a very large magnetic field was addressed within the MIT bag model [68], a very economic model in terms of parameters to be fixed (essentially one) and other ingredients usually hard to control in more sophisticated effective theories. The model is, of course, crude in numerical precision and misses the correct nature of the (crossover) transition. Nevertheless, it provides a simple setup for the discussion of some subtleties of vacuum and thermal contributions in each phase. It was shown in Ref. [68] that the influence of the magnetic field on the thermodynamics of both extreme energy domains is captured, so that the model furnishes a reasonable qualitative description of the behavior of the critical temperature in the presence of B, decreasing and saturating.

The fact that chiral models, even when coupled with the (static) Polyakov loop sector, seem to fail in the description of the behavior of T c ×eB, whereas the (assumedly simple) MIT bag approach finds a good qualitative agreement, suggests that the critical temperature in QCD is a confinement-driven observable. This was also hinted by a previous successful description of the behavior of the critical temperature as a function of the pion mass and isospin chemical potential, as compared to lattice data, where chiral models also failed even qualitatively [82–84]. If confinement dynamics plays a central role in guiding the functional behavior of T c , a the large-N c limit of QCD should provide an adequate and powerful framework to study associated magnetic thermodynamics. In fact, it was shown in Ref. [85] on very general grounds that the fact that the deconfining temperature decreases and tends to saturate for large B, although this last point cannot be proven in a model-independent way, depends solely on quarks behaving paramagnetically.

In the sequel we summarize results for the chiral and deconfining transitions obtained in the framework of the linear sigma model coupled to quarks and to the Polyakov loop, especially the prediction of a splitting of the two critical lines, and how they compare to other effective model approaches as well as to lattice QCD. Then we discuss the outcome of the magnetic MIT bag model that yields a behavior for the critical deconfining temperature compatible with the most recent lattice simulations and magnetic catalysis. We continue with a discussion of very recent results, starting with the rather general findings within the large-N c limit of magnetic QCD. Finally, we present our conclusions.

5.2 Modified Dispersion Relations and Integral Measures

In the presence of a classical, constant and uniform (Abelian) magnetic field, dispersion relations and momentum integrals will be modified. In order to compute vacuum and thermal determinants and Feynman diagrams, it is necessary to express these quantities in a convenient fashion. Lorentz invariance is broken by the preferred direction established by the external field, and Landau orbits redefine the new counting of quantum states [12].

For definiteness, let us take the direction of the magnetic field as the z-direction, \(\mathbf {B}=B \hat{\textbf{z}}\). One can compute, for instance, the modified effective potential or the modified pressure to lowest order by redefining the dispersion relations of charged scalar and spinor fields in the presence of B, using the minimal coupling shift in the gradient and the field equations of motion.Footnote 2 For this purpose, it is convenient to choose the gauge such that A μ=(A 0,A)=(0,−By,0,0).

For scalar fields with electric charge q, such as pions, one has

(5.1)
(5.2)

After decomposing ϕ into Fourier modes, except for the dependence in the coordinate y, one obtains

(5.3)

which has the form of a Schrödinger equation for a harmonic oscillator. Its eigenmodes correspond to the well-known Landau levels

(5.4)

where ω B =|q|B/m and ℓ is a positive (ℓ≥0) integer, and provide the new dispersion relation:

(5.5)

One can proceed in an analogous way for fermions with charge q. From the free Dirac equation (iγ μ ∂ μ −m)ψ=0, and the shift in ∂ μ , one arrives at the following Schrödinger equation

(5.6)

which yields the new dispersion relation for quarks:

(5.7)

where s=±1 is the spin projection in the \(\hat{\textbf{z}}\) direction.

It is also straightforward to show that integrals over four momenta and thermal sum-integrals acquire the following forms, respectively [44, 45, 86]:

(5.8)
(5.9)

where ℓ represents the different Landau levels and n stands for the Matsubara frequency indices [87].

5.3 PLSM q Effective Model and the Splitting of the Chiral and Deconfining Transition Lines

Let us consider the two-flavor linear sigma model coupled to quarks and to the Polyakov loop, the PLSM q effective model, in the presence of an external magnetic field [48].

The confining properties of QCD are encoded in the complex-valued Polyakov loop variable L. As a matter of fact, the Polyakov loop sector only provides a description of the behavior of the approximate order parameter for the Z(3) symmetry, which is explicitly broken by the presence of quarks. It is convenient for modeling the deconfining transition and has a good agreement with lattice results for most thermodynamic quantities such as the pressure and energy density, especially for the pure glue theory, but it does not provide a dynamical description of confinement.Footnote 3

The expectation value of the Polyakov loop L is an exact order parameter for color confinement in the limit of infinitely massive quarks:

(5.10)

where A 4=iA 0 is the matrix-valued temporal component of the Euclidean gauge field A μ and the symbol denotes path ordering. The integration takes place over compactified imaginary time τ, with periodic boundary conditions.

The chiral features of the model are encoded in the dynamics of the O(4) chiral field, which is an exact order parameter in the chiral limit, in which quarks and pions are massless degrees of freedom:

(5.11)

Here π is the isotriplet of the pseudoscalar pion fields and σ is the chiral scalar field which plays the role of an approximate order parameter of the chiral transition in QCD, since chiral symmetry is explicitly broken by the nonzero quark masses.

Within this effective model, the quark field ψ connects the Polyakov loop L and the chiral field ϕ, making a bridge between confining and chiral properties. Quarks are also coupled to the external magnetic field since the u and d quarks are electrically charged. Thus, it is clear that the external magnetic field will affect the chiral dynamics as well as the confining properties of the model, as much as the latter can be captured by the Polyakov loop sector.

This represents a natural generalization of the linear sigma model coupled to quarks [88], an effective theory that has been widely used to describe different aspects of the chiral transition, such as thermodynamic properties [89–102] and the nonequilibrium phase conversion process [103]. This generalization differs from previous ones [104–107] by the inclusion of a bridge via the covariant derivative and, of course, because of the modifications brought about by the magnetic field.

The Lagrangian of PLSM q describes the constituent quarks ψ, which interact with the meson fields σ, \(\pi^{\pm}= (\pi^{1} \pm i \pi^{2})/\sqrt{2}\) and π 0=π 3, the Abelian gauge field a μ =(a 0,a)=(0,−By,0,0), and the SU(3) gauge field A μ via the covariant derivative \(D^{(q)}_{\mu} = (\partial_{\mu} - i Q a_{\mu}- i A_{\mu})\) with the charge matrix Q=diag(+2e/3,−e/3). Its explicit form is given by

(5.12)

where \(D_{\mu}^{(\pi)} = \partial_{\mu}+ i e a_{\mu}\) is the covariant derivative acting on colorless pions.

The chiral potential has the form

(5.13)

where \(h = f_{\pi} m_{\pi}^{2}\), \(v^{2} = f^{2}_{\pi}-{m^{2}_{\pi}}/{\lambda}\), λ=20, f π ≈93 MeV and m π ≈138 MeV. The constituent quark mass is given by m q ≡m q (〈σ〉)=g〈σ〉, and, choosing g=3.3 at T=0, one obtains for the constituent quarks in the vacuum m q ≈310 MeV. At low temperatures quarks are not excited, and the model reproduces results from the usual linear σ-model without quarks.

The Polyakov potential adopted is given by [108–110]

(5.14)

where T 0≡T SU(3)=270 MeV is the critical temperature in the pure gauge case and a 0=16π 2/45≈3.51, a 1=−2.47, a 2=15.2, and b 3=−1.75. Below we follow a mean-field analysis in which the mesonic sector is treated classically whereas quarks represent fast degrees of freedom.

The one-loop corrections to the free energy Ω coming from quarks can be written as:

(5.15)

so that the expectation values of the condensates can be obtained by minimizing the free energy

(5.16)

at fixed values of temperature and magnetic field. The interaction piece Ω q (σ,L,T) can be split into a vacuum (temperature-independent but still magnetic-field dependent) contribution and a thermal correction. The vacuum term has the form

minus the standard vacuum correction in the absence of the magnetic field,

(5.17)

where we have defined the integral

(5.18)

and \(M^{2}_{\ell f} = m^{2}_{f} + 2 \ell|q_{f}| B\). The thermal (paramagnetic) contribution is given by [48]

(5.19)

where μ sℓ is the energy of the ℓth Landau level at zero longitudinal momentum, μ sℓ (σ)=[g 2 σ 2+(2ℓ+1−2s)|q|B]1/2, and the untraced Polyakov loop is such that \(\operatorname{Re} [\operatorname{Tr} \varPhi^{k} ] = \sum_{i=1}^{3} \cos(k \varphi_{i})\), the integer k corresponding to the winding number of the Polyakov loops [48].

For finite temperature and B=0 this model produces a crossover for both transitions. Figure 5.3 displays the condensates as functions of the temperature, and the critical temperature is defined by the change curvature in the curves. This occurs simultaneously for the chiral and deconfinement transitions within this model.

At zero temperature, the Polyakov loop variable does not play a role. The presence of a magnetic field enhances the chiral symmetry breaking, increasing the value of the chiral condensate, in line with the phenomenon of magnetic catalysis [14, 15, 17, 18, 33, 111]. This is shown in Fig. 5.4. It also deepens the minimum of the potential as B is increased, as illustrated in the same figure for several values of the magnetic field

The dependence of the chiral condensate on the magnetic field is approximately linear, as shown in Fig. 5.4. This is in line with results from chiral perturbation theory [29–31]. Recent lattice results [81] seem to deviate from a linear behavior for large B, growing faster, in better qualitative agreement with results from PNJL [52–55]. However, for larger values of B, all model calculations seem to deviate from the lattice data, whereas for very small B they all quantitatively agree [81].

Turning on the temperature, one can investigate the effects of the magnetic field on the thermodynamics and phase structure of strong interactions as captured by this model description. In the confining sector, the strong magnetic field affects the potential for the expectation value of the Polyakov loop via the intermediation of the quarks in three ways [48]: (i) the presence of the magnetic field intensifies the breaking of the global \({\mathbb {Z}}_{3}\) symmetry and makes the Polyakov loop real-valued, as shown in Fig. 5.2; (ii) the thermal contribution from quarks tends to destroy the confinement phase by increasing the expectation value of the Polyakov loop; (iii) on the contrary, the vacuum quark contribution tends to restore the confining phase by lowering the expectation value of the Polyakov loop.

Fig. 5.2
figure 2

Effects of temperature and magnetic field on quark confinement: The Polyakov loop potential at T=0.8T 0 (top) and T=1.2T 0 (bottom) and at zero magnetic field (left) and at eB=9T 2 (right). Extracted from Ref. [48]

Full size image
Fig. 5.3
figure 3

Expectation values of the order parameters for the chiral and deconfinement transitions as functions of the temperature. The filled circles represent the σ-condensate, and the empty circles stand for the expectation value of the Polyakov loop. In this plot the condensates are dimensionless. Extracted from Ref. [48]

Full size image
Fig. 5.4
figure 4

Upper: the expectation value of the (dimensionless, σ=ξv) condensate as a function of the magnetic field. Black dots are obtained from the PLSMq and the orange line is the linear fit. Lower: effective potential for the condensate at zero temperature for several values of the magnetic field B. Extracted from Ref. [48] (Color figure online)

Full size image

In fact, the vacuum correction from quarks has a crucial impact on the phase structure. If one disregards the vacuum contribution from the quarks, as was done in Refs. [44, 45], one finds that the confinement and chiral phase transition lines coincide. Moreover, in this case an increasing magnetic field lowers the equivalent chiral-confinement transition temperature. On the other hand, the inclusion of the vacuum contribution from quark loops in a magnetic field modifies completely the picture: confinement and chiral transition lines split, and both chiral and deconfining critical temperatures become increasing functions of the magnetic field. Both scenarios are shown in Fig. 5.5, which exhibit the full calculation of the phase diagram from the effective potential within the PLSM q effective model. The vacuum contribution from the quarks affects drastically the chiral sector as well. Our calculations also show that the vacuum contribution seems to soften the order of the phase transition: the first-order phase transition—which would be realized in the absence of the vacuum contribution—becomes a smooth crossover in the system with vacuum quark loops included.

Fig. 5.5
figure 5

Phase diagram in the B-T plane. Upper: without vacuum corrections: the critical temperatures of the deconfinement (the dash-dotted line) and chiral (the dashed line) transition coincide all the way, and decrease with B. Lower: with vacuum corrections: the critical temperatures of the deconfinement (the dash-dotted line) and chiral (the dashed line) transition coincide at B=0 and split at higher values of the magnetic field. A deconfined phase with broken chiral symmetry appears. The vertical line is the magnitude of the magnetic field that expected to be realized at LHC heavy-ion collisions [8, 9]. Extracted from Ref. [48]

Full size image

The modifications produced by strong magnetic fields over strong interactions seem very exciting, bringing new possibilities for the phase diagram: affecting the nature of the transitions, splitting different coexistence lines, possibly exhibiting new phases, increasing the breaking of \({\mathbb {Z}}_{3}\), and so on. As discussed in the Introduction, the second scenario has been also found in other effective models containing a chiral and a Polyakov loop sector [52–55, 67], as well as in preliminary lattice simulations [77, 78]. However, lattice simulations of magnetic QCD with physical masses and fine grids have shown that both critical temperatures actually go down for increasing B, saturating for very large fields [80], an unexpected behavior that is very different from the scenario depicted above.

This leads us to consider of a much simpler model that, yet, seems to contain the essential ingredients to describe the behavior of the deconfining line, and produces results that are in qualitative agreement with the lattice: the magnetic MIT bag model [68]. As will be clear in the discussion, the subtraction procedure in renormalization is subtle (which can be seen as the choice of the renormalization scale) but can be guided by known physical phenomena and lattice results.

5.4 Magbag—The Thermal MIT Bag Model in the Presence of a Magnetic Background

In the MIT bag model framework for the pressure of strong interactions, one needs the free quark pressure. As seen previously, the presence of a magnetic field in the \(\hat{\textbf{z}}\) direction affects this computation by modifying the dispersion relation to

$$ \omega_{\ell sf}(k_{z})=k_{z}^{2}+m_{f}^{2}+q_{f}B(2 \ell+s+1)\equiv k_{z}^{2}+M_{\ell sf}^{2} , $$
(5.20)

ℓ=0,1,2,… being the Landau level index, s=±1 the spin projection, f the flavor index, and q f the absolute value of the electric charge. Loop integrals are also affected as presented previously [44, 45, 86].

Since it has been shown that only very large magnetic fields do affect significantly the structure of the phase diagram for strong interactions [43–45, 51–55, 77, 78, 80], we can restrict the free quark pressure to the limit of very high magnetic fields, where it is possible to simplify some analytic expressions.

It is crucial to realize, however, that the lowest Landau level (LLL) approximation for the free gas pressure is not equivalent to the leading order of a large magnetic field expansion. For the zero-temperature, finite-B contribution to the pressure, the LLL is the energy level which less contributes in the limit of large B; the result being dominated by high values of ℓ. Nevertheless, the equivalence between the LLL approximation and the large B limit remains valid for the temperature-dependent part of the free pressure (as well as for the propagator), simplifying the numerical evaluation of thermal integrals [84].

The free magnetic contribution to the quark pressure has been considered in different contexts (usually, in effective field theories [44, 45, 49–51, 63, 64, 112]) and computed from the direct knowledge of the energy levels of the system, (5.20). The exact result, including all Landau levels, has to be computed from

$$ P_{q}= 2 N_c \sum_{\ell,s,f} \frac{q_f B}{2\pi} \int\frac{dk_z}{2\pi} \biggl\{ \frac{\omega_{\ell sf}(k_z)}{2} +T \ln \bigl[ 1+e^{-\omega_{\ell sf}(k_z)/T} \bigr] \biggr\} , $$
(5.21)

where the first term is a clearly divergent zero-point energy and the other one is the finite-temperature contribution for vanishing chemical potential. Since ω ℓsf grows with B, the largest the ℓ labeling the Landau level considered the larger the zero-point energy term becomes, being minimal for the LLL, corroborating the previous discussion. Thus, in the limit of large B, the LLL approximation is inadequate here. The decaying exponential dependence of the finite-temperature term on ω ℓsf , on the other hand, guarantees that the LLL dominates indeed this result for intense magnetic fields.

To obtain a good approximation for the large B limit of the free pressure, we choose to treat the full exact result and take the leading order of a \(x_{f}\equiv m_{f}^{2}/2q_{f}B\) expansion in the final renormalized expression. Let us then discuss the treatment of the divergent zero-point term. Despite being a zero-temperature contribution, the first term in (5.21) cannot be fully subtracted because it carries the modification to the pressure brought about by the magnetic dressing of the quarks. Using dimensional regularization and the zeta-function representation, which is also a type of regularization, for the sums over Landau levels and subtracting the pure vacuum term in (3+1) dimensions, one arrives at:

(5.22)

where a pole ∼(q f B)2[2/ε] still remains. This infinite contribution that survives the vacuum subtraction can be interpreted as a pure magnetic pressure coming from the artificial scenario adopted, with a constant and uniform B field covering the whole universe (analogous to the case of a cosmological constant). In this vein, one may neglect all terms ∼(q f B)2 and independent of masses and other couplings (as done, e.g. in Refs. [44, 45, 49, 50, 63, 64]), concentrating on the modification of the pressure of the quark matter under investigation. This can be seen as a choice for the renormalization scale after the renormalization of a ∼F μν F μν term representing the magnetic field, as discussed, e.g. in Refs. [63, 64]. We will come back to this point in the sequel.

The final exact result for the free pressure of magnetically dressed quarks is therefore

(5.23)

In Refs. [44, 45, 49, 50, 63, 64], the constant ζ′(−1,0)=−0.165421… was not subtracted. In the case of pions, however, the full subtraction ensures that magnetic catalysis, i.e. an enhancement of chiral symmetry breaking, at zero temperature [14, 15, 17, 18, 33, 111], is realized. On the other hand, if this term is left, the pion contribution to the effective potential for the chiral condensate at large magnetic fields will eventually raise the minimum instead of lowering it.

In the limit of large magnetic field (i.e. \(x_{f}=m_{f}^{2}/(2q_{f}B)\to0\)), we obtain

$$ \frac{P_{q}}{N_c}\stackrel{{\rm large}~ B}{=} \sum _f \frac{(q_fB)^2}{2\pi^2} [ x_f\ln \sqrt{x_f}\, ] +T \sum_{f} \frac{q_fB}{2\pi^{2}} \int dk_{z} \ln \bigl[ 1+e^{-\sqrt {k_{z}^{2}+m_{f}^{2}}/T} \bigr] . $$
(5.24)

Adding the free piece of the gluonic contribution and the bag constant , the pressure of the QGP sector in the presence of an intense magnetic field reads:

(5.25)

It is clear that, for \(\sqrt{eB}\) much larger than all other energy scales, the pressure in the QGP phase increases with the magnetic field, which seems to favor a steady drop in the critical temperature with increasing B that would lead to a crossing of the critical line with the T=0 axis at some critical value for the magnetic field. However, the behavior of T c (B) also depends on how the pions react to B, so that the outcome is not obvious.

In the confined sector, which we describe by a free pion gas, one may follow analogous steps in order to compute the contribution from the charged pions, which couple to the magnetic field, arriving at

(5.26)

where \(M^{2}_{\pi\ell}\equiv m_{\pi}^{2}+(2\ell+1)eB\) and \(x_{\pi }\equiv m_{\pi}^{2}/(2eB)\). In this final expression all terms ∼(q f B)2 and independent of masses and other couplings were subtracted, as discussed before. Notice that the spin-zero nature of the pions guarantees that all charged pion modes in a magnetic field, differently from what happens with the quark modes, are B-dependent. So, in the large magnetic field limit the thermal integral associated with π + and π − is exponentially suppressed by an effective mass \({\gtrsim}(m_{\pi}^{2}+eB)\), as was also noticed in Refs. [44, 45], and can be dropped. In this limit, we have

$$ P_{\pi^{+}}+P_{\pi^{-}}\stackrel{{\rm large}~ B}{=} - \frac{(e B)^2}{4\pi^2} \zeta^{(1,1)}(-1,1/2) ~x_{\pi} , $$
(5.27)

where ζ (1,1)(−1,1/2)=−ln(2)/2=−0.346574… . Neutral pions do not couple to the magnetic field and contribute only with the usual thermal integral [87].

As before, for \(\sqrt{eB}\) much larger than all other scales, the pion pressure rises with the magnetic field, as a consequence of the subtraction of all terms that are independent of temperature, masses and other couplings in the renormalization process, which renders the pressure positive. Differently from the quark pressure, however, the B=0 pion pressure takes over for temperatures of the order of the pion mass, which is not small and always enlarged by the presence of a magnetic field (given its scalar nature). Moreover, for large T, the magnetic pion pressures converge to (1/3) of the B=0 pressure, since π 0 is the only degree of freedom that contributes thermally for large B.

Each equilibrium phase should maximize the pressure, so that the critical line in the phase diagram can be constructed by directly extracting T c (B) from the equality of pressures. It is instructive, nevertheless, to consider a plot of the crossing pressures, as shown in Fig. 5.6. The figure shows, as expected, a decrease in the critical temperature (crossing points) as B is increased due to the corresponding positive shift of the QGP pressure. However, T c seems to be saturating at a constant value. One can see that the critical pressure (crossing point) goes down, but then it bends up again due to the increase in the pion pressure with B. This combination avoids a steady and rapid decrease of the critical temperature, as becomes clear in the phase diagram shown in Fig. 5.7. In fact, inspection of the zero-temperature limit of (5.24) and (5.27) shows that there is no value of magnetic field that allows for a vanishing critical temperature.

Fig. 5.6
figure 6

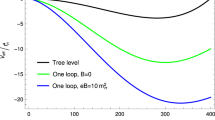
Crossing pion gas and QGP pressures as functions of the temperature for different values of the magnetic field: eB=0 (black, solid, right-most), \(20m_{\pi}^{2}\), \(40m_{\pi}^{2}\), \(60m_{\pi}^{2}\) (magenta, dash-dotted) and \(eB=100m_{\pi }^{2}\) (gray, solid, left-most), where m π =138 MeV is the vacuum pion mass. Extracted from Ref. [68] (Color figure online)

Full size image
Fig. 5.7
figure 7

Phase diagram in the presence of a strong magnetic field. We also keep the T c (B=0) point. The blue square represents a very conservative estimate for the maximum value of eB expected to be achieved in non-central collisions at the LHC with the formation of deconfined matter. The arrow marks the critical temperature for \(eB\approx210 m_{\pi}^{2}\) [113], expected to be found at the early universe. Extracted from Ref. [68] (Color figure online)

Full size image

The phase diagram in the plane T–eB shows that the critical temperature for deconfinement falls as we increase the magnetic field. However, instead of falling with a rate that will bring it to zero at a given critical value of eB, it falls less and less rapidly, tending to saturate at large values of B. Remarkably, this qualitative behavior agrees quite well with the most recent lattice results with physical masses [80].Footnote 4 As discussed in the Introduction, previous models [44, 45, 48, 52–57, 67], have predicted either an increase or an essentially flat behavior for the deconfinement critical line as B is increased to very large values. The same was true for previous lattice simulations [77, 78], which could be reproduced by the authors of Ref. [80] by increasing the quark masses to unphysical values.

The renormalization procedure in the presence of a constant and uniform magnetic field seems to be very subtle and crucial for the phenomenological outcome for the phase structure. B-dependent, mass-independent terms survive pure vacuum (B=0) subtraction and have to be subtracted either in an ad hoc fashion [68] or by including a background field counterterm associated with a term ∼F μν F μν representing the magnetic field [63, 64]. The latter brings a renormalization scale and, upon an appropriate choice, reproduces the former. Subtracting all purely magnetic terms in the pressures seems to be the appropriate choice since: (i) one guarantees that the pion pressure grows with increasing magnetic field at zero temperature, which is consistent with the well-known phenomenon of magnetic catalysis; (ii) lattice simulations usually measure derivatives of the pressure with respect to temperature and quark mass, and do not access derivatives with respect to B, so that purely B-dependent terms are not included in their results; and (iii) the effect of a purely magnetic contribution to the pressure would only shift the effective potential as a whole. In particular, there would be no modification on relative positions and heights of different minima that represent different phases of matter.

The qualitative success of the description of the deconfinement transition in the presence of an external magnetic field in terms of the MIT bag model suggests that confinement dynamics plays a central role in guiding the functional behavior of T c . In this case, a large N c investigation of the associated magnetic thermodynamics seems appropriate.

5.5 Large N c

Lattice QCD calculations [114] show that the deconfinement phase transition of pure glue SU(N c ) gauge theory becomes first order when N c ≥3 [115–122] with a critical temperature given by [123]

$$ \lim_{N_c\to\infty}\frac{T_c}{\sqrt{\sigma}}=0.5949(17) + \frac {0.458(18)}{N_c^2} , $$
(5.28)

where \(\sigma\sim(440~{\rm MeV})^{2}\) is the string tension. The thermodynamic properties of pure glue do not seem to change appreciably when N c ≥3 [124–126], which suggests that large N c arguments may indeed capture the main physical mechanism behind the deconfinement phase transition of QCD.

It has been shown in Ref. [85] that the deconfinement critical temperature must decrease in the presence of an external magnetic field in the large N c limit of QCD, provided that quarks exhibit a paramagnetic behavior. Assuming that N f /N c ≪1 and m q =0, the only contribution to the pressure of the confined phase that enters at is given by the vacuum (B=0) gluon condensate \(c_{0}^{4} N_{c}^{2} \sigma^{2}\). The gluon and quark condensates change in the presence of a magnetic field [30, 31, 127] but these modifications are negligible in the large N c limit. Besides, the gluon contribution to the deconfined pressure is blind to the magnetic field.

On the other hand, the quark contribution is affected by the magnetic field and has the form

$$ P_{\mathit{quark}}(T,eB)\sim N_c N_{\mathit{pairs}}(N_f) T^4 \tilde{f}_{\mathit{quark}} \bigl(T/\sqrt{\sigma},eB/T^2 \bigr) , $$
(5.29)

with N pairs (N f )/N c ≪1 being the number of pairs of quark flavors with electric charges {(N c −1)/N c ,−1/N c } in units of the fundamental charge. Only the largest (\({\sim} N_{c}^{0}\)) charge in each pair contributes to leading order in N f /N c . Notice that the function \(\tilde{f}_{\mathit{quark}}\) is positive definite and must increase monotonically with T for a fixed value of eB until it goes to 1 in the high temperature limit \(T \gg\sqrt{\sigma}\), eB. Thus, one should expect that the critical temperature as a function of the magnetic field, T c (eB), must decrease with respect to the pure glue critical temperature, \(T_{c}^{(0)}\), by an amount of . This can be seen directly by equating the pressures at T c , which yields [85]

$$ \frac{T_c(eB)}{\sqrt{\sigma}} f_\mathit{glue}^{1/4} \biggl(\frac{T_c(eB)}{\sqrt {\sigma}} \biggr)=\frac{c_2(N_\mathit{pairs},eB)}{c_{SB}} , $$
(5.30)

where we defined

(5.31)

Since c 2(N pairs ,eB)<c 0, one finds that \(T_{c}(eB)/T_{c}^{(0)}< 1\) by an amount ∼N f /N c [85]. Assuming that quarks behave paramagnetically for all values of B, then c 2(N pairs ,eB)<c 1(N f ), its equivalent in the case with B=0 and N f >0, and T c (eB) is also lower than the critical temperature in the presence of N f /N c flavors of massless quarks at B=0 [85].

In a free gas implementation of the deconfined phase f glue =1 and, for very strong magnetic fields, \(\tilde{f}_{\mathit{quark}}\sim eB/T_{c}^{2}\) [68], so that the magnetic suppression of the deconfinement critical temperature goes like eBN pairs /(N c σ). This simple implementation in the limits of low and high magnetic fields provides a scenario in which the slope in T c (eB) decreases for large fields, as illustrated in Fig. 5.8, which hints for a saturation of T c as a function of eB, as observed on the lattice [80] and in the magnetic MIT bag model [68], but cannot be obtained in a model-independent way.

Fig. 5.8
figure 8

Cartoon of the T c ×eB phase diagram in the large N c limit, using the approximation of free deconfined quarks and gluons. The numerical value 0.59 shown in the plot was extracted from Ref. [123]. Extracted from Ref. [85]

Full size image

5.6 Conclusions and Perspectives

The investigation of the effects brought about by the presence of a magnetic background on the thermal chiral and deconfining transitions is in its infancy yet. Nevertheless, the promise of the outcome of a rich phenomenology in mapping this new phase diagram of strong interactions is concrete.

First model calculations have revealed the possibility of modifications in the nature of the QCD phase transitions, and also the appearance of a new phase of strong interactions in the case of a splitting of the critical (chiral and deconfining) lines. Even if recent, more physical lattice simulations have drastically modified the initial picture, they have also shown that the magnetic background has a very non-trivial influence on strong interactions. For instance, the behavior of quark condensates at finite temperature is non-monotonic [81], rendering well-established vacuum phenomena such as magnetic catalysis more subtle at finite temperature.

The functional behavior of the critical temperatures still has to be understood more deeply. Although no model foresaw the fact that both, chiral and deconfining temperatures, decrease then saturate at a nonzero value according to the lattice [80], a posteriori the magnetic MIT bag model was successful to describe this behavior for deconfinement qualitatively [68] and seems to capture some essential ingredients. A model-independent analysis in the large-N c limit of QCD also points to this behavior [85], which is reassuring from the theoretical standpoint.

Another key ingredient in building an understanding of the physics of the quark-gluon plasma under these new conditions, which can be relevant for high-energy heavy-ion collision experiments, the primordial quark-hadron transition and magnetars is the standard perturbative investigation of magnetic QCD. The calculation of the pressure in thermal QCD to two loops in the strong sector using the full QED propagator in the lowest Landau level approximation is subtle but possible, as done originally in Ref. [84].

The computation makes use of the full magnetic propagator that was obtained by Schwinger [128], but can be cast in a more convenient form in terms of a sum over Landau levels as derived in Ref. [129] (see also Refs. [84, 130]). In particular, it has been shown in Ref. [84] that the chiral limit for the exchange diagram seems to be trivial for very large magnetic fields. Concretely, it can be written diagrammatically in the following compact form [84]:

(5.32)

which realizes the intuitive expectation that the nontrivial dynamics in an extremely intense magnetic field should be one-dimensional. Since gluons do not couple directly to the magnetic field, their dispersion relation maintains its three-dimensional character, which effectively results in a “massive” gluon in the dimensionally-reduced diagram. In the end the exchange contribution to the pressure is essentially an average over the effective gluon transverse mass \(m_{k}^{2}=k_{1}^{2}+k_{2}^{2}\) of the exchange diagram in (1+1)-dimensions with the Gaussian weight \((q_{f}B/2\pi) \exp[-m_{k}^{2}/2q_{f}B]\). Since the trace in the reduced diagram is proportional to \(m_{f}^{2}\), the chiral limit seems trivial [84]. A detailed analysis of the dependence of the pressure on the mass and temperature and a semiclassical interpretation of this result will be reported soon [131].

The nature of the phase diagram of strong interactions in the presence of a magnetic background is still open. Recent lattice data, especially when compared to effective model predictions, seem to indicate that confinement dynamics plays an important role in the phase structure that emerges and should be incorporated in any effective description. Comparison between lattice data with very different quark masses [77, 78, 80, 81] also show that the dependence of the critical temperatures on this parameter is non-trivial: T c increases at the percent level for large masses [77, 78] whereas it decreases appreciably for physical masses [80]. This competition between the effects from the magnetic field and quark masses on T c was also found in the large-N c QCD analysis of Ref. [85]. A more systematic analysis of this phenomenon on the lattice would be very helpful for the building of effective models.