Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Although social relationships and behaviors are inherently dynamically evolving, social interactions, represented by the paradigm of social networks [1] have long been studied as static entities, mostly because empirical longitudinal data have been scarce [2, 3], and often limited to relatively small groups of individuals. As new technologies pervade our daily life, digital traces of human activities are gathered at many different temporal and spatial scales and for large populations, and they promise to transform the way we measure, model and reason on social aggregates [4, 5] and socio-technical systems [6] that combine social dynamics and computer-supported interaction mechanisms (e.g., large scale on-line social networks like Twitter and Facebook). It is important to remark that, from a methodological point of view, data from technological and infrastructural proxies give access to behavioral networks defined in terms of the specific proxy at hand, and not to bona fide social networks. Digital traces have been already used as proxies to study many specific aspects of human behavior, such as geographic mobility [7–13], phone communications [14], email exchange or instant messaging [15–20], and even human mobility and proximity in indoor environments (http://www.sociopatterns.org) [21–24].

Due to the often high temporal resolution of emerging data sets on human interactions, the now customary representation of interactions in terms of static complex networks, which has led to countless interesting analyses and insights [1, 25–31], needs to be extended to take into account the dynamical properties of the interaction patterns, bringing forth the field of “temporal networks” [32]. This prompts fundamental and applied research on adapting and extending well-known networks observables, metrics and characterization techniques to the more complex case of a time-varying graph representations.

At the same time, the availability of high-resolution time-resolved data on human interactions does not mean that any research question should be addressed by using the full-scale and finest-resolution datasets, as they usually entail computational challenges due to the sheer size of their digital representations. Given a specific problem or research questions, understanding what is the most appropriate scale for coarse-graining the raw behavioral data, and what are the mathematical techniques and data representation that are best suited to create such synopses is a key problem in its own merit [33–35], and has been already identified as such in the specific case of epidemic simulation based on temporal social network data [36, 37].

In the context outline above, we review here recent research efforts, developed within the SocioPatterns collaboration (http://www.sociopatterns.org), based on large-scale datasets that describe human face-to-face interactions in various contexts, covering scientific conferences [21–23, 36, 38], hospital wards [39], schools [40], and museums [38].

2 Phenomenology

2.1 From Raw Proximity Data to Dynamical Networks

The data we describe here have been collected in deployments of the SocioPatterns (http://www.sociopatterns.org) social sensing infrastructure, described in [21]. This measurement infrastructure is based on wearable wireless devices that exchange low-power radio signals in a distributed fashion and use radio packet exchange rates to monitor for location and proximity of individuals. The proximity information is sent to radio receivers installed in the environment, which timestamp and log contact data. Participants are asked to wear such devices, embedded in unobtrusive wearable badges, on their chests, so that badges can exchange radio packets only when the individuals wearing them face each other at close range (about 1–1. 5 m). The onboard software of the devices is tuned so that the face-to-face proximity of two individuals wearing the badges can be assessed with a probability in excess of 99 % over an interval of 20 s. A “contact” between two individuals is then considered as established during a time period of 20 s if the devices worn by these individuals exchanged at least one radio packet during that interval. The contact is then considered as ongoing until a 20 s interval occurs such that no packet exchange between the devices is recorded: at that point the contact event is recorded together with its starting time and duration. Notice that in contrast to other temporal network datasets in which interactions are instantaneous events, here close-proximity and face-to-face contacts do have a finite duration.

The data gathered by the social sensing infrastructure thus give access, for each pair of participants, to the detailed list of their contacts, with starting and ending times: these data can be represented as a time-varying social network of contact within the monitored community. The temporal resolution of 20 s in assessing proximity sets the finest resolution for the temporal network representation we use, which, in the following, will be assumed to be an ordered sequence of graphs, each corresponding to a 20-s interval. Table 1 provides information and literature references on the temporal networks that will be discussed in the following.

Table 1 Partial list of the datasets on face-to-face proximity collected by the SocioPatterns collaboration during 2009 and 2010 and discussed in the present paper
Full size table

2.2 Microscopic View

For each pair of individuals i and j, the datasets contain a list of ℓ successive time intervals \(((t_{\mathit{ij}}^{(s,1)},t_{\mathit{ij}}^{(e,1)}),(t_{\mathit{ij}}^{(s,2)},t_{\mathit{ij}}^{(e,2)}),\cdots \,,(t_{\mathit{ij}}^{(s,\ell)},t_{\mathit{ij}}^{(e,\ell)}))\) during which i and j were detected to be in close-range face-to-face proximity, where t ij (s, a) refers to the starting time (hence the superscript s) and t ij (e, a) to the ending time of the time interval number a.

Several quantities of interest can be defined to summarize the contact patterns of each individual or pair of individuals, and to provide a statistical characterization of contact patterns. In particular, for each pair of individuals i and j (edge i-j), their list of contact time intervals yields a list of contact durations \((\Delta t_{\mathit{ij}}^{(1)},\cdots \,,\Delta t_{\mathit{ij}}^{(\ell)})\), with \(\Delta t_{\mathit{ij}}^{(a)} = t_{\mathit{ij}}^{(e,a)} - t_{\mathit{ij}}^{(s,a)}\) for a = 1, ⋯ , ℓ. Several notions of weight w ij for the edge i-j can be defined on the basis of this list of contact durations, yielding weighted contact networks that describe different aspects of the empirical sequence of contacts:

  • Edge presence:w ij p measures the contact occurrence (the superscript p stands for “presence”), with w ij p = 1 if at least one contact between i and j has been established, and 0 otherwise.

  • Frequency of occurrence: The frequency w ij n = l indicates how many distinct contact events have been registered between i and j, disregarding the length of each contact (the superscript n is for “number”).

  • Cumulative time in contact: The cumulative duration of the contact \(w_{\mathit{ij}}^{t} =\sum _{a}\Delta t_{\mathit{ij}}^{(a)}\) gives the sum of the durations of all contacts established between i and j (hence the superscript t).

At the level of each individual i, the above weights w can be aggregated over all individuals j who had a contact with i, i.e., \(s_{i} =\sum _{j}w_{\mathit{ij}}\), yielding the following notions of node strength:

  • \(s_{i}^{p} =\sum _{j}w_{\mathit{ij}}^{p}\) gives the number of distinct individuals with whom i has established at least one contact; i.e., the degree k i of i in the behavioral contact network.

  • \(s_{i}^{n} =\sum _{j}w_{\mathit{ij}}^{n}\) indicates the overall number of contacts in which i has been involved.

  • The cumulative contact time \(s_{i}^{t} =\sum _{j}w_{\mathit{ij}}^{t}\) corresponds to the total sum of the duration of all contacts involving individual i.Footnote 1

Of course all the quantities described above can be measured over the whole duration of the deployment, or for a restricted duration (for instance, 1 day, as is natural for conferences or the museum deployment we describe below). The choice of the aggregation time allows, for instance, to investigate the inter and intra-day variability of interaction patterns among different individuals.

A first way to uncover the complexity of the data is through a study of the statistical distributions of the duration of the contact events, and of the time intervals between contact events. As shown in Figs. 1 and 2 and discussed in [21], broad distributions spanning several orders of magnitude are observed in both cases: most contact durations and intervals between successive contacts are very short, but very long durations are also observed, and no characteristic timescale emerges. This bursty behavior is a well known feature of human dynamics and has been observed in a variety of systems driven by human actions [14, 48–50]. In the present case of close-range contacts, no simple functional form such as a power-law distribution or a log-normal distribution seems to fit the observed data over the full range of time intervals. However, it is important to highlight a few important aspects of the contact duration distributions of Fig. 1.

Fig. 1
figure 1

Distributions of the face-to-face contact durations measured in different environments

Full size image
Fig. 2
figure 2

Distributions of the time intervals between two successive contact events of a given individual, aggregated over the entire population

Full size image

The first observation is that the distributions approximately collapse on one another regardless of the specific context they refer to. This is remarkable as the datasets refer to very different social environments: exhibitions (SG), where visitors stream along a pre-defined path of a museum; Academic conferences (HT09, ESWC09, ESWC10), where the same tightly knit community shares a small number of social spaces for several days and meets according to a predefined schedule, large-scale conferences (SFHH) where many people do not know each other and very different social spaces coexist, such as plenary rooms and exhibition spaces. In the case of the primary school (PS), the distribution is slightly narrower, possibly due to strong schedule constraints such as the duration of breaks between lectures, or to the fact that young children tend to have less long face-to-face interactions than adults. Regardless of all these social, spatial and demographic differences, face-to-face contact behavior appears to obey the same bursty behavior across all contexts. This is an important fact for modelers, as it implies that processes relying on contact durations can be modeled by plugging into the model the empirically observed distribution, assumed to depend negligibly on the specifics of the contact situation being modeled.

A second observation deals with the origin of the contact duration heterogeneity of Fig. 1. It may be argued that the simultaneous presence of multiple timescales of human contact is responsible for the broad distribution we observe. However, as shown in [21] and related Supplementary Information, the contact durations restricted to single individuals do exhibit the same broad distribution observed for the entire social aggregate. This points to an intrinsic origin for the observed temporal heterogeneity, rooted in the way single persons arbitrate their social contacts and the use of their time. The temporal heterogeneity of contact durations, at the individual and collective level, undermines a number of simple representations for the contact network that implicitly assume some degree of statistical homogeneity. For example, when dealing with contact networks for epidemiological purpose, it is customary to summarize the contact networks between classes of individuals by using contact matrices [51] computed from averages of contact durations. Given the highly skewed character of the actual distributions measured by using state-of-the-art techniques, these representations need to be generalized in order to suitably capture temporal and structural heterogeneities that may play a crucial role in determining the evolution of dynamical processes over contact networks.

Perhaps the most striking feature of the observed distributions are their robustness: the distributions of contact durations are extremely similar for very different contexts, populations, activity timelines, and deployment conditions. In particular, we observe the same distribution in deployments corresponding to very different sampling of the population under study (from 30 % for SFHH to almost 100 % for PS, HT09). This confirms the results of [21] that showed the robustness of the contact duration distribution under further resampling of the data, aimed at simulating data loss or limited population sampling. Moreover, although human activity and contact patterns are highly non-stationary, as shown by an example in Fig. 3, the contact duration distributions measured over different time windows coincide [21], unveiling a statistical stationarity in an otherwise non-stationary signal. This is consistent with similar analyses on other temporal networks, such as proximity networks [52] and networks of cattle transfers between farms [53].

Fig. 3
figure 3

Timelines of the number of: nodes and links in 20-s instantaneous networks (top left), isolated nodes (top right), groups of 2 nodes (bottom left), groups of 3 nodes (bottom right) in the ESWC09 data set

Full size image

On the other hand, as displayed in Fig. 2, the distribution of time intervals between successive contacts involving the same individual typically do depend on the specific context at hand. The distributons are very similar for different conferences (HT09, ESWC09, ESWC10, SFHH), but narrower for the museum and the primary school cases. Moreover, in the school case (inset in Fig. 2), spatial and behavioral sampling due to selecting only those contacts that occur in the school playground significantly affects the distributions, even though their qualitative features stay unchanged. In general, this dependence on the context of the distribution of interval durations between successive contacts means that, contrary to pair-wise interactions, more complex temporal motifs that bear relevance to the causal structure of the temporal network may depend on the specific environment.

Similar to the case of contact durations, broad distributions are also observed for the lifetimes of simple structures in the contact network, such as groups of individuals of size n + 1 (n = 0 corresponds to an isolated person, n = 1 to a pair of individuals, and so on), as shown in Fig. 4. These broad distributions of group lifetimes become narrower for increasing n, i.e., larger groups are less stable than smaller ones.

Fig. 4
figure 4

Distributions of the lifetime (in seconds) of groups of size n + 1 (ESWC09)

Full size image

2.3 Aggregated Network View

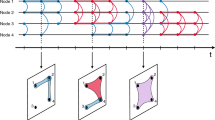
The sequence of contact events between individuals during a given time window defines an aggregated contact network at the population level, which is a static summary of the temporal network. In this network, each node is an individual, and a link between two nodes i and j denotes the fact that the corresponding individuals have been in contact at least once during the time window under consideration. Whereas the overall topological structure of the temporal network can be encoded in a static graph, the temporal activity of individual edges i − j can be summarized by suitably defined weights for the edges, such as the number of times w ij n the link was established or the cumulative duration w ij t of the contact events between i and j.

The time window considered for aggregation can range from the finest time resolution of 20 s up to the entire duration of the data set. In many contexts, it is natural to consider a specific temporal aggregation scale (i.e., daily), but different aggregation levels typically provide complementary views of the network dynamics at different scales.

Interestingly, and despite their static character, the structures of the aggregated contact networks unveil important information about the contact patterns of the population. Let us first consider the statistical distributions that are typically used to describe a network. The distributions of degree (number of distinct individuals with whom a given individual has been in contact) are typically narrow, with an exponential decay at large degrees and characteristic average values that depend on the particular context [38]. On the other hand, the distributions of the cumulative contact durations are broad: most pairs of individuals have been in face-to-face proximity for a short total amount of time, but a few cumulated contact durations are very long. No characteristic interaction timescale can be naturally defined, except for obvious temporal cutoffs due to the finite duration of the measurements. As already observed in the case of the distributions of contact durations, Fig. 5 shows the similarity of the distributions obtained in very different contexts: different populations, in which individuals behave with very different goals in different spatial and social environments, display a strikingly similar statistical behavior.

Fig. 5
figure 5

Weight distributions for the daily aggregated networks. The weight w ij t gives the cumulated amount of time spent in face-to-face interaction during 1 day by individuals i and j

Full size image

Despite their statistical similarities, the aggregated networks of face-to-face proximity might have very different structures, as revealed by a visual inspection of simple force-based network layouts. For instance, Fig. 6 shows that the aggregated network of interactions during a conference day is much more “compact” than the ones describing the interactions between museum visitors. In fact, as shown in [38], a typical daily aggregated network has a much smaller diameter in a conference context than in the museum case. This difference is due to the different patterns of presence of the attendees at the monitored venue, and also to the different social contexts: in conferences participants are present during the entire conference duration and are usually engaged in interacting with known individuals and in meeting new persons. Conversely, the distribution of visit durations in the museum case is close to a log-normal, with a geometric mean around 35 min, and the visitors’ main goal is not to meet other visitors but rather to explore the space following a partially pre-defined path. As a consequence, museum visitors are unlikely to interact directly with other visitors entering the venue more than one hour after or before them, thus preventing the aggregated network from having a short diameter: there is limited interaction among visitors entering the museum at different times, and the network diameter defines a path connecting visitors that enter the venue at successive times, mirroring the longitudinal dimension of the network. These findings show that aggregated network topology and longitudinal/temporal behavioral properties are deeply interwoven.

Fig. 6
figure 6

Daily aggregated networks in the HT09 and SG deployments. Nodes represent individuals and edges are drawn between nodes if at least one contact event was detected during the aggregation interval. Left: aggregated network for 1 day of the HT09 conference. Right: one representative day at the SG deployment. The network layouts were generated by using the force atlas graph layout implementation available in Gephi [54]

Full size image

Finally, the aggregated network of contacts among school children reported in Fig. 7 represents an intermediate case: children of each class form a cohesive structure with many links, but links between different classes, and in particular between children of different grades, are less frequent. This structure results from several combined factors that include (1) the spatial structure of the school, the grouping of students into classes, (2) the fixed association of school classes with given room for school activity, (3) the particular schedule of the school, according to which students do not go to the schoolyard or canteen at the same time and their movement as a group follows predefined spatio-temporal trajectories [40], (4) age-related homophily effects [55], which also play a role when children are free to move in the same space, such as in the playground. Overall, as shown in Fig. 7 the cumulative contact network displays a visible community structure that can be recalled using standard community-detection techniques. However, it is important to remark that the cumulated network projects out a lot of information on temporal communities, i.e., on nodes that share similar spatio-temporal trajectories and similar contact histories. For example, if a group X of nodes mixes strongly with a different group Y during a time interval [t 1, t 1 + T], and the second group of nodes Y has some connections with a third group Z during [t 2, t 2 + T], with t 2 > t 1 + T, the cumulative network representation will lose information on the group identities of X and Y and only show a single group X ∪Y with connections to Z. The problem of defining and identifying temporal communities in a time-varying networks [56, 57] is a central one when trying to mine out an activity schedule (such as the school schedule) from electronic records of human interactions, and requires to suitably define null models for temporal networks that incorporate the above described heterogeneities.

Fig. 7
figure 7

School (PS) daily aggregated social network. Only links that correspond to cumulated face-to-face proximity in excess of 5 min are shown. The color of nodes indicates the grade and class of students. Grey nodes are teachers. The network layout was generated by using the force atlas graph layout implementation available in Gephi [54]

Full size image

These few examples show how similar statistical properties in terms of heterogeneity of contact event durations and overall face-to-face presence can in fact hide very distinct structures of aggregated networks, that are shaped by the dynamical unfolding of the contacts: the study of static aggregated networks sheds in this respect some light on the system’s dynamics.

As in other cases of weighted networks [10], more insight can be gleaned by studying the correlations between the weights, which are here the trace of the contact dynamics, and the topology. Let us consider the strength s of each node, defined as the sum of the weights of all links inciding on it [10]. In our case, this corresponds, for each individual, to the cumulated time of interaction with other individuals. In social interaction contexts, it can be considered as at least as important as the number of distinct individuals contacted (the degree in the aggregated network), as it is a measure of the resources (time) an individual committed to social interactions. Correlations between the strength and the degree are of course expected: even for completely random durations of the contact events, a linear dependency of the average strength ⟨s(k)⟩ of nodes of degree k is obtained, with ⟨s(k)⟩ ∼ ⟨w⟩k, where ⟨w⟩ is the average link weight. A deviation of ⟨s(k)⟩ ∕ k from a horizontal line thus denotes the existence of non-trivial correlations: for instance, a decreasing ⟨s(k)⟩ ∕ k, as observed in large-scale phone call networks [14], indicates that individuals who call more distinct individuals spend on average less time in each call than individuals who have less links.

In the face-to-face behavioral networks we review here, two distinct behaviors have been observed, depending on the context, as shown in Fig. 8. In the museum data set (SG), ⟨s(k)⟩ ∕ (⟨w⟩k) has a clearly decreasing trend (that can be fitted by a power law with a negative exponent). On the other hand, for the aggregated networks describing the contacts in conferences (HT09 and ESWC10), ⟨s(k)⟩ ∕ (⟨w⟩k) displays consistently an increasing trend. In school settings, a rather flat ⟨s(k)⟩ ∕ (⟨w⟩k) is observed when the contacts occurring in the whole school (PS) are taken into account. This behavior has also been observed independently (Smieszek, private communication), in another dataset describing the proximity patterns of highschool students [24]. However, if only the contacts occurring in contexts where the children’s movements and contacts are not constrained (PS, playground) are considered, an increasing trend is found.

Fig. 8
figure 8

Correlation between node’s strength and degree, as measured by the average strength ⟨s(k)⟩ of nodes of degree k. The figure shows ⟨s(k)⟩ ∕ (⟨w⟩k), in several contexts. Distinct increasing and decreasing trends are observed, depending on the context

Full size image

The contrasting results obtained in different contexts show that processes such as information diffusion [58, 59], frequently occurring in social contexts, will unfold in different ways. The number of distinct persons encountered does not contain enough information to estimate the spreading potential of an individual: a super-linear dependence of ⟨s(k)⟩ with k hints at the importance of “super-spreader nodes” with large degree [58, 59] while a sub-linear behavior indicates that the decrease in the weights of individual contacts mitigates the expected super-spreading behavior of large degree nodes.

3 Modeling Face-to-Face Dynamical Contact Networks

The phenomenology outlined in the previous sections calls for the development of new modeling frameworks for dynamically evolving networks, as most modeling efforts have been until recently devoted to the case of static networks [26–30]. Among recent models of dynamical networks [52, 60–64], we review here a model of interacting agents developed in [63, 64] in order to describe how individuals interact at short times scales.

The model considers N agents who can either be isolated or form groups (cliques). Each agent i is characterized by two variables: (i) his/her coordination number n i  = 0, 1, 2. . . , N − 1 indicating the number of agents interacting with him/her, and (ii) the time t i at which n i was last changed. At each (discrete) time step, an agent i is chosen randomly. With a probability p n (t, t i ) that may depend on the agent’s state, on the present time t and on the last time t i at which i’s state evolved, i updates his/her state, under the following rules:

  1. (i)

     If i is isolated (n i  = 0), another isolated agent j is chosen with probability proportional to p 0(t, t j ), and i and j form a pair. The coordination number of both agents are then updated (n i  → 1 and n j  → 1).

  2. (ii)

     If the agent i is already in a group, (n i  = n > 0), with probability λ the agent i leaves the group; in this case, the coordination numbers are updated as n i  → 0, and n k  → n − 1 for all the other agents k of the original group. With probability (1 − λ) on the other hand i introduces an isolated agent j in the group, chosen with probability proportional to p 0(t, t j ). The coordination numbers of all the interacting agents are then changed according to the rules n j  → n + 1 and n k  → n + 1 (for all k in the group).

These rules define a dynamic network of contacts between the agents, whose properties depend on the probabilities p n , which control the tendency of the agents to change their state, and on the parameter λ, which determines the tendency either to leave groups or on the contrary to make them grow.

Constant probabilities p n correspond to Poissonian events of creation and deletion of links between individuals, and hence to narrow distributions of contact times. On the other hand, the introduction of memory effects in the definition of the p n is able to generate dynamical contact networks with properties similar to the ones of empirical data sets [63, 64]. In particular, a reinforcement principle can be implemented by considering that the probabilities p n (t, t′) that an agent with coordination number n changes his/her state decrease with the time elapsed since his/her last change of state. To this aim, we can impose p n (t, t′) = p n (t − t′), with p n decreasing functions of their arguments. This is equivalent to the assumption that the longer an agent is interacting in a group, the smaller is the probability that s/he will leave the group, and that the longer an agent is isolated, the smaller is the probability that s/he will form a new group.

The evolution equations of the number of agents in each state can be solved self-consistently at the mean-field level [63, 64] in various cases. One of the simplest is given by p n functions scaling as 1 ∕ (t − t′), \(p_{n}(t,t\prime) = \frac{b_{n}} {1+(t-t\prime)/N}\), with moreover b n  = b 1 for every n ≥ 1 in order to reduce the number of parameters (the model’s parameters are then b 0, b 1, and λ). The probability distributions of the time spent in each state can then be shown to be given by power-law distributions

$$\displaystyle\begin{array}{rcl} P_{0}(\tau )& \propto &{ \left (1+\tau \right )}^{-1-b_{0}(3\lambda -1)/(2\lambda -1)} \\ P_{n}(\tau )& \propto &{ \left (1+\tau \right )}^{-(n+1)b_{1}-1}\ \mbox{ for}\ n \geq 1.{}\end{array}$$
(1)

As shown in Fig. 9, these predictions are confirmed by numerical simulations.Footnote 2 The distributions of time intervals between successive contacts of an individual are as well power-law distributed, and the aggregated contact networks display features similar to the empirically observed ones.

Fig. 9
figure 9

Distribution P n (τ) of durations of groups of size n + 1, for N = 1, 000 agents with b 0 = b 1 = 0. 7, λ = 0. 8, and a number of time steps T max  = N ×105. The dashed lines correspond to the analytical predictions (1). From [64]

Full size image

The model can be easily extended to include an intrinsic heterogeneity between agents, possibly reflecting a difference in their “sociability”, or to model populations with a varying number of agents. For instance, it is possible to consider a museum-like situation in which agents enter the system, remain for a certain duration, and then leave without the possibility to re-enter it. Power-law distributions of contact durations are still observed, and the shape of the aggregated contact network closely resembles the ones observed in the museum setting. In addition, it would be possible to consider agents belonging to different groups with different mixing properties, in order to mimic as well for instance the contact dynamics in a school. Overall, this model’s versatility makes it an interesting tool for generating artificial dynamical contact networks.

4 Dynamical Processes on Dynamical Networks

Many networks are the support of dynamical processes of various nature, from random walks to synchronization or spreading phenomena [30]. Most related studies have however considered, as a first approach, dynamical phenomena unfolding on static networks. It has been shown how different topological characteristics impact the unfolding of phenomena such as epidemic spreading, with important consequences such as the suppression of the epidemic threshold in very heterogeneous networks [58].

To date, few research efforts have dealt with the fact that the networks supporting these phenomena might have a dynamics of their own. Through the study of toy models of co-evolution, in which the network dynamics itself is defined as a reaction to the process unfolding on top of it, it was shown that the interplay of these two dynamics can lead to interesting and sometimes counter-intuitive effects [60]. In this context, the study of dynamical processes on dynamical (temporal) networks can have a two-fold purpose. On the one hand, it can guide the design of more realistic models, applied for instance to epidemic spreading. Dynamical processes on temporal networks can be studied to understand the relative roles of the different time scales at play, and what level of information is actually needed for the description of these processes [36]. In addition to that, the use of very simple dynamical processes, such as random walks or deterministic spreading, can be considered among the techniques developed for the study and characterization of dynamical networks, such as the ones put forward in [32, 38, 53, 65, 66]. In particular, dynamical processes can serve to probe the role of causality constraints in temporal networks, comparing the outcome of a given process (i) on the dynamical network describing the real temporal sequence of events, and (ii) on aggregated networks in which the information about the precise order of events is discarded.

In this section we focus on a simple snowball SI model of epidemic spreading or information diffusion [59]. Individuals can be either in the susceptible (S) state, indicating that they have not been reached by the “infection” (or information) yet, or they can be in the infectious (I) state, meaning that they have been infected by the disease (or that they have received the information) and can further propagate it to other individuals. In the simplest, deterministic version of such a process, every contact between a susceptible individual and an infectious one results in a transmission event, which instantaneously turns the susceptible individual into an infected one according to S + I → 2I. In this simple model, infected individuals do not recover, i.e., once they transition to the infectious state they indefinitely remain in that state. The process is initiated by a single infected individual (“seed”), typically chosen at random. Despite its simplicity, such a schematic model provides interesting insight on causality constraints in dynamical networks, and on how different temporal contact patterns can lead to different outcomes. This is partially due to the fact that the SI process yields the fastest possible information propagation from the seed node to the rest of the network, thus bounding other more complex and realistic invasion processes.

4.1 SI Model as a Probe of Temporal Network Structure

Let us first consider the simplest measure of the unfolding of an SI process in a population, as given by the temporal evolution of the number of infected individuals (i.e., the incidence curve). Figure 10 shows that the incidence curves in different environments look qualitatively very different.

Fig. 10
figure 10

Incidence curves showing the number of infected individuals as a function of time for a susceptible-infectious (SI) process simulated over 1 day of HT09 (top-left panel), SG (top-right panel) and PS (bottom-left panel) temporal network data. In the HT09 and SG cases (top plots) each curve corresponds to a different seed node and is color-coded according to the starting time of the spreading process. In the PS case (bottom) school, each curve is an average over the dynamics simulated for different seed nodes belonging to a given class. The inset shows individual curves for different seeds chosen in two distinct classes

Full size image

In the case of a typical day at a conference (HT09, top-left panel) few transmission events occur until the conference participants gather for the coffee break at 11am, even if the seed was present early. A strong increase in the number of infected individuals is then observed, and a second strong increase occurs during the lunch break (12 p.m.). As a result of the concentration in time of transmission events, spreading processes initiated by different seeds all achieve very similar (and high) incidence levels after a few hours, regardless of the initial seed and of its arrival time. Even epidemics started by latecomers can reach about 80 % of the community.

A very different picture is observed in the museum case (top-right panel), where the arrival time of the seed individual has a strong impact on the epidemic size: at any point in time, the number of infected individuals is strongly correlated with the arrival time of the seed. This is due to the fact that visitors stream through the venue, and those who left before the arrival time of the seed cannot be reached by the infection. Furthermore, in many cases the daily aggregated network displays multiple disconnected components, so that the spreading process stops soon after the seed leaves and only reaches a very small portion of the total population [38]. Even on days with many visitors and a globally connected daily aggregated network, the incidence curves do not present sharp gradients as in the conference case, and later epidemics are unable to infect a large fraction of daily visitors.

In the school case (bottom-left panel) almost all students arrive at the beginning of the day, hence no effects due to heterogeneous arrival times can be observed. Similarly to the conference case, the simulated dynamics displays jumps in the number of infected individuals at specific times of the day, regardless of the seed node, and by the end of the day almost all individuals get infected. Heterogeneous invasion dynamics can be observed depending on the class of the seed node, and the differences can be related to the scheduled activities and movements of school children. Conversely, different choices for the seed node within a single class (bottom-left panel, inset) yield very similar incidence curves. This can be understood as a result of different within-class and cross-class contact patterns: contacts within individual classes are rather homogeneous compared to cross-class contacts, so that the SI process quickly reaches most nodes of the seed’s class. The invasion of other classes is controlled by slower temporal structures of the contact network, which are determined by the school schedule and determine the sensitivity on the initial class.

To characterize in a more quantitative fashion the importance of the temporal structure of the network on the spreading dynamics, we can consider the number of individuals who are reachable from the seed node through paths in the (daily) cumulative contact network, and compute what fraction of them are actually reached by an SI process that takes place over the temporal contact network. The value of this ratio displays markedly different distributions in the museum and in the conference case [38]: at a conference almost all the individuals who are reachable along the cumulative contact network always get infected by the end of the day, whereas in the museum case this ratio is often much smaller than 1. Therefore, studying the dynamics of a simple SI process can uncover differences in the temporal structure of human proximity networks that cannot be detected by using simpler statistical indicators (e.g., the probability distributions of contact durations). This calls for more work aimed at using generic dynamical processes over temporal networks to define a new class of time-aware network observables that can expose important differences and similarities.

4.2 Causality-Respecting Paths

The differences in spreading patterns outlined above are due to the causality constraints inherent in the temporal character of the contact network: for instance, if node i interacts first with node j and then with node k, a message or infectious agent can travel from j to k through i, but not in the opposite direction, while in a static network both events would be equally possible.

It is therefore interesting to study the spreading paths of the SI process on a temporal network and on the corresponding aggregated network, as mentioned in the above Sect. 4.1. To this aim, for each seed node we define a transmission network along which the infection effectively spreads in the temporal network (i.e., the network whose edges are given by S ↔ I contacts). Therefore, the distance along the transmission network between the seed node and another arbitrary node i gives the actual number of transmission events that occurred before the spreading process reached i, and consequently it is the length of the fastest path from the seed individual to the infected one which respects the causality constraints of the temporal network [53, 67, 68].

On the other hand, in an aggregated, static view of the contact network the spreading would follow the shortest path over the network aggregated from the time the seed first appears, as the infection can only spread along interactions occurring after the arrival of the seed node. We call this network a partially aggregated network.

As shown in Fig. 11, the distribution of lengths of the fastest paths turns out to be broader and shifted toward higher values than the corresponding shortest-path distributions. This holds both for the conference and for the museum case, and has also been observed in other cases [68]. The actual number of intermediaries is therefore larger on a temporal network than would be predicted by a propagation scheme based on a static network. This difference can be understood by considering a similar example as discussed above: if node i is infected and interacts with node j, who then interacts with node k before i interacts with k, the actual (fastest) spreading path between nodes i and k has path length 2, while the shortest path has a unitary path length.

Fig. 11
figure 11

Distribution of the path lengths n d from the seed node to all the infected individuals, computed over the transmission network (black circles) and over the partially aggregated networks (red pluses). For each day the distributions are computed by varying the choice of the seed node over all individuals

Full size image

In settings in which each transmission event has a cost, or is associated with the possibility of signal loss or attenuation, such differences might play an important role and temporal effects should accordingly be taken into account carefully.

4.3 Activity Clocks

The results of the previous subsection show that, depending on the environment and on the time at which the spreading process is initiated, different spreading dynamics can be obtained. In particular, the time at which a given node is reached by the information or infection may strongly depend on collective activity patterns. In the context of message routing in networks of mobile devices [69–72], the distribution of elapsed times between the generation of the message and its arrival at given nodes is often considered as a way to evaluate the performance of a spreading protocol [73–76]. However, the non-stationary and bursty behavior of the contact and proximity networks imply that the distribution of delays between message injection and message delivery at a given node may in fact depend importantly on the time of injection of a message, or on specific details of contact and activity patterns. The left panel of Fig. 12 shows this for the case of a message that spreads over the HT09 temporal contact network according to a simple SI process initiated at two different points in time: the distribution of arrival delays computed in terms of wall-clock time is extremely sensitive to the injection time of the message and displays strong heterogeneities that cannot be captured by any simple statistical model. It is thus important to devise more robust metrics for message delivery that factor out non-stationary behaviors and temporal heterogeneities, allowing on the one hand to carry out more objective comparisons of different protocols for message spreading, and on the other hand to validate the models of human mobility (and the ensuing temporal networks) that are used to design and inform such protocols.

Fig. 12
figure 12

Log-binned distribution of message arrival delays. The distributions are computed by simulating a simple SI process over the HT09 temporal contact network, for two different injection times of the initial message (blue crosses and red circles). Left: the delay interval is defined as the wall-clock time difference between the arrival of the message at a given node and the injection time of the message. Right: the delay interval distribution is computed by using node-specific activity clocks that only run when nodes have active links (proximity relations) to other nodes. That is, each node has a specific notion of “intrinsic” time that is defined as the cumulated time it spent in contact with other nodes

Full size image

Some progress in the direction outlined above can be made by giving up the global notion of wall-clock time in favor of a node-specific definition of time. We imagine that each node has its own clock, and that this clock only runs when the node is involved in one or more contacts. Since the clock measures the amount of time a given node has spent in interaction, we refer to this clock as an “activity clock”. All activity clocks are set to zero at the beginning of the spreading process, when the initial message is injected into the network. Thus, the activity clock of a node measures the amount of time during which that node could have received a message propagated along the links of the temporal network, i.e., it ignores the time intervals during which the node was disconnected from the rest of the network.

In this context, the message delivery delay for node i is defined as the value of its activity clock when the message is received, i.e., it is the elapsed time node i has spent in contact with others, from the injection time of the initial message up to the moment when the message is received by i. The right panel of Fig. 12 shows the distributions of delivery delays computed in terms of activity clocks. The distributions exhibit a smooth dependence on activity-clock time, without the strong heterogeneities observed when using wall-clock time. Most importantly, they now collapse onto one another, i.e., they are robust with respect to changes in the injection time of the message. Strikingly, they are also robust with respect to the context: as reported in [77], the same distribution is obtained for spreading processes simulated in conferences with very different schedules and contact densities.

It is important to remark that synthetic temporal networks of human contact are typically generated on the basis of a number of accepted models for the underlying human mobility in space. The quality of the models is often assessed on the basis of their ability to reproduce simple statistical observables of the temporal network, such as the probability distribution of contact durations and the distribution of times between successive contacts of a node. However, when computing the distributions of delivery delays for an SI process in terms of activity clocks, strong differences emerge between the accepted generative models and the empirical temporal networks. Specifically, as reported in [77], most of the accepted models yield delay distributions that are much narrower than those of Fig. 12, thus failing to reproduce the empirical phenomenology. This points to the need for further modeling work to design generative models of temporal networks that can correctly reproduce the empirical distributions. Notice that such differences only become visible on using activity clocks in combination with dynamical process on the temporal network, used as a probe of properties that cannot be captured by means of customary metrics. For example, the comparison between the left and right panels of Fig. 12 shows how suitable definitions of “time” based on activity metrics of the temporal network have the power to uncover regularities that are otherwise completely shadowed by the intrinsic heterogeneities of the system. At the same time these results call for more research in several directions. In particular, it would be important to:

  • Define and characterize activity clocks based on different types of node and edge metrics for temporal networks (e.g., defining time as the cumulated number of contact events, rather than as the elapsed time in contact),

  • Express in terms of activity clocks the evolution of simple dynamical processes taking place on temporal networks,

  • Model the form of the delay distributions observed in simulation for paradigmatic dynamical processes such as SI spreading taking place on temporal networks.

5 Conclusion

The study of empirical temporal networks is receiving increasing attention because of the availability of new data sources and because of their relevance for the detection, modeling and control of phenomena in a broad variety of socio-technical systems. To date, key questions are still open about temporal networks and dynamical processes over temporal networks.

Here we focused on high-resolution empirical temporal networks of human proximity, provided a phenomenological overview of some important properties, and reported on the impact that such properties have on paradigmatic epidemic-like processes that take place over temporal networks, with potential applications to diverse domains such as information spreading or epidemic modeling. We remark that the consolidated toolbox of statistical indicators, network metrics and generative models for static networks that has been developed over the last decade cannot be trivially generalized to the case of temporal networks. More research is thus needed in order to identify dynamical extensions of the observables designed for static network, to uncover dynamical network motifs [53, 66], and to explore entirely new characterization techniques that expose important features of the temporal-topological structure of the networks. In this respect, it will be probably fruitful to investigate simple dynamical processes over networks as a tool for uncovering relevant patterns, and as an aid to constrain and evaluate generative models for temporal networks.

We also notice that in the context of many applicative domains it is very difficult to characterize separately the dynamics of the network and that of the relevant dynamical process (e.g., the dynamics of a contact network and the dynamics of an epidemic unfolding over it): depending on the specific process, on its timescales, and on the set of properties of the process that one aims at modeling, the temporal structure of the network can have a profoundly different relevance. For example, it has been shown that for flu-like epidemic processes, with latent and infectious timescales of the order of a few days, the temporal structure of the underlying human contact networks is negligible if one aims at modeling just the peak time of the epidemics, and is important if the goal is to model the size of the epidemics [36]. Developing a more systematic understanding of the impact that the temporal structure of a network has on a given observable is an open challenge.

The above remarks are related to another important problem, that of coarse-graining temporal network data when either explicit node/edge attributes are available or node/edge activity patterns can be clustered into classes of similar behavior. When dealing with human contact networks, this is the case of many contexts in which the population under study is structured because of roles (e.g., hospitals) and/or spatio-temporal constraints on group mobility and interactions (e.g., schools). In particular, inferring behavioral classes from temporal network data requires algorithms to mine for dynamical communities of nodes or edges that extend those available for static networks, as a temporal network may have sharply defined classes of dynamical behavior that completely disappear on considering aggregated networks obtained by projecting out time. To this end, machine learning techniques based on node/edge features or on entire activity timelines may prove effective in uncovering and characterizing behavioral regularities hidden in temporal networks. When classes are known (e.g., explicit role-based classes within a hospital population), or discovered via time-aware community detection techniques, it is often insightful to consider aggregated representations of the data based on the class attributes, such as the contact matrices commonly used in epidemiology. These customary representations, though, have been defined and investigated in order to coarse-grain static interaction networks, and they need to be generalized so that they can be used to summarize temporal networks in a way which is suitable for the relevant applicative context.

Progress in the above directions of creating synopses of temporal network data would greatly help in defining “parsimonious” models for dynamical processes, that only retain the necessary amount of information about the underlying temporal network. This also calls for work on reconciling different scales of representation of temporal network data, so that properties and dynamical processes at different levels can be related to one another. In consideration of the coming deluge of behavioral information represented in the form of temporal networks, the ability to create parsimonious but informative representations will be an increasingly valuable asset for the applications of network science.