Selection of Vine Copulas

Abstract

Vine copula models have proven themselves as a very flexible class of multivariate copula models with regard to symmetry and tail dependence for pairs of variables. The full specification of a vine model requires the choice of a vine tree structure, the copula families for each pair copula term and their corresponding parameters. In this survey we discuss the different approaches, both frequentist and Bayesian, for these model choices so far and point to open problems.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

2.1 Introduction

The analysis of high-dimensional data sets requires flexible multivariate stochastic models that can capture the inherent dependency patterns. The copula approach, which separates the modeling of the marginal distributions from modeling the dependence characteristics, is a natural one to follow in this context. This development has spawned a tremendous increase in copula-based applications in the last 10 years, especially in the areas of finance, economics, and hydrology.

Considerable efforts have been undertaken to increase the flexibility of multivariate copula models beyond the scope of elliptical and Archimedean copulas. Vine copulas are among the best-received of such efforts. Vine copulas use (conditional) bivariate copulas as the so-called pair copula building blocks to describe a multivariate distribution (see [37]). A set of linked trees—the “vine”—describes a vine copula’s factorization of the multivariate copula density function into the density functions of its pair copulas (see [8, 9]). The article by [1] illustrates a first application of the vine copula concept using non-Gaussian pair copulas to financial data. The first comprehensive account of vine copulas is found in [45], a recent survey in [20], and the current developments of this active research area in [46].

Elliptical copulas as well as Archimedean copulas have been shown to be inadequate models to describe the dependence characteristics of real data applications (see, for example, [1, 23, 24]). As a pair copula construction, vine copulas allow different structural behaviors of pairs of variables to be modeled suitably, in particular so with regard to their symmetry, or lack thereof, strength of dependence, and tail dependencies. Such flexibility requires well-designed model selection procedures to realize the full potential of vine copulas as dependence models. Successful applications of vines can be found, amongst others, in [10, 12, 17, 22, 24, 32, 48, 51, 54, 61].

A parametric vine copula consists of three components: a set of linked trees identifying the pairs of variables and their conditioning variables, the copula families for each pair copula term given by the tree structure, and the corresponding copula parameters. The three-layered definition leads to three fundamental estimation and selection tasks: (1) Estimation of copula parameters for a chosen vine tree structure and pair copula families, (2) Selection of the parametric copula family for each pair copula term and estimation of the corresponding parameters for a chosen vine tree structure, and (3) Selection and estimation of all three model components. In this survey we address these tasks and give an overview of the statistical approaches taken so far. These range from frequentist to Bayesian methods.

The remainder of this paper is structured as follows. In Sect. 2.2 we provide the necessary methodical background on regular vines and regular vine copulas. We then discuss estimation of parameters of regular vine copulas in Sect. 2.3 and the selection of appropriate pair copulas in Sect. 2.4. Section 2.5 treats the joint selection of the regular vine tree structure, the copula families, and their parameters. Section 2.6 concludes with a discussion of available software and open problems.

2.2 Regular Vine Copulas

Copulas describe a statistical model’s dependence behavior separately from its marginal distributions [60]. As such, a copula is a multivariate distribution function with all marginal distributions being uniform: i.e. the copula associated with an n-variate cumulative distribution function F _1: n with univariate marginal distribution functions F ₁, …, F _n is a distribution function $C :{ \left [0,1\right ]}^{n} \rightarrow \left [0,1\right ]$ satisfying

$$\displaystyle{ F_{1:n}\left (\boldsymbol {\mathrm{x}}\right ) = C\left (F_{1}\left (x_{1}\right ),\ldots ,F_{n}\left (x_{n}\right )\right ),\quad \boldsymbol {\mathrm{x}} = {(x_{1},\ldots ,x_{n})}^{{\prime}}\in {\mathbb{R}}^{n}. }$$

If C is absolutely continuous, its density is denoted by c.

The factorization of multivariate copula densities into (conditional) bivariate copula densities is due to [8, 37], which were developed independently. The details of these factorizations are represented by the graph theoretical construction called regular vine to organize different decompositions. Graphs are defined in terms of a set of nodes N and a set of edges E connecting these nodes, i.e. E ⊂ N ×N. Vines are based on trees which are particular graphs where there is a unique sequence of edges between each two nodes.

Definition 2.1 (Regular Vine Tree Sequence). 

A set of linked trees $\mathcal{V} = \left (T_{1},T_{2},\ldots ,T_{n-1}\right )$ is a regular vine (R-vine) on n elements if

• 1. T ₁ is a tree with nodes $N_{1} =\{ 1,\ldots ,n\}$ and a set of edges denoted by E ₁.

• 2. For i = 2, …, n − 1, T _i is a tree with nodes N _i  = E _i − 1 and edge set E _i .

• 3. For i = 2, …, n − 1, if $a =\{ a_{1},a_{2}\}$ and $b =\{ b_{1},b_{2}\}$ are two nodes in N _i connected by an edge, then exactly one of the a _i equals one of the b _i (proximity condition).

In other words, the proximity condition requires that the edges corresponding to two connected nodes in tree T _i share a common node in tree T _i − 1. This ensures that the decomposition into bivariate copulas which is given below is well defined.

Two sub-classes of regular vines have been studied extensively in the literature: canonical vines (C-vines) and drawable vines (D-vines) (see [1, 45]). C-vines are characterized by a root node in each tree $T_{i},\ i \in \{ 1,\ldots ,n - 1\},$ which has degree n − i; that means that the root node is connected to all other nodes of the tree. D-vines, on the other hand, are uniquely characterized through their first tree which is, in graph theoretical terms, a path; this means that each node has degree of at most 2. Therefore the order of variables in the first tree defines the complete D-vine tree sequence.

Some more definitions are needed to introduce regular vine copulas: the complete union A _e of an edge $e =\{ a,b\} \in E_{i}$ in tree T _i of a regular vine $\mathcal{V}$ is defined by

$$\displaystyle\begin{array}{rcl} A_{e} = \left \{v \in N_{1} :\ \exists e_{m} \in E_{m},\ m = 1,\ldots ,i - 1,\text{ such that }v \in e_{1} \in \cdots \in e_{i-1} \in e\right \}.& &{}\end{array}$$

(2.1)

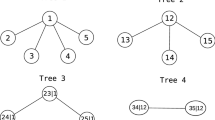
The conditioning set associated with $e =\{ a,b\}$ is defined as $D_{e} := A_{a} \cap A_{b}$ and the conditioned sets associated with $e =\{ a,b\}$ are defined as $\mathcal{C}_{e,a} := A_{a} \setminus D_{e}$ and $\mathcal{C}_{e,b} := A_{b} \setminus D_{e}$. Bedford and Cooke [8] showed that the conditioned sets are singletons, and we will therefore refer to edges by their labels $\{\mathcal{C}_{e,a},\mathcal{C}_{e,b}\vert D_{e}\}\ \hat{ =}\ \{ i(e),j(e)\vert$ An exemplary regular vine on five elements is shown in Fig. 2.1.

Fig. 2.1

Regular vine on five elements

Given these sets, we can specify a regular vine copula by associating a (conditional) bivariate copula with each edge of the regular vine, a so-called pair copula.

Definition 2.2 (Regular Vine Copula). 

A regular vine copula $C = \left (\mathcal{V},\mathcal{B}\left (\mathcal{V}\right )\right.$, ${\boldsymbol \theta }\left.\left (\mathcal{B}\left (\mathcal{V}\right )\right )\right )$ in $n$ dimensions is a multivariate distribution function such that for a random vector $\boldsymbol {\mathrm{U}} ={ \left (U_{1},\ldots ,U_{n}\right )}^{{\prime}}\sim C$ with uniform margins

• 1. $\mathcal{V}$ is a regular vine on n elements,

• 2. $\mathcal{B}(\mathcal{V}) = \left \{C_{i(e),j(e)\vert D(e)}\vert e \in E_{m},\ m = 1,\ldots n - 1\right \}$ is a set of n(n − 1) ∕ 2 copula families identifying the conditional distributions of $U_{i(e)},U_{j(e)}\vert \boldsymbol {\mathrm{U}}_{D(e)}$,

• 3. ${\boldsymbol \theta }(\mathcal{B}(\mathcal{V})) = \left \{{\boldsymbol \theta }_{i(e),j(e)\vert D(e)}\vert e \in E_{m},\ m = 1,\ldots n - 1\right \}$ is the set of parameter vectors corresponding to the copulas in $\mathcal{B}\left (\mathcal{V}\right )$.

There fore the full specification of a regular vine copula consists of three layers: the regular vine tree structure $\mathcal{V}$, the pair copula families $\mathcal{B} = \mathcal{B}(\mathcal{V})$, and the pair copula parameters ${\boldsymbol \theta }={\boldsymbol \theta } (\mathcal{B}(\mathcal{V}))$. Regular vine copulas which differ in the tree structure or in at least one pair copula family represent in general different statistical models. Notable exceptions from this are the multivariate Gaussian, Student’s t or Clayton copulas, which can be decomposed into bivariate Gaussian, Student’s t or Clayton copulas, respectively, in multiple ways (see [64]). The probability density function f _1: n at point $\boldsymbol {\mathrm{x}} = {(x_{1},\ldots ,x_{n})}^{{\prime}}\in {\mathbb{R}}^{n}$ of an n-dimensional regular vine-dependent distribution F _1: n is easily calculated as

$$\displaystyle\begin{array}{rcl} f_{1:n}\left (\boldsymbol {\mathrm{x}}\vert \mathcal{V},\mathcal{B},{\boldsymbol \theta }\right )& =& \left (\prod _{m=1}^{n-1}\prod _{ e=\{a,b\}\in E_{m}}\!\!\!c_{i(e),j(e)\vert D(e)}\left (F_{i(e)\vert D(e)},F_{j(e)\vert D(e)}\vert {\boldsymbol \theta }_{i(e),j(e)\vert D(e)}\right )\right ) \\ & & \times f_{1}\left (x_{1}\right )\cdots f_{n}\left (x_{n}\right ), {}\end{array}$$

(2.2)

where $F_{i(e)\vert D(e)} := F_{i(e)\vert D(e)}\left (x_{i(e)}\vert \boldsymbol {\mathrm{x}}_{D(e)}\right )$ and $F_{j(e)\vert D(e)} := F_{j(e)\vert D(e)}\left (x_{j(e)}\vert \boldsymbol {\mathrm{x}}_{D(e)}\right )$ (see [8]). These conditional distribution functions can be determined recursively tree-by-tree using the following relationship

$$\displaystyle{ \begin{array}{ll} F &_{i(e)\vert D(e)}\left (x_{i(e)}\vert \boldsymbol {\mathrm{x}}_{D(e)}\right ) = F_{\mathcal{C}_{e,a}\vert D_{e}}\left (x_{\mathcal{C}_{e,a}}\vert \boldsymbol {\mathrm{x}}_{D_{e}}\right ) \\ & = \frac{\partial C_{\mathcal{C}_{a,a_{ 1}},\mathcal{C}_{a,a_{2}}\vert D_{a}}\left (F_{\mathcal{C}_{a,a_{ 1}}\vert D_{a}}\big(x_{\mathcal{C}_{a,a_{1}}}\vert \boldsymbol {\mathrm{x}}_{D_{a}}\big),F_{\mathcal{C}_{a,a_{ 2}}\vert D_{a}}\big(x_{\mathcal{C}_{a,a_{2}}}\vert \boldsymbol {\mathrm{x}}_{D_{a}}\big)\right )} {\partial F_{\mathcal{C}_{a,a_{ 2}}\vert D_{a}}\big(x_{\mathcal{C}_{a,a_{2}}}\vert \boldsymbol {\mathrm{x}}_{D_{a}}\big)} ,\end{array} }$$

(2.3)

where $e =\{ a,b\}$ with $a =\{ a_{1},a_{2}\}$ as before (see [23] for details).

To facilitate inference, it is assumed that the pair copulas C _{i(e), j(e) | D(e)} only depend on the variables with indices in D(e) through the arguments F _{i(e) | D(e)} and F _{j(e) | D(e)}. This so-called simplifying assumption has been investigated by [35, 64]. In particular, [35] show examples where the assumption is not severe and [64] show that the multivariate Clayton copula is the only Archimedean copula which can be represented as a simplified vine. A critical look on the subject can be found in [2] who take a first step in building vine copulas of non-simplified nature.

Following expression (2.2), the likelihood L of a regular vine copula $C = \left (\mathcal{V},\mathcal{B},{\boldsymbol \theta }\right )$ given the observed data $\boldsymbol {\mathrm{x}}\,=\,{\left (\boldsymbol {\mathrm{x}}_{1},\ldots ,\boldsymbol {\mathrm{x}}_{N}\right )}^{{\prime}}\in {\mathbb{R}}^{N\times n}$ can be calculated as

$$\displaystyle{ L\left (\mathcal{V},\mathcal{B},{\boldsymbol \theta }\vert \boldsymbol {\mathrm{x}}\right ) =\prod _{ k=1}^{N}f_{ 1:n}\left (\boldsymbol {\mathrm{x}}_{k}\vert \mathcal{V},\mathcal{B},{\boldsymbol \theta }\right ). }$$

(2.4)

The corresponding log-likelihood is denoted by ℓ.

A regular vine copula is said to be truncated at level M if all pair copulas conditioning on M or more variables are set to bivariate independence copulas [14]. As a result, the iteration index m of the first product in (2.2) runs only up to m = M and the distribution is fully specified by $\big(\mathcal{V} = (T_{1},\ldots ,T_{M}),\mathcal{B}(\mathcal{V}),{\boldsymbol \theta }(\mathcal{B}(\mathcal{V}))\big)$.

In the following, we discuss in reverse order how the components of a regular vine copula can be selected and estimated. That is, we begin with estimation of the parameters ${\boldsymbol \theta }$, then treat the selection of appropriate copula families $\mathcal{B}$, and finally discuss the selection of vine trees $\mathcal{V}$.

2.3 Parameter Estimation for Given Vine Tree Structure and Pair Copula Families

Given a vine tree structure $\mathcal{V}$ and pair copula families $\mathcal{B} = \mathcal{B}(\mathcal{V})$, the challenge is to estimate the parameters ${\boldsymbol \theta }={\boldsymbol \theta } (\mathcal{B}(\mathcal{V}))$ of a regular vine copula for observed data $\boldsymbol {\mathrm{x}} \in {\mathbb{R}}^{N\times n}$. The crucial point here is to evaluate the conditional distribution functions F _{i(e) | D(e)}, which depend on the copulas of previous trees [see (2.3)].

2.3.1 Maximum Likelihood Estimation

Classically, parameters of a statistical model are often estimated using maximum likelihood techniques. Here, this means that regular vine copula parameters ${\boldsymbol \theta }$ and parameters of the marginal distributions are estimated by maximizing the likelihood (2.4) in terms of these parameters. For copulas, in particular if n > 2, the number of parameters to be estimated may, however, be too large, so that one typically either uses empirical distribution functions for the margins as proposed by [25, 26] or estimates parameters of the marginal distributions in a first step and then fixes these marginal parameters to their estimated values in the estimation of the copula parameters. The latter method is called inference functions for margins (IFM) by [38, 39].

But even when estimation of marginal and dependence parameters is separated, joint maximum likelihood estimation of regular vine copula parameters can be computationally intensive, since the vine decomposition involves n(n − 1) ∕ 2 bivariate copulas with corresponding parameters. Aas et al. [1] therefore proposed a sequential method: starting with the copulas of the first tree, this method proceeds tree-wise and estimates the parameters of the copulas in a tree by fixing the parameters of copulas in all previous trees.

Example 2.1 (Sequential Estimation). 

Let the 5-dimensional regular vine $\mathcal{V}$ of Fig. 2.1 be given with copulas $\mathcal{B}(\mathcal{V})$. In the first step, we estimate the parameters of the copulas C _1, 2, C _2, 3, C _3, 4, and C _3, 5 using maximum likelihood based on the transformed observations $F_{j}(x_{kj})$ for $x_{kj},\ k = 1,\ldots ,N,\ j = 1,\ldots ,5$. In the second tree, we then have to estimate, for instance, the parameter(s) of the copula C _{1, 3 | 2}. For this we form pseudo-observations $F_{1\vert 2}(x_{k1}\vert x_{k2},\hat{{\boldsymbol \theta }}_{1,2})$ and $F_{3\vert 2}(x_{k3}\vert x_{k2},\hat{{\boldsymbol \theta }}_{2,3}),\ k = 1,\ldots ,N,$ according to expression (2.3) and using the estimated parameters of copulas C _1, 2 and C _2, 3, respectively. Based on these pseudo-observations estimation of ${\boldsymbol \theta }_{1,3\vert 2}$ is again straightforward. All other copulas are estimated analogously.

Note that this strategy only involves the estimation of bivariate copulas and therefore is computationally much simpler than joint maximum likelihood estimation of all parameters at once. For more details, see [1] as well as [33] who investigates the asymptotic properties of this sequential approach. A comparison study of estimators for regular vine copulas can be found in [34].

If joint maximum likelihood estimates are desired, the sequential method can be used to obtain starting values for the numerical optimization. A detailed discussion how to compute score functions and the observed information matrix for regular vine copulas is provided by [65].

2.3.2 Bayesian Posterior Estimation

Bayesian statistics considers parameters ${\boldsymbol \theta }$ as random variables. As such, inference focuses on estimating the entire distribution of the parameters instead of only finding a point estimate. In particular, the so-called posterior distribution $p({\boldsymbol \theta }) := p({\boldsymbol \theta }\vert \boldsymbol {\mathrm{x}})$, the distribution of the parameters ${\boldsymbol \theta }$ given the observed data $\boldsymbol {\mathrm{x}}$, is the main object of interest. The unnormalized posterior density factorizes into the product of the likelihood function $L({\boldsymbol \theta }\vert \boldsymbol {\mathrm{x}})$ (2.4) and the prior density function $\pi ({\boldsymbol \theta })$:

$$\displaystyle{p({\boldsymbol \theta }) := p({\boldsymbol \theta }\vert \boldsymbol {\mathrm{x}}) = \frac{L({\boldsymbol \theta }\vert \boldsymbol{ \mathrm{x}}) \cdot \pi ({\boldsymbol \theta })} {f(\boldsymbol {\mathrm{x}})} \propto L({\boldsymbol \theta }\vert \boldsymbol {\mathrm{x}}) \cdot \pi ({\boldsymbol \theta }).}$$

The prior distribution incorporates a priori beliefs about the distribution of the parameters. It must not depend on, or be conditional upon, the observed data.

Markov chain Monte Carlo (MCMC) procedures clear the remaining obstacle of sampling from a distribution which is known only up to a constant. The trick is to simulate the run of a Markov chain whose equilibrium distribution is the targeted posterior distribution $p({\boldsymbol \theta })$ of the parameters ${\boldsymbol \theta }$. Upon convergence of the Markov chain, its states represent draws from the desired distribution.

The Metropolis–Hastings algorithm [31, 49] implements the simulation of such a Markov chain through an acceptance/rejection mechanism for the updates of the chain: in the first step, an update of the chain from its current state ${\boldsymbol \theta }$ to ${{\boldsymbol \theta }}^{{\ast}} \sim q(\cdot \vert {\boldsymbol \theta })$ is proposed. The proposal distribution q can be chosen almost arbitrarily. In the second step, the proposal is accepted with probability $\alpha :=\alpha ({\boldsymbol \theta }{,{\boldsymbol \theta }}^{{\ast}})$. The acceptance probability α is chosen such that convergence of the Markov chain to the targeted distribution is guaranteed by Markov chain theory [50]. The Metropolis–Hastings acceptance probability for convergence to the target distribution p( ⋅) is

$$\displaystyle{\alpha ({\boldsymbol \theta }{,{\boldsymbol \theta }}^{{\ast}}) = \frac{p{({\boldsymbol \theta }}^{{\ast}})} {p({\boldsymbol \theta })} \cdot \frac{q({\boldsymbol \theta }{\vert {\boldsymbol \theta }}^{{\ast}})} {q{({\boldsymbol \theta }}^{{\ast}}\vert {\boldsymbol \theta })}.}$$

The target distribution goes into the Metropolis–Hastings algorithm only at the evaluation of the acceptance probability α. It can be easily seen that it is sufficient to know the density function of the target distribution only up to a constant for this algorithm to work, given that α only depends on the ratio of two densities.

The following Metropolis–Hastings scheme to sample from the posterior distribution of the parameters ${\boldsymbol \theta }$ of a regular vine copula is proposed in [28, 51, 62]. The authors suggest normally distributed random walk proposals be used in the update step.

Algorithm 2.1 (Metropolis–Hastings Sampler for Parameter Estimation). 

1: Choose arbitrary starting values ${{\boldsymbol \theta }}^{0} = {(\theta _{1}^{0},\ldots ,\theta _{D}^{0})}^{{\prime}},$ where D := n(n − 1)∕2.

2: for each iteration r = 1,…,R do

3: Set ${{\boldsymbol \theta }}^{r} {={\boldsymbol \theta } }^{r-1}$.

4: for i = 1,…,D do

5: Draw $\theta _{i}^{r}$ from a $N(\theta _{i}^{r-1},\sigma _{i}^{2})$ distribution with probability density function $\phi _{(\theta _{i}^{r-1},\sigma _{i}^{2})}(\cdot )$.

6: Evaluate the Metropolis–Hastings acceptance probability of the proposal

$$\displaystyle{\alpha :=\alpha (\theta _{i}^{r-1},\theta _{ i}^{r}) = \frac{p{({\boldsymbol \theta }}^{{\ast}})} {p({\boldsymbol \theta })} \cdot \frac{\phi _{(\theta _{i}^{r},\sigma _{i}^{2})}(\theta _{i}^{r-1})} {\phi _{(\theta _{i}^{r-1},\sigma _{i}^{2})}(\theta _{i}^{r})} = \frac{L{({\boldsymbol \theta }}^{{\ast}}\vert \boldsymbol {\mathrm{x}})} {L({\boldsymbol \theta }\vert \boldsymbol {\mathrm{x}})} \cdot \frac{\pi {({\boldsymbol \theta }}^{{\ast}})} {\pi ({\boldsymbol \theta })} ,}$$

where ${{\boldsymbol \theta }}^{{\ast}} = {(\theta _{1}^{r},\ldots ,\theta _{i}^{r},\theta _{i+1}^{r-1},\ldots ,\theta _{D}^{r-1})}^{{\prime}}$ and ${\boldsymbol \theta }= {(\theta _{1}^{r},\ldots ,\theta _{i-1}^{r},\theta _{i}^{r-1},\ldots ,\theta _{D}^{r-1})}^{{\prime}}$.

7: Accept the proposal $\theta _{i}^{r}$ with probability α; if rejected, set $\theta _{i}^{r} =\theta _{ i}^{r-1}$.

8: end for

9: end for

10: return  ${({\boldsymbol \theta }}^{1},\ldots {,{\boldsymbol \theta }}^{R})$

2.4 Selection of the Pair Copula Families and their Parameters for a Known Vine Tree Structure

An n-dimensional regular vine copula with tree structure $\mathcal{V}$ is based on a set $\mathcal{B}(\mathcal{V})$ of n(n − 1) ∕ 2 bivariate copulas and their corresponding parameters. The copula families can be chosen arbitrarily, e.g., from the popular classes of Archimedean, elliptical or extreme-value copulas. Assuming that an appropriate vine structure $\mathcal{V}$ is chosen, the question is how to select adequate (conditional) pair copulas C _{i(e), j(e) | D(e)} and their parameters for given data $\boldsymbol {\mathrm{x}}$.

2.4.1 Sequential Selection

If a regular vine is truncated at level 1, the copulas in trees T ₂ to T _n − 1 are set to independence. The corresponding regular vine copula density reduces to the product of the unconditional bivariate copula densities C _i(e), j(e), which can be selected based on data $F_{i(e)}(x_{k,i(e)})$ and $F_{j(e)}(x_{k,j(e)}),\ k = 1,\ldots ,N$. Typical criteria for copula selection from a given set of families are information criteria such as the AIC as proposed by [11, 47]. The latter compares AIC-based selection to three alternative selection strategies: selection of family with highest p-value of a copula goodness of fit test based on the Cramér–von Mises statistic, with smallest distance between empirical and modeled dependence characteristics (Kendall’s τ, tail dependence), or with highest number of wins in pairwise comparisons of families using the test by [66]. In a large-scale Monte Carlo study the AIC turned out to be the most reliable selection criterion.

In a general regular vine, the selection of a pair copula C _{i(e), j(e) | D(e)}, however, depends on the choices for copulas in previous trees due to its arguments (2.3). Since a joint selection seems infeasible because of the many possibilities, one typically proceeds tree-by-tree as in the sequential estimation method. That is, instead of estimating the parameters ${\boldsymbol \theta }_{i(e),j(e)\vert D(e)}$ of C _{i(e), j(e) | D(e)}, the copula is selected first and then estimated, which usually coincides for most selection strategies. Given the selected and estimated copulas of previous trees, one then selects the copulas of the next tree.

Example 2.2 (Sequential Selection). 

Again consider the five-dimensional regular vine $\mathcal{V}$ of Fig. 2.1 but now with unknown copulas $\mathcal{B}(\mathcal{V})$. In the first tree, we select (and then estimate) the copulas C _1, 2, C _2, 3, C _3, 4, and C _3, 5 using our method of choice based on $F_{j}(x_{kj}),\ k = 1,\ldots ,N,\ j = 1,\ldots ,5$. Given these copulas, we then have to select conditional copulas in the second tree. In case of the copula C _{1, 3 | 2}, we therefore again form the pseudo-observations $F_{1\vert 2}(x_{k1}\vert x_{k2},\hat{{\boldsymbol \theta }}_{1,2})$ and $F_{3\vert 2}(x_{k3}\vert x_{k2},\hat{{\boldsymbol \theta }}_{2,3}),\ k = 1,\ldots ,N,$ according to expression (2.3) and then select (and estimate) C _{1, 3 | 2} based on them. This can be iterated for all trees.

Clearly this sequential selection strategy accumulates uncertainty in the selection and therefore the final model has to be carefully checked and compared to alternative models. For the latter, the tests for non-nested model comparison by [18, 66] may be used.

2.4.2 Reversible Jump MCMC-Based Bayesian Selection

Bayesian copula family and parameter selection aims at estimating the joint posterior distribution of the pair copula families $\mathcal{B} = \mathcal{B}(\mathcal{V})$ and parameters ${\boldsymbol \theta }={\boldsymbol \theta } (\mathcal{B}(\mathcal{V}))$. The posterior density function factorizes into the product of the likelihood function L (2.4) and the prior density function π: $p(\mathcal{B},{\boldsymbol \theta }) \propto L(\mathcal{B},{\boldsymbol \theta }\vert \boldsymbol {\mathrm{x}}) \cdot \pi (\mathcal{B},{\boldsymbol \theta })$.

As in Sect. 2.4.1, family selection is understood in the context of choosing from a pre-specified set $\boldsymbol {\mathrm{B}}$ of parametric pair copula families. Model sparsity can be induced through the choice of prior distributions which favor regular vine copulas with fewer parameters over those with more parameters.

Bayesian techniques to select the pair copula families of D-vine copulas are covered in [51, 52, 61]. The reversible jump MCMC algorithm presented in this section follows the latest developments of family selection methods for regular vine copulas laid out in [28].

Reversible jump MCMC is an extension of ordinary MCMC to sample from discrete-continuous posterior distributions. The sampling algorithm and the mathematics underpinning the convergence statements are an immediate generalization of the Metropolis–Hastings algorithm [27]. A reversible jump MCMC algorithm functions like an ordinary MCMC algorithm with one extra step built in: before, or after, updating the parameters, a “jump” to another model is attempted. That is called the “between-models move,” while the updating of the parameters only is called the “within-model move” [16].

Algorithm 2.2 implements a reversible jump MCMC sampler which samples from the joint posterior distribution of the pair copula families $\mathcal{B}$ and the parameters ${\boldsymbol \theta }$, given a regular vine tree structure $\mathcal{V}$. In each iteration, it first updates all parameters as in Algorithm 2.1. Then the pair copula families are updated along with their parameters one-by-one. The pair copula family proposals are drawn from a uniform distribution over $\boldsymbol {\mathrm{B}}$, while the parameter proposals are sampled from a (multivariate) normal distribution centered at the maximum likelihood estimates of the parameters.

Algorithm 2.2 (Reversible Jump MCMC Sampler for Family Selection). 

1: Choose arbitrary copula family and parameter starting values $({\boldsymbol {\mathcal{B}}}^{0}{,{\boldsymbol \theta }}^{0}) = ((\mathcal{B}_{1}^{0},{\boldsymbol \theta }_{1}^{0}),\ldots ,(\mathcal{B}_{D}^{0},{\boldsymbol \theta }_{D}^{0}))$, where D := n(n − 1)∕2.

2: for each iteration r = 1,…,R do

3: Set $({\mathcal{B}}^{r}{,{\boldsymbol \theta }}^{r}) = ({\mathcal{B}}^{r-1}{,{\boldsymbol \theta }}^{r-1})$.

4: Perform one update step of Algorithm 2.1 for the parameters ${{\boldsymbol \theta }}^{r}$; denote the updated parameter entries by ${{\boldsymbol \theta }}^{+}$.

5: for i = 1,…,D do

6: Draw $\mathcal{B}_{i}^{r}$ from a $\mathit{Unif }(\boldsymbol {\mathrm{B}})$ distribution.

7: Draw ${\boldsymbol \theta }_{i}^{r}$ from a multivariate $N(\hat{{\boldsymbol \theta }}_{i}^{r},\hat{\Sigma }_{i}^{r})$ distribution with probability density function $\phi _{(\hat{{\boldsymbol \theta }}_{i}^{r},\hat{\Sigma }_{i}^{r})}(\cdot )$. Here $\hat{{\boldsymbol \theta }}_{i}^{r}$ denotes the MLE of the copula parameters of the pair copula $\mathcal{B}_{i}^{r}$ and $\hat{\Sigma }_{i}^{r}$ denotes the estimated approximative covariance matrix of the parameter estimates $\hat{{\boldsymbol \theta }}_{i}^{r}$.

8: Evaluate the generalized Metropolis–Hastings acceptance probability of the proposal

$$\displaystyle\begin{array}{rcl} \alpha & :=& \alpha ((\mathcal{B}_{i}^{r-1},{\boldsymbol \theta }_{ i}^{+}),(\mathcal{B}_{ i}^{r},{\boldsymbol \theta }_{ i}^{r})) {}\\ & =& \frac{p({\boldsymbol {\mathcal{B}}}^{{\ast}}{,{\boldsymbol \theta }}^{{\ast}})} {p(\boldsymbol {\mathcal{B}},{\boldsymbol \theta })} \cdot \frac{\phi _{(\hat{{\boldsymbol \theta }}_{i}^{r-1},\hat{\Sigma }_{i}^{r-1})}({\boldsymbol \theta }_{i}^{+})} {\phi _{(\hat{{\boldsymbol \theta }}_{i}^{r},\hat{\Sigma }_{i}^{r})}({\boldsymbol \theta }_{i}^{r})} {}\\ & =& \frac{\pi ({\boldsymbol {\mathcal{B}}}^{{\ast}}{,{\boldsymbol \theta }}^{{\ast}})} {\pi (\boldsymbol {\mathcal{B}},{\boldsymbol \theta })} \cdot \frac{L({\boldsymbol {\mathcal{B}}}^{{\ast}}{,{\boldsymbol \theta }}^{{\ast}}\vert \boldsymbol {\mathrm{x}})} {L(\boldsymbol {\mathcal{B}},{\boldsymbol \theta }\vert \boldsymbol {\mathrm{x}})} \cdot \frac{\phi _{(\hat{{\boldsymbol \theta }}_{i}^{r-1},\hat{\Sigma }_{i}^{r-1})}({\boldsymbol \theta }_{i}^{+})} {\phi _{(\hat{{\boldsymbol \theta }}_{i}^{r},\hat{\Sigma }_{i}^{r})}({\boldsymbol \theta }_{i}^{r})} , {}\\ \end{array}$$

where ${\boldsymbol {\mathcal{B}}}^{{\ast}} = (\mathcal{B}_{1}^{r},\ldots ,\mathcal{B}_{i}^{r},\mathcal{B}_{i+1}^{r-1},\ldots ,\mathcal{B}_{D}^{r-1})$, $\boldsymbol {\mathcal{B}} = (\mathcal{B}_{1}^{r},\ldots ,\mathcal{B}_{i-1}^{r},\mathcal{B}_{i}^{r-1},\ldots ,\mathcal{B}_{D}^{r-1})$, ${{\boldsymbol \theta }}^{{\ast}}=({\boldsymbol \theta }_{1}^{r},\ldots ,{\boldsymbol \theta }_{i}^{r},{\boldsymbol \theta }_{i+1}^{+},\ldots ,{\boldsymbol \theta }_{D}^{+})$, and ${\boldsymbol \theta }= ({\boldsymbol \theta }_{1}^{r},\ldots ,{\boldsymbol \theta }_{i-1}^{r},{\boldsymbol \theta }_{i}^{+},\ldots ,{\boldsymbol \theta }_{D}^{+})$.

9: Accept the proposal $(\mathcal{B}_{i}^{r},\theta _{i}^{r})$ with probability α; if rejected, set $(\mathcal{B}_{i}^{r},\theta _{i}^{r}) = (\mathcal{B}_{i}^{r-1},\theta _{i}^{+})$.

10: end for

11: end for

12: return  $(({\mathcal{B}}^{1}{,{\boldsymbol \theta }}^{1}),\ldots ,({\mathcal{B}}^{R}{,{\boldsymbol \theta }}^{R}))$

2.5 Selection of Vine Tree Structure, Pair Copula Families, and Parameters

As pair copula families $\mathcal{B} = \mathcal{B}(\mathcal{V})$ and parameters ${\boldsymbol \theta }={\boldsymbol \theta } (\mathcal{B}(\mathcal{V}))$ both depend on the vine tree structure $\mathcal{V}$, the identification of adequate trees is crucial to the model selection of vine copulas. As it was already the case for pair copula selection in Sect. 2.4.1, it is again not feasible to simply try and fit all possible regular vine copulas $C = \left (\mathcal{V},\mathcal{B},{\boldsymbol \theta }\right )$ and then choose the “best” one. In particular, the number of possible regular vines on n variables is $\frac{n!} {2} \times {2}^{\left ({ n-2 \atop 2} \right )}$ as shown by [53]. This means that even if pair copulas and parameters were known, the number of different models would still be enormous.

This remains true even when the selection is restricted to the sub-classes of C- and D-vines, since there are still n! ∕ 2 different C- and D-vines in n dimensions, respectively (see [1]). It should, however, be noted that C- and D-vine copulas are most appropriate if their structure is explicitly motivated by the data. In particular, C-vine copulas may be used if there is a set of pivotal variables such as stock indices (see [12, 32]) and D-vine copulas are particularly attractive to model variables with temporal order (see [13, 61]). Nevertheless we describe how C- and D-vines can be selected for arbitrary data sets.

2.5.1 Top-Down and Bottom-Up Selection

Due to the proximity condition (see Definition 2.2) regular vine trees are closely linked with each other and have to be constructed carefully. Two construction strategies have been proposed in the literature: a top-down approach by [23] and a bottom-up method by [43]. Both strategies proceed sequentially tree-by-tree and respect the proximity condition in each step. We first describe the top-down, then the bottom-up method.

2.5.1.1 Top-Down Selection

Selecting regular vine trees top-down means that one starts with the selection of the first tree T ₁ and continues tree-by-tree up to the last tree T _n − 1. The first tree T ₁ can be selected as an arbitrary spanning tree. Given that a tree $T_{m},\ m \in \{ 1,\ldots ,n - 2\},$ has been selected, the next tree T _m + 1 is chosen respecting the proximity condition (see Definition 2.2). In other words, T _m + 1 can only be formed by (conditional) pairs $\{i(e),j(e)\vert D(e)\}$ which fulfill the proximity condition.

Example 2.3 (Top-Down Tree Selection). 

Assume that we have selected the first tree T ₁ as shown in Fig. 2.1. Then the question is which pairs $\{i(e),j(e)\vert D(e)\}$ are eligible for tree construction in the second tree T ₂. According to the proximity condition these are $\{1,3\vert 2\}$, $\{2,4\vert 3\}$, $\{2,5\vert 3\}$, and $\{4,5\vert 3\}$. Obviously, the last three pairs form a cycle and therefore only two of them can be selected for T ₂. One of the three possibilities is shown in Fig. 2.1.

To perform this iterative selection strategy a criterion is needed to select a spanning tree among the set of eligible edges, where a spanning tree simply denotes a tree on all nodes. Clearly, the log-likelihood ℓ _m of the pair copulas in tree T _m of a regular vine copula [see expression (2.4)] is given by

$$\displaystyle\begin{array}{rcl} \ell_{m}\left (T_{m},\mathcal{B}_{T_{m}},{\boldsymbol \theta }_{T_{m}}\vert \boldsymbol {\mathrm{x}}\right )& =& \sum _{k=1}^{N}\sum _{ e\in E_{m}}\log \left (c_{i(e),j(e)\vert D(e)}\right. \\ & & \times \,\left.\left (F_{i(e)\vert D(e)},F_{j(e)\vert D(e)}\vert {\boldsymbol \theta }_{i(e),j(e)\vert D(e)}\right )\right ),{}\end{array}$$

(2.5)

where we write $\mathcal{B}_{T_{m}} := \mathcal{B}(T_{m})$ and ${\boldsymbol \theta }_{T_{m}} :={\boldsymbol \theta } (\mathcal{B}(T_{m}))$.

A straightforward solution therefore would be to choose the tree such that (2.5) is maximized after having selected pair copulas with high log-likelihood for each (conditional) pair $\{i(e),j(e)\vert D(e)\}$ that fulfills the proximity condition. This solution, however, leads to highly over-parameterized models, since models with more parameters in which simpler models are nested will always give a higher likelihood. For instance, the Student’s t copula always has a higher likelihood than the Gaussian copula which is a special case of the Student’s t as the degrees of freedom tend to infinity.

Therefore we formulate the following algorithm in terms of a general weight ω assuming that we want to maximize it for each tree. The previously discussed strategy corresponds to choosing the pair copula log-likelihoods as weights.

Algorithm 2.3 (Sequential Top-Down Selection Based on Weights). 

1: Calculate the weight ω_i,j for all possible variable pairs $\{i,j\},1 \leq i < j \leq n$.

2: Select the maximum spanning tree, i.e.

$$\displaystyle{ T_{1} =\mathop{ \text{argmax}}\limits_{T = (N,E)\text{ spanning tree}}\quad \sum _{e\in E}\omega _{i(e),j(e)}. }$$

3: for each edge e ∈ E₁ do

4: Select a copula C_i(e),j(e).

5: Estimate the corresponding parameter(s) ${\boldsymbol \theta }_{i(e),j(e)}$.

6: For k = 1,…,N transform $F_{i(e)\vert j(e)}(x_{k,i(e)}\vert x_{k,j(e)},\hat{{\boldsymbol \theta }}_{i(e),j(e)})$ and $F_{j(e)\vert i(e)}(x_{k,j(e)}\vert x_{k,i(e)},\hat{{\boldsymbol \theta }}_{i(e),j(e)})$ using (2.3).

7: end for

8: for m = 2,…,n − 1 do

9: Calculate the weights ω_{i(e),j(e)|D(e)} for all conditional variable pairs $\{i(e),j(e)\vert D(e)\}$ that can be part of tree T_m. We denote this set of edges which fulfill the proximity condition by E_P.

10: Among these edges, select the maximum spanning tree, i.e.,

$$\displaystyle{ T_{m} =\mathop{ \text{argmax}}\limits_{T = (N,E)\text{spanning tree with }E \subset E_{P}}\quad \sum _{e\in E}\omega _{i(e),j(e)\vert D(e)}. }$$

11: for each edge e ∈ E_m do

12: Select a conditional copula C_{i(e),j(e)|D(e)}.

13: Estimate the corresponding parameter(s) $\boldsymbol{\theta}_{i(e),j(e)}$.

14: For k = 1,…,N transform $F_{i(e)\vert j(e)\cup D(e)}(x_{k,i(e)}\vert x_{k,j(e)},\boldsymbol {\mathrm{x}}_{k,D(e)}, \hat{{\boldsymbol \theta }}_{i(e),j(e)\vert D(e)})$ and $F_{j(e)\vert i(e)\cup D(e)}(x_{k,j(e)}\vert x_{k,i(e)},\boldsymbol {\mathrm{x}}_{k,D(e)},\hat{{\boldsymbol \theta }}_{i(e),j(e)\vert D(e)})$ using (2.3).

15: end for

16: end for

17: return  the sequential model estimate $(\hat{\mathcal{V}},\hat{\mathcal{B}},\hat{{\boldsymbol \theta }})$.

Clearly, this algorithm only makes a locally optimal selection in each step, since the impact on previous and subsequent trees is ignored. The strategy is, however, reasonable in light of the definition of regular vines (see Definition 2.2). The maximum spanning tree in lines 2 and 10 can be found, e.g., using the classical algorithms by Prim or Kruskal (see [19, Section 23.2]). Possible choices for the weight ω are, for example:

• The absolute empirical Kendall’s τ as proposed by [22, 23].

• The AIC of each pair copula corresponding to the discussion in Sect. 2.4.1.

• The (negative) estimated degrees of freedom of Student’s t pair copulas (see [48]).

• The p-value of a copula goodness of fit test and variants as proposed by [21].

Some remarks: First, taking the empirical Kendall’s τ as weight does not require to select and estimate pair copulas prior to the tree selection step. The other three weights require this, so that lines 4–5 and 12–13 in Algorithm 2.3 may be redundant in this case. Second, AIC weights also maximize the AIC of the entire tree, since the individual AICs sum like the log-likelihood. Third, the strategy proposed by [48] concentrates on tail dependence, since the algorithm will select pairs with estimated small degrees of freedom corresponding to a stronger deviation from Gaussianity with no tail dependence.

Copula goodness of fit tests based on the Cramér–von Mises statistic are considered in [21] to take into account the uncertainty of the pair copula fit. Corresponding p-values are calculated using fast bootstrap methods based on the multiplier approach developed and implemented in [40–42].

Finally, we like to note that the empirical Kendall’s τ as weight also approximatively maximizes (2.5), since the log-likelihoods of bivariate copulas tend to increase with increasing absolute values of Kendall’s τ. It, however, does not lead to over-parameterization, since copula selection and tree selection in a particular tree are independent. The strategy by [23] has therefore already been used successfully in applications with up to 52 variables (see [12]).

Recently, [36] proposed the construction of vines with non-parametric pair copulas based on empirical copula estimators. For vine tree selection [36] also advocate the use of empirical dependence measures such as Spearman’s ρ, since it does not require any parametric assumption on the pair copulas. Other dependence measures such as Blomqvist’s β could of course be used instead in the approaches by [23, 36].

Especially the strategy based on Kendall’s τ leads to regular vine copulas with decreasing dependence in higher order trees. This is advantageous to the vine structure, since numerical errors may add up and estimates become less precise as the number of conditioning variables increases. This has been exploited by [14] to identify appropriate truncation levels of regular vine copulas.

Algorithm 2.3 can easily be modified to select C- or D-vines instead of general regular vines. For C-vines the root node in each tree can simply be identified as the node with maximal sum of weights to all other nodes (see [22]). In the case of D-vines only the order of variables in the first tree has to be chosen. Since D-vine trees are paths on all nodes, so-called Hamiltonian paths, a maximum Hamiltonian path has to be identified. This problem is equivalent to a traveling salesman problem as discussed by [11]. As an NP-hard problem, there is no known efficient algorithm to find a solution.

2.5.1.2 Bottom-Up Selection

Rather than beginning with the first tree T ₁, [43] proposed a bottom-up selection strategy which starts with tree T _n − 1 and then sequentially selects trees T _m for m = n − 2, …, 1. Similar to top-down selection using Kendall’s τ by [23], this approach is also motivated by choosing a regular vine with weaker dependence in later trees. Here, dependence is, however, measured in terms of partial correlations. More precisely, each tree is selected such that the sum of absolute partial correlations as edge weights is minimized. This is feasible, since partial correlation estimates for each combination of variables can be obtained from the data without any parametric assumptions (see, e.g., [67]).

The bottom-up strategy by [43] thus selects tree T _n − 1 as the edge corresponding to the pair of variable with lowest absolute partial correlation given all other variables. Kurowicka [43] then provides conditions such that the proximity condition is satisfied when a tree $T_{m},\ m \in \{ 1,\ldots ,n - 2\},$ is selected given trees T _m + 1, …, T _n − 1. As before there may be several choices possible in the set of eligible edges.

Example 2.4 (Bottom-Up Tree Selection). 

Assume in Fig. 2.1 that we have selected T ₄ with edge $e =\{ a,b\} =\{ 1,5\vert 2,3,4\}$ as shown. Then $A_{a} =\{ 1,2,3,4\}$ and $A_{b} =\{ 2,3,4,5\}$ [see (2.1)]. Any choice of edges from A _a and A _b in tree T ₃ leads to a valid tree T ₄. For instance, the edges $\{1,2\vert 3,4\}$ and $\{4,5\vert 2,3\}$ are compatible with A _a and A _b , respectively, and would lead to another vine than the one shown in Fig. 2.1. In fact, it could be constructed as a D-vine with order 1, 4, 3, 2, 5.

Since partial correlations are equal to conditional correlations for elliptical distributions (see [5]), this strategy is particularly appropriate if all pair copula families are elliptical. In contrast to the top-down approach discussed above which requires the selection and estimation of pair copulas in each tree, this strategy chooses the vine tree structure without any assumption on the pair copula families. Having selected the vine tree structure, the selection of pair copulas can therefore proceed as discussed in Sect. 2.4.1.

2.5.2 Sequential Bayesian Tree Selection

Bayesian approaches to estimating the posterior distribution of the tree structure of a regular vine copula have only recently been developed. The sheer number of possible regular vine tree structures poses a relevant challenge to computationally efficient posterior evaluation.

This section presents a reversible jump MCMC-based approach proposed by [29] to obtain a sequential estimate of the posterior distribution of the regular vine tree structure $\mathcal{V}$, the pair copula families $\mathcal{B}$, and the copula parameters ${\boldsymbol \theta }$. The term “sequential estimation” is understood analogously to the notion discussed in Sect. 2.5.1.1 as a tree-by-tree procedure.

As in Sect. 2.4.2, model priors $\pi (\boldsymbol {\mathcal{V}},\boldsymbol {\mathcal{B}},{\boldsymbol \theta })$ which favor sparse models can serve to guard against selecting models with runaway complexity. On the other hand, the use of non-informative flat priors allows for tree-by-tree maximum likelihood estimation of the regular vine tree structure $\mathcal{V}$, the pair copula families $\mathcal{B}$, and the copula parameters ${\boldsymbol \theta }$. As a result, the posterior mode estimate of this procedure will agree with the model estimate of Algorithm 2.3, if flat priors are used. Again, the pair copula families are chosen from a set $\boldsymbol {\mathrm{B}}$ of parametric pair copula families.

For the sake of notational convenience and enhanced readability, the procedure is presented in two algorithms. Algorithm 2.4 gives the general outline of the sampling procedure. Algorithm 2.5 details the reversible jump MCMC algorithm to sample from the posterior distribution of tree T _m of the regular vine tree structure $\boldsymbol {\mathcal{V}} = (T_{1},\ldots ,T_{n-1})$.

Algorithm 2.4 implements the tree-by-tree selection procedure. As such, it calls Algorithm 2.5 for the actual posterior estimation. However, it condenses the posterior sample into the posterior mode estimate and organizes the move from selecting tree T _m to selecting tree T _m + 1. The posterior mode estimate $(\hat{T}_{m},\hat{\mathcal{B}}_{T_{m}},\hat{{\boldsymbol \theta }}_{T_{m}})$ of tree T _m is the most frequently sampled combination of tree structure T _m and pair copula families $\mathcal{B}_{T_{m}}$ parameterized at the mode of the posterior sample of the parameters ${\boldsymbol \theta }_{T_{m}}$ of this model.

Algorithm 2.4 (Outline of the Tree-by-Tree Sampling Algorithm). 

1: Sample from the posterior distribution of the first tree, $(T_{1},\mathcal{B}_{T_{1}},{\boldsymbol \theta }_{T_{1}})$: see Algorithm 2.5.

2: Set the tree estimate $(\hat{T}_{1},\hat{\mathcal{B}}_{T_{1}},\hat{{\boldsymbol \theta }}_{T_{1}})$ to the posterior mode.

3: for m = 2,…,n − 1 do

4: Sample from the posterior distribution of the m-th tree, $(T_{m},\mathcal{B}_{T_{m}},{\boldsymbol \theta }_{T_{m}})$, given the previous trees’ estimates $(\hat{T}_{1},\hat{\mathcal{B}}_{T_{1}},\hat{{\boldsymbol \theta }}_{T_{1}}),\ldots ,(\hat{T}_{m-1},\hat{\mathcal{B}}_{T_{m-1}},\hat{{\boldsymbol \theta }}_{T_{m-1}})$: see Algorithm 2.5.

5: Set the tree estimate $(\hat{T}_{m},\hat{\mathcal{B}}_{T_{m}},\hat{{\boldsymbol \theta }}_{T_{m}})$ to the posterior mode.

6: end for

7: return  the sequential Bayesian model estimate

$$\displaystyle{(\hat{\mathcal{V}},\hat{\mathcal{B}},\hat{{\boldsymbol \theta }}) = ((\hat{T}_{1},\ldots ,\hat{T}_{n-1}),(\hat{\mathcal{B}}_{T_{1}},\ldots ,\hat{\mathcal{B}}_{T_{n-1}}),(\hat{{\boldsymbol \theta }}_{T_{1}},\ldots ,\hat{{\boldsymbol \theta }}_{T_{n-1}})).}$$

Algorithm 2.5 samples from the posterior distribution of $(T_{m},\boldsymbol {\mathcal{B}}_{T_{m}},{\boldsymbol \theta }_{T_{m}})$ given the previously selected trees $((\hat{T}_{l},\hat{\boldsymbol {\mathcal{B}}}_{T_{l}},\hat{{\boldsymbol \theta }}_{T_{l}}),l = 1,\ldots ,m - 1)$. The within-model move of this algorithm to update the pair copula parameters ${\boldsymbol \theta }$ follows Algorithm 2.1. In the between-models move, the proposal trees are sampled as spanning trees which satisfy the proximity condition. Practitioners may note that this functionality is implemented, e.g., in the C++ boost library [59]. Edge weights can be used to fine-tune the variance of the proposal distribution: in our implementation, higher values for p ∈ (0, 1) increase the probability that the proposals for the tree structure, $T_{m}^{r}$, are similar to the current state $T_{m}^{r-1}$ of the sampling chain. As in Algorithm 2.2, the pair copula family proposals are sampled from a uniform distribution over $\boldsymbol {\mathrm{B}}$, and the parameter proposals are drawn from a (multivariate) normal distribution centered at the maximum likelihood estimates of the parameters.

Algorithm 2.5 (Reversible Jump MCMC Algorithm to Sample $(T_{m},\boldsymbol {\mathcal{B}}_{T_{m}},{\boldsymbol \theta }_{T_{m}})$). 

Denote the pair copula families of tree $T_{m} = (N_{m},E_{m})$ by $\boldsymbol {\mathcal{B}}_{T_{m}} = (\mathcal{B}_{e},e \in E_{m})$ , and the corresponding pair copula parameters by ${\boldsymbol \theta }_{T_{m}} = ({\boldsymbol \theta }_{e},e \in E_{m})$ .

1: Choose arbitrary, but valid, tree structure, copula family and parameter starting values $(T_{m}^{0},\boldsymbol {\mathcal{B}}_{T_{m}}^{0},{\boldsymbol \theta }_{T_{m}}^{0})$. If m ≥ 2, observe the proximity condition imposed on $T_{m}^{0}$.

2: for each iteration r = 1,…,R do

3: Set $(T_{m}^{r},\mathcal{B}_{T_{m}}^{r},{\boldsymbol \theta }_{T_{m}}^{r}) = (T_{m}^{r-1},\mathcal{B}_{T_{m}}^{r-1},{\boldsymbol \theta }_{T_{m}}^{r-1})$.

4: Perform one update step of Algorithm 2.1 for the pair copula parameters of tree T_m, ${\boldsymbol \theta }_{T_{m}}^{r}$; denote the updated parameter entries by ${\boldsymbol \theta }_{T_{m}}^{+}$.

5: Draw a spanning tree $T_{m}^{r}$ that satisfies the proximity condition from the proposal distribution

$$\displaystyle{ q(T_{m}^{r-1} = (N_{ m},E_{m}^{r-1}) \rightarrow T_{ m}^{r} = (N_{ m},E_{m}^{r})) \propto {p}^{\vert E_{m}^{r}\cap E_{ m}^{r-1}\vert }{(1-p)}^{\vert E_{m}^{r}\setminus E_{ m}^{r-1}\vert }. }$$

6: for each edge $e \in E_{m}^{r}$ do

7: Draw $\mathcal{B}_{e}^{r}$ from a $\mathit{Unif }(\boldsymbol {\mathrm{B}})$ distribution.

8: Draw ${\boldsymbol \theta }_{e}^{r}$ from a multivariate $N(\hat{{\boldsymbol \theta }}_{e}^{r},\hat{\Sigma }_{e}^{r})$ distribution with probability density function $\phi _{(\hat{{\boldsymbol \theta }}_{e}^{r},\hat{\Sigma }_{e}^{r})}(\cdot )$. Here $\hat{{\boldsymbol \theta }}_{e}^{r}$ denotes the MLE of the copula parameters of the pair copula $\mathcal{B}_{e}^{r}$ and $\hat{\Sigma }_{e}^{r}$ denotes the estimated approximative covariance matrix of the parameter estimates $\hat{{\boldsymbol \theta }}_{e}^{r}$.

9: end for

10: Set $\boldsymbol {\mathcal{B}}_{T_{m}}^{r} = (\mathcal{B}_{e}^{r},e \in E_{m}^{r})$, ${\boldsymbol \theta }_{T_{m}}^{r} = ({\boldsymbol \theta }_{e}^{r},e \in E_{m}^{r})$.

11: Evaluate the generalized Metropolis–Hastings acceptance probability of the proposal

$$\displaystyle\begin{array}{rcl} \alpha & :=& \alpha ((T_{m}^{r-1},\mathcal{B}_{ T_{m}}^{r-1},{\boldsymbol \theta }_{ T_{m}}^{+}),(T_{ m}^{r},\mathcal{B}_{ T_{m}}^{r},{\boldsymbol \theta }_{ T_{m}}^{r})) {}\\ & =& \frac{p({\mathcal{V}}^{{\ast}},{\boldsymbol {\mathcal{B}}}^{{\ast}}{,{\boldsymbol \theta }}^{{\ast}})} {p(\mathcal{V},\boldsymbol {\mathcal{B}},{\boldsymbol \theta })} \cdot \frac{\prod _{e\in E_{m}^{r-1}}\phi _{(\hat{{\boldsymbol \theta }}_{e}^{r-1},\hat{\Sigma }_{e}^{r-1})}({\boldsymbol \theta }_{e}^{+})} {\prod _{e\in E_{m}^{r}}\phi _{(\hat{{\boldsymbol \theta }}_{e}^{r},\hat{\Sigma }_{e}^{r})}({\boldsymbol \theta }_{e}^{r})} {}\\ & =& \frac{\pi ({\mathcal{V}}^{{\ast}},{\boldsymbol {\mathcal{B}}}^{{\ast}}{,{\boldsymbol \theta }}^{{\ast}})} {\pi (\mathcal{V},\boldsymbol {\mathcal{B}},{\boldsymbol \theta })} \cdot \frac{L({\mathcal{V}}^{{\ast}},{\boldsymbol {\mathcal{B}}}^{{\ast}}{,{\boldsymbol \theta }}^{{\ast}}\vert \boldsymbol {\mathrm{x}})} {L(\mathcal{V},\boldsymbol {\mathcal{B}},{\boldsymbol \theta }\vert \boldsymbol {\mathrm{x}})} \cdot \frac{\prod _{e\in E_{m}^{r-1}}\phi _{(\hat{{\boldsymbol \theta }}_{e}^{r-1},\hat{\Sigma }_{e}^{r-1})}({\boldsymbol \theta }_{e}^{+})} {\prod _{e\in E_{m}^{r}}\phi _{(\hat{{\boldsymbol \theta }}_{e}^{r},\hat{\Sigma }_{e}^{r})}({\boldsymbol \theta }_{e}^{r})} , {}\\ \end{array}$$

where ${\mathcal{V}}^{{\ast}} = (\hat{T}_{1},\ldots ,\hat{T}_{m-1},T_{m}^{r})$, $\mathcal{V} = (\hat{T}_{1},\ldots ,\hat{T}_{m-1},T_{m}^{r-1})$, ${\boldsymbol {\mathcal{B}}}^{{\ast}} = (\hat{\boldsymbol {\mathcal{B}}}_{T_{1}},\ldots ,\hat{\boldsymbol {\mathcal{B}}}_{T_{m-1}},\boldsymbol {\mathcal{B}}_{T_{m}}^{r})$, $\boldsymbol {\mathcal{B}} = (\hat{\boldsymbol {\mathcal{B}}}_{T_{1}},\ldots ,\hat{\boldsymbol {\mathcal{B}}}_{T_{m-1}},\boldsymbol {\mathcal{B}}_{T_{m}}^{r-1})$, ${{\boldsymbol \theta }}^{{\ast}} = (\hat{{\boldsymbol \theta }}_{T_{1}},\ldots ,\hat{{\boldsymbol \theta }}_{T_{m-1}},{\boldsymbol \theta }_{T_{m}}^{r})$, and ${\boldsymbol \theta }= (\hat{{\boldsymbol \theta }}_{T_{1}},\ldots ,\hat{{\boldsymbol \theta }}_{T_{m-1}},{\boldsymbol \theta }_{T_{m}}^{+})$.

12: Accept the proposal $(T_{m}^{r},\boldsymbol {\mathcal{B}}_{T_{m}}^{r},{\boldsymbol \theta }_{T_{m}}^{r})$ with probability α; if rejected, set $(T_{m}^{r},\boldsymbol {\mathcal{B}}_{T_{m}}^{r},{\boldsymbol \theta }_{T_{m}}^{r}) = (T_{m}^{r-1},\boldsymbol {\mathcal{B}}_{T_{m}}^{r-1},{\boldsymbol \theta }_{T_{m}}^{+})$.

13: end for

14: return  $((T_{m}^{1},\boldsymbol {\mathcal{B}}_{T_{m}}^{1},{\boldsymbol \theta }_{T_{m}}^{1}),\ldots ,(T_{m}^{R},\boldsymbol {\mathcal{B}}_{T_{m}}^{R},{\boldsymbol \theta }_{T_{m}}^{R}))$

2.6 Conclusions and Outlook

We have focused on the various model selection and estimation methods for regular vine copulas. Since a regular vine model is specified by three linked components, this results in three fundamental tasks with increasing complexity. We discussed frequentist and Bayesian approaches for each of these tasks. In particular this involved sequential approaches starting from the top tree until the last tree. The frequentist approaches are implemented in the R-packages CDVine [15, 57] for D- and C-vines and VineCopula [58] for regular vines, respectively.

In view of the linked nature of the vine tree structure the sequential approach is a natural approach. However as in the case of covariate selection in linear models, this might not yield the best fit to the data. In addition the approaches so far primarily considered in-sample fit and model comparisons. More empirical work is needed to validate the models in an out-of-sample performance study. However this is now feasible and tractable and is the subject of current investigations.

It has been recently recognized by [2] that even the flexible class of simplified regular vines might be insufficient for some data sets. This might be the result that the underlying joint density is not well approximated by a simplified regular vine density, where the conditional copula family terms are chosen to be independent of the conditioning value. Currently the proposed solution of [2] using non-parametric two-dimensional smoothing methods is limited to three dimensions and it will be a major challenge to extend the model and the selection methods to higher dimensions.

Other non-standard vine models occur when the pair copula terms depend on the conditioning time point, thus yielding models with time-varying copula parameters. These can also be seen as non-simplified vines in the special case that the conditioning variables follow a functional relationship to time. First parameter-driven time dependence was considered using an AR(1) dynamics in the copula parameters in the papers by [3, 4], while [62] follow a regime switching approach. Here only parameter estimation and assessment of the uncertainty of the parameters are considered so far. It has to be investigated if the additional flexibility of the copula families and the different vine tree structures is needed here.

This survey primarily focused on the selection and estimation problem of regular vines with parametric pair copula families. The approach of [36] can be compared to ones based on kernel methods as proposed in [7, 56].

Other data structures than multivariate continuous data have also gained by models based on pair copula constructions. In particular network structures were considered by [30, 44] in a primarily Gaussian setup and by [7] in a non-Gaussian setting. Here the network is modeled by a directed acyclic graph (DAG) model. While learning the network structure from data is a very complex task even in Gaussian DAG models, non-Gaussian learning algorithms are currently developed and investigated in [6].

Another very interesting multivariate data structure are discrete and mixed discrete-continuous outcomes which occur most often in the life sciences. Pair copula constructions using D-vines for discrete outcomes were recently developed in [55] together with highly efficient parameter estimation techniques. Current research is conducted to allow for mixed outcomes [63].

While these extensions are still concerned primarily with parameter estimation, it remains an important open challenge to find non-sequential solutions to the selection of regular vines when all three components have to be selected.