The Relationship Between Graphical Representations of Regular Vine Copulas and Polytrees

Abstract

Graphical models (GMs) are powerful statistical tools for modeling the (in)dependencies among random variables. In this paper, we focus on two different types of graphical models: R-vines and polytrees. Regarding the graphical representation of these models, the former uses a sequence of undirected trees with edges representing pairwise dependencies, whereas the latter uses a directed graph without cycles to encode independence relationships among the variables. The research problem we deal with is whether it is possible to build an R-vine that represents the largest number of independencies found in a polytree and vice versa. Two algorithms are proposed to solve this problem. One algorithm is used to induce an R-vine that represents in each tree the largest number of graphical independencies existing in a polytree. The other one builds a polytree that represents all the independencies found in the R-vine. Through simple examples, both procedures are illustrated.

1 Introduction

Graphical models (GMs) [7, 13] have been widely used for modeling the dependence structure of multivariate probability distributions through two closely related components: (i) The qualitative component is a graph where nodes correspond to random variables and edges to graphical relationships among them; (ii) The quantitative component is given by a set of local probability distributions that quantify the strength and uncertainty of the (in)dependencies encoded in the graph (or network). According to the type of the graph, directed and undirected, we can distinguish two different GMs: Bayesian networks (BNs) and Markov networks respectively. The interpretation of graphical (in)dependencies is different in directed and undirected graphs.

In this paper, we focus on two GMs representative of undirected and directed graphs, namely regular vine copulas [4, 12] (or simply R-vines) and a subclass of BNs called polytrees [8] respectively.

A copula is a probability distribution function with uniformly distributed margins [14, 17]. Copulas allow us to model the dependence structure of multivariate distributions and its margins separately. Despite the generality of the copula-based framework, it turns out that building high-dimensional joint copulas is a difficult problem [1].

Pair copula constructions (PCCs) [11] and their graphical model, called regular vines (R-vines) [3, 4], overcome the lack of flexibility of the copula-based modeling in the high-dimensional case. R-vines build multivariate copulas in terms of bivariate copulas (pair-copulas) taking advantage of the fact that the bivariate copulas are more tractable than multidimensional ones. Besides that, bivariate copulas of different families, can be combined in the same decomposition allowing the specification of different types of non-linear dependencies. The qualitative component of R-vines is specified by an R-vine structure (or graph) – a set of nested trees, where the variables are represented by nodes linked by edges, each associated with a pair-copula that captures certain types of pairwise dependence. It is in this sense that we say that R-vine structures encode dependence relationships rather than independencies relationships.

Polytrees (also known as singly connected networks) are directed acyclic graphs (DAGs) where there is no more than one undirected path that connects any two nodes (without undirected cycles). In these graphs, missing edges can represent either conditional independencies or conditional dependencies among random variables.

In general, Bayesian networks, particularly polytrees, have well-studied mathematical properties that have been developed throughout decades. In contrast, R-vines have boomed in the last few years. Previous works have addressed the question of the relationship between directed GMs and R-vines from different perspectives. In [9], a new method for learning the structure of a BN based on PCCs is introduced. In [10], a non-parametric Bayesian belief net as an alternative to a particular subclass of R-vines is introduced. The paper discusses the differences between both models and offers some guidelines on when to use one or the other from a quantitative perspective. In [2], a Bayesian network with pair-copulas is built using PCCs.

However, the problem of verifying whether the graphical independencies found in a polytree can be represented in an R-vine and vice versa has not been answered yet. In this work, we investigate the relationship between the graphical representations of R-vines and polytrees in both directions: (i) Given the graph of a polytree, we want to obtain an R-vine tree-structure that represents the largest number of independencies existing in the starting graph. To this end, a heuristic is proposed that, from the list of independences found in the polytree, performs this task locally, tree-by-tree of the R-vine. (ii) Given an R-vine, we want to build a polytree that represents the largest number of independences existing in the R-vine. Similarly, a heuristic is proposed that, based on the independence list extracted from the R-vine, builds a polytree that represents the independencies existing in the R-vine. These results are useful as they make it clear that properties and algorithms that can be applied to polytrees can be carried over to R-vines, and vice versa.

The paper is organized as follows: In Sects. 2 and 3, we provide the basic concepts as well as a short review of R-vines and polytrees respectively. In Sect. 4, we present the main contribution of this work: two algorithms that induce the graph of a R-vine from the graph of a polytree and vice versa. Section 5 offers a short summary and an outline of future work.

2 Regular Vines

Let $\mathbf {X}=\left( X_{1},\ldots ,X_{n}\right)$ be an n-dimensional random vector with joint density function $f:\mathbb {R}^{n}\rightarrow [0,\infty )$ and cumulative distribution function $F:\mathbb {R}^{n}\rightarrow \left[ 0,1\right]$. Furthermore, let $F_{i}:\mathbb {R}\rightarrow \left[ 0,1\right]$, $i=1,\ldots ,n$ be the corresponding marginal distributions of $X_{i}$¹. Capital letters denote variables and lower letters are their assignments.

A n-dimensional copula C is a multivariate probability distribution function for which the univariate margins are uniform: $C:\left[ 0,1\right] ^{n}\rightarrow \left[ 0,1\right]$ [14]. Copulas are used to describe the dependence structure among random variables.

The relevance of copulas in probabilistic modeling is given by Sklar’s theorem [17], which states that an n-dimensional (multivariate) distribution function F of a random continuous vector $\mathbf {X}=\left( X_{1},\ldots ,X_{n}\right) \in \mathbb {R}^{n}$ can be expressed in terms of its marginal distributions $F_{i}\left( x_{i}\right)$ and a unique copula C. Sklar’s theorem for densities is given by

$$\begin{aligned} f\left( x_{1},\ldots ,x_{n}\right) =c\left( F_{1}\left( x_{1}\right) ,\ldots ,F_{n}\left( x_{n}\right) \right) \cdot \prod _{i=1}^{n}f_{i}\left( x_{i}\right) \end{aligned}$$

(1)

where f and c denote the density functions corresponding to F and C respectively.

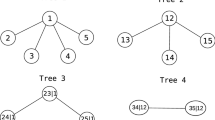
In (1), the copula c can be approximated by an PCC. This decomposition is represented graphically by an R-vine – a sequence of trees, of which each edge corresponds to a pair-copula. An R-vine is a probabilistic graphical model represented as a pair $\left( G,\mathbf {\theta }\right)$. G is the structural part that is composed of a sequence of trees $T_{1},T_{2,}\ldots ,T_{n-1}$, where the nodes of $T_{j}$ are edges in $T_{j-1}.$ Two nodes in $T_{j}$ (for $j\ge 2$) can only be adjacent if the corresponding edges in the previous tree have a common node (known as proximity condition) [2]. $\mathbf {\mathbf {\theta }}$ contains, for each edge of the trees, a pair-copula and its parameters. The number of edges in an R-vine is $n\left( n-1\right) /2$. Figure 1-(right panel) illustrates an R-vine copula $c_{_{12345}}$ for $n=5$ and its respective factorization.

We define an R-vine formally by following the definition given in [5]: If we denote $T_{j}=\left( N_{j},E_{j}\right)$, the tree of the decomposition at level j, where $N_{j}$ and $E_{j}$ denote the node and edge sets of the $j^{th}$ tree, the edge $e\in E_{j}$ joins two vertices of $N_{j}$, $X_{k\left( e\right) }$ and $X_{l\left( e\right) }$, which are determined by the set of indices $k\left( e\right)$ and $l\left( e\right)$ respectively. Then, in the pair-copula $c_{k\left( e\right) ,l\left( e\right) \mid D\left( e\right) },$ the nodes $X_{k\left( e\right) }$ and $X_{l\left( e\right) }$ are the conditioned nodes, whereas $\mathbf {X}_{D\left( e\right) }$, which represents a subvector of $\mathbf {X}$ determined by the indices in $D\left( e\right)$, is the conditioning set. Consequently, a regular vine distribution is the distribution of the random vector $\mathbf {X}=\left( X_{1},\ldots ,X_{n}\right)$ with marginal densities $f_{i}\left( x_{i}\right)$, $i=1,\ldots ,n$, and where the conditional density of $\left( X_{k\left( e\right) },X_{l\left( e\right) }\right)$ given $\mathbf {X}_{D\left( e\right) }$ is specified as $c_{k\left( e\right) ,l\left( e\right) |D\left( e\right) }$ for the R-vine copula with $n-1$ trees, set of nodes $\mathcal {\mathbf {N}}=\left\{ N_{1},\ldots N_{n-1}\right\}$ and set of edges $\mathcal {\mathbf {E}}=\left\{ E_{1},\ldots E_{n-1}\right\}$. If the dependence structure of $\mathbf {X}$ is represented by an R-vine copula, then the n-dimensional density $f_{\mathbf {R-vine}}\left( x_{1},\ldots ,x_{n}\right)$ is given by

$$\begin{aligned} \underset{\text {R-vine copula}}{\underbrace{\underset{j=1}{\prod ^{n-1}}\underset{e\in E_{j}}{\prod }c_{k\left( e\right) ,l\left( e\right) \mid D\left( e\right) }\left( F\left( x_{k\left( e\right) }\mid \mathbf {x}_{D\left( e\right) }\right) ,F\left( x_{l\left( e\right) }\mid \mathbf {x}_{D\left( e\right) }\right) \right) }}\cdot \underset{\text {Margins}}{\underbrace{\underset{i=1}{\prod ^{n}}f_{i}\left( x_{i}\right) }} \end{aligned}$$

(2)

In the approximation given in (2), only in the first tree are the pair-copulas unconditional as their arguments are marginal distributions. In the remaining trees, the pair-copulas are conditional as their arguments are conditional distributions. The number of variables in the conditioning set increases in one variable as we go deeper into the R-vine tree-structure: in the second tree, we have first-order conditional copulas; in the third tree, second-order conditional copulas, and so on; that is, in the tree j we have conditional copulas of the order $j-1$.

Fig. 1.

Example of a polytree (left panel) and an R-vine (right panel) where $n=5$. The polytree factorization is given as $p\left( x_{1}\right) \cdot p\left( x_{5}\right) \cdot p\left( x_{3}\mid x_{1},x_{5}\right) \cdot p\left( x_{2}\mid x_{3}\right) \cdot p\left( x_{4}\mid x_{3}\right)$. The R-vine factorization is given as $\underset{T_{1}}{\underbrace{c_{12}\cdot c_{23}\cdot c_{34}\cdot c_{45}}}\cdot \underset{T_{2}}{\underbrace{c_{13\mid 2}\cdot c_{24\mid 3}\cdot c_{25\mid 3}}}\cdot \underset{T_{3}}{\underbrace{c_{15\mid 23}\cdot c_{14\mid 23}}}\cdot \underset{T_{4}}{\underbrace{c_{45\mid 123}.}}$

2.1 Graphical (In)Dependence in R-vines

We define two types of edges (or links): dashed edges indicate linked nodes are independent and continuous edges indicate linked nodes are dependent with each other.

To provide the R-vine tree-structure with a semantic interpretation in terms of independencies, we define the vine-graphical independence criterion as follows.

Definition 1

(r-separation). Let $X_{k\left( e\right) }$, $X_{l\left( e\right) }$, $\mathbf {X}_{D\left( e\right) }$ three disjoint subsets in and R-vine. We say that $\mathbf {X}_{D\left( e\right) }$ r-separates $X_{k\left( e\right) }$ from $X_{l\left( e\right) }$ if there is a dashed edge in some tree that joins two vertices, on of them is associated with the vertices in $X_{k\left( e\right) }$ the other to the vertices in $X_{l\left( e\right) }$, and $\mathbf {X}_{D\left( e\right) }$ r-separates nodes $X_{k\left( e\right) }$ and $X_{l\left( e\right) }$.

When $\mathbf {X}_{D\left( e\right) }$ v-separates $X_{k\left( e\right) }$ and $X_{l\left( e\right) }$ in G, we write $I\left( X_{k\left( e\right) },X_{l\left( e\right) }\mid \right.$ $\left. X_{D\left( e\right) }\right) _{G}$ to indicate that this graphical conditional independence relationship is represented in the graph G. We write $D\left( X_{k\left( e\right) },X_{l\left( e\right) }\mid X_{D\left( e\right) }\right) _{G}$ to indicate that $X_{k\left( e\right) }$ and $X_{l\left( e\right) }$ are conditionally dependent given $\mathbf {X}_{D\left( e\right) }$ in the graph G.

3 Polytrees

3.1 Directed Graphs

Let $G=\left( \mathbf {X},\mathbf {E}\right)$ be a directed acyclic graph (DAG), consisting of the node set $\mathbf {X}$ and the edge set $\mathbf {E}$. Directed graphs only contain directed edges. A directed edge from node X to node Y is represented as $X\rightarrow Y$. A path from $X=X_{1}$ to $Y=X_{d}$ is a sequence of nodes $X_{1},\ldots ,X_{d}$ connected by edges in the graph G, where the edge $\left( X_{i},X_{i+1}\right) \in \mathbf {E}$, $i=1,\ldots ,d-1$. A cycle is a path where $X=Y$. We say that X is an ancestor of Y if we can find a path that, starting from X, reaches the node Y, such that $X\rightarrow ...\rightarrow Y$; correspondingly, Y is a descendant of X. An undirected path is a path in which the directions of the edges are not considered. The skeleton of G is the undirected graph obtained by eliminating the directions of edges from G. A head-to-head (h-h) connection is a subgraph $X\rightarrow Z\leftarrow Y$ in which Z is a h-h node (i.e., a node with convergent edges). A comprehensive introduction to graph theory and graphical models is found in [6].

3.2 Graphical (In)Dependence in DAGs

The concept of d-separation [15] is the graphical independence criterion that provides the DAG a semantic interpretation, allowing it to determine the independence relationships encoded by the topology of the network.

Definition 2

(d-separation). If $\mathbf {X}$, $\mathbf {Y}$ and $\mathbf {Z}$ are three disjoint subsets of nodes in a DAG G, then $\mathbf {Z}$ d-separates $\mathbf {X}$ from $\mathbf {Y}$ or, similarly, $\mathbf {X}$ and $\mathbf {Y}$ are graphically independent given $\mathbf {Z}$ if and only if along any undirected path between any node of $\mathbf {X}$ and any node of $\mathbf {Y}$ there is an intermediate node A such that (i) eitherA is a head-to-head node in the path and neither A nor its descendants are in $\mathbf {Z}$, or (ii) A is not a head-to-head node in the path and it is in $\mathbf {Z}$.

When $\mathbf {Z}$ d-separates $\mathbf {X}$ and $\mathbf {Y}$ in G, we write $I\left( \mathbf {X},\mathbf {Y}\mid \mathbf {Z}\right) _{G}$ to indicate that the independence relationship is given by the graph G. We write $D\left( \mathbf {X},\mathbf {Y}\mid \mathbf {Z}\right) _{G}$ to indicate that $\mathbf {X}$ and $\mathbf {Y}$ are conditionally dependent given $\mathbf {Z}$ in the graph G.

3.3 Dependence Models

Necessary definitions on dependence models are taken from [6]. The terms of the dependence and the independence models refer exclusively to the qualitative structure of the relationships existing in a set of variables. These models allow us to check which sets of variables are unconditionally or conditionally dependent or independent.

Definition 3

(Dependence Model). A model M of the variable set $\left\{ X_{1},\ldots ,X_{n}\right\}$ is called a dependence model if it allows to determine whether $I\left( \mathbf {X},\mathbf {Y}\mid \mathbf {Z}\right) _{M}$ is true for all the possible triples of subsets $\varvec{X}$, $\varvec{Y}$ and $\varvec{Z}$.

Two possible correspondences between a graphical representation G and a dependence model M are I-map and D-map.

Definition 4

(I-map). The graph G is an I-map of the dependence model M if $I\left( \mathbf {X},\mathbf {Y}\mid \mathbf {Z}\right) _{G}\Rightarrow I\left( \mathbf {X},\mathbf {Y}\mid \mathbf {Z}\right) _{M}$, i.e., if all independence relationships derived from G are verified in M.

Definition 5

(D-map). The graph G is a D-map of the dependence model M if $D\left( \mathbf {X},\mathbf {Y}\mid \mathbf {Z}\right) _{G}\Rightarrow D\left( \mathbf {X},\mathbf {Y}\mid \mathbf {Z}\right) _{M}$, i.e., if all dependence relationships derived from G are verified in M.

An I-map G of M includes some of the independence relationships of M, but not necessarily all of them. An I-map guarantees that the d-separated nodes correspond to independent variables in M, but does not guarantee that connected nodes correspond to dependent variables in M. On the other hand, a D-map G of M includes some of the dependence relationships of M, but not necessarily all of them. A D-map guarantees that connected nodes correspond to dependent variables in M, but does not guarantee that the d-separated nodes correspond to independent variables in M. Empty graphs (the set of edges is empty) and complete graphs (there is an edge between each pair of nodes) are called trivial D-maps and I-maps respectively.

3.4 Polytrees

Bayesian networks (BNs) are GMs based on DAGs. A BN is a pair $(G(\mathbf {X},\mathbf {E}),P)$, where G is a DAG, $\mathbf {X}$ and $\mathbf {E}$ are the set of variables (or nodes) and the set of directed edges in G respectively, and $P=\left\{ P\left( X_{1}\mid \mathbf {Pa}_{1}\right) ,\cdots ,P\left( X_{n}\mid \mathbf {Pa}_{n}\right) \right\}$ is a set of n conditional probability distribution functions (one for each variable) where $\mathbf {Pa}_{i}$ is the set of parents of $X_{i}$ in G. The set P defines a probability function given by

$$\begin{aligned} P\left( \mathbf {X}\right) =\prod _{i=1}^{n}P\left( X_{i}\mid \mathbf {Pa}_{i}\right) \end{aligned}$$

(3)

A particular subclass of BNs are polytrees (of course, (3) also applies to polytrees). In these networks, there is no more than one undirected path that connects any two nodes. Particular types of polytrees include chains: each node has at most one parent and/or only one child, and trees: each node has only one parent. The number of edges in a polytree is $n-1$. Figure 1-(left panel) shows a polytree where $n=5$ and its respective factorization.

4 The Graphical Relationship Between R-vines and Polytrees

This section proposes two methods that induce the graph of an R-vine from the graph of the polytree and vice versa, so that the resulting graph represents the largest number of independencies existing in the other graph.

4.1 From Polytrees to R-vines

We want to obtain an R-vine $G_{R-vine}$ that represents the largest number of independencies found in the polytree $G_{P}$. For this purpose, we propose Algorithm 1. To simplify the notation used in Definition 1, we use $X=X_{k\left( e\right) }$, $Y=X_{l\left( e\right) }$, and $\mathbf {V}=\mathbf {X}_{D\left( e\right) }$. Moreover, $\left| \mathbf {V}\right| =j-1$ denotes the cardinality of $\mathbf {V}$, and conditioning sets with cardinality $\left| \mathbf {V}\right|$ belong to the tree at the level $j=\left| \mathbf {V}\right| +1$.

We consider a dependence model M that contains the list of independencies and dependencies represented in the polytree $G_{P}$, $L_{I}$ and $L_{D}$ respectively. These lists are obtained via the d-separation criterion in Step 1. The elements of these lists have the form $I\left( X,Y\mid \mathbf {V}\right)$ and $D\left( X,Y\mid \mathbf {V}\right)$ respectively. Both lists are arranged in ascending order according to $\left| \mathbf {V}\right|$.

In Step 2, we obtain the first tree of $G_{R-vine}$, which is nothing more than the skeleton of the polytree. Notice that $T_{1}$ and the skeleton of the polytree have the same edge set, so that both structures represents the same set of unconditional dependencies.

In Steps 3 and 4, the next trees of $G_{R-vine}$ are built inside a for-loop that runs over the levels $j=2,\ldots ,n-1$. These trees are maximum weighted spanning trees (MWSTs) [16] that satisfy the R-vine properties. As the edge’s weight we use zero for continuous edges and one for dashed edges respectively. Afterward, each relation in $L_{D}$ of order $j-1$ suggests an edge, which is inserted in the graph if the following two conditions are satisfied: (i) the edge to be inserted does not introduce undirected cycles, which ensures that the resulting R-vine remains singly connected; (ii) the proximity condition holds. If both conditions are met, the boolean function $\varphi \left( T_{j},D_{i}\left( X,Y\mid \mathbf {V}\right) \right)$ is true.

Note that not all independencies found in the polytree can be represented in the R-vine, but those inserted exist in the polytree. On the other hand, we have that all the independence relationships represented in the R-vine exist in the polytree and we denote it as $I\left( G_{\text {R-vine}}\right) \subseteq I\left( G_{\text {P}}\right)$, thus the R-vine is an I-map of the dependence model M obtained from the polytree.

It is worth noting that if the R-vine is a D-vine – a subclass of R-vines where the trees have chain structure – we do not need to select MWSTs since the first tree determines completely the structure of the next trees [1]).

Example 1

Let us illustrate Algorithm 1 based on the polytree of Fig. 2-(left-panel).  

Step 1. :

Obtain $M=\left\{ L_{I},L_{D}\right\}$ from $G_{P}$.

$$\begin{aligned} L_{I}&=\left\{ I_{1}\left( 2,4\mid 3\right) ,I_{2}\left( 1,4\mid 3\right) ,I_{3}\left( 1,3\mid 4\right) ,I_{4}\left( 1,4\mid 2,3\right) \right\} \\ L_{D}&=\left\{ D_{1}\left( 1,3\mid 2\right) ,D_{2}\left( 1,4\mid 2\right) ,D_{3}\left( 1,2\mid 3,4\right) ,D_{4}\left( 1,3\mid 2,4\right) ,D_{5}\left( 2,3\mid 1,4\right) \right\} \end{aligned}$$

Step 2. :

From $T_{1}$ (Fig. 2-(right panel)) we obtain the connected nodes: $1-2,\,2-3,$ $3-4$.

Step 3. :

As $T_{1}$ is a chain (as in D-vines) we do not need to built an MWST at each level, but only determine if the edges are dashed or continuous. Next we pass to $T_{2}$, and from $L_{I}$ we see that $I_{1}\left( 2,4\mid 3\right)$ may be represented with the dashed edge $23\text {-}{\cdot }\text {-}34$. However, the dashed edges $13\text {-}{\cdot }\text {-}34$ and $14\text {-}{\cdot }\text {-}34$ corresponding to the relationships $I_{2}\left( 1,4\mid 3\right)$ and $I_{3}\left( 1,3\mid 4\right)$, respectively, cannot be inserted in $T_{2}$ since the nodes 13 and 14 do not belong to the node set of this tree, which are: 12, 23,  and 34.

Step 4. :

$D_{1}\left( 1,3\mid 2\right)$ can be represented by the continuous edge $12-23$ in $T_{2}$ without violating the graphical constraints that should hold an R-vine, which implies that $\varphi \left( T_{2},D_{1}\left( 1,3\mid 2\right) \right)$ is true.

Step 5. :

To build $T_{3}$, only $I_{4}$ has to be inserted. This can be done by means of the dashed edge $14\mid 2\text {-}{\cdot }\text {-}24\mid 3$.

 

Notice that the independence relationships represented in this R-vine structure, namely: $\left[ I_{1}\left( 2,4\mid 3\right) , I_{2}\left( 1,4\mid 2,3\right) \right]$, exist in $G_{\text {P}}$, thus this R-vine is an I-map of the dependence model obtained from the polytree. This way of building the structure of R-vines guarantees that only graphical independencies found in the polytree are inserted in the corresponding R-vine tree. Consequently, all the independencies represented in the R-vine are true in the polytree.

Fig. 2.

Illustration of Example 1: (left panel) polytree $G_{P}$; (right panel) the resulting R-vine $G_{R-vine}$.

4.2 From R-vines to Polytrees

Similarly to previous section, the idea of this section is to build a polytree $G_{P}$ that represents the largest numbers of independencies found in an R-vine $G_{R-vine}$. The heuristic proposed is shown in Algorithm 2.

We consider a denpendence model M that contains the list of independencies and dependencies represented in the R-vine $G_{R-vine}$, $L_{I}$ and $L_{D}$ respectively. Step 1 consists of extracting both lists: $L_{I}$ is represented by dashed lines and $L_{D}$ is represented by continuous lines via the v-separation criterion. In Step 2, we obtain the skeleton of $G_{P}$ that is no other than tree $T_{1}$ of $G_{R-vine}$. To extract $L_{I}$ and $L_{D}$, we can use the procedure given in [6]

Steps 3 and 4 are responsible for determining the direction of the edges of the polytree skeleton. Firstly, the algorithm goes through the list $L_{I}$ in order to insert the independence relationships. In Step 3, for each $I\left( X,Y\mid \mathbf {V}\right)$ the edges of the corresponding subgraph $X-\mathbf {V}-Y$ are oriented preventing any node of $\mathbf {V}$ from being a h-h. In Step 4, the algorithm goes through the list $L_{D}$ in order to insert those dependencies that do not eliminate any independencies previously represented. So, for each $D\left( X,Y\mid \mathbf {V}\right)$ the algorithm allows a node belonging to $\mathbf {V}$ to be a h-h if the independencies already inserted are still represented; otherwise, edges are not oriented towards any node of $\mathbf {V}$.

Notice that a complete R-vine structure (all its edges are continuous) is a trivial I-map of the dependence model obtained from the polytree. In the opposite case, if all the R-vine’s edges are discontinuous or continuous in the first tree, it is a trivial D-map of the dependence model obtained from polytree.

Example 2

Let us illustrate Algorithm 2 based on the R-vine of Fig. 3-(left panel).  

Step 1. :

Obtain $M=\left\{ L_{I},L_{D}\right\}$ from $G_{R-vine}$.

$L_{I}=\{I_{1}\left( 1,3\mid 2\right) \}$

$L_{D}=\{D_{1}\left( 2,4\mid 3\right) ,D_{2}\left( 1,4\mid 2,3\right) \}$

Step 2. :

The skeleton of $G_{P}$ is the tree $T_{1}$ of $G_{R-vine}$.

Step 3. :

By representing the independence $I_{1}$, the graphs of Fig. 3-(right panel, top) are obtained.

Step 4. :

To represent $D_{1}\left( 2,4\mid 3\right)$, the node 3 must be considered a head-to-head node. This is done by adding the directed edge $4\rightarrow 3$. This can be done without adding or removing independencies. However, the relationship $D_{2}$ cannot be represented since it can only be inserted as an independence in the polytree. Therefore, the final graph remains as shown in Fig. 3-(right panel, middle).

 

The resulting polytree, in addition to representing the same independence relationships existing in the R-vine structure, also includes others that are not verified in M (obtained from a polytree). As the independencies of the R-vine are a subset of those of the polytree, we can say that the R-vine is an I-map of M obtained from a polytree, and that the polytree is a D-map of M obtained from an R-vine as all the dependence relationships of the polytree exist in the R-vine. Notice that from the same R-vine, more that one polytree can be obtained, which is illustrated in Fig. 3-(right panel, bottom).

Example 3

Let us illustrate Algorithm 2 based on the R-vine of Fig. 4-(left panel).  

Step 1. :

Obtain $M=\left\{ L_{I},L_{D}\right\}$ from $G_{R-vine}$.

$L_{I}=\{(I_{1}\left( 2,5\mid 4\right) ,I_{2}\left( 3,5\mid 2,4\right) ,I_{3}\left( 1,5\mid 2,3,4\right) )\}$

$L_{D}=\{(D_{1}\left( 1,3\mid 2\right) ,D_{2}\left( 3,4\mid 2\right) ,D_{3}\left( 1,4\mid 2,3\right) )\}$

Step 2. :

The skeleton of $G_{P}$ is the tree $T_{1}$ of $G_{R-vine}$.

Step 3.:

By representing the independence relationships $I_{1}$, $I_{2}$ and $I_{3}$, the graphs of Fig. 4-(middle panel) are obtained. If we take a look at the last graph, we can see that in $G_{P}$ not only independencies found in $G_{R-vine}$ are represented, but also other independencies that are not visible in $L_{I}$. In order to preserve the same independence relationships, in the next step we proceed to insert the conditional dependencies that are in $L_{D}$.

Step 4. :

To represent $D_{1}\left( 1,3\mid 2\right)$, 2 must be considered as head-to-head node, this is done by changing the direction of the edge between the nodes 2 and 3. This can be performed without affecting independence relationships. Analogously, regarding relation $D_{2}$, the edge between 2 and 4 is redirected. Nevertheless, $D_{3}$ cannot be represented since it would change the existing independencies in the graph. Therefore, the final graph remains as shown in Fig. 4-(right panel).

 

Fig. 3.

Illustration of Example 2: (left panel) R-vine $G_{R-vine}$; (right panel) edge orientation to represent the relationships of $L_{I}=\left\{ I_{1}\right\}$ (top) and $L_{D}=\left\{ D_{1}\right\}$ (middle), and an example of another polytree that can be obtained from the R-vine on the left.

Fig. 4.

Illustration of Example 3: (left panel) starting R-vine $G_{R-vine}$; (middle panel) edge orientation to represent the independence relationships of $L_{I}=\left\{ I_{1},I_{2},I_{3}\right\}$ (from top to bottom); (right panel) edge orientation to represent the dependence relationships of $L_{D}=\left\{ D_{1},D_{2},D_{3}\right\}$.

5 Conclusions

In this work, we have studied the connection between the graphical representations of polytrees and R-vines. We have introduced two algorithms for translating between the underlying semantics of polytrees and regular vines from the graphical perspective.

We have shown that we can find an R-vine where all independencies it encodes exist in the polytree, although not all independencies existing in the polytree can be represented in an R-vine. Thus, the R-vine is an I-map of the dependence model obtained from the polytree. On the other hand, given an R-vine, the resulting polytree includes the same independence relationships existing in the R-vine and also others that are not true in the R-vine. As all the dependence relationships inserted in the polytree exist in the R-vine, the polytree is a D-map of the dependence model obtained from the R-vine. An ongoing topic demanding future work is the extension of this study to BNs with undirected cycles.