Asymptotic Methods for Random Tessellations

Abstract

In this chapter, we are interested in two classical examples of random tessellations which are the Poisson hyperplane tessellation and Poisson–Voronoi tessellation. The first section introduces the main definitions, the application of an ergodic theorem and the construction of the so-called typical cell as the natural object for a statistical study of the tessellation. We investigate a few asymptotic properties of the typical cell by estimating the distribution tails of some of its geometric characteristics (inradius, volume, fundamental frequency). In the second section, we focus on the particular situation where the inradius of the typical cell is large. We start with precise distributional properties of the circumscribed radius that we use afterwards to provide quantitative information about the closeness of the cell to a ball. We conclude with limit theorems for the number of hyperfaces when the inradius goes to infinity.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

6.1 Random Tessellations: Distribution Estimates

This section is devoted to the introduction of the main notions related to random tessellations and to some examples of distribution tail estimates. In the first subsection, we define the two main examples of random tessellations, namely the Poisson hyperplane tessellation and the Poisson–Voronoi tessellation. The next subsection is restricted to the stationary tessellations for which it is possible to construct a statistical object called typical cellZ via several techniques (ergodicity, Palm measures, explicit realizations). Having isolated the cell Z, i.e. a random polyhedron which represents a cell “picked at random” in the whole tessellation, we can investigate its geometric characteristics. In the last subsection, we present techniques for estimating their distribution tails.

This section is not intended to provide the most general definitions and results. Rather, it is aimed at emphasizing some basic examples. Quite often, we shall consider the particular case of the plane. A more exhaustive study of random tessellations can be found in the books [368, 386, 451, 489] as well as the surveys [108, 252].

6.1.1 Definitions

Definition 6.1 (Convex tessellation). 

A convex tessellation is a locally finite collection $\{\Xi _{n}\}_{n\in \mathbb{N}}$ of convex polyhedra of ${\mathbb{R}}^{d}$ such that $\cup _{n\in \mathbb{N}}\Xi _{n} = {\mathbb{R}}^{d}$ and Ξ _n and Ξ _m have disjoint interiors if n≠m. Each Ξ _n is called a cell of the tessellation.

The set $\mathbb{T}$ of convex tessellations is endowed with the σ-algebra generated by the sets

$$\left \{\{\Xi _{n}\}_{n\in \mathbb{N}} : \left [\cup _{n\in \mathbb{N}}\partial \Xi _{n}\right ] \cap K = \varnothing \right \}$$

where K is any compact set of ${\mathbb{R}}^{d}$.

Definition 6.2 (Random convex tessellation). 

A random convex tessellation is a random variable with values in $\mathbb{T}$.

Remark 6.1.

We can equivalently identify a tessellation $\{\Xi _{n}\}_{n\in \mathbb{N}}$ with its skeleton $\cup _{n\in \mathbb{N}}\partial \Xi _{n}$ which is a random closed set of ${\mathbb{R}}^{d}$.

Definition 6.3 (Stationarity, isotropy). 

A random convex tessellation is stationary (resp. isotropic) if its skeleton is a translation-invariant (resp. rotation-invariant) random closed set.

We describe below the two classical constructions of random convex tessellations, namely the hyperplane tessellation and the Voronoi tessellation. In the rest of the section, we shall only consider these two particular examples even though many more can be found in the literature (Laguerre tessellations [324], iterated tessellations [340], Johnson–Mehl tessellations [367], crack STIT tessellations [376], etc.).

Definition 6.4 (Hyperplane tessellation). 

Let Ψ be a point process which does not contain the origin almost surely. For every x ∈ Ψ, we define its polar hyperplane as $H_{x} =\{ y \in {\mathbb{R}}^{d} :\langle y - x,x\rangle = 0\}$. The associated hyperplane tessellation is the set of the closure of all connected components of ${\mathbb{R}}^{d} \setminus \cup _{x\in \varPsi }H_{x}$.

We focus on the particular case where Ψ is a Poisson point process. The next proposition provides criteria for stationarity and isotropy.

Proposition 6.1 (Stationarity of Poisson hyperplane tessellations). 

Let Ψ = Π _Λ be a Poisson point process of intensity measure Λ.

The associated hyperplane tessellation is stationary iff Λ can be written in function of spherical coordinates $(u,t) \in {\mathbb{S}}^{d-1} \times \mathbb{R}_{+}$ as

$$\Lambda (\mathit{du,dt}) = \lambda \,\mathit{dt}\,\varphi (\mathit{du})$$

(6.1)

where $\varphi$ is a probability measure on ${\mathbb{S}}^{d-1}$.

It is additionally isotropic iff $\varphi$ is the uniform measure σ _d−1 on ${\mathbb{S}}^{d-1}$.

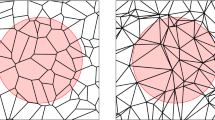
A so-called Poisson hyperplane tessellation (Poisson line tessellation in dimension two) is a hyperplane tessellation generated by a Poisson point process but it is quite often implied in the literature that it is also stationary and isotropic. Up to rescaling, we will assume in the rest of the chapter that its intensity λ is equal to one (Fig. 6.1).

Exercise 6.1.

Verify that a stationary and isotropic Poisson hyperplane tessellation satisfies the following property with probability one: for 0 ≤ k ≤ d, each k-dimensional face of a cell is the intersection of exactly (d − k) hyperplanes H _x , x ∈ Π _Λ , and is included in exactly 2^d − k cells.

This tessellation has been introduced for studying trajectories in bubble chambers by S.A. Goudsmit in [200] in 1945. It has been used in numerous applied works since then. For instance, R.E. Miles describes it as a possible model for the fibrous structure of sheets of paper [356, 357].

Fig. 6.1

Realizations of the isotropic and stationary Poisson line tessellation (a) and the planar stationary Poisson–Voronoi tessellation (b) in the unit square

Definition 6.5 (Voronoi tessellation). 

Let Ψ be a point process. For every x ∈ Ψ, we define the cell associated with x as

$$Z(x\vert \varPsi) =\{ y \in {\mathbb{R}}^{d} :\| y - x\| \leq \| y - x^{\prime}\|\ \forall x^{\prime} \in \varPsi ,x^{\prime}\neq x\}.$$

The associated Voronoi tessellation is the set $\{Z(x\vert \varPsi )\}_{x\in \varPsi }$.

Proposition 6.2 (Stationarity of Voronoi tessellations). 

The Voronoi tessellation associated with a point process Ψ is stationary iff Ψ is stationary.

A so-called Poisson–Voronoi tessellation is a Voronoi tessellation generated by a homogeneous Poisson point process. Up to rescaling, we will assume in the rest of the chapter that its intensity is equal to one.

Exercise 6.2.

Show that a Poisson–Voronoi tessellation is normal with probability one, i.e. every k-dimensional face of a cell, 0 ≤ k ≤ d, is included in exactly $d - k + 1$ cells.

This tessellation has been introduced in a deterministic context by R. Descartes in 1644 as a description of the structure of the universe (see also the more recent work [514]). It has been developed since then for many applications, for example in telecommunications [21, 173], image analysis [162] and molecular biology [185].

We face the whole population of cells in a random tessellation. How to study them? One can provide two possible answers:

• 1. Either you isolate one particular cell.

• 2. Or you try conversely to do a statistical study over all the cells by taking means.

An easy way to fix a cell consists in considering the one containing the origin.

Definition 6.6 (Zero-cell). 

If $o\not\in \cup _{n\in \mathbb{N}}\partial \Xi _{n}$ a.s., then the zero-cell (denoted by Z ₀) is the cell containing the origin. In the case of an isotropic and stationary Poisson hyperplane tessellation, it is called the Crofton cell.

The second point above will be developed in the next section. It is intuitively clear that it will be possible to show the convergence of means over all cells only if the tessellation is translation-invariant.

6.1.2 Empirical Means and Typical Cell

This section is restricted to the stationary Poisson–Voronoi and Poisson hyperplane tessellations. We aim at taking means of certain characteristics over all the cells of the tessellation. But of course, we have to restrict the mean to a finite number of these cells due to technical reasons. A natural idea is to consider those contained in or intersecting a fixed window, for example the ball B _R (o), then take the limit when the size of the window goes to infinity. Such an argument requires the use of an ergodic theorem and the first part of the section will be devoted to prepare and show an ergodic result specialized to our set-up. In the second part of the section, we use it to define the notion of the typical cell and we investigate several equivalent ways of defining it.

6.1.2.1 Ergodic Theorem for Tessellations

The first step is to realize the measurable space $(\Omega ,\mathcal{F})$ as $(\mathcal{N},\mathfrak{N})$ where $\mathcal{N}$ is the set of locally finite sets of ${\mathbb{R}}^{d}$ and $\mathfrak{N}$ is the σ-algebra generated by the functions #( ⋅ ∩ A), where A is any bounded Borel set. We define the shift $T_{a} : \mathcal{N}\,\rightarrow \,\mathcal{N}$ as the operation over the points needed to translate the tessellation by a vector $a \in {\mathbb{R}}^{d}$. In other words, for every locally finite set $\{x_{n}\}_{n\in \mathbb{N}}$, the underlying tessellation generated by $T_{a}(\{x_{n}\}_{n\in \mathbb{N}})$ is the translate by a of the initial tessellation generated by $\{x_{n}\}_{n\in \mathbb{N}}$.

Proposition 6.3 (Explicit shifts). 

For a Voronoi tessellation, T _a is the function which associates to every locally finite set $\{x_{n}\}_{n\in \mathbb{N}} \in \mathcal{N}$ the set $\{x_{n} + a\}_{n\in \mathbb{N}}$.

For a hyperplane tessellation, T _a is the function which associates to every locally finite set $\{x_{n}\}_{n\in \mathbb{N}} \in \mathcal{N}$ (which does not contain the origin) the set $\{x_{n} +\langle x_{n}/\|x_{n}\|,a\rangle x_{n}/\|x_{n}\|\}_{n\in \mathbb{N}}$.

Proof.

In the Voronoi case, the translation of the skeleton is equivalent with the translation of the nuclei which generate the tessellation.

In the case of a hyperplane tessellation, the translation of a fixed hyperplane preserves its orientation but modifies the distance from the origin. To prove the proposition, it suffices to notice that a polar hyperplane H _x is sent by a translation of vector a to H _y with $y = x +\langle u,a\rangle u$ where $u = \frac{x} {\|x\|}$. □ 

Proposition 6.4 (Ergodicity of the shifts). 

In both cases, T _a preserves the measure P (i.e. the distribution of the Poisson point process) and is ergodic.

Sketch of proof. Saying that T _a preserves the measure is another way of expressing the stationarity of the tessellation.

To show ergodicity, it is sufficient to prove that $\{T_{a} : a\,\in \,{\mathbb{R}}^{d}\}$ is mixing (cf. Definition 4.6), i.e. that for any bounded Borel sets A, B and $k,l \in \mathbb{N}$, we have as | a | → ∞

$$\mathbf{P}({\#}(\varPsi \cap A) = k;\;{\#}(T_{a}(\varPsi ) \cap B) = l)\;\rightarrow \;\mathbf{P}({\#}(\varPsi \cap A) = k)\mathbf{P}({\#}(\varPsi \cap B) = l).$$

(6.2)

In the Voronoi case, for | a | large enough, the two events $\{\#(\Phi \cap A) = k\}$ and $\{\#(T_{a}(\Phi ) \cap B) = l\}$ are independent since $A \cap (B - a) = \varnothing$. Consequently, the two sides of (6.2) are equal.

In the hyperplane case, the same occurs as soon as B is included in a set

$$\{x \in {\mathbb{R}}^{d} : \vert \langle x,a\rangle \vert \geq \epsilon \|x\|\|a\|\}$$

for some $\epsilon > 0$. Otherwise, we approximate B with a sequence of Borel subsets which satisfy this condition. □ 

In the next theorem, the main application of ergodicity for tessellations is derived.

Theorem 6.1 (Ergodic theorem for tessellations). 

Let N _R be the number of cells which are included in the ball B _R (o). Let $h : \mathcal{K}_{\mathrm{conv}}^{d} \rightarrow \mathbb{R}$ be a measurable, bounded and translation-invariant function over the set $\mathcal{K}_{\mathrm{conv}}^{d}$ of convex and compact sets of  ${\mathbb{R}}^{d}$ . Then almost surely,

$$\lim _{R\rightarrow \infty } \frac{1} {N_{R}}\sum _{\Xi \subset B_{R}(o)}h(\Xi ) = \frac{1} {\mathbf{E}(\nu _{d}{(Z_{0})}^{-1})}\mathbf{E}\left ( \frac{h(Z_{0})} {\nu _{d}(Z_{0})}\right ).$$

(6.3)

Proof.

The proof is done in three steps: use of Wiener’s continuous ergodic theorem, then rewriting the mean of h over cells included in B _R (o) as the sum of an integral and the rest, finally proving that the rest is negligible.

Step 1. :

The main ingredient is Wiener’s ergodic theorem applied to the ergodic shifts $\{S_{x} : x \in {\mathbb{R}}^{d}\}$. We have almost surely

$$\lim _{R\rightarrow \infty } \frac{1} {\nu _{d}(B_{R}(o))}\int \nolimits \nolimits _{B_{R}(o)} \frac{h(Z_{0}(T_{-x}\omega ))} {\nu _{d}(Z_{0}(T_{-x}\omega ))}\,dx = \mathbf{E}\left ( \frac{h(Z_{0})} {\nu _{d}(Z_{0})}\right ).$$

This can be roughly interpreted by saying that the mean in space (in the left-hand side) for a fixed sample ω is asymptotically close to the mean with respect to the probability law P.

Step 2. :

We have for almost every ω ∈ Ω that

$$\frac{1} {\nu _{d}(B_{R}(o))}\int \nolimits \nolimits _{B_{R}(o)} \frac{h(Z_{0}(T_{-x}\omega ))} {\nu _{d}(Z_{0}(T_{-x}\omega ))}\,dx = \frac{1} {\nu _{d}(B_{R}(o))}\sum _{\Xi \subset B_{R}(o)}h(\Xi ) + \mbox{ Rest}(R)$$

(6.4)

where

$$\mbox{ Rest}(R) = \frac{1} {\nu _{d}(B_{R}(o))}\sum _{\Xi :\Xi \cap \partial B_{R}(o)\neq \varnothing }\frac{\nu _{d}(\Xi \cap B_{R}(o))} {\nu _{d}(\Xi )} h(\Xi ).$$

In particular, if we define N _R ′ as the number of cells which intersect the boundary of the ball B _R (o), then there is a positive constant K depending only on h such that

$$\vert \mbox{ Rest}(R)\vert \leq K \frac{N_{R}^{\prime}} {\nu _{d}(B_{R}(o))}.$$

We observe that in order to get (6.3), it is enough to prove that the rest goes to 0. Indeed, when $h \equiv 1$, the equality (6.4) will provide that

$$\frac{N_{R}} {\nu _{d}(B_{R}(o))} = \frac{1} {\nu _{d}(B_{R}(o))}\int \nolimits \nolimits _{B_{R}(o)} \frac{1} {\nu _{d}(Z_{0}(T_{-x}\omega ))}\,dx-\mbox{ Rest}(R)\;\rightarrow \;\mathbf{E}(\nu _{d}{(Z_{0})}^{-1}).$$

Step 3. :

We have to show that Rest(R) goes to 0, that is what R. Cowan calls the insignificance of edge effects [132, 133]. In the sequel, we use his argument to show it and for sake of simplicity, we only consider the particular case of the two-dimensional Voronoi tessellation. Nevertheless, the method can be extended to any dimension by showing by induction that the number of k-faces hitting the boundary of the ball is negligible for every 0 ≤ k ≤ d.

Here, in the two-dimensional case, let us fix $\epsilon > 0$ and consider $R > \epsilon$. Let us denote by V _R the number of vertices of the tessellation in B _R (o) and by L _R the sum of the edge lengths inside B _R (o). A direct use of Wiener’s theorem applied to the functionals $V _{\epsilon }$ and $L_{\epsilon }$ on the sets $B_{R-\epsilon }(o)$ and $B_{R+\epsilon }(o)$ shows that the quantities $V _{R}/\nu _{d}(B_{R}(o))$ and $L_{R}/\nu _{d}(B_{R}(o))$ tend almost surely to constants.

We recall that a Voronoi tessellation is normal which means in particular that a fixed edge (resp. vertex) is contained in exactly two (resp. three) cells.

If a cell intersects the boundary of B _R (o), then we are in one of the three following cases:

• 1. No edge of the cell intersects $B_{R+\epsilon }(o) \setminus B_{R}(o)$.

• 2. Some edges but no vertex of the cell intersect $B_{R+\epsilon }(o) \setminus B_{R}(o)$.

• 3. At least one vertex of the cell is in $B_{R+\epsilon }(o) \setminus B_{R}(o)$.

The first case is satisfied by at most one cell, the second case by at most $\frac{2} {\epsilon }(L_{R+\epsilon } - L_{R})$ cells and the last one by at most $3(S_{R+\epsilon } - S_{R})$. Consequently, we get when R → ∞

$$\frac{N_{R}^{\prime}} {V _{2}(B_{R}(o))} \leq \frac{1} {V _{2}(B_{R}(o))} + 2\,\frac{L_{R+\epsilon } - L_{R}} {V _{2}(B_{R}(o))} + 3\,\frac{V _{R+\epsilon } - V _{R}} {V _{2}(B_{R}(o))} \rightarrow 0,$$

which completes the proof. □ 

Exercise 6.3.

Show a similar result for a Johnson–Mehl tessellation (defined in [367]).

Remark 6.2.

The statement of Theorem 6.1 still holds if condition “h bounded” is replaced with $\mathbf{E}(\vert h(Z_{0}){\vert }^{p})\,<\,\infty$ for a fixed p > 1 (see for example [196, Lemma 4]).

Remark 6.3.

When using this ergodic theorem for tessellations in practice, it is needed to have also an associated central limit theorem. Such second-order results have been proved for some particular functionals in the Voronoi case [20] and for the Poisson line tessellation [389] in dimension two. Recently, a more general central limit result for hyperplane tessellations has been derived from the use of U-statistics in [239].

The limit in the convergence (6.3) suggests the next definition for the typical cell, i.e. a cell which represents an “average individual” from the whole population.

Definition 6.7 (Typical cell 1). 

The typical cellZ is defined as a random variable with values in $\mathcal{K}_{\mathrm{conv}}^{d}$ and such that for every translation-invariant measurable and bounded function $h : \mathcal{K}_{\mathrm{conv}}^{d} \rightarrow \mathbb{R}$, we have

$$\mathbf{E}(h(Z)) = \frac{1} {\mathbf{E}(\nu _{d}{(Z_{0})}^{-1})}\mathbf{E}\left ( \frac{h(Z_{0})} {\nu _{d}(Z_{0})}\right ).$$

Remark 6.4.

Taking for h any indicator function of geometric events (for example {the cell is a triangle}, {the area of the cell is greater than 2}, etc.), we can define via the equality above the distribution of any geometric characteristic of the typical cell.

Remark 6.5.

One should keep in mind that the typical cell Z is not distributed as the zero-cell Z ₀. Indeed, the distribution of Z has a density proportional to ν₂ ^− 1 with respect to the distribution of Z ₀. In particular, since it has to contain the origin, Z ₀ is larger than Z. This is a d-dimensional generalization of the famous bus paradox in renewal theory which states that at your arrival at a bus stop, the time interval between the last bus you missed and the first bus you’ll get is actually bigger than the typical waiting time between two buses. Moreover, it has been proved in the case of a Poisson hyperplane tessellation that Z and Z ₀ can be coupled in such a way that Z ⊂ Z ₀ almost surely (see [352] and Proposition 6.6 below).

Looking at Definition 6.7, we observe that it requires to know either the distribution of Z ₀ or the limit of the ergodic means in order to get the typical cell. The next definition is an alternative way of seeing the typical cell without the use of any convergence result. It is based on the theory of Palm measures [323, 348]. For sake of simplicity, it is only written in the case of the Poisson–Voronoi tessellation but it can be extended easily to any stationary Poisson hyperplane tessellation.

Definition 6.8 (Typical cell 2 (Poisson–Voronoi tessellation)). 

The typical cellZ is defined as a random variable with values in $\mathcal{K}_{\mathrm{conv}}^{d}$ such that for every bounded and measurable function $h : \mathcal{K}_{\mathrm{conv}}^{d} \rightarrow \mathbb{R}$ and every Borel set B with 0 < ν _d (B) < ∞, we have

$$\mathbf{E}(h(Z)) = \frac{1} {\nu _{d}(B)}\mathbf{E}\left (\sum _{x\in B\cap \Pi }h(Z(x\vert \Pi ) - x)\right ).$$

(6.5)

This second definition is still an intermediary and rather unsatisfying one but via the use of Slivnyak–Mecke formula for Poisson point processes (see Theorem 4.5), it provides a way of realizing the typical cell Z.

Exercise 6.4.

Verify that the relation (6.5) does not depend on B.

Proposition 6.5 (Typical cell 3 (Poisson–Voronoi tessellation)). 

The typical cell Z is equal in distribution to the set Z(o) = Z(o|Π ∪{ o}), i.e. the Voronoi cell associated with a nucleus at the origin when this nucleus is added to the original Poisson point process.

Remark 6.6.

The cell Z(o) defined above is not a particular cell isolated from the original tessellation. It is a cell extracted from a different Voronoi tessellation but which has the right properties of a cell “picked at random” in the original tessellation. For any x ∈ Π, we define the bisecting hyperplane of [o, x] as the hyperplane containing the midpoint x ∕ 2 and orthogonal to x. Since Z(o) is bounded by portions of bisecting hyperplanes of segments [o, x], x ∈ Π, we remark that Z(o) can be alternatively seen as the zero-cell of a (non-stationary) Poisson hyperplane tessellation associated with the homogeneous Poisson point process up to a multiplicative constant.

The Poisson–Voronoi tessellation is not the only tessellation such that the associated typical cell can be realized in an elementary way. There exist indeed several ways of realizing the typical cell of a stationary and isotropic Poisson hyperplane tessellation. We present below one of the possible constructions of Z, which offers the advantage of satisfying Z ⊂ Z ₀ almost surely. It is based on a work [106] which is an extension in any dimension of an original idea in dimension two due to R.E. Miles [359] (Fig. 6.2).

Proposition 6.6 (Typical cell 3 (Poisson hyperplane tessellation)). 

The radius R _m of the largest ball included in the typical cell Z is an exponential variable of parameter the area of the unit sphere. Moreover, conditionally on R _m , the typical cell Z is equal in distribution to the intersection of the two independent following random sets:

• (i) a random simplex with inscribed ball $B_{R_{m}}(o)$ such that the vector $(u_{0},\ldots ,u_{d})$ of the d + 1 normal unit-vectors is independent of R _m and has a density proportional to the volume of the simplex spanned by $u_{0},\ldots ,u_{d}$.

• (ii) the zero-cell of an isotropic Poisson hyperplane tessellation outside $B_{R_{m}}(o)$ of intensity measure $\Lambda (du,dt)\,=\,\mathbf{1}(B_{R_{m}}{(o)}^{c})\,dt\,d\sigma _{d-1}(u)$ (in spherical coordinates).

Exercise 6.5.

When d = 2, let us denote by α, β, γ the angles between u ₀ and u ₁, u ₁ and u ₂, u ₂ and u ₀ respectively. Write the explicit density in (i) in function of α, β and γ.

Exercise 6.6.

We replace each hyperplane H _x from a Poisson hyperplane tessellation by a $\epsilon$-thickened hyperplane $H_{x}^{(\epsilon )} =\{ y \in {\mathbb{R}}^{d} : d(y,H_{x}) \leq \epsilon \}$ where $\epsilon > 0$ is fixed. Show that the distribution of the typical cell remains unchanged, i.e. is the same as for $\epsilon = 0$.

We conclude this subsection with a very basic example of calculation of a mean value: it is well-known that in dimension two, the mean number of vertices of the typical cell is 4 for an isotropic Poisson line tessellation and 6 for a Poisson–Voronoi tessellation. We give below a small heuristic justification of this fact: for a Poisson line tessellation, each vertex is in four cells exactly and there are as many cells as vertices (each vertex is the highest point of exactly one cell) whereas in the Voronoi case, each vertex is in three cells exactly and there are twice more vertices than cells (each vertex is either the highest point or the lowest point of exactly one cell).

Fig. 6.2

Realizations of the typical cells of the stationary and isotropic Poisson line tessellation (a) and the homogeneous planar Poisson–Voronoi tessellation (b)

In the next subsection, we estimate the distribution tails of some geometric characteristics of the typical cell.

6.1.3 Examples of Distribution Tail Estimates

Example 6.1 (Poisson hyperplane tessellation, Crofton cell, inradius). 

We consider a stationary and isotropic Poisson hyperplane tessellation, i.e. with an intensity measure equal to $\Lambda (du,dt) = dt\,d\sigma _{d-1}(u)$ in spherical coordinates (note that the constant λ appearing in (6.1) is chosen equal to one).

Let us denote by R _m the radius of the largest ball included in the Crofton cell and centered at the origin. Since it has to be centered at the origin, the ball $B_{R_{m}}(o)$ is not the real inball of the Crofton cell. Nevertheless, we shall omit that fact and call R _m the inradius in the rest of the chapter.

For every r > 0, we have

$$\begin{array}{rcl} \mathbf{P}(R_{m} \geq r)& =& \mathbf{P}(\varPi \cap B_{r}(o) = \varnothing ) \\ & =& \exp \left \{-\int \nolimits \nolimits _{0}^{r} \int \nolimits \nolimits _{{\mathbb{S}}^{d-1}}\,dt\,d\sigma _{d-1}(u)\right \} =\mathrm{ {e}}^{-d\kappa _{d}r} \\ \end{array}$$

where κ _d is the Lebesgue measure of the d-dimensional unit-ball. We can remark that it is the same distribution as the real inradius of the typical cell, i.e. the radius of the largest ball included in the typical cell with unfixed center (see [106, 356] and Proposition 6.6 above).

This result can be extended by showing that for every deterministic convex set K containing the origin, the probability $\mathbf{P}(K \subset Z_{0})$ is equal to $\exp \{-\frac{d} {2}\kappa _{d}V _{1}(K)\}$ where V ₁(K) is the mean width of K. In dimension two, the probability reduces to exp{ − P(K)} where P(K) is the perimeter of K.

Example 6.2 (Poisson–Voronoi tessellation, typical cell, inradius). 

We consider a homogeneous Poisson–Voronoi tessellation of intensity one in the rest of the section.

We realize its typical cell as Z(o) = Z(o | Π ∪{ o}) (see Proposition 6.5). We consider the radius R _m of the largest ball included in Z(o) and centered at the origin. We call it inradius with the same abuse of language as in the previous example. The radius R _m is larger than r iff for every x, $\|x\| = r$, x is in Z(o), i.e. B _r (x) does not intersect the Poisson point process Π. In other words, for every r > 0, we have

$$\begin{array}{rcl} \mathbf{P}(R_{m} \geq r)& =& \mathbf{P}\left (\Pi \cap \bigcup \nolimits _{x:\|x\|=r}B_{r}(x) = \varnothing \right ) \\ & =& \mathbf{P}(\Pi \cap B_{2r}(o) = \varnothing ) =\mathrm{ {e}}^{-{2}^{d}\kappa _{ d}{r}^{d} }.\end{array}$$

(6.6)

In general, for a deterministic convex set K containing the origin, we define the Voronoi flower $F(K)\,=\,\bigcup \nolimits _{x\in K}B_{\|x\|}(x)$ (Fig. 6.3). We can show the following equality:

$$\mathbf{P}(K \subset Z(o)) =\exp \{ -\nu _{d}(F(K))\}.$$

Exercise 6.7.

Verify that for any compact subset A of ${\mathbb{R}}^{d}$, the Voronoi flowers of A and of its convex hull coincide.

Example 6.3 (Poisson–Voronoi tessellation, typical cell, volume). 

The next proposition comes from a work due to E.N. Gilbert [187].

Proposition 6.7 (E.N. Gilbert [187]). 

For every t > 0, we have

$$\mathrm{{e}}^{-{2}^{d}t } \leq \mathbf{P}(\nu _{d}(Z) \geq t) \leq \frac{t - 1} {\mathrm{{e}}^{t-1} - 1}.$$

Proof.

Lower bound: It suffices to notice that $\nu _{d}(Z)\,\geq \,\nu _{d}(B_{R_{m}}(o))$ and apply (6.6).

Upper bound: :

Using Markov’s inequality, we get for every α, t ≥ 0

Fig. 6.3

Example of the Voronoi flower of a convex polygon

$$\mathbf{P}(\nu _{d}(Z) \geq t) \leq {(\mathrm{{e}}^{\alpha t} - 1)}^{-1}(\mathbf{E}(\mathrm{{e}}^{\alpha \nu _{d}(Z)}) - 1).$$

(6.7)

Let us consider now the quantity $f(\alpha ) = \mathbf{E}\left (\int \nolimits \nolimits _{Z(o)}\mathrm{{e}}^{\alpha \kappa _{d}\|{x\|}^{d} }\,dx\right )$. On one hand, we can show by Fubini’s theorem that for every α < 1,

$$f(\alpha ) = \int \nolimits \nolimits _{{\mathbb{R}}^{d}}\mathrm{{e}}^{\alpha \kappa _{d}\|{x\|}^{d} }\mathbf{P}(x \in Z(o))\,dx = \int \nolimits \nolimits _{{\mathbb{R}}^{d}}\mathrm{{e}}^{(\alpha -1)\kappa _{d}\|{x\|}^{d} }\,dx = \frac{1} {1 - \alpha }.$$

(6.8)

On the other hand, when comparing Z(o) with the ball centered at the origin and of same volume, we use an isoperimetric inequality to get a lower bound for the same quantity:

$$f(\alpha ) \geq \mathbf{E}\left (\int \nolimits \nolimits _{B_{{ (\nu _{d}(Z(o))/\kappa _{d})}^{1/d}}(o)}\mathrm{{e}}^{\alpha \kappa _{d}\|{x\|}^{d} }\,dx\right ) = \frac{1} {\alpha }\mathbf{E}(\mathrm{{e}}^{\alpha \nu _{d}(Z)}).$$

(6.9)

Combining (6.7), (6.8) with (6.9), we obtain that for every t > 0,

$$\mathbf{P}(\nu _{d}(Z) \geq t) \leq {(\mathrm{{e}}^{\alpha t} - 1)}^{-1} \frac{\alpha } {1 - \alpha }$$

and it remains to optimize the inequality in α by taking $\alpha = \frac{t-1} {t}$. □ 

Exercise 6.8.

Show the isoperimetric inequality used above.

Remark 6.7.

It has been proved since then (see Theorem 7.10 and [259]) that the lower bound provides the right logarithmic equivalent, i.e.

$$\lim _{t\rightarrow \infty }\frac{1} {t}\log \mathbf{P}(\nu _{d}(Z) \geq t) = -{2}^{d}.$$

In other words, distribution tails of the volumes of both the typical cell Z and its inball have an analogous asymptotic behaviour. This is due to D.G. Kendall’s conjecture (see the foreword of the book [489]) which was historically written for the two-dimensional Crofton cell. Indeed, it roughly states that cells with a large volume must be approximately spherical. After a first proof by I.N. Kovalenko [312], this conjecture has been rigorously reformulated and extended in many directions by D. Hug, M. Reitzner and R. Schneider (see Theorems 7.9 and 7.11 as well as [255, 256]).

Example 6.4 (Poisson–Voronoi tessellation, typical cell, fundamental frequency in dimension two). 

This last more exotic example is motivated by the famous question due to Kac [279] back in 1966: “Can one hear the shape of a drum?”. In other words, let us consider the Laplacian equation on Z(o) with a Dirichlet condition on the boundary, that is

$$\left \{\begin{array}{@{}l@{\quad }l@{}} \Delta f(x) = -\lambda f(x),\quad &\text{if}\ x \in Z(o),\\ f(x) = 0, \quad &\text{if} \ x \in \partial Z(o). \end{array} \right.$$

It has been proved that the eigenvalues satisfy

$$0 < \lambda _{1} \leq \lambda _{2} \leq \cdots \leq \lambda _{n} \leq \cdots < \infty.$$

Is it possible to recover the shape of Z(o) by knowing only its spectrum? In particular, λ₁ is called the fundamental frequency of Z(o). It is a decreasing function of the convex set considered. When the volume of the domain is fixed, Faber–Krahn’s inequality [40] says that it is minimal iff the domain is a ball. In such a case, we have $\lambda _{1}\,=\,j_{0}^{2}/{r}^{2}$ where r is the radius of the ball and j ₀ is the first positive zero of the Bessel function J ₀ [80].

The next theorem which comes from a collaboration with A. Goldman [198] provides an estimate for the distribution function of λ₁ in the two-dimensional case.

Theorem 6.2 (Fundamental frequency of the typical Poisson–Voronoi cell). 

Let μ ₁ denote the fundamental frequency of the inball of Z(o). Then when d = 2, we have

$$\lim _{t\rightarrow 0}\,t \cdot \log \mathbf{P}(\lambda _{1} \leq t) =\lim _{t\rightarrow 0}\,t \cdot \log \mathbf{P}(\mu _{1} \leq t) = -4\pi j_{0}^{2}.$$

Remark 6.8.

The larger Z(o) is, the smaller is λ₁. When evaluating the probability of the event {λ₁ ≤ t} for small t, the contribution comes from the largest cells Z(o). Consequently, the fact that the distribution functions for small λ₁ and small μ₁ have roughly the same behaviour is a new contribution for justifying D.G. Kendall’s conjecture.

Remark 6.9.

An analogous result holds for the Crofton cell of a Poisson line tessellation in the plane [196].

Sketch of proof.

Step 1. :

By a Tauberian argument (see [172], Vol. 2, Chap. 13, pages 442–448), we only have to investigate the behaviour of the Laplace transform $\mathbf{E}(\mathrm{{e}}^{-t\lambda _{1}})$ when t goes to infinity.

Step 2. :

We get a lower bound by using the monotonicity of the fundamental frequency (λ₁ ≤ μ₁) and the explicit distribution of $\mu _{1} = j_{0}^{2}/R_{m}^{2}$.

Step 3. :

In order to get an upper bound, we observe that almost surely

$$\mathrm{{e}}^{-t\lambda _{1} } \leq \varphi (t) =\sum _{n\geq 1}\mathrm{{e}}^{-t\lambda _{n} }$$

where $\varphi$ is called the spectral function of Z(o). It is known that the spectral function of a domain is connected to the probability that a two-dimensional Brownian bridge stays in that domain (see for example [279]). More precisely, we denote by W the trajectory of a standard two-dimensional Brownian bridge between 0 and 1 (i.e. a planar Brownian motion starting at 0 and conditioned on being at 0 at time 1) and independent from the point process. We have

$$\varphi (t) = \frac{1} {4\pi t}\int \nolimits \nolimits _{Z(o)}{\mathbf{P}}^{W}(x + \sqrt{2t}W \subset Z(o))\,dx$$

where P ^W denotes the probability with respect to the Brownian bridge W. We then take the expectation of the equality above with respect to the point process and we get the Laplace transform of the area of the Voronoi flower of the convex hull of W. We conclude by using results related to the geometry of the two-dimensional Brownian bridge [197]. □ 

Exercise 6.9.

In the case of the Crofton cell, express $\varphi (t)$ in function of the Laplace transform of the mean width of W.

6.2 Asymptotic Results for Zero-Cells with Large Inradius

In this section, we shall focus on the example of the Poisson–Voronoi typical cell, but the reader should keep in mind that the results discussed below can be extended to the Crofton cell and more generally to zero-cells of certain isotropic hyperplane tessellations (see [108, Sect. 3]). This section is devoted to the asymptotic behaviour of the typical cell, under the condition that it has large inradius. Though it may seem at first sight a very artificial and restrictive choice, we shall see that it falls in the more general context of D.G. Kendall’s conjecture and that this particular conditioning allows us to obtain very precise estimations for the geometry of the cell.

In the first subsection, we are interested in the distribution tail of a particular geometric characteristic that we did not consider before, the so-called circumscribed radius. We deduce from the general techniques involved an asymptotic result for the joint distribution of the two radii. In the second subsection, we make the convergence of the cell to the spherical shape more precise by showing limit theorems for some of its characteristics when the inradius goes to infinity. In this section, two fundamental models from stochastic geometry will be introduced as tools for understanding the geometry of the typical cell: random coverings of the circle/sphere and random polytopes generated as convex hulls of Poisson point processes in the ball.

6.2.1 Circumscribed Radius

We consider a homogeneous Poisson–Voronoi tessellation of intensity one and we realize its typical cell as Z(o) according to Proposition 6.5. With the same misuse of language as for the inradius, we define the circumscribed radiusR _M of the typical cell Z(o) as the radius of the smallest ball containing Z(o) and centered at the origin. We first propose a basic way of estimating its distribution and we proceed with a more precise calculation through a technique based on coverings of the sphere which provides satisfying results essentially in dimension two.

6.2.1.1 Estimation of the Distribution Tail

For the sake of simplicity, the following argument is written only in dimension two and comes from an intermediary result of a work due to S. Foss and S. Zuyev [176]. We observe that R _M is larger than r > 0 iff there exists x, $\|x\| = r$, which is in Z(o), i.e. such that $B_{\|x\|}(x)$ does not intersect the Poisson point process Π. Compared to the event {R _m  ≥ r}, the only difference is that “there exists x” is replacing “for every x” (see Example 2 of Sect. 6.1.3).

In order to evaluate this probability, the idea is to discretize the boundary of the circle and consider a deterministic sequence of balls $B_{\|z_{k}\|}(z_{k})$, 0 ≤ k ≤ (n − 1), $n \in \mathbb{N} \setminus \{ 0\}$ with $z_{k} = r(\cos (2\pi k/n),\sin (2\pi k/n))$. We call the intersection of two consecutive such disks a petal. If R _M  ≥ r, then one of these n petals has to be empty. We can calculate the area of a petal and conclude that for every r > 0, we have

$$\mathbf{P}(R_{M} \geq r) \leq n\exp \{ - {r}^{2}(\pi -\sin (2\pi /n) - (2\pi /n))\}.$$

(6.10)

In particular, when we look at the chord length in one fixed direction, i.e. the length l _u of the largest segment emanating from the origin in the direction u and contained in Z(o), we have directly for every r > 0,

$$\mathbf{P}(l_{u} \geq r) =\exp \{ -\pi {r}^{2}\},$$

which seems to provide the same logarithmic equivalent as the estimation (6.10) when n goes to infinity. This statement will be reinforced in the next section.

6.2.1.2 Calculation and New Estimation

This section and the next one present ideas and results contained in [107, 108]. The distribution of R _M can be calculated explicitly: let us recall that Z(o) can be seen as the intersection of half-spaces delimited by random bisecting hyperplanes and containing the origin. We then have R _M  ≥ r (r > 0) iff the half-spaces do not cover the sphere ∂B _r (o). Of course, only the hyperplanes which are at a distance less than r are necessary and their number is finite and Poisson distributed. The trace of a half-space on the sphere is a spherical cap with a (normalized) angular diameter α which is obviously less than 1 ∕ 2 and which has an explicit distribution. Indeed, α can be written in function of the distance L from the origin to the hyperplane via the formula $\alpha =\arccos (L/r)/\pi$. Moreover, the obtained spherical caps are independent. For any probability measure ν on [0, 1 ∕ 2] and $n\,\in \,\mathbb{N}$, we denote by P(ν, n) the probability to cover the unit-sphere with n i.i.d. isotropic spherical caps such that their normalized angular diameters are ν distributed. Following this reasoning, the next proposition connects the distribution tail of R _M with some covering probabilities P(ν, n) (Fig. 6.4).

Fig. 6.4

Covering of the circle of radius r when R _M  ≥ r

Proposition 6.8 (Rewriting of the distribution tail of R _M ). 

For every r > 0, we have

$$\mathbf{P}(R_{M} \geq r) =\mathrm{ {e}}^{-{2}^{d}\kappa _{ d}{r}^{d} }\sum _{n=0}^{\infty }\frac{{({2}^{d}\kappa _{ d}{r}^{d})}^{n}} {n!} (1 - P(\nu ,n))$$

(6.11)

where ν is a probability measure on [0,1∕2] with the density

$$f_{\nu }(\theta ) = d\pi \sin {(\pi \theta )\cos }^{d-1}(\pi \theta ),\quad \theta \in [0,1/2].$$

Exercise 6.10.

Verify the calculation of ν and do the same when the Poisson–Voronoi typical cell is replaced by the Crofton cell of a Poisson hyperplane tessellation.

The main question is now to evaluate the covering probability P(ν, n). In the two-dimensional case, it is known explicitly [475] so the preceding proposition provides in fact the exact calculation of the distribution tail of R _M . Unfortunately, the formula for P(ν, n) when ν is a continuous measure is not easy to handle but in the particular case where ν is simply a Dirac measure at a ∈ [0, 1] (i.e. all circular arcs have a fixed length equal to a), then it has been proved by W.L. Stevens [485] with very elementary arguments that for every $n \in {\mathbb{N}}^{{_\ast}}$, we have

$$P(\delta _{a},n) =\sum _{ k=0}^{n}{(-1)}^{k}\left ({ n \atop k} \right )(1 - ka)_{+}^{n-1}$$

(6.12)

where $x_{+}\,=\,\max (x,0)$ for every $x\,\in \,\mathbb{R}$. In particular, it implies the following relation for every a ∈ [0, 1]

$$\lim _{n\rightarrow \infty }\frac{1 - P(\delta _{a},n)} {n{(1 - a)}^{n-1}} = 1.$$

Exercise 6.11.

Calculate $P((1 - p)\delta _{0} + p\delta _{a},n)$ for $a,p \in [0,1],n \in {\mathbb{N}}^{{_\ast}}$

In higher dimensions, no closed formula is currently available for P(ν, n). The case where ν = δ _a with a > 1 ∕ 2 has been solved recently [103], otherwise bounds do exist in the particular case of a deterministic radius of the spherical caps [188, 222].

In dimension two, we can use Proposition 6.8 in order to derive an estimation of the distribution tail which is better than (6.10).

Theorem 6.3 (Distribution tail estimate of R _M in dimension two). 

For a sufficiently large r, we have

$$2\pi {r}^{2}\mathrm{{e}}^{-\pi {r}^{2} } \leq \mathbf{P}(R_{M} \geq r) \leq 4\pi {r}^{2}\mathrm{{e}}^{-\pi {r}^{2} }.$$

(6.13)

Sketch of proof. When using (6.11), we have to estimate P(ν, n), with ν chosen as in Proposition 6.8, but possibly without considering a too complicated explicit formula. In particular, since the asymptotic equivalent (6.12) for P(δ _a , n) seems to be quite simple, we aim at replacing the covering probability P(ν, n) with a covering probability P(δ _a , n) where a is equal to 1 ∕ 4, i.e. the mean of ν.

The problem is reduced to the investigation under which conditions we can compare two different covering probabilities P(μ₁, n) and P(μ₂, n) where μ₁, μ₂ are two probability measures on [0, 1]. We recall that μ₁ and μ₂ are said to be ordered according to the convex order, i.e. $\mu _{1} \prec _{\mathrm{conv}}\mu _{2}$, if $\langle f,\mu _{1}\rangle \leq \langle f,\mu _{2}\rangle$ for every convex function $f : [0,1] \rightarrow \mathbb{R}$ [374] (where $\langle f,\mu _{1}\rangle = \int \nolimits \nolimits fd\mu _{1}$). In particular, Jensen’s inequality says that $\delta _{a} \prec _{\mathrm{conv}}\nu$ and we can easily prove that $\nu \,\prec _{\mathrm{conv}}\,\frac{1} {2}(\delta _{0} + \delta _{2a})$. The next proposition shows how the convex ordering of distributions implies the ordering of the underlying covering probabilities.

Proposition 6.9 (Ordering of covering probabilities). 

If $\nu _{1}\,\prec _{\mathrm{conv}}\,\nu _{2}$ , then for every $n \in \mathbb{N}$, $P(\nu _{1},n) \leq P(\nu _{2},n)$.

Exercise 6.12.

Find a heuristic proof of Proposition 6.9.

Thanks to this proposition and the remark above, we can write

$$P(\delta _{1/4},n) \leq P(\nu ,n) \leq P((\delta _{0} + \delta _{1/2})/2,n),$$

then insert the two bounds in the equality (6.11) and evaluate them with Stevens’ formula (6.12). □ 

Remark 6.10.

Numerical estimates of P(R _M  ≥ r) with the formula (6.11) indicate that P(R _M  ≥ r) should be asymptotically equivalent to the upper bound of (6.13).

6.2.1.3 Distribution Conditionally on the Inradius

Why should we be interested in the behaviour of the typical cell when conditioned on the value of its inradius?

First, it is one of the rare examples of conditioning of the typical cell which can be made completely explicit. Indeed, conditionally on {R _m  ≥ r}, any point x of the Poisson point process is at distance larger than 2r from o so the typical cell Z(o) is equal in distribution to the zero-cell associated with the bisecting hyperplanes of the segments [o, x] where x is any point of a homogeneous Poisson point process in B _2r (o)^c.

Conditionally on {R _m  = r}, the distribution of Z(o) is obtained as previously, but with an extra-bisecting hyperplane generated by a deterministic point x ₀ at distance 2r.

The second reason for investigating this particular conditioning is that a large inradius implies a large typical cell. In other words, having R _m large is a particular case of the general setting of D.G. Kendall’s conjecture (see Remark 6.7). But we can be more precise about how the typical cell is converging to the spherical shape. Indeed, the boundary of the polyhedron is included in an annulus between the two radii R _m and R _M and so the order of decreasing of the difference $R_{M} - R_{m}$ will provide a satisfying way of measuring the closeness of Z(o) to a sphere. The next theorem provides a result in this direction.

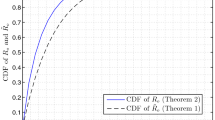
Theorem 6.4 (Asymptotic joint distribution of $(R_{m},R_{M})$). 

There exists a constant c > 0 such that for every $\frac{d-1} {d+1} < \delta < 1$ , we have

$$\mathbf{P}(R_{M} \geq r + {r}^{\delta }\mid R_{ m} = r) = \mathcal{O}(\exp \{-c{r}^{\beta }\}),\;\;r \rightarrow \infty ,$$

(6.14)

where $\beta = \frac{1} {2}\left [(d - 1) + \delta (d + 1)\right ]$.

Sketch of proof in dimension two. The joint distribution of the couple $(R_{m},R_{M})$ can be obtained explicitly via the same method as in Proposition 6.8. Indeed, the quantity $\mathbf{P}(R_{M}\,\geq \,r + s\mid R_{m}\,=\,r)$ can be rewritten as the probability of not covering the unit-sphere with random i.i.d. and uniform spherical caps. The only difference lies in the common distribution of the angular diameters of the caps which will now depend upon r since bisecting hyperplanes have to be at least at distance r from the origin. In dimension two, the covering probability can be estimated with an upper-bound due to L. Shepp [470], which implies the estimation (6.14).

Unfortunately, the method does not hold in higher dimensions because of the lack of information about random coverings of the sphere. Nevertheless, a different approach will be explained in the next section in order to extend (6.14) to d ≥ 3. □ 

Exercise 6.13.

For d = 2, estimate the minimal number of sides of the Poisson–Voronoi typical cell conditioned on {R _m  = r}.

Remark 6.11.

This roughly means that the boundary of the cell is included in an annulus centered at the origin and of thickness of order $R_{m}^{-(d-1)/(d+1)}$. The next problem would be to describe the shape of the polyhedron inside this annulus. For instance, in dimension two, a regular polygon which would be exactly “inscribed” in an annulus of thickness $R_{m}^{-1/3}$ would have about R _m ^2 ∕ 3 sides. Is it the same growth rate as the number of sides of the typical cell? The next section will be devoted to this problem. In particular, we shall see that indeed, this quantity behaves roughly as if the typical cell would be a deterministic regular polygon.

6.2.2 Limit Theorems for the Number of Hyperfaces

This section is based on arguments and results which come from a collaboration with T. Schreiber and are developed in [108–110]. When the inradius goes to infinity, the shape of the typical Poisson–Voronoi cell becomes spherical. In particular its boundary is contained in an annulus with a thickness going to zero and thus we aim at being more specific about the evolution of the geometry of the cell when R _m is large. For the sake of simplicity, we focus essentially on a particular quantity, which is the number of hyperfaces, but our methods can be generalized to investigate other characteristics, as emphasized in the final remarks.

6.2.2.1 Connection with Random Convex Hulls in the Ball

We start with the following observation: in the literature, there are more limit theorems available for random polytopes constructed as convex hulls of a Poisson point process than for typical cells of stationary tessellations (cf. Sects. 7.1 and 8.4.2). Models of random convex hulls have been probably considered as more natural objects to be constructed and studied. Our aim is first to connect our model of typical Poisson–Voronoi cell with a classical model of a random convex hull in the ball and then work on this possible link between the two in order to extend what is known about random polytopes and solve our current problem.

Conditionally on {R _m  ≥ r}, the rescaled typical cell $\frac{1} {r}Z(o)$ is equal in distribution to the zero-cell of a hyperplane tessellation generated by a Poisson point process of intensity measure ${(2r)}^{d}\mathbf{1}(x\,\in \,B_{1}{(o)}^{c})\,\nu _{d}(dx)$ [109]. In other words, via this scaling we fix the inradius of the polyhedron whereas the intensity of the underlying hyperplane process outside of the inball is now the quantity which goes to infinity.

The key idea is then to apply a geometric transformation to $\frac{1} {r}Z(o)$ in order to get a random convex hull inside the unit-ball B ₁(o). Let us indeed consider the inversion I defined by

$$I(x) = \frac{x} {\|{x\|}^{2}},\quad x \in {\mathbb{R}}^{d} \setminus \{ o\}.$$

In the following lines, we investigate the action of I on points, hyperplanes and the cell itself. The Poisson point process of intensity measure ${(2r)}^{d}\mathbf{1}(x\notin B_{1}(o))\,\nu _{d}(dx)$ is sent by I to a new Poisson point process Y _r of intensity measure ${(2r)}^{d}\mathbf{1}(x\,\in \,B_{1}(o)) \frac{1} {\|{x\|}^{2d}}\,\nu _{d}(dx)$. The hyperplanes are sent to spheres containing the origin and included in the unit ball, i.e. spheres $\partial B_{\|x\|/2}(x/2)$ where x belongs to the new Poisson point process Y _r in B ₁(o). The boundary of the rescaled typical cell $\frac{1} {r}Z(o)$ is sent to the boundary of a certain Voronoi flower, i.e. the union of balls $B_{\|x\|/2}(x/2)$ where x belongs to Y _r . In particular, the number of hyperfaces of the typical cell Z(o) remains unchanged after rescaling and can also be seen through the action of the inversion I as the number of portions of spheres on the boundary of the Voronoi flower in B ₁(o), that is the number of extreme points of the convex hull of the process Y _r . Indeed, it can be verified that the ball $B_{\|x\|/2}(x/2)$ intersects the boundary of the Voronoi flower of Y _r iff there exists a support hyperplane of the convex hull of Y _r which contains x.

6.2.2.2 Results

Let N _r be a random variable distributed as the number of hyperfaces of the typical cell Z(o) conditioned on {R _m  = r}.

We are now ready to derive limit theorems for the behaviour of N _r when r goes to infinity:

Theorem 6.5 (Limit theorems for the number of hyperfaces). 

There exists a constant a > 0 (known explicitly) depending only on d such that

$${\mathit{ar}}^{-\frac{d(d-1)} {d+1} }N_{r} \rightarrow 1\;\;\mbox{ in }{L}^{1}\ \text{and a.s. as}\ r \rightarrow \infty.$$

Moreover, the number N _r satisfies a central limit theorem when r →∞ as well as a moderate-deviation result: for every $\epsilon > 0$,

$$\mathop{\rm lim \ inf}\limits_{r\rightarrow \infty } \frac{1} {\log (r)}\log \left (-\log \left (\mathbf{P}\left \{{\biggl | \frac{N_{r}} {\mathbf{E}N_{r}} - 1\biggr |} \geq \epsilon \right \}\right )\right ) \geq \frac{d - 1} {3d + 5}.$$

Sketch of proof. The first two steps are devoted to proving the results for the number $\widetilde{N}_{r}$ of hyperfaces of Z(o) conditioned on {R _m  ≥ r}. In the last step, we explain how to adapt the arguments for the number N _r .

Step 1. :

We use the action of the inversion I to rewrite N _r as the number of vertices of the convex hull of the Poisson point process Y _r of intensity measure ${(2r)}^{d}\mathbf{1}(x \in B_{1}(o)) \frac{1} {\|{x\|}^{2d}}\,\nu _{d}(dx)$ in the unit ball. Limit theorems for the number of extreme points of a homogeneous set of points in the ball are classically known in the literature: indeed, a first law of large numbers has been established in [421] and generalized in [418]. A central limit theorem has been proved in [419] and extended by a precise variance estimate in [459]. Finally, a moderate deviations-type result has been provided in [110, 502] (see also Sects. 7.1 and 8.4.2 for more details).

Step 2. :

The only problem here is that we are not in the classical setting of all these previous works since the process Y _r is not homogeneous. Nevertheless, it can be overcome by emphasizing two points: first, when $\|x\|$ is close to one, the intensity measure of Y _r is close to (2r)^d ν _d (dx) and secondly, with high probability, only the points near the boundary of the unit sphere will be useful to construct the convex hull. Indeed, for any Poisson point process of intensity measure $\lambda f(\|x\|)\,\nu _{d}(dx)$ with $f : (0,1) \rightarrow \mathbb{R}_{+}$ a function such that lim _t → 1 f(t) = 1, it can be stated that the associated convex hull K _λ satisfies the following: there exist constants c, c′ > 0 such that for every $\alpha \in (0, \frac{2} {d+1})$, we have

$$\mathbf{P}(B_{1-c{\lambda }^{-\alpha }}(o)\not\subseteq K_{\lambda }) = \mathcal{O}(\exp \{-c^{\prime}{\lambda }^{1-\alpha (d+1)/2}\}).$$

(6.15)

The asymptotic result (6.15) roughly means that all extreme points are near ${\mathbb{S}}^{d-1}$ and included in an annulus of thickness ${\lambda }^{-2/(d+1)}$. It can be shown in the following way: we consider a deterministic covering of an annulus $B_{1}(o) \setminus B_{1-{\lambda }^{-\alpha }}(o)$ with a polynomial number of full spherical caps. When the Poisson point process intersects each of these caps, its convex hull contains $B_{1-c{\lambda }^{-\alpha }}(o)$ where c > 0 is a constant. Moreover, an estimation of the probability that at least one of the caps fails to meet the point process provides the right-hand side of (6.15).

To conclude, the estimation (6.15) allows us to apply the classical limit theory of random convex hulls in the ball even if the point process Y _r is not homogeneous.

Step 3. :

We recall that the difference between the constructions of Z(o) conditioned either on {R _m  ≥ r} or on {R _m  = r} is only an extra deterministic hyperplane at distance r from the origin. After the use of a rescaling and of the inversion I, we obtain that $\widetilde{N}_{r}$ (obtained with conditioning on {R _m  ≥ r}) is the number of extreme points of Y _r whereas N _r (obtained with conditioning on {R _m  = r}) is the number of extreme points of $Y _{r} \cup \{ x_{0}\}$ where x ₀ is a deterministic point on ${\mathbb{S}}^{d-1}$. A supplementary extreme point on ${\mathbb{S}}^{d-1}$ can “erase” some of the extreme points of Y _r but it can be verified that it will not subtract more than the number of extreme points contained in a d-dimensional polyhedron. Now the growth of extreme points of random convex hulls in a polytope has been shown to be logarithmic so we can consider that the effect of the extra point x ₀ is negligible (see in particular [48, 49, 375] about limit theorems for random convex hulls in a fixed polytope). Consequently, results proved for $\widetilde{N}_{r}$ in Steps 1–2 hold for N _r as well. □ 

Remark 6.12.

Up to now, the bounds on the conditional distribution of the circumscribed radius (6.14) was only proved in dimension two through techniques involving covering probabilities of the circle. Now applying the action of the inversion I once again, we deduce from (6.15) the generalization of the asymptotic result (6.14) to higher dimensions.

Remark 6.13.

The same type of limit theorems occurs for the Lebesgue measure of the region between the typical cell and its inball. Indeed, after application of I, this volume is equal to the μ-measure of the complementary of the Voronoi flower of the Poisson point process in the unit ball, where μ is the image of the Lebesgue measure under I. Limit theorems for this quantity have been obtained in [455, 456].

In a recent paper [111], this work is extended in several directions, including variance estimates and a functional central limit result for the volume of the typical cell. Moreover [111] contains an extreme value-type convergence for R _M which adds to (6.14) by providing a three-terms expansion of (R _M  − r) conditionally on {R _m  ≥ r}, when r goes to infinity. More precisely, it is proved that there exist explicit constants $c_{1},c_{2},c_{3} > 0$ (depending only on the dimension) such that conditionally on {R _m  ≥ r}, the quantity

$$\frac{{2}^{\frac{3d+1} {2} }\kappa _{d-1}} {d + 1} {r}^{\frac{d-1} {2} }{(R_{M} - r)}^{\frac{d+1} {2} } - c_{1}\log (r) - c_{2}\log (\log (r)) - c_{3}$$

converges in distribution to the Gumbel law when r → ∞.