Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

During the past decades, much attention has been given to the separation of mixed sources, in particular for the blind case where both the sources and the mixing process are unknown and only recordings of the mixtures are available. In several situations it is desirable to recover all sources from the recorded mixtures, or at least to segregate a particular source. Furthermore, it may be useful to identify the mixing process itself to reveal information about the physical mixing system.

In some simple mixing models each recording consists of a sum of differently weighted source signals. However, in many real-world applications, such as in acoustics, the mixing process is more complex. In such systems, the mixtures are weighted and delayed, and each source contributes to the sum with multiple delays corresponding to the multiple paths by which an acoustic signal propagates to a microphone. Such filtered sums of different sources are called convolutive mixtures. Depending on the situation, the filters may consist of a few delay elements, as in radio communications, or up to several thousand delay elements as in acoustics. In these situations the sources are the desired signals, yet only the recordings of the mixed sources are available and the mixing process is unknown.

There are multiple potential applications of convolutive blind source separation. In acoustics different sound sources are recorded simultaneously with possibly multiple microphones. These sources may be speech or music, or underwater signals recorded in passive sonar [52.1]. In radio communications, antenna arrays receive mixtures of different communication signals [52.2,3]. Source separation has also been applied to astronomical data or satellite images [52.4]. Finally, convolutive models have been used to interpret functional brain imaging data and biopotentials [52.5,6,7,8].

This chapter considers the problem of separating linear convolutive mixtures focusing in particular on acoustic mixtures. The cocktail-party problem has come to characterize the task of recovering speech in a room of simultaneous and independent speakers [52.9,10]. Convolutive blind source separation (BSS) has often been proposed as a possible solution to this problem as it carries the promise to recover the sources exactly. The theory on linear noise-free systems establishes that a system with multiple inputs (sources) and multiple output (sensors) can be inverted under some reasonable assumptions with appropriately chosen multidimensional filters [52.11]. The challenge lies in finding these convolution filters.

There are already a number of partial reviews available on this topic [52.12,13,14,15,16,17,18,19,20,21,22]. The purpose of this chapter is to provide a complete survey of convolutive BSS and identify a taxonomy that can organize the large number of available algorithms. This may help practitioners and researchers new to the area of convolutive source separation obtain a complete overview of the field. Hopefully those with more experience in the field can identify useful tools, or find inspiration for new algorithms. Figure 52.1 provides an overview of the different topics within convolutive BSS and in which section they are covered. An overview of published results is given in Sect. 52.7.

Fig. 52.1
figure 1

Overview of important areas within blind separation of convolutive sources

Full size image

The Mixing Model

First we introduce the basic model of convolutive mixtures. At the discrete time index t, a mixture of N source signals s(t) = [s 1(t),… , s N (t)]T are received at an array of M sensors. The received signals are denoted by x(t) = [x 1(t),… , x M (t)]T. In many real-world applications the sources are said to be convolutively (or dynamically) mixed. The convolutive model introduces the following relation between the m-th mixed signal, the original source signals, and some additive sensor noise v m (t):

(52.1)

The mixed signal is a linear mixture of filtered versions of each of the source signals, and a mnk represent the corresponding mixing filter coefficients. In practice, these coefficients may also change in time, but for simplicity the mixing model is often assumed stationary. In theory the filters may be of infinite length, which may be implemented as infinite impulse response (IIR) systems, however, in practice it is sufficient to assume K <∞. In matrix form the convolutive model can be written:

(52.2)

where A k is an M × N matrix that contains the k-th filter coefficients. v(t) is the M × 1 noise vector. In the z-domain the convolutive mixture (52.2) can be written:

(52.3)

where A(z) is a matrix with finite impulse response (FIR) polynomials in each entry [52.23].

Special Cases

There are some special cases of the convolutive mixture which simplify (52.2).

Instantaneous Mixing Model

Assuming that all the signals arrive at the sensors at the same time without being filtered, the convolutive mixture model (52.2) simplifies to

(52.4)

This model is known as the instantaneous or delayless (linear) mixture model. Here, A = A 0, is an M × N matrix containing the mixing coefficients. Many algorithms have been developed to solve the instantaneous mixture problem, see e.g., [52.17,24].

Delayed Sources

Assuming a reverberation-free environment with propagation delays the mixing model can be simplified to

(52.5)

where k mn is the propagation delay between source n and sensor m.

Noise Free

In the derivation of many algorithms, the convolutive model (52.2) is assumed to be noise-free, i.e.,

(52.6)

Over- and Underdetermined Sources

Often it is assumed that the number of sensors equals (or exceeds) the number of sources in which case linear methods may suffice to invert the linear mixing. However, if the number of sources exceeds the number of sensors the problem is underdetermined, and even under perfect knowledge of the mixing system linear methods will not be able to recover the sources.

Convolutive Model in the Frequency Domain

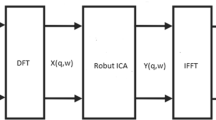
The convolutive mixing process (52.2) can be simplified by transforming the mixtures into the frequency domain. The linear convolution in the time domain can be written in the frequency domain as separate multiplications for each frequency:

(52.7)

At each frequency, ω = 2πf, A(ω) is a complex M × N matrix, X(ω) and V(ω) are complex M × 1 vectors, and similarly S(ω) is a complex N × 1 vector. The frequency transformation is typically computed using a discrete Fourier transform (DFT) within a time frame of length T starting at time t:

(52.8)

and correspondingly for S(ω, t) and V(ω, t). Often a windowed discrete Fourier transform is used:

(52.9)

where the window function w(τ) is chosen to minimize band overlap due to the limited temporal aperture. By using the fast Fourier transform (FFT) convolutions can be implemented efficiently in the discrete Fourier domain, which is important in acoustics as it often requires long time-domain filters.

Block-Based Model

Instead of modeling individual samples at time t one can also consider a block consisting of T samples. The equations for such a block can be written as:

The M-dimensional output sequence can be written as an MT × 1 vector:

(52.10)

where x T(t) = [x 1(t),⋯ , x M (t)]. Similarly, the N-dimensional input sequence can be written as an N(T + K − 1) × 1 vector:

(52.11)

From this the convolutive mixture can be expressed formally as:

(52.12)

where has the following form:

(52.13)

The block-Toeplitz matrix has dimensions MT × N(T + K − 1). On the surface, (52.12) has the same structure as an instantaneous mixture given in (52.4), and the dimensionality has increased by a factor T. However, the models differ considerably as the elements within and are now coupled in a rather specific way.

The majority of the work in convolutive source separation assumes a mixing model with a finite impulse response as in (52.2). A notable exception is the work by Cichocki, which also considers an autoregressive (AR) component as part of the mixing model [52.18]. The autoregressive moving-average (ARMA) mixing system proposed there is equivalent to a first-order Kalman filter with an infinite impulse response.

The Separation Model

The objective of blind source separation is to find an estimate y(t) that is a model of the original source signals s(t). For this, it may not be necessary to identify the mixing filters A k explicitly. Instead, it is often sufficient to estimate separation filters W l that remove the cross-talk introduced by the mixing process. These separation filters may have a feed-back structure with an infinite impulse response, or may have a finite impulse response expressed as feedforward structure.

Feedforward Structure

An FIR separation system is given by

(52.14)

or in matrix form

(52.15)

As with the mixing process, the separation system can be expressed in the z-domain as

(52.16)

and can also be expressed in block-Toeplitz form with the corresponding definitions for and [52.25]:

(52.17)

Table 52.1 summarizes the mixing and separation equations in the different domains.

Table 52.1 The convolutive mixing equation and its corresponding separation equation for different domains in which blind source separation algorithms have been derived
Full size table

Relation Between Source and Separated Signals

The goal in source separation is not necessarily to recover identical copies of the original sources. Instead, the aim is to recover model sources without interferences from other sources, i.e., each separated signal y n (t) should contain signals originating from a single source only (Fig. 52.3). Therefore, each model source signal can be a filtered version of the original source signals, i.e.,

(52.18)

as illustrated in Fig. 52.2. The criterion for separation, i.e., interference-free signals, is satisfied if the recovered signals are permuted, and possibly scaled and filtered versions of the original signals, i.e.,

(52.19)

where P is a permutation matrix, and Λ(z) is a diagonal matrix with scaling filters on its diagonal. If one can identify A(z) exactly, and choose W(z) to be its (stable) inverse, then Λ(z) is an identity matrix, and one recovers the sources exactly. In source separation, instead, one is satisfied with convolved versions of the sources, i.e., arbitrary diagonal Λ(z).

Fig. 52.2
figure 2

The source signals Y(z) are mixed with the mixing filter A(z). An estimate of the source signals is obtained through an unmixing process, where the received signals X(z) are unmixed with the filter W(z). Each estimated source signal is then a filtered version of the original source, i.e., G(z) = W(z)A(z). Note that the mixing and the unmixing filters do not necessarily have to be of the same order

Full size image
Fig. 52.3
figure 3

Illustration of a speech source. It is not always clear what the desired acoustic source should be. It could be the acoustic wave as emitted from the mouth. This corresponds to the signal as it would have been recorded in an anechoic chamber in the absence of reverberations. It could be the individual source as it is picked up by a microphone array, or it could be the speech signal as it is recorded on microphones close to the two eardrums of a person. Due to reverberations and diffraction, the recorded speech signal is most likely a filtered version of the signal at the mouth

Full size image

Feedback Structure

The mixing system given by (52.2) is called a feedforward system. Often such FIR filters are inverted by a feedback structure using IIR filters. The estimated sources are then given by the following equation, where the number of sources equals the number of receivers:

(52.20)

and u nml are the IIR filter coefficients. This can also be written in matrix form

(52.21)

The architecture of such a network is shown in Fig. 52.4. In the z-domain, (52.21) can be written as [52.26]

(52.22)

provided [I + U(z)]−1 exists and all poles are within the unit circle. Therefore,

(52.23)

The feedforward and the feedback network can be combined to a so-called hybrid network, where a feedforward structure is followed by a feedback network [52.27,28].

Fig. 52.4
figure 4

Recurrent unmixing (feedback) network given by equation (52.21). The received signals are separated by an IIR filter to achieve an estimate of the source signals

Full size image

Example: The TITO System

A special case, which is often used in source separation work is the two-input-two-output (TITO) system [52.29]. It can be used to illustrate the relationship between the mixing and unmixing system, feedforward and feedback structures, and the difference between recovering sources versus generating separated signals.

Figure 52.5 shows a diagram of a TITO mixing and unmixing system. The signals recorded at the two microphones are described by the following equations:

(52.24)
(52.25)

The mixing system is thus given by

(52.26)

which has the following inverse

(52.27)

If the two mixing filters a 12(z) and a 21(z) can be identified or estimated as and , the separation system can be implemented as

(52.28)
(52.29)

A sufficient FIR separating filter is

(52.30)

However, the exact sources are not recovered until the model sources y(t) are filtered with the IIR filter . Thus, the mixing process is invertible, provided that the inverse IIR filter is stable. If a filtered version of the separated signals is acceptable, we may disregard the potentially unstable recursive filter in (52.27) and limit separation to the FIR inversion of the mixing system with (52.30).

Fig. 52.5
figure 5

The two mixed sources s 1 and s 2 are mixed by an FIR mixing system. The system can be inverted by an alternative system if the estimates and of the mixing filters a 12(z) and a 12(z) are known. Furthermore, if the filter is stable, the sources can be perfectly reconstructed as they were recorded at the microphones

Full size image

Identification

Blind identification deals with the problem of estimating the coefficients in the mixing process A k . In general, this is an ill-posed problem, and no unique solution exists. In order to determine the conditions under which the system is blindly identifiable, assumptions about the mixing process and the input data are necessary. Even though the mixing parameters are known, this does not imply that the sources can be recovered. Blind identification of the sources refers to the exact recovery of sources. Therefore one should distinguish between the conditions required to identify the mixing system and the conditions necessary to identify the sources. The limitations for the exact recovery of sources when the mixing filters are known are discussed in [52.11,30,31]. For a recent review on identification of acoustic systems see [52.32]. This review considers systems with single and multiple inputs and outputs for the case of completely known sources as well as blind identification, where both the sources and the mixing channels are unknown.

Separation Principle

Blind source separation algorithms are based on different assumptions on the sources and the mixing system. In general, the sources are assumed to be independent or at least uncorrelated. The separation criteria can be divided into methods based on higher-order statistics (HOS), and methods based on second-order statistics (SOS). In convolutive separation it is also assumed that sensors receive N linearly independent versions of the sources. This means that the sources should originate from different locations in space (or at least emit signals into different orientations) and that there are at least as many sources as sensors for separation, i.e., M ≥ N.

Instead of spatial diversity a series of algorithms make strong assumptions on the statistics of the sources. For instance, they may require that sources do not overlap in the time-frequency domain, utilizing therefore a form of sparseness in the data. Similarly, some algorithms for acoustic mixtures exploit regularity in the sources such as common onset, harmonic structure, etc. These methods are motivated by the present understanding on the grouping principles of auditory perception commonly referred to as auditory scene analysis. In radio communications a reasonable assumption on the sources is cyclo-stationarity or the fact that source signals take on only discrete values. By using such strong assumptions on the source statistics it is sometimes possible to relax the conditions on the number of sensors, e.g., M < N. The different criteria for separation are summarized in Table 52.2.

Table 52.2 Assumptions made for separation
Full size table

Higher-Order Statistics

Source separation based on higher-order statistics is based on the assumption that the sources are statistically independent. Many algorithms are based on minimizing second and fourth order dependence between the model signals. A way to express independence is that all the cross-moments between the model sources are zero, i.e.,

(52.31)

for all τ, α, β ={ 1, 2,…}, and n ≠ n′. Here E[⋅] denotes the statistical expectation. Successful separation using higher-order moments requires that the underlying sources are non-Gaussian (with the exception of at most one), since Gaussian sources have zero higher cumulants [52.60] and therefore equations (52.31) are trivially satisfied without providing useful conditions.

Fourth-Order Statistics

It is not necessary to minimize all cross-moments in order to achieve separation. Many algorithms are based on minimization of second- and fourth-order dependence between the model source signals. This minimization can either be based on second and fourth order cross-moments or second- and fourth-order cross-cumulants. Whereas off-diagonal elements of cross-cumulants vanish for independent signals the same is not true for all cross-moments [52.61]. Source separation based on cumulants has been used by several authors. Separation of convolutive mixtures by means of fourth-order cumulants has also been addressed [52.35,61,62,63,64,65,66,67,68,69,70,71]. In [52.72,73,74], the joint approximate diagonalization of eigenmatrices (JADE) algorithm for complex-valued signals [52.75] was applied in the frequency domain in order to separate convolved source signals. Other cumulant-based algorithms in the frequency domain are given in [52.76,77]. Second- and third-order cumulants have been used by Ye et al. [52.33] for separation of asymmetric signals. Other algorithms based on higher-order cumulants can be found in [52.78,79]. For separation of more sources than sensors, cumulant-based approaches have been proposed in [52.70,80]. Another popular fourth-order measure of non-Gaussianity is kurtosis. Separation of convolutive sources based on kurtosis has been addressed in [52.81,82,83].

Nonlinear Cross-Moments

Some algorithms apply higher-order statistics for separation of convolutive sources indirectly using nonlinear functions by requiring:

(52.32)

where f(⋅) and g(⋅) are odd, nonlinear functions. The Taylor expansion of these functions captures higher-order moments and this is found to be sufficient for separation of convolutive mixtures. This approach was among of the first for separation of convolutive mixtures [52.53] extending an instantaneous blind separation algorithm by Herault and Jutten (H-J) [52.84]. In Back and Tsoi [52.85], the H-J algorithm was applied in the frequency domain, and this approach was further developed in [52.86]. In the time domain, the approach of using nonlinear odd functions has been used by Nguyen Thi and Jutten [52.26]. They present a group of TITO (2 × 2) algorithms based on fourth-order cumulants, nonlinear odd functions, and second- and fourth-order cross-moments. This algorithm has been further examined by Serviere [52.54], and also been used by Ypma et al. [52.55]. In Cruces and Castedo [52.87] a separation algorithm can be found, which can be regarded as a generalization of previous results from [52.26,88]. In Li and Sejnowski [52.89], the H-J algorithm has been used to determine the delays in a beamformer. The H-J algorithm has been investigated further by Charkani and Deville [52.57,58,90]. They extended the algorithm further to colored sources [52.56,91]. Depending on the distribution of the source signals, optimal choices of nonlinear functions were also found. For these algorithms, the mixing process is assumed to be minimum-phase, since the H-J algorithm is implemented as a feedback network. A natural gradient algorithm based on the H-J network has been applied in Choi et al. [52.92]. A discussion of the H-J algorithm for convolutive mixtures can be found in Berthommier and Choi [52.93]. For separation of two speech signals with two microphones, the H-J model fails if the two speakers are located on the same side, as the appropriate separating filters can not be implemented without delaying one of the sources and the FIR filters are constrained to be causal. HOS independence obtained by applying antisymmetric nonlinear functions has also been used in [52.94,95].

Information-Theoretic Methods

Statistical independence between the source signals can also be expressed in terms of the joint probability function (PDF). If the model sources y are independent, the joint PDF can be written as

(52.33)

This is equivalent to stating that model sources y n do not carry mutual information. Information-theoretic methods for source separation are based on maximizing the entropy in each variable. Maximum entropy is obtained when the sum of the entropy of each variable y n equals the total joint entropy in y. In this limit variables do not carry any mutual information and are hence mutually independent [52.96]. A well-known algorithm based on this idea is the Infomax algorithm by Bell and Sejnowski [52.97], which was significantly improved in convergence speed by the natural gradient method of Amari [52.98]. The Infomax algorithm can also be derived directly from model equation (52.33) using maximum likelihood [52.99], or equivalently, using the Kullback-Leibler divergence between the empirical distribution and the independence model [52.100].

In all instances it is necessary to assume, or model, the probability density functions p s (s n ) of the underlying sources s n . In doing so, one captures higher-order statistics of the data. In fact, most information-theoretic algorithms contain expressions rather similar to the nonlinear cross-statistics in (52.32) with f(y n ) =∂  ln p s (y n )/∂y n , and g(y n ) = y n . The PDF is either assumed to have a specific form or it is estimated directly from the recorded data, leading to parametric and nonparametric methods, respectively [52.16]. In nonparametric methods the PDF is captured implicitly through the available data. Such methods have been addressed [52.101,102,103]. However, the vast majority of convolutive algorithms have been derived based on explicit parametric representations of the PDF.

Infomax, the most common parametric method, was extended to the case of convolutive mixtures by Torkkola [52.59] and later by Xi and Reilly [52.104,105]. Both feedforward and feedback networks were used. In the frequency domain it is necessary to define the PDF for complex variables. The resulting analytic nonlinear functions can be derived as [52.106,107]

(52.34)

where p(Y) is the probability density of the model source Y ∈ℂ. Some algorithms assume circular sources in the complex domain, while other algorithms have been proposed that specifically assume noncircular sources [52.108,109].

The performance of the algorithm depends to a certain degree on the selected PDF. It is important to determine if the data has super-Gaussian or sub-Gaussian distributions. For speech commonly a Laplace distribution is used. The nonlinearity is also known as the Bussgang nonlinearity [52.110]. A connection between the Bussgang blind equalization algorithms and the Infomax algorithm is given in Lambert and Bell [52.111]. Multichannel blind deconvolution algorithms derived from the Bussgang approach can be found in [52.23,111,112]. These learning rules are similar to those derived in Lee et al. [52.113].

Choi et al. [52.114] have proposed a nonholonomic constraint for multichannel blind deconvolution. Nonholonomic means that there are some restrictions related to the direction of the update. The nonholonomic constraint has been applied for both a feedforward and a feedback network. The nonholonomic constraint was applied to allow the natural gradient algorithm by Amari et al. [52.98] to cope with overdetermined mixtures. The nonholonomic constraint has also been used in [52.115,116,117,118,119,120,121,122]. Some drawbacks in terms of stability and convergence in particular when there are large power fluctuations within each signal (e.g., for speech) have been addressed in [52.115].

Many algorithms have been derived from (52.33) directly using maximum likelihood (ML) [52.123]. The ML approach has been applied in [52.99,124,125,126,127,128,129,130,131,132]. Closely related to the ML are the maximum a posteriori (MAP) methods. In MAP methods, prior information about the parameters of the model are taken into account. MAP has been used in [52.23,133,134,135,136,137,138,139,140,141].

The convolutive blind source separation problem has also been expressed in a Bayesian formulation [52.142]. The advantage of a Bayesian formulation is that one can derive an optimal, possibly nonlinear, estimator of the sources enabling the estimation of more sources than the number of available sensors. The Bayesian framework has also been applied [52.135,137,143,144,145].

A strong prior on the signal can also be realized via hidden Markov models (HMMs). HMMs can incorporate state transition probabilities of different sounds [52.136]. A disadvantage of HMMs is that they require prior training and they carry a high computational cost [52.146]. HMMs have also been used in [52.147,148].

Second-Order Statistics

In some cases, separation can be based on second-order statistics (SOS) by requiring only uncorrelated sources rather then the stronger condition of independence. Instead of assumptions on higher-order statistics these methods make alternate assumptions such as the nonstationarity of the sources [52.149], or a minimum-phase mixing system [52.50]. By itself, however, second-order conditions are not sufficient for separation. Sufficient conditions for separation are given in [52.15,150]. The main advantage of SOS is that they are less sensitive to noise and outliers [52.13], and hence require less data for their estimation [52.34,50,150,151,152]. The resulting algorithms are often also easier to implement and computationally efficient.

Minimum-Phase Mixing

Early work by Gerven and Compernolle [52.88] had shown that two source signals can be separated by decorrelation if the mixing system is minimum-phase. The FIR coupling filters have to be strictly causal and their inverses stable. The condition for stability is given as |a 12(z)a 21(z)| < 1, where a 12(z) and a 21(z) are the two coupling filters (Fig. 52.5). These conditions are not met if the mixing process is non-minimum-phase [52.153]. Algorithms based on second-order statistic assuming minimum-phase mixing can be found in [52.41,42,50,51,52,154,155,156,157,158].

Nonstationarity

The fact that many signals are nonstationary has been successfully used for source separation. Speech signals in particular can be considered non-stationary on time scales beyond 10 ms [52.159,160]). The temporally varying statistics of nonstationarity sources provides additional information for separation. Changing locations of the sources, on the other hand, generally complicate source separation as the mixing channel changes in time. Separation based on decorrelation of nonstationary signals was proposed by Weinstein et al. [52.29], who suggested that minimizing cross-powers estimated during different stationarity times should give sufficient conditions for separation. Wu and Principe proposed a corresponding joint diagonalization algorithm [52.103,161] extending an earlier method developed for instantaneous mixtures [52.162]. Kawamoto et al. extend an earlier method [52.163] for instantaneous mixtures to the case of convolutive mixtures in the time domain [52.153,164] and frequency domain [52.165]. This approach has also been employed in [52.166,167,168,169] and an adaptive algorithm was suggested by Aichner et al. [52.170]. By combining this approach with a constraint based on whiteness, the performance can be further improved [52.171].

Note that not all of these papers have used simultaneous decorrelation, yet, to provide sufficient second-order constraints it is necessary to minimize multiple cross-correlations simultaneously. An effective frequency-domain algorithm for simultaneous diagonalization was proposed by Parra and Spence [52.149]. Second-order statistics in the frequency domain is captured by the cross-power spectrum,

(52.35)
(52.36)

where the expectations are estimated around some time t. The goal is to minimize the cross-powers represented by the off-diagonal elements of this matrix, e.g., by minimizing:

(52.37)

where Λ y (ω, t) is an estimate of the cross-power spectrum of the model sources and is assumed to be diagonal. This cost function simultaneously captures multiple times and multiple frequencies, and has to be minimized with respect to W(ω) and Λ y (ω, t) subject to some normalization constraint. If the source signals are nonstationary the cross-powers estimated at different times t differ and provide independent conditions on the filters W(ω). This algorithm has been successfully used on speech signals [52.172,173] and investigated further by Ikram and Morgan [52.174,175,176] to determine the trade-offs between filter length, estimation accuracy, and stationarity times. Long filters are required to cope with long reverberation times of typical room acoustics, and increasing filter length also reduces problems associated with the circular convolution in (52.36) (see Sect. 52.5.3). However, long filters increase the number of parameters to be estimated and extend the effective window of time required for estimating cross-powers, thereby potentially losing the benefit of the nonstationarity of speech signals. A number of variations of this algorithm have been proposed subsequently, including time-domain implementations [52.177,178,179], and other methods that incorporate additional assumptions [52.174,180,181,182,183,184,185,186,187]. A recursive version of the algorithm was given in Ding et al. [52.188]. In Robeldo-Arnuncio and Juang [52.189], a version with noncausal separation filters was suggested. Based on a different way to express (52.36), Wang et al. [52.148,190,191,192] proposed a slightly different separation criterion that leads to a faster convergence than the original algorithm by Parra and Spence [52.149].

Other methods that exploit nonstationarity have been derived by extending the algorithm of Molgedey and Schuster [52.193] to the convolutive case [52.194,195] including a common two-step approach of sphering and rotation [52.159,196,197,198,199]. (Any matrix, for instance matrix W, can be represented as a concatenation of a rotation with subsequent scaling, which can be used to remove second-order moments, i.e., sphering, and an additional rotation.)

In Yin and Sommen [52.160] a source separation algorithm was presented based on nonstationarity and a model of the direct path. The reverberant signal paths are considered as noise. A time-domain decorrelation algorithm based on different cross-correlations at different time lags is given in Ahmed et al. [52.200]. In Yin and Sommen [52.201] the cost function is based on minimization of the power spectral density between the source estimates. The model is simplified by assuming that the acoustic transfer function between the source and closely spaced microphones is similar. The simplified model requires fewer computations. An algorithm based on joint diagonalization is suggested in Rahbar and Reilly [52.152,152]. This approach exploits the spectral correlation between the adjacent frequency bins in addition to nonstationarity. Also in [52.202,203] a diagonalization criterion based on nonstationarity was used.

In Olsson and Hansen [52.138,139] the nonstationary assumption has been included in a state-space Kalman filter model.

In Buchner et al. [52.204], an algorithm that uses a combination of non-stationarity, non-Gaussianity, and nonwhiteness has been suggested. This has also been applied in [52.205,206,207]. In the case of more source signals than sensors, an algorithm based on nonstationarity has also been suggested [52.70]. In this approach, it is possible to separate three signals: a mixture of two nonstationary source signals with short-time stationarity and one signal that is long-term stationary. Other algorithms based on the nonstationary assumptions can be found in [52.208,209,210,211,212,213,214].

Cyclo-Stationarity

If a signal is assumed to be cyclo-stationary, its cumulative distribution is invariant with respect to time shifts of some period T multiples thereof. Further, a signal is said to be wide-sense cyclo-stationary if the signals mean and autocorrelation is invariant to shifts of some period T [52.215], i.e.,

(52.38)
(52.39)

An example of a cyclo-stationary signal is a random-amplitude sinusoidal signal. Many communication signals have the property of cyclo-stationarity, and voiced speech is sometimes considered approximately cyclo-stationary [52.216]. This property has been used explicitly to recover mixed sources in, e.g., [52.34,55,118,216,217,218,219,220,221,222]. In [52.220] cyclo-stationarity is used to solve the frequency permutation problem (see Sect. 52.5.1) and in [52.118] it is used as additional criteria to improve separation performance.

Nonwhiteness

Many natural signals, in particular acoustic signals, are temporally correlated. Capturing this property can be beneficial for separation. For instance, capturing temporal correlations of the signals can be used to reduce a convolutive problem to an instantaneous mixture problem, which is then solved using additional properties of the signal [52.25,38,39,40,41,42,43]. In contrast to instantaneous separation where decorrelation may suffice for nonwhite signals, for convolutive separation additional conditions on the system or the sources are required. For instance, Mei and Yin [52.223] suggest that decorrelation is sufficient provided the sources are an ARMA process.

Sparseness in the Time/Frequency Domain

Numerous source separation applications are limited by the number of available microphones. It is in not always guaranteed that the number of sources is less than or equal to the number of sensors. With linear filters it is in general not possible to remove more than M − 1 interfering sources from the signal. By using nonlinear techniques, in contrast, it may be possible to extract a larger number of source signals. One technique to separate more sources than sensors is based on sparseness. If the source signals do not overlap in the time-frequency (T-F) domain it is possible to separate them. A mask can be applied in the T-F domain to attenuate interfering signal energy while preserving T-F bins where the signal of interest is dominant. Often a binary mask is used giving perceptually satisfactory results even for partially overlapping sources [52.224,225]. These methods work well for anechoic (delay-only) mixtures [52.226]. However, under reverberant conditions, the T-F representation of the signals is less sparse. In a mildly reverberant environment (T 60 ≤200  ms) underdetermined sources have been separated with a combination of independent component analysis (ICA) and T-F masking [52.47]. The first N − M signals are removed from the mixtures by applying a T-F mask estimated from the direction of arrival of the signal (Sect. 52.6.1). The remaining M sources are separated by conventional BSS techniques. When a binary mask is applied to a signal, artifacts (musical noise) are often introduced. In order to reduce the musical noise, smooth masks have been proposed [52.47,227].

Sparseness has also been used as a postprocessing step. In [52.77], a binary mask has been applied as post-processing to a standard BSS algorithm. The mask is determined by comparison of the magnitude of the outputs of the BSS algorithm. Hereby a higher signal-to-interference ratio is obtained. This method was further developed by Pedersen et al. in order to segregate underdetermined mixtures [52.228,229]. Because the T-F mask can be applied to a single microphone signal, the segregated signals can be maintained as, e.g., in stereo signals.

Most T-F masking methods do not effectively utilize information from more than two microphones because the T-F masks are applied to a single microphone signal. However, some methods have been proposed that utilize information from more than two microphones [52.225,230].

Clustering has also been used for sparse source separation [52.140,141,230,231,232,233,234,235,236]. If the sources are projected into a space where each source groups together, the source separation problem can be solved with clustering algorithms. In [52.45,46] the mask is determined by clustering with respect to amplitude and delay differences.

In particular when extracting sources from single channels sparseness becomes an essential criterion. Pearlmutter and Zador [52.237] use strong prior information on the source statistic in addition to knowledge of the head-related transfer functions (HRTF). An a priori dictionary of the source signals as perceived through a HRTF makes it possible to separate source signals with only a single microphone. In [52.238], a priori knowledge is used to construct basis functions for each source signals to segregate different musical signals from their mixture. Similarly, in [52.239,240] sparseness has been assumed in order to extract different music instruments.

Techniques based on sparseness are further discussed in the survey by OʼGrady et al. [52.21].

Priors from Auditory Scene Analysis and Psychoacoustics

Some methods rely on insights gained from studies of the auditory system. The work by Bergman [52.241] on auditory scene analysis characterized the cues used by humans to segregate sound sources. This motivated computational algorithms that are referred to as computational auditory scene analysis (CASA). For instance, the phenomenon of auditory masking (the dominant perception of the signal with largest power) has motivated the use of T-F masking for many year [52.242]. In addition to the direct T-F masking methods outlined above, separated sources have been enhanced by filtering based on perceptual masking and auditory hearing thresholds [52.191,243].

Another important perceptual cue that has been used in source separation is pitch frequency, which typically differs for simultaneous speakers [52.135,137,138,147,244,245]. In Tordini and Piazza [52.135] pitch is extracted from the signals and used in a Bayesian framework. During unvoiced speech, which lacks a well-defined pitch they use an ordinary blind algorithm. In order to separate two signals with one microphone, Gandhi and Hasegawa-Johnson [52.137] proposed a state-space separation approach with strong a priori information. Both pitch and mel-frequency cepstral coefficients (MFCC) were used in their method. A pitch codebook as well as an MFCC codebook have to be known in advance. Olsson and Hansen [52.138] used an HMM, where the sequence of possible states is limited by the pitch frequency that is extracted in the process. As a preprocessing step to source separation, Furukawa et al. [52.245] use pitch in order to determine the number of source signals.

A method for separation of more sources than sensors is given in Barros et al. [52.244]. They combined ICA with CASA techniques such as pitch tracking and auditory filtering. Auditory filter banks are used in order to model the cochlea. In [52.244] wavelet filtering has been used for auditory filtering. Another commonly used auditory filter bank is the Gammatone filter-bank (see, e.g., Patterson [52.246] or [52.247,248]). In Roman et al. [52.248] binaural cues have been used to segregate sound sources, whereby interaural time and interaural intensity differences (ITD and IID) have been used to group the source signals.

Time Versus Frequency Domain

The blind source separation problem can either be expressed in the time domain

(52.40)

or in the frequency domain

(52.41)

A survey of frequency-domain BSS is provided in [52.22]. In Nishikawa et al. [52.249] the advantages and disadvantages of the time and frequency-domain approaches are compared. This is summarized in Table 52.3.

Table 52.3 Advantages and disadvantages of separation in the time and frequency domain
Full size table

An advantage of blind source separation in the frequency domain is that the separation problem can be decomposed into smaller problems for each frequency bin in addition to the significant gains in computational efficiency. The convolutive mixture problem is reduced to instantaneous mixtures for each frequency. Although this simplifies the task of convolutive separation a set of new problems arise: the frequency-domain signals obtained from the DFT are complex-valued. Not all instantaneous separation algorithms are designed for complex-valued signals. Consequently, it is necessary to modify existing algorithms correspondingly [52.5,250,251,252]. Another problem that may arise in the frequency domain is that there are no longer enough data points available to evaluate statistical independence [52.131]. For some algorithms [52.149] the frame size T of the DFT has to be much longer than the length of the room impulse response K (Sect. 52.5.3). Long frames result in fewer data samples per frequency [52.131], which complicates the estimation of the independence criteria. A method that addresses this issue has been proposed by Servière [52.253].

Frequency Permutations

Another problem that arises in the frequency domain is the permutation and scaling ambiguity. If separation is treated for each frequency bin as a separate problem, the source signals in each bin may be estimated with an arbitrary permutation and scaling, i.e.,

(52.42)

If the permutation P(ω) is not consistent across frequency then converting the signal back to the time domain will combine contributions from different sources into a single channel, and thus annihilate the separation achieved in the frequency domain. An overview of the solutions to this permutation problem is given in Sect. 52.6. The scaling indeterminacy at each frequency - the arbitrary solution for Λ(ω) - will result in an overall filtering of the sources. Hence, even for perfect separation, the separated sources may have a different frequency spectrum than the original sources.

Time-Frequency Algorithms

Algorithms that define a separation criteria in the time domain do typically not exhibit frequency permutation problems, even when computations are executed in the frequency domain. A number of authors have therefore used time-domain (TD) criteria combined with frequency-domain implementations that speed up computations [52.101,113,121,171,179,254,255,256,257]. However, note that second-order criteria may be susceptible to the permutation problem even if they are formulated in the time domain [52.184].

Circularity Problem

When the convolutive mixture in the time domain is expressed in the frequency domain by the DFT, the convolution becomes separate multiplications, i.e.,

(52.43)

However, this is only an approximation which is exact only for periodic s(t) with period T, or equivalently, if the time convolution is circular:

(52.44)

For a linear convolution errors occur at the frame boundary, which are conventionally corrected with the overlap-save method. However, a correct overlap-save algorithm is difficult to implement when computing cross-powers such as in (52.36) and typically the approximate expression (52.43) is assumed.

The problem of linear/circular convolution has been addressed by several authors [52.62,121,149,171,258]. Parra and Spence [52.149] note that the frequency-domain approximation is satisfactory provided that the DFT length T is significantly larger than the length of the un-mixing channels. In order to reduce the errors due to the circular convolution, the filters should be at least two times the length of the un-mixing filters [52.131,176].

To handle long impulse responses in the frequency domain, a frequency model which is equivalent to the time-domain linear convolution has been proposed in [52.253]. When the time-domain filter extends beyond the analysis window the frequency response is undersampled [52.22,258]. These errors can be mitigated by spectral smoothing or equivalently by windowing in the time domain. According to [52.259] the circularity problem becomes more severe when the number of sources increases.

Time-domain algorithms are often derived using Toeplitz matrices. In order to decrease the complexity and improve computational speed, some calculations involving Toeplitz matrices are performed using the fast Fourier transform. For that purpose, it is necessary to express the Toeplitz matrices in circulant Toeplitz form [52.23,121,171,195,260,261]. A method that avoids the circularity effects but maintains the computational efficiency of the FFT has been presented in [52.262]. Further discussion on the circularity problem can be found in [52.189].

Subband Filtering

Instead of the conventional linear Fourier domain some authors have used subband processing. In [52.142] a long time-domain filter is replaced by a set of short independent subband filters, which results in faster convergence as compared to the full-band methods [52.214]. Different filter lengths for each subband filter have also been proposed, motivated by the varying reverberation time of different frequencies (typically low frequencies have a longer reverberation time) [52.263].

The Permutation Ambiguity

The majority of algorithms operate in the frequency domain due to the gains in computational efficiency, which are important in particular for acoustic mixtures that require long filters. However, in frequency-domain algorithms the challenge is to solve the permutation ambiguity, i.e., to make the permutation matrix P(ω) independent of frequency. Especially when the number of sources and sensors is large, recovering consistent permutations is a severe problem. With N model sources there are N! possible permutations in each frequency bin. Many frequency-domain algorithms provide ad hoc solutions, which solve the permutation ambiguity only partially, thus requiring a combination of different methods. Table 52.4 summarizes different approaches. They can be grouped into two categories:

  1. 1.

    Consistency of the filter coefficients

  2. 2.

    Consistency of the spectrum of the recovered signals

The first exploits prior knowledge about the mixing filters, and the second uses prior knowledge about the sources. Within each group the methods differ in the way consistency across frequency is established, varying sometimes in the metric they use to measure distance between solutions at different frequencies.

Table 52.4 Categorization of approaches to solve the permutation problem in the frequency domain
Full size table

Consistency of the Filter Coefficients

Different methods have been used to establish consistency of filter coefficients across frequency, such as constraints on the length of the filters, geometric information, or consistent initialization of the filter weights.

Consistency across frequency can be achieved by requiring continuity of filter values in the frequency domain. One may do this directly by comparing the filter values of neighboring frequencies after adaptation, and pick the permutation that minimize the Euclidean distance between neighboring frequencies [52.74,269]. Continuity (in a discrete frequency domain) is also expressed as smoothness, which is equivalent with a limited temporal support of the filters in the time domain. The simplest way to implement such a smoothness constraint is by zero-padding the time-domain filters prior to performing the frequency transformation [52.264]. Equivalently, one can restrict the frequency-domain updates to have a limited support in the time domain. This method is explained in Parra et al. [52.149] and has been used extensively [52.119,122,161,174,188,190,192,201,269,283]. Ikram and Morgan [52.174,176] evaluated this constraint and point out that there is a trade-off between the permutation alignment and the spectral resolution of the filters. Moreover, restricting the filter length may be problematic in reverberant environments where long separation filters are required. As a solution they have suggest to relax the constraint on filter length after the algorithm converges to satisfactory solutions [52.176].

Another suggestion is to assess continuity after accounting for the arbitrary scaling ambiguity. To do so, the separation matrix can be normalized as proposed in [52.265]:

(52.45)

where Λ(ω) is a diagonal matrix and is a matrix with unit diagonal. The elements of , are the ratios between the filters and these are used to assess continuity across frequencies [52.48,220].

Instead of restricting the unmixing filters, Pham et al. [52.202] have suggested to require continuity in the mixing filters, which is reasonable as the mixing process will typically have a shorter time constant. A specific distance measure has been proposed by Asano et al. [52.267,284]. They suggest to use the cosine between the filter coefficients of different frequencies ω 1 and ω 2:

(52.46)

where a n (ω) is the n-th column vector of A(ω), which is estimated as the pseudo-inverse of W(ω). Measuring distance in the space of separation filters rather than mixing filters was also suggested because these may better reflect the spacial configuration of the sources [52.285].

In fact, continuity across frequencies may also be assessed in terms of the estimated spatial locations of sources. Recall that the mixing filters are impulse responses between the source locations and the microphone locations. Therefore, the parameters of the separation filters should account for the position of the source in space. Hence, if information about the sensor location is available it can be used to address the permutation problem.

To understand this, consider the signal that arrives at an array of sensors. Assuming a distant source in an reverberation-free environment the signal approximates a plane wave. If the plane wave arrives at an angle to the microphone array it will impinge on each microphone with a certain delay (Fig. 52.6). This delay τ is given by the microphone distance d, the velocity of the wave c, and the direction-of-arrival (DOA) angle θ:

(52.47)

Filters that compensate for this delay can add the microphone signals constructively (or destructively) to produce a maximum (or minimum) response in the DOA. Hence, the precise delay in filters (which in the frequency domain correspond to precise phase relationships) establishes a relationship between different frequencies that can be used to identify correct permutations. This was first considered by Soon et al. [52.286].

Fig. 52.6
figure 6

Linear array with M sensors separated by distance d. The sensors are placed in a free field. A source signal is considered coming from a point source a distance r away from the sensor array. The source signal is placed in the far field, i.e., r ≫ d. Therefore the incident wave is planar and the arrival angle θ is the same for all the sensors

Full size image

To be specific, each row in the separation matrix defines a directivity pattern, and therefore each row can be thought of as a separate beamformer. This directivity pattern is determined by the transfer function between the source and the filter output. The magnitude response of the n-th output is given by

(52.48)

where a(ω) is an M × 1 vector representing the propagation of a distant source with DOA θ to the sensor array. When M sensors are available, it is possible to place M − 1 nulls in each of the M directivity patterns, i.e., directions from which the arriving signal is canceled out. In an ideal, reverberation-free environment separation is achieved if these nulls point to the directions of the interfering sources. The locations of these nulls, as they may be identified by the separation algorithm, can be used to resolve the permutation ambiguity [52.77,81,131,266,287,288,289,290]. These techniques draw strong parallels between source separation solutions and beamforming. The DOAs do not have to be known in advance and can instead be extracted from the resulting separation filters. Note, however, that the ability to identify source locations is limited by the physics of wave propagation and sampling: distant microphones will lead to grading lobes which will confuse the source locations, while small aperture limits spatial resolution at low frequencies. Ikram and Morgan [52.175] extend the idea of Kurita et al. [52.266] to the case where the sensor space is wider than one half of the wavelength. Source locations are estimated at lower frequencies, which do not exhibit grating lobes. These estimates are then used to determine the correct nulls for the higher frequencies and hereby the correct permutations. In order to resolve permutations when sources arrive from the same direction, Mukai et al. [52.291] use a near-field model. Mitianoudis and Davies [52.268] suggested frequency alignment based on DOA estimated with the multiple signal classification (MuSIC) algorithm [52.292]. A subspace method has been used in order to avoid constraints on the number of sensors. Knaak et al. [52.222] include DOA information as a part of the BSS algorithm in order to avoid permutation errors. Although all these methods assume a reverberation-free environment they give reasonable results in reverberant environments as long as the source has a strong direct path to the sensors.

Two other methods also utilize geometry. In the case of moving sources, where only one source is moving, the permutation can be resolved by noting that only one of the parameters in the separation matrix changes [52.167]. If visual cues are available, they may also be used to solve the permutation ambiguity [52.148].

Instead of using geometric information as a separate step to solve the permutation problem Parra and Alvino include geometric information directly into the cost function [52.184,185]. This approach has been applied to microphone arrays under reverberant conditions [52.187]. Baumann et al. [52.72] have also suggested a cost function, which includes the DOA estimation. The arrival angles of the signals are found iteratively and are included in the separation criterion. Baumann et al. [52.73] also suggest a maximum-likelihood approach to solve the permutation problem. Given the probability of a permuted or unpermuted solution as function of the estimated zero directions, the most likely permutation is found.

Gotanda et al. [52.270] proposed a method to reduce the permutation problem based on the split spectral difference, and the assumption that each source is closer to one microphone. The split spectrum is obtained when each of the separated signals are filtered by the estimated mixing channels.

Finally, for iterative update algorithms a proper initialization of the separation filters can result in consistent permutations across frequencies. Smaragdis [52.250] proposed to estimate filter values sequentially starting with low frequencies and initializing filter values with the results of the previous lower frequency. This will tend to select solutions with filters that are smooth in the frequency domain, or equivalently, filters that are short in the time domain. Filter values may also be initialized to simple beamforming filters that point to estimated source locations. The separation algorithm will then tend to converge to solutions with the same target source across all frequencies [52.184,271].

Consistency of the Spectrum of the Recovered Signals

Some solutions to the permutation ambiguity are based on the properties of speech. Speech signals have strong correlations across frequency due to a common amplitude modulation.

At the coarsest level the power envelope of the speech signal changes depending on whether there is speech or silence, and within speech segments the power of the carrier signal induces correlations among the amplitude of different frequencies. A similar argument can be made for other natural sounds. Thus, it is fair to assume that natural acoustic signals originating from the same source have a correlated amplitude envelope for neighboring frequencies. A method based on this comodulation property was proposed by Murata et al. [52.159,196]. The permutations are sorted to maximize the correlation between different envelopes. This is illustrated in Fig. 52.7. This method has also been used in [52.198,199,203,263,287,293]. Rahbar and Reilly [52.152,209] suggest efficient methods for finding the correct permutations based on cross-frequency correlations.

Fig. 52.7
figure 7

For speech signals, it is possible to estimate the permutation matrix by using information on the envelope of the speech signal (amplitude modulation). Each speech signal has a particular envelope. Therefore, by comparison with the envelopes of the nearby frequencies, it is possible to order the permuted signals

Full size image

Asano and Ikeda [52.294] report that the method sometimes fails if the envelopes of the different source signals are similar. They propose the following function to be maximized in order to estimate the permutation matrix:

(52.49)

where is the power envelope of y and P(ω) is the permutation matrix. This approach has also been adopted by Peterson and Kadambe [52.232]. Kamata et al. [52.282] report that the correlation between envelopes of different frequency channels may be small, if the frequencies are too far from each other. Anemüller and Gramms [52.127] avoid the permutations since the different frequencies are linked in the update process. This is done by serially switching from low to high-frequency components while updating.

Another solution based on amplitude correlation is the so-called amplitude modulation decorrelation (AMDecor) algorithm presented by Anemüller and Kollmeier [52.126,272]. They propose to solve the source separation problem and the permutation problems simultaneously. An amplitude modulation correlation is defined, where the correlation between the frequency channels ω k and ω l of the two spectrograms Y a(ω, t) and Y b(ω, t) is calculated as

(52.50)

This correlation can be computed for all combinations of frequencies. This results in a square matrix C(Y a, Y b) with sizes equal to the number of frequencies in the spectrogram, whose k, l-th element is given by (52.50). Since the unmixed signals y(t) have to be independent, the following decorrelation property must be fulfilled

(52.51)

This principle also solves the permutation ambiguity. The source separation algorithm is then based on the minimization of a cost function given by the Frobenius norm of the amplitude-modulation correlation matrix.

A priori knowledge about the source distributions has also been used to determine the correct permutations. Based on assumptions of Laplacian distributed sources, Mitianopudis and Davies [52.134,251,276] propose a likelihood ratio test to test which permutation is most likely. A time-dependent function that imposes frequency coupling between frequency bins is also introduced. Based on the same principle, the method has been extended to more than two sources by Rahbar and Reilly [52.152]. A hierarchical sorting is used in order to avoid errors introduced at a single frequency. This approach has been adopted in Mertins and Russel [52.212].

Finally, one of the most effective convolutive BSS methods to date (Table 52.5) uses the statistical relationship of signal powers across frequencies. Rather than solving separate instantaneous source separation problems in each frequency band Lee et al. [52.277,278,280] propose a multidimensional version of the density estimation algorithms. The density function captures the power of the entire model source rather than the power at individual frequencies. As a result, the joint statistics across frequencies are effectively captured and the algorithm converges to satisfactory permutations in each frequency bin.

Table 52.5 An overview of algorithms applied in real rooms, where the SIR improvement has been reported
Full size table

Other properties of speech have also been suggested in order to solve the permutation indeterminacy. A pitch-based method has been suggested by Tordini and Piazza [52.135]. Also Sanei et al. [52.147] use the property of different pitch frequency for each speaker. The pitch and formants are modeled by a coupled HMM. The model is trained based on previous time frames.

Motivated by psychoacoustics, Guddeti and Mulgrew [52.243] suggest to disregard frequency bands that are perceptually masked by other frequency bands. This simplifies the permutation problem as the number of frequency bins that have to be considered is reduced. In Barros et al. [52.244], the permutation ambiguity is avoided due to a priori information of the phase associated with the fundamental frequency of the desired speech signal.

Nonspeech signals typically also have properties which can be exploited. Two proposals for solving the permutation in the case of cyclo-stationary signals can be found in Antoni et al. [52.273]. For machine acoustics, the permutations can be solved easily since machine signals are (quasi)periodic. This can be employed to find the right component in the output vector [52.221].

Continuity of the frequency spectra has been used by Capdevielle et al. [52.62] to solve the permutation ambiguity. The idea is to consider the sliding Fourier transform with a delay of one point. The cross-correlation between different sources are zero due to the independence assumption. Hence, when the cross-correlation is maximized, the output belongs to the same source. This method has also been used by Servière [52.253]. A disadvantage of this method is that it is computationally very expensive since the frequency spectrum has to be calculated with a window shift of one. A computationally less expensive method based on this principle has been suggested by Dapena and Servière [52.274]. The permutation is determined from the solution that maximizes the correlation between only two frequencies. If the sources have been whitened as part of separation, the approach by Capdevielle et al. [52.62] does not work. Instead, Kopriva et al. [52.86] suggest that the permutation can be solved by independence tests based on kurtosis. For the same reason, Mejuto et al. [52.275] consider fourth-order cross-cumulants of the outputs at all frequencies. If the extracted sources belong to the same sources, the cross-cumulants will be nonzero. Otherwise, if the sources belong to different sources, the cross-cumulants will be zero.

Finally, Hoya et al. [52.302] use pattern recognition to identify speech pauses that are common across frequencies, and in the case of overcomplete source separation, k-means clustering has been suggested. The clusters with the smallest variance are assumed to correspond to the desired sources [52.230]. Dubnov et al. [52.279] also address the case of more sources than sensors. Clustering is used at each frequency and Kalman tracking is performed in order to link the frequencies together.

Global Permutations

In many applications only one of the source signals is desired and the other sources are only considered as interfering noise. Even though the local (frequency) permutations are solved, the global (external) permutation problem still exists. Few algorithms address the problem of selecting the desired source signal from the available outputs. In some situations, it can be assumed that the desired signal arrives from a certain direction (e.g., the speaker of interest is in front of the array). Geometric information can determine which of the signals is the target [52.171,184]. In other situations, the desired speaker is selected as the most dominant speaker. In Low et al. [52.289], the most dominant speaker is determined on a criterion based on kurtosis. The speaker with the highest kurtosis is assumed to be the dominant. In separation techniques based on clustering, the desired source is assumed to be the cluster with the smallest variance [52.230]. If the sources are moving it is necessary to maintain the global permutation by tracking each source. For block-based algorithm the global permutation might change at block boundaries. This problem can often be solved by initializing the filter with the estimated filter from the previous block [52.186].

Results

The overwhelming majority of convolutive source separation algorithms have been evaluated on simulated data. In the process, a variety of simulated room responses have been used. Unfortunately, it is not clear whether any of these results transfer to real data. The main concerns are the sensitivity to microphone noise (often not better than −25 dB), nonlinearity in the sensors, and strong reverberations with a possibly weak direct path. It is suggestive that only a small subset of research teams evaluate their algorithms on actual recordings. We have considered more than 400 references and found results on real room recordings in only 10% of the papers. Table 52.5 shows a complete list of those papers. The results are reported as signal-to-interference ratio (SIR), which is typically averaged over multiple output channels. The resulting SIR are not directly comparable as the results for a given algorithm are very likely to depend on the recording equipment, the room that was used, and the SIR in the recorded mixtures. A state-of-the art algorithm can be expected to improve the SIR by 10-20 dB for two stationary sources. Typically a few seconds of data (2-10 s) will be sufficient to generate these results. However, from this survey nothing can be said about moving sources. Note that only eight (of over 400) papers reported separation of more than two sources, indicating that this remains a challenging problem.

Conclusion

We have presented a taxonomy for blind separation of convolutive mixtures with the purpose of providing a survey and discussion of existing methods. Further, we hope that this might stimulate the development of new models and algorithms which more efficiently incorporate specific domain knowledge and useful prior information.

In the title of the BSS review by Torkkola [52.13], it was asked: Are we there yet? Since then numerous algorithms have been proposed for blind separation of convolutive mixtures. Many convolutive algorithms have shown good performance when the mixing process is stationary, but still few methods work in real-world, time-varying environments. In these challenging environments, there are too many parameters to update in the separation filters, and too little data available in order to estimate the parameters reliably, while the less complicated methods such as null beamformers may perform just as well. This may indicate that the long demixing filters are not the solution for real-world, time-varying environments such as the cocktail-party situation.