Clause Learning and New Bounds for Graph Coloring

Abstract

Graph coloring is a major component of numerous allocation and scheduling problems.

We introduce a hybrid CP/SAT approach to graph coloring based on exploring Zykov’s tree: for two non-neighbors, either they take a different color and there might as well be an edge between them, or they take the same color and we might as well merge them. Branching on whether two neighbors get the same color yields a symmetry-free tree with complete graphs as leaves, which correspond to colorings of the original graph.

We introduce a new lower bound for this problem based on Mycielskian graphs; a method to produce a clausal explanation of this bound for use in a CDCL algorithm; and a branching heuristic emulating Brelaz on the Zykov tree.

The combination of these techniques in both a branch-and-bound and in a bottom-up search outperforms Dsatur and other SAT-based approaches on standard benchmarks both for finding upper bounds and for proving lower bounds.

G. Katsirelos—Partially supported by the french “Agence nationale de la Recherche”, project DEMOGRAPH, reference ANR-16-C40-0028.

1 Introduction

A coloring of a graph is a labeling of its vertices such that adjacent vertices have distinct labels. Let a labeling of the graph $G = (V,E)$ be a mapping from its set of vertices $V$ to the integers. A labeling $c$ such that $c ({v}) \ne c ({u})$ for every edge $({u}{v}) \in E$ is a coloring of $G$, and its cardinality is $|\{c ({v}) \mid v \in V \}|$. The chromatic number $\chi ({G})$ of a graph $G$ is the cardinality of its smallest coloring.

The problem of finding a minimum coloring of a graph is NP-hard, but has numerous applications. For instance when allocating frequencies, devices on nearby locations should not be assigned the same frequency to avoid interferences. The chromatic number of this distance-induced graph is therefore the minimum span of frequencies that is required [1, 18]. In compilers, finding an optimal register allocation can be cast as a coloring problem on an interference graph of value live ranges [3].

One of the oldest and most successful technique for coloring a graph is Brelaz’ Dsatur algorithm [2]: when branching, the vertex with highest degree of saturation is chosen and colored with the lexicographically least candidate. The degree of saturation of a vertex $v$ is the number of assigned colors within its neighborhood $N_{G}({v})$ in $G$. In case of a tie, the vertex with largest number of uncolored neighbors is chosen among the tied vertices. This heuristic is often used within a branch-and-bound algorithm with one variable per vertex whose domain is the set of possible colors. It is known as dom+deg in the CSP literature [6]. The standard approach for computing a bound in these algorithms is to compute a heuristic approximation of the clique number $\omega ({G})$ of the graph $G$ (e.g., the size of a maximal clique) since $\omega ({G}) \le \chi ({G})$. This bound is known to be weak for some polynomially recognizable classes of graphs, such as Mycielskian graphs, which are triangle-free graphs with arbitrarily large chromatic number [16]. Moreover, within the search tree explored using Brelaz’ heuristic, the clique has to be found only among vertices with degree of saturation equal to the number of colors in the current partial solution (i.e., adjacent to at least one vertex of every color used so far). Finally, this formulation exhibits value interchangeability [24]. One common way to break this symmetry is to arbitrarily color a clique, and never branch on colors larger than $k+1$ when extending a solution with k colors [14, 23, 25].

Satisfiability [13, 15] offers an attractive approach to coloring, in part because it is trivial to encode the problem. In satisfiability, we express problems with Boolean variables $\mathbf {X}$. We say that a literal l is either a variable x or its negation $\overline{x}$. Constraints are disjunctions of literals, written interchangably as sets of literals or as disjunctions, which are satisfied by an assignment if it assigns at least one literal to true. In order to encode graph coloring with satisfiability, one typically relies on color variables $x_{{v}{i}}$, where $x_{{v}{i}}$ being true means vertex $v$ takes color $i$. For every edge $({u}{v})$, there is a binary clause $\overline{x}_{v i} \vee \overline{x}_{u i}$ for every color $i$. Then, if K is the maximum number of colors, then there is a clause $\bigvee _{1 \le i \le K}x_{{u}{i}}$. Refinements to this encoding include Van Gelder’s log encoding versions, where $x_{{v}{j}}$ is true if the $j$-th bit of the binary encoding of the color taken by vertex $v$ is 1 [22]. However, the use of modern SAT solving techniques like restarting [7, 8] and clause learning [13] are not straightforward to combine with symmetry breaking such as that of van Hentenryck et al. [23]. They can only be easily combined with starting from an arbitrary coloring to a clique, but that is incomplete. The color6 solver [25] uses symmetry breaking branching but forgoes restarting to maintain complete symmetry breaking.

On the other hand, the search tree induced by Zykov’s deletion-contraction recurrence [26] has no color symmetry and using the clique number as lower bound is easier and more powerful than in the color variable formulation.

Let ${G} / {({u}{v})}$ be the graph obtained by contracting $u$ and $v$: the two vertices are identified to a single vertex $r({u})=r({v})=u$, every edge $({v}{w})$ is replaced by $({r({v})}{w})$ and self edges are discarded. Conversely, let ${G} + {({u}{v})}$ be the graph obtained by adding the edge $({u}{v})$. The Zykov reccurrence is thus:

$$\begin{aligned} \chi ({G})= & {} \min \{\chi ({{G} / {({u}{v})}}), \chi ({{G} + {({u}{v})}})\} \end{aligned}$$

(1)

Indeed, given a minimum coloring of $G$, either the vertices $u$ and $v$ have distinct colors and therefore it is also a coloring of ${G} + {({u}{v})}$, or they have the same color and it is a coloring of ${G} / {({u}{v})}$.

Example 1

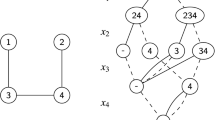
Fig. 1 illustrates the Zykov reccurrence. From the graph $G$ in Fig. 1a, we obtain the graph ${G} + {({c}{d})}$ shown in Fig. 1b by adding the edge $({c}{d})$ and the graph ${G} / {({c}{d})}$ shown in Fig. 1c. One of these two graphs has the same chromatic number as $G$.

Fig. 1.

Zykov reccurrence

This branching scheme was successfully used in a branch-and-price approach to coloring [14]. In the context of satisfiability, Schaafsma et al. showed that a clause encoding of Zykov formulation is not efficient [19]. For every non-edge $({u}{v})$, the edge variable $e_{{u}{v}}$ stands for the decision of contracting the vertices ($e_{{u}{v}} = 1$), or adding the edge ($e_{{u}{v}} = 0$). A difficulty is that a cubic number of clauses are required, three for every triplet $u$, $v$, $w$, in order to forbid that exactly two of the variables $e_{{u}{v}}, e_{{u}{w}}$ and $e_{{v}{w}}$ are true. This encoding proved too heavy and as a result less efficient than the formulations using color variables. However, Schaafsma et al. introduced a novel and clever way of taking advantage of Zykov’s idea: when learning a clause involving color variables, one can compactly encode all symmetric clauses using a single clause that only uses edge variables and propagates the same as if all the symmetric clauses were present.

In this work, we propose a constraint programming formulation of coloring in Sect. 2 that also uses the Zykov branching scheme. We use the idea of integrating constraint programming into clause learning satisfiability solvers by simply having each propagator label each pruning or failure by a clausal reason or explanation [10, 17] to alleviate the cost of keeping the edge variables consistent (Sect. 2.1) and to integrate a lower bound based on either cliques (Sect. 2.2) or a more general bound based on Mycielskians (Sect. 2.3). Together with effective branching heuristics (Sect. 2.4) and search strategies that emphasize either upper or lower bounds (Sect. 2.5), we get a solver that clearly outperforms the state of the art in satisfiability-based coloring (Sect. 3).

2 Clause-Learning Approach

In our approach, similar to that Schaafsma et al., we use a model which leads to the exploration of the tree resulting from application of the Zykov recurrence. We have one Boolean variable $e_{{u}{v}}$ for each non-edge of the input graph, that is for every $({u}{v}) \notin E$. When $e_{{u}{v}}$ is true, the vertices $v$ and $u$ are contracted, hence assigned the same color, and are separated otherwise, hence assigned different colors. We somewhat abuse notation in the sequel and write clauses using variables $e_{{u}{v}}$ even when $({u}{v}) \in E$ and assume that the variable is set to false at the root of the search tree.

With every (partial) assignment A to the edge variables, we can associate a graph $G _A$. For the empty assignment, we have $G _\emptyset = G$. For non-empty assignments it is the graph that results from contracting all vertices $u,v$ of $G$ for which A contains $e_{{u}{v}}$ and adding an edge between all pairs of vertices $u,v$ of $G$ for which A contains $\overline{e}_{u v}$. When $e_{{u}{v}}$ and $e_{{v}{w}}$ are both true, this means that we contract $u$ and $v$ and then contract $w$ and $r(v)$ and similarly for false literals. The operation of contracting vertices is associative and commutative, so we get the same graph $G _A$ regardless of the order in which we process the literals in A.

The property of having the same color is transitive, so if $e_{{u}{v}}$ and $e_{v w}$ are true, then so is $e_{{u}{w}}$. Similarly, if $e_{{u}{v}}$ is true and $e_{{v}{w}}$ is false, then $e_{u w}$ must also be false. We enforce this using the constraint

$$\begin{aligned} \textsc {Triangle}(\{e_{{u}{v}} \mid ({u}{v})\notin E \}) \end{aligned}$$

(2)

We can enforce GAC on this constraint using a decomposition of size $O(|V |^3)$:

$$\begin{aligned} (\overline{e}_{u v} \vee \overline{e}_{v w} \vee e_{{u}{w}})&\forall \text { distinct } u,v,w \in V \end{aligned}$$

(3)

Enforcing unit propagation on this decomposition therefore takes $O(|V |^3)$ time, amortized over a branch of the search tree. In our implementation, we have opted instead for a dedicated propagator for this, described in Sect. 2.1, whose complexity over a branch is only $O(|V |^2)$.

The model also includes a constraint Coloring which is satisfied by any assignment that corresponds to a coloring with fewer than k colors.

$$\begin{aligned} \textsc {Coloring}(\{e_{{u}{v}} \mid (u v)\notin E\}, k) \end{aligned}$$

(4)

This constraint is clearly NP-hard. We describe two incomplete propagators for it in Sects. 2.2 and 2.3. The first computes either the well known clique lower bound (Sect. 2.2) and the second a novel, stronger, bound (Sect. 2.3). If that bound meets or exceeds k, the propagator fails and produces an explanation. Neither of these bounds is cheap to compute, hence the propagator runs at a lower priority than unit propagation and the Triangle constraint.

Although we have experimented with pruning in this propagator, the rules we have found tend to be ineffective, in the sense that they generate very little pruning, barely reduce the overall search effort, and increase the overall runtime.

Discussion. Clearly, our approach is closely related to that of Schaafsma et al. However, there are some important differences. First, since we do not need the color variables to compute the size of the coloring, we completely eliminate the need for the clause rewriting scheme that they implement and get color symmetry-free search with no additional effort. In addition, since we our model uses a CP/SAT hybrid, we can use a constraint to compute a lower bound at each node, thus avoiding a potentially large number of conflicts.

The approach of Schaafsma et al. does not enforce triangle consistency except through the color variables (so that $X_v = X_u \iff e_{{u}{v}}$). In contrast, the triangle propagator maintains GAC on this constraint, without having to encode channeling between the edge variables and the color variables.

The main drawback of this model is that we need a large number of variables. This is especially problematic for large, sparse graphs, where the number of non-edges is quadratic in the number of vertices and significantly larger than the number of edges. Indeed, in 4 of the 125 instances we used in our experimental evaluation, our solver exceeded the memory limit.

The approach of Schaafsma et al. does not have the same limitation, as they introduce variables only when they are needed to rewrite a learnt clause, in a way similar to lazy model expansion [4]. It is possible that this approach of lazily introducing variables can be adapted to our model, but this, as well as other ways of reducing the memory requirements, remains future work.

2.1 Triangle Consistency Propagation

The propagator for the Triangle constraints works as follows: for each vertex $v$, we keep a bag $b(v)$ to which it belongs. Initially, $b(v) = \{v \}$ for all $v$. When we set $e_{{u}{v}}$ to true, we set $e_{u 'v '}$ to true for all $v ' \in b(v), u ' \in b(u)$. We also set $e_{u 'v '}$ to false for all $v ' \in b(v)$ and $u ' \in N({b(u}) \setminus N({b(v)})$.¹ Finally, we set $B = b(u) \cup b(v)$ and update $b(v ') = B$ for all $v ' \in B$. In the case where we set $e_{{u}{v}}$ to false, we set $e_{u 'v '}$ to false for all $v ' \in b(v), u ' \in b(u)$.

A small but important optimization is that if the propagator is invoked for $e_{{u}{v}}$ becoming true (resp. false) but $u$ and $v$ are already in the same bag (resp. already separated) then it does nothing. This ensures that it touches each non-edge exactly once, hence its complexity is quadratic over an entire branch. This is also optimal, since in the worst case every non-edge must be set either as a decision or by propagation.

This propagator uses the clauses (3) as explanations. The mapping from actions that it performs to explanations is fairly straightforward, using the vertices involved in the literal that woke the propagator as “pivots”. For example, if $b(v) = \{v, v '\}$, $b(u) = \{u, u '\}$ and it is woken on the literal $e_{{u}{v}}$, it sets $e_{u v '}$ using $(\overline{e}_{v v '} \vee \overline{e}_{u v} \vee e_{u v '})$ as the reason and then $e_{u 'v '}$ using $(\overline{e}_{u v '} \vee \overline{e}_{u u '} \vee e_{u 'v '})$.

2.2 Clique-Based Lower Bound

As we already discussed, an important advantage of the edge-variable based model is that computing a lower bound for the current subproblem is as easy as for the entire problem. For example, if the partial assignment in the current node is A, the clique number of the graph $G _A$ is a lower bound for the subproblem.

In order to find a large clique we use the following greedy algorithm. Let o be an ordering of the vertices, so we visit all vertices in the order $v _{o_1}, \ldots , v _{o_n}$. We maintain an initially empty list of cliques. For each vertex, we add to all the cliques which admit it and if no clique admits it we put it in a new singleton clique. When this finishes, we iterate over the vertices one more time and add them to all cliques which admit them, because in the first pass a vertex $v$ was not evaluated against cliques which were created after we processed $v$. We then pick the largest among these cliques as our lower bound.

If the lower bound meets or exceeds the upper bound k, the propagator reports a conflict. We construct a clausal conflict as follows: each vertex $v$ of the current graph is the result of the contraction of 1 or more vertices of the original graph. In keeping with the notation for the triangle consistency propagator, we call this the bag $b(v)$. We arbitrarily pick one vertex $r(v)$ from the bag of each vertex $v$ in the largest clique C, and set the explanation to

$$\begin{aligned} \bigvee _{v, u \in C} e_{r(v)r(u)} \end{aligned}$$

(5)

We have experimented with producing explanations with mixed-sign literals and found that they tend to be much shorter and speed up search in terms of number of conflicts per second, but significantly increase the overall effort required, both in runtime and number of conflicts.

Preprocessing and Vertex Ordering. We tried a few different heuristics for ordering the vertices of the graph, including the inverse of the degeneracy order [11], which tends to produce large cliques [5, 9]. However, we found that it works best to sort the vertices in order of decreasing bag size.

Lin et al. [12] recently proposed a reduction rule for graph coloring instances, which allowed them to reduce the size of large, sparse graphs.

Proposition 1

([12]). Let G be a graph with $\chi ({G}) \ge k$ and let I be an independent set of G such that for all $v \in I$, $d({v}) \le k$. Then, $k -1 \le \chi ({G \setminus I}) \le \chi ({G})$ and if $\chi ({G \setminus I}) = k-1$ then $\chi ({G})=k$.

The rule of Proposition 1 can be used with any lower bound and applied iteratively until no more reduction is possible. Besides the obvious advantage of trimming the graph this reduction also helps improve the lower bound found by a heuristic maximal clique algorithm. The reason is that whatever heuristic we use for finding a maximal clique may make a suboptimal choice and this preprocessing step removes some obviously suboptimal choices from consideration.

We have used this result for preprocessing, as Lin et al. did, but observed very little benefit in our instance set, which comprises smaller and denser graphs than the one that they used. We also used it, however, to improve the ordering for the greedy algorithm by placing such vertices at the end of the ordering. As we will show in Sect. 3, this has a small but measurable impact.

2.3 Mycielski-Based Bound

Although being a useful bound in practice, the clique number is both hard to compute and gives no guarantees on the quality of the bound. We propose here a new lower bound inspired by Mycielskian graph.

Definition 1

(Mycielskian graph [16]). The Mycielskian graph $\mu ({G})$ = ($\mu ({V})$, $\mu ({E})$) of $G$  = ($V$, $E$) is defined as follows:

• $\mu ({V})$ contains every vertex in $V$, and $|V |+1$ additional vertices, constituted of a set $U = \{u _i \mid v _i \in V \}$ and another distinct vertex $w$.

• For every edge $v _iv _j \in E$, $\mu ({E})$ contains $v _iv _j, v _iu _j$ and $u _iv _j$. Moreover, it contains all the edges between U and w.

The Mycielskian $\mu ({G})$ of a graph $G$, has the same clique number, however its chromatic number is $\chi ({G})+1$. Indeed, consider a coloring of $\mu ({G})$. For any vertex $v _i \in V$, we have $N({v _i}) \subseteq N({u _i})$, and therefore we can safely use the same color $v _i$ as for $u _i$. If follows that at least $\chi ({G})$ colors are required for the vertices in U, and since $N({w})=U$, then $w$ requires a $\chi ({G})+1$-th color. Mycielski introduced these graphs to demonstrate that triangle-free graphs can have arbitrarilly large chromatic numbers, hence the clique number does not approximate the chromatic number.

Fig. 2.

A 2-clique $M_2 = \mu ({\emptyset })$, its Mycielskians $M_3 = \mu ({M_2})$ and $M_4 = \mu ({M_3})$

The principle of our bound is a greedy procedure that can discover embedded “pseudo” Mycielskians. Indeed, the class of embedded graphs that we look for is significantly broader than set of “pure” Mycielskians $\{M_2, M_3, M_4,\ldots \}$. First, we look for a partial subgraph. Therefore, trivially, Mycielskians with extra edges also provide valid lower bounds. Moreover, we use as starting point a (potentially large) clique. Finally, the method we propose can also find Mycielskians modulo some vertex contractions. Clearly, those are also valid lower bounds since contracting vertices is equivalent to adding equality constraints to the problem.

Let $N_{G}({v})$ be the neighborhood of $v$ in the graph $G$. Suppose that we have a partial subgraph $H =(V _{H},E _{H})$ of $G$ such that $\chi ({H}) \ge k$. This can be for example a clique of size k. We define

$$\begin{aligned} S_v = \{ u \mid N_{H}({v}) \subseteq N_{G}({u})\} \end{aligned}$$

(6)

Suppose that there exists a vertex $w$ with at least one neighbor in every set $S_v$:

$$\begin{aligned} w \in \cap _{v \in V _{H}} N_{G}({S_v}) \end{aligned}$$

(7)

and let $u (v)$ be any element of $S_v$ such that $u (v) \in N_{G}({w})$ and $U=\{u (v) \mid v \in V\}$, then:

Lemma 1

The graph

$$\begin{aligned} H ' = (V \cup U \cup \{w \}, E \cup \bigcup _{v \in V}N_{H}({v}) \times u (v) \cup \bigcup _{u \in U}\{(u,w)\}) \end{aligned}$$

is such that $\chi ({H '}) \ge k+1$.

Proof

The proof follows from the facts that $H '$ is the Mycielskian graph of $H$ possibly with contracted vertices, and is embedded in $G$.

Suppose first that, for each $v \in V$, $u (v) \ne v$ and $w \not \in V$. Then we have $H '=\mu ({H})$ by using $u (v _i)$ for the vertex $u _i$, and $w$ for itself, in Definition 1.

Suppose now that $H ' \ne \mu ({H})$. This can only be because either:

• For some vertex $v _i$ of $H$, we have $u (v _i) = v _i$. In this case, consider the graph $\mu ({H})$ and contract $u _i$ and $v _i$. The resulting graph ${\mu ({H})} / {({u _i}{v _i})}$ has a chromatic number at least as high as $\mu ({H})$. However, it is isomorphic to $H '$.

• The vertex $w$ is the vertex $v _i$ from the original subgraph $H$. Here again contracting $v _i$ and $w$ in $\mu ({H})$ yields $H '$.

Notice that there is not a third case where $w$ is taken among U since, for any $v \in V _H$, we have $u (v) \not \in \cap _{v \in V _{H}} N_{G}({S_v})$ because $u (v)$ is not a neighbor of itself.

Finally, it is easy to see that $H '$ is embedded in $G$ since the edges added to $H '$ are all edges of $G$. $\square$

Example 2

Figure 3a shows the graph ${G} / {({c}{d})}$ obtained by contracting vertices c and d in the graph $G$ of Fig. 1. Let $H$ be the clique $\{a,b,c\}$. We have $S_{a}=\{a,e\}$, $S_{b}=\{b,f\}$ and $S_{c}=\{c\}$. Furthermore, $N_{G}({\{a,e\}}) \cap N_{G}({\{b,f\}}) \cap N_{G}({\{c\}}) = \{b,c,g\} \cap \{a,e,c,g\} \cap \{a,b,e,g,f\} = \{g\}$, from which we can conclude that this graph has chromatic number at least 4. As shown in Fig. 3b, when called with $H = \{a,b,c\}$ Algorithm 1 will extend it with a first layer $U = \{e,c,f\}$ and an extra vertex $w =g$. Notice that the graph obtained by adding the edge $({c}{d})$ has a 4-clique (see Fig. 1). Therefore, the graph $G$ in Fig. 1a also has a chromatic number of at least 4.

Fig. 3.

Embedded Mycielski

Algorithm 1 greedily extends a partial subgraph $H = (V _H, E _H)$ of the graph $G$ (with $\chi ({H}) \ge k$) into a larger partial subgraph $H ' = (V _H ',E _{H}')$, following the above principles. As long as this succeeds, in the outermost loop, we replace $H$ by $H '$ and iterate. The computed bound k is equal to $\chi ({H})$ plus the number of successful iterations.

We compute the sets $S_v$ (Eq. 6) and the set W of nodes with at least one neighbor in every $S_v$ in Loop 1. Then, if it is possible to extend $H$ (Line 4), we compute the pseudo Mycielskian $(V _{H}', E _{H}')$ as shown in Lemma 1 and replaces $H$ with it in Line 5 before starting another iteration.

Complexity. One iteration of Algorithm 1 requires $O(|V _{H}| \times |V |)$ bitset operations (Line 2 is 1 ‘AND’ operation and Line 3 is $O(|V |)$ ‘OR’ operations and 1 ‘AND’). The second part of the loop, starting from Line 4, runs in $O(|V _{H}|^2)$ time. Typically, the number of iterations is very small. In the worst case, it cannot be larger than $\log |V |$ since the number of vertices in $H$ is (more than) doubled at each iteration. It follows that Loop 1 is executed at most $2|V |$ times, and therefore, the worst case time complexity is $O(|V |^2)$ bitset operations (hence $O(|V |^3)$ time).

Explanation. Similarly to the clique based lower bound, the explanations that we produce here correspond to the set of all edges in the graph H:

$$\begin{aligned} \bigvee _{(v,u) \in E _H} e_{{u}{v}} \end{aligned}$$

(8)

Adaptive Application of the Mycielskian Bound. In our experiments, we found that trying to find a Mycielskian subgraph in every node of the search tree was too expensive and did not pay off in terms of total runtime. Therefore, we adapted a heuristic proposed by Stergiou [20] which allows us to apply this stronger reasoning less often. In particular, we only compute the clique lower bound by default. But everytime there is a conflict, whether by unit propagation or by bound computation, we compute the Mycielskian lower bound in the next node. If that causes a conflict, we keep computing this bound until we backtrack to a point where even the stronger bound does not detect a bound violation. This has the effect that we compute the cheaper clique lower bound most of the time, but learn clauses based on the stronger bound.

2.4 Branching Heuristic

Brelaz’ branching heuristic remains extremely competitive for finding good colorings, as evidenced by the performance of Dsatur in our experimental evaluation (Sect. 3). Moreover, Schaafsma et al. observed that branching on color variables was significantly better than branching on edge variables.

But adding the color variables is not really desirable. First, it adds the overhead of propagating the reified equality constraints. Second, using these variables to follow the Brelaz heuristic requires branching on them, which in trun requires that we use some kind of symmetry breaking method, like the rewriting scheme of Schaafsma et al. So it would be preferable to get the benefit of the more effective branching heuristic without needing to introduce color variables.

In order to get behavior similar to that of Brelaz’ heuristic in the edge variable model, we proceed as follows: we pick a maximal clique C in the current graph. We pick the vertex $v$ that maximises $|N({v}) \cap C|$, breaking ties by highest $|N({v}) \setminus C|$, and an arbitrary vertex $u \in C \setminus N({v})$². We then set $e_{{u}{v}}$ to true. This uses the current maximal clique to implicitly construct a coloring and uses that to choose the next vertex to color as Brelaz’ heuristic does. If the assignments $e_{{u}{v}}$ are refuted for all $u \in C$, then $v$ is adjacent to all vertices in C and so $C \cup \{v \}$ is a larger clique, which corresponds to using a new color in Brelaz’ heuristic.

This branching strategy can be more flexible than committing to a coloring by assigning the color variables. For example, unit propagation on learned clauses as we exlore a branch of the search tree can make it so that the maximal clique $C'$ at some deep level is not an extension of the maximal clique C at the root of the tree, i.e., $C \not \subseteq C'$. The Brelaz heuristic on the color variables commits to using C at the root, hence cannot take advantage of the information that $C'$ is a larger clique. The modification that we present here achieves this.

2.5 Solution Strategies

Previous satisfiability-based approaches to coloring have mostly ignored the optimization problem of finding an optimal coloring of a graph and instead attack the decision problem of whether a graph is colorable with k colors. In our setting, we have the flexibility to do both. In particular, we implemented two search strategies: branch-and-bound and bottom-up. The former uses a single instance of a solver, finds a solution and then tightens the upper bound in the Coloring constraint and continues searching. This is similar to the top-down approach one would use when solving a series of decision problems, starting from a heuristic upper bound and decreasing that until we generate an unsatisfiable instance, in which case we have identified the optimum. The advantage of the branch-and-bound approach is that it does not discard accumulated information between solution: learned clauses and heuristic scores for variables. Moreover, it more closely resembles the typical approach used in constraint programming systems.

The other approach we implemented is bottom-up: start from a lower bound (such as those described in Sect. 2.2 or 2.3) and keep increasing until we find a satisfiable instance, which gives the optimum. This has none of the advantages of the branch-and-bound approach, as it is not safe to reuse clauses from a more constrained problem in one that is less constrained. Moreover, it cannot generate upper bounds before it finds the optimum. But it gains from the fact that the more constrained problems it solves may be easier. One particular behavior we have observed is that sometimes the lower bound computed at the root coincides with the optimum and finding is quite easy with the bottom-up strategy, but finding that solution with branch-and-bound can be very hard.

3 Experimental Evaluation

We implemented several variations of our approach using MiniCSP³ as the underlying CDCL CSP solver, and retained two, one for each of the solution strategies described in Sect. 2.5.⁴ The former, cdcl, is a branch-and-bound algorithm, using Brelaz branching. The latter, cdcl $\uparrow$, is a bottom-up algorithm, using VSIDS. In both cases, we use the adaptive application of the Mycielskian bound, as explained in Sect. 2.3. When computing the Mycielskian bound, we apply Algorithm 1 on all of the maximal cliques, and keep the best outcome.

We compared with the state-of-art SAT-based solver color6 [25], a very efficient clause-learning algorithm for graph coloring proposed recently by Zhou et al. Similarly to our approach, it is based on a SAT solver (namely zChaff), however, it uses the color-based formulation. It was shown to outperform the state of the art on many instances. As color6 solves satisfiability instances only (testing whether a coloring with a specific number of colors exists), we implemented a branch-and-bound wrapper on top of it, denoted color6, as well as well as a wrapper that implements the bottom-up strategy, denoted color6 $\uparrow$. We used the lower and upper bounds computed by our approach (respectively the maximal clique algorithm described in Sect. 2.2 and a greedy run of Brelaz) as initial bounds for color6 and color6 $\uparrow$.

Moreover, we also compared with an implementation of Dsatur by Trick, and an integer programming formulation in CPLEX. The model we used for CPLEX is the trivial one using binary color variables (one for each vertex and each color), and one binary inequality per edge. However, observe that CPLEX actually computes maximal cliques in its preprocessing, so providing it with clique inequalities would have been useless. Moreover, we initialized the upper bound with the same method as for color6, and also arbitrarily fixed the colors of one maximal clique in order to break symmetries.

Unfortunately, we could not compare our method to the method of Schaafsma et al. (Minicolor) directly. Indeed, its implementation, generously provided by the authors, is difficult to use in the type of extensive experiments of the type we performed. Firstly, the algorithm is restricted to instances with at most 32 colors. Secondly it solves the satisfiability problem $\chi ({G}) \le K$ and uses a file converter. Finally, the changes made to Minisat’s code do not seem to be robust and we experienced several occurrences of assertion failures.

We used 125 benchmark instances from Trick’s graph coloring webpage (http://mat.gsia.cmu.edu/COLOR/color.html) and described in the proceedings of the workshop COLOR02 [21]. In the subsequent tables, however, we omit 22 of these instances that were trivial for every approach we used (i.e., that solved by every method to optimality). Every method was run with a time limit of one hour and a memory limit of 3.5 GB⁵ on 4 nodes, each with 35 Intel Xeon CPU E5-2695 v4 2.10 GHz cores running Linux Ubuntu 16.04.4.

Table 1. Comparison with top-down methods (by classes of instances)

Table 2. Comparison with bottom-up methods (by classes of instances)

The results in Tables 1 and 2 are averaged over instances from the same class and the number of instances in each class is given next to the class name. We show the ratio of instances for which a proof of optimality was found (‘opt’), as well as the average upper bound (‘ub’) and lower bound (‘lb’), for every method. The best results for each criterion are highlighted using colors. Table 1 focuses on top-down methods. cdcl is better on all but three classes of instances: Insertions, qg (quasigroup) and queen. Moreover, it finds the same coloring as the other methods in the Insertions class, and computes strictly more proofs of optimality than other solvers in the two other classes. Finally, on many classes it is strictly better than the second best solver (considering at least one criterion). Table 2 focuses on the two bottom-up methods. Here again there are far more classes where cdcl $\uparrow$ is better than classes (such as qg again) where the opposite is true. Moreover, although cdcl $\uparrow$ finds better lower bounds on two large classes (DSJ and flat) this does not translates to a higher proof ratio.

Table 3. Comparison with the state of the art: global results

Table 3 shows results aggregated across all instances. We report the average ratio of instance proven optimal (‘optimal’) in the first column. Then in the second to the fifth columns, we report the arithmetic (‘avg’) and geometric averages (‘gavg’) for both the lower and upper bounds. Finally, we report the mean normalised gap to the best upper bound, and to the best lower bound. Let b (resp. w) be the value found by best (resp. worst) method. In the case of the lower bound, b will be the maximum, while it will be the minimum for the upper bound. The normalised gap g(x) of the outcome x is:

$$\begin{aligned} g(x) = \left\{ \begin{array}{ll} 0 &{} \text {if}~b=w\\ (b-x)/(b-w) &{} \text {otherwise} \end{array} \right. \end{aligned}$$

A mean normalised gap of 0 (resp. 1) therefore indicates that the method systematically has the best (resp. worst) outcome.

Overall, the variants of cdcl are best for all criteria. CPLEX is third best for the number of optimality proofs. Although it requires a lot of memory, and is very poor in terms of solution quality, CPLEX often gives good lower bounds. This is not so surprising since the linear relaxation is quite potent on this formulation. For instance at the root node, since we fix the variables of a maximal clique, the lower bound from the linear relaxation can only be higher than that of our method. It should be noted, however, that in many cases it was not able to improve on the initial bounds provided to the model, even when memory was not an issue. color6 $\uparrow$ is second best for the lower bound, however, notice that the much larger mean normalised gap to the best lower bound than cdcl $\uparrow$ indicates that it was often close but rarely better than our approach. Finally, Dsatur, even though extremely simple, is still a very good method to actually find small colorings and is a close second best for the upper bound.

Table 4. Factor analysis: global results

Next, we tried to assess the impact of the new bounds, and of learning. To that purpose, we ran six variants. Let L denote the usage of clause learning, M the mycielskian-based lower bound and O the partition-based vertex ordering used to find maximal cliques, then $X \setminus S$ stands for the solver X where the options in S are turned off. The results reported in Table 4 clearly show the impact of each factor. There is an almost perfect correlation between turning off a feature, and moving down the ranking for any criterion. In particular, clause learning has clearly a very high impact as turning it off systematically and significantly degrades the performances on every criterion. Moreover, using the partition-based vertex ordering also has a very significant impact for such a simple technique. Finally the mycielskian-based lower bound also clearly helps. However, its impact on the upper bound is limited. For instance, with respect to cdcl $\setminus M$, it increases the proof ratio by 7.8% and the mean lower bound by 2.3%, but decreases the mean upper bound by only 0.3%.

4 Conclusions

We have presented a CP/SAT hybrid approach to graph coloring. The approach uses a new, sophisticated, lower bound that generalizes the clique bound and is inspired by Mycielskian graphs. We combined it with clause learning and effective primal heuristics for coloring to get a solver that in both its configurations outperforms the previous state of the art in satisfiability-based coloring, constraint programming based coloring, as well as a MIP model of the problem. The main disadvantage of the approach is that it requires one Boolean variable for each non-edge of the graph and hence cannot scale to large sparse graphs.