Determination of Constitutive Parameters in Inverse Problem Using Thermoelastic Data

Abstract

A new inverse problem formulation for identification of constitutive parameters in orthotropic materials from load-induced thermal information is developed using Levenberg-Marquardt Algorithm and Airy stress function. Inverse methods were used to determine the constitutive properties as well as the thermoelastic calibration factors of a loaded perforated graphite/epoxy laminated composite by processing noisy simulated thermoelastic data with an Airy stress function in complex variables. Equilibrium, compatibility, and traction-free condition on the boundary of the circular hole are satisfied using complex-variable formulation, conformal mapping and analytic continuation. The primary advantage of this new formulation is the direct use of load-induced thermal data to determine the constitutive parameters, separate the stresses, i.e., evaluate the individual stress components, including on the edge of the hole, and smooth the measured data, all from a single test. The inverse method algorithm determined the constitutive properties with errors less than 10%.

5.1 Introduction

The Airy stress function in complex variables was used extensively in determining stresses from measured data [1,2,3,4,5,6]. The Airy stress function can be processed with measured data using thermoelasticity (thermoelastic stress analysis, TSA) [1, 2], photoelasticity [3], digital image correlation [4], moiré [5] or strain gages [6]. These hybrid methods do not necessitate knowing the applied loads or external geometry. In addition, the proposed hybrid methods smooth the measured data and determine the individual stresses throughout, including on the edge of the hole. All of the prior applications of the mapping technique evaluated the stresses using the constitutive properties and TSA calibration factors found experimentally from standard tensile tests whereas the present approach only evaluated these parameters using the thermoelastic data.

In general, identification of a material constitutive parameters requires the use of inverse methods (IM). Avril and Pierron [7] reviewed several IM approaches and showed their general equivalency. Alshaya et al. [8] determined the constitutive properties of a symmetrically sided notched graphite/epoxy composite using recorded DIC displacement data and Airy stress function. Inverse method (IM) can be generally described as the iterative adjustments of parameters (constitutive properties) in a numerical model (in this case, an Airy stress function scheme) to minimize the difference between an experimentally measured quantity (thermoelastic data) and the numerically calculated quantity. In 2-D models, the degree of freedom is (number of nodes) × 2 – (number of constitutive parameters) – 1. For homogeneous, isotropic materials, the number of constitutive properties is two (E, ν); for homogeneous, orthotropic materials, the number of constitutive parameters are four (E ₁₁, E ₂₂, G ₁₂, ν ₁₂). For either case, the number of degrees of freedom is large and the problem is solved by minimizing least squares of the chosen cost function. The goal of this work is to evaluate the constitutive properties of a composite plate as well as the thermomechanical calibration factors of TSA using IM and Airy stress function scheme. The primary difference IM technique described here is that the specimen geometry is chosen so that an Airy stress function is known a priori and, therefore, the problem is statically determinant. The authors are unaware of prior utilization of mapping and complex variables to determine the constitutive properties in composites from thermoelastic data as well as the TSA calibration factors.

5.2 Thermoelastic Stress Analysis

Thermoelastic stress analysis (TSA) is a non-contacting, non-destructive experimental method for determining the full-field stresses in loaded members. By cyclically loading the structure to satisfy adiabatic reversible conditions, the stresses at a location are related to the stress-induced thermal information at that position. Under orthotropy, the thermoelastic system signal, S ^∗, is proportional to the following change in the linear combination of the normal stresses, σ ₁ and σ ₂, in the directions of material symmetry

$$ {S}^{\ast }=\Delta \left({K}_1{\sigma}_1+{K}_2{\sigma}_2\right) $$

(5.1)

where K ₁ and K ₂ are the orthotropic thermomechanical coefficients and can be determined experimentally.

5.3 Relevant Equations

5.3.1 Basic Equations

For plane problems having rectilinear orthotropy and no body forces, the Airy stress function, $\mathcal{F}$, can be expressed as a summation of two arbitrary analytical functions, F ₁(z ₁) and F ₂(z ₂), of the complex variables, z ₁ and z ₂, as [9]

$$ \mathcal{F}=2\mathit{\operatorname{Re}}\left[{F}_1\left({z}_1\right)+{F}_2\left({z}_2\right)\right] $$

(5.2)

such that z _j = x + μ _j y for j = 1, 2 and Re denotes the ‘real part’ of a complex number. The complex material properties μ ₁ and μ ₂ are two distinct roots of the following characteristic equation associated with the compatibility equation

$$ {\mu}^4+\left(\frac{E_{11}}{G_{12}}-2{\nu}_{12}\right){\mu}^2+\frac{E_{11}}{E_{22}}=0 $$

(5.3)

The 1- and 2-orientations are the directions of orthotropic material symmetry. The stresses in rectangular coordinates (x, y) of the physical z (=x + iy) plane can be expressed in terms of the stress functions. By introducing the new stress functions

$$ \Phi \left({z}_1\right)=\frac{d{F}_1\left({z}_1\right)}{d{z}_1},\kern0.5em \mathrm{and}\kern1.75em \Psi \left({z}_2\right)=\frac{d{F}_2\left({z}_2\right)}{d{z}_2} $$

(5.4)

one can write the stresses as

$$ {\sigma}_{xx}=2\mathit{\operatorname{Re}}\left[{\mu}_1^2{\Phi}^{\prime}\left({z}_1\right)+{\mu}_2^2{\Psi}^{\prime}\left({z}_2\right)\right] $$

(5.5)

$$ {\sigma}_{yy}=2\mathit{\operatorname{Re}}\left[{\Phi}^{\prime}\left({z}_1\right)+{\Psi}^{\prime}\left({z}_2\right)\right] $$

(5.6)

$$ {\sigma}_{xy}=-2\mathit{\operatorname{Re}}\left[{\mu}_1{\Phi}^{\prime}\left({z}_1\right)+{\mu}_2{\Psi}^{\prime}\left({z}_2\right)\right] $$

(5.7)

where primes denote differentiation with respect to the argument. Plane problems of elasticity classically involve determining the stress functions, Φ(z ₁) and Ψ(z ₂), throughout a component and subject to the boundary conditions around its entire edge. For a region of a component adjacent to a traction free-edge, Φ(z ₁) and Ψ(z ₂) can be related to each other by the conformal mapping and analytic continuation techniques. The stresses can then be expressed in terms of the single stress function, Φ(z ₁). Moreover, Φ(z ₁) will be represented by a truncated power-series expansion whose unknown complex coefficients are determined experimentally. Once Φ(z ₁) and Ψ(z ₂) are fully evaluated, the individual stresses are known from Eqs. (5.5) through (5.7). For a significantly large region of interest in a finite structure, it may also be necessary to satisfy other boundary conditions at discrete locations.

5.3.2 Conformal Mapping

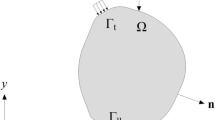
Conformal mapping is introduced to simplify the plane problem by mapping the region R _z of a complicated physical z = x + iy plane of a loaded structure into a region R _ζ of a simpler shape in the ζ = ξ + iη plane, the latter being a unit circle if one represents the stress function as a Laurent series, Fig. 5.1 [9,10,11]. The new coordinate system (and resulting geometry) is usually chosen to aid in solving the equations and the obtained solution from this simplified domain can then be mapped back to the original physical geometry for a valid solution.

Fig. 5.1

Mapping circular cutout in the physical z-plane into exteior region of a unit circle in ζ-plane

Assume that a mapping function of the form z = ω(ζ) exists and which maps R _ζ of the simpler plane into R _z of the more complicated physical plane. For orthotropy, auxiliary planes and their induced mapping functions are defined in terms of ζ _j = ξ + μ _j η, therefore z _j = ω_j(ζ _j), for j = 1, 2. The induced conformal mapping functions are one-to-one and invertible. The stress functions Φ(z ₁) and Ψ(z ₂) can be expressed as the following analytic functions of ζ ₁ and ζ ₂.

$$ \Phi \left({z}_1\right)=\Phi \left[{\upomega}_1\left({\zeta}_1\right)\right]\equiv \Phi \left({\zeta}_1\right)\kern2.5em \mathrm{and}\kern2.5em \Psi \left({z}_2\right)=\Psi \left[{\upomega}_2\left({\zeta}_2\right)\right]\equiv \Psi \left({\zeta}_2\right) $$

(5.8)

The derivatives of the stress functions with respect to their argument are

$$ {\Phi}^{\prime}\left({z}_1\right)={\Phi}^{\prime}\left({\zeta}_1\right)\frac{d{\zeta}_1}{d{z}_1}=\frac{\Phi^{\prime}\left({\zeta}_1\right)}{\upomega_1^{\prime}\left({\zeta}_1\right)}\kern2.25em \mathrm{and}\kern2.5em {\Psi}^{\prime}\left({z}_2\right)=\frac{\Psi^{\prime}\left({\zeta}_2\right)}{\upomega_2^{\prime}\left({\zeta}_2\right)} $$

(5.9)

The analyticity of the mapping functions satisfies the equilibrium and compatibility throughout region R _z of the physical plane.

5.3.3 Traction–Free Boundaries

Using the concept of analytic continuation, the stress functions for a region R _ζ adjacent to a traction-free boundary of the unit circle of an orthotropic material are related by [12]

$$ \Psi \left({\zeta}_2\right)=B\overline{\Phi \left(1/{\overline{\zeta}}_2\right)}+C\Phi \left({\zeta}_2\right) $$

(5.10)

where constants B and C are the following complex material properties

$$ B=\frac{{\overline{\mu}}_2-{\overline{\mu}}_1}{\mu_2-{\overline{\mu}}_2},\kern0.5em C=\frac{{\overline{\mu}}_2-{\mu}_1}{\mu_2-{\overline{\mu}}_2} $$

(5.11)

Equation (5.10) enable the elastic state of the structure to be expressed in terms of a single stress function, Φ(ζ ₁), the latter which can be represented by a Laurent series expansion. Equation (5.10) assumes ability to map the physical boundary of interest into the unit circle in the mapped plane. Reference [13] contains a more thorough derivation of Eq. (5.10).

5.3.4 Mapping Formulation

The objective here is to apply the approach to a region R _z adjacent to a traction-free boundary of a physical member provided an appropriate mapping function is available to map the region R _ζ into region R _z, where Γ_ζ, the exterior of a unit circle in the ζ-plane, goes to the physical traction-free boundary, Γ. For a region adjacent the circular notch of radius R, the following function

$$ {z}_j={\upomega}_{\mathrm{j}}\left({\zeta}_j\right)=\frac{R}{2}\left[\left(1-i{\mu}_j\right){\zeta}_j+\frac{1+i{\mu}_j}{\zeta_j}\right],\kern0.5em j=1,2 $$

(5.12)

maps the region of the exterior of a unit circle, R _ζ, of the ζ-plane into the region R _z of the z-physical plane, Fig. 5.2. The inverse of the induced mapping function is

$$ {\zeta}_j={\upomega}_{\mathrm{j}}^{-1}\left({z}_{\mathrm{j}}\right)=\frac{z_j\pm \sqrt{z_j^2-{R}^2\left(1+{\mu}_j^2\right)}}{R\left(1-i{\mu}_j\right)},\kern0.5em j=1,2 $$

(5.13)

Fig. 5.2

Flow chart of the inverse problem procedure for orthotropic material characterization using Airy stress function scheme

The branch of the square root in Eq. (5.13) is chosen such that |ζ _j|≥ 1 for j = 1, 2.

5.3.5 Mapping Collocation

The single stress function can be expresses as the following finite Laurent series

$$ \Phi \left({\zeta}_1\right)=\sum_{\begin{array}{c}j=-N\\ {}j\ne 0\end{array}}^N{A}_j{\zeta}_1^j $$

(5.14)

where A _j = a _j + ib _j are the unknown complex coefficients (a _j and b _j are both real numbers). The j = 0 term contributes to rigid-body motion and can be omitted. Substituting Eq. (5.14) into (5.10) yields

$$ \Psi \left({\zeta}_2\right)=\sum_{\begin{array}{c}j=-N\\ {}j\ne 0\end{array}}^N\left({\overline{A}}_jB{\zeta}_2^{-j}+{A}_jC{\zeta}_2^j\right) $$

(5.15)

where ${\overline{A}}_j$ is the complex conjugate of A _j. For a finite, simply connected region R _ζ, Φ(ζ ₁) is a single-valued analytic function. Orthotropic composite complex parameters are purely imaginary when the directions of material symmetry are parallel and perpendicular to the applied load and require that only odd terms be retained in the Laurent expansions. From Eqs. (5.5) through (5.8), the stresses can be written as

$$ {\sigma}_{xx}=2\sum_{\begin{array}{c}j=-N,-N+2,\dots \\ {}j\ne 0\end{array}}^N\mathit{\operatorname{Re}}\left\{j\left[\frac{\mu_1^2{\zeta_1}^{j-1}}{\upomega_1^{\prime}\left({\zeta}_1\right)}+\frac{C{\mu}_2^2{\zeta_2}^{j-1}}{\upomega_2^{\prime}\left({\zeta}_2\right)}\right]{A}_j-j{\mu}_2^2B\left[\frac{{\zeta_2}^{-j-1}}{\upomega_2^{\prime}\left({\zeta}_2\right)}\right]{\overline{A}}_j\right\} $$

(5.16)

$$ {\sigma}_{yy}=2\sum_{\begin{array}{c}j=-N,-N+2,\dots \\ {}j\ne 0\end{array}}^{\mathrm{N}}\mathit{\operatorname{Re}}\left\{j\left[\frac{{\zeta_1}^{j-1}}{\upomega_1^{\prime}\left({\zeta}_1\right)}+\frac{C{\zeta_2}^{j-1}}{\upomega_2^{\prime}\left({\zeta}_2\right)}\right]{A}_j- jB\left[\frac{{\zeta_2}^{-j-1}}{\upomega_2^{\prime}\left({\zeta}_2\right)}\right]{\overline{A}}_j\right\} $$

(5.17)

$$ {\sigma}_{xy}=-2\sum_{\begin{array}{c}j=-N,-N+2,\dots \\ {}j\ne 0\end{array}}^N\mathit{\operatorname{Re}}\left\{j\left[\frac{{\mu_1{\zeta}_1}^{j-1}}{\upomega_1^{\prime}\left({\zeta}_1\right)}+\frac{C{\mu}_2{\zeta_2}^{j-1}}{\upomega_2^{\prime}\left({\zeta}_2\right)}\right]{A}_j-j{\mu}_2B\left[\frac{{\zeta_2}^{-j-1}}{\upomega_2^{\prime}\left({\zeta}_2\right)}\right]{\overline{A}}_j\right\} $$

(5.18)

The only unknowns in these expressions for the stresses are the complex coefficients, A _j. The latter can be determined from thermoelastic data. Choosing the x-axis parallel to the stiffest orientation of the composite, i.e., 1-direction of an orthotropic composite material, the TSA signal S ^∗, Eq. (5.1), can be expressed as

$$ \begin{aligned}[b]{S}^{\ast }={\mathrm{K}}_1{\sigma}_{xx}+{K}_2{\sigma}_{yy}=2\sum_{\begin{array}{c}j=-N,-N+2,\dots \\ {}j\ne 0\end{array}}^N&\mathit{\operatorname{Re}}\left\{\left[\frac{j\left({K}_1{\mu}_1^2+{K}_2\right)}{\upomega_1^{\prime}\left({\zeta}_1\right)}{\zeta_1}^{j-1}+\frac{j\left({K}_1{\mu}_2^2+{K}_2\right)C}{\upomega_2^{\prime}\left({\zeta}_2\right)}{\zeta_2}^{j-1}\right]{A}_j\right.\\&\qquad\quad\left.-\left[\frac{j\left({K}_1{\mu}_2^2+{K}_2\right)B}{\upomega_2^{\prime}\left({\zeta}_2\right)}{\zeta_2}^{-j-1}\right]{\overline{A}}_j\right\} \end{aligned} $$

(5.19)

The only unknowns in these expressions for the stresses are the complex coefficients A _j = a _j + ib _j, the other quantities involve geometry (location) or material properties. Because the summation in Eqs. (5.16) through (5.18) involves only the odd values of N, the number of complex coefficients, A _j, is N + 1 and the number of real coefficients, a _j and b _j, is 2(N + 1). These coefficients can be determined from thermoelastic data, S ^∗. It should be noted that by using conformal mapping and analytic continuation techniques, Eqs. (5.16) through (5.18) imply that the induced stresses satisfy equilibrium and traction-free conditions in the adjacent portion of the entire boundary. However, unlike a classical boundary-value problem where one would typically evaluate the unknown coefficients, A _j, by satisfying the boundary and loading conditions around the entire shape, one can use a combination of the measured stresses and/or displacements from within region R _z to determine these unknown complex coefficients, A _j. Additional known boundary conditions may also be imposed at discrete locations. The concept of collecting measured data in a region R ^∗ adjacent to an edge Γ, mapping R _z into R _ζ such that Γ of the physical z-plane is mapped into the unit circle in the ζ-plane whereby the traction-free conditions on Γ are satisfied continuously, relating the two complex stress functions to each other, plus satisfying other loading conditions discretely on the boundary of the component beyond Γ will be referred to as the mapping-collocation technique.

The interior load induced thermal information S ^∗ at m different locations within region R ^∗ are employed. A system of simultaneous linear equations [S]_{m × 2(N + 1)}{c}_{2(N + 1) × 1} = {S ^∗}_m × 1, is formed whose matrix [S] consists of analytical expressions of TSA signals S ^∗, Eq. (5.19), vector {c} = {a _−N, b _−N, a _−N + 2, b _−N + 2, …, a _N − 2, b _N − 2, a _N, b _N} has 2(N + 1) unknown real coefficients, and vector {S ^∗} includes the m measured TSA signal values of S ^∗ such that m ≫ 2(N + 1). The best values of the coefficients A _j, in a least-squares numerical sense, are then be determined. The variables ζ _j = ξ + μ _j η are related to the physical locations z = x + iy through the inverse mapping function z _j = ω_j(ζ _j) of Eqs. (5.12) through (5.13).

5.4 Inverse Method Procedure

The particular inverse method used here is combining TSA signal produced from Airy stress function scheme with load induced thermal information measured by means of TSA. Through an iterative process that determines new constitutive parameters, the difference between measured TSA signals and the ones produced from Airy stress function is minimized. The function to be minimized is

$$ f\left({\widehat{S}}_{Airy},P\right)=\left\Vert r\right\Vert, \kern0.5em \mathrm{where}\ r={\widehat{S}}_{TSA}-{\widehat{S}}_{Airy} $$

(5.20)

where ${\widehat{S}}_{Airy}$ and ${\widehat{S}}_{TSA}$ are vector containing thermoelastic signals data determined by Airy stress function scheme and TSA respectively. P is a vector containing the constitutive parameters, E ₁, E ₂, ν ₁₂, G ₁₂, K ₁, K ₂ and ‖r‖ is the norm of r. Because Eq. (5.20) is nonlinear with respect to P, iterative procedures are appropriate methods for minimizing of $f\left({\widehat{v}}_{Airy},P\right)$ and determination of P. LMA (Levenberg-Marquardt Algorithm) is commonly used because it combines the benefits of Steepest Descent Method and Gauss-Newton Method. The LMA has the form [14]

$$ {P}_{i+1}={P}_i-{\left({J}^TJ+\lambda \cdotp \operatorname{diag}\left({J}^TJ\right)\right)}^{-1}{J}^Tr $$

(5.21)

where i is iteration number, J and J ^T are Jacobian and Jacobian transpose, determined by backward difference, ${J}_{m,n}=\frac{\partial {r}_m}{\partial {P}_n}$; m is number of nodal displacements and n is number of constitutive parameters (6 in this work), and λ is non-negative damping factor, adjusted each iteration step, adjusts between Steepest Descent Method and Gauss-Newton Method.

The primary disadvantage of LMA is the need for matrix inversion during each iteration. In most applications, reduced iterations compensate for the matrix inversion. After calculating a new P _i + 1. The constitutive parameters are checked for validity, i.e., a positive-definite stiffness matrix, and are adjusted if not valid. The validated P _i + 1 are inputs to a new analysis and the resulting nodal displacements are used to determine f _i + 1. If f _i + 1 < f _i, the constitutive parameters are updated, P _i + 1 → P _i, λ is reduced by a factor of 10, and the next iterations begins. If f _i + 1 > f _i, then λ is incrased by a factor of 10 and P _i is not updated. As λ → 0, LMA becomes exactly the Gauss-Newton Method.

5.5 Numerical Experiment

The developed inverse hybrid-TSA approach is utilized to analyze a finite-width tensile [0₁₃/90₅/0₁₃] graphite/epoxy orthotropic plate (E ₁ = 101 GPa, E ₂ = 24.9 GPa, G ₁₂ = 2.88 GPA, ν ₁₂ = 0.152 similar to the one used in Ref. [15]) with circular hole of radius R = 6.35 mm. The plate was loaded in the stiffest material direction (1-, x-direction), Fig. 5.3. Over-all laminate dimensions are 381 mm long and 38.1 mm wide. The coordinate origin is at the center of the plate and the response is symmetric about x- and y-axes. The thermoelastic coefficients K ₁ and K ₂ were evaluated from uniaxial tensile coupons loaded in the stiff and compliant laminate orientations of the orthotropic [0₁₃/90₅/0₁₃] composite plate. The values of the thermomechanical coefficients were determined to be K ₁ = 1.8 mU/MPa (12.38 U/psi) and K ₂ = 14.7 mU/MPa (101.25 U/psi). The unit U is used to signify the raw TSA output, in uncalibrated signal units [15].

Fig. 5.3

Schematic of symmetrically-loaded finite Gr/E [0₁₃/90₅/0₁₃] composite plate with central circular hole

Using simulated data as input is not a representation of the real situation when employing measured data and therefore not a sufficiently severe test of the present scheme. Pseudo-experimental errors were therefore imposed on the simulated input according to the following equation in order to simulate the scatter and/or error typically associated with measured information

$$ {S}_i^{\ast }=\left(1+E{R}_S\right){S}_{i,s}^{\ast } $$

where ${S}_i^{\ast }$ are simulated measured-input TSA signals at location i, E is the maximum absolute random error (user specified), R _S are independent random numbers (−1 ≤ R _S ≤ 1) and ${S}_{i,s}^{\ast }$ are ‘error-free’ values of the simulated TSA signals at the position i. The random errors of these TSA signals were independently generated at each input location. This was accomplished by evaluating R _S using a random number generation program. The maximum absolute error E at a location i is a controlled percentage of the simulated TSA signals ${S}_{i,s}^{\ast }$ at that location. For this numerical experiment, an absolute error of E = 20% was used. Using these ‘noisy’ input values at the 1326 locations of Fig. 5.4, the constitutive properties were determined and compared with the values used for the simulated measured-input displacement.

Fig. 5.4

Locations of m = 1326 data points used in the numerical experiment

5.6 Results

5.6.1 Evaluating Constitutive Properties

The results of this numerical experiment, based on 1326 input values of S ^∗ distributed as shown in Fig. 5.4, were used to evaluate 2 complex coefficients, A _k, (4 real coefficients). Table 5.1 shows the predicted constitutive properties using different initial guesses; ${E}_1^0,{E}_2^0,{G}_{12}^0,{\nu}_{12}^0,{K}_1^0,{K}_2^0$. Regardless of the initial guesses and the noisy implemented data, the method converges to the true value within 20 iterations. All the constitutive properties similarly converged as shown in Fig. 5.5.

Table 5.1 Identified constitutive parameters of orthotropic material using inverse method and Airy stress function scheme

Fig. 5.5

The convergence of the proposed inverse method for case (a)

5.6.2 Evaluating Stresses

Contour plots of the normalized longitudinal, transverse, and shear stresses in the region adjacent to the circular hole are shown in Fig. 5.6. The results shown in Fig. 5.6 demonstrate an excellent agreement with the simulated data. The results of this numerical experiment based on the discrete input values of S ^∗ agree virtually exactly with the FE-simulated values throughout region R _z. The maximum error of the predicted maximum values of σ _xx agrees within 1% of the maximum FE-predicted value. The results for σ _yy and σ _xy are similarly excellent. The u-displacement in Fig. 5.6a is also excellent even though it was derived from Airy stress scheme. These results illustrate the ability of the present hybrid inverse method to provide reliable stresses even with such bad or noisy input data and without the knowledge of the constitutive properties and TSA calibration factors. Such numerical experiments employing simulated test data from FE solution help verifying that there are no algebraic errors and substantiate that the system is numerically robust.

Fig. 5.6

Contour plot of (a) u-displacement, (b) σ _xx/σ ₀, (c) σ _yy/σ ₀, and (d) σ _xy/σ ₀ from hybrid scheme (left) and ANSYS (right)

5.7 Summary, Discussion and Conclusions

Stress analysis of materials can be accomplished by the determination of stress concentrations within structures. Determination such factors necessitates the need of using experimental techniques and knowing the constitutive properties of the structure material and TSA calibration factors. Stress analysis of any structure using only TSA signal data cannot be accomplished without prior knowledge of the constitutive properties of the within material and TSA calibration coefficients, so long as an Airy Stress Function exists to describe the geometry and load configuration. A new inverse hybrid method which processes the load-induced TSA signals with a stress function in complex variables, together with conformal mapping and analytic continuation concepts, provides the constitutive parameters, including TSA calibration factors, and the individual stresses on and in the neighborhood of a circular hole in a finite orthotropic composite plate, all from a single test. The new inverse problem formulation is developed using the Airy stress function, Levenberg-Marquardt Algorithm, and TSA signal data to determine the constitutive properties of a graphite/epoxy composite loaded in the strong/stiff direction. The primary advantage of this new formulation is the direct use of TSA signals data to determine constitutive properties as well as separating the stresses into three individual components. The inverse method algorithm determined the constitutive properties with errors less than 10%.