Abstract
We present a framework in Isabelle for verifying asymptotic time complexity of imperative programs. We build upon an extension of Imperative HOL and its separation logic to include running time. Our framework is able to handle advanced techniques for time complexity analysis, such as the use of the Akra–Bazzi theorem and amortized analysis. Various automation is built and incorporated into the auto2 prover to reason about separation logic with time credits, and to derive asymptotic behaviour of functions. As case studies, we verify the asymptotic time complexity (in addition to functional correctness) of imperative algorithms and data structures such as median of medians selection, Karatsuba’s algorithm, and splay trees.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
In studies of formal verification of computer programs, most of the focus has been on verifying functional correctness of a program. However, for many algorithms, analysis of its running time can be as difficult, or even more difficult than the proof of its functional correctness. In such cases, it is of interest to verify the run-time analysis, that is, showing that the algorithm, or a given implementation of it, does have the claimed asymptotic time complexity.
Interactive theorem provers are useful tools for performing such a verification, as their soundness is based on a small trusted kernel, hence long derivations can be made with a very high level of confidence. So far, the work of Guéneau et al. [6, 12] appears to be the only general framework for asymptotic time complexity analysis of imperative programs in an interactive theorem prover. The framework is built in Coq, based on Charguéraud’s CFML package [5] for verifying imperative programs using characteristic formulas.
We present a new frameworkFootnote 1 for asymptotic time complexity analysis in Isabelle/HOL [19]. The framework is an extension of Imperative HOL [2], which represents imperative programs as monads. Compared to [12], we go further in two directions. First, we incorporate the work of Eberl [11] on the Akra–Bazzi theorem to analyze several divide-and-conquer algorithms. Second, we extend the auto2 prover [21] to provide substantial automation in reasoning about separation logic with time credits, as well as deriving asymptotic behaviour of functions.
We also make use of existing work by Nipkow [18] on analysis of amortized complexity for functional programs. Based on this work, we verify the amortized complexity of imperative implementations of two data structures: skew heaps and splay trees.
Throughout our work, we place a great deal of emphasis on modular development of proofs. As the main theorems to be proved are concerned with asymptotic complexity rather than explicit constants, they do not depend on implementation details. In addition, by using an ad-hoc refinement scheme similar to that in [21], the analysis of an imperative program is divided into clearly-separated parts: proof of functional correctness, analysis of asymptotic behaviour of runtime functions, and reasoning about separation logic. Further separation of concerns is used in amortized analysis.
In summary, the main contributions of this paper are as follows:
-
We extend Imperative HOL and its separation logic to reason about running time of imperative programs (Sect. 2.1).
-
We introduce a methodology to organize the verification so that proofs can be divided cleanly into orthogonal parts (Sect. 3).
-
We extend the existing setup of the auto2 prover for separation logic to also work with time credits. We also set up various automation for proving asymptotic behaviour of functions in one or two variables (Sect. 4).
-
We demonstrate the broad applicability of our framework with several case studies (Sect. 5), including those involving advanced techniques for runtime analysis such as the use of the Akra–Bazzi theorem (for merge sort, median of medians selection, and Karatsuba’s algorithm) and amortized analysis (for dynamic arrays, skew heaps, and splay trees). We also provide an example (Knapsack problem) illustrating asymptotic complexity on two variables.
2 Background
In this section, we review some background material needed in our work. First, we briefly describe the extension of Imperative HOL to reason about running time of imperative programs. Then, we recapitulate the existing theory of asymptotic complexity in Isabelle, and Eberl’s formalization of the Akra–Bazzi theorem.
2.1 Imperative HOL with Time
Imperative HOL [2] is a framework for reasoning about imperative programs in Isabelle. Lammich and Meis later constructed a separation logic for this framework [17]. More details on both can be found in [16].
Atkey [1] introduced the idea of including time credits in separation logic to enable amortized resource analysis, in particular analysis of the running time of a program. He also provided a formalization of the logic in Coq. In this section, we describe how this idea is implemented by modifying Imperative HOL and its separation logic.
Basic Definitions. In ordinary Imperative HOL, a procedure takes a heap (of type  ) as input, and can either fail, or return a pair consisting of a return value and a new heap. In Imperative HOL with time, a procedure returns in addition a natural number when it succeeds, specifying the number of computation steps used. Hence, the type
) as input, and can either fail, or return a pair consisting of a return value and a new heap. In Imperative HOL with time, a procedure returns in addition a natural number when it succeeds, specifying the number of computation steps used. Hence, the type  for a procedure with return type
for a procedure with return type  is given by
is given by  .
.
In the separation logic for ordinary Imperative HOL, a partial heap is defined to be a heap together with a subset of used addresses (type  ). In our case, a partial heap can also contain a number of time credits. Hence, the new type for partial heaps is given by
). In our case, a partial heap can also contain a number of time credits. Hence, the new type for partial heaps is given by  .
.
An assertion (type  ) is, as before, a mapping from
) is, as before, a mapping from  to
to  that does not depend on values of the heap outside the address set. The notation \(((h,as),n) \vDash P\) means the partial heap ((h, as), n) satisfies the assertion P. The basic assertions have the same meaning as before, except they also require the partial heap to contain zero time credits. In addition we define the assertion \(\$n\), to specify a partial heap with n time credits and nothing else.
that does not depend on values of the heap outside the address set. The notation \(((h,as),n) \vDash P\) means the partial heap ((h, as), n) satisfies the assertion P. The basic assertions have the same meaning as before, except they also require the partial heap to contain zero time credits. In addition we define the assertion \(\$n\), to specify a partial heap with n time credits and nothing else.
The separating conjunction of two assertions is defined as follows (differences from original definition are marked in bold):
That is, time credits can be split in a separation conjunction in the same way as sets of addresses on the heap. In particular \(\$(n+m)=\$ n * \$ m\).
Hoare Triples. A Hoare triple  is a predicate of type
is a predicate of type

defined as follows:  holds if for any partial heap ((h, as), n) satisfying P, the execution of c on h is successful with new heap \(h'\), return value r, and time consumption t, such that \(n\ge t\), and the new partial heap \(((h',as'),n-t)\) satisfies Q(r), where \(as'\) is as together with the newly allocated addresses. With this definition of a Hoare triple with time, the frame rule continues to hold.
holds if for any partial heap ((h, as), n) satisfying P, the execution of c on h is successful with new heap \(h'\), return value r, and time consumption t, such that \(n\ge t\), and the new partial heap \(((h',as'),n-t)\) satisfies Q(r), where \(as'\) is as together with the newly allocated addresses. With this definition of a Hoare triple with time, the frame rule continues to hold.
Most basic commands (e.g. accessing or updating a reference, getting the length of an array) are defined to take one unit of computation time. Commands that operate on an entire array, for example initializing an array, or extracting an array into a functional list, are defined to take \(n+1\) units of computation time, where n is the length of the array. From this, we can prove Hoare triples for the basic commands. We give two examples (here  asserts that
asserts that  points to the array
points to the array  and \(\uparrow b\) asserts that b is true):
and \(\uparrow b\) asserts that b is true):


We define the notation  as a shorthand for
as a shorthand for  . The assertion
. The assertion  holds for any partial heap, and in particular can include any number of time credits. Hence, a Hoare triple of the form
holds for any partial heap, and in particular can include any number of time credits. Hence, a Hoare triple of the form  implies that the procedure c costs at most n time credits. We very often state Hoare triples in this form, and so only prove upper bounds on the computation time of the program.
implies that the procedure c costs at most n time credits. We very often state Hoare triples in this form, and so only prove upper bounds on the computation time of the program.
2.2 Asymptotic Analysis
Working with asymptotic complexity informally can be particularly error-prone, especially when several variables are involved. Some examples of fallacious reasoning are given in [12, Sect. 2]. In an interactive theorem proving environment, such problems can be avoided, since all notions are defined precisely, and all steps of reasoning must be formally justified.
For the definition of the big-O notation, or more generally Landau symbols, we use the formalization by Eberl [9], where they are defined in a general form in terms of filters, and therefore work also in the case of multiple variables.
In our work, we are primarily interested in functions of type  (for the single variable case) and
(for the single variable case) and  (for the two-variable case). Given a function g of one of these types, the Landau symbols \(O(g), \varOmega (g)\) and \(\varTheta (g)\) are sets of functions of the same type. In the single variable case, using the standard filter (
(for the two-variable case). Given a function g of one of these types, the Landau symbols \(O(g), \varOmega (g)\) and \(\varTheta (g)\) are sets of functions of the same type. In the single variable case, using the standard filter ( for limit at positive infinity), the definitions are as follows:
for limit at positive infinity), the definitions are as follows:
In the two-variable case, we will use the product filter  throughout. Expanding the definitions, the meaning of the Landau symbols are as expected:
throughout. Expanding the definitions, the meaning of the Landau symbols are as expected:
2.3 Akra–Bazzi Theorem
A well-known technique for analyzing the asymptotic time complexity of divide and conquer algorithms is the Master Theorem (see for example [7, Chap. 4]). The Akra–Bazzi theorem is a generalization of the Master Theorem to a wider range of recurrences. Eberl [11] formalized the Akra–Bazzi theorem in Isabelle, and also wrote tactics for applying this theorem in a semi-automatic manner. Notably, the automation is able to deal with taking ceiling and floor in recursive calls, an essential ingredient for actual applications but often ignored in informal presentations of the Master theorem.
In this section, we state a slightly simpler version of the result that is sufficient for our applications. Let \(f : \mathbb {N} \rightarrow \mathbb {R}\) be a non-negative function defined recursively as follows:
where \(x_0 \in \mathbb {N}\), \(g(x)\ge 0\) for all \(x\ge x_0\), \(a_i \ge 0\) and each \(h_i(x) \in \mathbb {N}\) is either \(\lceil b_i \cdot x \rceil \) or \(\lfloor b_i \cdot x \rfloor \) with \(0< b_i < 1\), and \(x_0\) is large enough that \(h_i(x) < x\) for all \(x\ge x_0\).
The parameters \(a_i\) and \(b_i\) determine a single characteristic value p, defined as the solution to the equation
Depending on the relation between the asymptotic behaviour of g and \(\varTheta (x^p)\), there are three main cases of the Akra–Bazzi theorem:
-
Bottom-heavy: if \(g \in O(x^q)\) for \(q < p\) and \(f(x)>0\) for sufficiently large x, then \(f \in \varTheta (x^p)\).
-
Balanced: if \(g \in \varTheta (x^p\ln ^{a}x)\) with \(a\ge 0\), then \(f \in \varTheta (x^p\ln ^{a+1}x)\).
-
Top-heavy: if \(g \in \varTheta (x^q)\) for \(q > p\), then \(f \in \varTheta (x^q)\).
All three cases are demonstrated in our examples (in Karatsuba’s algorithm, merge sort, and median of medians selection, respectively).
3 Organization of Proofs
In this section, we describe our strategy for organizing the verification of an imperative program together with its time complexity analysis. The strategy is designed to achieve the following goals:
-
Proof of functional correctness of the algorithm should be separate from the analysis of memory layout and time credits using separation logic.
-
Analysis of time complexity should be separate from proof of correctness.
-
Time complexity analysis should work with asymptotic bounds \(\varTheta \) most of the time, rather than with explicit constants.
-
Compositionality: verification of an algorithm should result in a small number of theorems, which can be used in the verification of a larger algorithm. The statement of these theorems should not depend on implementation details.
We first consider the general case and then describe the additional layer of organization for proofs involving amortized analysis.
3.1 General Case
For a procedure with name  , we define three Isabelle functions:
, we define three Isabelle functions:
-
 The functional version of the procedure.
The functional version of the procedure. -
 The imperative version of the procedure.
The imperative version of the procedure. -
 The runtime function of the procedure.
The runtime function of the procedure.
The definition of  should be stated in terms of runtime functions of procedures called by
should be stated in terms of runtime functions of procedures called by  , in a way parallel to the definition of
, in a way parallel to the definition of  . If
. If  is defined by recursion,
is defined by recursion,  should also be defined by recursion in the corresponding manner.
should also be defined by recursion in the corresponding manner.
The theorems to be proved are:
-
1.
The functional program
 satisfies the desired correctness property.
satisfies the desired correctness property. -
2.
A Hoare triple stating that
 implements
implements  and runs within
and runs within  .
. -
3.
The running time
 satisfies the desired asymptotic behaviour.
satisfies the desired asymptotic behaviour. -
4.
Combining 1 and 2, a Hoare triple stating that
 satisfies the desired correctness property, and runs within
satisfies the desired correctness property, and runs within  .
.
Here the proof of Theorem 2 is expected to be routine, since the three definitions follow the same structure. Theorem 3 should involve only analysis of asymptotic behaviour of functions, while Theorem 1 should involve only reasoning with functional data structures. In the end, Theorems 3 and 4 present an interface for external use, whose statements do not depend on details of the implementation or of the proofs.
We illustrate this strategy on the final step of merge sort. The definitions of the functional and imperative programs are shown side by side below. Note that the former is working with a functional list, while the latter is working with an imperative array on the heap.

The runtime function of the procedure is defined as follows:

The theorems to be proved are as follows. First, correctness of the functional algorithm  :
:

Second, a Hoare triple asserting the agreement of the three definitions:

Third, the asymptotic time complexity of  :
:

Finally, Theorems 1 and 2 are combined to prove the final Hoare triple for external use, with  replaced by
replaced by  .
.
3.2 Amortized Analysis
In an amortized analysis, we fix some type of data structure and consider a set of primitive operations on it. For simplicity, we assume each operation has exactly one input and output data structure (extension to the general case is straightforward). A potential function P is defined on instances of the data structure and represents time credits that can be used for future operations. Each procedure f is associated an actual runtime \(f_{\text {t}}\) and an amortized runtime \(f_{\text {at}}\). They are required to satisfy the following inequality: let a be the input data structure of f and let b be its output data structure, thenFootnote 2
The proof of inequality (3) usually involves arithmetic, and sometimes the correctness of the functional algorithm. For skew heaps and splay trees, the analogous results are already proved in [18], and only slight modifications are necessary to bring them into the right form for our use.
The organization of an amortized analysis in our framework is as follows. We define two assertions: the raw assertion  stating that the address a points to an imperative data structure refining t, and the amortized assertion, defined as
stating that the address a points to an imperative data structure refining t, and the amortized assertion, defined as

where P is the potential function.
For each primitive operation implemented by  , we define
, we define  ,
,  , and
, and  as before, where
as before, where  is the actual runtime. We further define a function
is the actual runtime. We further define a function  to be the proposed amortized runtime. The theorems to be proved are as follows (compare to the list in Sect. 3):
to be the proposed amortized runtime. The theorems to be proved are as follows (compare to the list in Sect. 3):
-
1.
The functional program
 satisfies the desired correctness property.
satisfies the desired correctness property. -
2.
A Hoare triple using the amortized assertion stating that
 implements
implements  and runs within
and runs within 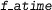 , which is a consequence of the following:
, which is a consequence of the following:-
2a.
A Hoare triple using the raw assertion stating that
 implements
implements  and runs within
and runs within  .
. -
2b.
The inequality between amortized and actual runtime.
-
2a.
-
3.
The amortized runtime
 satisfies the desired asymptotic behaviour.
satisfies the desired asymptotic behaviour. -
4.
Combining 1 and 2, a Hoare triple stating that
 satisfies the desired correctness property and runs within
satisfies the desired correctness property and runs within  .
.
In the case of data structures (and unlike merge sort), it is useful to state Theorem 4 in terms of yet another, abstract assertion which hides the concrete reference to the data structure. This follows the technique described in [21, Sect. 5.3]. Theorems 3 and 4 are the final results for external use.
We now illustrate this strategy using splay trees as an example. The raw assertion is called  . The basic operation in a splay tree is the “splay” operation, from which insertion and lookup can be easily defined. For this operation, the functions
. The basic operation in a splay tree is the “splay” operation, from which insertion and lookup can be easily defined. For this operation, the functions  ,
,  , and
, and  are defined by recursion in a structurally similar manner. Theorem 2a takes the form:
are defined by recursion in a structurally similar manner. Theorem 2a takes the form:

Let  be the potential function on splay trees. Then the amortized assertion is defined as:
be the potential function on splay trees. Then the amortized assertion is defined as:

The amortized runtime for splay has a relatively simple expression:

The difficult part is showing the inequality relating actual and amortized runtime (Theorem 2b):

which follows from the corresponding lemma in [18]. Note the requirement that t is a binary search tree. Combining 2a and 2b, we get Theorem 2:

The asymptotic bound on the amortized runtime (Theorem 3) is:

The functional correctness of  (Theorem 1) states that it maintains sortedness of the binary search tree and its set of elements:
(Theorem 1) states that it maintains sortedness of the binary search tree and its set of elements:

The abstract assertion hides the concrete tree behind an existential quantifier:

The final Hoare triple takes the form ( denotes the cardinality of
denotes the cardinality of  ):
):

4 Setup for Automation
In this section, we describe automation to handle two of the steps mentioned in the previous section: one working with separation logic (for Theorem 2), and the other proving asymptotic behaviour of functions (for Theorem 3).
4.1 Separation Logic with Time Credits
First, we discuss automation for reasoning about separation logic with time credits. This is an extension of the setup discussed in [21] for reasoning about ordinary separation logic. Here, we focus on the additional setup concerning time credits.
The basic step in the proof is as follows: suppose the current heap satisfies the assertion  and the next command has the Hoare triple
and the next command has the Hoare triple

where  is the pure part of the precondition, apply the Hoare triple to derive the successful execution of c, and some assertion on the next heap. In ordinary separation logic (without \(\$ T\) and \(\$ T'\)), this involves matching \(P'\) with parts of P, proving the pure assertions b, and then applying the frame rule. In the current case, we additionally need to show that \(T'\le T\), so \(\$ T\) can be rewritten as \(\$ T=\$(T'+T'')=\$ T'*\$ T''\).
is the pure part of the precondition, apply the Hoare triple to derive the successful execution of c, and some assertion on the next heap. In ordinary separation logic (without \(\$ T\) and \(\$ T'\)), this involves matching \(P'\) with parts of P, proving the pure assertions b, and then applying the frame rule. In the current case, we additionally need to show that \(T'\le T\), so \(\$ T\) can be rewritten as \(\$ T=\$(T'+T'')=\$ T'*\$ T''\).
In general, proving this inequality can involve arbitrarily complex arguments. However, due to the close correspondence in the definitions of  and
and  , the actual tasks usually lie in a simple case, and we tailor the automation to focus on this case. First, we normalize both T and \(T'\) into polynomial form:
, the actual tasks usually lie in a simple case, and we tailor the automation to focus on this case. First, we normalize both T and \(T'\) into polynomial form:
where each \(c_i\) and \(d_j\) are constants, and each \(p_i\) and \(q_j\) are non-constant terms or 1. Next, for each term \(d_j q_j\) in \(T'\), we try to find some term \(c_i p_i\) in T such that \(p_i\) equals \(q_j\) according to the known equalities, and \(d_j \le c_i\). If such a term is found, we subtract \(d_j p_i\) from T. This procedure is performed on T in sequence (so \(d_2 q_2\) is searched on the remainder of T after subtracting \(d_1 q_1\), etc.). If the procedure succeeds with \(T''\) remaining, then we have \(T = T' + T''\).
The above procedure suffices in most cases. For example, given the parallel definitions of  and
and  in Sect. 3.1, it is able to show that
in Sect. 3.1, it is able to show that  runs in time
runs in time  . However, in some special cases, more is needed. The extra reasoning often takes the following form: if s is a term in the normalized form of T, and \(s \ge t\) holds for some t (an inequality that must be derived during the proof), then the term s can be replaced by t in T.
. However, in some special cases, more is needed. The extra reasoning often takes the following form: if s is a term in the normalized form of T, and \(s \ge t\) holds for some t (an inequality that must be derived during the proof), then the term s can be replaced by t in T.
In general, we permit the user to provide hints of the form

where the operator \(\cdot \ge _t\cdot \) is equivalent to \(\cdot \ge \cdot \), used only to remind auto2 that the fact is for modification of time credit only. Given this instruction, auto2 attempts to prove \(s\ge t\), and when it succeeds, it replaces the assertion \(h_i \vDash P * \$ T\) on the current heap with  , where the new time credit \(T'\) is the normalized form of \(T-s+t\). This technique is needed in case studies such as binary search and median of medians selection (see the explanation for the latter in Sect. 5).
, where the new time credit \(T'\) is the normalized form of \(T-s+t\). This technique is needed in case studies such as binary search and median of medians selection (see the explanation for the latter in Sect. 5).
4.2 Asymptotic Analysis
The second part of the automation is for analysis of asymptotic behaviour of runtime functions. Eberl [9] already provides automation for Landau symbols in the single variable case. In addition to incorporating it into our framework, we add facilities for dealing with function composition and the two-variable case.
Because side conditions for the Akra–Bazzi theorem are in the \(\varTheta \) form, we mainly deal with \(\varTheta \) and \(\varTheta _2\), stating the exact asymptotic behaviours of running time functions. However, since running time functions themselves are very often only upper bounds of the actual running times, we are essentially still proving big-O bounds on running times of programs.
In our case, the general problem is as follows: given the definition of  in terms of some
in terms of some  (runtime of procedures called by
(runtime of procedures called by  ), simple terms like 4n or 1, or recursive calls to
), simple terms like 4n or 1, or recursive calls to  , determine the asymptotic behaviour of
, determine the asymptotic behaviour of  .
.
To begin with, we maintain a table of the asymptotic behaviour of previously defined runtime functions. The attribute  adds a new theorem to this table. This table can be looked-up by the name of the procedure.
adds a new theorem to this table. This table can be looked-up by the name of the procedure.
We restrict ourselves to asymptotic bounds of the form
where a and b are natural numbers. In the two-variable case, we work with asymptotic bounds of the form

This suffices for our present purposes and can be extended in the future. Note that this restriction does not mean our framework cannot handle other complexity classes, only that they will require more manual proofs (or further setup of automation).
Non-recursive Case. When the runtime function is non-recursive, the analysis proceeds by determining the asymptotic behaviour in a bottom-up manner.
To handle terms of the form  where s is linear, we use the following composition rule: if \(u\in \varTheta ({\text {polylog}}(a,b))\), and \(v\in \varTheta (\lambda n.\ n)\), then \(u\circ v\in \varTheta ({\text {polylog}}(a,b))\). Composition in general is quite subtle: the analogous rule does not hold if u is the exponential functionFootnote 3.
where s is linear, we use the following composition rule: if \(u\in \varTheta ({\text {polylog}}(a,b))\), and \(v\in \varTheta (\lambda n.\ n)\), then \(u\circ v\in \varTheta ({\text {polylog}}(a,b))\). Composition in general is quite subtle: the analogous rule does not hold if u is the exponential functionFootnote 3.
The asymptotic behaviour of a sum is determined by the absorption rule: if \(g_1\in O(g_2)\), then \(\varTheta (g_1+g_2)=\varTheta (g_2)\). Here, we make use of existing automation in [9] for deciding inclusion of big-O classes of polylog functions. The rule for products is straightforward.
The combination of these three rules can solve many examples automatically. E.g. this (artificial) example: if \(f_1\in \varTheta (\lambda n.\ n)\) and \(f_2\in \varTheta (\lambda n. \ln n)\), then

Analogous results are proved in the two-variable case (note that unlike in the single variable case, not all pairs of  functions are comparable. e.g. \(O(m^2n+mn^2)\)). For example, the following can be automatically solved: if additionally \(f_3\in \varTheta (\lambda (m,n).\ mn)\) and \(f_4\in \varTheta (\lambda (m,n).\ m + n)\), then
functions are comparable. e.g. \(O(m^2n+mn^2)\)). For example, the following can be automatically solved: if additionally \(f_3\in \varTheta (\lambda (m,n).\ mn)\) and \(f_4\in \varTheta (\lambda (m,n).\ m + n)\), then

Recursive Case. There are two main classes of results for analysis of recursively-defined runtime functions: the Akra–Bazzi theorem and results about linear recurrences. For both classes of results, applying the theorem reduces the analysis of a recursive runtime function to the analysis of a non-recursive function, which can be solved using automation described in the previous part.
The Akra–Bazzi theorem is discussed in Sect. 2.3. Theorems about linear recurrences allow us to reason about for-loops written as recursions. They include the following: in the single variable case, if f is defined by induction as
where \(g\in \varTheta (\lambda n.\ n)\), then \(f\in \varTheta (\lambda n.\ n^2)\).
In the two-variable case, if f satisfies
where \(g\in \varTheta (\lambda n.\ n)\), then \(f\in \varTheta _2(\lambda (n,m).\ nm)\).
As an example, consider the problem of showing  complexity of
complexity of  , defined in Sect. 3.1. This applies the balanced case of the Akra–Bazzi theorem. Using this theorem, the goal is reduced to:
, defined in Sect. 3.1. This applies the balanced case of the Akra–Bazzi theorem. Using this theorem, the goal is reduced to:

(the non-recursive calls run in linear time). This can be shown automatically using the method described in the previous section, given that  ,
,  , and
, and  have already been shown to be linear.
have already been shown to be linear.
5 Case Studies
In this section, we present the main case studies verified using our framework. The examples can be divided into three classes: divide-and-conquer algorithms (using the Akra–Bazzi theorem), algorithms that are essentially for-loops (using linear recurrences), and amortized analysis.
We measure the complexity of a proof by counting the number of steps in the proof: each lemma statement counts as one step and each hint provided by the user as an additional step. In the table below, #Hoare counts the number of steps for proving the Hoare triples (Theorems 2 and 4). #Time counts the number of steps for reasoning about runtime functions (Theorem 3). We also list the ratio (Ratio) between the sum of #Hoare and #Time to the number of lines of the imperative program (#Imp). This ratio measures the overhead for verifying the imperative program with runtime analysis. In particular this does not include verifying the correctness of the functional program (Theorem 1). In addition we list the total lines of code for each case study.
#Imp | #Time | #Hoare | Ratio | LOC | |
|---|---|---|---|---|---|
Binary search | 11 | 10 | 14 | 2.18 | 82 |
Merge sort | 38 | 11 | 12 | 0.61 | 121 |
Karatsuba | 58 | 18 | 28 | 0.79 | 250 |
Select | 51 | 41 | 31 | 1.41 | 447 |
Insertion sort | 15 | 3 | 4 | 0.47 | 42 |
Knapsack | 27 | 9 | 8 | 0.63 | 113 |
Dynamic array | 55 | 19 | 37 | 1.02 | 424 |
Skew heap | 25 | 38 | 21 | 2.36 | 257 |
Splay tree | 120 | 51 | 37 | 0.73 | 447 |
Using our automation the average overhead ratio is slightly over 1. On a dual-core laptop with 2 GHz each, processing all the examples takes around ten minutes. The development of the case studies, together with the framework itself, took about 4 person months.
Next we give details for some of the case studies.
Karatsuba’s Algorithm. The functional version of Karatsuba’s algorithm for multiplying two polynomials is verified in [8]. To simplify matters, we further restrict us to the case where the two polynomials are of the same degree.
The recursive equation is given by:
Here g(n) is the sum of the running times corresponding to non-recursive calls, which can be automatically shown to be linear in n. Then the Akra–Bazzi method gives the solution \(T(n)\in \varTheta (n^{log_2 3})\) (bottom-heavy case).
Median of Medians Selection. Median of medians for quickselect is a worst-case linear-time algorithm for selecting the i-th largest element of an unsorted array [7, Sect. 9.3]. In the first step of the algorithm, it chooses an approximate median p by dividing the array into groups of 5 elements, finding the median of each group, and finding the median of the medians by a recursive call. In the second step, p is used as a pivot to partition the array, and depending on i and the size of the partitions, a recursive call may be made to either the section \(x<p\) or the section \(x>p\). This algorithm is particularly interesting because its runtime satisfies a special recursive formula:
where g(n) is linear in n. The Akra–Bazzi theorem shows that T is linear (top-heavy case).
Eberl verified the correctness of the functional algorithm [10]. There is one special difficulty in verifying the imperative algorithm: the length of the array in the second recursive call is not known in advance, only that it is bounded by \(\lceil 7n/10\rceil \). Hence, we need to prove monotonicity of T, as well as provide the hint \(T(\lceil 7n/10\rceil ) \ge _t T(l)\) (where l is the length of the array in the recursive call) during the proof.
Knapsack. The dynamic programming algorithm solving the Knapsack problem is used to test our ability to handle asymptotic complexity with two variables. The time complexity of the algorithm is \(\varTheta _2(nW)\), where n is the number of items, and W is the capacity of the sack. Correctness of the functional algorithm was proved by Simon Wimmer.
Dynamic Array. Dynamic Arrays [7, Sect. 17.4] are one of the simpler amortized data structures. We verify the version that doubles the size of the array whenever it is full (without automatically shrinking the array).
Skew Heap and Splay Tree. For these two examples, the bulk of the analysis (functional correctness and justification of amortized runtime) is done in [18]. Our work is primarily to define the imperative version of the algorithm and verifying its agreement with the functional version. Some work is also needed to transform the results in [18] into the appropriate form, in particular rounding the real-valued potentials and runtime functions into natural numbers required in our framework.
6 Related Work
We compare our work with recent advances in verification of runtime analysis of programs, starting from those based on interactive theorem provers to the more automatic methods.
The most closely-related is the impressive work by Guéneau et al. [12] for asymptotic time complexity analysis in Coq. We now take a closer look at the similarities and differences:
-
Guéneau et al. give a structured overview of different problems that arise when working informally with asymptotic complexity in several variables, then solve this problem by rigorously defining asymptotic domination (which is essentially \(f\in O(g)\)) with filters and develop automation for reasoning about it. We follow the same idea by building on existing formalization of Landau symbols with filters in Isabelle [9], then extend automation to also handle the two-variable case.
-
While they package up the functional correctness together with the complexity claims into one predicate
 , we choose to have two separate theorems (the Hoare triple and the asymptotic bound).
, we choose to have two separate theorems (the Hoare triple and the asymptotic bound). -
While their automation assists in synthesizing recurrence equations from programs, they leave their solution to the human. In contrast, we write the recurrence relation by hand, which can be highly non-obvious (e.g. in the case of median of medians selection), but focus on solving the recurrences for the asymptotic bounds automatically (e.g. using the Akra–Bazzi theorem).
-
Their main examples include binary search, the Bellman–Ford algorithm and union-find, but not those requiring applications of the Master theorem or the Akra–Bazzi method. We present several other advanced examples, including applications of the Akra–Bazzi method, and those involving amortized analysis.
Wang et al. [20] present TiML, a functional programming language which can be annotated by invariants and specifically also with time complexity annotations in types. The type checker extracts verification conditions from these programs, which are handled by an SMT solver. They also make the observation that annotational burden can be lowered by not providing a closed form for a time bound, but only specifying its asymptotic behaviour. For recursive functions, the generated VCs include a recurrence (e.g. \(T(n-1) + 4n \le T(n)\)) and one is left to show that there exists a solution for T which is additionally in some asymptotic bound, e.g. \(O(n^2)\). By employing a recurrence solver based on heuristic pattern matching they make use of the Master Theorem in order to discharge such VCs. In that manner they are able to verify the asymptotic complexity of merge sort. Additionally they can handle amortized complexity, giving Dynamic Arrays and Functional Queues as examples. Several parts of their work rely on non-verified components, including the use of SMT solvers and the pattern matching for recurrence relations. In contrast, our work is verified throughout by Isabelle’s kernel.
On the other end of the scale we want to mention Automatic Amortized Resource Analysis (AARA). Possibly the first example of a resource analysis logic based on potentials is due to Hofmann and Jost [15]. They pioneer the use of potentials coded into the type system in order to automatically extract bounds in the runtime of functional programs. Hoffmann et al. successfully developed this idea further [13, 14]. Carbonneaux et al. [3, 4] extend this work to imperative programs and automatically solve extracted inequalities by efficient off-the-shelf LP-solvers. While the potentials involved are restricted to a specific shape, the analysis performs well and at the same time generates Coq proof objects certifying their resulting bounds.
7 Conclusion
In this paper, we presented a framework for verifying asymptotic time complexity of imperative programs. This is done by extending Imperative HOL and its separation logic with time credits. Through the case studies, we demonstrated the ability of our framework to handle complex examples, including those involving advanced techniques of time complexity analysis, such as the Akra–Bazzi theorem and amortized analysis. We also showed that verification of amortized analysis of functional programs [18] can be converted to verification of imperative programs with little additional effort.
One major goal for the future is to extend Imperative HOL with while and for loops, and add facilities for reasoning about them (both functional correctness and time complexity). Ultimately, we would like to build a single framework in which all deterministic algorithms typically taught in undergraduate study (for example, those contained in [7]) can be verified in a straightforward manner.
The Refinement Framework by Lammich [16] is a framework for stepwise refinement from specifications via deterministic algorithms to programs written in Imperative HOL. It would certainly be interesting to investigate how to combine this stepwise refinement scheme with runtime analysis.
Notes
- 1.
Available online at https://github.com/bzhan/Imperative_HOL_Time.
- 2.
In many presentations, the amortized runtime \(f_{\text {at}}\) is simply defined to be \(f_{\text {t}} + P(b) - P(a)\). Our approach is more flexible in allowing \(f_{\text {at}}\) to be defined by a simple formula and isolating the complexity to the proof of (3).
- 3.
References
Atkey, R.: Amortised resource analysis with separation logic. In: Gordon, A.D. (ed.) ESOP 2010. LNCS, vol. 6012, pp. 85–103. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11957-6_6
Bulwahn, L., Krauss, A., Haftmann, F., Erkök, L., Matthews, J.: Imperative functional programming with Isabelle/HOL. In: Mohamed, O.A., Muñoz, C., Tahar, S. (eds.) TPHOLs 2008. LNCS, vol. 5170, pp. 134–149. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-71067-7_14
Carbonneaux, Q., Hoffmann, J., Reps, T., Shao, Z.: Automated resource analysis with Coq proof objects. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10427, pp. 64–85. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63390-9_4
Carbonneaux, Q., Hoffmann, J., Shao, Z.: Compositional certified resource bounds. In: Grove, D., Blackburn, S. (eds.) PLDI 2015, pp. 467–478. ACM (2015)
Charguéraud, A.: Characteristic formulae for the verification of imperative programs. In: Proceedings of the 16th ACM SIGPLAN International Conference on Functional Programming, ICFP 2011, pp. 418–430. ACM, New York (2011). https://doi.org/10.1145/2034773.2034828
Charguéraud, A., Pottier, F.: Verifying the correctness and amortized complexity of a union-find implementation in separation logic with time credits. J. Autom. Reason. (2017). https://doi.org/10.1007/s10817-017-9431-7
Cormen, T.H., Leiserson, C.E., Rivest, R.L., Stein, C.: Introduction to algorithms, 3rd edn. MIT Press, Cambridge (2009)
Divasón, J., Joosten, S., Thiemann, R., Yamada, A.: The factorization algorithm of Berlekamp and Zassenhaus. Archive of formal proofs. Formal proof development, October 2016. http://isa-afp.org/entries/Berlekamp_Zassenhaus.html
Eberl, M.: Landau symbols. Archive of formal proofs. Formal proof development, July 2015. http://isa-afp.org/entries/Landau_Symbols.html
Eberl, M.: The median-of-medians selection algorithm. Archive of formal proofs. Formal proof development, December 2017. http://isa-afp.org/entries/Median_Of_Medians_Selection.html
Eberl, M.: Proving divide and conquer complexities in Isabelle/HOL. J. Autom. Reason. 58(4), 483–508 (2017)
Guéneau, A., Charguéraud, A., Pottier, F.: A fistful of dollars: formalizing asymptotic complexity claims via deductive program verification. In: Ahmed, A. (ed.) ESOP 2018. LNCS, vol. 10801, pp. 533–560. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89884-1_19
Hoffmann, J., Aehlig, K., Hofmann, M.: Multivariate amortized resource analysis. In: ACM SIGPLAN Notices, vol. 46, pp. 357–370. ACM (2011)
Hoffmann, J., Das, A., Weng, S.C.: Towards automatic resource bound analysis for OCaml. In: ACM SIGPLAN Notices, vol. 52, pp. 359–373. ACM (2017)
Hofmann, M., Jost, S.: Type-based amortised heap-space analysis. In: Sestoft, P. (ed.) ESOP 2006. LNCS, vol. 3924, pp. 22–37. Springer, Heidelberg (2006). https://doi.org/10.1007/11693024_3
Lammich, P.: Refinement to imperative/HOL. In: Urban, C., Zhang, X. (eds.) ITP 2015. LNCS, vol. 9236, pp. 253–269. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-22102-1_17
Lammich, P., Meis, R.: A separation logic framework for imperative HOL. Archive of formal proofs. Formal proof development, November 2012. http://isa-afp.org/entries/Separation_Logic_Imperative_HOL.html
Nipkow, T.: Amortized Complexity Verified. In: Urban, C., Zhang, X. (eds.) ITP 2015. LNCS, vol. 9236, pp. 310–324. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-22102-1_21
Nipkow, T., Wenzel, M., Paulson, L.C. (eds.): Isabelle/HOL. LNCS, vol. 2283. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45949-9
Wang, P., Wang, D., Chlipala, A.: TiML: a functional language for practical complexity analysis with invariants. Proc. ACM Program. Lang. 1(OOPSLA), 79 (2017)
Zhan, B.: Efficient verification of imperative programs using auto2. In: Beyer, D., Huisman, M. (eds.) TACAS 2018. LNCS, vol. 10805, pp. 23–40. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89960-2_2
Acknowledgments
This work is funded by DFG Grant NI 491/16-1. We thank Manuel Eberl for his impressive formalization of the Akra–Bazzi method and the functional correctness of the selection algorithm, and Simon Wimmer for the formalization of the DP solution for the Knapsack problem. We thank Manuel Eberl, Tobias Nipkow, and Simon Wimmer for valuable feedback during the project. Finally, we thank Armaël Guéneau and his co-authors for their stimulating paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Zhan, B., Haslbeck, M.P.L. (2018). Verifying Asymptotic Time Complexity of Imperative Programs in Isabelle. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds) Automated Reasoning. IJCAR 2018. Lecture Notes in Computer Science(), vol 10900. Springer, Cham. https://doi.org/10.1007/978-3-319-94205-6_35
Download citation
DOI: https://doi.org/10.1007/978-3-319-94205-6_35
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-94204-9
Online ISBN: 978-3-319-94205-6
eBook Packages: Computer ScienceComputer Science (R0)




 The functional version of the procedure.
The functional version of the procedure. The imperative version of the procedure.
The imperative version of the procedure. The runtime function of the procedure.
The runtime function of the procedure. satisfies the desired correctness property.
satisfies the desired correctness property. implements
implements  and runs within
and runs within  .
. satisfies the desired asymptotic behaviour.
satisfies the desired asymptotic behaviour. satisfies the desired correctness property, and runs within
satisfies the desired correctness property, and runs within  .
. satisfies the desired correctness property.
satisfies the desired correctness property. implements
implements  and runs within
and runs within 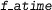 , which is a consequence of the following:
, which is a consequence of the following: implements
implements  and runs within
and runs within  .
. satisfies the desired asymptotic behaviour.
satisfies the desired asymptotic behaviour. satisfies the desired correctness property and runs within
satisfies the desired correctness property and runs within  .
. , we choose to have two separate theorems (the Hoare triple and the asymptotic bound).
, we choose to have two separate theorems (the Hoare triple and the asymptotic bound).