Abstract
Cycloids are particular Petri nets for modelling processes of actions or events. They belong to the fundaments of Petri’s general systems theory and have very different interpretations, ranging from Einstein’s relativity theory to elementary information processing gates. Despite their simple definitions, their properties are still not completely understood. This contribution provides for the first time a formal definition together with new results concerning their structure. For instance, it is shown that the minimal length of a cycle is the length of a local basic circuit, possibly decreased by an integer multiple of the number of semi-active transitions.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
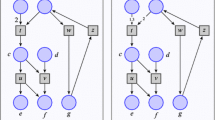
Cycloids were discovered by C. A. Petri to describe fundamental processes running in time and space. They are based on Minkowski’s spacetime model, but use causal dependence instead of numeric distance. They have been introduced in [7] in the section on physical spaces to illustrate the shift from Galilei to Lorentz transformation. Of particular importance to Petri was his discovery that fundamental gates of boolean circuits, such as XOR-transfer, majority-transfer, or Quine-transfer, are topologically equivalent to some of his cycloids (see Fig. 9). In private communication with the author, he explained that he discovered this relationship by pure diligence without any methodical approach. Petri usually introduced the concept using the regimen or organization rule for people carrying buckets to extinguish a fire [7] or by cars driving in line on a road with varying distances as shown in Fig. 1 (from [9]). In the corresponding causal and infinite net, cars are represented by black tokens moving forward in time and space, whereas the gaps are moving also forward in time but in the opposite spacial directionFootnote 1. As the concept considerably differs from Minkowski’s space and is based uniquely on causal dependencies, we call it Petri spaceFootnote 2. Petri defined the slowness of the system by the quotient of the difference of the numbers of gap units and cars (in a suitable section of a case), divided by the sum of the numbers of gaps and cars. In the example this is \(w := \frac{gaps-cars}{gaps+cars} = \frac{12-4}{12+4}= \frac{1}{2}\). In [9] he wrote: “The concept of slowness is a key to understanding repetitive group behaviour. It can be applied to organization, to workflow (just-in-time production), and to physical systems”.Footnote 3 In the report [11], Stehr states that the nets of Fig. 2 have slowness \(w=0\) on the left-hand side and slowness \(w=1/3\) on the right-hand. Intuitively it is visible that the first net is “faster” as more transitions can occur concurrently. But the parameters \(\alpha \) and \(\beta \), which have been used by Petri to define the slowness, are not directly visible from the net. In this paper we show how to compute these parameters.
In this context systems are considered as finite repetitive structures. They are constructed by folding the Petri space. In a first step, a finite space is assumed. Hence after some finite number of steps the initial state is reached again. This is modelled by folding the Petri space in such a way that transitions a and b (as well as d and c) of Fig. 3 are identified. The resulting still infinite net is called a time orthoid ([7], p. 37), as it extends infinitely in temporal direction.
Next, the analogous step is done with respect to time, i.e. transitions a and d are identified. The resulting net is finite, and all the four vertices a, b, c and d are identified. In the middle of the figure, the resulting net is represented by the output of a cycloid toolFootnote 4. On the right hand side, a redesign is shown emphasizing the cyclic structureFootnote 5. Note that the cycle leading in a straight line from transition a via 3 other transitions to transition c, the latter identified with a in the folding, corresponds to the cycle t1, t2, t3, t4 in the right-hand side nets. Other examples generated with that tool are given in the Figs. 6 and 8.
The aims of this paper are threefold:
-
From the lectures and seminars, Petri gave in the years 1988–2004 at the University of Hamburg, there is a lot of unpublished knowledge in hand-written scripts by Petri and in the notes and the memory of the persons which attended the events [6]. Some of this knowledge is put into writing in this paper.
-
The introduction of cycloids in [7] is rather short. This paper provides formal definitions that allow to prove some properties.
-
New properties of cycloids are found, like symmetry properties or length-of-shortest-cycles, that allow new analytic procedures.
We acknowledge the work of Uwe Fenske, who collected much of the material mentioned above and contributed formal Definitions 2, 3 and 8 as well as Lemma 4 in a thesis [1]. This thesis also contains a large number of explanations and motivations of Petri’s concepts. Later he implemented the cycloid tool mentioned above, which allowed to create numerous examples by the construction of cycloid systems in form of RENEW nets. We also acknowledge Peter Langner who wrote the web tool “Cycloids’ Characteristics” [5], which was very useful to investigate cycloids in the form of the fundamental parallelogram (see Figs. 6 and 8). We further acknowledge the help of Lawrence Cabac who provided a plug-in for the computation of cycles from a RENEW net. Finally thanks to Uwe Fenske, Mark-Oliver Stehr, Bernd Neumann and Olaf Kummer for comments on this paper, the latter for suggesting Theorem 5(b) and (c).
2 Nets, Net Systems and Petri Space
Definition 1
A net \( \mathcal {N}_{} \) is defined by a triple (S, T, F) where S is a set, called set of state elements or places, a set T of transitions and a flow relation F, with the following restrictions:

An element from \(X \mathrel {:=}S \cup T\) is said to be a net element of \( \mathcal {N}_{} \).
\(^{\mathord {\scriptscriptstyle ^\bullet }} x \mathrel {:=}F^{-1}[x]\)Footnote 6, \(x^{\mathord {\scriptscriptstyle ^\bullet }} \mathrel {:=}F[x]\) denote the input and output elements of an element x, respectively.
A transition \(t \in T\) is active in a marking \(M\subseteq S\) if \( \; 0 \le |^{\mathord {\scriptscriptstyle ^\bullet }} t \cap M| = |^{\mathord {\scriptscriptstyle ^\bullet }}t|\) and \( t^{\mathord {\scriptscriptstyle ^\bullet }} \cap \;M = \emptyset \). In this case the follower marking \(M'\) is defined and given by \(M' = M \backslash ^{\mathord {\scriptscriptstyle ^\bullet }} t \cup t^{\mathord {\scriptscriptstyle ^\bullet }} \).
A transition \(t \in T\) with \(|^{\mathord {\scriptscriptstyle ^\bullet }}t| \ge 2\) is semi-active in a marking \(M\subseteq S\) if \( \; 0< |^{\mathord {\scriptscriptstyle ^\bullet }} t \cap M| < |^{\mathord {\scriptscriptstyle ^\bullet }}t|\) and \( t^{\mathord {\scriptscriptstyle ^\bullet }} \cap \;M = \emptyset \).
A transition \(t \in T\) with \(|^{\mathord {\scriptscriptstyle ^\bullet }}t| \ge 1\) is input-marked or marked in a marking \(M\subseteq S\) if \( \; 0 < |^{\mathord {\scriptscriptstyle ^\bullet }} t \cap M| \le |^{\mathord {\scriptscriptstyle ^\bullet }}t|\) and \( t^{\mathord {\scriptscriptstyle ^\bullet }} \cap \;M = \emptyset \).
A net (S, T, F) together with an initial marking \(M_0\) is called a net system.
Active transitions follow the usual definition: \( ^{\mathord {\scriptscriptstyle ^\bullet }} t \subseteq M \) and \( t^{\mathord {\scriptscriptstyle ^\bullet }} \cap \;M = \emptyset \). For a semi-active transition there are some, but not sufficiently many input tokens. A transition, with \(|^{\mathord {\scriptscriptstyle ^\bullet }}t| \ge 2\), is marked if it is active or semi-active.
Definition 2
A \(Petri\;space\) is defined by the net
\(\mathcal {PS}_{1} \mathrel {:=}(S_1, T_1, F_1)\) where

\(S^\rightarrow _{1}\) is called set of forward places and \(S^\leftarrow _{1}\) the set of backward places.
The introduced denominations of the Petri space elements are shown in Fig. 4 and should be compared with Fig. 1. Contrary to the Minkowski space, the Petri space is independent of an embedding into  . It is therefore suitable for the modelling in transformed coordinates as in non-Euclidian space models. However, the reader will wonder that we will apply linear algebra, for instance using equations of lines. This is done only to determine the relative position of points. It can be understood by first topologically transforming and embedding the space into
. It is therefore suitable for the modelling in transformed coordinates as in non-Euclidian space models. However, the reader will wonder that we will apply linear algebra, for instance using equations of lines. This is done only to determine the relative position of points. It can be understood by first topologically transforming and embedding the space into  , calculating the position and then transforming back into the Petri space. Distances, however, are not computed with respect to the Euclidean metric, but by counting steps in the grid of the Petri space.
, calculating the position and then transforming back into the Petri space. Distances, however, are not computed with respect to the Euclidean metric, but by counting steps in the grid of the Petri space.
3 Cycloids
Definition 3
A cycloid is a net  , defined by parameters
, defined by parameters  Footnote 7 as a quotient of the Petri space \(\mathcal {PS}_{1} \mathrel {:=}(S_1, T_1, F_1)\) (Definition 2) with respect to the equivalence relation \(\mathord {\equiv }\subseteq X_1 \mathbin \times X_1\) withFootnote 8
Footnote 7 as a quotient of the Petri space \(\mathcal {PS}_{1} \mathrel {:=}(S_1, T_1, F_1)\) (Definition 2) with respect to the equivalence relation \(\mathord {\equiv }\subseteq X_1 \mathbin \times X_1\) withFootnote 8

Isomorphic nets are denominated as cycloids, as well.
From [1] we cite the following lemma.
Lemma 4
The natural application with respect to \(\mathord {\equiv }\subseteq X_1 \mathbin \times X_1\) and explicitely specified by \(f_ {\mathord {\equiv }}:X_1\rightarrow X\), \(f_ {\mathord {\equiv }}(x_{\xi ,\eta }) = [\![x_{\xi ,\eta }]\!]_{\equiv }\) and the property \( f_ {\mathord {\equiv }}(x_{\xi ,\eta }) = f_ {\mathord {\equiv }}(x_{\xi +m\alpha +n\gamma ,\,\eta -m\beta +n\delta }) \) for arbitrary  is a net morphism, and particularly a folding and a quotient.
is a net morphism, and particularly a folding and a quotient.
Proof
Following [10] the map \(f_ {\mathord {\equiv }}\) is a morphism if and only if
\(\mathord {\equiv }\; \cap \; (S_1 \times T_1 ) = \emptyset \). This holds in our case as property (b) of Definition 1 is preserved by \(f_ {\mathord {\equiv }}\). Also by [10] \(f_ {\mathord {\equiv }}\) is a folding and a quotient. \(\square \)
As we are interested in exploring the structure of cycloids from their para-meters, symmetries are of importance. The first symmetry will be used in later sections, namely that the structure is preserved by exchanging \(\alpha \) with \(\beta \), and \(\gamma \) with \(\delta \), respectively. This symmetry describes the exchange of forward by backward lines, which are terms used by Petri. If ordinary time and space coordinates are considered (see Fig. 1 and [7]) it describes the reversal of space orientation. The second and third symmetry are a kind of shearing of the cycloid. They have an interesting application in Sect. 6.
Theorem 5
The following cycloids are isomorphic to \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta ) \):
-
(a)
\(\mathcal {C}(\beta ,\alpha ,\delta ,\gamma ) \),
-
(b)
\(\mathcal {C}(\alpha ,\beta ,\gamma - \alpha ,\delta +\beta ) \) if \(\gamma > \alpha \) and
-
(c)
\(\mathcal {C}(\alpha ,\beta ,\gamma + \alpha ,\delta -\beta ) \) if \(\delta > \beta \).
Proof
-
(a)
We show that the mapping \(\varphi : X_1 \rightarrow X_1\) defined by \(\varphi (x_{\xi ,\eta }) := x_{\eta +\beta ,\xi -\alpha }\) is an isomorphism that is congruent to \(\equiv \). To avoid confusion we denote the second cycloid by \(\mathcal {C}'(\alpha ',\beta ',\gamma ',\delta ') \), i.e. \(\alpha ' = \beta \), \(\beta ' = \alpha \), \(\gamma ' = \delta \), \(\delta ' = \gamma \).
\(\varphi \) is an isomorphism on the Petri space since \(\varphi (x_{\xi ,\eta }) = \varphi (x_{\xi ',\eta '})\,\Rightarrow \,\eta +\beta = \eta '+\beta \wedge \xi -\alpha = \xi '-\alpha \,\Rightarrow \,(\xi ,\eta ) = (\xi ',\eta ') \), i.e. \(\varphi \) is injective and by similar arguments also surjective.
It remains to show, that \(\varphi \) is congruent, i.e. \(x_{\xi ,\eta } \equiv x_{\xi _1,\eta _1} \; \Rightarrow \; \varphi (x_{\xi ,\eta }) \equiv \varphi (x_{\xi _1,\eta _1})\). For easier reading, we omit the letter x and calculate with the indices only: with \(\varphi (\xi ,\eta ) = (\xi ',\eta ')\) and \(\varphi (\xi _1,\eta _1) = (\xi _1',\eta '_1)\) we now prove \((\xi ,\eta ) \equiv (\xi _1,\eta _1)\,\Rightarrow \,(\xi ',\eta ') \equiv (\xi '_1,\eta '_1)\). By the definition of \(\equiv \) we have \((\xi _1,\eta _1) = (\xi +m\alpha +n\gamma ,\eta -m\beta +n\delta )\) for some
 and $$\begin{aligned} \begin{aligned} (\xi '_1,\eta '_1)&= (\eta -m\beta +n\delta +\beta ,\xi +m\alpha +n\gamma -\alpha ) \\&= (\eta +\beta -m\beta +n\delta ,\xi -\alpha +m\alpha +n\gamma ) \\&= (\xi '+m'\alpha '+n'\gamma ',\eta '-m'\beta '+n'\delta ') \end{aligned} \end{aligned}$$
and $$\begin{aligned} \begin{aligned} (\xi '_1,\eta '_1)&= (\eta -m\beta +n\delta +\beta ,\xi +m\alpha +n\gamma -\alpha ) \\&= (\eta +\beta -m\beta +n\delta ,\xi -\alpha +m\alpha +n\gamma ) \\&= (\xi '+m'\alpha '+n'\gamma ',\eta '-m'\beta '+n'\delta ') \end{aligned} \end{aligned}$$with \(m'=-m \) and \( n'=n\), hence \((\xi '_1,\eta '_1)\equiv (\xi ',\eta ') \). (b) Since \(\xi + m\alpha +n(\gamma -\alpha ) = \xi + (m-n)\alpha +n\gamma \) and \(\eta -m\beta +n(\delta +\beta ) = \eta -(m-n)\beta +n\delta \), the equivalence relation folding the Petri space is the same as the original one of Definition 2. The analogous argument proves part (c). \(\square \)
For proving properties of cycloids particular denotations are needed. Petri used the letters O, P, R and Q for the vertices of the fundamental parallelogram ([7], p. 41). Equations, vectors and distances with respect to these vertices will be used (see Fig. 5).
Lemma 6
For a cycloid \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) the vertices with their coordinates in clockwise order are \(O = (0,0)\) (origin), \(P = (\alpha ,-\beta )\) (space), \(R = (\alpha +\gamma ,\delta -\beta )\)(space and time) and \(Q = (\gamma ,\delta )\) (time). For pairs (A, B) of such nodes the following table gives the equation for the line \(\overline{AB} \) through A and B in column 2, the vector \(\overrightarrow{AB}\) from A to B in column 3 and the distance d(A, B) between A and B.
(A, B) | Equation for \(\overline{AB} \) | Vector \(\overrightarrow{AB}\) | Distance d(A, B) |
|---|---|---|---|
(O, P) | \(\eta = - \frac{\beta }{\alpha } \xi \) | \(\left( \begin{array}{c}\alpha \\ beta\end{array}\right) = \mathbf {a}_s\) | \(\alpha +\beta \) |
(O, Q) | \(\eta = \frac{\delta }{\gamma } \xi \) | \(\left( \begin{array}{c}\gamma \\ \delta \end{array}\right) = \mathbf {a}_t\) | \(\gamma +\delta \) |
(P, R) | \(\eta = \frac{\delta }{\gamma } (\xi -\alpha )-\beta \) | \(\left( \begin{array}{c}\gamma \\ \delta \end{array}\right) \) | \(\gamma +\delta \) |
(Q, R) | \(\eta = \frac{-\beta }{\alpha } (\xi -\gamma )+\delta \) | \(\left( \begin{array}{c}\alpha \\ beta\end{array}\right) \) | \(\alpha +\beta \) |
(P, Q) | \(\eta = \frac{\beta +\delta }{\gamma -\alpha } (\xi -\alpha ) - \beta \) | \(\left( \begin{array}{c}-\alpha +\gamma \\ \beta +\delta \end{array}\right) \) | \(|\alpha -\gamma |+\beta +\delta \) |
(O, R) | \(\eta = \frac{\delta -\beta }{\alpha +\gamma } \xi \) | \(\left( \begin{array}{c}\alpha +\gamma \\ \delta -\beta \end{array}\right) \) | \(\alpha +\gamma +|\beta -\delta |\) |
Proof
The vectors \(\overrightarrow{OP}\) and \(\overrightarrow{OQ}\) are obvious (see Fig. 5), while the vector \(\overrightarrow{OR}\) is the sum of both. \(\overrightarrow{PR}\) equals \(\overrightarrow{OQ}\) and \(\overrightarrow{PQ} = \overrightarrow{OQ}- \overrightarrow{OP}\). Similarly the equations for the lines \(\overline{OP} \) and \(\overline{OQ} \) are obvious (see Fig. 5). The equation for \(\overline{PR} \) is a shift of value \(\alpha \) of \(\overline{OQ} \) in \(\xi \)-direction and of value \(-\beta \) in \(\eta \)-direction. In a similar way \(\overline{QR}\) is a shift of \(\overline{OP} \). The slope of \(\overline{QR}\) and \(\overline{OQ}\) follow from \(\overline{OP}\) and \(\overline{PR}\), respectively. The slope of \(\overline{PQ}\) follows from \(\overrightarrow{PQ}\) while its \(\eta \)-intercept is computed by ordinary methods. To prove column 4, observe that the distance is different from Euclidean geometrie, as the steps between points of the grid are counted. Therefore \(d(\left( \begin{array}{c} a \\ b \end{array}\right) , \left( \begin{array}{c} c \\ d \end{array}\right) )\) = \(|a-c|+|b-d|\). \(\square \)
The number of transitions of a cycloid is frequently used by Petri and called area A ([7], p. 40). He gave a geometrical proof in his lectures, which was described in [1]. In the proof below we use a property of determinants. This will be useful when considering cycloids in higher dimensions.
Theorem 7
-
(a)
A cycloid \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) has \(A = |T| = \alpha \delta +\beta \gamma \) transitions and \(|S| = 2 \;|T| \) places.
-
(b)
The set T of transitions of such a cycloid is the union of three setsFootnote 9, called Upper Area UA, Middle Area MA and Lower Area LA. These sets are:
-
1.
Upper Area for
 :
:
-
2.
Middle Area 1 for \(\gamma \le \alpha \) and \(\gamma \le \xi \le \alpha \):

-
3.
Middle Area 2 for \(\alpha \le \gamma \) and \(\alpha \le \xi \le \gamma \):

-
4.
Lower Area for \( \max (\alpha ,\gamma ) \le \xi \le \alpha + \gamma \):

-
1.
Proof
-
(a)
It is well-known that the volume A of a parallelepiped of n vectors is the determinant of the matrix having these vectors as columns. In our case we have two vectors in two dimensions: \(A = det(\overrightarrow{OP}\;\overrightarrow{OQ}) = \bigg \vert \begin{array}{cc}\alpha &{}\gamma \\ -\beta &{}\delta \end{array} \bigg \vert = \alpha \delta + \beta \gamma \). For each transition \(t_{\xi ,\eta }\) there are two places \(s^\rightarrow _{\xi ,\eta }\) and \(s^\leftarrow _{\xi ,\eta }\), hence \(|S| = 2 \;|T| \).
-
(b)
The Upper Area is a triangle bordered by the lines \(\overline{OP} \), \(\overline{OQ} \) and \(\xi = min(\alpha ,\gamma )\) (see Fig. 5 and the table of Lemma 6). The Middle Area depends on the value of \(\alpha \le \gamma \), but the proof also applies. The same holds for the Lower Area. The special case \(\alpha = \gamma \) is covered by all four cases. \(\square \)
4 Cycloid Systems
As in most Petri net models, a net structure together with an initial marking is called a net system as it gives rise to dynamic processes. The first formal definition of an initial marking for cycloids is given by Kummer [3, 4]. For the cycloid \(\mathcal {C}(4,4,2,2)\) he gives three live initial markings having different reachability sets. This shows that the right choice of an initial marking is important. In the same year, but not known by Kummer, Petri published the following informal definition ([7], p. 38): We provide each cycloid with a standard marking by marking the earliest case in the fundamental parallelogram. In his earlier lecturesFootnote 10 Petri gave an interpretation: shift the space repetition vector \(\overrightarrow{OP} = \mathbf {a}_s\) (see Fig. 5) in the direction of the time repetition vector \(\overrightarrow{OQ} = \mathbf {a}_t\) until it does not meet any crossing point (i.e. transitions) of the Petri space grid. The edges of the grid which are crossed in this way are the locations of the intended initial marking. To formalize this approach, we select transitions lying between the line \(\overline{OP}\) (having equation \(\eta = -\frac{\beta }{\alpha }\xi \)) and the line \(\eta = -\frac{\beta }{\alpha }(\xi +1)\). The latter results from \(\overline{OP}\) by a shift of distance 1 in negative \(\xi \)-direction. For each such transition \(t_{\xi ,\eta }\) a token is located in its forward place \(s^\rightarrow _{\xi ,\eta }\). In a similar way, tokens are introduced in backward places of transitions between lines \(\eta = -\frac{\beta }{\alpha }\xi \) and the line \(\eta = -\frac{\beta }{\alpha }\xi -1\), i.e. the line shifted by 1 in negative \(\eta \)-direction. Between any two of such marked places there is no directed path in the Petri grid. Therefore these marked places are causally independentFootnote 11, as required for a marking. The definition of Fenske and Kummer are very similar and generate the same reachability set. From the difference it becomes apparent that Petri’s informal definition is not unambiguous. In Petri’s handwritten script [6] we found the cycloid \(\mathcal {C}(4,3,4,3)\) (see Fig. 6), which is used for illustration. Also in Fig. 6 the corresponding cycloid system is shown in two different representations, together with their standard initial marking.
Definition 8
For a cycloid \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) constructed as a quotient from the Petri space \(\mathcal {PS}_{1} = (S_1, T_1, F_1)\) by the equivalence relation \(\equiv \) we define a cycloid system by adding the following standard initial markingFootnote 12

Cycloid system \(\mathcal {C}(4,3,4,3)\) from [6] and redesign.
A proof that a cycloid system is strongly connected, live, safe and secure is given in [1], drafting upon propositions by Stehr [12]Footnote 13. The next lemma shows properties that are useful for designing the initial marking and are used in the following proofs. Parts (a) and (b) of the lemma show that the coordinates of the first and the lastFootnote 14 marked transitions \(t_{1,0}\) and \(t_{\alpha ,1-\beta }\) are the same in all cycloids with \(\alpha \ge \beta \). (c) proves a more general regularity, namely that the backward input places of all marked transitions are marked. Part (d) is useful to show that some of these transitions are semi-active, and (e) and (f) will be used to prove that coordinates of a marked transition fulfil a certain condition.
Lemma 9
Let \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) be a cycloid system with \(\alpha \ge \beta \) and initial marking \(M_0\). (See Figs. 4 and 7 for the following properties.)
-
(a)
\(t_{1,0}\) is active.
-
(b)
\(t_{\alpha ,1-\beta }\) is active if \(\alpha = \beta \), but is semi-active if \(\alpha > \beta \).
-
(c)
The backward input place is marked for all marked transitions.
-
(d)
If \(s^\leftarrow _{\xi ,\eta -1} \in M_0\) then \(s^\rightarrow _{\xi ,\eta } \notin M_0\).
-
(e)
If \(t_{\xi ,\eta }\) is a marked transition, then \(t_{\xi ,\eta - 1}\) is not.
-
(f)
If \(t_{\xi -1,\eta +1}\) and \(t_{\xi ,\eta }\) are marked transitions, then \(s^\rightarrow _{\xi -1,\eta } \in M_0\).
Proof
-
(a)
The coordinates of the input places of \(t_{1,0}\) are (0, 0) and \((1,-1)\) and therefore satisfy the conditions (1) and (2) of Definition 8 due to \(\alpha \ge \beta \).
-
(b)
The coordinates of the backward input place of \(t_{\alpha ,1-\beta }\) are \((\alpha ,-\beta )\) and satisfy the condition (2). Condition (1) for the forward input place \(s^\rightarrow _{\alpha -1,1-\beta }\) is equivalent to \(\beta \ge \beta +1-\frac{\beta }{\alpha }\; \wedge \beta < \beta +1\) and requires \(\alpha = \beta \) (as we assumed \(\alpha \ge \beta \)).
-
(c)
As for a marked transition \(t_{\xi ,\eta }\) at least one input place is marked in \(M_0\), it is sufficient to show that the backward input place is marked if the forward input place is marked: if \(s^\rightarrow _{\xi -1,\eta } \in M_0\) then \(s^\leftarrow _{\xi ,\eta -1} \in M_0\). In fact, from the first part of condition (1) for \(s^\rightarrow _{\xi -1,\eta } \), namely \(\eta \le - \frac{\beta }{\alpha }(\xi -1)\) and using \(\alpha \ge \beta \) it follows \(\eta - 1\le - \frac{\beta }{\alpha }\xi \) which is the first part of condition (2) for \(s^\leftarrow _{\xi ,\eta -1}\). The same holds for the second part of the conditions.
-
(d)
If \(s^\rightarrow _{\xi ,\eta } \in M_0\) then (by condition (1)) \(\eta \le -\frac{\beta }{\alpha }\xi \) which is in contradiction to the second part of condition (2) for \(s^\leftarrow _{\xi ,\eta -1}\), hence \(s^\rightarrow _{\xi ,\eta } \notin M_0\).
-
(e)
The following property has to be proved: if one of the two (or both) input places \(s^\rightarrow _{\xi -1,\eta }\) or \(s^\leftarrow _{\xi ,\eta -1}\) of \(t_{\xi ,\eta }\) are marked then by (c) the backward input place \(s^\leftarrow _{\xi ,\eta -2}\) of \(t_{\xi ,\eta -1}\) is not marked. Indeed, let be \(s^\rightarrow _{\xi -1,\eta } \in M_0\), i.e. \(\eta \le -\frac{\beta }{\alpha } ( \xi -1) \wedge \eta > -\frac{\beta }{\alpha }\xi \) implying \( \eta \le -\frac{\beta }{\alpha }\xi + \frac{\beta }{\alpha } \le -\frac{\beta }{\alpha }\xi +1 \) (condition (*)). Assuming \(s^\leftarrow _{\xi ,\eta -2}\) be marked leads to \(\eta -2 > - \frac{\beta }{\alpha }\xi - 1\) and \(\eta > -\frac{\beta }{\alpha }\xi +1\) in contradiction to condition (*). The second case for \(s^\leftarrow _{\xi ,\eta -1}\) is similar.
-
(f)
If \(t_{\xi -1,\eta +1}\) is a marked transition, then by (c) \(s^\leftarrow _{\xi -1,\eta } \in M_0\) (see Fig. 4) and by the first part of condition (2) it follows \(\eta \le -\frac{\beta }{\alpha }(\xi -1)\). This is the same condition (2) for \(s^\rightarrow _{\xi -1,\eta }\). If \(t_{\xi ,\eta }\) is a marked transition, then by (c) \(s^\leftarrow _{\xi ,\eta -1} \in M_0\) and by the second part of condition (2) it follows \(\eta -1 >-\frac{\beta }{\alpha }\xi -1\). This is equivalent to the same condition (2) for \(s^\rightarrow _{\xi -1,\eta }\). \(\square \)
As we are interested to find the cycloid parameters from the cycloid system in any representation we introduce new parameters \(\mu , \mu _a, \mu _0\) and \(\tau ,\tau _a, \tau _0\) corres-ponding to the initial marking and the initially active transitions, respectively.
Definition 10
For a cycloid system \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) with initial marking \(M_0\) the following system parameters are defined:
-
(a)
\(\tau _0 := |\{t |\;\;|{}^{\mathord {\scriptscriptstyle ^\bullet }} t\cap M_0| \ge 1\}|\) is the number of transitions initially marked.
-
(b)
\(\tau _a := |\{t |\;\;|{}^{\mathord {\scriptscriptstyle ^\bullet }} t\cap M_0| = 2\}|\) is the number of initially active transitions.
-
(c)
\(\tau := |\{t |\;\;|{}^{\mathord {\scriptscriptstyle ^\bullet }} t\cap M_0| = 1\}|\) is the number of initially semi-active transitions.
-
(d)
\(\mu _0 := |M_0| \) is the number of tokens in the initial marking.
-
(e)
\(\mu _a \) is number of tokens activating initially active transitions.
-
(f)
\(\mu \) is number of tokens activating initially semi-active transitions.
Tokens contributing to \(\mu _a\) and \(\mu \) are called active and semi-active tokens, respectively.
Lemma 11
The number of tokens of the initial marking \(M_0\) is \(\mu _0 = \alpha + \beta \).
Proof
The transitions generating the forward tokens in Definition 8 have the number of \(\beta \) coordinates \((0,0), (\xi _1,1), \cdots , (\xi _{\beta - 1},\beta - 1)\), while those generating the backwards tokens have \(\alpha \) coordinates \( (1,\eta _1),(2,\eta _2) \cdots , (\alpha ,\eta _{\alpha })\). The total number is \(\alpha + \beta \). \(\square \)
Petri [6] called the tokens of the former and latter class forward and backwards flow tokens, respectively. Their total number corresponds to the distance \(d(O,P) = \alpha +\beta \) (see Lemma 6).
Lemma 12
The number of semi-active tokens of the initial marking \(M_0\) is \(\mu = |\alpha - \beta |\).
Proof
First, we assume \(\alpha \ge \beta \). We define a path, called m-path, containing all marked transitions as nodes. The edges connect marked transitions \(t_{\xi ,\eta }\) and \(t_{\xi +1,\eta '}\) with \(1\le \xi \le \alpha \).Footnote 15 By Lemma 9(a) and (b) the first transition is \(t_{1,0}\) and the last is \(t_{\alpha ,1-\beta }\). From this we have for the \(\eta \)-coordinates \(0\le \eta \le 1- \beta \), with the following property.
The edges of the m-path are composed of edges of (vector-)type \((1,-1)\) (diagonal in the \(\xi \)-\(\eta \)-grid) and of type (1, 0) (following a line \(\eta =const\)), since the type \((0,-1)\) is excluded by Lemma 9(e): if \(t_{\xi ,\eta }\) is a marked transition in \(M_0\) then \(t_{\xi ,\eta - 1}\) is not. By (c) and (d) of the same lemma the backward input place of each marked transition is marked, but the forward output place is not. Therefore a (place on a) (1, 0)-edge is not marked and the transition at the higher-\(\xi \)-end of this edge is semi-active. Furthermore the forward input place of a transition at the end of a \((1,-1)\)-edge is marked by Lemma 9(f). Therefore this transition is active. As a consequence a token is semi-active if and only if it marks the place on a (1, 0)-type edge and the number of semi-active tokens equals the number of (1, 0)-edges on the m-path.
Both types of edges, (1, 0) and \((1,-1)\) have the number 1 in their \(\xi \)-component. Therefore the number of all edges of the m-path is the difference of the \(\xi \)-components of the first transition \(t_{1,0}\) and the last transition \(t_{\alpha ,1-\beta }\), namely \(|1 - \alpha |\). With respect to the \(\eta \)-component only \((1,-1)\) contribute. Therefore their number is the difference of the \(\eta \)-components of the first and the last transition, namely \(|0-(1-\beta )|\). The number of (1, 0)-edges is their difference \(|1 - \alpha |-|0-(1-\beta )| = |1-\alpha |- |\beta - 1| = |\alpha - \beta |\). This proves the number of semi-active tokens to be \( |\alpha - \beta |\). To revoke the assumption \(\alpha \ge \beta \) we apply Theorem 5(a) by swapping \(\alpha \) and \(\beta \) keeping the structure isomorphic. \(\square \)
Example 13
To illustrate the proof, consider Fig. 7. It shows the case \(\alpha = \beta = 6\). There are 6 active transitions with coordinates \((1,0),(2,-1),\cdots ,(6,-5) \) forming a m-path. The case \(\alpha = 6\) and \(\beta ' = 3\) is represented in the same picture. The new origin \(O'\) is in the point \((0,-\alpha +\beta ') = (0,-3)\). The coordinates with respect to the new origin are distinguished by apostrophes. The nodes of the m-path have the coordinates \((1',0'),(2',0'),(3',-1'),(4',-1'),(5',-2'),\) \((6',-2')\). The path contains two (1, 1)-edges and three (1, 0)-edges. It is evident that the number of (1, 0)-edges equals the distance of the two origins 0 and \(0'\), which is \(\alpha - \beta ' = 3\). The initial marking is shown by small circles on edges, hence 3 transitions are active and 3 are semi-active. To show a case with two consecutive (1, 1)-edges, consider the case \(\alpha = 6\) and \(\beta ''= 4\).
Theorem 14
Let \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) be a cycloid system with initial marking \(M_0\)
-
(a)
\(\tau _0 =max\{\alpha ,\beta \}\)
-
(b)
\(\tau _a = min\{\alpha ,\beta \} \)
-
(c)
\(\tau = |\alpha -\beta |\)
-
(d)
\(\mu _0 = \alpha +\beta \)
-
(e)
\(\mu _a = 2 \cdot min\{\alpha ,\beta \}\)
-
(f)
\(\mu = |\alpha -\beta |\).
Proof
The propositions of (d) and (f) are proved in the preceding lemmata.
For (e) we use \(\mu _a = \mu _0 - \mu = \alpha +\beta -|\alpha -\beta |\). For \(\alpha \ge \beta \) this gives \(\alpha +\beta -(\alpha -\beta ) = 2\cdot \beta \). In the same way, for \(\alpha < \beta \) we obtain \(\alpha +\beta -(\beta - \alpha ) = 2\cdot \alpha \), hence \(\mu _a = 2 \cdot min\{\alpha ,\beta \}\). The first three propositions follow immediately: There are as many semi-active transitions as semi-active tokens: \(\tau = \mu = |\alpha -\beta |\). Each active transition has two active input tokens: \(\tau _a = \frac{1}{2} \cdot \mu _a = min\{\alpha ,\beta \}\). Finally, \(\tau _0 = \tau _a + \tau = min\{\alpha ,\beta \} + |\alpha -\beta | \), which is \(\beta + \alpha - \beta = \alpha \) if \(\alpha \ge \beta \) and \(\alpha + \beta - \alpha = \beta \) if \(\alpha < \beta \). \(\square \)
In his article [7] Petri introduces the notion of slowness by \(w = \frac{|\alpha -\beta |}{\alpha +\beta }\). Using our notation, the slowness of a cycloid is the ratio \(\mu \slash \mu _0\) of semi-active tokens relative to all tokens in the initial marking. The more tokens are semi-active, the higher is the slowness. In the left-hand example of Fig. 2 we have minimal slowness \(w=0\) as all tokens are active, while on the right-hand side \(w=\frac{1}{3}\) as a third of all tokens is semi-active. While Petri’s definition of slowness is non-probabilistic, in a personal communication he wrote: “Slowness is a mass or group phenomenon. The formula is valid for very large numbers of objects following a uniformly distributed behaviour. By a simple rule-of-thumb, a distribution proceeds as its slowest part”.
5 Minimal Cycloid Cycles
As another parameter which is independent of a fundamental parallelogram re-presentation, we now look for the length of minimal cycles. In his lecture notes [6] Petri mentions the “number of segments in local basic circuit” as \(\gamma + \delta \) in connection with his investigations on security. As we will see in this section, this is in fact the length of a minimal cycloid circuit in some cases, but no further results of Petri are known on the topic. As we investigate the property of minimal cycles using the fundamental parallelogram, we first state that such a cycle always appears as a normal form containing a vertex O, P, Q or R.
Lemma 15
For any cycloid \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta ) \) there is a minimal cycle containing the origin O in its fundamental parallelogram representation.
Proof
It is obvious that a cycloid contains cycles (closed paths). Consider a fixed minimal cycle and a transition \(t_{\xi _0,\eta _0}\) contained in this cycle. The mapping \(\varphi : X_1 \rightarrow X_1\) defined by \(\varphi (x_{\xi ,\eta }) := x_{\xi -\xi _0,\eta -\eta _0}\) is an automorphism that is congruent to \(\equiv \). Therefore there is a also a minimal cycle containing \(t_{\xi ,\eta }\) which is the origin \(O =(0,0)\) in the Petri space. \(\square \)
As shown in Fig. 8, the edges of a path can leave the limiting lines of the fundamental parallelogram. We first consider the opposite case.
Definition 16
Let \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) be a cycloid. A path or a cycle is called internal if it does not leave the limiting lines of the fundamental parallelogram. The internal minimal cycle index is defined by

If the parameters are given by context, the internal index is denoted by \(i_0\).
Theorem 17
The length of a minimal internal cycle of a cycloid \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) is \(cyc_0(\alpha ,\beta ,\gamma ,\delta ) = \gamma + \delta + i_0 \cdot (\alpha - \beta )\).
Proof
As we argued above, with respect to paths and cycles in the fundamental parallelogram and by Lemma 15, it is sufficient to consider the paths between the vertices O, P, Q and R. Therefore we can reduce our investigations to the paths (A, B), as given in the second column of the following table. The minimal paths between (O, Q) and (P, R) are the same and have the length of the distance \(d(O,Q) = d(P,R) = \gamma + \delta \) by Lemma 6. Such a path is always possible, as already observed by Petri, in contrast to paths between O and P or Q and R. For any such internal path, due to \( \overrightarrow{OP}= \overrightarrow{QR} = (\alpha ,-\beta )\) a step in negative \(\eta \)-direction would be included, which is impossible.
Case | (A, B) | Path possible | Path length | \( i_0\) |
|---|---|---|---|---|
I | (O, Q), (P, R) | True | \(\gamma +\delta \) | 0 |
II | (P, Q) | \(\alpha \le \gamma \) | \(-\alpha +\beta +\gamma +\delta \) | \({-}1\) |
III | (O, R) | \(\beta \le \delta \) | \(\alpha -\beta +\gamma +\delta \) | 1 |
(O, P), (Q, R) | False |
The paths between (P, Q) and (O, R) are only possible under specific conditions, however. (P, Q) is possible if the \(\xi \)-coordinate of P is not greater than that of Q, i.e. \(\alpha \le \gamma \). (O, R) is possible if and only if \(R = (\alpha +\gamma ,\delta -\beta )\) (Lemma 6) has a non-negative \(\eta \)-coordinate, i.e. \(\delta \ge \beta \). Due to these conditions the signs for the absolute value in Lemma 6 for \(d(P,Q) =|\alpha -\gamma |+\beta +\delta =\gamma - \alpha +\beta +\delta \) and \(d(O,R) =\alpha +\gamma +|\beta -\delta | = \alpha +\gamma +\delta -\beta \) can be omitted (column 4). With the values for \(i_0\) in the fifth column of the preceding table, the formula \(cyc_0(\alpha ,\beta ,\gamma ,\delta ) = \gamma + \delta + i_0 \cdot (\alpha - \beta )\) reproduces the values in the fourth column. It remains to find out which of the three cases I, II and III gives the length of the minimal cycle. Let us compare, for instance, case I with case II. \(\gamma +\delta \le -\alpha +\beta +\gamma +\delta \) is equivalent to \(\alpha \le \beta \), which gives the entry of the line I and column II of the following table. Similarly, comparing case II with case III gives \(-\alpha +\beta +\gamma +\delta \le \alpha -\beta +\gamma +\delta \Leftrightarrow \beta \le \alpha \). The other entries in the table are computed in the same way.
Case | I | II | III |
|---|---|---|---|
I | \(\alpha \le \beta \) | \(\beta \le \alpha \) | |
II | \(\beta \le \alpha \) | \(\beta \le \alpha \) | |
III | \(\alpha \le \beta \) | \(\alpha \le \beta \) |
Compiling these results, in the case of \(\alpha \le \beta \) we obtain III \(\le \) I \(\le \) II, where the case identifier stands for the cycle length. Case III is the winner if it is possible, i.e. under the condition \(\alpha \le \beta \; \wedge \; \beta \le \delta \) with cycle length \(\alpha -\beta +\gamma +\delta \). This is just the right condition, namely giving \(i_0 = 1\) in Definition 16 and the correct cycle length in Theorem 17. If case III is not possible, we obtain case I as the minimal cycle length with condition \(\alpha \le \beta \; \wedge \; \beta > \delta \) and \(i_0 = 0\) which gives again the correct cycle length \(\gamma + \delta \) in Theorem 17.
The case \(\beta \le \alpha \) is deduced from the case \(\alpha \le \beta \) by using the isomorphism of Theorem 5 applying the substitution \([\alpha \rightarrow \beta , \beta \rightarrow \alpha , \gamma \rightarrow \delta , \delta \rightarrow \gamma ]\). \(\square \)
As shown by the cycle \(t_1, t_2, t_3,t_4,t_5,t_6 \) of length 6 in the cycloid at the left-hand side of Fig. 8, a minimal cycle is not necessarily internal. Looking on the corresponding fundamental parallelogram on the right-hand side, the cycle can be obtained by starting in the origin, proceeding in \(\xi \)-direction until meeting the line \(\overline{QR_1}\). The example is chosen in such a way that the \(\xi \)-axis and the line \(\overline{QR}\) intersect in a point in the Petri space, namely the point \(R_3\) in Fig. 8, which is equivalent to \( R_1\). Geometrically, the point is obtained by unfoldingFootnote 16 the fundamental parallelogram \(i-1= 2\) times. As shown in the proof below we will obtain \(i = \frac{\delta }{\beta } = 3\). The vector \(\overrightarrow{OR_3}\) can be calculated by adding \(\overrightarrow{OQ}\) and i times the vector \(\overrightarrow{QR_1} = \overrightarrow{OP_1}\). This vector is \(\overrightarrow{OR_3} = \left( \begin{array}{c}\gamma +i\cdot \alpha \\ \delta -i\cdot \beta \end{array}\right) = \left( \begin{array}{c}6\\ 0\end{array}\right) \) with length \(|\overrightarrow{OR_3}| = \gamma + \delta + i\cdot (\alpha -\beta ) = 6 \). The case where the intersect of the lines is not in the Petri space is treated in the proof.
Definition 18
The minimal cycle index of a cycloid \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) is defined by
If the parameters are given by context, the index is denoted by i.
Theorem 19
The length of a minimal cycle of a cycloid \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) is
If the parameters are given by context the cycle index is denoted by i.
Proof
With respect to paths and cycles in the fundamental parallelogram and by Lemma 15 it is sufficient to consider paths starting in the origin O.
-
(a)
We first consider the case \(\alpha \le \beta \). As will be justified below, the best choice is a line starting in the origin O in direction \(\xi \), i.e. having the equation \(\eta =0\). It meets the line \(\overline{QR}\) with equation \(\eta = \frac{-\beta }{\alpha } (\xi -\gamma )+\delta \) (see Lemma 6) in a point X. If this point is equivalent to Q or R (with respect to \(\equiv \)), then \(d(O,X) = cyc\) is the length of the cycle in question. Hence, setting \(\xi =cyc\) and \(\eta =0\) in the equation above, we obtain: \(0 = \frac{-\beta }{\alpha } (cyc-\gamma )+\delta \Leftrightarrow \frac{\beta }{\alpha } (cyc-\gamma )=\delta \Leftrightarrow cyc =\delta \frac{\alpha }{\beta } +\gamma \Leftrightarrow cyc =\delta \frac{\alpha }{\beta } +\gamma + \delta -\delta \Leftrightarrow cyc = \gamma + \delta +\frac{\delta }{\beta }(\alpha -\beta )\).
If X is equivalent to Q or R with respect to \(\equiv \) then \(\frac{\delta }{\beta }\) is an integer. If this is not the case, we compute X in a different way. In fact, X can be obtained by the following vector equation \(\overrightarrow{OX} = \overrightarrow{OQ} + j \cdot \overrightarrow{OP} = \left( \begin{array}{c}\gamma \\ \delta \end{array}\right) + j \cdot \left( \begin{array}{c}\alpha \\ beta\end{array}\right) = \left( \begin{array}{c}\gamma +j\cdot \alpha \\ \delta -j\cdot \beta \end{array}\right) \) for some integer j. The length of this vector is \(|\overrightarrow{OX}| = \gamma +j\cdot \alpha +\delta -j\cdot \beta = \gamma + \delta + j\cdot (\alpha -\beta ) \). Comparing \(|\overrightarrow{OX}| = \gamma + \delta + j\cdot (\alpha -\beta ) \) with \(cyc = \gamma + \delta +\frac{\delta }{\beta }(\alpha -\beta )\) from case (a) we conclude \(j \le \frac{\delta }{\beta } \le j+1\). Due to the causality structure of the cycloid the transition with respect to \(j+1 = \lceil \frac{\delta }{\beta }\rceil \) is not directly reachable, hence \(j = \lfloor \frac{\delta }{\beta }\rfloor \). This gives \(cyc = \gamma + \delta + \lfloor \frac{\delta }{\beta }\rfloor \cdot (\alpha - \beta )\) in the case \(\alpha \le \beta \). The optimality of the choice of a line in case a) becomes evident here, since a smaller value of i results in a longer cycle, whereas a greater value of i is impossible due to the causality structure of the cycloid.
-
(b)
For the alternative case we look at the isomorphic cycloid \(\mathcal {C}(\beta ,\alpha ,\delta ,\gamma ) \) (by interchanging \(\alpha \) and \(\beta \), as well as \(\gamma \) and \(\delta \), see Theorem 5 which has a minimal cycle of the same length, hence \(cyc = \gamma + \delta + \lfloor \frac{\gamma }{\alpha }\rfloor \cdot (\beta -\alpha )\) also in the case \(\alpha >\beta \). Both cases together verify the theorem. \(\square \)
Remark: Using Petri’s terminology and the notion of semi-active transition, the minimal length of a cycle is the length \(\gamma +\delta \) of a local basic circuit, possibly decreased by an integer multiple i of the number \(\tau = |\alpha - \beta |\) of semi-active transitions.
Note that Theorems 17 and 19 are consistent in the following sense. The internal minimal cycle length is obtained without unfolding the fundamental parallelogram. This means that the index i is 0 or 1. If we replace \(\lfloor \frac{\delta }{\beta }\rfloor \) by \(min\{1,\lfloor \frac{\delta }{\beta }\rfloor \}\) and \(-\lfloor \frac{\gamma }{\alpha }\rfloor \) by \(max\{-1,-\lfloor \frac{\gamma }{\alpha }\rfloor \}\) in Definition 18, we obtain Theorem 17 from Theorem 19.
6 Computing Cycloid Parameters from System Parameters
Next we exploit our results to find the fundamental parallelogram representation of a cycloid from its net presentation using the system parameters \(\tau _0, \tau _a, A\) and cyc. The corresponding equivalence is denoted as \(\sigma \)-equivalence. The letter \(\sigma \) emphasizes the use of the shortest cycle length cyc, whereas the other parameters are more natural. It also gives room for other equivalences like \(\lambda \)-equivalence, where the longest cycle length is used, instead. Similar to the theory of regions, the following procedures do not necessarily give a unique result. But for \(\alpha \ne \beta \) the resulting cyloids are isomorphic.
Definition 20
Cycloids with identical system parameters \(\tau _0, \tau _a, A\) and cyc are called \(\sigma \)-equivalent.
Theorem 21
Given a cycloid \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) in its net representation where the parameters \(\tau _0, \tau _a, A\) and cyc are known (but the parameters \(\alpha ,\beta ,\gamma ,\delta \) are not). Then a \(\sigma \)-equivalent cycloid \(\mathcal {C}(\alpha ',\beta ',\gamma ',\delta ')\) can be computed by the formulas \(\alpha ' = \tau _0\), \(\beta ' = \tau _a\) and, if \(\alpha ' \ne \beta '\) the positive solutions of \(\gamma ' \; \mathbf {mod}\; \alpha ' = \frac{\alpha '\cdot cyc - A}{\alpha '-\beta '}\) and \(\delta ' = \frac{1}{\alpha '}(A - \beta '\cdot \gamma ')\). These equations may result in different cycloids which are isomorphic, however. If \(\alpha ' = \beta '\) then \(\gamma ' = \lceil \frac{cyc}{2}\rceil \) and \(\delta ' = \lfloor \frac{cyc}{2}\rfloor \) can be used.
Proof
As by Theorem 5 for the case \(\alpha \le \beta \), there is an isomorphic solution for \(\alpha \ge \beta \) we can restrict to the latter case. Hence by Theorem 14 we can choose \(\alpha ' = \tau _0\) and \(\beta ' = \tau _a\), giving \(\alpha '=\alpha \) and \(\beta ' = \beta \).
For computing \(\gamma '\) and \(\delta '\) we use the following equations if \(\alpha \ne \beta \): from \(A = \alpha \delta '+\beta \gamma '\) we obtain \(\delta ' = \frac{A}{\alpha }-\frac{\beta }{\alpha }\gamma '\) and insert this value into the formula for cyc in the case \(\alpha \ge \beta \): \(cyc = \gamma ' + \delta ' + \lfloor \frac{\gamma '}{\alpha }\rfloor \cdot (\beta -\alpha ) = \gamma ' + \frac{A}{\alpha }-\frac{\beta }{\alpha }\gamma ' + \lfloor \frac{\gamma '}{\alpha }\rfloor \cdot (\beta -\alpha )\). This is equivalent to \(\gamma ' - \alpha \cdot \lfloor \frac{\gamma '}{\alpha }\rfloor = \frac{\alpha \cdot cyc - A}{\alpha -\beta }\). Using \( \gamma ' - \alpha \cdot \lfloor \frac{\gamma '}{\alpha }\rfloor = \gamma ' \; \mathbf {mod}\; \alpha \) we obtain one or more (positive) solutions \(\gamma '\), which also give the same number of solutions for \(\delta ' = \frac{A}{\alpha }-\frac{\beta }{\alpha }\gamma '\). If \(\gamma _1\) and \(\gamma _2\) are two different such solutions, we have \(\gamma _2 = \gamma _1 + k\cdot \alpha \) for some  . W.l.o.g. assume \(k \ge 1\). Then for \(\delta _2\) we obtain \(\delta _2 = \frac{A}{\alpha }-\frac{\beta }{\alpha }\gamma _2 = \delta _1 - k \cdot \beta \). Hence applying Theorem 5(c) (k-times) the resulting cycloids \(\mathcal {C}(\alpha ,\beta ,\gamma _1,\delta _1)\) and \(\mathcal {C}(\alpha ,\beta , \gamma _1 + k\cdot \alpha ,\delta _1 - k \cdot \beta )\) are isomorphic.
. W.l.o.g. assume \(k \ge 1\). Then for \(\delta _2\) we obtain \(\delta _2 = \frac{A}{\alpha }-\frac{\beta }{\alpha }\gamma _2 = \delta _1 - k \cdot \beta \). Hence applying Theorem 5(c) (k-times) the resulting cycloids \(\mathcal {C}(\alpha ,\beta ,\gamma _1,\delta _1)\) and \(\mathcal {C}(\alpha ,\beta , \gamma _1 + k\cdot \alpha ,\delta _1 - k \cdot \beta )\) are isomorphic.
If \(\alpha ' = \beta '\) then the minimal cycle length is always \( \gamma '+\delta ' \). To verify again the same values \(cyc' = cyc\) and \(A'=A\) in \(\mathcal {C}(\alpha ',\beta ',\gamma ',\delta ')\), we observe: \(cyc' = \gamma ' + \delta ' = \lceil \frac{cyc}{2}\rceil + \lfloor \frac{cyc}{2}\rfloor = cyc\) and \(A' = \alpha \delta '+\beta \gamma ' = \alpha (\delta '+\gamma ') = \alpha \cdot cyc' = \alpha \cdot cyc = A\). \(\square \)
Example 22
For the cycloid system on the left-hand side of Fig. 2 we obtain \(\alpha ' = \tau _0 = 3\), \(\beta ' = \tau _a = 3\) and \(\alpha ' = \tau _0 = 4\), \(\beta ' = \tau _a = 2\) for the right-hand net of the same figure. To compute \(\gamma '\) and \(\delta '\) we start with the net on the right-hand side with \(A=6\) transitions and \(cyc = 2\). As \(\alpha ' \ne \beta '\) we obtain \(\gamma ' \; \mathbf {mod}\; \alpha ' = \frac{\alpha '\cdot cyc - A}{\alpha '-\beta '} = \frac{4\cdot 2 - 6}{4-2} = 1\). The set of positive solutions of \(\gamma ' \; \mathbf {mod}\; 4 = 1\) is  . Using these values we obtain
. Using these values we obtain
\(\delta ' = \frac{1}{\alpha '}(A - \beta '\cdot \gamma ') = \frac{1}{4}(6 - 2\cdot \gamma ') = \{1,-1,-3,\cdots \}\). Therefore \(\gamma ' = 1, \delta ' =1\) is a unique positive solution. To compute \(\gamma '\) and \(\delta '\) for the net on the left-hand side (\(A=6\), \(cyc = 2\)) we obtain \(\gamma ' = \lceil \frac{2}{2}\rceil = 1\) \(\delta ' = \lfloor \frac{2}{2}\rfloor = 1\), since \(\alpha ' = \beta '\).
Example 23
For the cycloid system of Fig. 6 we obtain \(\alpha ' = \tau _0 = 4\), \(\beta ' = \tau _a = 3, A = 24, cyc = 6\). As \(\alpha ' > \beta '\) we consider \(\gamma ' \; \mathbf {mod}\; \alpha ' = \frac{\alpha '\cdot cyc - A}{\alpha '-\beta '} = \frac{4\cdot 6 - 24}{4-3} = 0\). The set of positive solutions of \(\gamma ' \; \mathbf {mod}\; 4 = 0\) is  . Using these values we obtain \(\delta ' = \frac{1}{\alpha '}(A - \beta '\cdot \gamma ') = \frac{1}{4}(24 - 3\cdot \gamma ') \). Hence the set of values for \((\gamma ',\delta ')\) reduces to \( \{(0,\frac{3}{2}),(4,3),(0,8),\cdots \}\). Therefore \(\gamma ' = 4, \delta ' =3\) is a unique positive integer solution.
. Using these values we obtain \(\delta ' = \frac{1}{\alpha '}(A - \beta '\cdot \gamma ') = \frac{1}{4}(24 - 3\cdot \gamma ') \). Hence the set of values for \((\gamma ',\delta ')\) reduces to \( \{(0,\frac{3}{2}),(4,3),(0,8),\cdots \}\). Therefore \(\gamma ' = 4, \delta ' =3\) is a unique positive integer solution.
Example 24
Consider the cycloid \(\mathcal {C}(3,2,8,2)\) with \(A = 22\) and \(cyc = 8\). Then \(\alpha '= 3\), \(\beta ' = 2\) and \(\gamma ' \;\mathbf {mod}\; 3 = \frac{\alpha '\cdot cyc - A}{\alpha '-\beta '} = \frac{3\cdot 8- 22}{3-2} = 2\) has a set of solutions \(\gamma ' \in \{\cdots -1,2,5,8,11,\cdots \}\) and with \(\delta ' = \frac{1}{\alpha '}(A - \beta '\cdot \gamma ') = \frac{1}{3}(22 - 2\cdot \gamma ')\) also \((\gamma ',\delta ') \in \{\cdots (-1,8),(2,6),(5,4),(8,2),(11,0),\cdots \}\). As only positive integer values for \(\gamma '\) and \(\delta '\) are possible, we obtain two cycloids \(\mathcal {C}(3,2,2,6)\) and \(\mathcal {C}(3,2,5,4)\) that are \(\sigma \)-equivalent to the initial cycloid \(\mathcal {C}(3,2,8,2)\). All three cycloids are isomorphic due to Theorem 5.
Example 25
As mentioned in the introduction, the topological equivalence of elementary gates of information processing on the bit level to particular cycloids is an important result of Petri’s work. In a mail from August 28, 2007 Petri wrote that the “oscillator” is the easiest example for the “surprising” construction of a cycloid from the XOR-gate, which he called a “Pattern of Group Behaviour” based on the same topology. Petri wrote that he first found such an equivalence in the year 1964 by the example of the Quine-Transfer. Let us come back to the XOR-gate shown on the right-hand side of Fig. 9 and its redesign in the middle. By reorientation of the arcs, Petri built the net on the left hand side. It becomes a cycloid system by adding a token to the place \(a_0\) in order to obtain a live net, as in a marked graph each cycle has to contain exactly one token. The net is known as “oscillator net” or “four seasons net” (equivalent to Fig. 3).
Here our result helps Petri’s construction: initially marked transitions: \(\alpha '=\tau _0 =|\{a,b\}| =2\), initially active transitions \(\beta '=\tau _a =|\{a\}| =1\), minimal cycle length \(cyc = 2\) and \(A =4\), hence \(\gamma ' \mathbf {mod}\; 2 = \frac{\alpha '\cdot cyc - A}{\alpha '-\beta '} = \frac{2\cdot 2 - 4}{2-1}=0\) and \(\delta ' = \frac{1}{\alpha '}(A - \beta '\cdot \gamma ')= 2 - \frac{\gamma '}{2}\). The set of solutions for \((\gamma ',\delta ')\) is \( \{\cdots (0,2),(2,1),(4,0),\cdots \}\). Therefore \(\gamma ' = 2\) and \(\delta ' =1\) is a unique positive integer solution, giving the cycloid \(\mathcal {C}(2,1,2,1)\), as shown in Petri’s slide of Fig. 9.
7 Conclusion
In this paper a formal definition for the model of cycloids is given, enabling proofs of known and new properties. This has been done on the basis of C. A. Petri’s formal and informal papers, some of which are internal for the Hamburg research group on General Net Theory. To prepare new results and also as a mathematical tool box for further research, some technical properties are derived. The main theorem gives a compact formula for the length of minimal cycloid cycles. Together with three other system parameters, this allowed to compute the cycloid parameters \(\alpha , \beta , \gamma \) and \(\delta \) solely from the cycloid net. At the end, some examples are given, including some suggested by C. A. Petri himself.
Notes
- 1.
In the net, the gaps are also ordinary black tokens, but represented here by a cross to distinguish them from the cars.
- 2.
- 3.
See more about the notion of slowness in Sect. 4.
- 4.
The cycloid model generator cyclogen written by Fenske, in combination with the RENEW tool.
- 5.
The net is known as “oscillator net” or “four seasons net”. See also Fig. 9.
- 6.
\(F^{-1}[x]\) is the relational image of the element x with respect to the inverse of the relation F.
- 7.
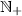 denotes the set of positive integers.
denotes the set of positive integers. - 8.
\(\mathord {\equiv }[A]\) is the relational image of the set A with respect to the relation \(\mathord {\equiv }\).
\([\![x]\!]_{\equiv }\) denotes the equivalence class to which x belongs in the quotient \(X_1/_\equiv \).
- 9.
These sets are not disjoint.
- 10.
Reported by Fenske.
- 11.
They are in the concurrency relation co.
- 12.
We will use the term initial marking, for short.
- 13.
- 14.
First and last with respect to the space dimension.
- 15.
It may be helpful for the reader to consider Fig. 7, which illustrates the proof and is explained afterwards.
- 16.
Such unfoldings of the fundamental parallelogram have been frequently used by Petri, see “Nets, Time and Space” [7], Fig. 11, for instance.
References
Fenske, U.: Petris Zykloide und Überlegungen zur Verallgemeinerung. Diploma thesis (2008)
Girault, C., Valk, R. (eds.): Petri Nets for System Engineering - A Guide to Modelling, Verification and Applications. Springer, Berlin (2003). https://doi.org/10.1007/978-3-662-05324-9. 585 p.
Kummer, O.: Axiomatic Systems in Concurrency Theory. Logos Verlag Berlin, Berlin (2001)
Kummer, O., Stehr, M.-O.: Petri’s axioms of concurrency a selection of recent results. In: Azéma, P., Balbo, G. (eds.) ICATPN 1997. LNCS, vol. 1248, pp. 195–214. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-63139-9_37
Langner, P.: Cycloids’ Characteristics (2013). http://cycloids.adventas.de/
Petri, C.A.: Collection of Handwritten Scripts on Cycloids. Lecture University of Hamburg (1990/1991)
Petri, C.A.: Nets, time and space. Theor. Comput. Sci. 153, 3–48 (1996)
Petri, C.A.: Slides of the Lecture “Systematik der Netzmodellierung”, Hamburg (2004). http://www.informatik.uni-hamburg.de/TGI/mitarbeiter/profs/petri_eng.html
Petri, C.A., Valk, R.: On the Physical Basics of Information Flow - Results obtained in cooperation Konrad Zuse. http://www.informatik.uni-hamburg.de/TGI/mitarbeiter/profs/petri_eng.html (2008)
Smith, E., Reisig, W.: The semantics of a net is a net - an exercise in general net theory. In: Voss, K., Genrich, J., Rozenberg, G. (eds.) Concurrency and Nets, pp. 461–479. Springer, Berlin (1987). https://doi.org/10.1007/978-3-642-72822-8_29
Stehr, M.O.: System specification by cyclic causality constraints. Technical report 210, Department of Informatics, University Hamburg (1998)
Stehr, M.O.: Characterizing security in synchronization graphs. Petri Net Newsl. 56, 17–26 (1999)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Valk, R. (2018). On the Structure of Cycloids Introduced by Carl Adam Petri. In: Khomenko, V., Roux, O. (eds) Application and Theory of Petri Nets and Concurrency. PETRI NETS 2018. Lecture Notes in Computer Science(), vol 10877. Springer, Cham. https://doi.org/10.1007/978-3-319-91268-4_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-91268-4_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-91267-7
Online ISBN: 978-3-319-91268-4
eBook Packages: Computer ScienceComputer Science (R0)








 and
and 
 :
:







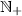 denotes the set of positive integers.
denotes the set of positive integers.