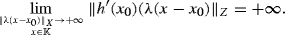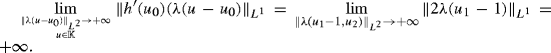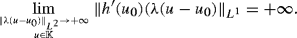Abstract
In this chapter we first present some theoretic concepts related to the strong duality in the infinite-dimensional setting. Then, we apply such results to the general financial equilibrium economy, studying also the dual formulation of the problem, analyzing both the sector’s and the system’s viewpoints and deriving the contagion phenomenon. Further, we provide an evolutionary Markowitz-type measure of the risk with a memory term. Finally, we apply Assumption S to the elastic-plastic torsion problem for linear operators and investigate the existence of Lagrange multipliers to the elastic-plastic torsion problem for nonlinear monotone operators, providing an example of the so-called Von Mises functions and searching for radial solutions.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
1 The Strong Duality in the Infinite-Dimensional Setting
The duality theory we intend to study can be summarized as follows.
Let \(f: S \to \mathbb {R},\) g : S → Y, h : S → Z be three mappings, where S here and in what follows is a convex subset of a real normed space X, Y is a real normed space ordered by a convex cone C, Z is a real normed space and consider the optimization problem:
where θ Z is the zero element in the space Z.
The Lagrange dual problem is:
where
is the dual cone of C and Z ∗ is the dual space of Z.
Then, we say that the strong duality holds for problems (1) and (2) if and only if problems (1) and (2) admit a solution and the optimal values coincide.
The already classical results by Rockafellar [47], Holmes [36], Borwein and Lewis [3] give sufficient conditions in order that the strong duality between problems (1) and (2) holds.
All these conditions use concepts such as:
-
the core:
$$\displaystyle \begin{aligned}Core \, C : = \left \{x \in C: Cone \, (C + \{\ x \}) = X \right \};\end{aligned}$$ -
the intrinsic core:
$$\displaystyle \begin{aligned}Intrinsic \,\, Core \,\, C := \left \{ c \in C: \forall c' \in \mbox{ aff } (C) \setminus \{c\}, \mbox{ we have } (c, c') \cap C \ne \emptyset \right \},\end{aligned}$$where aff (C) is the affine hull of C and \((a,b) := \left \{ (1 - t) a + tb : t \in (0,1)\right \};\)
-
strong quasi-relative interior of C :
$$\displaystyle \begin{aligned}sqri \,\, C : = \left \{ x \in C: Cone \,\, (C - \{x\}) \mbox{ is a closed linear subspace of } X \right \}.\end{aligned}$$
Such concepts (see [3, 36, 39, 47]) require the nonemptiness of the ordering cone, which defines the cone constraints in convex optimization and variational inequalities. However, the ordering cone of almost all the known problems, stated in infinite dimensional spaces, has the interior (and all the above generalized interior concepts) empty. Hence, the above interior conditions cannot be used to guarantee the strong duality. This is the case, for example, of optimization problems or variational inequalities connected with evolutionary financial network equilibrium problems, the obstacle problem, the elastic-plastic torsion problem, the infinite-dimensional bilevel problem, which use non-negative cones of Lebesgue or Sobolev spaces (see [1, 8, 10,11,12,13,14, 22, 24, 25, 27, 31, 34, 35, 37, 46, 49]).
Only recently, in [16, 42, 43] the authors introduced new conditions called S, S′, NES, which turn out to be necessary and sufficient conditions for the strong duality and really useful in the applications. These conditions do not require the nonemptiness of the interior of the ordering cone. This new strong duality theory was then refined in [13, 17, 19, 37, 45].
Now we present in detail these new conditions.
1.1 Assumption S
Let us first recall that for a subset C ⊆ X and x ∈ X the tangent cone to C at x is defined as
If x ∈ clC (the closure of C) and C is convex, we have
where the \(cone A = \{ \lambda x:\ x \in A, \ \lambda \in \mathbb {R}^+\}\) denotes the cone hull of a general subset A of the space.
Definition 1
Given the mappings f, g, h and the set K as above, we say that Assumption S is fulfilled at a point x 0 ∈ K if and only if
where
Now we recall the main theorem on strong duality based on Assumption S (see [13, 16, 17, 19, 45]).
Theorem 1
Assume that the functions \(f:S \longrightarrow \mathbb {R}\) , g : S→Y are convex and that h : S→Z is an affine-linear mapping. Assume that the Assumption S is fulfilled at the optimal solution x 0 ∈ K of the problem (1) . Then also problem (2) is solvable and if \(\overline {u} \in C^*\) , \(\overline {v} \in Z^*\) are optimal solutions to (2) , we have
and the optimal values of the two problems coincide; namely
Moreover it is seen in [4] that Assumption S is also a necessary condition for the strong duality.
An important consequence of the strong duality is the usual relationship between a saddle point of the so-called Lagrange functional
and the solution to (1) and (2). Indeed, we have the following theorem (see [16] and [23]).
Theorem 2
Let the assumptions of Theorem 1 be fulfilled. Then, \(x_0 \in \mathbb {K}\) is an optimal solution to (1) if and only if there exist \(\bar u \in C^*,\) \(\bar v \in Z^*\) such that \((x_0, \bar u, \bar v)\) is a saddle point of the Lagrange functional, namely:
and
1.2 Assumption S′
Assumption S′ requires additional hypotheses on the mappings f, g, h and works on directional derivatives. Sometimes it is easier to use with respect to Assumption S.
Let us assume that f, g, h have directional derivative at x 0 ∈ K in every direction x − x 0 with arbitrary x ∈ S.
Definition 2
We say that Assumption S ′ is fulfilled at the point x 0 ∈ K if and only if
where
The next theorem holds (see [42]).
Theorem 3
Let X and Z be real normed spaces, let Y be a real normed space ordered by a closed convex cone C. Let S be a convex subset of X and let \(f: S \longrightarrow \mathbb {R}\) be a given convex functional, let g : S→Y be a convex mapping and let h : S→Z an affine-linear mapping. Assume that f, g have a directional derivative at x 0 ∈ K solution to problem (1) in every direction x − x 0 with arbitrary x ∈ S. Then, the strong duality holds if and only if Assumption S ′ is fulfilled.
1.3 Strong Duality in the Case of Nonlinear Equality Constrains
Let us assume that h is no longer an affine-linear mapping, but, for instance, a convex one, since it depends on the sign of v. Then the constraint set \(\mathbb {K}\) is no longer convex. As a consequence, the usual optimality conditions for the convex functions on convex sets cannot be applied. Moreover, if we consider the Lagrange functional
where \(\bar u \in C^*\) and \(\bar v \in Z^*,\) even if h is convex as well as g, L is not, in general, a convex functional. In order to overcome these difficulties, some strong duality results have been elaborated under Assumption S′, but introducing additional conditions (see [44] Theorem 2).
Theorem 4
Let (X, ∥⋅∥X), (Y, ∥⋅∥Y), (Z, ∥⋅∥Z) be real Banach spaces with an ordering closed convex cone X +, C and D, respectively. Let S be an open convex subset of X, let \(f:S \to \mathbb {R}\) be a convex functional such that f is Fréchet-differentiable at a minimal point \(x_0 \in \mathbb {K},\) let g : S → Y and h : S → Z be convex functions with respect to the cones C and D, respectively, both Gâteaux-differentiable at x 0. Assume also:
-
(i)
f′(x 0)(x) ≤ 0, ∀x ∈ S ∩ X +;
-
(ii)
g′(x 0)(x) ∈ − C ∀x ∈ S ∩ X +;
-
(iii)
h′(x 0)(S ∩ X +) = D;
-
(iv)
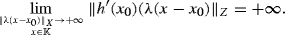
If Assumption S ′ is fulfilled at x 0, then the strong duality holds.
Example 1
Let us consider the following problem (see [44]):
where
We set:
We note that f attains its minimum value in \(\mathbb {K}\) in correspondence of the couple of constant functions u 0 = (1, 0). Now, we verify that all assumptions of Theorem 4 are satisfied. Indeed:
-
(i)
\(f'(u_0)(u) = \displaystyle \int _0^T - u_1(t) \, dt \leq 0,\) \(\forall (u_1, u_2) \in L^2([0,T], \mathbb {R}^2_+);\)
-
(ii)
g′(u 0)(u) = (−u 1, −u 2) ∈ − C, \(\forall (u_1, u_2) \in L^2([0,T], \mathbb {R}^2_+);\)
-
(iii)
h′(u 0)(u) = 2u 1 ≥ 0, \(\forall (u_1, u_2) \in L^2([0,T], \mathbb {R}^2_+);\)
-
(iv)
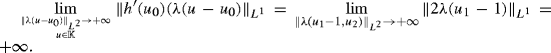
In order to have the strong duality, it remains to prove that also Assumption S′ holds true. Let
We need to verify that:
taking into account that:
and
where λ n ≥ 0, \(n \in \mathbb {N},\) \(v_n \in L^2([0,T], \mathbb {R}^2)^+,\) \(u_n \in L^2([0,T], \mathbb {R}^2) \setminus \mathbb {K},\) α n ≥ 0, \(\forall n \in \mathbb {N}.\)
From (4) it follows:
Example 2
Now, we present an example where assumption (i) is not satisfied (see [44]).
Let us consider the problem:
where
We set:
We note that f attains its minimum value in \(\mathbb {K}\) in correspondence of the couple of constant functions u 0 = (1, 0). Assumption (i) of Theorem 4 is not satisfied. Indeed:
-
(i)
\(f'(u_0)(u) = \displaystyle \int _0^1 u_1(t) \, dt \geq 0,\) \(\forall (u_1, u_2) \in L^2([0,1], \mathbb {R}^2_+);\)
-
(ii)
g′(u 0)(u) = (−u 1, −u 2) ∈ − C, \(\forall (u_1, u_2) \in L^2([0,1], \mathbb {R}^2_+);\)
-
(iii)
h′(u 0)(u) = 2u 1 ≥ 0, \(\forall (u_1, u_2) \in L^2([0,1], \mathbb {R}^2_+);\)
-
(iv)
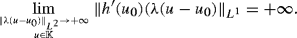
As in the previous example, it is easy to show that also Assumption S′ holds true. Since we have (see also formula (2.5) in [44]):
and (3) holds true, it follows, from an easy calculation, that the maximum over C + and v ∈ Z ∗ is achieved when
for some \(\bar u_2 \geq 0.\) Therefore,

As we have seen, not all the assumptions of Theorem 4 are fulfilled. Hence, if strong duality holds, then we would have:
It is enough to choose, for instance, (u 1, u 2) = (2, 0) to get a contradiction, since:
1.4 NES (Non Empty Subdifferential Condition)
This new necessary and sufficient condition is the one which requires a smaller number of assumptions on the functions. Recall that a subdifferential of a convex function \(f: S \to \mathbb {R},\) where S is a subset of a real normed space X, at \(\overline {x} \in S\) is defined by
For y ∈ Y , let us define a closed convex subset of Y as
with C the closed convex ordering cone of Y .
If on Y × Z, we consider the norm ∥(y, z)∥Y ×Zł = ∥y∥Y + ∥z∥Z, let us define
by
Definition 3 (Assumption NES)
We say that the Condition NES is fulfilled for the triple f, g, h with respect to K if and only if
Taking into account that \(\varphi (\theta _{Y \times Z}) = \displaystyle \inf _{\substack {x \in S \\ - g(x) \in C\\ h(x) = \theta _Z}} f(x)= \inf _{x \in \mathbb {K}} f(x),\) (6) means that there exist (y ∗, z ∗) ∈ Y ∗× Z ∗ such that
Then, we have the following result (see [43] Theorem 3.2).
Theorem 5
Let us assume that \(\displaystyle \inf _{x \in \mathbb {K}} f(x) \in \mathbb {R}.\) Then, the strong duality holds for problems (1) and (2) if and only if the Condition NES holds for f, g, h.
Now, the following result easily follows.
Corollary 1
Assume that \(f:S \to \mathbb {R},\) g : S → Y are convex functions and let h : S → Z be an affine-linear mapping. Then Assumption S is fulfilled at the optimal solution \(x_0 \in \mathbb {K}\) of problem (1) , if and only if Condition NES holds for f, g, and h with respect to \(\mathbb {K}.\)
Similarly, keeping in consideration the main result in [42], we have the following result.
Corollary 2
Let X and Z be real normed spaces, let Y be a real normed space ordered by a closed convex cone C. Let S be a convex subset of X and let \(f: S\to \mathbb {R}\) be a given convex functional, let g : S → Y be a convex mapping and let h : S → Z an affine-linear mapping. Assume that f, g have a directional derivative at x 0 ∈ K solution to problem (1) in every direction x − x 0 with arbitrary x ∈ S. Then, Assumption S′ is fulfilled at x 0 if and only if Condition NES holds for f, g, h with respect to \(\mathbb {K}.\)
As for Assumptions S and S′, also Condition NES is really useful in the applications as we can see in the next sections.
2 Applications to the General Financial Equilibrium Problem
In this chapter we apply Assumption S, which was introduced in Sect. 1.1, to a general equilibrium model of financial flows and prices (see also [15]).
2.1 Presentation of the Model
We consider a financial economy consisting of m sectors, for example households, domestic business, banks and other financial institutions, as well as state and local governments, with a typical sector denoted by i, and of n instruments, for example mortgages, mutual funds, saving deposits, money market funds, with a typical financial instrument denoted by j, in the time interval [0, T]. Let s i(t) denote the total financial volume held by sector i at time t as assets, and let l i(t) be the total financial volume held by sector i at time t as liabilities. Further, we allow markets of assets and liabilities to have different investments s i(t) and l i(t), respectively. Since we are working in the presence of uncertainty and of risk perspectives, the volumes s i(t) and l i(t) held by each sector cannot be considered stable with respect to time and may decrease or increase. For instance, depending on the crisis periods, a sector may decide not to invest on instruments and to buy goods as gold and silver. At time t, we denote the amount of instrument j held as an asset in sector i’s portfolio by x ij(t) and the amount of instrument j held as a liability in sector i’s portfolio by y ij(t). The assets and liabilities in all the sectors are grouped into the matrices \(x(t), \,y(t) \in \mathbb {R}^{m \times n},\) respectively. At time t we denote the price of instrument j held as an asset and as a liability by r j(t) and by (1 + h j(t))r j(t), respectively, where h j is a nonnegative function defined into [0, T] and belonging to \(L^{\infty }([0,T], \mathbb {R}).\) We introduce the term h j(t) because the prices of liabilities are generally greater than or equal to the prices of assets. In this manner we describe, in a more realistic way, the behaviour of the markets for which the liabilities are more expensive than the assets. We group the instrument prices held as an asset nd as a liability into the vectors r(t) = [r 1(t), r 2(t), …, r i(t), …, r n(t)]T and (1+h(t))r(t) = [(1+h 1(t))r 1(t), (1+h 2(t))r 2(t), …, (1+h i(t))r i(t), …, (1+h n(t))r n(t)]T, respectively. In our problem the prices of each instrument appear as unknown variables. Under the assumption of perfect competition, each sector will behave as if it has no influence on the instrument prices or on the behaviour of the other sectors, but on the total amount of the investments and the liabilities of each sector.
We choose as a functional setting the very general Lebesgue space
with the norm
Then, the set of feasible assets and liabilities for each sector i = 1, …, m becomes
and the set of all feasible assets and liabilities becomes
Now, we introduce the ceiling and the floor price associated with instrument j, denoted by \(\overline {r}_j\) and by \( \underline {r}_j\), respectively, with \(\overline {r}_j(t) > \underline {r}_j(t) \geq 0\), a.e. in [0, T]. The floor price \( \underline {r}_j(t)\) is determined on the basis of the official interest rate fixed by the central banks, which, in turn, take into account the consumer price inflation. Then the equilibrium prices \(r^*_j(t)\) cannot be less than these floor prices. The ceiling price \(\overline {r}_j(t)\) derives from the financial need to control the national debt arising from the amount of public bonds and of the rise in inflation. It is a sign of the difficulty on the recovery of the economy. However it should be not overestimated because it produced an availability of money.
In detail, the meaning of the lower and upper bounds is that to each investor a minimal price \( \underline {r}_j\) for the assets held in the instrument j is guaranteed, whereas each investor is requested to pay for the liabilities in any case a minimal price \((1+h_j) \underline {r}_j\). Analogously each investor cannot obtain for an asset a price greater than \(\overline {r}_j\) and as a liability the price cannot exceed the maximum price \((1+h_j) \overline {r}_j\).
We denote the given tax rate levied on sector i’s net yield on financial instrument j, as τ ij. Assume that the tax rates lie in the interval [0, 1) and belong to \(L^\infty ([0,T], \mathbb {R})\). Therefore, the government in this model has the flexibility of levying a distinct tax rate across both sectors and instruments.
We group the instrument ceiling and floor prices into the column vectors \(\overline {r}_j(t) = (\overline {r}_n(t))_{j=1, \ldots , n},\) and \( \underline {r}_j(t) = ( \underline {r}_j(t))_{j=1, \ldots , n},\) respectively, and the tax rates τ ij into the matrix \(\tau (t) \in L^2([0,T], \mathbb {R}^{m \times n}).\)
The set of feasible instrument prices is:
where \( \underline {r}\) and \(\overline {r}\) are assumed to belong to \(L^2([0,T], \mathbb {R}^n)\).
In order to determine for each sector i the optimal distribution of instruments held as assets and as liabilities, we consider, as usual, the influence due to risk-aversion and the optimality conditions of each sector in the financial economy, namely the desire to maximize the value of the asset holdings while minimizing the value of liabilities. An example of risk aversion is given by the well-known Markowitz quadratic function based on the variance-covariance matrix denoting the sector’s assessment of the standard deviation of prices for each instrument (see [40, 41]). In our case, however, the Markowitz utility or other more general ones are assumed to be time-dependent in order to incorporate the adjustment in time which depends on the previous equilibrium states.
Then, we introduce the utility function U i(t, x i(t), y i(t), r(t)), for each sector i, defined as follows:
where the term − u i(t, x i(t), y i(t)) represents a measure of the risk of the financial agent and r j(t)(1 − τ ij(t))[x i(t) − (1 + h j(t))y i(t)] represents the value of the difference between the asset holdings and the value of liabilities. We suppose that the sector’s utility function U i(t, x i(t), y i(t)) is defined on \([0, T ] \times \mathbb {R}^n\times \mathbb {R}^n\), is measurable in t and is continuous with respect to x i and y i. Moreover we assume that \(\displaystyle \frac {\partial u_i}{\partial x_{ij}}\) and \(\displaystyle \frac {\partial u_i}{\partial y_{ij}}\) exist and that they are measurable in t and continuous with respect to x i and y i. Further, we require that ∀i = 1, …, m, ∀j = 1, …, n, and a.e. in [0, T] the following growth conditions hold true:
and
where α i, β ij, γ ij are non-negative functions of \(L^\infty ([0, T ], \mathbb {R})\). Finally, we suppose that the function u i(t, x, y) is concave.
In Sect. 2.5 we define a utility function of Markowitz type.
Now, we establish the equilibrium conditions for the prices which express the equilibration of the total assets, the total liabilities and the portion of financial transactions per unit F j employed to cover the expenses of the financial institutions including possible dividends and manager bonus. Indeed, the equilibrium condition for the price r j of instrument j is the following:
where (x ∗, y ∗, r ∗) is the equilibrium solution for the investments as assets and as liabilities and for the prices. In other words, the prices are determined taking into account the amount of the supply, the demand of an instrument and the charges F j, namely if there is an actual supply excess of an instrument as assets and of the charges F j in the economy, then its price must be the floor price. If the price of an instrument is positive, but not at the ceiling, then the market of that instrument must clear. Finally, if there is an actual demand excess of an instrument as liabilities in the economy, then the price must be at the ceiling.
Now, we can give different but equivalent equilibrium conditions, each of which is useful to illustrate particular features of the equilibrium.
Definition 4
A vector of sector assets, liabilities and instrument prices \(\displaystyle (x^*(t), y^*(t), r^*(t)) \in P \times \mathcal {R}\) is an equilibrium of the dynamic financial model if and only if ∀i = 1, …, m, ∀j = 1, …, n, and a.e. in [0, T], it satisfies the system of inequalities


and equalities


where \(\mu ^{(1)*}_i(t)\), \(\mu ^{(2)*}_i(t) \in L^2([0, T ], \mathbb {R})\) are Lagrange multipliers, and verifies conditions (9) a.e. in [0, T].
We associate with each financial volumes s i and l i held by sector i the functions \(\mu ^{(1)*}_i(t)\) and \(\mu ^{(2)*}_i(t)\), related, respectively, to the assets and to the liabilities and which represent the “equilibrium disutilities” per unit of sector i. Then, (10) and (12) mean that the financial volume invested in instrument j as assets \(x^*_{ij}\) is greater than or equal to zero if the j-th component \(\displaystyle - \frac {\partial u_i(t, x^*, y^*)}{\partial x_{ij}} - (1- \tau _{ij}(t)) r_j^* (t)\) of the disutility is equal to \(\mu ^{(1)*}_i(t)\), whereas if \(\displaystyle - \frac {\partial u_i(t, x^*, y^*)}{\partial x_{ij}} - (1- \tau _{ij}(t)) r_j^* (t)> \mu ^{(1)*}_i(t)\), then \(x^*_{ij}(t)=0\). The same occurs for the liabilities.
The functions \(\mu ^{(1)*}_i(t)\) and \(\mu ^{(2)*}_i(t)\) are the Lagrange multipliers associated a.e. in [0, T] with the constraints \(\displaystyle \sum _{j=1}^n x_{ij}(t) - s_i(t) =0\) and \(\displaystyle \sum _{j=1}^n y_{ij}(t) - l_i(t) =0\), respectively. They are unknown a priori, but this fact has no influence because we will prove in the following theorem that Definition 4 is equivalent to a variational inequality in which \(\mu ^{(1)*}_i(t)\) and \(\mu ^{(2)*}_i(t)\) do not appear (see [2] Theorem 2.1.).
Theorem 6
A vector \(\displaystyle ( x^*, y^*, r^*) \in P \times \mathcal {R}\) is a dynamic financial equilibrium if and only if it satisfies the following variational inequality:
Find \(( x^*, y^*, r^*) \in \displaystyle P \times \mathcal {R}\):
Remark 1
We would like to explicitly remark that our definition of equilibrium conditions (Definition 4) is equivalent to the equilibrium definition given by a vector \(( x^*, y^*, r^*) \in \displaystyle P \times \mathcal {R}\) satisfying
∀(x i, y i) ∈ P i, and (9). We prefer to use Definition 4, since it is expressed in terms of equilibrium disutilities.
Now, we would like to give an existence result. First of all, we remind some definitions. Let X be a reflexive Banach space and let \(\mathbb {K}\) be a subset of X and X ∗ be the dual space of X.
Definition 5
A mapping \(A: \mathbb {K} \to X^*\) is pseudomonotone in the sense of Brezis (B-pseudomonotone) iff
-
1.
For each sequence u n weakly converging to u (in short \(u_n \rightharpoonup u\)) in \(\mathbb {K}\) and such that limsupn〈Au n, u n − v〉≤ 0 it results that:
$$\displaystyle \begin{aligned} \liminf_n \langle A u_n, u_n -v \rangle \geq \langle A u, u-v \rangle, \quad \forall v \in \mathbb{K}.\end{aligned} $$ -
2.
For each \(v \in \mathbb {K}\) the function u↦〈Au, u − v〉 is lower bounded on the bounded subset of \(\mathbb {K}\).
Definition 6
A mapping \(A: \mathbb {K} \to X^*\) is hemicontinuous in the sense of Fan (F-hemicontinuous) iff for all \(v \in \mathbb {K}\) the function u↦〈Au, u − v〉 is weakly lower semicontinuous on \(\mathbb {K}\).
The following existence result does not require any kind of monotonicity assumptions.
Theorem 7
Let \(\mathbb {K} \subset X\) be a nonempty closed convex bounded set and let \(A:\mathbb {K} \subset E \to X^*\) be B-pseudomonotone or F-hemicontinuous. Then the variational inequality
admits a solution.
2.2 The Duality for the Financial Equilibrium Problem
Now, in order to study the duality for the financial equilibrium problem, let us set:
Then the Lagrange functional is
where \((x,y,r) \in L^2([0,T], \mathbb {R}^{2mn + n}), \) λ (1), \(\lambda ^{(2)} \in L^2([0,T], \mathbb {R}^{mn}_+),\) μ (1), μ (2) ∈ L 2([0, T], \(\mathbb {R}^{m}), \) \(\rho ^{(1)}, \rho ^{(2)} \in L^2([0,T], \mathbb {R}^{n}_+)\) and λ (1), λ (2), ρ (1), ρ (2) are the Lagrange multipliers associated, a.e. in [0, T], with the sign constraints x i(t) ≥ 0, y i(t) ≥ 0, \(r_j(t)- \underline {r}_j(t) \ge 0,\) \( \overline {r}_j(t) - r_j(t) \ge 0,\) respectively whereas the functions μ (1)(t) and μ (2)(t) are the Lagrange multipliers associated, a.e. in [0, T], with the equality constraints \(\displaystyle \sum _{j=1}^n x_{ij}(t) - s_i(t) =0\) and \(\displaystyle \sum _{j=1}^n y_{ij}(t) - l_i(t) =0\), respectively. Hence, applying Theorem 1, the following result can be provided (see [2]):
Theorem 8
Let \(\displaystyle (x^*, y^*, r^*) \in P \times \mathcal {R}\) be a solution to variational inequality (14) and let us consider the associated Lagrange functional (16) . Then, the strong duality holds and there exist λ (1)∗, λ (2)∗ \(\in L^2([0,T], \mathbb {R}^{mn}_+),\) \(\mu ^{(1)*}, \mu ^{(2)*} \in L^2([0,T], \mathbb {R}^{m}),\) \(\rho ^{(1)*}, \rho ^{(2)*} \in L^2([0,T],\mathbb {R}^n_+)\) such that (x ∗, y ∗, r ∗, λ (1)∗, λ (2)∗, μ (1)∗, μ (2)∗, ρ (1)∗, ρ (2)∗) is a saddle point of the Lagrange functional, namely
\(\forall (x, y, r) \in L^2([0,T], \mathbb {R}^{2mn + n}),\) \( \forall \lambda ^{(1)}, \lambda ^{(2)} \in L^2([0,T], \mathbb {R}^{mn}_+), \) \( \forall \mu ^{(1)}, \mu ^{(2)} \in L^2([0,T], \mathbb {R}^{m}), \) \( \forall \rho ^{(1)}, \rho ^{(2)} \in L^2([0,T], \mathbb {R}^n_+)\) and, a.e. in [0, T],
Formula (18) represents the Deficit Formula. Indeed, if \(\rho ^{(1)*}_j(t)\) is positive, then the prices are minimal and there is a supply excess of instrument j as an asset and of the charge F j(t), namely the economy is in deficit and, for this reason, \(\rho ^{(1)*}_j(t)\) is called the deficit variable and represents the deficit per unit.
Analogously if \(\rho ^{(2)*}_j(t)\) is positive, then the prices are maximal and there is a demand excess of instrument j as a liability, namely there is a surplus in the economy. For this reason \(\rho ^{(2)*}_j(t)\) is called the surplus variable and represents the surplus per unit.
From (18) it is possible to obtain the Balance Law
Finally, assuming that the taxes τ ij(t), i = 1, …, m, j = 1, …, n, have a common value θ(t), and the increments h j(t), j = 1, …, n, have a common value i(t), otherwise we can consider the average values (see Remark 7.1 in [2]), the significant Liability Formula follows
2.3 The Viewpoints of the Sector and of the System
The financial problem can be considered from two different perspectives: one from the Point of View of the Sectors, which try to maximize the utility and a second point of view, that we can call System Point of View, which regards the whole equilibrium, namely the respect of the previous laws. For example, from the point of view of the sectors, l i(t), for i = 1, …, m, are liabilities, whereas for the economic system they are investments and, hence, the Liability Formula, from the system point of view, can be called “Investments Formula”. The system point of view coincides with the dual Lagrange problem (the so-called “shadow market”) in which \(\rho ^{(1)}_j(t)\) and \(\rho ^{(2)}_j(t)\) are the dual multipliers, representing the deficit and the surplus per unit arising from instrument j. Formally, the dual problem is given by
Find \((\rho ^{(1)*}, \rho ^{(2)*}) \in L^2([0,T], \mathbb {R}^{2n}_+)\) such that
Indeed, taking into account inequality (17), we get
\(\forall \lambda ^{(1)}, \lambda ^{(2)} \in L^2([0,T], \mathbb {R}^{mn}_+),\) \(\mu ^{(1)}, \mu ^{(2)} \in L^2([0,T], \mathbb {R}^{m}), \) \(\rho ^{(1)}, \rho ^{(2)} \in L^2([0,T], \mathbb {R}^{n}_+).\)
Choosing λ (1) = λ (1)∗, λ (2) = λ (2)∗, μ (1) = μ (1)∗, μ (2) = μ (2)∗, we obtain the dual problem (23)
Note that, from the System Point of View, also the expenses of the institutions F j(t) are supported from the liabilities of the sectors.
Remark 2
Let us recall that from the Liability Formula we get the following index E(t), called “Evaluation Index”, that is very useful for the rating procedure:
where we set
From the Liability Formula we obtain

If E(t) is greater or equal than 1, the evaluation of the financial equilibrium is positive (better if E(t) is proximal to 1), whereas if E(t) is less than 1, the evaluation of the financial equilibrium is negative.
2.4 The Contagion Problem
Let us note that in the balance law:
if
namely the sum of all the deficit exceeds the sum of all the surplus, the balance of all the financial entities is negative (see also [18]). In this case we say that a negative contagion is determined and we can assume that the insolvencies of individual entities propagate through the entire system. It is sufficient that only one deficit \(\rho _j^{(1)*}(t)\) is large to obtain, even if the other \(\rho _j^{(2)*}(t)\) are lightly positive, a negative balance for the all system.
When condition (25) is verified, we get E(t) ≤ 1 and, hence, also E(t) is a significant indicator that the financial contagion happens.
In [20] a regularity result of \(\rho ^{(1)*}_j(t)\), \(\rho ^{(2)*}_j(t)\), has been proved. Let us set


with
Let us note that \(\mathcal {K} \) is a convex, bounded and closed subset of \(L^2([0,T], \mathbb {R}^{2mn+n})\). Moreover assumption (8) implies that A is lower semicontinuous along line segments.
The following result holds true (see [20] Theorem 2.4):
Theorem 9
Let \(A \in C^0([0,T], \mathbb {R}^{2mn+n}) \) be strongly monotone in x and y, monotone in r, namely, there exists α such that, for t ∈ [0, T],
∀ν 1 = (x 1, y 1, r 1), \( \nu _2= (x_2, y_2, r_2) \in \mathbb {R}^{2mn+n}\).
Let \( \underline {r}(t) \) , \(\overline {r}(t)\) , h(t), F(t) ∈ \( C^0([0,T],\mathbb {R}^n_+)\) , let \(\tau (t)\in C^0([0,T],\mathbb {R}^{mn})\) and let \(s, l \in C^0([0,T], \mathbb {R}^m)\) , satisfying the following assumption (β):
-
there exists δ 1(t) ∈ L 2([0, T]) and \(c_1 \in \mathbb {R} \) such that, for a.a. t ∈ [0, T]:
$$\displaystyle \begin{aligned} \| s(t)\| \le \delta_1 (t) + c_1 ; \end{aligned}$$ -
there exists δ 2(t) ∈ L 2([0, T]) and \(c_2 \in \mathbb {R} \) such that, for a.a. t ∈ [0, T]:
$$\displaystyle \begin{aligned} \| l(t)\| \le \delta_2 (t) + c_2 . \end{aligned}$$
Then the Lagrange variables, ρ (1)∗(t), ρ (2)∗(t), which represent the deficit and the surplus per unit, respectively, are continuous too.
2.5 An Example of a Markowitz-Type Risk Measure
We generalize and provide an evolutionary Markowitz-type measure of the risk proposed with a memory term. This function is effective, namely an existence theorem for the general financial problem holds (see [21]). In this way we cover a lack providing the existence of a significant evolutionary measure of the risk. The particular, but significant, example of utility function is:
where Q i denotes the sector i’s assessment of the standard deviation of prices for each instrument j.
3 Applications to the Elastic-Plastic Torsion Problem
In this chapter we apply Assumption S to the elastic-plastic torsion problem.
3.1 Presentation of the Problem
The elastic-plastic torsion problem and its relationships with obstacle problem have been deeply investigated in years 1965–1980. Later on these studies have been resumed, with particular regards to existence and properties of Lagrange multipliers. The existence of Lagrange multipliers is strictly related to strong duality theory.
The problem arises from aerodynamics and has been formulated by R. Von Mises (see [53]): the elastic-plastic torsion problem of a cylindrical bar with cross section Ω is to find a function u(x) which vanishes on the boundary ∂Ω and, together with its first derivatives, is continuous on Ω; nowhere on Ω the gradient of u must have an absolute value (modulus) less than or equal to a given positive constant τ; whenever in Ω the strict inequality holds, the function u must satisfy the differential equation Δu = −2μθ, where the positive constants μ and θ denote the shearing modulus and the angle of twist per unit length, respectively.
From the Von Mises formulation it follows that the cross section Ω is divided into two regions: an elastic region E = {x ∈ Ω : |Du(x)| < 1} and a plastic region P = {x ∈ Ω : |Du(x)| = 1}.
This problem is a free boundary one and a suitable tool for studying this kind of problems is the variational inequality theory. To this end, let us consider the following variational inequality:Find \(\displaystyle u \in K= \left \{ v \in H_{0}^{1, \infty }(\varOmega ): |Dv| = \sum _{i=1}^{n} \left ( \frac {\partial v}{\partial x_{i}} \right )^2 \leq 1 \;\mbox{a.e. on}\; \varOmega \right \} \) such that
with \(\varOmega \subset \mathbb {R}^n\) open bounded convex set with Lipschitz boundary ∂Ω, F ∈ L p(Ω), p > 1.
As it is well known, (29) admits a unique solution u ∈ W 2, p(Ω) ∩ K (see [6, 7]).
In literature, in the planar case the existence and the properties of a smooth solution of the elastic-plastic torsion problem have been studied by Ting ([50,51,52]), whereas multidimensional case has been studied by Brezis in [5], who proved the existence of a Lagrange multiplier for (29), assuming F = cost > 0, namely, if u is the solution of variational inequality (29), then there exists a unique μ ∈ L ∞(Ω), μ ≥ 0 a.e. in Ω such that:
that is the solution of (29) solves the elastic-plastic torsion problem.
Conversely, if u ∈ K and there exists μ satisfying (30), then it is easily proved that u is the solution of (29).
In virtue of this equivalence the variational inequality (29) is the elastic-plastic torsion problem formulated by Von Mises.
Moreover, in this case, the solution to elastic-plastic torsion problem coincides with the solution to obstacle problem and is nonnegative.
Only recently the relationship between problems (29) and (30) has been clarified in the case of general linear operators and nonlinear monotone operators. In this section we will describe these results, together with the study of radial solutions to the elastic-plastic torsion.
3.2 The Elastic-Plastic Torsion Problem for Linear Operators
First, we establish the existence of Lagrange multipliers associated to a general linear operator. In particular we prove that the Lagrange multipliers associated to the elastic-plastic torsion problem for linear operators always exist and, in general, they result as a Radon measure. This result is proved using the classical strong duality.
Moreover, the result may be generalized, namely, it is possible to prove that the L p Lagrange multipliers exist if and only if Assumption S holds and this is a consequence of the new strong duality described in Sect. 1.1.
Let us now describe the problem in detail.
Let \(\varOmega \subset \mathbb {R}^n\) be an open bounded domain either convex or with boundary of class C 1, 1. Let us consider the linear elliptic operator
with associated bilinear form on \(H^{1, \infty }_{0}(\varOmega ) \times H^{1, \infty }_{0}(\varOmega )\) given by
where
Let us consider the variational inequality:
Find \(\displaystyle u \in K= \left \{ v \in H_{0}^{1, \infty }(\varOmega ): \sum _{i=1}^{n} \left ( \frac {\partial v}{\partial x_{i}} \right )^2 \leq 1, \; \mbox{a.e. on}\; \varOmega \right \} \) such that:
As it is well known, variational inequality (33) admits a unique solution u ∈ K and, if F ∈ L p(Ω), p > 1, u ∈ W 2, p(Ω) ∩ K (see [6, 7]).
We are able to prove the existence of a Lagrange multiplier for variational inequality (33) as a Radon measure (see [28, 30]).
Theorem 10
Under the above assumptions on Ω and \(\mathcal {L}\) , let F ∈ L p(Ω), p > 1, and u ∈ K ∩ W 2, p(Ω) be the solution to problem (33) . Then there exists \( \overline \mu \in (L^{\infty }( \varOmega ))^*\) such that
The theorem means that, if we consider a solution u of variational inequality (33), then conditions (34) are satisfied. Moreover it is possible to show that, as a consequence of conditions (34), the solution of variational inequality (33) is also a solution of the elastic-plastic torsion problem and vice versa.
We mention the paper [9], in which the authors prove the existence of a Lagrange multiplier as a positive Radon measure under different assumptions and using a different technique.
In order to prove Theorem 10 we use the strong duality property in the classical sense (see [26, 38]) and its consequence on the existence of saddle points of the Lagrange functional. We briefly recall them.
Theorem 11 (Classical Strong Duality Property)
Let S be a nonempty subset of a real linear space X; (Y, ∥⋅∥) be a partially ordered real normed space with ordering cone C; \(f: S \to \mathbb {R}\) be a given objective functional; g : S → Y be a given constraint mapping; let the composite mapping \((f,g): S \to \mathbb {R} \times Y \) be convex-like with respect to product cone \(\mathbb {R}_+ \times C \) in \(\mathbb {R} \times Y\) . Let the constraint set be given as \(\mathbb {K}:= \{ v \in S : g(v) \in -C \} \) which is assumed to be nonempty. Let the ordering cone C have a nonempty interior int(C). If the primal problem
is solvable and the generalized Slater condition is satisfied, namely there is a vector \(\hat v \in S\) with \(g(\hat v) \in - int(C)\) , then the dual problem
is also solvable and the extremal values of the two problems are equal. Moreover, if u is the optimal solution to problem (35) and \(\overline \mu \in C^*\) is a solution of the problem (36) , it results
Theorem 12
Under the same assumptions as above, suppose the ordering cone C to be closed. Then a point \((u,\overline \mu ) \in S \times C^*\) is a saddle point of the Lagrange functional L if and only if u is a solution of the primal problem (35) , \(\overline \mu \) is a solution of the dual problem (36) and the extremal values of the two problems are equal.
Indeed, let u ∈ K ∩ W 2, p(Ω) be the solution to (33). Let us rewrite the variational inequality (33) as the minimum problem
where
Let us set \(S= X= H^{1, \infty }_0(\varOmega )\), Y = L ∞(Ω),
Since f and g are convex on the space \( H^{1, \infty }_0(\varOmega )\), then the composite mapping (f, g) is convex-like with respect to the product cone \(\mathbb {R}_{+} \times C\) in \(\mathbb {R} \times Y\). Moreover, we are able to prove that int(C)≠∅ and that generalized Slater condition is verified. Then, every assumption of Theorem 11 is verified and, since the primal problem is solvable, it follows that the dual problem
is also solvable and the extremal values of the two problems coincide. Moreover, if u is a solution of the problem (38) and \(\overline \mu \in C^*\) is a solution of the problem (39), condition (37) holds, namely
Finally, since the ordering cone C is closed, we may apply Theorem 12, from which it follows
In conclusion, since
from (40), (41) we obtain that, if u is a solution of (33), then of the primal problem (38), there exists \( \overline \mu \in C^*\) solution of the dual problem (39) and the following conditions are satisfied:
namely, Theorem 10 is proved.
Moreover, if \(\overline \mu \in (L^{\infty }(\varOmega ))^*,\) \(\overline \mu \) can be expressed by a Radon’s integral with respect to the finitely additive measure Ψ:
Ψ is finitely additive, has a bounded total variation and is absolutely continuous with respect to the Lebesgue measure, that is m(B) = 0 implies Ψ(B) = 0.
From this properties of \(\overline \mu \) and conditions (34) it is possible to prove that the solution of variational inequality (33) is also a solution of the elastic plastic torsion problem and vice versa.
In order to obtain a regularization of this result, namely to obtain the existence of a Lagrange multiplier for variational inequality (33) as a L ∞ function, it is necessary to consider the convex set K in \(H_0^1(\varOmega )\), that is
But in this case the interior of the ordering cone, which defines the sign constraints, is empty, then it is not possible to apply the classical strong duality theory. It is necessary to apply the new strong duality principle described in Sect. 1.1 and, then, we obtain the following characterization in terms of Assumption S of the elastic-plastic torsion problem (see Theorem 3.4 in [19]).
Theorem 13
Let u ∈ K ∇∩ W 2, p(Ω) be the solution to problem
Then there exists \(\bar \mu \in L^{\infty }(\varOmega )\) such that
if and only if the solution u of (42) verifies Assumption S.
The theorem means that, if the solution of (42) verifies Assumption S, then conditions (43) are satisfied, that is the solution of (42) is a solution of the elastic-plastic torsion problem; vice versa if u ∈ W 2, p(Ω) verifies (43), and, then, in particular, is a solution of the elastic-plastic torsion problem, then u solves (42) and verifies Assumption S.
The thesis is achieved rewriting the variational inequality (42) as the minimum problem
where
with the settings
Assuming that Assumption S holds, from Theorem 1 it follows that there exists \(\bar \mu \in C^*= \displaystyle \left \{\mu \in L^{\infty }(\varOmega ) : \right . \) \( \left . \; \int _{\varOmega } \mu \,v \, dx \ge 0, \; \forall v \in L^1(\varOmega )\right \}\) such that
Then the thesis is obtained using Theorem 2 and (46). Vice versa assuming that conditions (43) hold, it is possible to show that u verifies Assumption S and, finally, it is easy to verify that u is a solution to variational inequality (42).
3.3 The Elastic-Plastic Torsion Problem for Nonlinear Monotone Operators
Second, we are aimed at the investigation of the existence of Lagrange multipliers associated to the following nonlinear problem (see [7] for the existence and the regularity of solutions to (47)):
In particular, we are able to prove that the Lagrange multiplier is always a Radon measure when the operator is strictly monotone, whereas the Lagrange multiplier is a L p function when the operator is strongly monotone (see [32]). The first result is proved using classical strong duality theory, whereas for the second one we apply the new strong duality theory described in Sect. 1.1.
From now on we assume that \(\varOmega \subset \mathbb {R}^n\) is an open bounded convex set with Lipschitz boundary ∂Ω and a is an operator of class C 2. In a first step we suppose that the operator is strictly monotone, namely
In a first theorem we are able to prove the equivalence between elastic-plastic torsion problem and obstacle problem.
Theorem 14
Under the above assumptions on Ω and a, if a(0) = 0 and F ≡ const., the solution u of (47) coincides with the solution of
where
In a second theorem we prove the existence of Lagrange multipliers for problem (47) as a Radon measure.
Theorem 15
Under the above assumptions on Ω and a, let F ∈ L p(Ω), p > 1, and u ∈ K be the solution to (47) . Then there exists \( \overline \mu \in (L^{\infty }( \varOmega ))^*\) such that
From conditions (50) it follows that, if u belongs to the elastic region E, \(\overline \mu \equiv 0\) and then u is a solution of the elliptic equation Au = F a.e. in Ω, where \(A= -\sum _{i=1}^n \frac {\partial a_i(Du)}{\partial x_i}\) and, in particular, a solution of (47) solves the elastic-plastic torsion problem. Conversely it is easily proved that, if u ∈ K satisfies conditions (50), then u solves variational inequality (47).
The proof of Theorem 15 is based on the following steps. First we rewrite variational inequality (47) as the minimum problem
where
Then, setting \(S= X= W^{1, \infty }_0(\varOmega )\), Y = L ∞(Ω),
as in the linear case (see [29, 30]) we are able to prove that the assumptions of Theorems 11 and 12 hold. Consequently, if u is a solution of (47), then of the problem (51), there exists \(\overline \mu \in C^*\) solution of the dual problem
and \((u, \overline \mu )\) is a saddle point of the so called Lagrange functional
namely
Via variational arguments we obtain that
Then from (37), (55), we obtain conditions (50).
If now we assume strong monotonicity assumption
we are able to prove the following regularization theorem concerning Lagrange multipliers.
Theorem 16
Under the same assumptions on Ω as above, let a satisfy strong monotonicity assumption (56) , with a(0) = 0, let F be a positive constant and u ∈ K ∩ W 2, p(Ω) be the solution to problem (47) . Then there exists \(\bar \mu \in L^p(\varOmega )\) such that
Of course, as for the linear problem, it is easy to prove that, if u ∈ K and there exists \(\bar \mu \) satisfying (57), then u is also the solution to problem (47).
Let us notice that, if u is the solution to problem (47), in virtue of Theorem 14, it is the solution of problem (49). In particular, since f ≡ const. > 0, a is monotone and a(0) = 0, it is possible to prove that u is the solution of the problem
where
Finally, we are able to prove that the elastic region coincides with the set where u does not touch the obstacle, namely
Theorem 17
Under the same assumptions on Ω, a and f as in Theorem 16 , setting
it results
In order to prove Theorem 16, we should apply strong duality theory in the case \(X=S= H_0^{1}(\varOmega )\), but in this case, as we already observed, the ordering cone C = {w ∈ L 1(Ω) : w(t) ≥ 0 a.e. in Ω} has an empty interior, then the classical strong duality theory cannot be applied.
It is necessary to use the new strong duality theory described in Sect. 1.1.
To this end, let us consider variational inequality (47) under assumption (56) and let u ∈ K be the solution to (47). From the regularity results in [7] it follows that, if F ∈ L p(Ω), 1 < p < ∞, u belongs to W 2, p(Ω) ∩ K. In particular, if p > n, Du belongs to \(C^{0, \alpha }(\overline \varOmega )\). From Theorem 14, it follows that u is a solution to problem (49). Since strong monotonicity holds and u is regular, it also solves the problem
where
Moreover, since f is positive and a monotone, with a(0) = 0, u is also the solution to
where
Now, we may rewrite problem (60) as an optimization problem. Let us set
where
As we already observed, u ∈ K 2 ∩ W 2, p(Ω) is the solution of (60) and let us remark that
We are able to prove that, assuming
the optimization problem (62) fulfills Assumption S. Then the strong duality and Theorem 2 hold, from which we get, via variational arguments, that there exists \( \overline \mu \in C\) such that
From Theorem 17, that is achieved using delicate tools of nonlinear partial differential equations, conditions (57) follow.
Remark 3
Another way to reach the strong duality is to verify Assumption NES. Indeed, in this particular setting, our map
is defined by
In particular, in virtue of (61),
then it results
and we are able to prove that, setting μ = (Aδ − f) ⋅ χ {x ∈ Ω: u(x)=δ(x)},
In any case, the strong duality holds.
3.4 Von Mises Functions
We now provide an example of the so-called “Von Mises functions”, namely of solutions of the elastic-plastic torsion problem, associated to nonlinear monotone operators, which are not obtained by means of the obstacle problem in the case F = constant.
We consider an operator \(a(p): \mathbb {R}^n \rightarrow \mathbb {R}^n\), of class C 2, strictly monotone. Let \(\varOmega \subseteq \mathbb {R}^n\) with boundary ∂Ω ∈ C 2, 1 = W 3, ∞, \(P= \varGamma _{\mu } = \left \{x \in \varOmega : \; \delta (x) = d(x, \partial \varOmega ) < \mu \right \}\), E = Ω ∖ P.
As it is well known μ can be chosen in such a way that for every x ∈ Γ μ there is a unique closest point from ∂Ω to x and δ(x) owns the same regularity of ∂Ω on Γ μ. Then δ(x) ∈ W 3, p(P), ∀p > 1, and its trace δ ∕∂P ∈ W 3−1∕p, p(∂P).
Let
and w(x) ∈ W 3, p(E), ∀p > 1, the solution of
We can directly prove that, in E, G(Dw) = |Dw|2 − 1 verifies
Then we may apply maximum principle to G(Dw), from which it follows |Dw| < 1 in E.
The function u(x) ∈ W 2, p(Ω), ∀p > 1,
arises.
Setting
it results
namely
Moreover
and by means of maximum principle we can prove
that is u is a solution of an elastic-plastic torsion problem.
3.5 Radial Solutions
Finally, we search for radial solutions to the elastic-plastic torsion problem, assuming the free term to belong to L p(Ω) (see [33]). In particular, for n = 2, we investigate the nature of the torsion and when the transition from the elastic case to the plastic one happens. We are able to find the explicit solution u ∈ W 2, p(Ω) and the Lagrange multiplier \(\overline \mu \in L^p(\varOmega )\) in the two admissible cases, namely, when the elastic and the plastic regions both exist and when the torsion is only elastic. Moreover, we characterize the free boundary and obtain a necessary and sufficient condition in order that the plastic region exists. Finally, we provide some examples.
To this aim, let us assume that Ω is the ball of \(\mathbb {R}^n\) of radius 1 centered at the origin, and F ∈ L p(Ω), p > n, is of radial type, namely F(x) = f(|x|) = f(ρ), with |x| = ρ.
We search for solutions to (43) such that u(x) ∈ W 2, p(Ω) and \(\overline \mu (x) \in L^p(\varOmega )\) are of radial type, namely \(\overline \mu (x)= \mu (|x|) = \mu (\rho ) \), u(x) = φ(|x|) = φ(ρ). In this case, since u(x) = φ(ρ), \(\frac {\partial u}{\partial x_i}= \varphi ' (\rho ) \frac {x_i}{\rho }\), \(\varDelta u = \varphi '' + \frac {n-1}{\rho } \varphi '(\rho ),\) |Du| = φ′(ρ), bearing in mind that u ∈ K, conditions (43 ) become
Under the following assumptions: there exists \(\overline {\rho } \in (0,1)\) such that
where \(C_{\overline \rho }(0)\) is the closed ball of radius \(\overline \rho \) centered at the origin, namely
and
we are able to prove the following result.
Theorem 18
Under conditions (69) , (71) , the region \([0, \overline \rho ]\) is an elastic region and the region \([\overline \rho , 1]\) is a plastic region. Moreover, the solution φ to (68) is
and it results to be φ(ρ) ∈ W 2, p(0, 1) and μ(ρ) ∈ L p(0, 1).
If Eq. (70) does not admit any solution \(\overline \rho \in (0,1)\), namely ∀ρ ∈ (0, 1)
the plastic region does not exist. The case
is not admissible, since it implies
Then, we are able to prove the following result.
Theorem 19
Under condition (71) , if
then, [0,1] is an elastic region. Moreover, the solution φ to (68) is
It results to be φ(ρ) ∈ W 2, p(0, 1).
Example 3
Let us consider a first example, namely F = const = k > 0. In this case we obtain the same results as in [48], p. 15.
If we consider a first case, F = k > 2, the plastic region exists, since
namely, \(\overline \rho = \frac {2}{k} < 1\) is the solution to (70).
Then, by (72) we get the continuous function
It is easily seen that u ∈ W 2, p(Ω).
Moreover, the Lagrange multiplier μ(ρ) exists and belongs to L p([0, 1]):
If we consider the other case F = const = k, 0 < k ≤ 2, the plastic region does not exist, since \(\overline \rho = \frac {2}{k} \ge 1\) is the solution to (70).
Then, the torsion is all elastic and by (73) we get the continuous function
φ(ρ) as in (74) and μ = 0 verify conditions (68) in [0, 1]. Moreover u ∈ W 2, p(Ω).
Let us now consider problem (68) with \(\displaystyle f (\rho )= \frac {k }{\rho ^{\alpha }}\), 0 < α < 1.
The condition α < 1 ensures that F(x) ∈ L p(Ω), \(2=n <p< \frac 2{\alpha }\). Moreover, condition (71) is verified.
If we consider the case k > 2 − α, the plastic region exists, since
namely, \(\overline \rho = \left ( \frac {2-\alpha }{k}\right )^{\frac 1{1-\alpha }} <1\) is the solution to (70).
Then, by (72) we get the continuous function
It is easily seen that u ∈ W 2, p(Ω).
Moreover, the Lagrange multiplier μ(ρ) exists and belongs to L p([0, 1]):
Finally, if we consider the other case 0 < k ≤ 2 − α, the plastic region does not exist, since \(\overline \rho = \left ( \frac {2-\alpha }{k}\right )^{\frac 1{1-\alpha }} \ge 1\) is the solution to (70).
Then, the torsion is all elastic and by (73) we get the continuous function
φ(ρ) as in (75) and μ = 0 verify conditions (68) in [0, 1]. Moreover, u ∈ W 2, p(Ω).
References
A. Barbagallo, A. Maugeri, Duality theory for a dynamic oligopolistic market equilibrium problem. Optimization 60, 29–52 (2011)
A. Barbagallo, P. Daniele, S. Giuffrè, A. Maugeri, Variational approach for a general financial equilibrium problem: the deficit formula, the balance law and the liability formula. A path to the economy recovery. Eur. J. Oper. Res. 237(1), 231–244 (2014)
J.M. Borwein, V. Jeyakumar, A.S. Lewis, M. Wolkowicz, Constrained approximation via convex programming. University of Waterloo. Preprint (1988)
R.I. Bot, E.R. Csetnek, A. Moldovan, Revisiting some duality theorems via the quasirelative interior in convex optimization. J. Optim. Theory Appl. 139(1), 67–84 (2008)
H. Brezis, Moltiplicateur de Lagrange en Torsion Elasto-Plastique. Arch. Rational Mech. Anal. 49, 32–40 (1972)
H. Brezis, Problèmes Unilatéraux. J. Math. Pures Appl. 51, 1–168 (1972)
H. Brezis, G. Stampacchia, Sur la régularité de la solution d’inéquations elliptiques. Bull. Soc. Math. Fr. 96, 153–180 (1968)
V. Caruso, P. Daniele, A network model for minimizing the total organ transplant costs. Eur. J. Oper. Res. (2017). https://doi.org/10.1016/j.ejor.2017.09.040
V. Chiadó-Piat, D. Percivale, Generalized Lagrange multipliers in elastoplastic torsion, J. Differ. Equ. 114, 570–579 (1994)
M.G. Cojocaru, P. Daniele, A. Nagurney, Projected dynamical systems and evolutionary variational inequalities via Hilbert spaces and applications. J. Optim. Theory Appl. 127, 549–563 (2005)
P. Daniele, Dynamic Networks and Evolutionary Variational Inequalities (Edward Elgar Publishing, Cheltenham, 2006)
P. Daniele, Evolutionary variational inequalities and applications to complex dynamic multi-level models. Transp. Res. Part E 46, 855–880 (2010)
P. Daniele, S. Giuffrè, General infinite dimensional duality and applications to evolutionary network equilibrium problems. Optim. Lett. 1, 227–243 (2007)
P. Daniele, S. Giuffrè, Random variational inequalities and the random traffic equilibrium problem. J. Optim. Theory Appl. 167(1), 363–381 (2015)
P. Daniele, S. Giuffrè, S. Pia, Competitive financial equilibrium problems with policy interventions. J. Ind. Manag. Optim. 1(1), 39–52 (2005)
P. Daniele, S. Giuffrè, G. Idone, A. Maugeri, Infinite dimensional duality and applications. Math. Ann. 339, 221–239 (2007)
P. Daniele, S. Giuffrè, A. Maugeri, Remarks on general infinite dimensional duality with cone and equality constraints. Commun. Appl. Anal. 13(4), 567–578 (2009)
P. Daniele, S. Giuffrè, M. Lorino, A. Maugeri, C. Mirabella, Functional inequalities and analysis of contagion in the financial networks, in Handbook of Functional Equations – Functional Inequalities, ed. by Th.M. Rassias. Optimization and Its Applications, vol. 95 (Springer, Berlin, 2014), pp. 129–146
P. Daniele, S. Giuffrè, A. Maugeri, F. Raciti, Duality theory and applications to unilateral problems. J. Optim. Theory Appl. 162(3), 718–734 (2014)
P. Daniele, S. Giuffrè, M. Lorino, Functional inequalities, regularity and computation of the deficit and surplus variables in the financial equilibrium problem. J. Glob. Optim. 65, 575–596 (2016)
P. Daniele, M. Lorino, C. Mirabella, The financial equilibrium problem with a Markowitz-type memory term and adaptive, constraints. J. Optim. Theory Appl. 171, 276–296 (2016)
P. Daniele, A. Maugeri, A. Nagurney, Cybersecurity investments with nonlinear budget constraints: analysis of the marginal expected utilities, in Operations Research, Engineering, and Cyber Security, ed. by N.J. Daras, T.M. Rassias. Springer Optimization and Its Applications, vol. 113 (Springer, Berlin, 2017), pp. 117–134
M.B. Donato, The infinite dimensional Lagrange multiplier rule for convex optimization problems. J. Funct. Anal. 261(8), 2083–2093 (2011)
M.B. Donato, A. Maugeri, M. Milasi, C. Vitanza, Duality theory for a dynamic Walrasian pure exchange economy. Pac. J. Optim. 4, 537–547 (2008)
S. Giuffrè, Strong solvability of boundary value contact problems. Appl. Math. Optim. 51(3), 361–372 (2005)
S. Giuffrè, Elements of duality theory, in Topics in Nonlinear Analysis and Optimization, ed. by Q.H. Ansari (World Education, Delhi, 2012), pp. 251–267
S. Giuffrè, S. Pia, Weighted traffic equilibrium problem in non pivot Hilbert spaces with long term memory, in AIP Conference Proceedings Rodi, September 2010, vol. 1281, pp. 282–285
S. Giuffrè, A. Maugeri, New results on infinite dimensional duality in elastic-plastic torsion. Filomat 26(5), 1029–1036 (2012)
S. Giuffrè, A. Maugeri, Lagrange multipliers in elastic-plastic torsion, in AIP Conference Proceedings Rodi, September 2013, vol. 1558, pp. 1801–1804
S. Giuffrè, A. Maugeri, A measure-type Lagrange multiplier for the elastic-plastic torsion. Nonlinear Anal. 102, 23–29 (2014)
S. Giuffrè, G. Idone, A. Maugeri, Duality theory and optimality conditions for generalized complementary problems. Nonlinear Anal. 63, e1655–e1664 (2005)
S. Giuffrè, A. Maugeri, D. Puglisi, Lagrange multipliers in elastic-plastic torsion problem for nonlinear monotone operators. J. Differ. Equ. 259(3), 817–837 (2015)
S. Giuffrè, A. Pratelli, D. Puglisi, Radial solutions and free boundary of the elastic-plastic torsion problem. J. Convex Anal. 25(2), 529–543 (2018)
J. Gwinner, F. Raciti, Random equilibrium problems on networks. Math. Comput. Model. 43, 880–891 (2006)
J. Gwinner, F. Raciti, On a class of random variational inequalities on random sets. Numer. Funct. Anal. Optim. 27, 619–636 (2006)
R.B. Holmes, Geometric Functional Analysis (Springer, Berlin, 1975)
G. Idone, A. Maugeri, Generalized constraints qualification and infinite dimensional duality. Taiwan. J. Math. 13, 1711–1722 (2009)
J. Jahn, Introduction to the Theory of Nonlinear Optimization, 3rd edn. (Springer, Berlin, 2007)
V. Jeyakumar, H. Wolkowicz, Generalizations of slater constraint qualification for infinite convex programs. Math. Program. 57, 85–101 (1992)
H.M. Markowitz, Portfolio selection. J. Financ. 7, 77–91 (1952)
H.M. Markowitz, Portfolio Selection: Efficient Diversification of Investments (Wiley, New York, 1959)
A. Maugeri, D. Puglisi, A new necessary and sufficient condition for the strong duality and the infinite dimensional Lagrange Multiplier rule. J. Math. Anal. Appl. 415(2), 661–676 (2014)
A. Maugeri, D. Puglisi, Non-convex strong duality via subdifferential. Numer. Funct. Anal. Optim. 35, 1095–1112 (2014)
A. Maugeri, D. Puglisi, On nonlinear strong duality and the infinite dimensional Lagrange multiplier rule. J. Nonlinear Convex Anal. 18(3), 369–378 (2017)
A. Maugeri, F. Raciti, Remarks on infinite dimensional duality. J. Glob. Optim. 46, 581–588 (2010)
A. Maugeri, L. Scrimali, New approach to solve convex infinite-dimensional bilevel problems: application to the pollution emission price problem. J. Optim. Theory Appl. 169(2), 370–387 (2016)
R.T. Rockafellar, Conjugate duality and optimization, in Conference Board of the Mathematical Science Regional Conference Series in Applied Mathematics, vol. 16 (Society for Industrial and Applied Mathematics, Philadelphia, 1974)
J.F. Rodrigues, Obstacle Problems in Mathematical Physics. Mathematics Studies, vol. 134 (Elsevier, Amsterdam, 1987)
L. Scrimali, Infinite dimensional duality theory applied to investment strategies in environmental policy. J. Optim. Theory Appl. 154, 258–277 (2012)
T.W. Ting, Elastic-plastic torsion of a square bar. Trans. Am. Math. Soc. 113, 369–401 (1966)
T.W. Ting, Elastic-plastic torsion problem II. Arch. Ration. Mech. Anal. 25, 342–366 (1967)
T.W. Ting, Elastic-plastic torsion problem III. Arch. Ration. Mech. Anal 34, 228–244 (1969)
R. Von Mises, Three remarks on the theory of the ideal plastic body, in Reissner Anniversary Volume (Edwards, Ann Arbor, 1949)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Colajanni, G., Daniele, P., Giuffrè, S., Maugeri, A. (2018). Nonlinear Duality in Banach Spaces and Applications to Finance and Elasticity. In: Rassias, T. (eds) Applications of Nonlinear Analysis . Springer Optimization and Its Applications, vol 134. Springer, Cham. https://doi.org/10.1007/978-3-319-89815-5_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-89815-5_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89814-8
Online ISBN: 978-3-319-89815-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)