Computation of Invariant Curves in the Analysis of Periodically Forced Neural Oscillators

Abstract

Background oscillations, reflecting the excitability of neurons, are ubiquitous in the brain. Some studies have conjectured that when spikes sent by one population reach the other population in the peaks of excitability, then information transmission between two oscillating neuronal groups is more effective. In this context, phase locking relationships between oscillating neuronal populations may have implications in neuronal communication as they assure synchronous activity between brain areas. To study this relationship, we consider a population rate model and perturb it with a time-dependent input. We use the stroboscopic map and apply powerful computational methods to compute the invariant objects and their bifurcations as the perturbation parameters (frequency and amplitude) are varied. The analysis performed shows the relationship between the appearance of synchronous and asynchronous regimes and the invariant objects of the stroboscopic map.

1 Introduction

Since it was first reported in 1929 by Hans Berger [2], neural oscillatory activity has been a topic of great interest and debate in neuroscience. Although its role is not fully understood, electroencephalographic patterns evidence its importance in brain function. In particular, oscillations have been linked to many different processes as memory or perception [4]. Although oscillatory behaviour can occur across different brain scales, this work will focus on oscillations generated by neuronal ensembles or populations.

Neurons are the fundamental cells within the brain, and they basically communicate through electrical impulses [6]. Neurons integrate inputs from neighbouring neurons across dendrites. When these inputs cause the neuron membrane potential to reach a certain critical value or threshold, the neuron will respond with a characteristic voltage change of large amplitude and short time duration ($\approx$1 ms) known as action potential or spike. This action potential then travels along the axon of the neuron to the axon terminal, where its effect will be felt by the neighbouring neurons (Fig. 1). Neurons can be excitatory or inhibitory, depending on the effect of the connection (synapse) on the receiving neuron: inputs from an excitatory (inhibitory) neuron depolarize (hyperpolarize) the membrane potential of the receiving neuron.

Fig. 1

Schematic of a neuron with different synaptic connections. It can be seen how axon terminals from neighbouring neurons contact the dendrites of the receiving neuron

In this paper, we explore the oscillatory activity emerging from a neuronal network consisting of a single population of excitatory neurons and a single population of inhibitory neurons (E-I network). Under the appropriate stimulus, the firing of the excitatory population activates the inhibitory population that, on its turn, suppresses the excitatory activity. Once the inhibitory effect has vanished, if the stimulus remains, the excitatory neurons will fire again generating an oscillatory pattern. The excitability of the excitatory population is not the same for all the phases of the cycle due to the inhibitory action. Indeed, when the excitatory population receives an external input at the phase in which the inhibition is not present, the excitatory cells can respond effectively, while if the inhibition is present, the input might be ignored (see Fig. 2). This mechanism, known as communication through coherence, has been invoked to explain neural communication between brain areas [7]. In this context, two neuronal groups with underlying oscillatory activity communicate much effectively when they are properly phase-locked so that the windows for inputs and outputs are open at the same times. Although the functional role of the brain oscillations is still unknown, a growing number of studies have recently suggested that in several cognitive tasks (such as sensory perception, working memory, and attention), synchronized background oscillations may coordinate computations involving different brain areas [15].

Fig. 2

Oscillations arise from the interaction between the inhibition and the excitation. We illustrate how different phases of the oscillation may have different excitability properties due to the inhibition as suggested in [18]

A simplified framework for studying this situation is to consider the effect of an external oscillatory input onto a network model consisting of excitatory and inhibitory cells showing oscillations. For such network we consider the simplest canonical model describing the mean firing rates of the excitatory and inhibitory populations: the Wilson–Cowan equations [20]. As the parameters of this model can be chosen so that the system shows oscillations we can simulate the framework of interest.

In particular, we focus on oscillations of the Wilson–Cowan model arising from a Hopf bifurcation. The periodic forcing of such bifurcation has been studied in classical papers [9], and recently, in the neuroscience context [19]. In this work, we aim to understand the different mechanisms which give rise to synchronous activity between the E-I network and the external $T'$-periodic input. As we study a periodic perturbation, we consider the stroboscopic map (i.e. the time-$T'$ map of the flow) and identify an attracting invariant curve of the map, where the dynamics on it can be understood by means of the rotation number. The rotation number indicates the relationship between the period of the forced oscillator and the external forcing; rational values of this magnitude correspond to synchronous regions while irrational values correspond to asynchronous regions. Thus, assuming the existence of an invariant curve, we compute the rotation number as the amplitude and the frequency of the external periodic input are varied and identify the synchronous solutions. We also identify regions where this computation fails, which correspond to the breakdown of the invariant curve. To provide a full understanding of the dynamics beyond the breakdown of the invariant curve, we compute the fixed points of the map as well as their bifurcations. Bifurcations of the fixed points can be related to the breakdown of the invariant curve. Thus, we apply powerful computational methods [11] to compute the invariant curve and its internal dynamics, which provide a framework that enlarges the comprehension of the dynamics generated by the periodic forcing.

2 Mathematical Model

A neuronal population can be modelled as a neuronal network consisting of N neurons connected through synapses. If each neuron is described by a system of n differential equations, a network of N neurons will be described by a system of $N \cdot n$ equations. This approach, although generates very accurate results, considers a high dimensional system, that requires a high computational effort to integrate it and makes the mathematical analysis difficult. As an alternative to this approach, there exist mean field models, which use a single variable to describe the mean activity of a population. These models have a reduced number of equations and are suitable for analysis. One of the most famous rate models are the Wilson–Cowan equations [20]:

Fig. 3

Schematic of a neuronal network modelled by the mean field model (1)

$$\begin{aligned} \begin{aligned} \tau _e \frac{dE}{dt} = -E + (1-r_eE)S_e(c_1E - c_2I + P), \\ \tau _i \frac{dI}{dt} = -I + (1-r_iI)S_i(c_3E - c_4I + Q), \end{aligned} \end{aligned}$$

(1)

where the variables E and I correspond to the fraction of neurons of the excitatory and the inhibitory populations respectively which are emitting an action potential at time t. The coupling constants $c_i$ determine the strength of connexions between neuronal populations. P and Q are the (constant) external inputs which are injected to E and I populations, respectively (see Fig. 3). Coupling constants $c_i$ are positive, whereas external currents P and Q can be either positive or negative depending whether its action is excitatory or inhibitory.

Assuming that a population k is receiving an input x, the proportion of cells which will fire as a result of this input is modelled by the response function $S_k(x)$, a sigmoidal function defined as:

$$\begin{aligned} S_k(x) = \frac{1}{1+e^{-a_k(x-\theta _k)}}, \quad \quad \quad \quad \quad \quad \text{ with } \quad k = e, i, \end{aligned}$$

where the parameters $\theta _k$ and $a_k$ are the position of the maximum slope and the value of this maximum slope, respectively.

Neurons have a refractory period $r_k$ during which they can not respond to external inputs. The factor $(1-r_kk)$ in Eq. (1), represents the proportion of neurons of the population k which are able to be excited. In [14] it is shown how this term only rescales the parameters on the nonlinearities $S_k(x)$ and does not change the qualitative behaviour of the system. For this reason, from now on, we will consider $r_k = 0$.

2.1 Dynamical Analysis

In this subsection we study the most important objects (critical points and limit cycles) of system (1) and their bifurcations. Nullclines of (1), when $r_e = r_i = 0$, are given by

$$\begin{aligned} \begin{aligned} E = f_e(I, Q) = \frac{1}{c_3}[S_i^{-1}(I) + c_4I - Q],\\ I = g_i(E, P) = \frac{1}{c_2}[c_1E - S_e^{-1}(E) + P]. \end{aligned} \end{aligned}$$

(2)

As it can be seen in Eq. (2), P and Q translate nullclines and thus determine their intersection. Consequently, the name and position of the critical points of the system will depend on the values of P and Q (Fig. 4 left). For this reason parameters P and Q will be considered as bifurcation parameters.

Choosing the set of constants adequately, the Wilson–Cowan equations show oscillatory behaviour [20]. In particular, as it can be seen in Fig. 4 (right), oscillations in the Wilson–Cowan model reproduce the oscillatory mechanism stated in the introduction: for a strong enough input value P, the excitatory activity will increase, activating the inhibitory cells which, in its turn, will suppress the excitatory activity and in consequence, the inhibitory activity. Once the inhibitory effect has vanished, the external input P –if still present–, will activate the excitatory cells again, generating an oscillatory pattern. The following set of parameters $\mathscr {P}$ ensures the existence of oscillations for some (P, Q) stimulus values and for this reason they will be the default parameters used throughout the work:

$$\begin{aligned} \begin{aligned} \mathscr {P} = \{&c_{1}=13, c_2=12, a_e=1.3, \theta _e = 4, r_e=0, \tau _e=1\\&c_3=6, \ c_4=3, \ a_i=2, \ \theta _i = 1.5, \ r_i=0, \ \tau _i=1 \}. \end{aligned} \end{aligned}$$

(3)

Fig. 4

Left: Nullclines and phase space for the set of parameters $\mathscr {P}$ given in (3) and (P, Q) = (2.5, 0). There exists a limit cycle $\gamma$ and an unstable focus $P_1$. Right: Dynamics for system (1) over the limit cycle $\gamma$. The oscillations arise from the interactions between the excitatory inhibitory populations

As system (1) is 2-dimensional and the phase space is bounded, using Poincaré-Bendixon theorem it is enough to require that the system has a unique unstable critical point to guarantee the existence of a periodic orbit (oscillations). Such oscillations are going to appear across Hopf, Saddle-Node on Invariant Circle (SNIC bifurcation) and Homoclinic bifurcation  [3, 12]. As a first step to find these bifurcations we look for bifurcations of the critical points of the system. Thus, by defining DX(E, I, P, Q) the Jacobian matrix of system (1), we can look for points (E, I, P, Q) satisfying (2) and conditions Tr $DX(E, I, P, Q) = 0$ for the Hopf bifurcation and Det $DX(E, I, P, Q) = 0$ for the Saddle-Node bifurcation. As we are dealing with non linear equations, the computation of the bifurcation diagram (Fig. 5) requires computational methods for continuation of curves [17].

Fig. 5

Bifurcation diagram for the Wilson–Cowan system (1) as a function of external stimulii P and Q. Parameters for system (1) are given by the set $\mathscr {P}$ in (3)

3 Non Autonomous Perturbation

In this section we will study the effects of a $T'$-periodic non-autonomous perturbation onto the Wilson–Cowan equations (1). Concretely we will study the following model:

$$\begin{aligned} \begin{aligned} \tau _e \frac{dE}{dt}&= -E + S_e(c_1E - c_2I + P + A p(t)), \\ \tau _i \frac{dI}{dt}&= -I + S_i(c_3E - c_4I + Q), \end{aligned} \end{aligned}$$

(4)

where A is the amplitude of the perturbation and p(t) is the $T'$-periodic function:

$$\begin{aligned} p(t) = 1 + \cos (\frac{2\pi t}{T'}), \end{aligned}$$

modelling the activity of an external excitatory population.

3.1 The Stroboscopic Map

The stroboscopic map is the most natural approach when considering the study of $T'$-periodic perturbations. It is defined by

$$\begin{aligned} F_{A}:\mathbb {R}^{2}\rightarrow & {} \mathbb {R}^{2}, \nonumber \\ x\rightarrow & {} F_{A}(x) = \phi _A(t_0 + T'; t_0, x), \end{aligned}$$

(5)

where $\phi _A(t; t_0, x)$ is the solution of (4) such that $\phi _A(t_0; t_0, x) = x$.

As it is well known, the fixed points and invariant curves of the stroboscopic map (5) correspond to periodic and quasiperiodic solutions of system (4) respectively. For instance, if $\gamma (t) = \phi _A(t; t_0, x)$ is a solution of system (4) and $[F_A(x)]^q = x$, then by definition $\phi _A(t_0 + qT'; t_0, x) = x$ and therefore $\gamma (t)$ is periodic of period $qT'$. Analogously, if $\gamma (t) = \phi _A(t; t_0, x)$ is a periodic orbit of period T of (4) with $\frac{T'}{T}=\frac{p}{q}$, $p,q \in \mathbb {N}$, then

$$\begin{aligned}{}[F_{A}(x)]^q = \phi _A(t_0 + qT'; t_0, x) = \phi _A(t_0 + pT; t_0, x) = x, \end{aligned}$$

(6)

that is, fixed points x for the map $[F_{A}(x)]^q$ will correspond to periodic orbits of the system (4). In the neuroscience context, relationship (6) indicates that a p:q phase locking state has been established between the population and the perturbation. In the Wilson–Cowan model this means that the neuronal population variables E and I have completed p revolutions in the same time that the perturbation p(t) has completed q revolutions. By contrast, if $\gamma (t) = \phi _A(t; t_0, x)$ is periodic of period T but $\frac{T'}{T} \notin \mathbb {Q}$, then $[F_{A}(x)]^n \ne x$ $\forall$ n $\in$ $\mathbb {N}$ and $[F_{A}(x)]^n$ fills densely $\varGamma _A = \{ \overline{\phi _A(t_0 + nT'; t_0, x), n \in \mathbb {N}} \}$ which is an invariant curve for $F_{A}(x)$. So, depending on the amplitude A and the period $T'$ of the perturbation, the system in (4) can display either a p:q synchronous regime synchronous regime or an asynchronous regime .

3.2 Computing the Rotation Number in the Perturbed Framework

In this section we will explain how to compute the rotation number. Consider the set of parameters $\mathscr {P}$ defined in (3), and let (P, Q) $=$ (2.5, 0). As bifurcation diagram on Fig. 5 shows, for this set of parameters the unperturbed Wilson–Cowan equations (1) display an unstable focus $P_1$ and an attracting limit cycle $\gamma$ of period $T \approx 5.26$.

When $A=0$ the phase portrait described by the stroboscopic map (5) is the same as the one generated by the unperturbed system (1). In particular, $F_0(P_1) = P_1$ and $F_0(\gamma ) \subseteq \gamma$, $\forall$ $T'$, that is, $P_1$ and $\gamma$ are an unstable fixed point and an attracting invariant curve for the map (5), respectively. When applying a $T'$-periodic continuous perturbation, as both objects $P_1$ and $\gamma$ are normally hyperbolic, they will continue existing for weak enough perturbations, and they can be studied as invariant objects for the stroboscopic map $F_{A}$ when $A \ne 0$. In particular, while the unstable focus $P_1 = P_1(A)$ will remain an unstable fixed point for the stroboscopic map $F_{A}$, the attracting limit cycle $\gamma$ will become an attracting invariant curve $\varGamma _A$. Over the invariant curve $\varGamma _A$ we can define and compute the rotation number.

The rotation number is defined for any continuous orientation preserving map of the circle

$$\begin{aligned} \begin{aligned} f:\mathbb {T}&\rightarrow \mathbb {T}\\ \theta&\mapsto f(\theta ) \end{aligned} \end{aligned}$$

as

$$\begin{aligned} \rho = \lim _{n\rightarrow \infty } \frac{\theta _n - \theta _0}{n}, \quad \quad \quad \theta _n = f^n(\theta _0). \end{aligned}$$

(7)

As it is well known, $\rho$ exists and is independent of the point $\theta _0$ [1]. Moreover, if $\rho = \frac{p}{q} \in \mathbb {Q}$, the map f has, at least, one periodic point $\theta ^*$ of period q. On the other hand, under some regularity assumptions, if $q \in \mathbb {R} \setminus \mathbb {Q}$, the map f is conjugated to a rotation of angle $\rho$ and the orbit of every point $\theta$ fill densely $\mathbb {T}$.

In our case, one can take $f := f_A = F_{A |_{\begin{array}{c} \varGamma _A \end{array}}}$ and compute the rotation number as follows: given a point $x \in \varGamma _A$, define the angle $\theta$ between the line from $P_1(A)$ to x and the positive E-axis. Then, given a point $x_0 \in \varGamma _A$ for $x_n = f_{n}^{A}(x_0)$, one can compute the rotation number in (7).

When computing $\rho$ numerically, usually the limit to infinity is substituted by a large enough number of iterations but the convergence to $\rho$ is very slow. We used the methods presented in [16], which refine the computation of rotation numbers saving computational effort and accelerating the convergence of the method.

Recall that if $\rho = \frac{p}{q}$ with $p,q \in \mathbb {N}$ there exists a $\theta ^*$ such that $f_{A}^q(\theta ^*) = \theta ^*$, and the corresponding point $x^*$ is a q-periodic orbit of $F_A$, which turns p times around the invariant curve $\varGamma _A$. This indicates the appearance of a given p:q phase locking regime in system (4).

In Fig. 6 we show the computation of the rotation number for some amplitude values A and varying $T'$. We observe the classical Devil’s Staircase function [1]. The function shows intervals on the x-axis (showing the ratio $\frac{T'}{T}$) for which the rotation number $\rho (T')$ is constant (there exists a solution of (4) which is phase-locked to the periodic perturbation). For small positive amplitudes, the largest intervals correspond to the phase locked states 1:1 ($\rho =1$) and 1:2 ($\rho =\frac{1}{2}$) (Fig. 6 top). The phase-locked intervals widen as the amplitude is increased (Fig. 6 bottom). The rotation number displays a discontinuity at some values of $T'$ jumping suddenly to $\rho =1$ as the amplitude is increased. As the rotation number is defined over the invariant curve $\varGamma _A$, this discontinuity may indicate a bifurcation or the breakdown of the invariant curve appearing for non-weak amplitudes that we will investigate in the next sections.

Fig. 6

Rotation number computed for different amplitudes in the perturbed Wilson–Cowan model (4). Parameters used were the set $\mathscr {P}$ in (3), and (P, Q) $=$ (2.5, 0)

3.3 Bifurcation Analysis

In order to understand the dynamics that occur in system (4) depending on the period $T'$ and the amplitude A of the perturbation, we will begin by computing bifurcations for the fixed points of the stroboscopic map (5).

Given a map depending in one parameter $\alpha \in \mathbb {R}$:

$$\begin{aligned} \begin{aligned} F:\mathbb {R}^n \times \mathbb {R}&\rightarrow \mathbb {R}^n\\ (x, \alpha )&\rightarrow F(x,\alpha ). \end{aligned} \end{aligned}$$

(8)

If there exists ($x_0, \alpha _0$) such that

• 1. $F(x_0, \alpha _0) = x_0$

• 2. $DF(x_0, \alpha _0)$ has eigenvalues $\lambda$ with $|\lambda | \ne 1$,

then $x_0$ is called a hyperbolic fixed point and it is known that for $\alpha \simeq \alpha _0$, there exists $x_{\alpha }$ fixed point of $F(x_{\alpha },\alpha )$ of the same topological type of $x_0$. Otherwise, when (2) fails we call $\alpha _0$ a bifurcation value.

Thus, bifurcation values of the map F must satisfy being fixed points of the map (8) and also a bifurcation condition $\varPhi _{BIF}$. Mathematically,

$$\begin{aligned} G(x, \alpha ) = {\left\{ \begin{array}{ll} F(x,\alpha ) - x = 0 \\ \varPhi _{BIF}(x,\alpha ) = 0. \end{array}\right. } \end{aligned}$$

(9)

We look for bifurcations of the fixed points of the map defined in (6) for $q=1$. We found two bifurcations of fixed points (see Fig. 7): Saddle-Node (SN) and Neimark-Sacker (NS). At it is well known, a SN bifurcation occurs when one of the real eigenvalues for the fixed point equals one, whereas a NS bifurcation occurs when a fixed point has a pair of complex eigenvalues whose modulus equals one. In a 2D system the conditions which must be satisfied at these bifurcation values are written as

$$\begin{aligned} \varPhi _{SN}= & {} det(DF - Id) = 0, \\ \varPhi _{NS}= & {} Tr(DF) - 1 = 0, \end{aligned}$$

where we denote by DF the Jacobian matrix of the map F evaluated at the fixed point, whose computation requires the integration of a second order variational system [17].

Fig. 7

Bifurcation diagram for the stroboscopic map $F_A$ of the perturbed Wilson–Cowan system (4). Parameters used were the set $\mathscr {P}$ and (P, Q) = (2.5, 0). Two bifurcations were found: Neimark-Sacker (green curve) and Saddle-Node (cyan curve). The solid line corresponds to a SN between a saddle and a stable node whereas the dashed line corresponds to a SN between a saddle and an unstable node. Constant amplitudes, for which rotation numbers in Fig. 6 were computed, were drawn respecting the same color code. Inside the yellow area there exists a stable fixed point for the map $F_A$ corresponding to a 1:1 phase locking relationship

Computations depicted in Fig. 7 also enlight the rotation number results shown in Fig. 6. One guesses that discontinuities on the rotation number in Fig. 6 can be caused by the disappearance of the invariant curve (which exists for small amplitudes) across a Neimark-Sacker bifurcation. To give a complete description of the dynamics, besides the computation of the fixed points and its bifurcations we are going to compute the invariant curves to check its persistence and relate its disappearance with the discontinuities observed in the rotation number curves.

3.4 Computation of Invariant Curves

As it was observed in Sect. 3.3, the computation of invariant curves is needed to provide a full description of the dynamics generated by the perturbation in (4). The framework developed in [5] allows us to compute a parameterization of the invariant curve $\varGamma _A$ issuing from the unperturbed limit cycle $\gamma$. We now briefly review the method and refer the reader to [5] for a detailed description of the method.

Given a map $F: \mathbb {R}^2 \rightarrow \mathbb {R}^2$ having an invariant curve $\varGamma _A$, we look for a parameterization $K : \mathbb {T} \rightarrow \mathbb {R}^2$ of this invariant curve by solving the following invariance equation

$$\begin{aligned} F(K(\theta )) = K(f(\theta )), \end{aligned}$$

(10)

where $K(\theta )$ and the dynamics inside the curve $f(\theta )$ are both unknown. Differentiating (10) we find the invariance equation for the tangent bundle $DK(\theta )$:

$$\begin{aligned} DF(K(\theta ))DK(\theta ) = DK(f(\theta ))Df(\theta ), \end{aligned}$$

(11)

and imposing the invariance of the normal (stable) bundle of $K(\theta )$, denoted by $N(\theta )$, we have the following invariance equation

$$\begin{aligned} DF(K(\theta ))N(\theta ) = N(f(\theta ))\varLambda _N(\theta ), \end{aligned}$$

(12)

where $\varLambda _N(\theta )$ denotes the linearised dynamics over $N(\theta )$.

In order to express in a more compact way the invariance equations (11) and (12) we introduce the matrices $P(\theta ) = \begin{pmatrix} DK(\theta )&N(\theta ) \end{pmatrix}$, and $\varLambda (\theta ) = \text {Diag}(Df(\theta ), \varLambda _N(\theta ))$:

$$\begin{aligned} DF(K(\theta ))P(\theta ) = P(f(\theta )) \varLambda (\theta ). \end{aligned}$$

(13)

Therefore, if we express the linear map $DF(K(\theta ))$ in the basis provided by $P(\theta )$, it becomes diagonal. Taking profit of this adapted invariant frame, a Newton method is performed. As it is usual in Newton methods, we assume given the approximation for the unknowns $K(\theta )$, $f(\theta )$, $N(\theta )$ and $\varLambda _N(\theta )$ and we compute better approximations:

$$\begin{aligned} \bar{K}(\theta )= & {} K(\theta ) + \varDelta K(\theta ),\end{aligned}$$

(14)

$$\begin{aligned} \bar{f}(\theta )= & {} f(\theta ) + \varDelta f(\theta ),\end{aligned}$$

(15)

$$\begin{aligned} \bar{N}(\theta )= & {} N(\theta ) + \varDelta N(\theta ),\end{aligned}$$

(16)

$$\begin{aligned} \bar{\varLambda }_N(\theta )= & {} \varLambda _N(\theta ) + \varDelta \varLambda _N(\theta ). \end{aligned}$$

(17)

To determine the correction terms $\varDelta K(\theta )$, $\varDelta f(\theta )$, $\varDelta N(\theta )$, $\varDelta \varLambda _N(\theta )$, the Newton method performed is split in two substeps. In the first one, we look for corrections $\varDelta K(\theta )$ and $\varDelta f(\theta )$. We begin by substituting expressions (14) and (15) into the invariance equation (10), and then expanding in Taylor series around K and f respectively and neglecting quadratically small terms, we obtain

$$\begin{aligned} 0 = E(\theta ) + DF(K(\theta )) \varDelta K(\theta ) - DK(f(\theta ))\varDelta f(\theta ) - \varDelta K(f(\theta )) \end{aligned}$$

(18)

where $E(\theta ) = F(K(\theta )) - K(f(\theta ))$ is the error for the approximated solution.

Writing Eq. (18) in the adapted frame provided by $P(\theta )$, that is, writing $\varDelta K(\theta ) = P(\theta )\xi (\theta )$, we obtain the following cohomological equation

$$\begin{aligned} \eta (\theta ) = \varLambda (\theta )\xi (\theta ) - \xi (f(\theta )) -\begin{pmatrix}\varDelta f(\theta ) \\ 0\end{pmatrix} \end{aligned}$$

where $\eta (\theta ) = -(P(f(\theta )))^{-1}E(\theta )$ is the error of the approximate solution in the adapted frame. $\eta (\theta )$ is a vector which has tangent and normal components, each of them having different equations

$$\begin{aligned} \eta ^{T}(\theta )= & {} {\varLambda _T}(\theta )\xi ^{T}(\theta ) - \xi ^{T}(f(\theta )) - \varDelta f(\theta ),\\ \eta ^{N}(\theta )= & {} {\varLambda _N}(\theta )\xi ^{N}(\theta ) - \xi ^{N}(f(\theta )), \end{aligned}$$

where unknowns $\xi ^{T}$ and $\xi ^{N}$, can be computed separately by means of a fixed point method.

So far, we have find the corrections $\varDelta K(\theta )$ and $\varDelta f(\theta )$. Then one can proceed to the second substep of the Newton method. Analogously to the first substep, by substituting the Eqs. (16) and (17) in the invariance equation (12) and applying the same methodology as in the first substep one can find the new corrections for the normal bundle $\varDelta N(\theta )$ and its linearised dynamics $\varDelta \varLambda _N(\theta )$. See [5] for more details.

We have reviewed the principal steps of the method. Next we are going to provide some details about the computation of the initial seeds for the Newton method in our problem. For a small perturbation, one can use as initial seed the invariant curve for the unperturbed system. Having an unperturbed system which displays a limit cycle $\gamma (t)$ of period T, we can define $\theta = \frac{t}{T}$ as an angular variable which parameterizes the limit cycle $\varGamma _0(\theta ) = \gamma (\theta T)$. Therefore, as initial seed for the parameterization K and the dynamics on it when A is small we will take $K_0(\theta ) = \varGamma _0(\theta )$ and $f_0(\theta ) = \theta + \frac{T'}{T}$.

In order to find an initial seed for the normal bundle and its dynamics, we need to compute the derivative of the limit cycle respect its normal bundle direction. For that aim we use methods in [10], which provide an analytical solution for the value of that derivative. In particular they parameterize the stable manifold $\mathscr {M}$ of the unperturbed limit cycle $\gamma$ by using an angular variable $\theta$ over the limit cycle and a variable $\sigma$ which moves in the transverse direction to the limit cycle. Dynamics of both variables $\theta$ and $\sigma$ are given by:

$$\begin{aligned} \begin{aligned} \dot{\theta }&= 1/T,\\ \dot{\sigma }&= \lambda \sigma /T, \end{aligned} \end{aligned}$$

(19)

where T and $\lambda$ are the period and the characteristic exponent of the limit cycle $\gamma$ respectively. By using variables $\theta$ and $\sigma$ we look for a parameterization for $\mathscr {M}$ $K(\theta , \sigma )$ such that, by (19):

$$\begin{aligned} \left( \frac{1}{T}\partial _{\theta } + \frac{\lambda \sigma }{T}\partial _{\sigma }\right) K (\theta , \sigma ) = X(K (\theta , \sigma )), \end{aligned}$$

(20)

where X is the vector field (1). Expanding $K(\theta , \sigma )$ one gets:

$$\begin{aligned} K(\theta , \sigma ) = K_0(\theta ) + \sigma K_1(\theta ) + \mathscr {O}({\sigma }^2), \end{aligned}$$

(21)

were it is clear that $K_0 = \varGamma _0$, and by using (19) it is easy to see that

$$\begin{aligned} F(K(\theta , \sigma )) = K\left( \theta + \frac{T'}{T}, \sigma e^{\frac{\lambda T'}{T}}\right) , \end{aligned}$$

(22)

and therefore, differentiating (22) respect to $\sigma$:

$$\begin{aligned} \frac{\partial F(K(\theta , \sigma ))}{\partial \sigma }_{|_{\begin{array}{c} \sigma =0 \end{array}}} = DF(K_0(\theta )) K_1(\theta ) = e^{\frac{\lambda T'}{T}} K_1(\theta ), \end{aligned}$$

(23)

and comparing expressions (23) and (12) it is clear that over the unperturbed limit cycle, $N(\theta ) = K_1(\theta )$ and $\varLambda _N(\theta ) = e^{\frac{\lambda T'}{T}}$.

In [10] is demonstrated that to obtain $K_1(\theta )$ is only necessary to compute the fundamental matrix $\varPhi (t)$ ($\varPhi (0)=Id$), of the variational equations on the periodic $\gamma (t)$. Then, if we denote by v the eigenvector of the monodromy matrix $\varPhi (T)$ associated to the eigenvalue $e^{\lambda }$, $K_1(\theta )$ is given by $K_1(\theta ) = e^{-\lambda \theta } \varPhi (T \theta ) v$.

In order to explain rotation number discontinuities we apply this method to compute invariant curves for system (4) which complete the bifurcation diagram analysis in Fig. 7. If we fix $\frac{T'}{T} = 0.965$ we expect to cross a SN bifurcation for an amplitude $A_{SN} \simeq 0.014$. This is exactly what Fig. 8 shows: for a value of $A = 0.01 < A_{SN}$ there exists an invariant curve whose dynamics have no crossings with the fixed points of $f(\theta ) = \theta$. By contrast for $A = 0.02 > A_{SN}$ two crossings appear between $f^A(\theta )$ and $f(\theta ) = \theta$ indicating the presence of two fixed points over the invariant curve. This can be seen in another way when looking at the rotation number results: for $A = 0.01$ rotation number was different from 1, whereas it was equal to 1 for $A = 0.02$ which showed fixed points.

Fig. 8

(Left) Invariant curve for the stroboscopic map with different amplitudes and $\frac{T'}{T}$ = 0.965. (Right) Dynamics $f(\theta )$ over the invariant curve

By contrast when fixing $\frac{T'}{T} = 0.85$ a NS bifurcation is expected to be crossed at $A \simeq 0.062$. This is exactly what Fig. 9 shows: as the amplitude is increased, the invariant curve shrinks, but there are no crossings between the dynamics $f^A(\theta )$ and the line of fixed points. These results are consistent with rotation number results in Fig. 6. When looking at values of $\rho$ at $\frac{T'}{T} = 0.85$, when $A = 0.05 < A_{NS}$ a rotation number different from one appears as it is expected in an invariant curve with no fixed points over it. By contrast, for $A = 0.07 > A_{NS}$ as there is no invariant curve, rotation number calculations do not work. Nevertheless, a value for $\rho (0.85) = 1$ was computed. This result is a consequence of having a fixed point dynamics calculated assuming that an orientation preserving map is defined. So, although the dynamics tend to a fixed point we assume that each iteration of the map gives a complete revolution before returning to the fixed point.

Fig. 9

(Left) Invariant curve for the stroboscopic map with different amplitudes and $\frac{T'}{T}$ = 0.85. (Right) Dynamics $f(\theta )$ over the invariant curve

4 Dynamics of the Stroboscopic Map

Section 3 was devoted to the introduction of the stroboscopic map, its invariant objects and its bifurcations, providing techniques to compute all of them. In this section we aim at using all the tools provided in Sect. 3 to give a full description of the stroboscopic map dynamics for the perturbed system (4) close to the 1:1 phase-locking area by describing the evolution of all invariant objects of the system. Finally, will distinguish asynchronous from synchronous areas and study its implications for neuroscience.

4.1 Phase Space Analysis

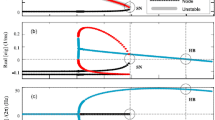
As the bifurcation analysis in Fig. 7 shows, there exist two possible bifurcations depending on the period $T'$ and the amplitude of the perturbation: a Neimark-Sacker (NS) and a Saddle-Node (SN) bifurcation. Moreover, a Bogdanov-Takens bifurcation occurs at (A, $\frac{T'}{T}$) $\simeq$ (0.023, 0.9388) delimiting the NS and SN bifurcation curves. As different bifurcations will generate different dynamics, we will present phase portraits for the stroboscopic map at the crossing of both bifurcations in order to provide a description of the dynamics of the system (4) close to resonance 1:1. More precisely, we will restrict the analysis of dynamics to the range of $\frac{T'}{T}$ values that we have shown in Fig. 7, this is from 0.8 to 1 where the rotation number presented discontinuities.

Fig. 10

Dynamics when a Saddle-Node bifurcation is crossed. Fixed points and invariant curves were computed using provided numerical methods

For values of $T'$ such that 0.9388 $< \frac{T'}{T}<$ 1, the phase portrait for system (4) can be seen in Fig. 10. In region $A_1$, the attracting invariant curve $\varGamma _A$ generated from unperturbed limit cycle $\gamma$ has no fixed points of $F_A$, and an unstable focus $P_1$ exists inside $\varGamma _A$. Once the Saddle-Node bifurcation (solid blue line) is crossed (region B), there appear two fixed points on the invariant curve $\varGamma _A$: a stable node $P_2$ and a saddle $P_3$. The invariant curve consists of the union of the saddle $P_3$, its unstable invariant manifolds, and the stable node $P_2$. When increasing the amplitude (region C), $P_1$ becomes an unstable node (dashed gray line). If the amplitude is increased further, $P_1$ will coalesce with $P_3$ in a unstable Saddle-Node bifurcation (dashed blue line) leaving the stable node $P_2$ as the unique fixed point (region D). As one may note it is possible to pass from area $A_1$ to area C, without passing from B. When entering in the area $A_2$ the unstable focus $P_1$ can become an unstable node before crossing the SN bifurcation.

Fig. 11

Dynamics when a Neimark-Sacker bifurcation is crossed. Fixed points and invariant curves were computed using provided numerical methods

For values of $T'$ such that 0.8 $< \frac{T'}{T}<$ 0.9388, the phase portrait for system (4) can be seen in Fig. 11. The attracting invariant curve $\varGamma _A$ has no fixed points of $F_A$, and an unstable focus $P_1$ exists inside $\varGamma _A$ (region A). As the amplitude A is increased, this situation persists until we reach the Neimark-Sacker bifurcation (green curve), where the curve $\varGamma _A$ collapses with $P_1$ and disappears while $P_1$ becomes a stable focus (region B).

Phase space analysis performed gives a fully understanding of the dynamics for the perturbed system (4), demonstrating the presence of a fixed point for the map $F_A$ and thus explaining discontinuities and results for rotation number. For a given amplitude, discontinuities in the rotation number are expected to appear for the exact value of $\frac{T'}{T}$ for which a NS bifurcation appears.

4.2 From Synchronous to Asynchronous Behaviour

As fixed points for the stroboscopic map correspond to periodic orbits of the system (4), the disappearance of stable fixed points across bifurcations separates the synchronous from the asynchronous regime. Computing the bifurcation curves of system (4) is the most natural way for delimiting and studying a given phase locking relationship. In Fig. 12 we show the stable solutions for a synchronous and an asynchronous state. It can be seen how the phase or time lag between the system and the perturbation is constant in the synchronous regime whereas it is not the case in the asynchronous.

Fig. 12

(Top) Synchronous solution of system (4) for $A = 0.02$ and $\frac{T'}{T} = 0.965$. (Bottom) Asynchronous solution of system (4) for $A = 0.04$ and $\frac{T'}{T} = 0.85$

As various theories suggest synchrony between oscillating activity of two neuronal populations may have very important implications in neural communication [13]. In particular, this time lag difference may underlie a possible mechanism for selection of transmitted information [8].

5 Summary

We have considered a periodic perturbation of the Wilson–Cowan equations and we have looked for synchronous and asynchronous regimes. In particular, we have studied phase locking relationships through the rotation number. Computations of this magnitude showed discontinuities which have been understood through the computation of the main invariant objects (fixed points and invariant curves) of the stroboscopic map close to the resonance 1:1. We have shown how powerful computational methods for invariant curves provide a further understanding of the dynamics generated by a periodic perturbation. Thus, this work aims at providing powerful tools to study interactions of brain rhythms in the brain.