Abstract
We consider the following strong variant of private information retrieval (PIR). There is a large database x that we want to make publicly available. To this end, we post an encoding X of x together with a short public key \(\mathsf{pk}\) in a publicly accessible repository. The goal is to allow any client who comes along to retrieve a chosen bit \(x_i\) by reading a small number of bits from X, whose positions may be randomly chosen based on i and \(\mathsf{pk}\), such that even an adversary who can fully observe the access to X does not learn information about i.
Towards solving this problem, we study a weaker secret key variant where the data is encoded and accessed by the same party. This primitive, that we call an oblivious locally decodable code (OLDC), is independently motivated by applications such as searchable symmetric encryption. We reduce the public-key variant of PIR to OLDC using an ideal form of obfuscation that can be instantiated heuristically with existing indistinguishability obfuscation candidates, or alternatively implemented with small and stateless tamper-proof hardware.
Finally, a central contribution of our work is the first proposal of an OLDC candidate. Our candidate is based on a secretly permuted Reed-Muller code. We analyze the security of this candidate against several natural attacks and leave its further study to future work.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
A private information retrieval (PIR) protocol allows a client to retrieve an item from a remote database while hiding which item is retrieved even from the servers storing the database. PIR has been studied both in a multi-server setting, where security should only hold against non-colluding servers [9, 10], and in a single-server setting [27]. In both settings, the main focus of the large body of work on PIR has been on minimizing the communication complexity.
Improving the computational complexity of PIR turned out to be much more challenging. If no preprocessing of the database is allowed, the computational complexity of the servers must be at least linear in the database size [4]. While preprocessing was shown to be helpful in the multi-server setting [4], the existence of sublinear-time single-server PIR protocols has been a longstanding open question, with no negative results or (even heuristic) candidate solutions.
In this work we consider the following strong variant of sublinear-time PIR that we call public-key PIR (pk-PIR). Suppose we want to allow efficient and privacy-preserving access to a large database \(x\in \{0,1\}^n\). To this end, we encode x into a (possibly bigger) database \(X=(X_1,\ldots ,X_N)\) and post X together with a short public key \(\mathsf{pk}\) in a publicly accessible repository. We want to allow any client who comes along to retrieve a chosen bit \(x_i\) by reading a small number of bits from X (sublinear in n), where the positions of these bits may be randomly chosen based on i and \(\mathsf{pk}\). (Note that X can be over any alphabet, but the total number of bits read by the decoder should be o(n).) More concretely, there is a randomized decoder that given i and \(\mathsf{pk}\) picks a small set \(I\subset [N]\) of positions to be read, and using \(X_I\), \(\mathsf{pk}\), and its secret randomness recovers \(x_i\).
We would like to achieve the following strong security guarantee: even an adversary who knows \(\mathsf{pk}\) and can fully observe the access to X, including both the positions I and the contents \(X_I\) of symbols being read, does not learn information about i. Since we are interested in efficient solutions that transfer less than n bits of information, one should settle for computational (rather than information-theoretic) security against computationally bounded observers [10].
Our notion of pk-PIR can be viewed as a variant of single-server PIR with preprocessing [4] (see Sect. 1.1 for a detailed discussion). It can also be viewed as a variant of oblivious RAM (ORAM) [19] which is weaker in that it only supports “read” operations, but is qualitatively stronger in that the same encrypted database can be repeatedly used without being updated. Unlike the standard notion of ORAM, pk-PIR can support a virtually unlimited number of accesses by an arbitrary number of stateless clients who do not trust each other. An efficient realization of pk-PIR can be extremely useful for enabling privacy-preserving public access to a large static database.
Main tool: OLDC. We reduce pk-PIR to the design of a new primitive that we call an oblivious locally decodable code (OLDC). Intuitively, OLDC can be thought of as a simpler secret-key variant of pk-PIR. An OLDC encoder randomly maps the database x into an encoded database X by using a short secret key \(\mathsf{sk}\). The decoder may use \(\mathsf{sk}\) to determine the set I of symbols of X it reads and also for recovering \(x_i\) from \(X_I\), where the same key \(\mathsf{sk}\) can be used for polynomially many invocations of the decoder. As in pk-PIR (and standard LDC), we require the decoder to have sublinear locality, namely to read o(n) bits of X. There are two significant differences in the notion of security. First, the observer does not have access to the secret key \(\mathsf{sk}\) used for decoding. Second, it does not even have access to the contents of the symbols \(X_I\). All the observer can see is the positions I of the symbols being read.
On the non-triviality of OLDC. The relaxed security goal makes OLDC conceivably easier to realize than pk-PIR. However, whether such OLDC exists is still far from obvious. In fact, one might be tempted to try to prove that OLDC is just too strong to exist. In Appendix A we argue that ruling out the existence of OLDC is unlikely, as it would require proving strong data structure lower bounds that seem beyond the reach of current techniques.
On the other hand, there is also no hope to prove the existence of OLDC unconditionally; in fact, we prove that any OLDC implies a one-way function. Another source of non-triviality comes from the following general property of OLDC. With overwhelming probability over the choice of \(\mathsf{sk}\), the encoder and (probabilistic) decoder defined by \(\mathsf{sk}\) should satisfy the following requirement: the probability that a given codeword symbol is read by the decoder is essentially independent of the query index i. Using known results, this means that any OLDC can be easily converted into a closely related “smooth code”Footnote 1 [24], or even into a standard LDC that allows for local decoding in the presence of a constant fraction of errors [26]. Since there is only a handful of known smooth code and LDC constructions, this severely limits the pool of potential OLDC candidates.
On the usefulness of OLDC. Unlike standard notions of PIR (but similarly to ORAM), OLDC does not apply to the case of publicly accessible data, in the sense that a client who has the key to access the encoded data can learn the queries i of others who access the same encoded data. However, OLDC can still be useful in many application scenarios. For instance, by applying an OLDC on top of a data structure (e.g., one supporting near-neighbor searches), one can implement general forms of searchable symmetric encryption [13, 36], avoiding the access pattern leakage of current practical approaches without the need to update the encoded data as in an ORAM-based approach.
From OLDC to pk-PIR. Before describing our candidate OLDC construction, we explain the transformation from OLDC to pk-PIR. Conceptually, the transformation is similar to an obfuscation-based construction of public-key encryption from secret-key encryption. The idea is to have the pk-PIR encoder produce an encrypted and authenticated version of the symbols of the OLDC encoding X, and emulate the OLDC decoder by obfuscating the code for generating I from i and \(\mathsf{pk}\) together with the code for recovering \(x_i\) from \(X_I\). An additional authentication mechanism is needed to ensure that the decoder is indeed fed with \(X_I\) for the same I it generated.
Unlike the simpler case of encryption [34], here we cannot instantiate the construction using indistinguishability obfuscation (iO). Instead, we need to rely on an ideal “virtual black-box” obfuscation primitive [3]. This primitive can be heuristically instantiated using existing iO candidates (e.g., the ones from [14, 15]) or provably instantiated by relying on ideal multi-linear maps [2]. Alternatively, the decoder can be implemented directly by using small and stateless tamper-proof hardware or a secure co-processor. The latter setting does not seem to trivialize the problem, and can potentially provide an implementable variant of our construction that is not curbed by the inefficiency of current software-based obfuscation methods.
An OLDC candidate. A central contribution of our work is the first proposal of an OLDC candidate, which we describe below. The encoding is just a secretly permuted version of a standard locally decodable code obtained from Reed-Muller codes (cf. [24]): the secret key defines a (pseudo-)random permutation, and the encoder applies a Reed-Muller encoding to x and then permutes the result according to the permutation defined by the secret key. The parameters are chosen such that decoding is done by probing \(O(\lambda \cdot n^{\epsilon })\) (permuted) points along a degree-\(\lambda \) curve, where \(\lambda \) is a security parameter and \(\epsilon >0\) can be an arbitrarily small constant that determines the (polynomial) storage overhead. Decoding is done via interpolation, where it is crucial that the interpolation points be kept secret to defeat a simple linearization attack we describe.
Assuming the security of this OLDC candidate, we get pk-PIR based on ideal obfuscation and one-way functions, where the client reads \(\mathsf{poly}(\lambda )\cdot n^\epsilon \) bits for an arbitrarily small constant \(\epsilon >0\). As noted above, ideal obfuscation can be heuristically replaced by existing iO candidates, leading to an explicit candidate construction of pk-PIR. Alternatively, it can be implemented by small and stateless tamper-proof hardware.
Roughly speaking, the security of our OLDC candidate reduces to an intractability assumption defined by a“randomized puzzle” obtained by first sampling polynomially many random low-degree curves (where each curve has a different color), and then randomly shuffling the pieces of the puzzle, i.e., the colored points of the space. The assumption is that it is hard to distinguish the shuffled pieces of the puzzle from pieces of a similar puzzle where the low-degree curves are replaced by high-degree curves, or even by totally random functions. Note that unlike standard physical puzzles, or computational puzzles that are motivated by problems such as DNA sequencing, the local independence property of random low-degree curves ensures that there is no local information to help determine whether two pieces are likely to fit next to each other.
Being unable to reduce the security of our OLDC candidate to any well studied assumption, we establish its plausible security by showing that it defeats several relevant types of attacks. This may be an inevitable state of affairs, as it is often the case in cryptography that ambitious new goals call for new assumptions. On the other hand, we show that several weaker variants of the construction can be broken by linearization attacks. This includes variants in which the global permutation is replaced by one that randomly permutes only one of the coordinates in the space.
Finally, it is useful to note that other ad-hoc pseudorandomness assumptions related to specific classes of efficiently decodable codes have successfully withstood the test of time. This includes the conjectured pseudorandomness of noisy Reed-Solomon codes [31] (despite early attacks on a specialized variant [6, 7]) and assumptions related to unbroken instances of the McEliece cryptosystem [28] (despite some broken variants [35]). In contrast, several attempts to base single-server PIR or public-key encryption on noisy Reed-Muller or Reed-Solomon codes have been irreparably broken [5, 11, 12, 25]. Our OLDC candidate does not fit in the latter category, since neither the OLDC primitive nor our concrete intractability assumption seem to imply single-server PIR or even public-key encryption.
Future directions. The problem considered in this work is a rare remaining example for a major “feasibility” goal in cryptography that is not clearly impossible to achieve, and yet is not readily solved by using an ideal form of obfuscation and standard cryptographic assumptions. The main question we leave open is that of further evaluating the security of our OLDC candidate, either by showing it insecure or by reducing its security (or the security of another candidate) to a well studied assumption. There is of course a third possibility that the candidate will survive the test of time and become “well studied” without a security reduction to an earlier assumption. A second natural open question is to obtain a construction of pk-PIR from OLDC via iO. Some evidence against this is given by the fact that single-server PIR cannot be based on iO and one-way functions using standard proof techniques [1]. Finally, it would be very interesting to come up with a direct candidate construction of pk-PIR that does not rely on any form of general-purpose obfuscation.
1.1 Related Work
Sublinear-time PIR. The question of PIR with sublinear server computation was first studied in [4]. The main model considered in [4] is that of PIR with polynomial-time preprocessing. This model allows each server to apply a one-time, polynomial-time preprocessing to the database in order to enable faster processing of queries.
Our notion of pk-PIR can be seen as a variant of the single-server model from [4] (Definition 2) with the following differences. Our model is more restrictive in that it does not allow the client to send a query which is answered by the server. This has the advantage of not requiring the data to be stored on a single computer—the encoded database can be dispersed over the network, or written “up in the sky” or on the pages of a book, and can be accessed by clients directly. By default, we also restrict the decoder to be non-adaptive (given the public key), whereas the general version of the model from [4] can use multiple rounds of interaction. On the other hand, our model is more liberal in that it allows the encoding of the database to be randomized. This randomization is essential for our solutions, even in the secret-key case of OLDC.
The results of [4] on PIR with preprocessing include a weak lower bound on the tradeoff between storage and server computation, positive results in the multi-server model, and a barrier to proving strong negative results for single-server solutions with adaptive queries (see Appendix A). They also obtain positive results for sublinear-time PIR in alternative models, including the case of amortizing the computational work required for processing multiple queries simultaneously and protocols with single-use preprocessing. The question of reducing the amortized computational cost of multi-query PIR was subsequently studied in [21, 22].
Other notions of keyed LDC. A very different notion of LDC with (private or public) keys was considered in [20, 33]. The goal of these works is to make use of the keys towards improving the efficiency of LDCs, rather than hide the access pattern.
1.2 Independent Work
The problem we consider has been independently studied by Canetti et al. [8]. The two works consider the same problem of sublinear-time PIR with preprocessing and propose similar candidate solutions based on secretly permuted Reed-Muller codes. The notion of OLDC (resp., pk-PIR) from the present work corresponds to the notion of designated-client (resp., public-client) doubly-efficient PIR from [8]. (In this work we make the additional restriction of non-adaptive queries.) We provide an overview of the main differences between the two works below.
The main contributions of [8] beyond those of this work include: (1) A different variant of the designated-client (OLDC) candidate in which the curve evaluation points used by the decoder are fixed (or made public) but some of the points on the curve are replaced by random noise. A combination of random noise with secret evaluation points is also proposed as a potentially more conservative candidate. (2) A search-to-decision reduction for a restricted case of the above fixed-evaluation-point variant, where the location of the noise elements is the same for all queries. (3) An efficient variant of the designated client scheme, that is secure in the bounded-query case assuming one way functions.
The main contributions of this work beyond those of [8] include: (1) A general transformation from (designated-client) OLDC to (public-client) pk-PIR by applying VBB obfuscation to the query generation algorithm and an authenticated version of the decoding algorithm. This yields an explicit candidate construction of pk-PIR. (2) Two types of barriers: A “data structures barrier,” suggesting that even a very strong form of pk-PIR, with deterministic encoder and non-adaptive queries, would be difficult to unconditionally rule out; and an “LDC barrier,” showing that OLDC implies traditional LDC, effectively imposing a limitation on the space of possible candidates. (3) Ruling out (under standard assumptions) a natural “learning” approach for generically breaking constructions based on secret linear codes, by using the power of span programs. (4) A proof that any OLDC implies a one-way function.
2 Preliminaries
Notation. The security parameter is denoted by \(\lambda \). A function \(\nu :\mathbb {N}\rightarrow \mathbb {N}\) is said to be negligible if for every positive polynomial \(p(\cdot )\) and all sufficiently large \(\lambda \) it holds that \(\nu (\lambda )<{1}/{p(\lambda )}\). We use [n] to denote the set \(\{1,\ldots ,n\}\). We use \(d \leftarrow \mathcal {D}\) to denote the process of sampling d from the distribution \(\mathcal {D}\) or, if \(\mathcal {D}\) is a set, a uniform choice from it. We denote by \(S_N\) the symmetric group on N elements.
2.1 Standard Cryptographic Tools
We refer the reader to, e.g. [17] for treatment of standard cryptographic primitives, including pseudorandom function (PRF) families \((\mathsf{Gen},\mathsf{Eval})\), pseudorandom permutations \(\mathsf{PRP}\), semantically secure symmetric-key encryption schemes \((\mathsf{Gen},\mathsf{Enc},\mathsf{Dec})\), and message authentication codes \((\mathsf{Gen},\mathsf{Tag},\mathsf{Verify})\).
2.2 Virtual Black-Box Obfuscation
Intuitively, a program obfuscator serves to “scramble” a program, hiding implementation details, while preserving its input/output functionality. The notion of Virtual Black-Box (VBB) obfuscation was first formally studied by [3]. We consider a notion with auxiliary input.
Definition 1
(VBB Obfuscator [3]). Let \(\mathcal {C}= \{\mathcal {C}_n\}_{n \in \mathbb {N}}\) be a family of polynomial-size circuits, where \(\mathcal {C}_n\) is a set of boolean circuits operating on inputs of length n. And let \(\mathcal {O}\) be a PPT algorithm, which takes as input an input length \(n \in \mathbb {N}\), a circuit \(C \in \mathcal {C}_n\), a security parameter \(1^\lambda \), and outputs a boolean circuit \(\mathcal {O}(C)\) (not necessarily in \(\mathcal {C}\)). \(\mathcal {O}\) is a virtual black-box (VBB) obfuscator for the circuit family \(\mathcal {C}\) if there exists a negligible function \(\nu \) such that:
-
1.
(Preserving Functionality): For every \(n \in \mathbb {N}\), and every \(C \in \mathcal {C}_n\), and every \(x \in \{0,1\}^n\), with all but \(\nu (\lambda )\) probability over the coins of \(\mathcal {O}\), we have \((\mathcal {O}(C,1^n,1^\lambda ))(x) = C(x)\).
-
2.
(Polynomial Slowdown): There exists a polynomial \(p(\cdot )\) such that for every \(n,\lambda \in \mathbb {N}\) and \(C \in \mathcal {C}\), the circuit \(\mathcal {O}(C,1^n,1^\lambda )\) is of size at most \(p(|C|,n,\lambda )\).
-
3.
(Virtual Black-Box): For every (non-uniform) polynomial-size adversary \(\mathcal {A}\), there exists a (non-uniform) polynomial-size simulator \(\mathcal {S}\) such that, for every \(n \in \mathbb {N}\) every \(C \in \mathcal {C}_n\) and every auxiliary input z,
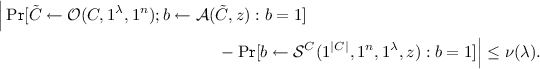
3 Oblivious LDC and Public-Key PIR
In this section, we formally introduce the notions of oblivious locally decodable codes and public-key private information retrieval. For simplicity, we consider a database x consisting of n bits.
3.1 Oblivious LDC
A standard locally decodable code (LDC) is an error-correcting code that simultaneously offers resilience to errors and a local decoding procedure, which can recover any message bit \(x_i\) with good success probability by probing few, randomly selected, bits of the encoding. Intuitively, an oblivious LDC (OLDC) is an LDC with the additional property that the sets of symbols being read computationally do not reveal the respective queried indices i. Unlike the standard goal of LDCs, we do not explicitly require any error correction capability, but such a capability is in some sense implied by our security requirement (see Remark 2 below).
Note that Oblivious LDC is a “secret-key” notion of public-key PIR, where to generate valid queries one must hold the secret key \(\mathsf{sk}\) that was used within the encoding procedure. As in other secret key primitives, we need to ensure that the same \(\mathsf{sk}\) can be used to hide any polynomial number of queries.
Definition 2
(Oblivious LDC). An Oblivious LDC is a tuple of PPT algorithms \((\mathsf{G},\mathsf{E},\mathsf{Q},\mathsf{D})\) with the following syntax:
-
\(\mathsf{G}(1^\lambda )\) is a probabilistic key generation algorithm, which takes as input a security parameter \(1^\lambda \) and outputs a secret sampling key \(\mathsf{sk}\).
-
\(\mathsf{E}(1^\lambda ,\mathsf{sk},x)\) is a probabilistic encoder, which takes as input a security parameter \(1^\lambda \), secret key \(\mathsf{sk}\), and database \(x=(x_1,\ldots ,x_n)\) with \(x_i \in \{0,1\}\), and outputs \(X=(X_1,...,X_N)\) with \(X_i \in \{0,1\}^L\).
-
\(\mathsf{Q}(1^\lambda , 1^n, i,\mathsf{sk};r)\) is a probabilistic query sampler which takes as input: a security parameter \(1^\lambda \), database size \(1^n\), index \(i \in [n]\), secret key \(\mathsf{sk}\), and randomness r used within the query generation, and outputs a list of q indices \(I \in [N]^q\).
-
\(\mathsf{D}(1^\lambda , 1^n, i,X_I,\mathsf{sk},r)\) is a deterministic decoder. It takes as input: a security parameter \(1^\lambda \), database size \(1^n\), an index \(i \in [n]\), a vector of q queried database symbols \(X_I \in (\{0,1\}^L)^q\), secret key \(\mathsf{sk}\), and secret randomness r used within the corresponding execution of \(\mathsf{Q}\). The output of \(\mathsf{D}\) is a decoded database symbol (presumably \(x_i\)).
The algorithms \((\mathsf{G},\mathsf{E},\mathsf{Q},\mathsf{D})\) should satisfy the following correctness, non-triviality and security guarantees:
-
Correctness: Honest execution of \(\mathsf{G}, \mathsf{E},\mathsf{Q},\mathsf{D}\), successfully returns the requested data items. That is, for every \(x=(x_1,\dots ,x_n)\) and every \(i \in [n]\),

-
Non-triviality: There exists \(\epsilon > 0\) such that for every \(\lambda \), and all sufficiently large n, the number of queried bits satisfies \(Lq < n^{1-\epsilon }\).
-
Security: No efficient adversary can distinguish the memory accesses dictated by \(\mathsf{Q}\) on input query index \(i_0\) and \(i_1\), for a randomly sampled \(\mathsf{sk}\). Namely, for every non-uniform PPT adversary \(\mathcal {A}\), there exists a negligible function \(\nu \) such that the distinguishing advantage of \(\mathcal {A}\) in the following game is bounded by \(\nu (\lambda )\):
-
1.
\(\mathsf{sk}\leftarrow \mathsf{G}(1^\lambda )\): The challenger samples a secret key \(\mathsf{sk}\).
-
2.
\((i_0,i_1,\mathsf{aux}) \leftarrow \mathcal {A}^{\mathsf{Q}_\mathsf{sk}(\cdot )}(1^\lambda )\): \(\mathcal {A}\) selects a challenge index pair \(i_0 \ne i_1 \in [n]\), and auxiliary information \(\mathsf{aux}\), given oracle access to the randomized functionality \(\mathsf{Q}_\mathsf{sk}(\cdot )\), which on input \(i \in [n]\) outputs a list of indices \(I \in [N]^q\) sampled as \(I \leftarrow \mathsf{Q}(1^\lambda ,1^n,i,\mathsf{sk})\).
-
3.
\(b \leftarrow \{0,1\}\); \(I^* \leftarrow \mathsf{Q}(1^\lambda ,1^n,i_b,\mathsf{sk})\): The challenger selects a random bit and generates a sample query for the chosen index \(i_b\).
-
4.
\(b' \leftarrow \mathcal {A}^{\mathsf{Q}_\mathsf{sk}(\cdot )}(\mathsf{aux},I^*)\): \(\mathcal {A}\) outputs a guess for b, given the challenge \(I^*\), and continued oracle access to \(\mathsf{Q}_\mathsf{sk}(\cdot )\) as defined above.
-
5.
\(\mathcal {A}\)’s advantage in the challenge game is defined as \(\Pr [b'=b] - 1/2\), over the randomness of the challenger (and \(\mathcal {A}\)).
-
1.
Remark 1
The above security definition is specified for a single challenge query. However, since security holds also given access to the query (“encrypt”) oracle, then by a straightforward hybrid argument, this definition directly implies computational indistinguishability for any polynomial number of queries, analogous to semantic security of symmetric-key encryption.
Remark 2
(Relation to LDC). Analogous to PIR, OLDCs are a close relative to standard LDCs, whose focus is on local recoverability of data given symbol errors or erasures. Indeed, the OLDC security requirement implies that with overwhelming probability over the choice of \(\mathsf{sk}\), the encoder and (probabilistic) decoder defined by \(\mathsf{sk}\) must read any given codeword symbol with probability essentially independent of the queried index i. This property holds directly for information theoretic PIR; for OLDC, the security guarantees are only computational, but such a probability disparity would constitute an efficient distinguisher (and thus cannot exist). Thus, in a similar fashion to the PIR-implies-LDC construction, a simple modification to the OLDC (by dropping “low-weight” symbols and duplicating “high-weight” ones) then yields a related smooth code (i.e., with a local decoding procedure where each codeword symbol is read with roughly equal probability); see “Smooth encodings and PIR” in [24]. This in turn directly yields an LDC correctable against erasures, or against errors in a low but nontrivial error regime, and can further be transformed into a standard LDC that allows for local decoding in the presence of a constant fraction of errors [26]. This means that future OLDC candidates inherently must come out of LDC techniques.
We prove that within the nontrivial regime of parameters, OLDC necessarily implies the existence of one-way functions. Interestingly, several straightforward approaches toward this assertion are not valid. In particular, one cannot make a direct use of an OLDC to devise a symmetric-key encryption scheme, since correctness of OLDC decoding is only guaranteed given the randomness used to generate the query indices, and indistinguishability of OLDC query index sets is only guaranteed when the corresponding codeword symbols themselves are unknown. The proof considers two distributions: One with a list of query sets \(I_{r_i}\) for random query indices \(r_i\) together with the real indices \(r_i\), and the second with a similar list of query sets \(I_{r_i}\) together with uncorrelated random indices \(r'_i\). Note that we must necessarily make use of the fact that the OLDC decoder can make many queries, as bounded-query OLDC exists unconditionally (e.g., using a k-wise independent functions).
Proposition 1
(OLDC Implies OWF). Suppose OLDC exists. Then one-way functions must exist.
Proof
Let \((\mathsf{G},\mathsf{E},\mathsf{Q},\mathsf{D})\) be an OLDC with parameters as above. We demonstrate two distributions which are (by OLDC security) computationally indistinguishable, but are (by OLDC correctness) statistically far [16]. Consider the following pair of distributions, for a parameter \(\ell \in \mathbb {N}\):
OLDC security directly dictates that \(D_1(1^\lambda ,\ell ),D_2(1^\lambda ,\ell )\) are computationally indistinguishable for any polynomial \(\ell =\ell (\lambda )\). We now argue that for appropriate choice of \(\ell \) they must be statistically far.
To do so, we first consider an intermediate step, roughly corresponding to the above distributions together with the secret key \(\mathsf{sk}\). Given \(\mathsf{sk}\), the OLDC decoding correctness will require the distributions to be statistically far (by the impossibility of information theoretic PIR). This does not yet suffice for our final goal, as given \(\mathsf{sk}\) the distributions are no longer computationally close. However, with some amplification this will enable us to prove that the distributions remain statistically far even when \(\mathsf{sk}\) is removed.
For any \(\mathsf{sk}\) in the support of \(\mathsf{G}(1^\mathsf{sk})\), consider a related pair of distributions \(D^\mathsf{sk}_1,D^\mathsf{sk}_2\) sampled as
For any ensemble of keys \(\{\mathsf{sk}_\lambda \}_{\lambda }\) in the support of \(\mathsf{G}\), the statistical distance between \(D^{\mathsf{sk}_\lambda }_1\) and \(D^{\mathsf{sk}_\lambda }_2\) must be non-negligible, as the contrary would imply the existence of information theoretically secure 1-server PIR with server-to-client communication sublinear in n:
-
To query index \(i \in [n]\), the client samples \((\mathsf{sk}, (I_r,r)) \leftarrow D^{\mathsf{sk}_\lambda }_1\) (where the execution of \(\mathsf{Q}\) takes randomness \(\mathsf{rand}\)) and sends the tuple \((\mathsf{sk}, (I_r, r-i))\) to the server.
-
On input \((\mathsf{sk},(I,r'))\), the server responds by OLDC-encoding the \(r'\)-shifted database (i.e., \(x'\) where \(x'_j = x_{j + r' \pmod n}~ \forall j \in [n]\)) as \(X \leftarrow \mathsf{E}(1^\lambda ,\mathsf{sk},x')\), and sending the codeword symbols \(X_I\).
-
To decode, the client executes \(x_i = \mathsf{D}(1^\lambda ,1^n,i,X_I,\mathsf{sk},\mathsf{rand})\).
Correctness and communication complexity follow from OLDC decoding and non-triviality. Note that the desired \(x_i\) will be be mapped to position r via the \((r-i)\) shift. Statistical privacy of the PIR holds by the statistical indistinguishability of \(D'_1\) and \(D'_2\) (by implying an index-i query \((\mathsf{sk},(I_r,r+i))\) is statistically close to \((\mathsf{sk},(I_r,r'+i))\), which is the query distribution for a random index).
As the final step, we show that if we consider several such \((I_r,r)\) query pairs, then non-negligible statistical distance must be maintained even when we remove \(\mathsf{sk}\) from the distribution (at which point we can no longer use OLDC correctness arguments directly). Intuitively, this must hold, otherwise omitting \(\mathsf{sk}\) would yield a secret-key encryption scheme with information theoretic security.
More formally, since the sampling of \((I_r,r)\) and \((I_r,r')\) are independent conditioned on a given value of \(\mathsf{sk}\), we may directly amplify the (non-negligible) statistical distance of \(D_1^{\mathsf{sk}_\lambda }\) and \(D_2^{\mathsf{sk}_\lambda }\) to be \(1-\nu (\lambda )\) for negligible function \(\nu \) by including a sufficiently large polynomial number \(\ell _1(\lambda )\) of sample pairs \((I_{r_i},r_i)\) or \((I_{r_i},r'_i)\), respectively (as in \(D_1(1^\lambda )\) and \(D_2(1^\lambda )\) above), together with \(\mathsf{sk}\). In particular, for any choice of \(\{\mathsf{sk}_\lambda \}_\lambda \), one can reliably transmit a bit (with possibly inefficient decoding) \(b \in \{0,1\}\) by sending a sample
(where this notation is shorthand for the distributions described above). This is preserved for the larger value \(\ell ^*(\lambda ) = 2|\mathsf{sk}_\lambda | \ell _1(\lambda )\), enabling reliable transmission of \(2|\mathsf{sk}_\lambda |\) bits of information. Further, it is maintined over a random choice of \(\mathsf{sk}_\lambda \leftarrow \mathsf{G}(1^\lambda )\).
Now, suppose that for this choice of \(\ell ^*\) the original pair of distributions \(D_1(1^\lambda ,\ell ^*(\lambda )),D_2(1^\lambda ,\ell ^*(\lambda ))\) are statistically close. These distributions correspond directly to the \(\ell ^*(\lambda )\)-sample distributions above (which enable transmission of \(2|\mathsf{sk}_\lambda |\) bits) but with \(\mathsf{sk}\) omitted. That is, we have just demonstrated an information theoretically secure symmetric-key encryption scheme for messages of length greater than twice the key size \(|\mathsf{sk}_\lambda |\), a contradiction to Shannon’s impossibility. Thus, assuming OLDC it must be that \(D_1(1^\lambda ,\ell ^*(\lambda )),D_2(1^\lambda ,\ell ^*(\lambda ))\) are computationally indistinguishable but statistically far.
3.2 Public-Key PIR
Definition 3
(pk-PIR). A Public-Key PIR (with preprocessing) is a tuple of PPT algorithms \((\mathsf{Gen},\mathsf{Encode},\mathsf{Query},\mathsf{Decode})\) acting on a size-n database with the following syntax:
-
\(\mathsf{Gen}(1^\lambda )\): On input the security parameter, \(\mathsf{Gen}\) outputs a secret encoding key \(\mathsf{sk}\) and a public sampling key \(\mathsf{pk}\).
-
\(\mathsf{Encode}(1^\lambda ,\mathsf{sk}, x)\): On input a secret encoding key and database \(x \in \{0,1\}^n\), \(\mathsf{Encode}\) outputs a compiled database \(X \in (\{0,1\}^L)^N\).
-
\(\mathsf{Query}(\mathsf{pk}, i)\): On input the public key and index \(i \in [n]\), the algorithm \(\mathsf{Query}\) outputs a sample-specific decoding key \(\mathsf{sk}_i\) and a list of indices \(I \in [N]^q\) for some q.
-
\(\mathsf{Decode}(\mathsf{sk}_i, X_I)\): On input a query-specific decoding key \(\mathsf{sk}_i\) (as generated by \(\mathsf{Query}\)) and values \(X_I \in (\{0,1\}^L)^q\), the algorithm outputs a decoded value \(x' \in \{0,1\}\).
The algorithms \((\mathsf{Gen},\mathsf{Encode},\mathsf{Query},\mathsf{Decode})\) should satisfy the following correctness and security guarantees:
-
Correctness: Honest execution of \(\mathsf{Gen}, \mathsf{Encode}, \mathsf{Query}\), and \(\mathsf{Decode}\) successfully recovers requested data items. That is, for every \(i \in [n]\),

-
Non-triviality: There exists \(\epsilon > 0\) such that for every \(\lambda \), and all sufficiently large n, the number of queried bits satisfies \(Lq < n^{1-\epsilon }\).
-
Security: No efficient adversary, given access to a public key and encoded database, can distinguish the memory accesses dictated by \(\mathsf{Query}\) on input query index \(i_0\) and \(i_1\). Namely, for every non-uniform PPT adversary \(\mathcal {A}\), there exists a negligible function \(\nu \) such that the distinguishing advantage of \(\mathcal {A}\) in the following game is bounded by \(\nu (\lambda )\):
-
1.
\((x,\mathsf{aux}) \leftarrow \mathcal {A}(1^\lambda )\): \(\mathcal {A}\) selects a database \(x \in \{0,1\}^n\) and auxiliary information \(\mathsf{aux}\).
-
2.
\((\mathsf{sk},\mathsf{pk}) \leftarrow \mathsf{Gen}(1^\lambda )\); \(X \leftarrow \mathsf{Encode}(1^\lambda ,\mathsf{sk},x)\): The challenger samples a key pair and encodes the database x.
-
3.
\((i_0,i_1,\mathsf{aux}') \leftarrow \mathcal {A}(\mathsf{pk},X,\mathsf{aux})\): \(\mathcal {A}\) selects a challenge index pair \(i_0 \ne i_1 \in [n]\).
-
4.
\(b \leftarrow \{0,1\}\); \((\mathsf{sk}_i,I^*) \leftarrow \mathsf{Query}(\mathsf{pk},i_b)\): The challenger selects a random bit and generates a sample query (and key \(\mathsf{sk}_i\)) for the chosen index \(i_b\).
-
5.
\(b' \leftarrow \mathcal {A}(\mathsf{aux}',I^*)\): \(\mathcal {A}\) outputs a guess for b, given the challenge index list \(I^*\).
-
6.
\(\mathcal {A}\)’s advantage in the challenge game is defined as \(\Pr [b'=b] - 1/2\), over the randomness of the challenger (and \(\mathcal {A}\)).
-
1.
Remark 3
As with OLDCs, the pk-PIR security definition is specified for a single challenge query, but extends via a straightforward hybrid argument for any polynomial number of queries (this time analogous to semantic security of public-key encryption).
4 Oblivious LDC Candidate
We propose an approach for constructing Oblivious LDCs via Reed-Muller codes. At a high level, we use the standard LDC based on Reed-Muller codes (with a constant number of variables m and query complexity \(\tilde{O}(n^{1/m})\)), except that we randomly permute the codeword symbols. A more explicit description follows.
Let \(\mathbb {F}\) be a finite field and let \(d,m \in \mathbb {N}\) with \(d\lambda +1 < |\mathbb {F}|\). We consider an (m, d)-Reed-Muller code over \(\mathbb {F}\), namely the code defined by m-variate polynomials of degree \(\le d\) over \(\mathbb {F}\). The codeword corresponding to a polynomial p consists of the values of p on all points in \(\mathbb {F}^m\). We use a secret (pseudo-random) permutation over \(\mathbb {F}^m\) to order the codeword symbols (e.g., [30]). To decode the value of the polynomial p at a target point \(\alpha \in \mathbb {F}^m\), the decoder picks a random degree-\(\lambda \) parameterized curve beginning at \(\alpha \), and recovers \(p(\alpha )\) by reading the values of p on a random sequence of \(d\lambda +1\) distinct parameter values along the curve (excluding the initial parameter value).
We formally describe the construction below, viewing the number of variables m and degree bound d as parameters that determine the database size n.
Construction 1
((m, d) RM-Based Oblivious LDC Candidate). Let \(n = {m+d \atopwithdelims ()d}\). Fix a canonical set of n points in \(\mathbb {F}^m\) in general position, denoted by \(\mathbf {\alpha }_i\) for \(i \in [n]\). Let \(N = |\mathbb {F}|^m\), and fix a correspondence between \(\mathbf {a} \in \mathbb {F}^m\) and \(j_{\mathbf {a}} \in [N]\). Consider the following tuple of PPT algorithms.
-
\(\mathsf{G}(1^\lambda )\): Sample a key describing a pseudorandom permutation \(\pi \in S_N\), via \(\pi \leftarrow \mathsf{PRP}(1^\lambda )\). Output \(\mathsf{sk}=\pi \).
-
\(\mathsf{E}(1^\lambda ,\mathsf{sk},x)\):
-
1.
For message \(x = (x_1,\dots ,x_n) \in \mathbb {F}^n\), define the corresponding m-variable d-degree polynomial \(P_x \in \mathbb {F}[Z_1,\ldots ,Z_m]\) as the low-degree interpolation of evaluations \(P_x(\mathbf {\alpha }_i) = x_i\). Denote the resulting codeword by \(X' \in \mathbb {F}^{N}\) indexed by points \(\mathbf {a} \in \mathbb {F}^m\) (recall \(N=|\mathbb {F}|^m\)), given componentwise as the evaluations of \(P_x\) at every point in \(\mathbb {F}^m\): i.e., \(\forall \mathbf {a} \in \mathbb {F}^m\), take \(X'[\mathbf {a}] := P_x(\mathbf {a})\).
-
2.
Permute the indices of \(X'\) via \(\pi \). That is, let \(X = (X'_{\pi (1)},\dots ,X'_{\pi (N)})\).
-
3.
Output X.
-
1.
-
\(\mathsf{Q}(1^\lambda ,1^n,i,\mathsf{sk}; r)\):
-
1.
Parse \(\mathsf{sk}= \pi \in S_N\).
-
2.
Sample a random degree-\(\lambda \) parametric curve \(C = \{(p_1(t),\dots ,p_m(t)) : t \in \mathbb {F}\} \subset \mathbb {F}^m\) that intersects the ith distinguished point \(\mathbf {\alpha }_i \in \mathbb {F}^m\), for queried index \(i \in [n]\). Concretely, C is defined by letting \(p_h\) be a random univariate polynomial of degree \(\le \lambda \) such that \(p_h(0)=(\alpha _i)_h\).
-
3.
Select a random sequence \((t_0,\dots ,t_{d\lambda }) \in \mathbb {F}^{d\lambda +1}\) of \(d\lambda +1\) distinct nozero parameter values, using the randomness r. For each \(\ell =0,\dots ,d\lambda \), let \(\mathbf {b}_\ell = (p_1(t_\ell ),\dots ,p_m(t_\ell )) \in \mathbb {F}^m\) be the corresponding point on C, and let \(j_{\mathbf {b}_\ell } \in [N]\) be the associated index.
-
4.
Output \(I = (\pi (j_{\mathbf {b}_0}),\dots ,\pi (j_{\mathbf {b}_{d\lambda }})) \in [N]^{d\lambda }\) (i.e., the list of \(\pi \)-permuted indices) as the list of query indices.
-
1.
-
\(\mathsf{D}(1^\lambda ,1^n,i,X_I,\mathsf{sk},r)\):
-
1.
Parse \(X_I = (X_0,\dots ,X_{d\lambda })\), \(\mathsf{sk}=\pi \) the pseudorandom permutation, and \(r = (t_0,\dots ,t_{d\lambda })\).
-
2.
The choice of parameter evaluation points \(t_1,\dots ,t_{d\lambda }\) determines a corresponding list of Lagrange polynomial interpolation coefficients \(c_0,\dots ,c_{d\lambda } \in \mathbb {F}\).
-
3.
Output the linear combination \(x'_i = \sum _{\ell =0}^{d\lambda } c_\ell X_\ell \in \mathbb {F}\).
-
1.
Choice of parameters. Viewing the number of variables \(m\ge 2\) as constant, the code dimension is \(\varTheta (d^m)\). We can therefore encode \(x\in \{0,1\}^n\) by letting \(d=O(n^{1/m})\) and \(|\mathbb {F}|=O(d\lambda )\). The code length is now \(|\mathbb {F}|^m=O(\lambda ^m\cdot n)\) and the number of queries used for local decoding is \(d\lambda +1=O(\lambda \cdot n^{1/m})\).
Consider the Oblivious LDC security game for the candidate construction above. The challenger samples a random secret permutation \(\pi \) of the points in \(\mathbb {F}^m\) (corresponding to [N]). The adversary is given oracle access to the query-generation algorithm \(\mathsf{Q}_\mathsf{sk}\). In this case, the index set \(I \leftarrow \mathsf{Q}_\mathsf{sk}(i)\) corresponds to a collection of \(\pi \)-permuted points in the space \(\mathbb {F}^m\) which (before the permutation) were an oversampling of a low-degree curve in \(\mathbb {F}^m\).
Security of the candidate would say that, given access to polynomial many samples of this type for desired query indices i, an efficient adversary still cannot discern a fresh query index sample for some \(i_0\) from \(i_1\). In particular, it must be the case that he cannot learn the secret permutation given access to these samples.
We treat the security of the proposed scheme with respect to the following conjecture. Roughly, it states that a permuted “puzzle” of colored low-degree curves in m-dimensional space \(\mathbb {F}^m\) is computationally indistinguishable from the same number of colored points selected at random from \(\mathbb {F}^m\).
Conjecture 1
(Permuted Low-Degree Polynomials). Let \(m \in \mathbb {N}\) be a dimension parameter and \(d=d_m(n)\) the minimal integer for which \(n \ge {m+d \atopwithdelims ()d}\). For every efficient non-uniform \(\mathcal {A}= (\mathcal {A}_1,\mathcal {A}_2)\) there exists a negligible \(\nu \) such that
where \(\mathbb {F}\) is a finite field satisfying \(|\mathbb {F}|>d\lambda +1\), and for any \(\pi \in S_{(\mathbb {F}^m)}\) and \(v \in \mathbb {F}^m\), the probabilistic algorithm \(\mathsf{Samp}_b(\pi ,v)\) does the following:
-
If \(b=0\):
-
1.
Select m random degree-\(\lambda \) polynomials \(p_1,\dots ,p_m \leftarrow \mathbb {F}[Z]\) where \(\forall i \in [m], ~p_i(0)=v_i\). This determines a curve in \(\mathbb {F}^{m}\), given by the points \(\{ (p_1(t),\dots ,p_m(t)) : t \in \mathbb {F}\}\).
-
2.
Sample \(d\lambda +1\) distinct random points on this curve, defined by nonzero parameters \(t_0,\dots ,t_{d\lambda } \leftarrow \mathbb {F}\).
-
3.
Output these points (in order), but with each point permuted by \(\pi : \mathbb {F}^m \rightarrow \mathbb {F}^m\). That is,
$$\begin{aligned} \Big ( \pi \big ( p_1(t_i), \dots , p_m(t_i) \big ) \Big )_{i =0}^{d\lambda } \in (\mathbb {F}^{m})^{d\lambda +1}. \end{aligned}$$
-
1.
-
If \(b=1\): Output \(d\lambda + 1\) random points in \(\mathbb {F}^m\): \((w_0,\dots ,w_{d\lambda }) \leftarrow (\mathbb {F}^m)^{d\lambda +1}\).
Proposition 2
Suppose that Conjecture 1 holds for dimension \(m\ge 2\). Then Construction 1 is a secure Oblivious LDC with communication complexity \(\lambda ^m \cdot \tilde{O}(n^{1/m})\).
Proof
The complexity is derived in “Choice of parameters” above. For the security of the OLDC it suffices to prove a version of Conjecture 1 with the following changes. In the first step \(\mathcal{A}_1\) picks a pair of points \((v_0,v_1)\). After the second step, \(\mathcal{A}_2\) is given a single instance of \(\mathsf{Samp}_0(\pi ,v_b)\). Finally, the third step is modified so that \(\mathsf{Samp}_0\) is used instead of \(\mathsf{Samp}_b\). Conjecture 1 implies that for both choices of b, the view of \(\mathcal{A}_2\) is indistinguishable from a random and independent set of points. Hence, the advantage of \(\mathcal{A}_2\) in guessing b is negligible.
We remark that we choose to present the simplest proposed candidate in this style whose security is plausible. One may consider several natural more complex extensions, such as including additional “distractor” indices in the query list I whose values will be ignored within the decoding. Such inclusion will correspond to introduction of error symbols within the permuted codeword.
4.1 Generalized and Toy Versions of Conjecture
We explore both a generalization and a specific instance of the Permuted Low-Degree Polynomials conjecture above.
Generalization: Permuted Puzzles. As discussed in the Introduction, our main conjecture is a particular instance of a broader class of distinguishing tasks of “permuted puzzles.” We think of a puzzle as describing: (1) a distribution of structured functions from \(\mathbb {F}^m\) to some range R (e.g., the class of pixel maps defining images of dogs), and (2) a corresponding distribution of unstructured functions (e.g., the class of all pixel maps with the same general color balance). The corresponding Permuted Puzzle Conjecture considers a random secret permutation \(\pi \) of the “puzzle pieces” (i.e., the input space \(\mathbb {F}^m\)), and states that one cannot efficiently distinguish between an arbitrary polynomial collection of permuted samples from \(\mathsf{Structured}\) from permuted samples from \(\mathsf{Unstructured}\), where each sample is permuted with the same \(\pi \).
Definition 4
(Puzzle). We refer to an m-dimensional puzzle over \(\mathbb {F}\) with range R as defined by a pair of efficiently samplable distributions \((\mathsf{Structured},\mathsf{Unstructured})\), each over the class of functions \(\{ f : \mathbb {F}^m \rightarrow R \}\).
Conjecture 2
(Permuted Puzzle Conjecture). The Permuted Puzzle Conjecture with respect to the m-dimensional puzzle \((\mathsf{Structured},\mathsf{Unstructured})\) states that for every efficient non-uniform \(\mathcal {A}\), there exists a negligible \(\nu \) such that

where \(\mathcal {O}_\pi \) is an oracle that takes as input \(b \in \{ \mathsf{struct}, \mathsf{unstruct} \}\) and performs the following:
-
If \(b = \mathsf{struct}\): Sample \(f \leftarrow \mathsf{Structured}\), output \(f \circ \pi \).
-
If \(b = \mathsf{unstruct}\): Sample \(f \leftarrow \mathsf{Unstructured}\), output \(f \circ \pi \).
For example, the Permuted Low-Degree Polynomials Conjecture 1 is a particular case of the permuted puzzle conjecture, where \(\mathsf{Structured}\) consists of functions \(f: \mathbb {F}^m \rightarrow \{0,1\}\) which evaluate to 1 precisely on \((d\lambda +1)\) points on a degree-\(\lambda \) parametric curve, and \(\mathsf{Unstructured}\) consists of all functions \(\mathbb {F}^m \rightarrow \{0,1\}\) which have \((d\lambda +1)\) nonzero outputs (but in an arbitrary placement).
Specific Instance: Toy Conjecture. To encourage investigation of the core Permuted Low-Degree Polynomials conjecture, we put forth a simple toy variant, which constitutes an easier version of the simplest parameter setting. In particular, it considers the case of dimension \(m=2\), and takes the first-coordinate polynomial to be the identity function: that is, including the value of the curve parameter explicitly. This variant brings the problem closer to typical settings of coding theory, and may thus be a useful starting point toward addressing coding-based cryptanalytic attacks. We pursue this strategy in the discussion of cryptanalysis in Sect. 4.2 below.
Conjecture 3
(Toy Conjecture). Let \(|\mathbb {F}| \approx \lambda ^2\). Let \(p_1,\dots ,p_m\) be random degree-\(\lambda \) polynomials over \(\mathbb {F}\), for \(m = \lambda ^{100}\). Let \(q_1,\dots ,q_m\) be random functions from \(\mathbb {F}\) to \(\mathbb {F}\).
Then the following two distributions are computationally indistinguishable, over the choice of random permutation \(\pi \leftarrow S_{\mathbb {F}\times \mathbb {F}}\) over \(\mathbb {F}\times \mathbb {F}\). Here, elements of each set \(S_i\) or \(T_i\) appear in canonical sorted order (not ordered by \(x \in \mathbb {F}\)).
-
1.
Permuted low-degree polynomials: \((S_1,\dots ,S_m)\), for \(S_i = \{ \pi (x,p_i(x)) : x \in \mathbb {F}\}\).
-
2.
Permuted random functions: \((T_1,\dots ,T_m)\), for \(T_i = \{ \pi (x, q_i(x)) : x \in \mathbb {F}\}\).
4.2 Discussion on Cryptanalysis
We briefly address a selection of relevant cryptanalytic techniques with respect to the candidate construction, as well as attacks on simplified versions of the construction. We focus on the Toy Conjecture 3 (i.e., \(m=2\) dimensions, where the first-coordinate polynomial is the identity function), as an attack on the primary conjecture is necessarily also an attack on this easier version.
Permuting Individual Coordinates. To develop intuition, we first consider weaker (i.e., easier to break) variants of the Toy Conjecture, and show that these are not secure. In these variants, instead of choosing the permutation \(\pi \) from the entire space \(S_{\mathbb {F}\times \mathbb {F}}\), we sample from a restricted class that permutes one or both coordinates of \(\mathbb {F}\times \mathbb {F}\) independently. In particular:
-
1.
Permute only second coordinate: \(\pi \leftarrow id \times S_\mathbb {F}\). In this case, the permuted low-degree curves are given as sets of points \(\big \{ (t, \pi _2(p(t))) \big \} \subseteq \mathbb {F}\times \mathbb {F}\).
This weakened version is not secure. The exposure of the parameter values t themselves in the clear reveals a linear constraint on the corresponding second coordinate symbols, corresponding to Lagrange interpolation where the coefficients are known. As discussed and generalized in the second category of Linearization attacks below, this enables an adversary with sufficiently many samples to learn the preimages of \(\pi \).
-
2.
Permute only first coordinate: \(\pi \leftarrow S_\mathbb {F}\times id\). In this case, the permuted low-degree curves are given as sets of points \(\big \{ (\pi _1(t), p(t)) \big \} \subseteq \mathbb {F}\times \mathbb {F}\).
This weakened version is also not secure. One can view this as the problem of distinguishing “noisy” Reed-Solomon codewords from uniformly random vectors in \(\mathbb {F}^{|\mathbb {F}|}\), where the “noise” is a permutation of the codeword symbols. Since the resulting “noisy” codewords are still codewords in a linear code, they are contained in some low-dimensional subspace. Thus, the adversary may simply check the dimension of the span of sufficiently many samples to determine whether the structured or unstructured case holds.
Standard Decoding Attacks. Coding-theoretic attacks are a natural attempt to refute the Toy Conjecture 3; as above, the attacker’s task is similar to the task of distinguishing “noisy” Reed-Solomon codewords from uniformly random vectors. As noted above, when the “noise” is a permutation acting on either coordinate independently, the linearity of the underlying code provides an attack. Similarly, if the “noise” did not include a permutation, and only included standard coding-theoretic noise (that is, if \(S_i\) were of the form \(\{ (x, p_i(x) + e_i(x) ) \, :\, x \in \mathbb {F} \}\) for a sparse \(e_i(x)\)), then standard decoding algorithms (for example Reed-Solomon list-decoding, or the multi-dimensional extension of Coppersmith and Sudan [11]) might apply. However, because the noise takes the form of a permutation, it is not at all clear how to apply such techniques in this setting.
Similarly, an attacker might hope to adapt attacks on instantiations of the McEliece cryptosystem [28] with Reed-Solomon codes in the place of Goppa codes, since these attacks are aimed at distinguishing a permutation applied to a Reed-Solomon generator matrix from uniformly random; such attacks might apply directly in the setting where the \(S_i\) are of the form \(\{ ( \pi (x), p_i(x) + e_i(x) ) \, :\, x \in \mathbb {F}\}\). However, there are two reasons that these sorts of attacks are not directly applicable to the general Toy Conjecture 3. First, the permuation acts on the entire space \(\mathbb {F}\times \mathbb {F}\), rather than just on the first coordinate. Second, these attacks require knowledge of the public key—the scrambled generator matrix—and in the Oblivious LDC setting the attacker is not privy to this information.
Linearization Attacks. Generalizing the discussion above on permuting individual coordinates, linearization-style attacks can be used to break any version of the above candidate construction satisfying the following simplified properties:
-
1.
Encoding is linear & public:
In this case, each encoded database entry \(X_j\) corresponds to a known linear combination of the original database entries \(x_j\), i.e. to a known n-dimensional coefficient vector \(c^{(j)} \in \mathbb {F}^n\) for which \(X_j = \sum _{i=1}^n c^{(j)}_i x_i\). In this case we can assume without loss of generality that the decoder is also linear. Indeed, for a random database x, a set of linear combinations of \(x_j\) can be used to infer a given target \(x_i\) with better than 1/2 success probability if and only if it spans \(x_i\). Given a query set \(I \in [N]^q\), we can simply determine whether a given basis vector \(\mathbf {e}_i\) lies in the span of the vectors \(c^{(j)}\) corresponding to the queried locations. By correctness and linearity of the decoder, this must be the case for the true queried index i. But, since the number of queries \(q < n/2\), this cannot be the case for most indices \(i' \ne i\).
In particular, this means that if \(\mathsf{Encode}\) is a linear procedure, then it must utilize secret randomness. In our candidate construction, this is achieved by use of the secret permutation \(\pi \). Namely, \(\mathsf{Encode}\) corresponds to implementing a fixed public linear Reed-Muller encoding procedure composed with a random permutation matrix.
-
2.
Decoding is linear & public, encoding is linear:
In this case, even if the encoding is randomized and secret, but the decoding is linear and public, we can launch a simple linearization attack. As above, linear encoding means each encoded symbol \(X_j\) corresponds to some n-dimensional coefficient vector \(c^{(j)} \in \mathbb {F}^n\) (for which \(X_j = \sum _{i=1}^n c^{(j)}_i x_i\)). Define nN linearization variables, corresponding to the unknown values of \(\{c^{(j)}_i\}_{i \in [n],j\in [N]}\). Plugging in the known linear decoding function, each received query sample \(I \in [N]^q\) on input \(i \in [n]\) (whose data value \(x_i\) is known) yields a fresh linear constraint on these variables.
In particular, this means that a simplified version of our candidate construction in which the \(d\lambda +1\) parameter values \(t_0,\dots ,t_{d\lambda } \in \mathbb {F}\) are fixed (and public) would be broken, as well as the simplified variant discussed in “Permuting Individual Coordinates” above where the parameter values are random but public. We avoid this issue in our proposed candidate by sampling a random set of such values for each query, and passing this information along to the decoder (but not revealing it directly). In effect, each distinct subset of parameter values induces a distinct linear function for the decoding, corresponding to the different value of Lagrange interpolation coefficients.
Generic Learning Approach. Assuming the existence of pseudorandom functions in NC\(^1\) [18, 32] (a mild assumption that follows from most standard cryptographic assumptions), we can rule out the following hypothetical generic attack that applies to constructions based on permuted linear LDCs. The generic attack views every symbol of X as a hidden vector which specifies some linear combination of x. By repeatedly invoking the decoder on index i, one can get polynomially many samples of sets of hidden vectors which span a given target vector t. If this information could be used to learn the hidden vectors, or even just distinguish between samples that span t and ones that do not, this would give rise to a distinguishing attack.
However, the existence of pseudorandom functions in NC\(^1\), together with the fact that span programs [23] can efficiently simulate NC\(^1\) functions, imply that an attack as above cannot work in general. For simplicity we restrict the attention to the case where t is the unit vector \(e_1\) and the field size is fixed.
Proposition 3
Suppose there is a pseudorandom function in NC\(^1\). Then, for any finite field \(\mathbb {F}\), there are PPT algorithms \((\mathsf{Gen},\mathsf{Query})\) such that \(\mathsf{Gen}(1^\lambda )\), on a security parameter \(\lambda \), outputs a secret key \(\mathsf{sk}\) and a matrix \(M\in \mathbb {F}^{N\times n}\), and \(\mathsf{Query}(\mathsf{sk},b)\) outputs a row index set \(I_b\subseteq [N]\), and the following conditions hold.
-
For the pair \((M,I_1)\) obtained by running \(\mathsf{Gen}(1^\lambda )\) and then \(\mathsf{Query}(\mathsf{sk},1)\), the set of \(I_1\)-rows of M spans the unit vector \(e_1\in \mathbb {F}^n\) except with
 failure probability.
failure probability. -
For the pair \((M,I_0)\) obtained by running \(\mathsf{Gen}(1^\lambda )\) and then \(\mathsf{Query}(\mathsf{sk},0)\), the set of \(I_0\)-rows of M does not span \(e_1\) except with
 failure probability.
failure probability. -
For any polynomial \(p(\lambda )\), the distribution ensembles \(\{(I^1_0,\ldots ,I^{p(\lambda )}_0)\}_\lambda \) and \(\{(I^1_1,\ldots ,I^{p(\lambda )}_1)\}_\lambda \) are computationally indistinguishable, where \((I^1_b,\ldots ,I^{p(\lambda )}_b)_\lambda \) is obtained by letting \((\mathsf{sk},M)\leftarrow \mathsf{Gen}(1^\lambda )\) and then \(I^j_b\leftarrow \mathsf{Query}(\mathsf{sk},b)\) for \(j=1,\ldots ,p(\lambda )\).
Proof
Let \(\mathsf{Gen}(1^\lambda )\) generate a boolean formula F of size N computing a PRF described by a secret evaluation key \(\mathsf{sk}\) on an input \(x\in \{0,1\}^\lambda \). (The existence of polynomial-time \(\mathsf{Gen}\) follows from the existence of a PRF in NC\(^1\).) Using the known simulation of formulas by span programs [23], one can efficiently construct \(2\lambda \) matrices \(M_{i,0},M_{i,1}\) over \(\mathbb {F}\), \(1\le i\le \lambda \), each with \(n\le N\) columns and a total of N rows, such that \(F(x)=1\) if and only if the unit vector \(e_1\in \mathbb {F}^n\) is spanned by the rows of the \(\lambda \) matrices \(M_{i,x_i}\). The matrix M output by \(\mathsf{Gen}\) is the matrix whose rows contain all rows of \(M_{i,b}\) in order.
The algorithm \(\mathsf{Query}(\mathsf{sk},b)\) samples a random x such that \(F(x)=b\), and outputs the index set \(I_b\) of the rows of \(M_{i,x_i}\) as rows of M. Since \(F=F_\mathsf{sk}\) is a PRF, \(F(x)=b\) holds for roughly a half of the inputs, and so such an x can be sampled with negligible failure probability by trying \(\lambda \) random candidates. Finally, since F is indistinguishable from a random function, polynomially many samples of inputs x for which \(F(x)=0\) are indistinguishable from polynomially many samples of inputs x for which \(F(x)=1\). Since the row indices in \(I_b\) are determined by the input, this implies the required indistinguishability condition.
Overall, while there are certainly some simplified variants of the Toy Conjecture 3 that are not secure, it seems that the stated version is not immediately susceptible to natural attack strategies. We hope that this Toy Conjecture will be the subject of further study (either with the goal of refuting or confirming it), as this will lead to a better understanding of our core Permuted Low-Degree Polynomials Conjecture.
5 Oblivious LDC to Public-Key PIR
We demonstrate a general transformation from any Oblivious LDC to a construction of Public-Key PIR, assuming virtual black-box program obfuscation. Recall the core differences between the two primitives are: (1) querying an OLDC (and decoding the retrieved values) requires the secret encoding key, and (2) OLDC security holds only if the codeword remains private. The transformation uses obfuscation to safely enable public querying and decoding (without revealing \(\mathsf{sk}\) directly). The codeword will be published in encrypted form, and the obfuscated program will additionally contain the decryption key. Finally, to protect against malicious decoding queries, all queries generated by the obfuscated program will be authenticated by a MAC, which will be verified before answering.
Theorem 2
Suppose Oblivious LDCs exist. Then, assuming one-way functions, there exists a secure Public-Key PIR in the virtual black-box obfuscation hybrid model.
Proof
We present a general transformation from any oblivious LDC \((\mathsf{G},\mathsf{E},\mathsf{Q},\mathsf{D})\) to a public-key PIR scheme \((\mathsf{Gen},\mathsf{Encode},\mathsf{Query},\mathsf{Decode})\) in Construction 3, assuming the following tools (each of which, aside from VBB obfuscation itself, are implied by one-way functions):
-
Let \(\mathcal {O}\) be a VBB circuit obfuscator secure with auxiliary input.
-
Let \((\mathsf{Gen}_\mathsf{SKE},\mathsf{Enc},\mathsf{Dec})\) be a semantically secure symmetric encryption scheme.
-
Let \((\mathsf{Gen}_\mathsf{MAC},\mathsf{Tag},\mathsf{Verify})\) be a secure deterministic MAC.Footnote 2
-
Let \((\mathsf{Gen}_\mathsf{PRF}, \mathsf{Eval}_\mathsf{PRF})\) be a pseudorandom function family.
Construction 3
(pk-PIR from Oblivious LDC)
-
\(\mathsf{Gen}(1^\lambda , x)\):
-
1.
Sample \(P \leftarrow \mathsf{Samp}(1^\lambda )\), defined as follows:
-
– Sample an oblivious LDC key \(\mathsf{sk}_\mathsf{LDC}\leftarrow \mathsf{G}(1^\lambda )\).
-
– Sample a SKE key \(\mathsf{sk}_\mathsf{SKE}\leftarrow \mathsf{Gen}_\mathsf{SKE}(1^\lambda )\).
-
– Sample a MAC key \(\mathsf{sk}_\mathsf{MAC}\leftarrow \mathsf{Gen}_\mathsf{MAC}(1^\lambda )\).
-
– Sample a PRF key \(k \leftarrow \mathsf{Gen}_\mathsf{PRF}(1^\lambda )\).
-
– Let P be as in Fig. 1, with \(\mathsf{sk}_\mathsf{LDC},\mathsf{sk}_\mathsf{SKE},\mathsf{sk}_\mathsf{MAC},k\) hardcoded.
-
-
2.
Obfuscate the program as \(\tilde{P} \leftarrow \mathcal {O}(P,1^\lambda ,1^n)\).
-
3.
Output \(\mathsf{sk}:= (\mathsf{sk}_\mathsf{LDC},\mathsf{sk}_\mathsf{SKE},\mathsf{sk}_\mathsf{MAC},k)\) and \(\mathsf{pk}:= \tilde{P}\).
-
1.
-
\(\mathsf{Encode}(1^\lambda ,\mathsf{sk}, x)\):
-
1.
Encode x using the oblivious LDC: i.e., \(X'' \leftarrow \mathsf{E}(1^\lambda ,\mathsf{sk}_\mathsf{LDC},x)\).
-
2.
Encrypt each item in the encoded database (using \(\mathsf{sk}_\mathsf{SKE}\) from above): For \(j=1,\dots ,N\), let \(X'_j \leftarrow \mathsf{Enc}_{\mathsf{sk}_\mathsf{SKE}}(X''_j)\).
-
3.
MAC each item in the encrypted database (using \(\mathsf{sk}_\mathsf{MAC}\) from above): For \(j=1,\dots ,N\), compute \(\mathsf{tag}_j = \mathsf{Tag}(\mathsf{sk}_\mathsf{MAC}, (j,X'_j))\), and define \(X_j = (X'_j, \mathsf{tag}_j)\).
-
4.
Output the database \(X = (X_1,\dots ,X_N)\).
-
1.
-
\(\mathsf{Query}(\mathsf{pk}, i)\): Sample randomness \(r \leftarrow \{0,1\}^\lambda \). Evaluate
 . Output \(\mathsf{sk}_i = (c, \mathsf{tag}_Q)\) and query index set I.
. Output \(\mathsf{sk}_i = (c, \mathsf{tag}_Q)\) and query index set I. -
\(\mathsf{Decode}(\mathsf{sk}_i, X_I)\): Parse \(\mathsf{sk}_i = (c,\mathsf{tag}_Q)\). Output

 .
.
Suppose, for contradiction, that Construction 3 is not a secure pk-PIR: that is, that there exists a non-negligible function \(\alpha \) and non-uniform polynomial-time \(\mathcal {A}=(\mathcal {A}_1,\mathcal {A}_2,\mathcal {A}_3)\) who wins in the pk-PIR security challenge game with advantage \(\alpha \). We will demonstrate a contradiction via a sequence of related games.
-
Game 0. Real pk-PIR security game.
By definition of the pk-PIR security game, we have that \(\mathcal {A}\) satisfies
$$\begin{aligned} \Pr \Big [ (x,\mathsf{aux}) \leftarrow \mathcal {A}_1(1^\lambda ); (\mathsf{sk},\mathsf{pk}) \leftarrow \mathsf{Gen}(1^\lambda ); X \leftarrow \mathsf{Encode}(1^\lambda ,\mathsf{sk},x); \\ (i_0,i_1,\mathsf{aux}') \leftarrow \mathcal {A}_2(\mathsf{pk},X,\mathsf{aux}); b \leftarrow \{0,1\}; (\mathsf{sk}_{i_b},I) \leftarrow \mathsf{Query}(\mathsf{pk},i_b); \\ b' \leftarrow \mathcal {A}_3(\mathsf{aux}',I) : b'=b \Big ] \ge \alpha . \end{aligned}$$(1)
-
Game 1. VBB security. In this step, we show that the adversary \(\mathcal {A}\) must still be able to successfully distinguish in the pk-PIR security game given only black-box access to the program P in the place of seeing the actual obfuscated code \(\mathsf{pk}= \tilde{P}\).
Formally, consider Expression (1) above. By the pigeonhole principle applied over index pairs \((i_0,i_1) \in [n^2]\), there must exist a fixed choice of \((i_0^*,i_1^*) \in [n]^2\) for which
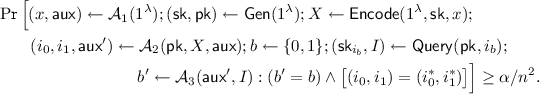
For this choice of \((i_0^*,i_1^*) \in [n]^2\), define a new adversary \(\mathcal {A}_{(i_0^*,i_1^*)}=(\mathcal {A}_1,\mathcal {A}_2,\mathcal {A}'_3)\) where \(\mathcal {A}'_3(\mathsf{aux}',I)\) outputs \(\mathcal {A}_3(\mathsf{aux}',I)\) if \((i_0,i_1)=(i_0^*,i_1^*)\) and \(\bot \) otherwise. Then
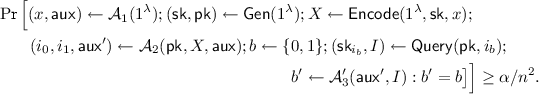
Plugging in the particular procedure for \(\mathsf{Gen}\) (consisting of sampling \((P,\mathsf{sk}) \leftarrow \mathsf{Samp}(1^\lambda )\) and then obfuscating \(\tilde{P} \leftarrow \mathcal {O}(P,1^\lambda ,1^n)\), and taking \(\mathsf{pk}:= \tilde{P}\)), of \(\mathsf{Query}\) (which samples randomness \(r \leftarrow \{0,1\}^\lambda \) and evaluates the obfuscated program at input
 ), and making use of the correctness of the obfuscator (so that
), and making use of the correctness of the obfuscator (so that  ), this implies
), this implies 
For \(i \in [n]\), define the distribution \((P, (\mathsf{aux},X,I)) \leftarrow \mathsf{InstSamp}_i(1^\lambda )\) by:
-
1.
\((x,\mathsf{aux}) \leftarrow \mathcal {A}_1(1^\lambda )\).
-
2.
\((P,\mathsf{sk}) \leftarrow \mathsf{Samp}(1^\lambda )\) (where \(\mathsf{Samp}\) samples keys and takes
\(\mathsf{sk}= (\mathsf{sk}_\mathsf{LDC},\mathsf{sk}_\mathsf{SKE},\mathsf{sk}_\mathsf{MAC},k)\) as specified in \(\mathsf{Gen}\) in Construction 3).
-
3.
\(X \leftarrow \mathsf{Encode}(1^\lambda ,\mathsf{sk},x)\) (where \(\mathsf{Encode}\) is specified in Construction 3).
-
4.
\(r \leftarrow \{0,1\}^\lambda \);
 .
. -
5.
Output \((P, (\mathsf{aux},X,I))\).
Then (for the same \((i^*_0,i^*_1) \in [n]^2\) as above) we have

Note that while the challenge I is sampled using either \(i_0^*\) or \(i_1^*\) instead of \(i_0\) or \(i_1\) as selected by \(\mathcal {A}\), this does not affect the probabilities since \(\mathcal {A}'_3\) will anyway output \(\bot \) in the case that \((i_0,i_1)\ne (i_0^*,i_1^*)\).
For the same \((i^*_0,i^*_1) \in [n]^2\) as above, define the algorithm \(\mathcal {B}_{(i^*_0,i^*_1)}\) that, on input an obfuscated program \(\tilde{P}\), and a triple \((\mathsf{aux},X,I)\), executes as follows:
-
1.
Run \((i_0,i_1,\mathsf{aux}') \leftarrow \mathcal {A}_2(\tilde{P}, X,\mathsf{aux})\).
-
2.
Output \(b' \leftarrow \mathcal {A}'_3(\mathsf{aux}',I)\).
Then, plugging in \(\mathcal {B}_{(i^*_0,i^*_1)}\) notation to the expression above we have

Now, by the VBB security of the obfuscator \(\mathcal {O}\), then for the algorithm \(\mathcal {B}_{(i^*_0,i^*_1)}\) there exists a corresponding simulator \(\mathcal {S}_{(i^*_0,i^*_1)}\) such that for every auxiliary input \(z = (\mathsf{aux},X,I)\),

Therefore it must be the case that
$$\begin{aligned}&\Pr \Big [ b \leftarrow \{0,1\}; (P, (\mathsf{aux},X,I)) \leftarrow \mathsf{InstSamp}_{i^*_b}(1^\lambda ); \nonumber \\&b' \leftarrow (\mathcal {S}_{(i^*_0,i^*_1)})^{P(\cdot )}(1^{|P|},1^n,1^\lambda , (\mathsf{aux},X,I)) : b'=b \Big ] \ge \alpha /n^2 - 2\nu (\lambda ). \end{aligned}$$(2)That is, the simulator \((\mathcal {S}_{(i^*_0,i^*_1)})\) wins an analogous pk-PIR challenge (on a fixed choice of challenge indices \((i^*_0,i^*_1)\)), given only black-box oracle access to the program P instead of its obfuscated code.
-
1.
-
Game 2. MAC security. In this game, we consider the same experiment as in Eq. (2), but where the simulator \(\mathcal {S}_{(i_0^*,i_1^*)}\) instead interacts with a modified (stateful) oracle, \(P_{\mathsf{MAC}}\) defined below. \(P_\mathsf{MAC}\) acts precisely as P but self destructs if it ever receives as input a valid MAC tag that was not generated by the program itself (or appearing in the given encoded database X).
(Stateful) program \(P_\mathsf{MAC}\):
Hardcoded: Program P, and encoded database \(X = ( (\mathsf{data}\mathsf{CT}^\mathsf{real}_1,\mathsf{tag}^\mathsf{real}_1),\dots ,\) \((\mathsf{data}\mathsf{CT}^\mathsf{real}_N,\mathsf{tag}^\mathsf{real}_N))\).
-
Initialize \(\mathsf{ValidTagList}\leftarrow \emptyset \).
-
For each input
 :
:-
1.
Let
 .
. -
2.
Add new message-tag pair to the list: \(\mathsf{ValidTagList}\leftarrow \mathsf{ValidTagList}\cup \{ ( (i,I,c), \mathsf{tag}_Q) \}\).
-
3.
Output \((I,c,\mathsf{tag}_Q)\).
-
1.
-
For each input
 :
:-
1.
If either of the following holds, set \(\mathsf{ForgedTag}\leftarrow 1\). Otherwise, \(\mathsf{ForgedTag}\leftarrow 0\).
-
For some \(j \in I\), \(\mathsf{Verify}(\mathsf{sk}_\mathsf{MAC}, (j,\mathsf{data}\mathsf{CT}_j), \mathsf{tag}_j) = 1\) and \(\mathsf{data}\mathsf{CT}_j \ne \mathsf{data}\mathsf{CT}^\mathsf{real}_j\).
-
\(\mathsf{Verify}(\mathsf{sk}_\mathsf{MAC}, (i, I,c), \mathsf{tag}_Q) = 1\) and \(((i,I,c),\mathsf{tag}_Q) \notin \mathsf{ValidTagList}\).
-
-
2.
If \(\mathsf{ForgedTag}= 1\): then \(\mathsf{selfdestruct}\).
-
3.
Else, output
 .
.
-
1.
Claim
For \((i_0^*,i_1^*), \mathsf{InstSamp}\) defined in Game 1, and \(P_\mathsf{MAC}\) as above, there exists a negligible function \(\nu _2\) for which
Proof
Follows directly by the security of the MAC. Namely, if the expression in Eq. (3) differs from that in Eq. (2) by more than a negligible amount, this would imply that the non-uniform polynomial algorithm \(\mathcal {S}_{(i_0^*,i_1^*)}\) succeeds with non-negligible probability in generating a fresh message-tag pair, given black-box access to the program P. But, such an algorithm can be directly used to win with non-negligible probability in the MAC security game, since the outputs of the program P can be simulated given only query access to the algorithms \(\mathsf{Tag}\) and \(\mathsf{Verify}\) for a challenge key.
-
Game 3. Correctness of SKE and Oblivious LDC. In this step, instead of actually running the oblivious LDC decoder \(\mathsf{D}\) on a “\(\mathsf{decode}\)” request to the program, we will respond in one of two ways: (1) if the request is invalid or includes message-tag pair that was not generated earlier by the program or X (i.e., the case where \(P_\mathsf{MAC}\) would self-destruct) then output \(\bot \); (2) otherwise, the decode request corresponds directly to a previously asked
 request for some index \(i \in [n]\), in which case we will directly output the database value \(x_i\).
request for some index \(i \in [n]\), in which case we will directly output the database value \(x_i\).
(Stateful) program \(P_\mathsf{correct}\):
Hardcoded: Program P, plaintext database \(x = x_1,\dots ,x_n\), encoded database \(X = ( (\mathsf{data}\mathsf{CT}^\mathsf{real}_1,\mathsf{tag}^\mathsf{real}_1),\dots ,(\mathsf{data}\mathsf{CT}^\mathsf{real}_N,\mathsf{tag}^\mathsf{real}_N))\).
-
Initialize \(\mathsf{QueryList}\leftarrow \emptyset \).
-
For each input
 :
:-
1.
Let
 .
. -
2.
Add new query pair to the list: \(\mathsf{QueryList}\leftarrow \mathsf{QueryList}\cup \{ ((i,I,c), \mathsf{tag}_Q) \}\).
-
3.
Output \((I,c,\mathsf{tag}_Q)\).
-
1.
-
For each input
 :
:-
1.
If either of the following holds, set \(\mathsf{ForgedTag}\leftarrow 1\). Otherwise, \(\mathsf{ForgedTag}\leftarrow 0\).
-
For some \(j \in I\), \(\mathsf{Verify}(\mathsf{sk}_\mathsf{MAC}, (j,\mathsf{data}\mathsf{CT}_j), \mathsf{tag}_j) = 1\) and \(\mathsf{data}\mathsf{CT}_j \ne \mathsf{data}\mathsf{CT}^\mathsf{real}_j\).
-
\(\mathsf{Verify}(\mathsf{sk}_\mathsf{MAC}, (i, I,c), \mathsf{tag}_Q) = 1\) and \(((i,I,c),\mathsf{tag}_Q) \notin \mathsf{QueryList}\).
-
-
2.
If \(\mathsf{ForgedTag}= 1\): then \(\mathsf{selfdestruct}\).
-
3.
If \(((i,I,c),\mathsf{tag}_Q) \in \mathsf{QueryList}\), output \(x_i\).
-
4.
Else output \(\bot \).
-
1.
Claim
For \((i_0^*,i_1^*), \mathsf{InstSamp}\) defined in Game 1, and \(P_\mathsf{correct}\) as above, there exists a negligible function \(\nu _3\) for which
Proof
Note that \(P_\mathsf{MAC}\) and \(P_\mathsf{correct}\) identically treat  inputs (including an identical update of respective lists \(\mathsf{ValidTagList}\) and \(\mathsf{QueryList}\)). Suppose an input is received of the form
inputs (including an identical update of respective lists \(\mathsf{ValidTagList}\) and \(\mathsf{QueryList}\)). Suppose an input is received of the form  , for which \(\mathsf{ForgedTag}= 0\) (otherwise, if \(\mathsf{ForgedTag}=1\), both \(P_\mathsf{MAC}\) and \(P_\mathsf{correct}\) self destruct). In particular, this means two things:
, for which \(\mathsf{ForgedTag}= 0\) (otherwise, if \(\mathsf{ForgedTag}=1\), both \(P_\mathsf{MAC}\) and \(P_\mathsf{correct}\) self destruct). In particular, this means two things:
-
The triple \((I,c,\mathsf{tag}_Q)\) was generated as the output of the program on some input
 . By the definition of the
. By the definition of the  portion of the programs, this means there exists \((r_1,r_2)\) for which \(I = \mathsf{Q}(1^\lambda ,1^n,i,\mathsf{sk}_\mathsf{LDC};r_1)\) and \(c = \mathsf{Enc}_{\mathsf{sk}_\mathsf{SKE}}(r_1;r_2)\).
portion of the programs, this means there exists \((r_1,r_2)\) for which \(I = \mathsf{Q}(1^\lambda ,1^n,i,\mathsf{sk}_\mathsf{LDC};r_1)\) and \(c = \mathsf{Enc}_{\mathsf{sk}_\mathsf{SKE}}(r_1;r_2)\). -
The input values \((\mathsf{data}\mathsf{CT}_j)_{j \in I}\) are the true values of the encoded database at the indices specified by I (i.e., \(X_I\)). Now, recall that X was generated (within \(\mathsf{InstSamp}_{i_b^*}\), defined in Game 1, where \(\mathsf{Samp},\mathsf{Encode}\) are defined as in Fig. 1) by: sampling an oblivious LDC key as \(\mathsf{sk}_\mathsf{LDC}\leftarrow \mathsf{G}(1^\lambda )\); encoding x via the oblivious LDC as \(X'' \leftarrow \mathsf{E}(1^\lambda ,\mathsf{sk}_\mathsf{LDC},x)\); encrypting each coordinate of the encoded database as \(\mathsf{data}\mathsf{CT}_j \leftarrow \mathsf{Enc}_{\mathsf{sk}_\mathsf{SKE}}(X''_j) ~\forall j \in [N]\); MACing each encrypted coordinate as \(\mathsf{tag}_j \leftarrow \mathsf{Tag}(\mathsf{sk}_\mathsf{MAC},(j,\mathsf{data}\mathsf{CT}_j))\) \(\forall j \in [N]\); and taking final output values \(X_j = (\mathsf{data}\mathsf{CT}_j,\mathsf{tag}_j) ~\forall j \in [N]\).
Now, consider the steps of the  portion of \(P_\mathsf{MAC}\) that are replaced within \(P_\mathsf{correct}\):
portion of \(P_\mathsf{MAC}\) that are replaced within \(P_\mathsf{correct}\):
-
1.
For each \(j \in I\): Decrypt \(\mathsf{data}_j = \mathsf{Dec}_{\mathsf{sk}_\mathsf{SKE}}(\mathsf{data}\mathsf{CT}_j)\).
By correctness of the SKE, we have that \(\mathsf{data}_j = X''_j\) (as defined above) for each j.
-
2.
Decrypt \(r_1 = \mathsf{Dec}_{\mathsf{sk}_{\mathsf{SKE}}}(c)\).
By correctness of the SKE, we have that \(\mathsf{Dec}_{\mathsf{sk}_\mathsf{SKE}}(c) = r_1\), for the randomness value \(r_1\) used in \(\mathsf{Q}\) to generate I.
-
3.
Output \(D(1^\lambda ,1^n,i, (\mathsf{data}_j)_{j \in I}, \mathsf{sk}_\mathsf{LDC}, r_1)\).
In our notation, this is \(D(1^\lambda ,1^n,i, X''_I, \mathsf{sk}_\mathsf{LDC}, r_1)\), where \(I = \mathsf{Q}(1^\lambda ,1^n,i,\) \(\mathsf{sk}_\mathsf{LDC};r_1)\).
By correctness of decoding for the Oblivious LDC, this value is thus the queried ith data value, \(x_i\).
Therefore, the programs \(P_\mathsf{MAC}\) and \(P_\mathsf{correct}\) are in fact identical. The claim follows.
Game 4. PRF security. We now replace the pseudorandom values \((r_1,r_2)\) with truly random values.
(Stateful) program \(P_\mathsf{PRF}\):
Hardcoded: \(\mathsf{sk}_\mathsf{LDC},\mathsf{sk}_{\mathsf{SKE}},\mathsf{sk}_\mathsf{MAC}\), Plaintext database \(x = x_1,\dots ,x_n\), encoded database \(X = ( (\mathsf{data}\mathsf{CT}^\mathsf{real}_1,\mathsf{tag}^\mathsf{real}_1),\dots ,(\mathsf{data}\mathsf{CT}^\mathsf{real}_N,\mathsf{tag}^\mathsf{real}_N))\).
-
Initialize \(\mathsf{QueryList}\leftarrow \emptyset \).
-
Initialize \(\mathsf{OutputList}\leftarrow \emptyset \).
-
Input
 :
:-
1.
If there exists a pair
 , then output \((i,c,\mathsf{tag}_Q)\).
, then output \((i,c,\mathsf{tag}_Q)\). -
2.
Else, let \((r_1, r_2) \leftarrow \{0,1\}^\lambda \times \{0,1\}^\lambda \). (This was previously pseudo-randomness).
-
3.
Let \(I = \mathsf{Q}(1^\lambda ,1^n,i,\mathsf{sk}_\mathsf{LDC}; r_1)\).
-
4.
Let \(c = \mathsf{Enc}_{\mathsf{sk}_\mathsf{SKE}}(r_1; r_2)\).
-
5.
Let \(\mathsf{tag}_Q = \mathsf{MAC}_{\mathsf{sk}_\mathsf{MAC}}(i, I, c)\).
-
6.
Add new query pair to the list: \(\mathsf{QueryList}\leftarrow \mathsf{QueryList}\cup \{ ((i,I,c),\mathsf{tag}_Q) \}\).
-
7.
Add new output value to the list:
 .
. -
8.
Output \((I,c,\mathsf{tag}_Q)\).
-
1.
-
Input
 : Compute and output
: Compute and output  , as in Game 3.
, as in Game 3.
Claim
For \((i_0^*,i_1^*), \mathsf{InstSamp}\) defined in Game 1, and \(P_\mathsf{PRF}\) as above, there exists a negligible function \(\nu _4\) for which
Proof
Follows directly by the security of the PRF. Note that Step 1 ensures consistency if the same input  is received more than once.
is received more than once.
-
Game 5. SKE security. We consider a new program \(P_\mathsf{SKE}\) that replaces each \(c \leftarrow \mathsf{Enc}(r_1)\) in \(P_\mathsf{PRF}\) with an encryption of 0, i.e. \(c \leftarrow \mathsf{Enc}(0)\). (Note that each encryption in \(P_\mathsf{PRF}\) indeed uses true, freshly sampled randomness \(r_2\).) In addition, we modify the \(\mathsf{InstSamp}\) procedure so that instead of including encryptions of the encoded database as X, we now simply generate N fresh encryptions of 0 (and MAC the resulting ciphertexts).
Formally, define the new distribution \((P, (\mathsf{aux},X,I)) \leftarrow \mathsf{InstSamp}^{\mathsf{Enc}(0)}_i(1^\lambda )\), for \(i \in [n]\), by:
-
1.
\((x,\mathsf{aux}) \leftarrow \mathcal {A}_1(1^\lambda )\).
-
2.
\((P,\mathsf{sk}) \leftarrow \mathsf{Samp}(1^\lambda )\) (where \(\mathsf{Samp}\) is defined in \(\mathsf{Gen}\) in Construction 3).
-
3.
For \(j=1,\dots ,N\):
-
(a)
Sample CT of 0: \(\mathsf{data}\mathsf{CT}_j \leftarrow \mathsf{Enc}_{\mathsf{sk}_\mathsf{SKE}}(0)\).
-
(b)
MAC each item: \(\mathsf{tag}_j \leftarrow \mathsf{Tag}(\mathsf{sk}_\mathsf{MAC}, (j,\mathsf{data}\mathsf{CT}_j))\).
-
(c)
Let \(X_j = (\mathsf{data}\mathsf{CT}_j,\mathsf{tag}_j)\).
-
(a)
-
4.
\(r \leftarrow \{0,1\}^\lambda \);
 .
. -
5.
Output \((P, (\mathsf{aux},X,I))\).
(Stateful) program \(P_\mathsf{SKE}\):
Hardcoded: \(\mathsf{sk}_\mathsf{LDC},\mathsf{sk}_{\mathsf{SKE}},\mathsf{sk}_\mathsf{MAC}\), Plaintext database \(x = x_1,\dots ,x_n\), encoded database \(X = ( (\mathsf{data}\mathsf{CT}^\mathsf{real}_1,\mathsf{tag}^\mathsf{real}_1),\dots ,(\mathsf{data}\mathsf{CT}^\mathsf{real}_N,\mathsf{tag}^\mathsf{real}_N))\).
-
Initialize \(\mathsf{QueryList}\leftarrow \emptyset \).
-
Initialize \(\mathsf{OutputList}\leftarrow \emptyset \).
-
Input
 :
:-
1.
If there exists a pair
 , then output \((I,c,\mathsf{tag}_Q)\).
, then output \((I,c,\mathsf{tag}_Q)\). -
2.
Let \(I \leftarrow \mathsf{Q}(1^\lambda ,1^n,i,\mathsf{sk}_\mathsf{LDC})\).
-
3.
Let \(c \leftarrow \mathsf{Enc}_{\mathsf{sk}_\mathsf{SKE}}(0)\). (Previously encrypted the randomness used in \(\mathsf{Q}\)).
-
4.
Let \(\mathsf{tag}_Q = \mathsf{MAC}_{\mathsf{sk}_\mathsf{MAC}}(i, I, c)\).
-
5.
Add new query pair to the list: \(\mathsf{QueryList}\leftarrow \mathsf{QueryList}\cup \{ (i,I,c) \}\).
-
6.
Add new output value to the list:

-
7.
Output \((I,c,\mathsf{tag}_Q)\).
-
1.
-
Input
 :
:Compute and output
 , as in Game 3.
, as in Game 3.
Claim
For \((i_0^*,i_1^*)\) as in Game 1, and \(\mathsf{InstSamp}^{\mathsf{Enc}(0)}_i, P_\mathsf{SKE}\) as above, there exists a negligible function \(\nu _5\) for which
Proof
Follows by the semantic security of the SKE and a standard hybrid argument.
-
Game 6. Oblivious LDC security. In our final step, we argue that Eq. (6) cannot hold for non-negligible \(\alpha \). The reason is because interaction with the program \(P_\mathsf{SKE}\) can be completely simulated given only access to the challenge oracle for the Oblivious LDC security game. Therefore, the combined (non-uniform polynomial-time) adversary which runs the simulator \(\mathcal {S}_{(i^*_0,i^*_1)}\) and simulates the answers of its oracle \(P_\mathsf{SKE}(\cdot )\) serves as an Oblivious LDC adversary, who successfully distinguishes between the challenge I sampled via \(\mathsf{InstSamp}^{\mathsf{Enc}(0)}_{i_0^*}\) from that sampled via \(\mathsf{InstSamp}^{\mathsf{Enc}(0)}_{i_1^*}\).
Claim
For \((i_0^*,i_1^*)\) as in Game 1, and \(\mathsf{InstSamp}^{\mathsf{Enc}(0)}_i, P_\mathsf{SKE}\) as in Game 5, there exists a negligible function \(\nu _6\) for which
Proof
Suppose, to the contrary, the probability expression in Eq. (7) is equal to some non-negligible function \(\beta (\lambda )\).
Consider following the Oblivious LDC adversary \(\mathcal {B}_\mathsf{LDC}\):
-
1.
An Oblivious LDC challenge key is sampled as \(\mathsf{sk}\leftarrow \mathsf{G}(1^\lambda )\). \(\mathcal {B}_\mathsf{LDC}\) receives oracle access to \(\mathsf{Q}_\mathsf{sk}(\cdot )\) (which on input \(i \in [n]\) outputs \(I \leftarrow \mathsf{Q}(1^\lambda ,1^n,i,\mathsf{sk})\)).
-
2.
\(\mathcal {B}_\mathsf{LDC}\) simulates the remaining (non-LDC) items in \(\mathsf{InstSamp}^{\mathsf{Enc}(0)}\):
-
(a)
Simulate \(\mathcal {A}_1\) to obtain \((x,\mathsf{aux}) \leftarrow \mathcal {A}_1(1^\lambda )\).
-
(b)
Sample \(\mathsf{sk}_\mathsf{SKE}\leftarrow \mathsf{Gen}_\mathsf{SKE}(1^\lambda ); \mathsf{sk}_\mathsf{MAC}\leftarrow \mathsf{Gen}_\mathsf{MAC}(1^\lambda )\); and \(k \leftarrow \mathsf{Gen}_\mathsf{PRF}(1^\lambda )\).
-
(c)
For \(j=1,\dots ,N\):
-
i.
Sample CT of 0: \(\mathsf{data}\mathsf{CT}_j \leftarrow \mathsf{Enc}_{\mathsf{sk}_\mathsf{SKE}}(0)\).
-
ii.
MAC each item: \(\mathsf{tag}_j \leftarrow \mathsf{Tag}(\mathsf{sk}_\mathsf{MAC}, (j,\mathsf{data}\mathsf{CT}_j))\).
-
iii.
Let \(X_j = (\mathsf{data}\mathsf{CT}_j,\mathsf{tag}_j)\).
-
i.
-
(a)
-
3.
\(\mathcal {B}_\mathsf{LDC}\) selects the Oblivious LDC challenge index pair \((i_0^*,i_1^*) \in [n]^2\), and receives a challenge index sequence I generated as \(I \leftarrow \mathsf{Q}(1^\lambda ,1^n,i_b^*,\mathsf{sk})\) for randomly selected \(b \leftarrow \{0,1\}\).
-
4.
\(\mathcal {B}_\mathsf{LDC}\) simulates \(b' \leftarrow (\mathcal {S}_{(i_0^*i_1^*)})^{P_\mathsf{SKE}(\cdot )}(1^{|P|},1^n,1^\lambda ,(\mathsf{aux},X,I))\), for the values of \((\mathsf{aux},X,I)\) as generated in Step 2.
For each query made by \(\mathcal {S}_{(i_0^*i_1^*)}\) to the oracle \(P_\mathsf{SKE}(\cdot )\), \(\mathcal {B}_\mathsf{LDC}\) simulates the response:
-
In Step 2 of the computation for an input of the form
 , \(\mathcal {B}_\mathsf{LDC}\) makes a query to its oracle \(\mathsf{Q}_\mathsf{sk}(\cdot )\) on the input index i.
, \(\mathcal {B}_\mathsf{LDC}\) makes a query to its oracle \(\mathsf{Q}_\mathsf{sk}(\cdot )\) on the input index i. -
In all other steps, \(\mathcal {B}_\mathsf{LDC}\) simulates precisely.
-
-
5.
\(\mathcal {B}_\mathsf{LDC}\) outputs the guess bit \(b'\).
By construction, the advantage of \(\mathcal {B}_\mathsf{LDC}\) in the Oblivious LDC security challenge for \((\mathsf{G},\mathsf{E},\mathsf{Q},\mathsf{D})\) is precisely \(\beta \). Therefore, it must be the case that \(\beta \) is negligible.
Combining Games 1–6, we have that the original advantage \(\alpha \) of the adversary \(\mathcal {A}\) in the Public-Key PIR security challenge game must be negligible. That is, \((\mathsf{Gen},\mathsf{Encode},\mathsf{Query},\mathsf{Decode})\) of Construction 3 is a secure Public-Key PIR. This concludes the proof of Theorem 2.
Combining Proposition 2 and Theorem 2, we obtain the following main theorem.
Theorem 4
Suppose the Permuted Low-Degree Polynomials Conjecture holds (Conjecture 1), and one-way functions exist. Then given ideal obfuscation (alternatively, a \(\mathsf{poly}(\lambda )\)-size, stateless hardware token), there is a pk-PIR scheme with communication and computation complexity \(\mathsf{poly}(\lambda )\cdot n^{\epsilon }\), for every \(\epsilon >0\).
6 Conclusion and Open Problems
In this work we put forward two new cryptographic primitives: pk-PIR, a public-key variant of single-server PIR with preprocessing, and OLDC, its secret-key variant. We propose a candidate implementation for OLDC and reduce pk-PIR to OLDC via ideal obfuscation. Our work leaves open many interesting directions for further research. For example:
-
Further study the Permuted Low-Degree Polynomials Conjecture and more general instances of the Permuted Puzzles problem.
-
Can a construction of OLDC be based on standard cryptographic assumptions? Alternatively, can it be based on standard assumptions together with ideal obfuscation?
-
Are there OLDC candidates that provide a better tradeoff between storage overhead and decoding complexity?
-
Does a general transformation from OLDC to pk-PIR follow from indistinguishability obfuscation?
-
Is there a direct candidate construction of pk-PIR that does not rely on any form of general-purpose obfuscation?
Notes
- 1.
A smooth code supports a local decoding procedure in which each codeword symbol is read with roughly the same probability.
- 2.
Note that a pseudorandom function can also be used directly for this purpose; however, we use separate notation for clarity to emphasize the two uses.
- 3.
We ran this problem by several relevant experts, who were unaware of any negative results or implications to other well studied problems in complexity theory.
References
Asharov, G., Segev, G.: Limits on the power of indistinguishability obfuscation and functional encryption. In: IEEE 56th Annual Symposium on Foundations of Computer Science, FOCS 2015, Berkeley, CA, USA, 17–20 October 2015, pp. 191–209 (2015)
Barak, B., Garg, S., Kalai, Y.T., Paneth, O., Sahai, A.: Protecting obfuscation against algebraic attacks. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 221–238. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_13
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S.P., Yang, K.: On the (im)possibility of obfuscating programs. J. ACM 59(2), 6 (2012)
Beimel, A., Ishai, Y., Malkin, T.: Reducing the servers computation in private information retrieval: PIR with preprocessing. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 55–73. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44598-6_4
Bleichenbacher, D., Kiayias, A., Yung, M.: Decoding of interleaved reed solomon codes over noisy data. In: Baeten, J.C.M., Lenstra, J.K., Parrow, J., Woeginger, G.J. (eds.) ICALP 2003. LNCS, vol. 2719, pp. 97–108. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-45061-0_9
Bleichenbacher, D., Nguyen, P.Q.: Noisy polynomial interpolation and noisy Chinese remaindering. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 53–69. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_4
Boneh, D.: Finding smooth integers in short intervals using CRT decoding. J. Comput. Syst. Sci. 64(4), 768–784 (2002)
Canetti, R., Holmgren, J., Richelson, S.: Towards doubly efficient private information retrieval. In: TCC 2017. IACR Cryptology ePrint Archive 2017: 568 (2017)
Chor, B., Gilboa, N.: Computationally private information retrieval (extended abstract). In: Proceedings of the Twenty-Ninth Annual ACM Symposium on the Theory of Computing, El Paso, Texas, USA, 4–6 May 1997, pp. 304–313 (1997)
Chor, B., Kushilevitz, E., Goldreich, O., Sudan, M.: Private information retrieval. J. ACM 45(6), 965–981 (1998). Earlier version in Proceedings of FOCS 2005
Coppersmith, D., Sudan, M.: Reconstructing curves in three (and higher) dimensional space from noisy data. In: Proceedings of the 35th Annual ACM Symposium on Theory of Computing, 9–11 June 2003, San Diego, CA, USA, pp. 136–142 (2003)
Coron, J.-S.: Cryptanalysis of a public-key encryption scheme based on the polynomial reconstruction problem. In: Bao, F., Deng, R., Zhou, J. (eds.) PKC 2004. LNCS, vol. 2947, pp. 14–27. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24632-9_2
Curtmola, R., Garay, J.A., Kamara, S., Ostrovsky, R.: Searchable symmetric encryption: Improved definitions and efficient constructions. J. Comput. Secur. 19(5), 895–934 (2011)
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: FOCS (2013)
Garg, S., Miles, E., Mukherjee, P., Sahai, A., Srinivasan, A., Zhandry, M.: Secure obfuscation in a weak multilinear map model. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 241–268. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_10
Goldreich, O.: A note on computational indistinguishability. Inf. Process. Lett. 34(6), 277–281 (1990)
Goldreich, O.: Foundations of Cryptography - Basic Tools. Cambridge University Press, Cambridge (2001)
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM 33(4), 792–807 (1986)
Goldreich, O., Ostrovsky, R.: Software protection and simulation on oblivious rams. J. ACM 43(3), 431–473 (1996)
Hemenway, B., Ostrovsky, R.: Public-key locally-decodable codes. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 126–143. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_8
Ishai, Y., Kushilevitz, E., Ostrovsky, R., Sahai, A.: Batch codes and their applications. In: Proceedings of the 36th Annual ACM Symposium on Theory of Computing, Chicago, IL, USA, 13–16 June 2004, pp. 262–271 (2004)
Ishai, Y., Kushilevitz, E., Ostrovsky, R., Sahai, A.: Cryptography from anonymity. In: Proceedings of 47th Annual IEEE Symposium on Foundations of Computer Science (FOCS 2006), 21–24 October 2006, Berkeley, California, USA, pp. 239–248 (2006)
Karchmer, M., Wigderson, A.: On span programs. In: Proceedings of the Eight Annual Structure in Complexity Theory Conference, San Diego, CA, USA, 18–21 May 1993, pp. 102–111 (1993)
Katz, J., Trevisan, L.: On the efficiency of local decoding procedures for error-correcting codes. In: Proceedings of the Thirty-Second Annual ACM Symposium on Theory of Computing, 21–23 May 2000, Portland, OR, USA, pp. 80–86 (2000)
Kiayias, A., Yung, M.: Cryptanalyzing the polynomial-reconstruction based public-key system under optimal parameter choice. In: Lee, P.J. (ed.) ASIACRYPT 2004. LNCS, vol. 3329, pp. 401–416. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30539-2_28
Kopparty, S., Meir, O., Ron-Zewi, N., Saraf, S.: High-rate locally-correctable and locally-testable codes with sub-polynomial query complexity. In: Proceedings of the 48th Annual ACM SIGACT Symposium on Theory of Computing, STOC 2016, Cambridge, MA, USA, 18–21 June 2016, pp. 202–215 (2016)
Kushilevitz, E., Ostrovsky, R.: Replication is not needed: single database, computationally-private information retrieval. In: FOCS, pp. 364–373 (1997)
McEliece, R.J.: A public-key cryptosystem based on algebraic coding theory. Deep Space Netw. Prog. Rep. 44, 114–116 (1978)
Miltersen, P.B., Nisan, N., Safra, S., Wigderson, A.: On data structures and asymmetric communication complexity. J. Comput. Syst. Sci. 57(1), 37–49 (1998)
Morris, B., Rogaway, P., Stegers, T.: How to encipher messages on a small domain. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 286–302. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_17
Naor, M., Pinkas, B.: Oblivious polynomial evaluation. SIAM J. Comput. 35(5), 1254–1281 (2006)
Naor, M., Reingold, O.: Number-theoretic constructions of efficient pseudo-random functions. J. ACM 51(2), 231–262 (2004)
Ostrovsky, R., Pandey, O., Sahai, A.: Private locally decodable codes. In: Arge, L., Cachin, C., Jurdziński, T., Tarlecki, A. (eds.) ICALP 2007. LNCS, vol. 4596, pp. 387–398. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73420-8_35
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: Symposium on Theory of Computing, STOC 2014, New York, NY, USA, 31 May–03 June 2014, pp. 475–484 (2014)
Sidelnikov, V.M., Shestakov, S.O.: On insecurity of cryptosystems based on generalized Reed-Solomon codes. Discret. Math. Appl. 2, 439–444 (2009)
Song, D.X., Wagner, D., Perrig, A.: Practical techniques for searches on encrypted data. In: 2000 IEEE Symposium on Security and Privacy, Berkeley, California, USA, 14–17 May 2000, pp. 44–55 (2000)
Acknowledgments
We thank David Cash, Ronald Cramer, Venkat Guruswami, Tancrède Lepoint, Daniel Wichs, and Chaoping Xing for helpful discussions.
This work was done in part while the first three authors were visiting the Simons Institute for the Theory of Computing, supported by the Simons Foundation and by the DIMACS/Simons Collaboration in Cryptography through NSF grant #CNS-1523467. EB was supported in part by ISF grant 1861/16, AFOSR Award FA9550-17-1-0069, and ERC Grant no. 307952. YI was supported in part by NSF-BSF grant 2015782, BSF grant 2012366, ISF grant 1709/14, ERC grants 259426 and 742754, DARPA/ARL SAFEWARE award, NSF Frontier Award 1413955, NSF grants 1619348, 1228984, 1136174, and 1065276, a Xerox Faculty Research Award, a Google Faculty Research Award, an equipment grant from Intel, and an Okawa Foundation Research Grant. This material is based upon work supported by the DARPA through the ARL under Contract W911NF-15-C-0205. RP was supported in part by NSF Award CNS-1561209, NSF Award CNS-1217821, AFOSR Award FA9550-15-1-0262, a Microsoft Faculty Fellowship, and a Google Faculty Research Award. MW is supported in part by NSF grant CCF-1657049. The views expressed are those of the authors and do not reflect the official policy or position of the DoD, the NSF, or the U.S. Government.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Barriers to Proving Impossibility of OLDC
A Barriers to Proving Impossibility of OLDC
In this section we argue that ruling out the existence of OLDC is unlikely, as it would imply data structure lower bounds that seem beyond the reach of current techniques.
When considering a relaxed notion of OLDC that allows for adaptive decoding (i.e., decoding proceeds in rounds, where the location of each symbol read by the decoder may depend on the contents of the previous ones) there is a known barrier which was already pointed out in [4, 29]: proving strong lower bounds in the adaptive setting requires strong branching program lower bounds. However, no such connection is known in the non-adaptive case.
We argue that ruling out the existence of OLDC is very unlikely, as it would require proving strong data structure lower bounds. To be concrete, consider the following question:
Is it possible to preprocess any circuit \(C:\{0,1\}^k\rightarrow \{0,1\}\) of size \(k^{100}\) into a data structure D of size poly(k) such that for any input q, C(q) can be evaluated by non-adaptively probing \(k^{10}\) bits of D?
While this type of “dream data structure” seems extremely unlikely to exist, ruling it out seems beyond the reach of current techniques.Footnote 3 Given such a hypothetical data structure, we can take existing single-server PIR protocols (e.g., the one from [27]) and just let D be the data structure corresponding to the circuit \(C_x\) that computes the answer given the client’s PIR query. For instance, for the concrete dream data structure formulated above, we can take an instance of the protocol from [27] where the queries are of size k, the database is of size \(n=k^{98}\), and the circuit \(C_x\) is of size \(k^{100}\). This would result in an OLDC that makes \(k^{10}\ll n\) probes to the encoded database. In fact, this OLDC is stronger than our default notion in that has a deterministic encoder and does not make use of any secret key.
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Boyle, E., Ishai, Y., Pass, R., Wootters, M. (2017). Can We Access a Database Both Locally and Privately?. In: Kalai, Y., Reyzin, L. (eds) Theory of Cryptography. TCC 2017. Lecture Notes in Computer Science(), vol 10678. Springer, Cham. https://doi.org/10.1007/978-3-319-70503-3_22
Download citation
DOI: https://doi.org/10.1007/978-3-319-70503-3_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70502-6
Online ISBN: 978-3-319-70503-3
eBook Packages: Computer ScienceComputer Science (R0)





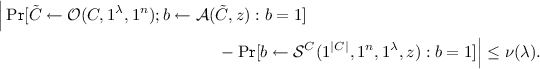


 failure probability.
failure probability. failure probability.
failure probability. . Output
. Output 
 .
.
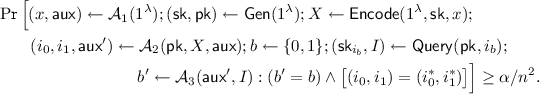
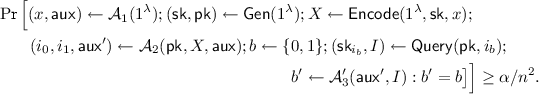
 ), and making use of the correctness of the obfuscator (so that
), and making use of the correctness of the obfuscator (so that  ), this implies
), this implies 
 .
.


 :
: .
. :
: .
. request for some index
request for some index  :
: .
. :
: . By the definition of the
. By the definition of the  portion of the programs, this means there exists
portion of the programs, this means there exists  :
: , then output
, then output  .
. : Compute and output
: Compute and output  , as in Game 3.
, as in Game 3. .
. :
: , then output
, then output 
 :
: , as in Game 3.
, as in Game 3. ,
, 