Keywords

1 Introduction

Software testing is an important activity of the software development life cycle that aims at revealing failures in a Software Under Test (SUT). Among many activities that help improving software quality, testing is still the most popular method, even though being expensive. Although testing is usually done manually in industrial applications, its automation has been a burgeoning interest of many researchers [1, 2]. Automation reduces cost and time and improves the quality degree of the testing activity.

Test data generation is the activity of finding a set of input values with the aim of detecting more failures of software systems. In the graph-based, structural approach to test data generation, the given software artifact (e.g., the source code concerned in this paper) is modeled as a graph. Control Flow Graph (CFG) is a graph that is obtained from source code for this purpose. According to the graph based criteria, some parts of the resulting graph should be covered by the test data. The simplest criteria are node coverage, edge coverage, and edge-pair coverage. The edge-pair criterion can be logically extended to the Complete Path Coverage (CPC) criterion. Because of the possibility of infinite number of test requirements, CPC is not practical for programs with loops. To resolve this issue, some solutions have been proposed by researchers, including a coverage criterion based on the prime path notion [4]. Unlike CPC, which is not practical, Prime Path Coverage (PPC) is a practical criterion that subsumes all other graph-based, structural coverage criteria. Thus, in this paper, we consider PPC as the coverage criterion.

The emphasis on the prime path coverage is due to the fact that covering prime paths may reveal failures that cannot be detected using other criteria. For instance, Fig. 1 shows a sample program along with its CFG. It contains a fault in line 11 (i.e., c = 0) which causes an exception (division by zero) in the second iteration of the existing loop. Based on the test requirements represented in Table 1, we can reveal the failure if we traverse path 7 which results when using the prime path coverage as the test criterion. Other coverage criteria may never find this fault.

Fig. 1.
figure 1

(a) The sample program (b) The corresponding CFG

Full size image
Table 1. Test paths according to node, edge and prime path coverage for the given example
Full size table

Test data generation is an expensive and time consuming activity. Therefore, development of methods to automate this activity is necessary. One approach for automatic test data generation is symbolic execution [6] that assigns symbolic values to program parameters in order to formulate program paths in terms of logical constraints. These constraints should be solved to find values which cause the program to follow specific paths. The main issue with this approach is that it is dependent on the capabilities of constraint solvers. Constraint solvers either are unable to resolve complex constraints or resolve such constraints in a computationally expensive way. Loop-dependent or array-dependent variables, pointer references and calls to external libraries whose implementations are unknown also introduce issues for this approach.

Dynamic methods are another automatic approach which generate test data through executing the SUT and determining the visited program locations via some form of program instrumentation. Program instrumentation is done to trace run-time information such as branch distance (detailed in Sect. 2). To do this, some extra statements will be added inside the original program before every predicate. These statements should not alter the behavior of the original program.

Using meta-heuristic algorithms is a category of dynamic methods called Search Based Software Testing (SBST). To apply this approach, the input domain of the SUT forms the search space, and a fitness function is defined which evaluates and scores different inputs to the SUT according to the given test criteria and test requirements. All the information needed by a meta-heuristic algorithm (e.g., if the given test data lead to traversing a specific location of the program) can be extracted from the execution of the instrumented SUT, accordingly.

The fitness function plays an important role in successful and efficient searches in meta-heuristic algorithms. A well-defined fitness function improves the likelihood of finding a proper solution. It also can result in consuming fewer system resources [7]. The fitness functions that have already been proposed for search based test data generation methods are divided into two categories: Branch Predicate Distance Function (BPDF) and Approximation level, which are described in Sect. 2.

As shown in Fig. 1, in order to cover prime paths, the test data generation method should be capable to cover those test paths that pass through loops one or more times. Therefore, a search-based test data generation method which regards the prime path coverage criterion needs an appropriate fitness function. To the best of our knowledge, only two works [8, 21] exist proposing fitness functions that can support the prime path coverage criterion. We refer to these fitness functions as NEHD [8] and BP1 [21]. However, the mentioned works are based on GA, while swarm intelligence algorithms have shown considerable results in the optimization problems [19].

NEHD has been designed to measure the Hamming distance from the first order to the nth order between two paths to consider the notion of sequences of branches. It results in time intensive calculations for long paths because the fitness function must continuously search for the number of combinations of branches from 1 to n order at each stage. Therefore, according to [20] the method of [8] has a poor efficiency.

BP1 is the linear combination of two measures, BPDF and Approximation level. BDPF is normalized in the range [0,1] but the Approximation level is not normalized despites the importance of normalization [18]. In this situation, normalization is essential to consider equal weights for the two measures of the fitness function (BPDF and Approximation level) for guiding individuals in the search process (Sect. 4).

We propose a new search-based approach for test data generation which aims at covering prime paths more effectively and more efficiently through two contributions: (1) we apply Ant Colony Optimization (ACO) and Particle Swarm Optimization (PSO) as two prominent swarm intelligence algorithms for test data generation, and (2) we propose a new normalized fitness function. ACO is a powerful method for finding shortest paths in dynamic networks. But, it is not always straightforward to apply it to other problems such as function optimization or searching n-dimensional spaces [10]. Thus, we should adapt ACO for the test generation problem in this paper.

The results of our experiments show that the customized ACO and PSO have better average coverage and better average time in comparison to GA. Also, ACO leads to a better average coverage comparing with PSO while, it has a worse average time.

The rest of the paper is structured as follows. In the next section, we review the basic ACO, PSO, and the current fitness functions for test data generation. The third section provides a brief overview of some related works. In Sect. 4, the customized ACO algorithm and the new fitness function are addressed. Then, the experimental analysis and results are presented and discussed in Sect. 5, followed by the conclusion and outline of the future works in Sect. 6.

2 Background

2.1 Basic ACO

ACO is one of the swarm intelligence algorithms [19, 28] whose application in various problems is known. Like many other meta-heuristic algorithms, the main idea of ACO is inspired by observing the natural behavior of living organisms. In ACO, different behaviors of ants in their community have been the source of inspiration.

ACO algorithms were originally conceived to find the shortest route in traveling salesman problems. In ACO, several ants travel across the edges that connect the nodes of a graph while depositing virtual pheromones. Ants that travel the shortest path will be able to make more return trips and deposit more pheromones in a given amount of time. Consequently, that path will attract more ants in a positive feedback loop. However, in nature, if more ants choose a longer path during the initial search, that path will become reinforced even if it is not the shortest. To overcome this problem, ACO assumes that virtual pheromones evaporate, thus reducing the probability that long paths are selected.

Several types of ACO algorithms have been developed with variations to address the specificities of the problems to be solved. Here, we briefly describe the basic ACO algorithm, known as the ant system [9]. Initially, ants are randomly distributed on the nodes of the graph. Each artificial ant chooses an edge from its location with a probabilistic rule that takes into account the length of the edge and the value of pheromones on that edge, as shown in Fig. 2 a virtual ant arriving from node A considers which edge to choose next on the basis of pheromone levels \( \tau_{ij} \) and visibilities \( \eta_{ij} \) (inverse of distance). The edge to node A is not considered because that node has already been visited. Once all ants have completed a full tour of the graph, each of them retraces its own route while depositing on the traveled edges a value of pheromones inversely proportional to the length of the route. Before restarting the ants from random locations for another search, the pheromones on all edges evaporate by a small quantity. The pheromone evaporation, combined with the probable choice of the edge, ensures that ants eventually converge on one of the shortest paths, but some ants continue to travel also on slightly longer paths.

Fig. 2.
figure 2

Choosing an edge with a probabilistic rule

Full size image

Because the basic ACO is suitable for search space with graph structure, a customization of the ACO is required to make this algorithm applicable for the test data generation problem with an n-dimensional search space.

2.2 PSO

In PSO [3], each particle keeps track of a position which is the best solution it has achieved so far as pbx; and the globally optimal solution is stored as gbest. The basic steps of PSO are as follow.

  1. 1.

    Initialize N particles with random positions \( px_{i} \) and velocities \( vi \) on the search space. Evaluate every particle’s current fitness \( f(px_{i} ) \). Initialize \( pbxi = px_{i} \) and \( gbest = i \), \( f(px_{i} ) = min(f(pbx_{0} ),\, f(pbx_{2} ), \ldots , f(pbx_{n} )); \)

  2. 2.

    Check whether the criterion (i.e. desired fitness function) is met. If the criterion is met, loop ends; else continue;

  3. 3.

    Change velocities according to formula (1):

    $$ v_{i} = v_{i} + c1\left( {pbx_{i} - px_{i} } \right) + c2 (pbx_{gbest} - px_{i} ) $$
    (1)

where \( \upomega \) is an intra weight c 1 , c 2 are learning factors.

  1. 4.

    Change positions according to formula (2):

    $$ px_{i} = px_{i} + vi $$
    (2)
  2. 5.

    Evaluate every particle’s fitness \( f(px_{i} ) \); if \( f(px_{i} ) \, < \,f(pbx_{i} ) \) then \( pbx_{i} \, = \, px_{i} \);

  3. 6.

    Update \( gbest \) and loop to step 2.

2.3 Fitness Functions for Test Data Generation

In this section, an overview of the two general categories of fitness functions [5], BPDF and Approximation level, is given. After that, BP1 and NEHD which support the coverage of prime paths are explained.

In a CFG, each decision node is associated with a branch predicate. The outgoing edges from decision nodes are labeled with true or false values of the corresponding predicate. To traverse a path during execution, it is necessary to find appropriate values for the input variables such that they satisfy all of the related branch predicates. One way to define a proper fitness function to guide such a search is using BPDF [5] that examines the branching node at which the actual path deviated from the intended path. Its objective is to measure how close this test data is to fulfill the branch predicate condition that would have sent it down the intended path. For instance, suppose that branch predicate C is (a = b) and f is the BPDF-based fitness function. When |a − b| = 0, then f = 0; otherwise, f = |a − b| + k where factor k is a positive constant which is always added if the predicate is not true. In this way, the fitness function returns a non-negative value if the predicate is false, and zero when it is true. A complete list of branch distance formulas for different relational predicate types is presented in [1].

The other way to define fitness functions is using Approximation level [5]. The Approximation level indicates how close the actual path taken was to reaching the partial aim (for example, the number of correct nodes the test data encountered or how often that path was generated). In the case of correct nodes, test data with higher Approximation levels are judged to be more fit than those with low values.

The Normalized Extended Hamming Distance (NEHD) is designed to measure the Hamming distance from the first order to the nth order between two paths. But, according to [20] the method proposed in [8] has a poor efficiency.

The fitness function BP1 is a linear combination of BDPF and Approximation level that has the form shown in formula 3.

$$ BP1 = NC - \frac{EP}{MEP} $$
(3)

  • NC is the value of the path similarity metric computed based on the number of coincident nodes between the executed path and the target one, starting from the entry node up to the node where the executed path is different from the target one. This value can vary from 1 to the number of nodes in the target path. In the case similarity = 1, only the entry node is common to both paths.

  • EP is the absolute value of the BDPF associated with the branch which is deviated from the target path.

  • MEP is the BDPF maximum value among the candidate solutions that executed the same nodes of the intended path.

\( \frac{EP}{MEP} \) is a measure of the candidate solution error with respect to all the solutions that executed the right path up to the same deviation predicate. This value is used as a solution penalty. Thus, the search dynamics is characterized by the co-existence of two objectives: maximize the number of nodes correctly executed with respect to the intended path and minimize the predicate function of the reached predicates. It should be noted that the range of BP1 is between 0 and the length of the target path (because of NC) so when the target path is long, the significance of the BPDF parameter is deceased. The reason is that BPDF is in the range [0,1] and it is linearly combined with the Approximation level part.

Experimental results [5] show that BP1 has a better performance than NEHD [5, 20]. BP1 has two parts where the first part is normalized between [0,1] but the second part is not normalized. The importance of normalization is shown in [7, 18]. In this paper, we use a normalized fitness function based on BP1.

3 Related Work

In this section, we review the related work for test data generation based on various meta-heuristic algorithms. In the literature, there are many works addressing search based test data generation [1, 2]. In this section, we review the prominent methods that center around different meta-heuristic algorithms.

Jones [22] and Pargas [16] investigated the usage of GA for automated test data generation regarding branch coverage. Their experiments on several small programs showed that in general, GA significantly outperforms the random method. Harman and McMinn [24] performed an empirical study on GA-based test data generation for large-scale programs and validated its effectiveness over other search algorithms such as hill climbing. Fraser et al. [25] have implemented a tool named EvoSuite to generate a whole test suite for satisfying the given coverage goals. The default coverage criterion used by EvoSuite is branch coverage, but there is also rudimentary support for some coverage criteria in the context of mutation and data flow testing. In their tool, GA and Memetic are used to generate JUnit test suites for classes in Java.

Simulated Annealing (SA) is a well-known search algorithm which solves complex optimization problems using the idea of neighborhood search. Tracey et al. proposed a framework to generate test data based on SA [26] with the aim of overcoming some of the problems associated with the application of local search. In this method, test data can be generated for specific paths without loops, or for specific statements or branches. Also, Cohen et al. adopted SA to generate test data for combinatorial testing [27].

Windisch et al. applied PSO to generate test data [29]. They compared their method with a GA-based technique in terms of the convergence characteristic. Mao et al. have built a new method, called TDGen-PSO [17] which has exhibited better performance comparing with GA and SA.

ACO has shown a comparable effect on solving optimization problems in comparison to other meta-heuristic search algorithms like GA [32,33,34]. Applying ACO for solving the problems in software testing have been investigated in [35]. ACO was adopted in [36, 37] to produce test sequences (not test data) for state-based software testing.

Li et al. [31] used ACO to generate test data in accordance with the branch coverage criterion. Unlike our approach, this work transforms the search space (to a graph form) instead of adapting the ACO algorithm. In addition, [31] has not provided any implementation and evaluation for its idea. Mao et al. [30] used ACO to generate test data for the branch coverage criterion. They set the pheromone to each ant in the colony; thus, pheromone is not distributed in the search space. By defining pheromone in each ant, a memory is dedicated to each ant so ACO has in fact converted to a memory-based algorithm [10] like PSO. Their findings show that ACO is better than GA and SA in this regard. Ayari et al. proposed an ACO-based method for mutation testing [23]. Their measure for test data adequacy is the mutation score. Meanwhile, their experimental analysis is based on just two benchmark programs. Bauersfeld et al. used ACO to find input sequences for testing applications with Graphical User Interface (GUI) [19].

As two approaches capable of covering prime paths, Lin et al. [8] and Bueno et al. [21] introduced methods for test data generation based on the GA algorithm. They proposed NEHD and BP1 as their fitness function, respectively. These works are based on GA while scalability and performance of evolutionary algorithms are questionable [13, 14]. In addition, as reported in [19], swarm intelligence algorithms have shown considerable results in the optimization problems.

In this paper, we propose a new search based approach for test data generation which aims at covering prime paths more effectively and more efficiently through a new normalized fitness function and using ACO and PSO as two prominent swarm intelligence algorithms. A customization of the ACO is required to make this algorithm applicable for the test data generation problem.

4 Test Data Generation

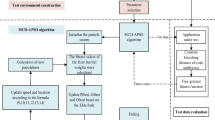
The aim of this work is to produce a set of test data to satisfy the given test paths. There is no restriction on test paths and they can involve prime paths as well. For this purpose, our method considers every test path as a target, separately, and repeats the data generation process until the target path is covered or the maximum number of iterations is exceeded. For PSO, we use its basic algorithm, explained in Sect. 2, so in this section, we only explain our customization on ACO. A top-level view of the algorithm is shown in Fig. 3. For each test path of the program, ants are randomly scattered in the search space. The instrumented program is executed by a test data \( td \) which is determined by the location of a specific ant in the search space. According to the covered path, the fitness value is computed. Then, for each ant of the population, local search, global search, and pheromone updating are performed iteratively.

Fig. 3.
figure 3

Algorithm for test data generation

Full size image

4.1 The Customized ACO

The basic ACO algorithm is mainly used in discrete optimization problems which are formulated on the graph structure. We customize the basic ACO to generate test data in an n-dimensional space. The test data generation can be formally described as follows: Given a program under test P, suppose it has d input variables represented by vector \( X_{k} = (x_{k} , x_{k} , \ldots ,x_{k} ) \) can be treated as the position vector of an ant in ACO. For each input variable \( x_{i} (1\, \le \,i\, \le \,d) \), assume it takes its values from domain \( {\text{D}}_{i} \). Thus, the corresponding input domain of the whole program is \( {\text{D}} = {\text{D}}_{1} \times {\text{D}}_{2} \times \ldots \times {\text{D}}_{d} \).

In the basic ACO, the search space has a graph structure. Thus, the neighbor area of an ant is the set of the adjacent nodes of its corresponding position in the graph. Since the structure of the test data generation problem does not form a graph, the basic ACO algorithm must be modified such that it can be applied on the non-graph structure of the problem. For the test data generation problem, each ant’s position can be viewed as a test data and represented as a vector in input domain D. For any ant \( {\text{k }}(1\, \le \,{\text{k}}\, \le \,{\text{n}}) \), its position can be denoted as \( X_{k} = (x_{k} , x_{k} , \ldots ,x_{k} ) \) is the number of input variables and therefore the number of dimensions).

A major challenge for applying ACO to test data generation is the form of pheromone because the search space is continuing and it does not have either node or edge for defining pheromone on it. To tackle this problem, we partition the search space by partitioning every domain of each input variable to b equivalent parts that can be any number dividable by the range of input domain. The best value for b is obtained from sensitivity analysis which is explained more in Sect. 5.

The number of partitions for each input variable is determined separately. To illustrate partitioning, consider a program with two inputs x and y. If we partition the input domain of x to b1 parts and the input domain of y to b2 parts, there are totally φ = b1 × b2 partitions on the 2-dimensional space (Fig. 4). Each partition has a special pheromone value. Therefore, the number of pheromones in the search space is equal to the number of partitions in this space.

Fig. 4.
figure 4

A sample partitioned search space

Full size image

Local Search.

During the local search, each ant looks for a better solution in its own neighborhood area. To compute the neighbors of ant k, we must consider it in the n-dimensional space D. The neighbors of ant with position vector \( X_{k} = (x_{k1} ,x_{k2} , \ldots ,x_{kd} ) \) have the position vector \( Xk^{\prime } = (x_{k1}^{\prime } ,x_{k2}^{\prime } , \ldots x_{kd}^{\prime } ) \) where \( x_{ki}^{\prime } = x_{ki} + s,\quad - 1\, \le \,s\, \le \,1 \) and \( X_{k}^{\prime } \ne X \). If an input has integer domain, s is 0 or 1 or −1. For a continues variable, three random numbers are selected for s. In a 2-dimensional search space, the location of an ant can be (1, 1). Thus, the positions of the neighbors are: (0, 1), (1, 0), (0, 0), (2, 1), (1, 2), (2, 2), (2, 0), (0, 2). The number of neighbors for an ant in a d-dimensional space is 3d − 1 as it is shown in Fig. 5.

Fig. 5.
figure 5

The number of neighbors in local search based on the number of domains

Full size image

The rule for local search or local transfer of ant’s position can be represented as follows: ant k transfers from \( Xk \) to a new position \( Xk^{\prime } \) if the fitness of \( Xk^{\prime } \) is better than that of \( {\text{Xk}} \) \( (i.e., \;Fitness\left( {Xk^{\prime } } \right)\, < \,Fitness(Xk)) \), and \( Xk^{\prime } \) has the best fitness value among \( Xk^{\prime } \) neighbors. Otherwise, the ant must stay at its current position (i.e., \( Xk \)). It should be mentioned that according to our implementation, the best fitness value is 0. Thus, a lower value is considered as a better fitness.

Global Search.

The previous step is an activity of local optimization for each ant in the colony. But, this is not sufficient to find a high-quality solution because, at the local transfer stage, there might be an ant with no movement since it could not find a neighboring position with better fitness value. This situation is known as local optima trap [10] which could be resolved by an action called global transfer.

For any ant k in the colony \( (1\, \le \,{\text{k}}\, \le \,{\text{n}}), \) if its fitness is lower than the average level, i.e., \( {\text{Fitness}}({\text{X}}_{k} ) \, > \,{\text{Fitness}}_{avg} \), a random number \( q \) is selected. \( {\text{Fitness}}_{avg} \) is the average fitness of whole ant colony and \( q \) is a random number from 0 to 1. When \( {\text{Fitness}}({\text{X}}_{k} ) \, > \, {\text{Fitness}}_{avg} \) and \( q \, < \,q0 \), the position of ant k is randomly set in the whole search space (\( q0 \) is a preset parameter). When \( {\text{Fitness}}({\text{X}}_{k} )\, > \, {\text{Fitness}}_{avg} \) and \( q \, \ge \, q0 \), the position of ant k is randomly set to a position in a partition which has a maximum value of pheromone. With doing global search any ant that has in the local optima situation is transferred with probability \( q0 \) to a random position in the whole search space and with a probability \( 1\, - \, q0 \) to a position which has a maximum value of pheromone.

Update Pheromone.

After doing global and local search for all ants in each run, the pheromone is updated (Fig. 3). To update pheromone value in every partition, the following rule is used:

$$ \tau \left( j \right) \leftarrow \left( {1 - \alpha } \right) \times \tau \left( j \right) + \alpha \, \times \,number\,of\,ants\,in\,partition \,j. $$
(4)

Where \( \alpha \in \) (0, 1) is a pheromone evaporation rate, \( \tau \left( j \right) \) represents the value of pheromone in the jth partition; j stands for the partition index.

4.2 Fitness Function

We represent a test path by sequences of characters which are the labels of edges in the CFG of the SUT. Therefore, for test data generation, the fitness function is calculated for the target path and the path traversed by any test data. To formulate the fitness function considering the order of the branches, both branch distance and Approximation level are used. The fitness function FT that is used to evaluate each candidate solution has the form shown in formula 5 and has two separately normalized parts. One part relates to the branch distance and the other relates to the Approximation level. Each part has the value between 0 and 1. Thus, FT is ranged from 0 to 2.

$$ FT = \left( {1 - \frac{NC}{TP}} \right) + \frac{EP}{EP + \beta } $$
(5)

  • NC is the value of the path similarity metric. (described in Sect. 2.3)

  • TP is the length of the target path, thus (1 − NC/TP) has a normalized value between 0 and 1. The value zero is the optimal value for this part of FT.

  • EP is the value of branch distance. (described in Subsect. 2.3)

  • β is a parameter for the normalization proposed in [18]; based on the experiment done in [18], we set it to 1.

It should be mentioned that the normalization function that we used (i.e. \( \frac{EP}{Ep + \beta } \)) is the same as what proposed in [18]. By using this function instead of \( \frac{EP}{MEP} \) (in BP1), there is no need to calculate MEP which leads to more efficiency.

In contrast to BP1, the values of fitness are normalized between 0 and 2, and fitness = 0 means the target path is fully met. Normalization is separately done for two parts of FT because the two parts of the fitness function would have the same share to conduct the individuals.

5 Experiments

In this section, we assess our proposed approach, which uses two prominent swarm intelligence algorithms PSO and ACO, against the GA-based method proposed in [21]. As mentioned before, it is shown by experiment in [20] that the method proposed in [8] has low efficiency. Thus, we do not compare our approach with [8]. To perform the experiment, all the three algorithms have been implemented with the same fitness function, proposed in Subsect. 4.2. We define the following two criteria as evaluation metrics:

  • Average Coverage (AC), i.e., the average percentage of covered test paths in repeated runs.

  • Average Time (AT), i.e., the average execution time (in milliseconds) of realizing test path coverage.

5.1 Experimental Setup

We selected a set of benchmark programs from the literature. Most of these programs, including “Triangle Type” (1), “Power xy” (2), “Remainder” (3), “GCD” (4), “LCM” (5) and “ComputeTax” (6), are commonly used in software testing research. Table 2 shows the number of lines of code (LoC) and the number of prime paths (No. PP) of each program.

Table 2. Programs selected for the experiment
Full size table

We manually instrumented each original program without changing its semantics. Then, we constructed the corresponding CFG by using Control flow graph factory tool [12] and extracted a list of prime paths using the tool available in [11].

Before using GA, ACO, and PSO, their parameters must be initialized. The chosen values are shown in Table 3.

Table 3. Parameter setup
Full size table

5.2 Experimental Results

The experimental results are presented in Table 4. The results show that our customized ACO is better than GA in terms of both criteria. Furthermore, our customized ACO has equal or better average coverage comparing with the PSO algorithm. However, PSO reaches the solution in less time in comparison to ACO because this algorithm is basically less complex.

Table 4. Comparison between the customized ACO, PSO, and GA
Full size table

In the customized ACO, selecting the best value for parameter “b” (i.e. the number of parts) is important, therefore, the sensitivity analysis is done for this parameter. To do this, we calculate the values of the two evaluation criteria with different number of parts. As can be seen in Figs. 6 and 7, the average coverage and average time are increased with increasing the number of parts, but when we reach to the maximum coverage, we do not have any change in the average coverage with increasing the number of the parts. Also, the best value of parameter b for programs “Triangle Type” and “Synthetic” is 5000, for “compute tax” is 50000, for “Remainder” and “LCM” is 1000 and for “Pow xy” and “GCD” is 500. In each program, when parameter b is set to this value, the least average time and the most average coverage are gained.

Fig. 6.
figure 6

Average coverage against the number of partitions

Full size image
Fig. 7.
figure 7

Average time against the number of partitions

Full size image

6 Conclusions and Future Works

In this paper, we have presented a search-based test data generation approach to cover prime paths of the program under test. The proposed approach uses ACO and PSO as two prominent swarm intelligence algorithms and a new normalized fitness function. We customized the ACO algorithm by combining it with the idea of input space partitioning. Also, the proposed fitness function is a normalization of the fitness function BP1 proposed in the [2]. We compared the customized ACO, PSO, and GA when all of these three algorithms are applied with the proposed fitness function. The results have shown that our method is stronger than GA in terms of both evaluation criteria. In addition, the results manifest that in comparing with PSO, the customized ACO results in a better coverage, but has worse efficiency. As future work, we will consider the following research areas:

  • The main reason that causes the swarm intelligence algorithms do not widely apply in the test data generation problem is the search space of the string type. Most swarm intelligence based algorithms work on the structural search space, while the input domain of the string variables does not have a defined neighborhood concept.

  • Using the static structure of the program in the partitioning of the search space (i.e. defining parameter “b” in the customized ACO).

  • Multiple path test data generation (i.e. in each run, we consider multiple paths as target instead of one path) by swarm intelligence algorithms is another issue that could be considered in the future. There are approaches for multiple test path generation by evolutionary algorithms, but they cannot be applied directly using the swarm intelligence (i.e., population-based) algorithms.