Abstract
We present VINTE, a theorem prover for conditional logics for counterfactual reasoning introduced by Lewis in the seventies. VINTE implements some internal calculi recently introduced for the basic system \(\mathbb {V}\) and some of its significant extensions with axioms \(\mathbb {N}\), \(\mathbb {T}\), \(\mathbb {C}\), \(\mathbb {W}\) and \(\mathbb {A}\). VINTE is inspired by the methodology of  and it is implemented in Prolog. The paper shows some experimental results, witnessing that the performances of VINTE are promising.
and it is implemented in Prolog. The paper shows some experimental results, witnessing that the performances of VINTE are promising.
Supported by the Project TICAMORE ANR-16-CE91-0002-01, by the EU under Marie Skłodowska-Curie Grant Agreement No. [660047], and by the Project “ExceptionOWL”, Università di Torino and Compagnia di San Paolo, call 2014.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Conditional logics are extensions of classical logic by a conditional operator  . They have a long history [11], and recently they have found an interest in several fields of AI and knowledge representation. Just to mention a few (see [1] for a complete bibliography), they have been used to reason about prototypical properties, to model belief change [8], to reason about access control policies [5], to formalize epistemic change in a multi-agent setting [2, 4]. Conditional logics can also provide an axiomatic foundation of nonmonotonic reasoning [9]: here a conditional
. They have a long history [11], and recently they have found an interest in several fields of AI and knowledge representation. Just to mention a few (see [1] for a complete bibliography), they have been used to reason about prototypical properties, to model belief change [8], to reason about access control policies [5], to formalize epistemic change in a multi-agent setting [2, 4]. Conditional logics can also provide an axiomatic foundation of nonmonotonic reasoning [9]: here a conditional  is read “normally, if A then B”.
is read “normally, if A then B”.
In early seventies, Lewis proposed a formalization of conditional logics in order to represent a kind of hypothetical reasoning that cannot be captured by the material implication of classical logic [10]. His original motivation was to formalize counterfactuals, that is to say, conditionals of the form “if A were the case then B would be the case”, where A is false. The family of logics studied by Lewis is semantically characterized by sphere models, a particular kind of neighbourhood models introduced by Lewis himself. In Lewis’ terminology, a sphere denotes a set of worlds; in sphere models, each world is equipped with a nested system of such spheres. From the viewpoint of the given world, inner sets represent the “most plausible worlds”, while worlds belonging only to outer sets are considered as less plausible. In order to treat the conditional operator, Lewis takes as primitive the comparative plausibility connective \( \preccurlyeq \): a formula \(A \preccurlyeq B\) means “A is at least as plausible as B”. The conditional  can be then defined as “A is impossible” or “\(A \wedge \lnot B\) is less plausible than \(A \wedge B\)”. However, the latter assertion is equivalent to the simpler one “\(A \wedge \lnot B\) is less plausible than A”Footnote 1.
can be then defined as “A is impossible” or “\(A \wedge \lnot B\) is less plausible than \(A \wedge B\)”. However, the latter assertion is equivalent to the simpler one “\(A \wedge \lnot B\) is less plausible than A”Footnote 1.
In previous works [6, 16] we have introduced internal, standard, cut-free calculi for most logics of the Lewis family, namely logics \( \mathbb {V}\), \( \mathbb {V}\mathbb {N}\), \( \mathbb {V}\mathbb {T}\), \( \mathbb {V}\mathbb {W}\), \( \mathbb {V}\mathbb {C}\), \( \mathbb {V}\mathbb {A}\) and \( \mathbb {V}\mathbb {N}\mathbb {A}\). Here we describe a Prolog implementation of the invertible calculi \( {\mathcal {I}_{\mathcal {L}}^{\mathsf {i}}} \) introduced in [6]. The program, called VINTE, gives a decision procedure for the respective logics, and it is inspired by the methodology of  [3]. The idea is that each axiom or rule of the sequent calculi is implemented by a Prolog clause of the program. The resulting code is therefore simple and compact: the implementation of VINTE for \(\mathbb {V}\) consists of only 3 predicates, 21 clauses and 57 lines of code. We provide experimental results by comparing VINTE with the following theorem provers for conditional logics: CondLean [12], GoalD
\(\mathcal {U}\)CK [13] and NESCOND [14, 15], and we show that the performances of VINTE are quite promising. The program VINTE, as well as all the Prolog source files, are available for free usage and download at http://193.51.60.97:8000/vinte/.
[3]. The idea is that each axiom or rule of the sequent calculi is implemented by a Prolog clause of the program. The resulting code is therefore simple and compact: the implementation of VINTE for \(\mathbb {V}\) consists of only 3 predicates, 21 clauses and 57 lines of code. We provide experimental results by comparing VINTE with the following theorem provers for conditional logics: CondLean [12], GoalD
\(\mathcal {U}\)CK [13] and NESCOND [14, 15], and we show that the performances of VINTE are quite promising. The program VINTE, as well as all the Prolog source files, are available for free usage and download at http://193.51.60.97:8000/vinte/.
2 Lewis’ Conditional Logics
We consider the conditional logics defined by Lewis in [10]. The set of conditional formulae is given by \( \mathcal {F}{::}= p \mid \bot \mid \mathcal {F}\rightarrow \mathcal {F}\mid \mathcal {F}\preccurlyeq \mathcal {F}, \) where \(p \in \mathcal {V}\) is a propositional variable. The other boolean connectives are defined in terms of \(\bot ,\rightarrow \) as usual. Intuitively, a formula \(A \preccurlyeq B\) is interpreted as “A is at least as plausible as B”.
As mentioned above, Lewis’ counterfactual implication  can be defined in terms of comparative plausibility \( \preccurlyeq \) as
can be defined in terms of comparative plausibility \( \preccurlyeq \) as

The semantics of this logic is defined by Lewis in terms of sphere semantics:
Definition 1
A sphere model (or model) is a triple  , consisting of a non-empty set W of elements, called worlds, a mapping
, consisting of a non-empty set W of elements, called worlds, a mapping  , and a propositional valuation
, and a propositional valuation  . Elements of
. Elements of  are called spheres. We assume the following conditions: for every
are called spheres. We assume the following conditions: for every  we have \(\alpha \ne \emptyset \), and for every
we have \(\alpha \ne \emptyset \), and for every  we have \(\alpha \subseteq \beta \) or \(\beta \subseteq \alpha \). The latter condition is called sphere nesting.
we have \(\alpha \subseteq \beta \) or \(\beta \subseteq \alpha \). The latter condition is called sphere nesting.
The valuation  is extended to all formulae by:
is extended to all formulae by:  ;
;  ;
;  . For \(w \in W\) we also write \(w \Vdash A\) instead of
. For \(w \in W\) we also write \(w \Vdash A\) instead of  . As for spheres, we write \( \alpha \Vdash ^{\forall }A \) meaning \( \forall x \in \alpha . x \Vdash A\) and \( \alpha \Vdash ^{\exists } A \) meaning \( \exists x \in \alpha . x \Vdash A \)
Footnote 2. Validity and satisfiability of formulae in a class of models are defined as usual. Conditional logic \(\mathbb {V}\) is the set of formulae valid in all sphere models.
. As for spheres, we write \( \alpha \Vdash ^{\forall }A \) meaning \( \forall x \in \alpha . x \Vdash A\) and \( \alpha \Vdash ^{\exists } A \) meaning \( \exists x \in \alpha . x \Vdash A \)
Footnote 2. Validity and satisfiability of formulae in a class of models are defined as usual. Conditional logic \(\mathbb {V}\) is the set of formulae valid in all sphere models.
Extensions of \(\mathbb {V}\) are semantically given by specifying additional conditions on the class of sphere models, namely:
-
normality: for all \( w \in W\) we have
 ;
; -
total reflexivity: for all \( w \in W\) we have
 ;
; -
weak centering: normality holds and for all
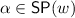 we have \(w \in \alpha \);
we have \(w \in \alpha \); -
centering: for all \( w \in W\) we have
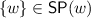 ;
; -
absoluteness: for all \( w,v \in W\) we have
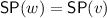 Footnote 3.
Footnote 3.
Extensions of \(\mathbb {V}\) are denoted by concatenating the letters for these properties: \(\mathbb {N}\) for normality, \(\mathbb {T}\) for total reflexivity, \(\mathbb {W}\) for weak centering, \(\mathbb {C}\) for centering, and \(\mathbb {A}\) for absoluteness. All the above logics can be characterized by axioms in a Hilbert-style system [10, Chap. 6]. The modal axioms formulated in the language with only the comparative plausibility operator are presented in Table 1 (where \(\vee \) and \(\wedge \) bind stronger than \(\preccurlyeq \)). The propositional axioms and rules are the standard ones.
3 Internal Calculi for Conditional Logics
Table 2 presents calculi \({\mathcal {I}_{\mathcal {L}}^{\mathsf {i}}}\), where \(\mathcal {L}\) ranges over the logics \(\mathbb {V},\mathbb {V}\mathbb {N},\mathbb {V}\mathbb {T},\mathbb {V}\mathbb {W},\mathbb {V}\mathbb {C},\mathbb {V}\mathbb {A},\) \(\mathbb {V}\mathbb {N}\mathbb {A}\), introduced in [6]. The basic constituent of sequents are blocks of the form \(\left[ A_1, \ldots , A_m \vartriangleleft A \right] \), with \( A_1, \ldots , A_m, A \) formulas, representing disjunctions of \(\preccurlyeq \)-formulas. A sequent is a tuple \(\varGamma \Rightarrow \varDelta \), where \(\varGamma \) is a multiset of conditional formulae, and \(\varDelta \) is a multiset of conditional formulae and blocks. The formula interpretation of a sequent is given by:

As usual, given a formula \(G \in \mathcal {L}\), in order to check whether G is valid we look for a derivation of \(\Rightarrow G\). Given a sequent \(\varGamma \Rightarrow \varDelta \), we say that it is derivable if it admits a derivation, namely a tree whose root is \(\varGamma \Rightarrow \varDelta \), every leaf is an instance of \(\mathsf {init}\) or \(\bot _L\) or \(\top _R\), and every non-leaf node is (an instance of) the conclusion of a rule having (an instance of) the premises of the rule as children.
In [6] it is shown that:
Theorem 1
The calculi \({\mathcal {I}_{\mathcal {L}}^{\mathsf {i}}} \) are sound and complete for the respective logics.
In [6] it has been also shown that the calculi \({\mathcal {I}_{\mathcal {L}}^{\mathsf {i}}}\) can be used in a decision procedure for the logic \(\mathcal {L}\) as follows. Since contractions and weakenings are admissible we may assume that a derivation of a duplication-free sequent (containing duplicates neither of formulae nor of blocks) only contains duplication-free sequents: whenever a (backwards) application of a rule introduces a duplicate of a formula already in the sequent, it is immediately deleted in the next step using a backwards application of weakening. While officially our calculi do not contain the weakening rules, the proof of admissibility of weakening yields a procedure to transform a derivation with these rules into one without. Since all rules have the subformula property, the number of duplication-free sequents possibly relevant to a derivation of a sequent is bounded in the number of subformulae of that sequent, and hence enumerating all possible loop-free derivations of the above form yields a decision procedure for the logic.
Theorem 2
Proof search with the blocking technique above for a sequent \( \varGamma \Rightarrow \varDelta \) in calculus \( {\mathcal {I}_{\mathcal {L}}^{\mathsf {i}}} \) always comes to an end in a finite number of steps.
As usual, in order to implement such a decision procedure, we have to control the application of the rules to avoid the introduction of duplicated sequents. Concerning the rule \(\preccurlyeq _L^\mathsf {i}\), the principal formula \(A \preccurlyeq B\) is copied into the premisses, then we have to avoid that, in a backward application of the rule, such formula is redundantly applied by using the same block \(\left[ \varSigma \vartriangleleft C \right] \). Since no rule, with the exception of \(\mathsf {jump}\), remove formulas from blocks, we allow a backward application of \(\preccurlyeq _L^\mathsf {i}\) to a sequent \(\varGamma , A \preccurlyeq B \Rightarrow \varDelta , \left[ \varSigma \vartriangleleft C \right] \) if neither \(\left[ B, \varSigma \vartriangleleft C \right] \) nor \(\left[ \varSigma ' \vartriangleleft C \right] \), where \(B, \varSigma \subset \varSigma '\) belong to \(\varDelta \), and neither \(\left[ \varSigma \vartriangleleft A \right] \) nor \(\left[ \varSigma ' \vartriangleleft A \right] \), where \(\varSigma \subset \varSigma '\) belong to \(\varDelta \). Similarly for the \(\mathsf {com}^\mathsf {i}\) rule, which can be applied backward to blocks \(\left[ \varSigma _1 \vartriangleleft A \right] \) and \(\left[ \varSigma _2 \vartriangleleft B \right] \) if neither \(\left[ \varSigma _1, \varSigma _2 \vartriangleleft A \right] \) nor \(\left[ \varSigma _1, \varSigma _2 \vartriangleleft B \right] \) are introduced redundantly in the premisses. For rules like \(\mathsf {W}^\mathsf {i}\), whose premisses contain the principal formula, we just need to check whether the formulas introduced in the premisses by a backward application of the rule already belong to such premisses or not. In the first case, the application of the rule is blocked. As an example, if \(\mathsf {W}^\mathsf {i}\) is applied to \(\Rightarrow \left[ A \vee B \vartriangleleft C \right] \), then the premiss is \(\Rightarrow \left[ A \vee B \vartriangleleft C \right] , A \vee B\), that becomes \((*) \ \Rightarrow \left[ A \vee B \vartriangleleft C \right] , A, B\) after an application of the rule \(\vee _R\). The rule \(\mathsf {W}^\mathsf {i}\) can be further applied to \((*)\), since \(A \vee B\) does not belong to the right-hand side of the sequent, then obtaining the premiss \(\Rightarrow \left[ A \vee B \vartriangleleft C \right] , A, B, A \vee B\), and at this point neither \(\mathsf {W}^\mathsf {i}\) nor \(\vee _R\) can be further applied.
4 Design of VINTE
In this section we present a Prolog implementation of the internal calculi \( {\mathcal {I}_{\mathcal {L}}^{\mathsf {i}}} \) recalled in Sect. 3. The program, called VINTE (\(\mathbb {V}\): INTernal calculi and Extensions), is inspired by the “lean” methodology of  , even if it does not follow its style in a rigorous manner. The program comprises a set of clauses, each one of them implements a sequent rule or axiom of \( {\mathcal {I}_{\mathcal {L}}^{\mathsf {i}}} \). The proof search is provided for free by the mere depth-first search mechanism of Prolog, without any additional ad hoc mechanism.
, even if it does not follow its style in a rigorous manner. The program comprises a set of clauses, each one of them implements a sequent rule or axiom of \( {\mathcal {I}_{\mathcal {L}}^{\mathsf {i}}} \). The proof search is provided for free by the mere depth-first search mechanism of Prolog, without any additional ad hoc mechanism.
VINTE represents a sequent with a pair of Prolog lists [Gamma,Delta], where Gamma and Delta represent the left-hand side and the right-hand side of the sequent, respectively. Elements of Gamma are formulas, whereas elements of Delta can be either formulas or pairs [Sigma,A], where Sigma is a Prolog list, representing a block \(\left[ \varSigma \vartriangleleft A \right] \). Symbols \(\top \) and \(\bot \) are represented by constants true and false, respectively, whereas connectives \(\lnot \), \(\wedge \), \(\vee \), \(\rightarrow \), \(\preccurlyeq \), and  are represented by -,
are represented by -,  , ?,
, ?,  , and
, and  . Propositional variables are represented by Prolog atoms. As an example, the Prolog pair
. Propositional variables are represented by Prolog atoms. As an example, the Prolog pair

is used to represent the sequent

The calculi \( {\mathcal {I}_{\mathcal {L}}^{\mathsf {i}}} \) are implemented by the predicate

This predicate succeeds if and only if the sequent \(\varGamma \Rightarrow \varDelta \) represented by the pair of lists [Gamma,Delta] is derivable. When it succeeds, the output term ProofTree matches with a representation of the derivation found by the prover. For instance, in order to prove that the formula \((A \preccurlyeq B) \vee (B \preccurlyeq A)\) is valid in \(\mathbb {V}\), one queries VINTE with the goal:  Each clause of prove implements an axiom or rule of \( {\mathcal {I}_{\mathcal {L}}^{\mathsf {i}}} \). To search a derivation of a sequent \(\varGamma \Rightarrow \varDelta \), VINTE proceeds as follows. First of all, if \(\varGamma \Rightarrow \varDelta \) is an instance of either \(\bot _L\) or \(\top _R\) or \(\mathsf {init}\), the goal will succeed immediately by using one of the following clauses for the axioms:
Each clause of prove implements an axiom or rule of \( {\mathcal {I}_{\mathcal {L}}^{\mathsf {i}}} \). To search a derivation of a sequent \(\varGamma \Rightarrow \varDelta \), VINTE proceeds as follows. First of all, if \(\varGamma \Rightarrow \varDelta \) is an instance of either \(\bot _L\) or \(\top _R\) or \(\mathsf {init}\), the goal will succeed immediately by using one of the following clauses for the axioms:

If \(\varGamma \Rightarrow \varDelta \) is not an instance of the ending rules, then the first applicable rule will be chosen, e.g. if \(\varDelta \) contains a formula  , then the clause implementing the \(\preccurlyeq _R\) rule will be chosen, and VINTE will be recursively invoked on the unique premise of such a rule. VINTE proceeds in a similar way for the other rules. The ordering of the clauses is such that the application of the branching rules is postponed as much as possible, with the exception of the rule \(\mathsf {jump}\) which is the last rule to be applied. As an example, the clause implementing \(\preccurlyeq _L^\mathsf {i}\) is as follows:
, then the clause implementing the \(\preccurlyeq _R\) rule will be chosen, and VINTE will be recursively invoked on the unique premise of such a rule. VINTE proceeds in a similar way for the other rules. The ordering of the clauses is such that the application of the branching rules is postponed as much as possible, with the exception of the rule \(\mathsf {jump}\) which is the last rule to be applied. As an example, the clause implementing \(\preccurlyeq _L^\mathsf {i}\) is as follows:

In line 4, the auxiliary predicate remove_duplicates is invoked in order to remove duplicated formulas in the multiset of formulas \(B, \varSigma \). This is equivalent to apply weakening if the formula B already belongs to \(\varGamma \). Another auxiliary predicate, memberOrdSet, is then invoked in lines 5 and 6 in order to implement the decision procedure described at the end of Sect. 3: Prolog ordsets are used in order to deal with the equivalence of lists where formulas occur in different orders. Since the rule is invertibile, Prolog cut \(\mathtt{!}\) is used in line 6 to eventually block backtracking. The \(\mathsf {jump}\) rule is implemented as follows:

This is the only non invertible rule, and a backtracking point is introduced by the choice of the block \(\left[ \varSigma \vartriangleleft A \right] \) in \(\varDelta \) to which apply the rule.
The implementation of the calculi for extensions of \(\mathbb {V}\) is very similar. The only significant difference is in the more sophisticated mechanism needed to ensure termination. As an example, in system implementing the calculus for \(\mathbb {V}\mathbb {C}\), the predicate prove is equipped by a further parameter, called AppliedC, containing the list of formulas of the form \(A \preccurlyeq B\) to which the rule \(\mathsf {C}^\mathsf {i}\) has been already applied in the current branch. The code implementing the rule \(\mathsf {C}^\mathsf {i}\) is as follows:

Line 3 shows how this parameter is used in order to avoid multiple application of \(\mathsf {C}^\mathsf {i}\) to the same formula \(A \preccurlyeq B\) in a given branch, then the consequent loop in the proof search: if \(A \preccurlyeq B\) belongs to AppliedC, then the rule \(\mathsf {C}^\mathsf {i}\) has been already applied to it in the current branch and it is no longer applied; otherwise, the predicate prove is recursively invoked on the premisses of the rule, and \(A \preccurlyeq B\) is added to the list of formulas already employed for applications of \(\mathsf {C}^\mathsf {i}\).
VINTE can be used by means of a simple web interface, implemented in php and allowing the user to check whether a conditional formula is valid by using his computer as well as his mobile device. The web interface also allows the user to choose the conditional system to adopt, namely \(\mathbb {V}\) or one of the extensions mentioned in Sect. 2. When a formula is valid, VINTE builds a pdf file showing a derivation in the invertible calculi recalled in Sect. 3 as well as the  source file. Prolog source codes and experimental results are also available. Some pictures of VINTE are shown in Figs. 1 and 2.
source file. Prolog source codes and experimental results are also available. Some pictures of VINTE are shown in Figs. 1 and 2.
When the user wants to check whether a formula F is valid, then (i) he selects the conditional logic to use, (ii) he types F in the form and (iii) clicks the button in order to execute the calculi presented in Sect. 3.
5 Performance of VINTE
The performance of VINTE seems to be promising. We have tested it by running SICStus Prolog 4.0.2 on an Apple MacBook Pro, 2.7 GHz Intel Core i7, 8 GB RAM machine. In absence of theorem provers specifically tailored for Lewis’ logics, we have compared the performances of VINTE with those of the following theorem provers for conditional logics:
-
CondLean 3.1, implementing labelled sequent calculi [12];
-
GoalD \(\mathcal {U}\)CK, implemented a goal-directed proof procedure [13];
All the above mentioned theorem provers take into account conditional logics based on the selection function semantics [11], namely conditional logic CK and extensions with axioms ID, MP, CEM, CSO, that are weaker than the ones considered by VINTE, then the experimental results are only partially significant and only aim at conjecturing that the performance of VINTE is promising.
We have performed two kinds of experiments: 1. we have tested the four provers on randomly generated formulas, fixing different time limits; 2. we have tested VINTE for system \(\mathbb {V}\mathbb {N}\) and NESCOND over a set of valid formulas in the logic CK, therefore also valid in \(\mathbb {V}\mathbb {N}\) [10].
Concerning 1 (Table 3), we have tested the four provers over 2000 random sequents with 20 formulas built from 7 different atomic variables and with a high level of nesting (10): both VINTE and NESCOND are able to answer in all cases within 1 s, whereas CondLean 3.1 is not able to conclude anything in 55 cases over 1000. Performance of GoalD \(\mathcal {U}\)CK is even worse, since it fails to answer in 174 cases. The differences seem much more significant when considering sequents with more formulas (100) and with a higher level of nesting (20): with a time limit of 5 ms, GoalD \(\mathcal {U}\)CK is faster than CondLean 3.1 and NESCOND, since it is not able to answer only in 136 cases over 1000, against 173 timeouts of CondLean 3.1 and 479 timeouts of NESCOND. VINTE is able to answer again in all cases, and only NESCOND is also able to complete all the tests, when the time limit is extended to 1 s. We have repeated the above experiments by considering implementations of VINTE for extensions of \(\mathbb {V}\), obtaining the results summarized in Table 4.
As mentioned, since the four provers take into account different logics, in general they give a different answer over the same - randomly generated - sequent. Then, this kind of tests over CK formulas could be considered not very significant. Instead, we should test VINTE over a set of significant formulas for the specific Lewis’ logics that it is designed for: to this aim, we are currently developing a set of benchmarks for VINTE drawn by valid instances of Lewis’ axioms.
Concerning 2, we have considered 76 valid formulas obtained by translating K valid formulas provided by Heuerding in conditional formulas: \(\Box A\) is replaced by  Footnote 4, whereas \(\diamond A\) is replaced by
Footnote 4, whereas \(\diamond A\) is replaced by  . We have compared the performance of VINTE, implementation for \(\mathbb {V}\mathbb {N}\), with those of NESCOND, the best prover among those taken into account for conditional logics based on the selection function semantics [15]. As expected, the performance of NESCOND is still significantly better than those of VINTE: fixing a time limit of 1ms, NESCOND is able to check the validity of the considered formula in the 86 % of cases, whereas VINTE is able to answer only in the 11 % of cases. However, VINTE is able to reach a percentage of successes of 37 % by extending the time limit to 1 s, and over 60% in 3 s (even if, in this last case, NESCOND is not able to answer only in 2 cases over 76). Obviously, this result is justified by the fact that VINTE supports stronger systems of conditional logics with respect to NESCOND, which is specifically tailored for CK and all the proposed results are restricted to such weaker system supported by both provers.
. We have compared the performance of VINTE, implementation for \(\mathbb {V}\mathbb {N}\), with those of NESCOND, the best prover among those taken into account for conditional logics based on the selection function semantics [15]. As expected, the performance of NESCOND is still significantly better than those of VINTE: fixing a time limit of 1ms, NESCOND is able to check the validity of the considered formula in the 86 % of cases, whereas VINTE is able to answer only in the 11 % of cases. However, VINTE is able to reach a percentage of successes of 37 % by extending the time limit to 1 s, and over 60% in 3 s (even if, in this last case, NESCOND is not able to answer only in 2 cases over 76). Obviously, this result is justified by the fact that VINTE supports stronger systems of conditional logics with respect to NESCOND, which is specifically tailored for CK and all the proposed results are restricted to such weaker system supported by both provers.
6 Conclusions and Future Issues
We have presented VINTE, a theorem prover implementing internal calculi for Lewis’ conditional logics introduced in [6]. Our long term project is to develop both calculi and theorem provers for the whole family of Lewis’ logics. One further step in this direction is represented by the hypersequent calculi for containing both uniformity (all worlds have the same set of accessible worlds) and total reflexivity presented in [7]. Notice that an implementation of hypersequent calculi is an interesting task in itself.
We also aim at improving the performances of VINTE by implementing standard refinements and heuristics. We also intend to extend VINTE to handle countermodel generation for unprovable formulas. Last, as mentioned in the previous section, we are currently developing a set of benchmarks for VINTE for a more detailed analysis of the performances of the theorem prover.
Notes
- 1.
It is worth noticing that in turn the connective \(\preccurlyeq \) can be defined in terms of
 .
. - 2.
Employing this notation, satisfiability of a \( \preccurlyeq \)-formula in a model becomes the following: \(x \Vdash A\preccurlyeq B \) iff for all
 . \( \alpha \Vdash ^{\forall } \lnot B \) or \( \alpha \Vdash ^{\exists } A \).
. \( \alpha \Vdash ^{\forall } \lnot B \) or \( \alpha \Vdash ^{\exists } A \). - 3.
It is worth noticing that absoluteness can be equally stated as local absoluteness:
 it holds
it holds  .
. - 4.
It is worth noticing that this translation introduces an exponential blowup.
References
Alenda, R., Olivetti, N., Pozzato, G.L.: Nested sequent calculi for normal conditional logics. J. Log. Comput. 26(1), 7–50 (2016)
Baltag, A., Smets, S.: The logic of conditional doxastic actions. Texts Log. Games 4, 9–31 (2008). Special Issue on New Perspectives on Games and Interaction
Beckert, B., Posegga, J.: leanTAP: lean tableau-based deduction. J. Autom. Reason. 15(3), 339–358 (1995)
Board, O.: Dynamic interactive epistemology. Games Econ. Behav. 49(1), 49–80 (2004)
Genovese, V., Giordano, L., Gliozzi, V., Pozzato, G.L.: Logics in access control: a conditional approach. J. Log. Comput. 24(4), 705–762 (2014)
Girlando, M., Lellmann, B., Olivetti, N., Pozzato, G.L.: Standard sequent calculi for Lewis’ logics of counterfactuals. In: Michael, L., Kakas, A. (eds.) JELIA 2016. LNCS, vol. 10021, pp. 272–287. Springer, Cham (2016). doi:10.1007/978-3-319-48758-8_18
Girlando, M., Lellmann, B., Olivetti, N., Pozzato, G.L.: Hypersequent calculi for Lewis’ conditional logics with uniformity and reflexivity. In: Nalon, C., Schmidt, R.A. (eds.) TABLEAUX 2017. LNCS (LNAI), vol. 10501, pp. 131–148. Springer, Cham (2017)
Grahne, G.: Updates and counterfactuals. J. Log. Comput. 8(1), 87–117 (1998)
Kraus, S., Lehmann, D., Magidor, M.: Nonmonotonic reasoning, preferential models and cumulative logics. Artif. Intell. 44(1–2), 167–207 (1990)
Lewis, D.: Counterfactuals. Blackwell, Hoboken (1973)
Nute, D.: Topics in Conditional Logic. Reidel, Dordrecht (1980)
Olivetti, N., Pozzato, G.L.: CondLean 3.0: improving condlean for stronger conditional logics. In: Beckert, B. (ed.) TABLEAUX 2005. LNCS (LNAI), vol. 3702, pp. 328–332. Springer, Heidelberg (2005). doi:10.1007/11554554_27
Olivetti, N., Pozzato, G.L.: Theorem proving for conditional logics: condlean and goalduck. J. Appl. Non-Class. Log. 18(4), 427–473 (2008)
Olivetti, N., Pozzato, G.L.: NESCOND: an implementation of nested sequent calculi for conditional logics. In: Demri, S., Kapur, D., Weidenbach, C. (eds.) IJCAR 2014. LNCS (LNAI), vol. 8562, pp. 511–518. Springer, Cham (2014). doi:10.1007/978-3-319-08587-6_39
Olivetti, N., Pozzato, G.L.: Nested sequent calculi and theorem proving for normal conditional logics: the theorem prover NESCOND. Intelligenza Artificiale 9(2), 109–125 (2015)
Olivetti, N., Pozzato, G.L.: A standard internal calculus for Lewis’ counterfactual logics. In: Nivelle, H. (ed.) TABLEAUX 2015. LNCS, vol. 9323, pp. 270–286. Springer, Cham (2015). doi:10.1007/978-3-319-24312-2_19
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Girlando, M., Lellmann, B., Olivetti, N., Pozzato, G.L., Vitalis, Q. (2017). VINTE: An Implementation of Internal Calculi for Lewis’ Logics of Counterfactual Reasoning. In: Schmidt, R., Nalon, C. (eds) Automated Reasoning with Analytic Tableaux and Related Methods. TABLEAUX 2017. Lecture Notes in Computer Science(), vol 10501. Springer, Cham. https://doi.org/10.1007/978-3-319-66902-1_9
Download citation
DOI: https://doi.org/10.1007/978-3-319-66902-1_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-66901-4
Online ISBN: 978-3-319-66902-1
eBook Packages: Computer ScienceComputer Science (R0)





 ;
; ;
;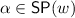 we have
we have 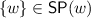 ;
;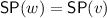


 .
. .
.  it holds
it holds  .
.