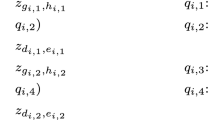Rotation-Based Formulation for Stable Matching

Abstract

We introduce new CP models for the many-to-many stable matching problem. We use the notion of rotation to give a novel encoding that is linear in the input size of the problem. We give extra filtering rules to maintain arc consistency in quadratic time. Our experimental study on hard instances of sex-equal and balanced stable matching shows the efficiency of one of our propositions as compared with the state-of-the-art constraint programming approach.

1 Introduction

In two-sided stable matching problems the objective is to assign some agents to other agents based on their preferences [14]. The classic exemplar of such problems is the well known stable marriage (SM) problem, first introduced by Gale and Shapley [6]. In SM the two sets of agents are called men and women. Each man has a preference list over the women and vice versa. The purpose is to find a matching where each man (respectively woman) is associated to at most one woman (respectively man) that respects a criterion called stability. A matching M in this context is stable if any pair $\langle m, w \rangle$ (where m is a man and w is a woman) that does not belong to M satisfies the property that m prefers his partner in M to w or w prefers her partner in M to m.

This family of problems has gained considerable attention as it has a wide range of applications such as assigning doctors to hospitals, students to college, and in kidney exchange problems. The stable marriage problem itself can be solved in $O(n^2)$ time [6] where n is the maximum number of men/women. This is also true for the general case of many-to-many stable matching; the complexity $O(n^2)$ is given in the proof of Theorem 1 in [1]. However, when facing real world situations the problem often considers additional optimality criteria. In many cases, the problem becomes intractable and specialized algorithms for solving the standard version are usually hard to adapt. The use of a modular approach such as constraint programming is very beneficial to tackle such cases.

Many constraint programming approaches exist in the literature for stable matching problems. Examples of these concern stable marriage [7, 21, 22], hospital residents (HR) [13, 20], many-to-many stable matching [3], and stable room-mates [17]. Despite the fact that many-to-many stable matching generalizes HR and SM, it has not gained as much attention as SM and HR in the constraint programming community. In this paper, we follow this line of research by proposing an effective and efficient model for all three variants of stable matching: one-to-one, many-to-one, and many-to-many. Our propositions are based on a powerful structure called rotations. The latter has been used to model the stable room-mates problem in [9] (p. 194) and [4, 5].

We leverage some known properties related to rotations in order to propose a novel SAT formulation of the general case of many-to-many stable matching. We show that unit propagation on this formula ensures the existence of a particular solution. Next, we use this property to give an algorithm that maintains arc consistency if one considers many-to-many stable matching as a (global) constraint. The overall complexity for arc consistency is $O(L^2)$ time where L is total input size of all preference lists. Our experimental study on hard instances of sex-equal and balanced stable matching show that our approach outperforms the state-of-the-art constraint programming approach [20].

The remainder of this paper is organized as follows. In Sect. 2 we give a brief overview of constraint programming. We present the stable matching problem in Sect. 3 as well as various concepts related to rotations. In Sect. 4 we propose a novel formulation of stable matching based on the notion of rotation. We show in Sect. 5 some additional pruning rules and show that arc consistency can be maintained in $O( L^2)$ worst case time complexity. Lastly, in Sect. 6 we present an empirical experimental study on two hard variants of stable matching and show that one of our new models outperforms the state-of-the-art constraint programming approach in the literature.

2 Constraint Programming

We provide a short formal background related to constraint programming. Let $\mathcal{X}$ be a set of integer variables. A domain for $\mathcal{X}$, denoted by $\mathcal{D}$, is a mapping from variables to finite sets of integers. For each variable $x_{}$, we call $\mathcal{{D}}{({x_{}})}$ the domain of the variable $x_{}$. A variable is called assigned when $\mathcal{{D}}{({x_{}})} = \{v\}$. In this case, we say that v is assigned to $x_{}$ and that ${x_{}}$ is set to v. A variable is unassigned if it is not assigned. A constraint C defined over $[x_{{1}},\ldots ,x_{{k}}]$ ($k\in \mathbb {N}^*$) is a finite subset of $\mathbb {Z}^k$. The sequence $[x_{{1}},\ldots ,x_{{k}}]$ is the scope of C (denoted by $\mathcal{X}(C)$) and k is called the arity of C. A support for C in a domain $\mathcal{D}$ is a k-tuple $\tau$ such that $\tau \in C$ and $\tau [i] \in \mathcal{{D}}{({x_{i}})}$ for all $i \in [1,\ldots ,k]$. Let $x_{i} \in \mathcal{X}(C)$ and $v \in \mathcal{{D}}{({x_{i}})}$. We say that the assignment of v to $x_{}$ has a support for C in $\mathcal{D}$ iff there exists a support $\tau$ for C in $\mathcal{D}$ such that $\tau [i]=v$. The constraint C is arc consistent (AC) in $\mathcal{D}$ iff $\forall i \in [1,\ldots ,k]$, $\forall v \in \mathcal{{D}}{({x_{i}})}$, the assignment of v to $x_{i}$ has a support in $\mathcal{D}$. A filtering algorithm (or propagator) for a constraint C takes as input a domain $\mathcal{D}$ and returns either $\emptyset$ if there is no support for C in $\mathcal{D}$ (i.e., failure) or a domain $\mathcal{D}'$ such that any support for C in $\mathcal{D}$ is a support for C in $\mathcal{D}'$, $\forall x_{} \in \mathcal{X}(C)$, $\mathcal{D}'(x_{}) \subseteq \mathcal{{D}}{({x_{}})}$, and $\forall x_{} \notin \mathcal{X}(C)$, $\mathcal{D}'(x_{}) = \mathcal{{D}}{({x_{}})}$. A Boolean variable has an initial domain equal to $\{0, 1\}$ (0 is considered as false and 1 as true). A clause is a disjunction of literals where a literal is a Boolean variable or its negation. Clauses are usually filtered with an algorithm called unit propagation [16].

Let $\mathcal{X}$ be a set of variables, $\mathcal{D}$ be a domain, and $\mathcal{C}$ be a set of constraints defined over subsets of $\mathcal{X}$. The constraint satisfaction problem (CSP) is the question of deciding if an $|\mathcal{X}|-$tuple of integers $\tau$ exists such that the projection of $\tau$ on the scope of every constraint $C \in {\mathcal{C}}$ is a support for C in $\mathcal{D}$. We consider in this paper classical backtracking algorithms to solve CSPs by using filtering algorithms at every node of the search tree [19].

3 Stable Matching

We consider the general case of the many-to-many stable matching problem. We follow the standard way of introducing this problem by naming the two sets of agents as workers and firms [14]. We use a notation similar to that of [3].

Let $n_{F}, n_{W}\in \mathbb {N}^*$, ${F}=\{f_{{1}}, f_{{2}}, \ldots , f_{{n_{F}}} \}$ be a set of firms, ${W}=\{w_{{1}}, w_{{2}}, \ldots , w_{{n_{W}}} \}$ be a set of workers, and $n=\max \{n_{F},n_{W}\}$. Every firm $f_{{i}}$ has a list, $P_{{f_{{i}}}}$, of workers given in a strict order of preference (i.e., no ties). The preference list of a worker $w_{{i}}$ is similarly defined. We denote by $P_{{{W}}}=\{P_{{w_{{i}}}}~|~ i \in [1,n_{W}]\}$ the set of preferences of workers, and by $P_{{{F}}}=\{P_{{f_{{j}}}}~|~ j \in [1,n_{F}]\}$ the set of preferences of firms. We use L to denote the sum of the sizes of the preference lists. Note that the size of the input problem is O(L). Therefore we shall give all our complexity results with respect to L.

For every firm $f_{{j}}$ (respectively, worker $w_{{i}}$), we denote by $q_{{f_{{j}}}}$ (respectively, $q_{{w_{{i}}}}$) its quota. We denote by $q_{{{W}}}=\{q_{{w_{{i}}}}~|~ i \in [1,n_{W}]\}$ the set of quota for workers, and by $q_{{{F}}}=\{q_{{f_{{j}}}}~|~ j \in [1,n_{F}]\}$ the set of quotas for firms. We use the notation $w_{{i}} \succ _{{f_{{k}}}} w_{{j}}$ when a firm $f_{{k}}$ prefers worker $w_{{i}}$ to worker $w_{{j}}$. The operator $\succ _{{w_{{k}}}}$ is defined similarly for any worker $w_{{k}}$.

A pair $\langle {w_{{i}}}, {f_{{j}}}\rangle$ is said to be acceptable if $w_{{i}} \in P_{{f_{{j}}}}$ and $f_{{j}} \in P_{{w_{{i}}}}$. A matching ${M}$ is a set of acceptable pairs. Let ${M}(w_{{i}})=\{f_j ~|~ \langle {w_{{i}}}, {f_{{j}}}\rangle \in {M}\}$, and ${M}(f_{{j}})=\{w_i ~|~ \langle {w_{{i}}}, {f_{{j}}}\rangle \in {M}\}$. A worker $w_{{i}}$ (respectively, firm $f_{{j}}$) is said to be under-assigned in ${M}$ if $| {M}(w_{{i}}) | < q_{{w_{{i}}}}$ (respectively, $| {M}(f_{{j}}) | < q_{{f_{{j}}}}$). We define for every worker $w_{{i}}$, $last_{{{M}}}(w_{{i}})$ as the least preferred firm for $w_{{i}}$ in ${M}(w_{{i}})$ if ${M}(w_{{i}}) \ne \emptyset$. For every firm $f_{{j}}$, $last_{{{M}}}(f_{{j}})$ is similarly defined. A pair $\langle {w_{{i}}}, {f_{{j}}}\rangle \notin {M}$ is said to be blocking ${M}$ if it is acceptable such that the following two conditions are true:

• $w_{{i}}$ is under-assigned in ${M}$ or $\exists f_{{k}} \in {M}(w_{{i}})$ and $f_{{j}} \succ _{{w_{{i}}}} f_{{k}}$.

• $f_{{j}}$ is under-assigned in ${M}$ or $\exists w_{{l}} \in {M}(f_{{j}})$ and $w_{{i}} \succ _{{f_{{j}}}} w_{{l}}$.

Definition 1

(Stability). A matching ${M}$ is (pairwise) stable if $\forall w_{{i}} \in {W}$, $| {M}(w_{{i}}) | \le q_{{w_{{i}}}}$, $\forall f_{{j}} \in {F}$, $| {M}(f_{{j}}) | \le q_{{f_{{j}}}}$, and there is no blocking pair for ${M}$.

An instance of the many-to-many stable matching problem is defined by the tuple $\langle {W},{F}, P_{{{W}}}, P_{{{F}}}, q_{{{W}}}, q_{{{F}}} \rangle$. The problem is to find a stable matching if one exists.

A pair $\langle {w_{{i}}}, {f_{{j}}}\rangle$ is stable if there exists a stable matching ${M}$ containing $\langle {w_{{i}}}, {f_{{j}}}\rangle$, unstable otherwise. A pair $\langle {w_{{i}}}, {f_{{j}}}\rangle$ is fixed if it is included in all stable matchings.

Let ${M}, {M}'$ be two stable matchings. A worker $w_{{i}}$ prefers ${M}$ no worse than ${M}'$ (denoted by ${M}\succeq _{{w_{{i}}}} {M}'$) if (1) ${M}(w_{{i}}) = {M}'(w_{{i}})$ or (2) $|{M}(w_{{i}})| \ge |{M}'(w_{{i}})|$ and $last_{{{M}}}(w_{{i}}) \succ _{{w_{{i}}}} last_{{{M}'}}(w_{{i}})$. It should be noted that every worker (respectively, firm) is assigned to the same number of firms (respectively, workers) in every stable matching [1]. So the condition $|{M}(w_{{i}})| \ge |{M}'(w_{{i}})|$ is always true in the case of many-to-many stable matching. Let ${M}, {M}'$ be two different stable matchings. We say that ${M}$ dominates ${M}'$ (denoted by ${M}\succeq _{{{W}}} {M}'$) if ${M}\succeq _{{w_{{i}}}} {M}'$ for every worker $w_{{i}}$. This is called the worker-oriented dominance relation. The firm-oriented dominance relation ( $\succeq _{{{F}}}$ ) is similarly defined for firms.

The authors of [1] showed that a stable matching always exists and can be found in $O(n^2)$ time. More precisely, the complexity of finding a stable matching is O(L). Moreover, they showed that there always exist worker-optimal and firm-optimal stable matchings (with respect to $\succeq _{{{W}}}$ and $\succeq _{{{F}}}$). We denote these two matchings by ${M}_0$ and ${M}_z$, respectively.

Example 1

(An instance of many-to-many stable matching (from [3]). Consider the example where $n_{W}=5, n_{F}=5$, and for all $1\le i,j\le 5$, $q_{{w_{{i}}}}=q_{{f_{{j}}}}=2$. The preference lists for workers and firms are given in Table 1.

Table 1. Example of preference lists

There exist seven stable matchings for this instance:

• ${M}_0= \{\langle {w_{{1}}}, {f_{{1}}}\rangle ,~ \langle {w_{{1}}}, {f_{{2}}}\rangle$, $\langle {w_{{2}}}, {f_{{2}}}\rangle ,~ \langle {w_{{2}}}, {f_{{3}}}\rangle$, $\langle {w_{{3}}}, {f_{{3}}}\rangle ,~ \langle {w_{{3}}}, {f_{{4}}}\rangle$, $\langle {w_{{4}}}, {f_{{4}}}\rangle$, $\langle {w_{{4}}}, {f_{{5}}}\rangle$, $\langle {w_{{5}}}, {f_{{5}}}\rangle ,~ \langle {w_{{5}}}, {f_{{1}}}\rangle \}$

• ${M}_1 = \{\langle {w_{{1}}}, {f_{{1}}}\rangle , \langle {w_{{1}}}, {f_{{3}}}\rangle$, $\langle {w_{{2}}}, {f_{{2}}}\rangle , \langle {w_{{2}}}, {f_{{3}}}\rangle$, $\langle {w_{{3}}}, {f_{{5}}}\rangle , \langle {w_{{3}}}, {f_{{4}}}\rangle$, $\langle {w_{{4}}}, {f_{{4}}}\rangle , \langle {w_{{4}}}, {f_{{5}}}\rangle$, $\langle {w_{{5}}}, {f_{{2}}}\rangle , \langle {w_{{5}}}, {f_{{1}}}\rangle \}$

• ${M}_2 = \{\langle {w_{{1}}}, {f_{{4}}}\rangle , \langle {w_{{1}}}, {f_{{3}}}\rangle$, $\langle {w_{{2}}}, {f_{{2}}}\rangle , \langle {w_{{2}}}, {f_{{3}}}\rangle$, $\langle {w_{{3}}}, {f_{{5}}}\rangle , \langle {w_{{3}}}, {f_{{4}}}\rangle$, $\langle {w_{{4}}}, {f_{{1}}}\rangle , \langle {w_{{4}}}, {f_{{5}}}\rangle$, $\langle {w_{{5}}}, {f_{{2}}}\rangle , \langle {w_{{5}}}, {f_{{1}}}\rangle \}$

• ${M}_3 = \{\langle {w_{{1}}}, {f_{{4}}}\rangle , \langle {w_{{1}}}, {f_{{5}}}\rangle$, $\langle {w_{{2}}}, {f_{{2}}}\rangle , \langle {w_{{2}}}, {f_{{3}}}\rangle$, $\langle {w_{{3}}}, {f_{{1}}}\rangle , \langle {w_{{3}}}, {f_{{4}}}\rangle$, $\langle {w_{{4}}}, {f_{{1}}}\rangle , \langle {w_{{4}}}, {f_{{5}}}\rangle$, $\langle {w_{{5}}}, {f_{{2}}}\rangle , \langle {w_{{5}}}, {f_{{3}}}\rangle \}$

• ${M}_4 = \{\langle {w_{{1}}}, {f_{{4}}}\rangle , \langle {w_{{1}}}, {f_{{5}}}\rangle$, $\langle {w_{{2}}}, {f_{{2}}}\rangle , \langle {w_{{2}}}, {f_{{3}}}\rangle$, $\langle {w_{{3}}}, {f_{{1}}}\rangle , \langle {w_{{3}}}, {f_{{2}}}\rangle$, $\langle {w_{{4}}}, {f_{{1}}}\rangle , \langle {w_{{4}}}, {f_{{5}}}\rangle$, $\langle {w_{{5}}}, {f_{{4}}}\rangle , \langle {w_{{5}}}, {f_{{3}}}\rangle \}$

• ${M}_5 = \{\langle {w_{{1}}}, {f_{{4}}}\rangle , \langle {w_{{1}}}, {f_{{5}}}\rangle$, $\langle {w_{{2}}}, {f_{{2}}}\rangle , \langle {w_{{2}}}, {f_{{1}}}\rangle$, $\langle {w_{{3}}}, {f_{{1}}}\rangle , \langle {w_{{3}}}, {f_{{4}}}\rangle$, $\langle {w_{{4}}}, {f_{{3}}}\rangle , \langle {w_{{4}}}, {f_{{5}}}\rangle$, $\langle {w_{{5}}}, {f_{{2}}}\rangle , \langle {w_{{5}}}, {f_{{3}}}\rangle \}$

• ${M}_z= {M}_6 = \{\langle {w_{{1}}}, {f_{{4}}}\rangle , \langle {w_{{1}}}, {f_{{5}}}\rangle$, $\langle {w_{{2}}}, {f_{{2}}}\rangle , \langle {w_{{2}}}, {f_{{1}}}\rangle$, $\langle {w_{{3}}}, {f_{{1}}}\rangle , \langle {w_{{3}}}, {f_{{2}}}\rangle$, $\langle {w_{{4}}}, {f_{{3}}}\rangle$, $\langle {w_{{4}}}, {f_{{5}}}\rangle$, $\langle {w_{{5}}}, {f_{{4}}}\rangle , \langle {w_{{5}}}, {f_{{3}}}\rangle \}$

In this instance, $\langle {w_{{1}}}, {f_{{1}}}\rangle$ is a stable pair since $\langle {w_{{1}}}, {f_{{1}}}\rangle \in {M}_0$ and $\langle {w_{{2}}}, {f_{{4}}}\rangle$ is not stable since it is not included in any stable matching. Regarding the dominance relation, we have ${M}_1 \succeq _{{{W}}} {M}_2$, and ${M}_2 \succeq _{{{W}}} {M}_3$, Using transitivity, we obtain ${M}_1 \succeq _{{{W}}} {M}_3$, Note that ${M}_4$ and ${M}_5$ are incomparable.    $\square$

In the following, we introduce a central notion in this paper called rotation. Consider the matching ${M}_{0}$ from the instance given in Example 1 and the list of pairs $\rho _0 = [\langle {w_{{1}}}, {f_{{2}}}\rangle , \langle {w_{{5}}}, {f_{{5}}}\rangle , \langle {w_{{3}}}, {f_{{3}}}\rangle ]$. Notice that every pair in $\rho _0$ is part of ${M}_{0}$. Consider now the operation of shifting the firms in a cyclic way as follows: $f_{{2}}$ is paired with $w_{{5}}$, $f_{{5}}$ is paired with $w_{{3}}$, and $f_{{3}}$ is paired with $w_{{1}}$. This operation changes ${M}_0$ to ${M}_1$. In this case, we say $\rho _0$ is a rotation.

Formally, for any stable matching ${M}\ne {M}_z$ and any worker $w_{{i}}$ such that ${M}(w_{{i}}) \ne \emptyset$, we define $r_{{M}}(w_{{i}})$ to be the most preferred firm $f_{{j}}$ for $w_{{i}}$ such that $w_{{i}} \succ _{{f_{{j}}}} last_{{{M}}}(f_{{j}})$ and $\langle w_{{i}}, f_{{j}} \rangle \notin {M}$. In other words, given $\langle w_{{i}}, f_{{j}} \rangle \notin {M}$, $r_{{M}}(w_{{i}})$ is a firm that is the most preferred firm to $w_{{i}}$ such that it prefers $w_{{i}}$ to her worst assigned partner in M.

Definition 2

(Rotation [2]). A rotation $\rho$ is an ordered list of pairs $[\langle {w_{{i_0}}}, {f_{{j_0}}}\rangle$, $\langle {w_{{i_1}}}, {f_{{j_1}}}\rangle ,$ ..., $\langle {w_{{i_{t-1}}}}, {f_{{j_{t-1}}}}\rangle ]$ such that $t \in [2, \min (n_{W},n_{F})]$, $i_{k} \in [1,n_{W}]$, $j_{k} \in [1,n_{F}]$ for all $0 \le k < t$ and there exists a stable matching ${M}$ where $\langle {w_{{i_k}}}, {f_{{j_k}}}\rangle \in {M}$, $w_{{i_k}} = last_{{{M}}}(f_{{j_k}})$, and $f_{{j_k}}= r_{{M}}(w_{{i_{k+1 ~mod~ t}}})$ for all $0 \le k < t$. In this case we say that $\rho$ is exposed in ${M}$.

Let $\rho$ be a rotation exposed in a stable matching ${M}$. The operation of eliminating a rotation $\rho$ from ${M}$ consists of removing each pair $\langle {w_{{i_k}}}, {f_{{j_k}}}\rangle \in \rho$ from ${M}$, then adding $\langle {w_{{i_{k+1 ~mod~t}}}}, {f_{{j_{k}}}}\rangle$. The new set of pairs, denoted by ${{M}}_{/{\rho }}$ constitutes a stable matching that is dominated (w.r.t. workers) by ${M}$ [3, 8]. We say that $\rho$ produces $\langle {w_{{i}}}, {f_{{j}}}\rangle$ if $\langle {w_{{i}}}, {f_{{j}}}\rangle \in {{M}}_{/{\rho }} \setminus {M}$.

The following three lemmas are either known in the literature [3] or are a direct consequence of [3].

Lemma 1

In every stable matching ${M}\ne {M}_z$, there exists (at least) a rotation that can be exposed in ${M}$.

Lemma 2

Every stable matching ${M}\ne {M}_0$ can be obtained by iteratively eliminating some rotations, without repetition, starting from ${M}_0$.

Lemma 3

Any succession of eliminations leading from ${M}_0$ to ${M}_z$ contains all the possible rotations (without repetition).

We say that a rotation $\rho _1$ precedes another rotation $\rho _2$ (denoted by $\rho _1 \prec \prec {} \rho _2$) if $\rho _1$ is exposed before $\rho _2$ in every succession of eliminations leading from ${M}_0$ to ${M}_z$. Note that this precedence relation is transitive and partial. That is, $\rho _1 \prec \prec {} \rho _2 \wedge \rho _2 \prec \prec {} \rho _3$, implies $\rho _1 \prec \prec {} \rho _3$, and there might exist two rotations $\rho _1$, and $\rho _2$ where neither $\rho _1 \prec \prec {} \rho _2$ nor $\rho _2 \prec \prec {} \rho _1$.

Example 2

(Rotation precedence). In the previous example we have $\rho _0 \prec \prec {} \rho _1$, $\rho _1 \prec \prec {} \rho _2$, $\rho _2 \prec \prec {} \rho _3$, $\rho _2 \prec \prec {} \rho _4$. By transitivity we obtain $\rho _0 \prec \prec {} \rho _4$. Note that in this example neither $\rho _3 \prec \prec {} \rho _4$ nor $\rho _4 \prec \prec {} \rho _3$.    $\square$

Let $R$ be the set of all rotations. The precedence relation $\prec \prec$ with $R$ forms the rotation poset $\Pi _R$. Let $G=(V_G,A_G)$ be the directed graph corresponding to the rotation poset. That is, every vertex corresponds to a rotation, and there is an arc $(\rho _{j},\rho _{i}) \in A_G$ iff $\rho _{j} \prec \prec \rho _{i}$. The construction of $R$ and G can be performed in O(L) time [3]. For each rotation $\rho _{i} \in R$, we denote by ${{N}^-}(\rho _{i})$ the set of rotations having an outgoing edge towards $\rho _{i}$, i.e., these rotations dominate $\rho _{i}$. We introduce below the notion of closed subset and a very important theorem.

Definition 3

(Closed subset). A subset of rotations $S \subseteq V_G$ is closed iff $\forall \rho _{i} \in S$, $\forall \rho _{j} \in V_G$, if $\rho _{j} \prec \prec \rho _{i}$, then $\rho _{j} \in S$.

Theorem 1

(From [2]). There is a one-to-one correspondence between closed subsets and stable matchings.

The solution corresponding to a closed subset S is obtained by eliminating all the rotations in S starting from ${M}_0$ while respecting the order of precedence between the rotations. Recall from Lemma 2 that every stable matching ${M}\ne {M}_0$ can be obtained by iteratively eliminating some rotations, without any repetition, starting from ${M}_0$. The closed subset corresponding to a stable matching ${M}$ is indeed the set of rotations in any succession of eliminations of rotations leading to ${M}$. Notice that ${M}_0$ corresponds to the empty set and that ${M}_z$ is the set of all rotations.

We denote by $\varDelta$ the set of stable pairs. Let $\langle {w_{{i}}}, {f_{{j}}}\rangle$ be a stable pair. There exists a unique rotation containing $\langle {w_{{i}}}, {f_{{j}}}\rangle$ if $\langle {w_{{i}}}, {f_{{j}}}\rangle \notin {M}_z$ [3]. We denote this rotation by $\rho _{{e_{{i}{j}}}}$. Similarly, $\forall \langle {w_{{i}}}, {f_{{j}}}\rangle \in \varDelta \setminus {M}_0$ there exists a unique rotation $\rho$ such that eliminating $\rho$ produces $\langle {w_{{i}}}, {f_{{j}}}\rangle$. We denote by $\rho _{{p_{{i}{j}}}}$ the rotation that produces the stable pair $\langle {w_{{i}}}, {f_{{j}}}\rangle \in \varDelta \setminus {M}_0$. Notice that it is always the case that $\rho _{{p_{{i}{j}}}} \prec \prec \rho _{{e_{{i}{j}}}}$ for any stable pair that is not part of ${M}_0\cup {M}_z$.

Example 3

(The rotations $\rho _{e_{{i}{j}}}$ and $\rho _{p_{{i}{j}}}$ ). For the previous example, we have $\rho _{e_{{2}{3}}}=\rho _4$, and $\rho _{p_{{3}{1}}}=\rho _2$ since $\rho _2$ produces the pair $\langle {w_{{3}}}, {f_{{1}}}\rangle$.   $\square$

Lastly, we denote by $FP$ the set of fixed pairs, $SP$ is the set of stable pairs that are not fixed, and $NSP$ is the set of non stable pairs. Note that $\langle {w_{{i}}}, {f_{{j}}}\rangle \in FP$ iff $\langle {w_{{i}}}, {f_{{j}}}\rangle \in {M}_0\cap {M}_z$. These three sets can be constructed in O(L) [3].

4 A Rotation-Based Formulation

We first show that the problem of finding a stable matching can be formulated as a SAT formula using properties from rotations. Next, we show that for any input domain $\mathcal{D}$, if unit propagation is performed without failure, then there exists necessarily a solution in $\mathcal{D}$. Recall that there exists an algorithm (called the Extended Gale-Shapley algorithm) to find a solution to the many-to-many stable matching that runs in O(L) time [1, 3]. However, using a CP formulation such as the one that we propose in this section is very beneficial when dealing with NP-Hard variants of the problem.

In out model, a preprocessing step is performed to compute ${M}_0$, ${M}_z$, $SP$, $FP$, $NSP$, the graph posed, $\rho _{{e_{{i}{j}}}}$ for all $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\setminus {M}_z$, and $\rho _{{p_{{i}{j}}}}$ for all $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\setminus {M}_0$. This preprocessing is done in O(L) time [3].

4.1 A SAT Encoding

We introduce for each pair $\langle {w_{{i}}}, {f_{{j}}}\rangle$ a Boolean variable $x_{{{i}},{{j}}}$. The latter is set to true iff $\langle {w_{{i}}}, {f_{{j}}}\rangle$ is part of the stable matching. Moreover, we use for each rotation $\rho _{k}$ a Boolean variable $r_{k}$ (called rotation variable) to indicate whether the rotation $\rho _{k}$ is in the closed subset that corresponds to the solution.

Observe first that for all $\langle {w_{{i}}}, {f_{{j}}}\rangle \in FP$, $x_{{{i}},{{j}}}$ has to be true, and for all $\langle {w_{{i}}}, {f_{{j}}}\rangle \in NSP$, $x_{{{i}},{{j}}}$ has to be false.

We present three lemmas that are mandatory for the soundness and completeness of the SAT formula. Let M be a stable matching and S its closed subset (Theorem 1).

Lemma 4

$\forall \langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_0:$ $\langle {w_{{i}}}, {f_{{j}}}\rangle \in M$ iff $\rho _{{e_{{i}{j}}}} \notin S.$

Proof

$\Rightarrow$ Suppose that $\rho _{{e_{{i}{j}}}} \in S$. Let Sequence be an ordered list of the rotations in S such that exposing the rotations of S starting from ${M}_0$ leads to M. For all $a \in [1, |S|]$, we define $M'_a$ to be the stable matching corresponding the closed subset $S'_{a}=\{Sequence[k] ~|~ k \in [1, a] \}$. We also use $M'_0$ to denote the particular case of ${M}_0$ and $S'_0 =\emptyset$. Notice that $M'_{|S|} = M$ and $S'_{|S|}=S$. Let $a \in [1, |S|]$ such that $Sequence[a]=\rho _{{e_{{i}{j}}}}$. We know that exposing the rotation $\rho _{{e_{{i}{j}}}}$ from $S'_{a-1}$ moves worker $w_{{i}}$ to a partner that is worse than $f_{{i}}$. For any matching $M'_b$ where $b \in [a, |S|]$, $w_{{i}}$ either has the same partners in $M'_{b-1}$ or is assigned a new partner that is worse than $f_{{i}}$. Hence $\langle {w_{{i}}}, {f_{{j}}}\rangle$ cannot be part of $M'_{|S|}= M$.

$\Leftarrow$ $\langle {w_{{i}}}, {f_{{j}}}\rangle$ must be part of the solution since it is part of ${M}_0$ and $\rho _{{e_{{i}{j}}}} \notin S$.    $\square$

Lemma 5

$\forall \langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_z:$ $\langle {w_{{i}}}, {f_{{j}}}\rangle \in M$ iff $\rho _{{p_{{i}{j}}}} \in S.$

Proof

$\Rightarrow$ Suppose that $\rho _{{p_{{i}{j}}}} \notin S$. The pair $\langle {w_{{i}}}, {f_{{j}}}\rangle$ cannot be produced when eliminating rotations in S since $\rho _{{p_{{i}{j}}}}$ is unique. Therefore ${\rho _{{p_{{i}{j}}}}} \in S$.

$\Leftarrow$ Suppose that $\rho _{{p_{{i}{j}}}} \in S$. The pair $\langle {w_{{i}}}, {f_{{j}}}\rangle$ must be part of the solution since $\rho _{{p_{{i}{j}}}} \in S$ and it can never be eliminated by any rotation since $\langle {w_{{i}}}, {f_{{j}}}\rangle \in {M}_z$.   $\square$

Lemma 6

$\forall \langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\setminus ({M}_0\cup {M}_z):$ $\langle {w_{{i}}}, {f_{{j}}}\rangle \in M$ iff $\rho _{{p_{{i}{j}}}} \in S \wedge \rho _{{e_{{i}{j}}}} \notin S.$

Proof

$\Rightarrow$ Suppose that $\langle {w_{{i}}}, {f_{{j}}}\rangle$ is part of M.

• If $\rho _{{p_{{i}{j}}}} \notin S$, then $\langle {w_{{i}}}, {f_{{j}}}\rangle$ can never be produced when eliminating rotations in S. Therefore ${\rho _{{p_{{i}{j}}}}} \in S$.

• If $\rho _{{e_{{i}{j}}}} \in S$, similarly to the proof of Lemma 4, we can show that the pair $\langle {w_{{i}}}, {f_{{j}}}\rangle$ cannot be part of the solution.

$\Leftarrow$ Suppose that $\rho _{{p_{{i}{j}}}} \in S$ and $\rho _{{e_{{i}{j}}}} \notin S$. The pair $\langle {w_{{i}}}, {f_{{j}}}\rangle$ must be part of the solution since it is produced by $\rho _{{p_{{i}{j}}}}$ and not eliminated since $\rho _{{e_{{i}{j}}}} \notin S$.   $\square$

Using Lemmas 4, 5 and 6, we can formulate the problem of finding a stable matching as follows.

$$\begin{aligned} \forall \rho _{i} \in R, \forall \rho _{j} \in {{N}^-}(\rho _{i}): ~ \lnot {r_{i}} \vee {r_{j}} \end{aligned}$$

(1)

$$\begin{aligned} \forall \langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_0: \lnot {x_{{{i}},{{j}}}} \vee \lnot {r_{{e_{{i}{j}}}}} ~;~ {x_{{{i}},{{j}}}} \vee {r_{{e_{{i}{j}}}}} \end{aligned}$$

(2)

$$\begin{aligned} \forall \langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_z: \lnot {x_{{{i}},{{j}}}} \vee {r_{{p_{{i}{j}}}}} ~;~{x_{{{i}},{{j}}}} \vee \lnot {r_{{p_{{i}{j}}}}} \end{aligned}$$

(3)

$$\begin{aligned} \forall \langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\setminus ({M}_0\cup {M}_z): \lnot {x_{{{i}},{{j}}}} \vee {r_{{p_{{i}{j}}}}} ~;~ \lnot {x_{{{i}},{{j}}}} \vee \lnot {r_{{e_{{i}{j}}}}} ~;~ {x_{{{i}},{{j}}}} \vee \lnot {r_{{p_{{i}{j}}}}} \vee {r_{{e_{{i}{j}}}}} \end{aligned}$$

(4)

$$\begin{aligned} \forall \langle {w_{{i}}}, {f_{{j}}}\rangle \in FP: {x_{{{i}},{{j}}}} \end{aligned}$$

(5)

$$\begin{aligned} \forall \langle {w_{{i}}}, {f_{{j}}}\rangle \in NSP: \lnot {x_{{{i}},{{j}}}} \end{aligned}$$

(6)

We denote this formula by $\varGamma$. Clauses 1 make sure that the set of rotation variables that are set to true corresponds to a closed subset. Clauses 2, 3, and 4 correspond (respectively) to Lemmas 4, 5, and 6. Lastly, Clauses 5 and 6 handle the particular cases of fixed and non stable pairs (respectively). Observe that each clause is of size at most 3. Moreover, since the the number of edges in the graph poset is bounded by O(L) [3], then the size of this formula is O(L).

The only CP formulation for the case of many-to-many stable matching was proposed in [3]. It is a straightforward generalization of the CSP model proposed for the hospital/residents problem in [13]. The authors use $q_{{w_{{i}}}}$ variables per worker, and $q_{{f_{{j}}}}$ variables per firm. The variables related to a worker $w_{{i}}$ represent the rank of the firm assigned at each position (out of the $q_{{w_{{i}}}}$ available positions). A similar set of variables is used for firms. The model contains $|{W}| \times (\sum _i q_{{w_{{i}}}} + |{F}| \times (1 + {\sum _j q_{{f_{{j}}}}} \times (2 + \sum _i (q_{{w_{{i}}}}-1 )) ))$ constraints related to workers. Likewise, $|{F}| \times (\sum _j q_{{f_{{j}}}} + |{W}| \times (1 + {\sum _i q_{{w_{{i}}}}} \times (2 + \sum _j (q_{{f_{{j}}}}-1 )) ))$ constraints are used for firms.

4.2 Properties Related to Unit Propagation

In the following, we show that once unit propagation is performed without failure then there exists necessarily a solution.

Suppose that $\mathcal{D}$ is a domain where unit propagation has been performed without failure. Let $S_1$ be the set of rotation variables that are set to 1.

Lemma 7

$S_1$ is a closed subset.

Proof

Let $\rho _{i}$ be a rotation in $S_1$ and let $\rho _{j}$ be rotation such that $\rho _{j} \prec \prec \rho _{i}$. Unit propagation on Clauses 1 enforces $r_{j}$ to be true. Therefore $\rho _{j} \in S_1$. Hence $S_1$ is a closed subset.   $\square$

Let $M_1$ be the stable matching corresponding to $S_1$ (Theorem 1). We show that $M_1$ is part of the solution space in $\mathcal{D}$.

Lemma 8

For any $x_{{{i}},{{j}}}$ that is set to 1, $\langle {w_{{i}}}, {f_{{j}}}\rangle \in M_1$.

Proof

The case where $\langle {w_{{i}}}, {f_{{j}}}\rangle$ is a fixed pair or non stable is trivial. Take a non-fixed stable pair $\langle {w_{{i}}}, {f_{{j}}}\rangle$ and suppose that $\mathcal{{D}}{({x_{{{i}},{{j}}}})} =\{1\}$. There are three cases to distinguish.

• 1. $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_0$: Unit propagation on Clauses 2 enforces $r_{{e_{{i}{j}}}}$ to be false. Therefore, $\rho _{{e_{{i}{j}}}} \notin S_1$. Hence by Lemma 4 we obtain: $\langle {w_{{i}}}, {f_{{j}}}\rangle \in M_1$.

• 2. $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_z:$ Unit propagation on Clauses 3 enforces $r_{{p_{{i}{j}}}}$ to be true. Therefore, $\rho _{{p_{{i}{j}}}} \in S_1$. Hence by Lemma 5 we obtain: $\langle {w_{{i}}}, {f_{{j}}}\rangle \in M_1$.

• 3. $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\setminus ({M}_0\cup {M}_z):$ Unit propagation on Clauses 4 enforces $r_{{p_{{i}{j}}}}$ to be true and $r_{{e_{{i}{j}}}}$ to be false. Therefore, $\rho _{{p_{{i}{j}}}} \in S_1$, $\rho _{{e_{{i}{j}}}} \notin S_1$. Hence by Lemma 6 we obtain: $\langle {w_{{i}}}, {f_{{j}}}\rangle \in M_1$.    $\square$

Lemma 9

For any $x_{{{i}},{{j}}}$ that is set to 0, $\langle {w_{{i}}}, {f_{{j}}}\rangle \notin M_1$.

Proof

The case where $\langle {w_{{i}}}, {f_{{j}}}\rangle$ is a fixed pair or non-stable is trivial. Take a non-fixed stable pair $\langle {w_{{i}}}, {f_{{j}}}\rangle$ and suppose that $\mathcal{{D}}{({x_{{{i}},{{j}}}})} =\{0\}$. There are three cases to distinguish.

• 1. $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_0$: Unit propagation on Clauses 2 enforces $r_{{e_{{i}{j}}}}$ to be true. Therefore, $\rho _{{e_{{i}{j}}}} \in S_1$. Hence by Lemma 4 we obtain: $\langle {w_{{i}}}, {f_{{j}}}\rangle \notin M_1$.

• 2. $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_z:$ Unit propagation on Clauses 3 enforces $r_{{p_{{i}{j}}}}$ to be false. Therefore, $\rho _{{p_{{i}{j}}}} \notin S_1$. Hence by Lemma 5 we obtain: $\langle {w_{{i}}}, {f_{{j}}}\rangle \notin M_1$.

• 3. $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\setminus ({M}_0\cup {M}_z)$: We distinguish two cases:

  • (a) $\mathcal{{D}}{({\rho _{{p_{{i}{j}}}}})}\ne \{1\}$: In this case $\rho _{{p_{{i}{j}}}} \notin S_1$ hence by Lemma 6 we obtain: $\langle {w_{{i}}}, {f_{{j}}}\rangle \notin M_1$

  • (b) $\mathcal{{D}}{({\rho _{{p_{{i}{j}}}}})} =\{1\}$: In this case, unit propagation on Clauses 4 enforces $r_{{e_{{i}{j}}}}$ to be true. Therefore, $\rho _{{e_{{i}{j}}}} \in S_1$. Hence by Lemma 6 we obtain: $\langle {w_{{i}}}, {f_{{j}}}\rangle \notin M_1$.    $\square$

Recall that $\varGamma$ denotes the SAT formula defined in Sect. 4.1.

Theorem 2

Let $\mathcal{D}$ be a domain such that unit propagation is performed without failure on $\varGamma$. There exists at least a solution in $\mathcal{D}$ that satisfies $\varGamma$.

Proof

We show that $M_1$ corresponds to a solution under $\mathcal{D}$. To do so, one needs to set every unassigned variable to a particular value. We propose the following assignment. Let $x_{{{i}},{{j}}}$ be an unassigned variable. Note that $\langle {w_{{i}}}, {f_{{i}}}\rangle$ has to be part of $SP$.

• 1. If $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_0:$ $x_{{{{i}}},{{{j}}}}$ is set to 1 if $\rho _{{e_{{i}{j}}}} \notin S_1$; and 0 otherwise.

• 2. If $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_z:$ $x_{{{{i}}},{{{j}}}}$ is set to 1 if $\rho _{{p_{{i}{j}}}} \in S_1$; and 0 otherwise.

• 3. If $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\setminus ({M}_0\cup {M}_z):$ $x_{{{{i}}},{{{j}}}}$ is set to 1 if $\rho _{{p_{{i}{j}}}} \in S_1 \wedge \rho _{{e_{{i}{j}}}} \notin S_1$; and 0 otherwise.

This assignment corresponds to a solution as a consequence of Lemmas 4, 5, 6, 8, and 9. Therefore, once unit propagation is established without failure, we know that there exists at least one solution.    $\square$

5 Arc Consistency

We propose in this section a procedure to filter more of the search space. We assume in the rest of this section that I is a stable matching instance defined by $\langle {W},{F}, P_{{{W}}}, P_{{{F}}}, q_{{{W}}}, q_{{{F}}} \rangle$ using the same notations introduced in Sect. 3.

Let $\mathcal{X}(M2M)= \{x_{{{1}},{{1}}}, \ldots x_{{{n_{W}}},{{n_{F}}}} , r_{1}, \ldots r_{|R|} \}$ be the set of Boolean variables defined in Sect. 4.1. We define the many-to-many stable matching constraint as $M2M(I, \mathcal{X}(M2M))$. Given a complete assignment of the variables in $\mathcal{X}(M2M)$, this constraint is satisfied iff the set M of pairs corresponding to Boolean variables $x_{{{i}},{{j}}}$ that are set to 1 is a solution to I and the set of rotations corresponding to Boolean variables $r_{k}$ that are set to 1 is the closed subset corresponding to M.

Example 4 shows an instance with a particular domain where unit propagation on $\varGamma$ is not enough to establish arc consistency on the M2M constraint.

Example 4

(Missing Support). Consider the example where $n_{W}=4, n_{F}=4$, and for all $1\le i,j\le 4$, $q_{{w_{{i}}}}=q_{{f_{{j}}}}=1$. The preference lists for workers and firms are given in Table 2.

Table 2. Preference lists

Consider the domain such that all the variables are unassigned except for $x_{{{1}},{{4}}}$, $x_{{{3}},{{1}}}$, $x_{{{3}},{{3}}}$, $x_{{{4}},{{2}}}$, and $x_{{{4}},{{3}}}$ where the value 0 is assigned to each of these variables. Unit propagation on the encoding $\varGamma$ of this instance does not trigger a failure. It also does not change the domain of $x_{{{2}},{{1}}}$ (i.e., $\{0,1\}$). However, the assignment of 1 to $x_{{{2}},{{1}}}$ does not have a support in $\mathcal{D}$ for M2M.    $\square$

In the following, we assume that unit propagation is established on an input domain $\mathcal{D}$ and that it propagated the clauses without finding a failure. In the rest of this section, we use the term ‘support’ to say ‘support for $M2M(I, \mathcal{X}(M2M))$’. We shall use unit propagation to find a support for any assignment using the property we showed in Theorem 2.

In order to construct supports, we need to introduce the following two lemmas.

Lemma 10

For any rotation $\rho _{i}$ where $\mathcal{{D}}{({r_{i}})} =\{0,1\}$, assigning 1 to $r_{i}$ has a support.

Proof

Consider the set of rotations $S = S_1 \cup \{ r_{j} ~|~ r_{j} \prec \prec r_{i} \}$. Clearly S is a closed subset (Lemma 7). Let M be the corresponding stable matching of S. We show that M corresponds to a valid support.

By construction, we have any variable $x_{{{i}},{{j}}}$ set to 1 is part of M and any variable set to 0 is not. Consider now the rotation variables. Recall that $S_1$ is the set of rotation variables that are set to 1. Observe that $\{ r_{j} | r_{j} \prec \prec r_{i} \}$ can only contain rotations that are unassigned because otherwise, unit propagation would assign 0 to $r_{i}$. In our support, every rotation variable whose rotation is in $\{ r_{j} | r_{j} \prec \prec r_{i} \}$ is set to 1. Consider $x_{{{i}},{{j}}}$ an unassigned variable. We set $x_{{{i}},{{j}}}$ as follows

• 1. If $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_0:$ $x_{{{{i}}},{{{j}}}}$ is set to 1 if $\rho _{{e_{{i}{j}}}} \notin S$; and 0 otherwise.

• 2. If $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_z:$ $x_{{{{i}}},{{{j}}}}$ is set to 1 if $\rho _{{p_{{i}{j}}}} \in S$; and 0 otherwise.

• 3. If $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\setminus ({M}_0\cup {M}_z):$ $x_{{{{i}}},{{{j}}}}$ is set to 1 if $\rho _{{p_{{i}{j}}}} \in S \wedge \rho _{{e_{{i}{j}}}} \notin S$; and 0 otherwise.

This assignment corresponds by construction to M as a consequence of Lemmas 4, 5, 6, 8, and 9.    $\square$

Lemma 11

For any rotation $\rho _{i}$ where $\mathcal{{D}}{({r_{i}})} =\{0,1\}$, assigning 0 to $r_{i}$ has a support.

Proof

Recall that $S_1$ is the set of rotation variables that are set to 1 and that $M_1$ is its corresponding stable matching. By construction, we can show that $M_1$ corresponds to a support.    $\square$

Consider now an unassigned variable $x_{{{i}},{{j}}}$. Notice that $\langle {w_{{i}}}, {f_{{i}}}\rangle \in SP$. Lemma 12 show that there is always a support for 0.

Lemma 12

For any unassigned variable $x_{{{i}},{{j}}}$, assigning 0 to $x_{{{i}},{{j}}}$ has a support.

Proof

We distinguish three cases:

• 1. $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_0:$ Observe that $\rho _{{e_{{i}{j}}}}$ is unassigned. We know by Lemma 10 that assigning 1 to $r_{{e_{{i}{j}}}}$ has a support. In this support 0 is assigned to $x_{{{i}},{{j}}}$.

• 2. $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_z:$ In this case $\rho _{{p_{{i}{j}}}}$ is unassigned. We know by Lemma 11 that assigning 0 to $r_{{p_{{i}{j}}}}$ has a support. In this support, 0 is assigned to $x_{{{i}},{{j}}}$.

• 3. $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\setminus ({M}_0\cup {M}_z):$ Note that 0 cannot be assigned to $\rho _{{p_{{i}{j}}}}$ because otherwise $x_{{{i}},{{j}}}$ would be set to 0. We distinguish two cases:

  • (a) $\rho _{{p_{{i}{j}}}}$ is set to 1: In this case $\rho _{{e_{{i}{j}}}}$ is unassigned (otherwise $x_{{{i}},{{j}}}$ would be assigned). We know by Lemma 10 that assigning 1 to $r_{{e_{{i}{j}}}}$ has a support. In this support 0 is assigned to $x_{{{i}},{{j}}}$.

  • (b) $\rho _{{p_{{i}{j}}}}$ is unassigned: We know by Lemma 11 that assigning 0 to $r_{{p_{{i}{j}}}}$ has a support. In this support 0 is assigned to $x_{{{i}},{{j}}}$.    $\square$

In the case of finding supports when assigning 1 to $x_{{{i}},{{j}}}$, there are three cases. These cases are detailed in Lemmas 13, 14, and 15.

Lemma 13

If $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_0$, then assigning 1 to $x_{{{i}},{{j}}}$ has a support.

Proof

In this case $\rho _{{e_{{i}{j}}}}$ is unassigned. We know by Lemma 11 that assigning 0 to $r_{{e_{{i}{j}}}}$ has a support. In this support 1 is assigned to $x_{{{i}},{{j}}}$.   $\square$

Lemma 14

If $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\cap {M}_z$, then assigning 1 to $x_{{{i}},{{j}}}$ has a support.

Proof

In this case $\rho _{{p_{{i}{j}}}}$ is unassigned. We know by Lemma 10 that assigning 1 to $r_{{p_{{i}{j}}}}$ has a support. In this support $x_{{{i}},{{j}}}$ is set to 1.    $\square$

Let $\mathcal{D}^1_{x_{{{i}},{{j}}}}$ be the domain identical to $\mathcal{D}$ except for $\mathcal{{D}}{({x_{{{i}},{{j}}}})}=\{1\}$.

Lemma 15

If $\langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\setminus {M}_0\cup {M}_z$, then

• If  $\mathcal{{D}}{({r_{{p_{{i}{j}}}}})} = \{1\}$, then assigning 1 to $x_{{{i}},{{j}}}$ has a support.

• Otherwise, we have $\mathcal{{D}}{({r_{{p_{{i}{j}}}}})} = \{0,1\}$ and assigning 1 to $x_{{{i}},{{j}}}$ has a support iff unit propagation on $\mathcal{D}^1_{x_{{{i}},{{j}}}}$ does not fail.

Proof

For the first case, we can argue that $\rho _{{e_{{i}{j}}}}$ is unassigned (otherwise $x_{{{i}},{{j}}}$ would be assigned). By Lemma 11, we have a support if we set $r_{{e_{{i}{j}}}}$ to 0. In this support $x_{{{i}},{{j}}}$ is set to 1.

For the second case, we have necessarily $\mathcal{{D}}{({r_{{p_{{i}{j}}}}})} = \{0,1\}$ (otherwise $x_{{{i}},{{j}}}$ would be assigned) and it is easy to see that there exists a support iff unit propagation does not fail on $\mathcal{D}^1_{x_{{{i}},{{j}}}}$ by Theorem 2.    $\square$

We summarize all the properties of the previous lemmas in Algorithm 1. This algorithm shows a pseudo-code to maintain arc consistency on $M2M(I, \mathcal{X}(M2M))$. In this algorithm, UP($\mathcal{D}$) is the output domain after performing unit propagation on a domain $\mathcal{D}$. The output of UP($\mathcal{D}$) is $\emptyset$ iff a failure is found.

Suppose that $\mathcal{D}$ is a domain where unit propagation is established without failure. First, for any variable that is set to a value v, the assignment of v to this variable has a support in $\mathcal{D}$ since there exists necessarily a solution (Theorem 2). Second, we know that any assignment of any rotation variable has a support in $\mathcal{D}$ by Lemmas 10 and 11. Also, the assignment of 0 to any unassigned variable $x_{{{i}},{{j}}}$ has a support (Lemma 12). Lastly, by Lemmas 13, 14, and 15, we know that we need to check supports only for the assignment of 1 to some particular unassigned variables $x_{{{i}},{{j}}}$. These variables correspond to the pairs of the set $\varPsi =\{\langle {w_{{i}}}, {f_{{j}}}\rangle | \langle {w_{{i}}}, {f_{{j}}}\rangle \in SP\wedge \langle {w_{{i}}}, {f_{{j}}}\rangle \notin {M}_0\cup {M}_z\wedge \mathcal{{D}}{({r_{{p_{{i}{j}}}}})} = \{0,1\} \}$ (Lemma 15).

Algorithm 1 first performs unit propagation on the input domain $\mathcal{D}$ in Line 1. If a failure is not found, we loop over the pairs in $\varPsi$ in Line 2 and call unit propagation on the new domain $\mathcal{D}^1_{x_{{{i}},{{j}}}}$ in Line 3 for each $\langle {w_{{i}}}, {f_{{j}}}\rangle \in \varPsi$. If this call results in failure then $x_{{{i}},{{j}}}$ does not have a support for the value 1. In this case, such a variable is set to 0 in Line 4.

We discuss now the complexity of Algorithm 1. Observe first that since the SAT formula contains only clauses of size at most 3, and since the number of clauses is O(L), then unit propagation takes O(L) time. Notice that by using the two-watched literal procedure [16], there is no data structure to update between the different calls. Lastly, observe that the number of calls to unit propagation in Line 3 is bounded by the number of unassigned variables. Therefore the worst-case time complexity to maintain arc consistency is $O(U_x \times L)$ where $U_x$ is the number of unassigned $x_{{{i}},{{j}}}$ variables. Therefore the overall complexity is $O(L^2)$.

6 Experimental Results

In the absence of known hard problems for many to many stable matching, we propose to evaluate our approach on two NP-hard variants of stable marriage called sex-equal stable matching and balanced stable matching [14]. Let M be a stable marriage. Let $C^m_M$ (respectively $C^w_M$) be the sum of the ranks of each man’s partner (respectively woman’s partner). In balanced stable matching, the problem is to find a stable matching M with the minimum value of $max\{C^m_M, C^w_M \}$. In sex-equal stable matching, the problem is to find a stable matching M with the minimum value of $|C^m_M - C^w_M|$ [14]. Modeling these problems in constraint programming is straightforward by using an integer variable $X_{i}$ for each man $m_{i}$ whose domain represents the rank of the partner of $m_{i}$.

We implemented our two propositions in the Mistral-2.0 [10] solver (denoted by fr for the first formulation and ac for the arc consistency algorithm) and we compare them against the bound ($\mathcal{D}$) consistency algorithm of [20] implemented in the same solver (denoted by bc). We restrict the search strategy to branch on the sequence $[X_{1}, \ldots , X_{n}]$ since it is sufficient to decide the problem. We used four different heuristics: a lexicographic branching (lx) with random value selection (rd); lx with random min/max value selection (mn); activity based search (as) [15]; and impact-based search (is) [18]. We use geometric restarts and we run 5 randomization seeds. There is a time cutoff of 15 min for each model on each instance.

We first run all the configurations on purely random instances with complete preference lists of size up to $500 \times 500$ and observed that these instances are extremely easy to solve for all configurations without valuable outcome. We therefore propose to use a new benchmark of hard instances.

Irving and Leather [12] described a family of stable marriage instances, where the number of solutions for stable matching grows exponentially. In this family, the number of stable matchings g(n) for an instance of size $n \times n$ respects the recursive formula $g(n) \ge 2 \times {g(n/2)}^2$, and $g(1)=1$, where n, the number of men, is of the form $2^k$. To give an idea of the exponential explosion, when $n=16$, the number of solutions is 195472, and when $n=32$, the number of solutions is 104310534400. We generate instances of sizes $n \in \{32, 64, 128, 256 \}$ as follows. For each size, we generate the instance as in [12], then swap $\alpha \%$ of n random pairs from the preference lists of men. We apply the same swapping procedure for woman. We generated 50 instances for each size with $\alpha =10$, $\alpha =20$, and $\alpha =30$. This gives us a total of 600 instances available in http://siala.github.io/sm/sm.zip.

In the following figures we represent every configuration by “A-B” where A$\in \{\textit{fr}, \textit{ac}, \textit{bc}\}$ is the constraint model for stability and B $\in \{$ lx-rd, lx-mn, as, is $\}$ is the search strategy. In Figs. 1a and  2b we give the cactus plots of proving optimality for these instances on the two problems. That is, after a given CPU time in seconds (y-axis), we give the percentage of instances proved to optimality for each configuration on the x-axis. In Figs. 1a and  2b we study the quality of solutions by plotting the normalized objective value of the best solution found by the configuration h (x-axis) after a given time in seconds (y-axis) [11]. Let h(I) be the objective value of the best solution found using model h on instance I and lb(I) (resp. ub(I)) the lowest (resp. highest) objective value found by any model on I. We use a normalized score in the interval [0, 1]: $score(h,I)= \frac{ub(I) - h(I) + 1}{ub(I) - lb(I) + 1}$. The value of score(h, I) is equal to 1 if h has found the best solution for this instance among all models, decreases as h(I) gets further from the optimal objective value, and is equal to 0 if and only if h did not find any solution for I. Note that for $\textit{fr}$ and $\textit{ac}$ the CPU time in all there figures includes the O(L) preprocessing step that we mentioned at the beginning of Sect. 4.

Fig. 1.

Performance cactus, sex equal stable matching

Fig. 2.

Performance cactus, balanced stable matching

These figures show that the arc consistency model (ac) does not pay off as it considerably slows down the speed of exploration. It should be noted that between bc and ac  there is no clear winner. The SAT formulation (fr), on the other hand, outperforms both bc and ac using any search strategy. This is true for both finding proofs of optimality and finding the best objective values. In fact, fr clearly finds better solutions faster than any other approach.

Lastly, we note that the best search strategy for sex-equal stable matching is, surprisingly, the one branching lexicographically using a random value selection (Figs. 1a and b). For the case of balanced stable matching, clearly impact-based search is the best choice for finding proofs (Fig. 2a) whereas activity based search finds better solutions (Fig. 2b).

7 Conclusion

We addressed the general case of many-to-many stable matching in a constraint programming context. Using fundamental properties related to the notion of rotation in stable matching we presented a novel SAT formulation of the problem then showed that arc consistency can be maintained in quadratic time. Our experimental study on two hard variants of stable matching called sex-equal and balanced stable matching showed that our SAT formulation outperforms the best CP approach in the literature. In the future, it would be interesting to experimentally evaluate our propositions on hard variants in the many-to-many setting.