Improved Integral Attack on HIGHT

Abstract

HIGHT is a lightweight block cipher with 64-bit block length and 128-bit security, and it is based on the ARX-based generalized Feistel network. HIGHT became a standard encryption algorithm in South Korea and also is internationally standardized by ISO/ICE 18033-3. Therefore, many third-party cryptanalysis against HIGHT have been proposed. Especially, impossible differential and integral attacks are applied to reduced-round HIGHT, and the current best attack under the single-key setting is 27 rounds using the impossible differential attack. In this paper, we propose an improved integral attack against HIGHT. We first propose new 19-round integral characteristics by using the propagation of the division property, and they are improved by two rounds compared with previous integral characteristics. Finally, we can attack 28-round HIGHT by appending 9-round key recovery. Moreover, we can attack 29-round HIGHT if the full code book is used, and it improves by two rounds compared with previous best attack.

1 Introduction

The lightweight cryptography is one of the most actively discussed topics in the community of symmetric-key cryptographers. The motivation of the lightweight symmetric-key cryptography is to design high-performance and secure symmetric-key ciphers under the area-constraining environments. Such ciphers are expected to be proper for radio frequency identification (RFID), sensor network, and Internet of Things (IoT). Nowadays, a huge number of such ciphers have been proposed, and please refer to [2], where a list of lightweight ciphers is well summarized.

The generalized Feistel network (GFN) is suited to the design of lightweight block ciphers because each F-function is very small. LBlock [23] and TWINE [19] are examples of such ciphers. HIGHT, which was proposed by Hong et al. at CHES 2006 [7], is also a lightweight block cipher adopting the GFN. Moreover, HIGHT was standardized by ISO/IEC 18033-3 [8]. HIGHT only consists of three operations, i.e., modular additions over 256, bitwise rotations, and bitwise XOR. Such structure is often called ARX, and HIGHT is regarded as an ARX-based generalized Feistel network. Some ARX-based ciphers have been proposed, but there are many unsolved problems in the security analysis compare with the S-box-based ciphers. Therefore, HIGHT standardized by ISO/IEC is one of the most attractive ARX-based ciphers and is well analyzed.

In the related-key setting, the full HIGHT was already broken using the related-key rectangle attack [10]. On the other hand, impossible differential and integral attacks have been often applied to HIGHT under the single-key setting, but the full HIGHT has not been attacked yet. The current best attack is proposed by Chen using the impossible differential attack and 27-round HIGHT is attacked [3] (Table 1).

Table 1. Comparison of attack results on HIGHT.

In this paper, we propose the current best attack by using the improved integral attacks. The integral attack consists of two parts; an integral characteristic and key recovery. In the integral characteristic, attackers first prepare a set of chosen plaintexts, where the XOR of the part of all corresponding states after several encryption rounds is always 0 for all secret keys. Then, in the key recovery, they guess round keys used in the last several rounds and evaluate whether the XOR of partially decrypted texts is 0 or not. If the correct key is guessed, the XOR is 0 because of the integral characteristic. Therefore, if the XOR is not 0, the guessed round key is discarded.

The integral cryptanalysis on HIGHT was first evaluated by the designers [7]. They showed 12-round integral characteristics with $2^8$ chosen plaintexts, and 16-round HIGHT is attacked by using the characteristic. However, the error of this 12-round characteristics was pointed out by Zhang et al., and they showed that the correct integral characteristics with $2^8$ chosen plaintexts cover only 11 rounds [25]. Moreover, they improved the 11-round characteristic to 17-round one by using the higher-order integral characteristics. As a result, 22-round HIGHT is attacked by using the 17-round characteristic. Then, the key recovery part is dramatically improved by Sasaki and Wang. They first proposed the meet-in-the-middle technique for the key recovery of the integral attack [14], which is useful to reduce the time complexity. Moreover, they proposed the bitwise partial-sum technique and optimized the key recovery [15]. As a result, 26-round HIGHT is attacked. Note that both improvements use the same 17-round characteristic by Zhang et al.

In this paper, we first show new 19-round integral characteristics, which is improved by two rounds than previous 17-round one. Our new characteristic is found by the propagation of the division property [21]. The division property is a general technique to find integral characteristics and recently applied to a wide range of block ciphers. New 18-round integral characteristics with $2^{63}$ chosen plaintexts are found by the propagation of the division property, and 18-round characteristics are extended to 19-round ones. Then, we show that 28-round HIGHT can be attacked by using this extended 19-round characteristic. Moreover, we show that 29-round HIGHT can be attacked by using the same characteristic if the full code book is used. Since the previous best attack is up to 27 rounds, our new attacks are the current best attack under the single-key setting.

2 Preliminaries

2.1 Specification of HIGHT

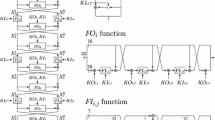
HIGHT is a block-cipher proposed at CHES 2006 by Hong et al. [7]. The block size is 64 bits and the key size is 128 bits. It adopts the type-2 generalized Feistel network with 8 branches and 32 rounds. Please refer to [7] for details. Note that a figure with an incorrect subkey order is showed in [7], and the designers later fixed the problem [1].

Encryption. The 64-bit plaintext and ciphertext are considered as concatenations of 8 bytes and denoted by $P = P_{7} \Vert P_{6} \Vert \cdots \Vert P_{0}$ and $C = C_{7} \Vert C_{6} \Vert \cdots \Vert C_{0}$, respectively. The input of the $(r+1)$-th round function is represented as $X^{r} = X^{r}_{7} \Vert X^{r}_{6} \Vert \cdots \Vert X^{r}_{0}$ for $r = 0,1,\ldots ,32$. At first, the plaintext is loaded into an internal state $X^{0}_{7} \Vert X^{0}_{6} \Vert \cdots \Vert X^{0}_{0}$ as follows.

$$\begin{aligned} X^{0}_{0}&= P_{0} \boxplus WK_{0},&X^{0}_{1}&= P_{1},&X^{0}_{2}&= P_{2} \oplus WK_{1},&X^{0}_{3}&= P_{3}, \\ X^{0}_{4}&= P_{4} \boxplus WK_{2},&X^{0}_{5}&= P_{5},&X^{0}_{6}&= P_{6} \oplus WK_{3},&X^{0}_{7}&= P_{7}, \end{aligned}$$

where $WK_{i}$ denotes 8-bit whitening keys for $i = 0,1,\ldots ,7$. The operation $\boxplus$ denotes addition mod $2^{8}$. Then, the value $X^{r}_{7} \Vert X^{r}_{6} \Vert \cdots \Vert X^{r}_{0}$ is updated as Fig. 1 for $r = 0,1,\ldots ,31$, where $F_{0}(x) = (x \lll 1) \oplus (x \lll 2) \oplus (x \lll 7)$ and $F_{1}(x) = (x \lll 3) \oplus (x \lll 4) \oplus (x \lll 6)$. The operation about $(x \lll s)$ denotes an s-bit left rotation of an 8-bit value x, and $SK_{i}$ denotes the i-th 8-bit subkey for $i = 0,1,\ldots ,127$. The swap of the byte position is omitted in the last round.

Fig. 1.

Round function procedure of HIGHT

The internal state between F and the key addition is defined by $Y^{r}_{1},Y^{r}_{3},Y^{r}_{5},Y^{r}_{7}$, and the internal state after the key addition is defined by $Z^{r}_{1},Z^{r}_{3},Z^{r}_{5},Z^{r}_{7}$. Finally, the ciphertext is generated from $X^{32}$ by applying the post whitening as follows.

$$\begin{aligned} C_{0}&= X^{32}_{0} \boxplus WK_{4},&C_{1}&= X^{32}_{1},&C_{2}&= X^{32}_{2} \oplus WK_{5},&C_{3}&= X^{32}_{3}, \\ C_{4}&= X^{32}_{4} \boxplus WK_{6},&C_{5}&= X^{32}_{5},&C_{6}&= X^{32}_{6} \oplus WK_{7},&C_{7}&= X^{32}_{7}. \end{aligned}$$

Decryption. The decryption process is explained in the similar to the encryption process. This operation is identical to an operation for encryption apart from the following two modifications.

• 1. All $\boxplus$ operations are replaced by $\boxminus$ operations except for the $\boxplus$ operations connecting $SK_{i}$ and outputs of $F_{0}$, where the operation about $\boxminus$ denotes subtraction mod $2^{8}$.

• 2. The order in which the keys $WK_{i}$ and $SK_{i}$ are applied is reversed.

Key Schedule. The 128-bit master key is considered as a concatenation of 16 bytes and denoted by $K = K_{15} \Vert K_{14} \Vert \cdots \Vert K_{0}$. In the key schedule, 4 whitening keys for plaintexts are first generated from the master key as $(WK_0,WK_1,WK_2,WK_3)=(K_{12},K_{13},K_{14},K_{15})$, and 4 whitening keys for ciphertexts are generated from the master key as $(WK_4,WK_5,WK_6,WK_7)=(K_{0},K_{1},K_{2},K_{3})$. Moreover, the 128 subkeys are generated as

$$\begin{aligned} {\left\{ \begin{array}{ll} SK_{16 \cdot i + j} = K_{j - i \mod 8} \boxplus \delta _{16 \cdot i + j}, \\ SK_{16 \cdot i + j + 8} = K_{(j - i \mod 8) + 8} \boxplus \delta _{16 \cdot i + j + 8}, \end{array}\right. } \end{aligned}$$

where $\delta _i$ is a constant.

2.2 Integral Characteristics and Division Property

The integral attack was first proposed by Daemen et al. to evaluate the security of Square [5], and then it was formalized by Knudsen and Wagner [9]. The integral attack consists of two parts; construction of an integral characteristic and key recovery. In this subsection, we focus on the first part, and the second part is described in the next subsection.

The most common integral characteristic exploits the set of chosen plaintexts such that the sum of chosen bits in texts encrypted a certain number of rounds is always 0 for all secret keys. Assume that m-bit encrypted texts hold this characteristic in the target block cipher. Then, since the probability that the ideal block cipher holds this characteristic is $2^{-m}$, the distinguishing attack is directly derived from the integral characteristic.

Division Property. The division property, which was recently proposed in [21, 22], is a general method to find integral characteristics, and it is defined as follows.

Definition 1

(Division Property [21, 22]). Let ${\mathbb {X}}$ be a multiset whose elements take a value of ${\mathbb {F}}^{n}_{2}$. When the multiset ${\mathbb {X}}$ has the division property ${\mathcal {D}}^{1^n}_{{\mathbb {K}}}$, where ${\mathbb {K}}$ denotes a set of m-dimensional vectors whose i-th element takes 0 or 1, it fulfills the following conditions:

$$\begin{aligned} \bigoplus _{\varvec{x} \in {\mathbb {X}}} \varvec{x}^{\varvec{u}} = {\left\{ \begin{array}{ll} unknown &{} if\,\, there\,\, exist\,\, \varvec{k} \in {\mathbb {K}} \ \text {s.t.} \ \varvec{u} \succeq \varvec{k}, \\ 0 &{} otherwise, \end{array}\right. } \end{aligned}$$

where $\varvec{x}^{\varvec{u}} = \prod _{i=1}^n x[i]^{u[i]}$, and $\varvec{u} \succeq \varvec{k}$ if $u[i] \ge k[i]$ for all i. Here, x[i] denotes the i-th bit of x from the least significant bit (lsb).

Todo and Morii showed the propagation rules of the division property for three basic operations; copy, xor, and and [22].

Let $I=\{i_1,i_2,\ldots ,i_{|I|}\}$ be the index of active plaintext bits. Then, the division property of such chosen plaintexts becomes ${\mathcal {D}}_{\varvec{k}}^{1^n}$, where $k_i=1$ if $i \in I$ and $k_i=0$ otherwise. Then, to search for integral characteristics, division trail is evaluated.

Definition 2

(Division Trail [24]). Let us consider the propagation of the division property

$$\begin{aligned} \{\varvec{k}\} \overset{\underset{\mathrm {def}}{}}{=} {\mathbb {K}}_0 \rightarrow {\mathbb {K}}_1 \rightarrow {\mathbb {K}}_2 \rightarrow \cdots \rightarrow {\mathbb {K}}_r, \end{aligned}$$

where ${\mathcal {D}}_{{\mathbb {K}}_i}$ be the division property after i-round propagation. Moreover, for any vector $\varvec{k}^*_{i+1} \in {\mathbb {K}}_{i+1}$, there must exist a vector $\varvec{k}^*_{i} \in {\mathbb {K}}_{i}$ such that $\varvec{k}^*_{i}$ can propagate to $\varvec{k}^*_{i+1}$ by the propagation rule of the division property. Furthermore, for $(\varvec{k}_0, \varvec{k}_1,\ldots , \varvec{k}_r) \in ({\mathbb {K}}_0 \times {\mathbb {K}}_1 \times \cdots \times {\mathbb {K}}_r)$ if $\varvec{k}_{i}$ can propagate to $\varvec{k}_{i+1}$ for all $i \in \{0,1,\ldots ,r-1\}$, we call $(\varvec{k}_0 \rightarrow \varvec{k}_1 \rightarrow \cdots \rightarrow \varvec{k}_r)$ an r-round division trail.

Let $E_k$ be the target r-round block cipher. Then, if there is no division trail $\varvec{k}_0 \xrightarrow {E_k} \varvec{k}_r=\varvec{e}_i$, the i-th bit of r-round ciphertexts is always balanced. In [20, 21], and [22], all possible division trails are evaluated by using a breadth-first search. Unfortunately, it is practically infeasible to apply this method to block ciphers whose block length exceeds 32 because the size of ${\mathbb {K}}_i$ is extremely large.

MILP-Aided Propagation Search. A mixed-integer linear programming (MILP) was introduced to cryptanalysis by Mouha et al. in [11]. Then, the MILP has been successfully applied to various cryptanalyses [4, 13, 17, 17, 18, 24]. The MILP is an optimization or feasibility program where variables are restricted to integers. An MILP model ${\mathcal {M}}$ consists of variables ${\mathcal {M}}.var$, constraints ${\mathcal {M}}.con$, and an objective function ${\mathcal {M}}.obj$, and the following is an example of MILP.

Example 1

$$\begin{aligned} {\mathcal {M}}.var&\leftarrow x,y,z \text{ as } \text{ binary. } \\ {\mathcal {M}}.con&\leftarrow x + 2 y + 3 z \le 4 \quad \text{ and } \quad x + y \ge 1 \\ {\mathcal {M}}.obj&\leftarrow \text{ maximize } x + y + 2z \end{aligned}$$

The answer of the model ${\mathcal {M}}$ is 3, where $(x,y,z)=(1,0,1)$.

MILP solver can solve such optimization program, and it returns infeasible if there is no feasible solution. Moreover, if there is no objective function, the MILP solver only evaluates whether this model is feasible or not.

Xiang et al. showed that all division trails are efficiently evaluated by using the MILP in [24], where three division trails for basic operations are modeled as follows.

Proposition 1

(MILP model for COPY). Let $a \xrightarrow {COPY} (b_1,b_2,\ldots ,b_m)$ be a division trail of COPY, where one bit is copied to m bits. The following inequalities are sufficient to describe the propagation of the division property for copy.

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {M}}.var \leftarrow a,b_1,b_2,\ldots ,b_m\,\, as\,\, binary. \\ {\mathcal {M}}.con \leftarrow a = b_1 + b_2 + \cdots + b_m \end{array}\right. } \end{aligned}$$

Proposition 2

(MILP model for XOR). Let $(a_1, a_2, \ldots , a_m) \xrightarrow {XOR} b$ be a division trail of XOR, where the XOR of m bits is computed. The following inequalities are sufficient to describe the propagation of the division property for xor.

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {M}}.var \leftarrow a_1,a_2,\ldots ,a_m,b \,\,as\,\, binary. \\ {\mathcal {M}}.con \leftarrow a_1 + a_2 + \cdots + a_m = b \end{array}\right. } \end{aligned}$$

Proposition 3

(MILP model for 2-bit AND). Let $(a_1, a_2) \xrightarrow {AND} b$ be a division trail of AND, where the AND of 2 bits is computed. The following inequalities are sufficient to describe the propagation of the division property for and.

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {M}}.var \leftarrow a_1,a_2,b \,\,as\,\, binary. \\ {\mathcal {M}}.con \leftarrow b \ge a_i \,\,for\,\, all \,\, i\in \{1,2\} \end{array}\right. } \end{aligned}$$

In [24], an additional constraint $b-a_1-a_2 \le 0$ is used, but it is redundant. Namely, even if the redundant constraint is not used, it does not affect the result of MILP.

We first create the MILP model for a target block cipher by using Proposition 1, 2, and 3. Then, the division property of plaintexts is constrained according to the index I of active plaintext bits. Moreover, the division property of the i-th bit of ciphertexts is constrained to 1 when the i-th bit of ciphertexts is evaluated, and the division property of the other bits is constrained to 0. If the MILP solver judges that the model is infeasible, the i-th bit of ciphertexts is balanced. Please refer to [24] in detail.

2.3 Key Recovery and Bitwise Partial-Sum Technique

Supposing that $\kappa$-bit secret key is involved to evaluate the integral characteristic with $2^{|I|}$ texts from ciphertexts, the trivial key recovery requires $2^{|I|+\kappa }$ time complexity. Ferguson et al. proposed the partial-sum technique to reduce the time complexity in [6]. In this technique, we first store the frequency of ciphertexts into a memory, ciphertexts are partially decrypted by guessing the part of involved keys, and reduce the size of the memory. Since the complexity is the product of the memory size and the partially guessed key size, the attacker can reduce the whole complexity by partial decryption and compressing the data size step by step.

Table 2. Summary of the complexity of the bytewise and bitwise partial-sum

Sasaki and Wang proposed the bitwise partial-sum technique, which improves the complexity of the partial-sum technique for ARX designs [15]. Suppose that n-bit variables X, Y and n-bit unknown key K. Also suppose that $2^{2n}$ pairs of (X, Y) are given to the attacker, and the goal of the attacker is to compute Z by exhaustively guessing K, where the following two operations are considered.

$$\begin{aligned} Z&= (X \oplus K) \boxplus Y,&Z&= (X \boxplus K) \oplus Y. \end{aligned}$$

The complexity to compute Z is $2^{2n} \cdot 2^{n} = 2^{3n}$ operations. The bitwise partial-sum can reduce the complexity to $n \cdot 2^{2n+1}$ by computing Z bit by bit.

In practice, we need to evaluate the complexity for mod subtraction because of analyzing on decryption. At first, n-bit variable ${\bar{Y}}$ and ${\bar{K}}$ denote inverse elements corresponding to Y and K, respectively. Then, the following equations can be easily derived.

$$\begin{aligned} (X \oplus K) \boxminus Y&= (X \oplus K) \boxplus {\bar{Y}},&(X \boxminus K) \oplus Y&= (X \boxplus {\bar{K}}) \oplus Y. \end{aligned}$$

Hence, we can consider that the mod subtraction is equivalent to the mod addition are equivalent as far as guessing all values of ${\bar{Y}}$ and ${\bar{K}}$, and use same procedure shown by [15]. The complexities to compute the above equations with the bytewise and bitwise partial-sum is given in Table 2.

3 New Integral Characteristics on HIGHT

3.1 Previous 17-Round Integral Characteristics

Zhang et al. first showed 11-round integral characteristics with $2^8$ chosen plaintexts in [25]. Moreover, they extended the characteristics to 17-round ones by using the higher-order integral as

$$\begin{aligned} ({\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {C}})&\xrightarrow {17R} ({\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {B}}_{0},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}}), \\ ({\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {C}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}})&\xrightarrow {17R} ({\mathcal {B}}_{0},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}}), \end{aligned}$$

where ${\mathcal {B}}_{0}$ denotes that the lsb of the byte is balanced [25]. Moreover, ${\mathcal {A}}$ denotes that every value appears the same number in the multiset, ${\mathcal {C}}$ denotes that the value is fixed to a constant for all texts in the multiset and ${\mathcal {U}}$ denotes that the multiset is indistinguishable from one of n-bit random values.

3.2 New Integral Characteristics Based on Division Property

We first propose some new 18-round integral characteristics, which are found by the propagation of the division property. As the unique structure of HIGHT, there are modular constant additions and modular additions of two values. Such additions are represented by the combination of half and full adders, and we generate the MILP model by simulating these adders by three propagation rules.

MILP Model for Modular Additions.

We first consider the MILP model for half and full adders. In the half adder, the input is two bits a and b, and the output is the sum s and the carry c. Then, s and c are computed as

$$\begin{aligned} c = a \wedge b, \qquad s = a \oplus b. \end{aligned}$$

In the full adder, the input is three bits a, b, and x, and the output is the sum s and the carry c. Then, s and c are computed as

$$\begin{aligned} c = (a \wedge b) \oplus (x \wedge (a \oplus b)), \qquad s = a \oplus b \oplus x. \end{aligned}$$

halfAdder and fullAdder in Algorithm 1 generates the MILP model of the division property for halfAdder and fullAdder, respectively. Here, halfAdder consists of 6 ${\mathcal {M}}.vars$ and 5 ${\mathcal {M}}.cons$, and fullAdder consists of 13 ${\mathcal {M}}.vars$ and 10 ${\mathcal {M}}.cons$. Moreover, modAdd in Algorithm 1 shows the MILP model of the division property for modular addition of two n-bit values, where $(6 + 13 \times (n-2) + 1)$ ${\mathcal {M}}.vars$ and $(5 + 10 \times (n-2) + 1)$ ${\mathcal {M}}.cons$ are used. Constant round keys are modular added to the state in HIGHT, and modAddConst in Algorithm 1 shows the MILP model of the division property. In the constant addition, corresponding division property is always 0. Therefore, additions of the lsb and msb are simply represented, and it is enough to use halfAdder for additions of other bits. Therefore, $2 + 6 \times (n-2) + 1$ ${\mathcal {M}}.vars$ and $1 + 5 \times (n-2) + 1$ ${\mathcal {M}}.cons$ are used.

New 18-Round Integral Characteristics. We implemented an MILP model of the division property for HIGHT. The algorithm to search for integral characteristics is described in Algorithm 2 of Appendix A. To find the longest integral characteristics, we choose one constant bit from 64 plaintext bits, i.e., 64 sets of $2^{63}$ chosen plaintexts are tried out. As a result, we found six 18-round integral characteristics as

$$\begin{aligned}&\text {IC1}&({\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}}_{0})&\xrightarrow {18R} ({\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {B}}_{0},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}}), \\&\text {IC2}&({\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}}_{0},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}})&\xrightarrow {18R} ({\mathcal {B}}_{0},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}}), \\&\text {IC3}&({\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}}_{0},{\mathcal {A}},{\mathcal {A}})&\xrightarrow {18R} ({\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {B}}_{1,0},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}}), \\&\text {IC4}&({\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}}_{1},{\mathcal {A}},{\mathcal {A}})&\xrightarrow {18R} ({\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {B}}_{1,0},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}}), \\&\text {IC5}&({\mathcal {A}},{\mathcal {A}}_{0},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}})&\xrightarrow {18R} ({\mathcal {B}}_{1,0},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}}), \\&\text {IC6}&({\mathcal {A}},{\mathcal {A}}_{1},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}})&\xrightarrow {18R} ({\mathcal {B}}_{1,0},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}}), \end{aligned}$$

where ${\mathcal {A}}_{i}$ denotes seven bits except for i-th bit are active and i-th bit is constant, and ${\mathcal {B}}_{1,0}$ denotes that the lsb and the second lsb are balanced¹.

3.3 Extended 19-Round Integral Characteristics

We propose how to extend six 18-round integral characteristics to 19-round ones by appending one round to the plaintext side. Especially, we do not need to guess secret keys for extensions from IC1, IC2, IC3 and IC5, and it does not require the use of the full code book. Unfortunately, other two extensions requires guessing the part of secret keys, but we can easily append one round by using the full code book.

Fig. 2.

IC1, 2

Fig. 3.

IC3, 5

Fig. 4.

IC4, 6

Extending IC1 and IC2. We consider the extension from IC1 and IC2, where the round function using $F_0$ is involved (see Fig. 2). Then, the lsb of the left half of the output is represented as

$$\begin{aligned} L[0] \oplus (F_0(R) \boxplus SK)[0]&= L[0] \oplus F_0(R)[0] \oplus SK[0]. \end{aligned}$$

When the lsb of the left half of the plaintext takes a value ${\mathcal {X}} = F_{0}(R)[0]$, the lsb of the left half of the output is always constant. As a result, we can get two 19-round integral characteristics as

$$\begin{aligned}&\text {IC1'}&({\mathcal {A}}^{7} \Vert {\mathcal {X}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}})&\xrightarrow {19R} ({\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {B}}_{0},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}}), \\&\text {IC2'}&({\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}}^{7} \Vert {\mathcal {X}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}})&\xrightarrow {19R} ({\mathcal {B}}_{0},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}}), \end{aligned}$$

without guessing any bit of secret key, where ${\mathcal {A}}^{i}$ denotes that i bits are active.

Extending IC3 and IC5. We consider the extension from IC3 and IC5, where the round function using $F_1$ is involved (see Fig. 3). Then, the lsb of the left half of the output is represented as

$$\begin{aligned} L[0] \boxplus (F_1(R) \oplus SK)[0]&= L[0] \oplus F_1(R)[0] \oplus SK[0]. \end{aligned}$$

When the lsb of the left half of the plaintext takes a value ${\mathcal {X}} = F_{1}(R)[0]$, the lsb of the left half of the output is always constant. As a result, we can get two 19-round integral characteristics as

$$\begin{aligned}&\text {IC3'}&({\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}}^{7} \Vert {\mathcal {X}},{\mathcal {A}})&\xrightarrow {19R} ({\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {B}}_{1,0},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}}), \\&\text {IC5'}&({\mathcal {A}},{\mathcal {A}},{\mathcal {A}}^{7} \Vert {\mathcal {X}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}})&\xrightarrow {19R} ({\mathcal {B}}_{1,0},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}}), \end{aligned}$$

without guessing any bit of secret key.

Extending IC4 and IC6. We consider the extension from IC4 and IC6 (see Fig. 4). The second lsb is constant in these integral characteristics instead of the lsb. Then, the second lsb of the left half of the output is represented as

$$\begin{aligned} L[1] \oplus F_1(R)[1] \oplus SK[1] \oplus (L[0] \times (F_1(R)[0] \oplus SK[0])). \end{aligned}$$

When the second lsb of the left half of the plaintext takes a value ${\mathcal {X}} = F_1(R)[1] \oplus (L[0] \times (F_1(R)[0] \oplus SK[0]))$, the output second lsb is constant. Then,

$$\begin{aligned}&\text {IC4'}&({\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}}^{6} \Vert {\mathcal {X}} \Vert A^{1},{\mathcal {A}})&\xrightarrow {19R} ({\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {B}}_{1,0},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}}), \\&\text {IC6'}&({\mathcal {A}},{\mathcal {A}},{\mathcal {A}}^{6} \Vert {\mathcal {X}} \Vert A^{1},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}},{\mathcal {A}})&\xrightarrow {19R} ({\mathcal {B}}_{1,0},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}},{\mathcal {U}}). \end{aligned}$$

Unfortunately, these extension requires guessing SK[0] and the full code book.

These integral characteristics could not be detected by MILP-aided tool. In our procedure that how to extend integral characteristics, we have to compose the set of chosen plaintexts which include some non-linear part, represented as ${\mathcal {X}}$. On the other hand, the division property provide the completely linear and generalized set of chosen plaintexts. As a result, the MILP-aided tool using the division property can find 18-round integral characteristics but cannot find 19-round ones.

4 28-Round Attack on HIGHT Without Full Code Book

4.1 Whitening Key Addition to Integral Characteristics

In Sect. 3.3, we showed new 19-round integral characteristics, but we cannot use each characteristic directly because whitening key is added to plaintexts at first. In this section, we propose how to add the whitening to six 19-round integral characteristics.

First, we add the whitening to IC1’ or IC2’, where the XOR is used as the addition. Then, the whitening key is linearly involved to the lsb of the left half of the output. Therefore, even if there is the whitening, we can use IC1’ without guessing the key.

Next, we add the whitening to IC3’ or IC5’, where the modular addition is used as the addition. Then, the whitening key is nonlinearly involved to the lsb of the left half of the output. Unfortunately, this requires guessing the whitening key, and the use of the full code book is required to add the whitening. Similarly, the full code book is required to add the whitening to IC4’ or IC6’.

As a result, we can add the whitening to IC1’ and IC2’ without using the full code book. Other four integral characteristics can be added the whitening when the full code book is used. Hereafter, we only use IC1’ and IC2’ to avoid the use of the full code book in this section.

4.2 Meet-in-the-Middle Technique

Let us consider the integral attack using IC1’. Then, $X^{19}_{3}[0]$ is balanced and can be written as a linear combination of two variables $X^{20}_{4}[0]$ and $Z^{19}_{3}[0]$, where $X^{r}_{i}[j]$ denotes the j-th bit of the $X^{r}_{i}$. In the meet-in-the-middle technique [14], each sum is independently computed from ciphertexts, and secret keys satisfying $\bigoplus Z^{19}_{3}[0] = \bigoplus X^{20}_{4}[0]$ are recovered by using the computation like the meet-in-the-middle attack. Furthermore, for HIGHT, this concept is extended by exploiting more linearity inside the round function in [15]. Since the complexity for computing $\bigoplus Z^{19}_{3}[0]$ is much bigger than the one for $\bigoplus X^{20}_{4}[0]$, we reduce the number of subkeys involved $\bigoplus Z^{19}_{3}[0]$. We focus on that $Z^{19}_{3}[0]$ is computed by $SK_{77}[0] \boxplus Y^{19}_{3}[0]$, and this is represented as $Z^{19}_{3}[0] = SK_{77}[0] \oplus Y^{19}_{3}[0]$ because the lsb of the modular addition is a XOR. Therefore, $SK_{77}[0]$ can be removed, namely $\bigoplus X^{20}_{4}[0] = \bigoplus Y^{19}_{3}[0]$. Furthermore, by utilizing the linearity of $F_{0}$, i.e., $Y^{19}_{3}[0] = X^{20}_{3}[7] \oplus X^{20}_{3}[6] \oplus X^{20}_{3}[1]$, we can move more subkey bits, and finally get the following equation.

$$\begin{aligned} \bigoplus (X^{20}_{4}[0] \oplus X^{21}_{4}[7] \oplus X^{21}_{4}[6] \oplus X^{21}_{4}[1]) = \bigoplus (Z^{20}_{3}[7] \oplus Z^{20}_{3}[6] \oplus Z^{20}_{3}[1]). \end{aligned}$$

(1)

Unfortunately, 13-byte keys are involved to the right half of Eq. (1), and we cannot append 9 rounds like [15]. Moreover, 14-byte keys are involved when IC2’ is used. Alternatively, we attack 28-round HIGHT from the 2-nd round to 29-th round with whitening keys. Then, 12-byte keys and 13-byte keys are involved when IC1’ and IC2’ are used, respectively. We detail the analyses of the involved keys about each $Z^{r}_{i}$ in Table 5 of Appendix B.

We prepare the 28-round HIGHT from the 2-nd to 29-th round and apply IC1’ to 19-round between 2-nd and 20-th round. Then, $X^{20}_{3}[0]$ is balanced, and we finally get the following equation.

$$\begin{aligned} \bigoplus (X^{21}_{4}[0] \oplus X^{22}_{4}[7] \oplus X^{22}_{4}[6] \oplus X^{22}_{4}[1]) = \bigoplus (Z^{21}_{3}[7] \oplus Z^{21}_{3}[6] \oplus Z^{21}_{3}[1]). \end{aligned}$$

(2)

4.3 Attack Procedure

We use the relationship between the whitening key, subkey and master key in Table 3.

Table 3. Relationship between Whitening key, Subkey and Master key from 1-st to 29-th round

Fig. 5.

Partial decryption for $\bigoplus (Z^{21}_{3}[7] \oplus Z^{21}_{3}[6] \oplus Z^{21}_{3}[1])$ on 28-round attack

Since the computation for the right-hand side of Eq. (2) requires much more complexity than the left-hand side, we only explain the procedure to obtain the right-hand side of Eq. (2) and evaluate the time complexity. The partial decryption for obtaining $\bigoplus (Z^{21}_{3}[7] \oplus Z^{21}_{3}[6] \oplus Z^{21}_{3}[1])$ is shown in Fig. 5. We first describe our procedure with the bytewise partial-sum technique as following steps:

• 1. The analysis starts from at most $2^{64}$ ciphertexts of $(C_{0},\ldots ,C_{7})$.

• 2. $K_{1} \text { and } K_{2}$ are guessed and the data is compressed into $2^{56}$ texts.

• 3. $K_{2}$ has been already guessed, so $K_{3}$ is guessed and the data is converted into $2^{56}$ texts.

• 4. $K_{15}$ is guessed and the data is compressed into $2^{48}$ texts.

• 5. $K_{3}$ has been already guessed, so $K_{4}$ is guessed and the data is converted into $2^{48}$ texts.

• 6. $K_{8}$ is guessed and the data is converted into $2^{48}$ texts.

• 7. $K_{11}$ is guessed and the data is compressed into $2^{40}$ texts.

• 8. $K_{1}$ has been already guessed, so $K_{0}$ is guessed and the data is converted into $2^{40}$ texts.

• 9. $K_{9}$ is guessed and the data is converted into $2^{40}$ texts.

• 10. $K_{12}$ is guessed and the data is converted into $2^{40}$ texts.

• 11. $K_{7}$ is guessed and the data is compressed into $2^{32}$ texts.

• 12. $K_{3}$ has been already guessed, so the data is converted into $2^{32}$ texts.

• 13. $K_{0}$ has been already guessed, so the data is converted into $2^{32}$ texts.

• 14. $K_{8}$ has been already guessed, so the data is converted into $2^{32}$ texts.

• 15. $K_{13}$ is guessed and the data is compressed into $2^{24}$ texts.

• 16. $K_{4}$ has been already guessed, so the data is compressed into $2^{16}$ texts.

• 17. $K_{12}$ has been already guessed, so the data is compressed into $2^{8}$ texts.

• 18. $K_{0}$ has been already guessed, so the data is compressed into 1 text of $Z^{21}_{3}$. Then, we can calculate the value of $\bigoplus (Z^{21}_{3}[7] \oplus Z^{21}_{3}[6] \oplus Z^{21}_{3}[1])$.

This procedure and its time complexity evaluation is summarized in Table 4. Step 11 and 15 requires the dominant time complexity, where $2^{128}$ round function computations is used for the bytewise partial sum. We apply the bitwise partial sum to Step 11 and 15 to reduce the complexities. Step 11 starts from $2^{40}$ texts of $(X^{27}_{0},X^{26}_{3},X^{26}_{4},X^{26}_{5},X^{27}_{7})$, and the goal is obtaining $2^{32}$ texts of $(X^{27}_{0},X^{25}_{3},X^{26}_{5},X^{27}_{7})$ with guessing $K_{7}$. We then apply the bitwise partial sum to guess $K_{7}$. Referring Table 2, its time complexity is reduced to $n \cdot (2^{80+39+1}) = 2^{123}$ round functions, where $n = 8$. In Step 15, we can also reduce the time complexity about $2^{128}$ to $n \cdot (2^{88+31+1}) = 2^{123}$ round functions, similarly. Finally, the time complexity in the key recovery is estimated by Step 11 and 15 because the complexities of other steps are negligible compared with $2^{123}$. Hence, the time complexity of the key recovery is about $2^{124}$ round functions(RF).

Table 4. Summary of the computation for $\bigoplus (Z^{21}_{3}[7] \oplus Z^{21}_{3}[6] \oplus Z^{21}_{3}[1])$.

Since only one integral characteristic with one balance bit is used, this key recovery only reduces the 1-bit of information on the master key. Therefore, we finally exhaustively searches $2^{127}$ master keys. As a result, the whole complexity of our attack is $2^{124} \text { RF} + 2^{127} \text { Enc} \approx 2^{127} \text { Enc}$.

5 29-Round Attack on HIGHT with Full Code Book

When the use of the full code book is acceptable, we can attack 29-round HIGHT, where one round is added to the plaintext side from the 28-round attack. Therefore, while 28-round HIGHT from the 2-nd to 29-th round is attacked in Sect. 4, the natural 29-round HIGHT is attacked.

We briefly describe the overview of our 29-round attack. We first prepare the set of chosen texts for the input of the 2-nd round function such that it brings 19-round integral characteristics, i.e., $X^{20}_3[0]$ is balanced, and it is the same as the 28-round attack. Next, we guess the round key in the 1-st round and whitening keys, and get the set of corresponding plaintexts. Since the set of plaintexts depends on the guessed keys, 29-round attack requires the use of the full code book. Moreover, the position of the guessed keys depends on each characteristic, and Appendix C shows it in detail. Finally, we execute the key recovery that is the same as that for the 28-round attack.

We first try to execute 29-round attack using the 19-round integral characteristic IC1’. To prepare the set of plaintexts, we have to guess the value of $K_{14}$ and $K_{2}$. Unfortunately, $K_{14}$ is not involved to the key recovery shown in Table 4. Therefore, the complexity of each step always requires $2^{8}$ times, and the time complexity in Step 11 and 15 is over $2^{128}$ even if the bit-wise partial sum is applied. As a result, we cannot use IC1’. We next try to execute 29-round attack using the 19-round integral characteristic IC3’. Note that the position of balanced byte is the same as that by IC1’, i.e., $X^{20}_3[0]$ is balanced. Therefore, we can use the same procedure for the key recovery. To prepare the set of plaintexts, we have to guess the value of $K_{15}$ and $K_{3}$, which are already guessed in Step 4 and 3 in the key recovery, respectively. Hence, we add two bytes to the guessed keys in Step 1–2 and one byte to them in Step 3, and the complexity does not change after Step 4. Therefore, even if IC3’ is used, the complexity of the key recovery is still $2^{124} \text { RF}$ because the dominant part is in Step 11 and 15. Moreover, when IC4’ is used, we have to guess the value of not only $K_{15}$ and $K_{3}$ but also the lsb of $K_{4}$ and $K_{12}$, but all additional guessing keys have been already guessed in the key recovery. Therefore, similarly to the key recovery using IC3’, the dominant complexity is still $2^{124} \text { RF}$. Since we can execute the key recovery using both IC3’ and IC4’ in the same time, 2 bits of information of the master key is recovered. As a result, the whole complexity of our attack is $2^{124} \text { RF} + 2^{126} \text { Enc} \approx 2^{126} \text { Enc}$.

6 Conclusions

In this paper, we first proposed 19-round integral characteristics by using the propagation of the division property. These characteristics are improved by two rounds compared with previous ones. Then, we showed the attack against 28-round HIGHT by appending 9-round key recovery. We attacked 28-round HIGHT with $2^{63}$ data size and $2^{127}$ time complexity. Moreover, we showed another attack on 29-HIGHT with $2^{64}$ data size and $2^{126}$ time complexity. These attacks are the best known attack against HIGHT under the single-key setting.

Appendices

A Detailed MILP Model for HIGHT

In this appendix, the detailed algorithm to search for integral characteristics on HIGHT is described.

As a result of running the Algorithm 2 with our machine (CPU: i5-6500 @ 3.20 GHz, 3.20 GHz/RAM: 8.00 GB/64-bit operating system, x64 base processor), it took about 50 min.

B Involved Key Size in Key Recovery

In this appendix, the detailed analyses of the involved key size in the calculation of $Z^{r}_{i}$ is described.

Table 5. The number of involved key bytes in calculation of $Z^{r}_{i}$

C Detailed Addition of Whitening Layer

In this appendix, we described detailed procedure how to add the whitening layer to three 19-round integral characteristics. The first 2-round procedure on HIGHT is shown in Fig. 6. Please refer to Table 3 in order to know the relationship between the round keys and the master keys.

Fig. 6.

1-st and 2-nd round procedure of HIGHT

We consider the extension from IC1’ and the lsb of $X^{2}_{0}$ is represented as

$$\begin{aligned} X^{2}_{0}[0]&= X^{1}_{7}[0] \oplus SK_{7}[0] \oplus F_0(X^{1}_{6})[0] \\&= X^{0}_{6}[0] \oplus WK_{3}[0] \oplus SK_{7}[0] \oplus F_0(F_1(X^{0}_{4} \boxplus WK_{2}) \oplus SK_{2} \boxplus X^{0}_{5})[0]. \end{aligned}$$

We can ignore the value of $WK_{3}[0]$ and $SK_{7}[0]$ because $X^{2}_{0}[0]$ is added linearly by them using XOR. But we cannot ignore that this extension requires guessing the value of $K_{14}$ and $K_{2}$ as $WK_{2}$ and $SK_{2}$, respectively. Next, we consider the extension from IC3’. In case of considering the lsb, we can regard the modular addition as the XOR. So the lsb of $X^{2}_{2}$ is represented as

$$\begin{aligned} X^{2}_{2}[0]&= X^{1}_{1}[0] \oplus SK_{4}[0] \oplus F_1(X^{1}_{0})[0] \\&= X^{0}_{0}[0] \oplus WK_{0}[0] \oplus SK_{4}[0] \oplus F_1(F_0(X^{0}_{6} \oplus WK_{3}) \boxplus SK_{3} \oplus X^{0}_{7})[0]. \end{aligned}$$

This extension requires guessing the value of $K_{15}$ and $K_{3}$ as $WK_{3}$ and $SK_{3}$, respectively. Finally, we consider the extension from IC4’ and the second lsb is represented as

$$\begin{aligned} X^{2}_{2}[1]&= X^{1}_{1}[1] \oplus F_1(X^{1}_{0})[1] \oplus SK_{4}[1] \oplus (X^{1}_{1}[0] \times (F_1(X^{1}_{0})[0] \oplus SK_{4}[0])), \end{aligned}$$

where each $X^{1}$ are represented as follows:

$$\begin{aligned} X^{1}_{1}[1]&= X^{0}_{0}[1] \oplus WK_{0}[1] \oplus (X^{0}_{0}[0] \times WK_{0}[0])), \\ X^{1}_{1}[0]&= X^{0}_{0}[0] \oplus WK_{0}[0], \\ X^{1}_{0}&= F_0(X^{0}_{6} \oplus WK_{3}) \boxplus SK_{3} \oplus X^{0}_{7}. \end{aligned}$$

This extension requires guessing the value of $K_{4}[0], K_{12}[0], K_{15}$ and $K_{3}$ as $SK_{4}[0], WK_{0}[0], WK_{3}$ and $SK_{3}$, respectively.