Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Fuzzy Cognitive Maps (FCMs), proposed by Kosko [11], comprise a very suitable tool for modeling and simulation purposes. Without loss of generality, we can define FCMs as recurrent neural networks that produce a state vector at each iteration. From the structural perspective, FCM-based models comprise a set of neural processing entities called concepts (or simply neurons) and a set of causal relations defining a weight matrix. One of the advantages of cognitive mapping relies on the interpretability attached to the causal network, where both neurons and weights have a precise meaning for the problem domain.

The reader can find several interesting applications of these cognitive neural networks in [18], while the survey in [19] is devoted to their extensions. Meanwhile, due to the relevance of the weight matrix in designing the cognitive model, several supervised learning methods have been introduced to compute the weights characterizing the system under investigation (e.g., [1, 16, 28, 30, 31]). Estimating a high-quality weight matrix is a key issue towards building the forecasting model; otherwise, the system interpretation will not be meaningful even if the FCM reasoning is still transparent.

One field where FCMs have found great applicability is related to the time series prediction [9, 10, 12, 13, 24, 25, 27]. In [26] the authors focused on the learning mechanism and causality estimation from the perspective of time series. Multivariate, interval-valued time series are addressed using fuzzy grey cognitive maps in [8], where near-continuous time series are transformed into intervals of increasing or decreasing values. Modifications of the learning algorithm to better deal with time series prediction are proposed in [7]. Likewise, FCMs and time lags in time series prediction are considered in [20]. After this, not much attention seems to be paid to the issue of lagging effects in time series.

The power of FCMs does not lay in superior forecasting in time series analysis. Indeed, looking only at fitness measures for fitted and predicted data, specialized techniques like even the well-known ARIMA methods [3] are able to outperform an FCM. However, the weight matrix, which is the center of an FCM-based model, provides a degree of transparency that cannot be easily achieved with other forecasting models. As a further advantage, a discovered weight matrix, constrained or not, can be presented to experts for either validation of the model or as input for supporting the policy making process.

Regrettably, FCM-based forecasting models tend to converge to a fixed-point when performing the inference process. While this feature is highly attractive in simulation and pattern classification situations [17], its effect on time series scenarios is less desirable. More explicitly, if the network converges to a fixed-point, then the forecasting model will not fit the time series, unless the data points match with the fixed-point, which is rather unlikely.

In this paper, we investigate the use of FCMs in time series prediction in the context of a real case study. Particularly, our paper introduces two contributions, moving from theory to practice. The first contribution is related to the study of four neural updating rules and their impact over the accuracy achieved by the cognitive forecasting model. As a second contribution, we adopt the proposed models to predict the future influx of a prosecutor’s office in a Belgian province using both demographic and economic features. The numerical simulations have shown that selecting a specific neural updating rule may improve the model accuracy; however, further investigation is required.

This paper follows the principles and structure of Design Science, as proposed by Peffers et al. in [22]. Section 2 introduces the Fuzzy Cognitive Maps, while Sect. 3 describes the theoretical problem to be confronted. Section 4 presents some alternatives to cope with the identified problem. Section 5 is devoted to the numerical analysis by using a real-world case study, whereas Sect. 6 discusses the results and outlines the future research directions.

2 Fuzzy Cognitive Maps

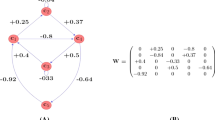
The semantics behind an FCM-based system can be completely defined using a 4-tuple \((\mathcal {C},\mathcal {W},\mathcal {A},f)\) where \(\mathcal {C} = \{C_1,C_2,C_3,\ldots ,C_M\}\) is the set of M neural processing entities, \(\mathcal {W} : \mathcal {C} \times \mathcal {C} \rightarrow [-1,1]\) is a function that attaches a causal value \(w_{ij}\) to each pair of neurons \((C_i,C_j)\) and the value \(w_{ij}\) denotes the direction and intensity of the edge connecting the cause \(C_i\) and the effect \(C_j\). This function describes a causal weight matrix that defines the behavior of the investigated system [11]. On the other hand, the function \(\mathcal {A} : \mathcal {C} \rightarrow A_i^{(t)}\) computes the activation degree \(A_i \in \mathfrak {R}\) of each neuron \(C_i\) at the discrete-time step t, where \(t = \{1,2, \ldots ,T\}\). Finally, the transfer function \(f: \mathfrak {R} \rightarrow I\) retains the activation degree of each neuron confined into the activation space.

Causal relations have an associated numerical value in the \([-1,1]\) range that govern the intensity of the relationships between the concepts defining the system semantics. Let \(w_{ij}\) be the weight associated with the connection between two neurons \(C_i\) and \(C_j\). Generally speaking, the interpretation of causal influences between two neural entities can be summarized as follows:

  • If \(w_{ij}>0\), this indicates that an increment (decrement) in the neuron \(C_i\) will produce an increment (decrement) on \(C_j\) with intensity \(|w_ij|\).

  • If \(w_{ij}<0\), this indicates that an increment (decrement) in the neuron \(C_i\) will produce a decrement (increment) on \(C_j\) with intensity \(|w_ij|\).

  • If \(w_{ij}=0\) (or very close to 0), this denotes the absence of a causal relationship from \(C_i\) upon \(C_j\).

Equation 1 shows the updating rule attached to an FCM-based system, where \(A^{(t)}\) is the vector of activation values at the tth iteration step, and W is the weight matrix defining the causal relations between concepts. The f(x) function is introduced to normalize the values and is often defined as a sigmoid function (see Eq. 2). It is worth mentioning that, in this model, a neuron cannot influence itself, so the main diagonal of W only contains zeros.

$$\begin{aligned} \varvec{A}^{(t+1)} = f(\varvec{W} \times \varvec{A}^{(t)}) \end{aligned}$$
(1)
$$\begin{aligned} f(x)= \dfrac{a}{1+exp(- \lambda x)} - b \end{aligned}$$
(2)

The features that turn FCMs into an attractive artefact for scientists and decision makers are multiple. (1) Their visual and transparent structure enables domain experts to introduce their knowledge into the model. (2) By applying learning techniques to an FCM, a weight matrix can be discovered. This weight matrix provides insights into the internal mechanism of the analyzed system, thus contributing to the decision-making process. (3) By modeling complex structures of dependencies between several concepts, the FCM is not constraint to focus on a single variable, but can simulate a system as a whole.

3 Problem Statement

The output of a neural processing entity in an FCM-based network produces a time-series-like sequence. In most FCM models, convergence is a desired (sometimes mandatory) feature when iterating the causal model. Understanding and encouraging convergence features have been studied actively in recent papers by Nápoles et al. [15, 17]. In contrast, time series typically display a more chaotic behavior. More explicitly, when an iteration t in an FCM is equated with a time observation k in a time series, measures have to be taken to reconcile the conflicting requirements coming to the convergence features.

As an alternative we can adopt a modified updating rule that uses different strategies to avoid the convergence issue. In this paper, we describe and compare different models and study their effect on the outcome.

As a practical example, we could compute a specific weight matrix \(W^{(t)}\) to predict the next value [13]. Besides the increased complexity towards learning the weight sets, and an inherently increased capacity for over-fitting, the multiplex nature of the weight sets decrease their transparency in decision-making scenarios. On top of it, predictions for future values can only be obtained if those future weight matrices are known as well.

A form of one-step-prediction is also used in [21]. Instead of using predicted values \(A^{(t)}\) to calculate \(A^{(t+1)}\), this adaptation uses the real values stored in the row data records. This approach seems adequate to analyze historical data; however, but it cannot solve the convergence issue when forecasting future values using the learned model (i.e., with no actual values available).

This paper proposes a modified strategy that addresses the aforementioned issues while maintaining the advantages of using cognitive mapping. Concretely, our model should satisfy the following requirements:

  1. 1.

    The prediction of chaotic time series with controlled chaos features.

  2. 2.

    The multiple-step-ahead predictions.

  3. 3.

    To preserve high prediction rates.

  4. 4.

    To preserve the transparency of the weight matrix.

4 Proposed Solutions

This paper proposes a modification of the FCM updating rule by introducing ARIMA-inspired components. Regardless the transfer function [4], Eq. 3 is selected as benchmark. In contrast with Eq. 1, it is allowed for neurons to influence themselves in the next iteration. In other words, the main diagonal of the weight matrix W can take values in the \([-1,1]\) range.

$$\begin{aligned} \varvec{A}^{(t+1)} = f(\varvec{A}^{(t)} + \varvec{W} \times \varvec{A}^{(t)}) \end{aligned}$$
(3)

Previous proposals advocate for the time series analysis using one-step ahead predictions [21, 23]. In these approaches, \(A_i^{(t+1)}\) is not calculated based on the calculated \(A_i^{(t)}\), but on the real, actual record \(R_i^{(t)}\). In a more generic form, this could be translated into Eq. 4, where part of the concepts are considered independent variables. Let \(\varvec{C^-}\) be the set of independent variables and \(C_i \in \varvec{C^-}\), then \(R_i^{(t)}\) the actual value in the data set will be used to calculate the activation value in the next iteration. These variables are providing independent input before each iteration. For the remaining variables, \(C_i \in \varvec{C^*}\), the \(A_i^{(t)}\) calculated activation values will be used to evolve the model.

$$\begin{aligned} \varvec{A}^{(t+1)} = f(\varvec{A}^{(t)} + \varvec{W}_{c^*} \times \varvec{A}^{(t)} + \varvec{W}_{c^-} \times \varvec{R}^{(t)}) \end{aligned}$$
(4)

Note that the model assumes that an iteration t coincides with an observation at time k in the time series. In this interpretation, the evolution through the iterations is implicitly considered as an evolution over time.

In our solution, we propose the introduction of ARIMA-inspired components to strengthen the applicability of FCM in the domain of time series analysis. Firstly, instead of using \(A_i^{(t)}\) as a base for calculating \(A_i^{(t+1)}\), a moving average will be introduced. On top of that, to avoid a converging time series, a weight amplification method is proposed. Just like ARIMA uses the auto-correlation parameters, the FCM would use correlation between concepts to increase or decrease the effect of the attributed weights.

$$\begin{aligned} \varvec{A}^{(t+1)} = \hat{f}(\varvec{MAC}_{window}^{(t)} + \hat{g}(\varvec{W}) \times \varvec{A}^{(t)}) \end{aligned}$$
(5)

The modified reasoning rule is depicted in Eq. 5. \(MAC_{window}^{(t)}\) denotes the moving average of the concept values for a time period \([t-window:t]\). The amplification of the weight effects is defined as \(\hat{g}(x)\) in Eq. 6, where \(\rho ^{window}_t\) is a matrix of Pearson Coefficients [29].

$$\begin{aligned} \hat{g}(W) = \rho ^{window}_t \times W \end{aligned}$$
(6)

Aiming at confining the activation values into the allowed interval, we adopt a modified version of the sigmoid function 2 (see Eq. 7). The parameters of this function are set to \(a=1.2\), \(b=0.2\) and \( \lambda = 1\).

$$\begin{aligned} \hat{f}(x)= {\left\{ \begin{array}{ll} \dfrac{1.2}{1+exp(-x)} - 0.2, &{} \text {if}\ \hat{f}(x) \ge 0 \\ 0, &{} \text {otherwise} \end{array}\right. } \end{aligned}$$
(7)

5 Demonstration

5.1 Dataset

The proposed models are applied to support the prosecutors in the Belgian criminal justice system. Accurately forecasting criminal activity and the demand on the criminal justice system enables authorities to proactively plan resources, which is particularly important because there has been variation in the intensity of crime over the last years, both over time and geographic units.

We follow the traditional law and economics literature on criminal behavior, which goes back to [2]. The size of the police force (POL, \(C_4\)) is a critical component of the price of committing crime because a larger police force is associated with a higher probability of apprehension and therefore an increased price of committing crime [5, 6, 14]. Furthermore, socio-economic (SOC) and demographic (DEM) variablesFootnote 1 that are expected to affect crime are included in the form of the proportion of young, single males (\(C_5\)), poverty (\(C_6\)) and unemployment (\(C_7\)) are included as well. Equation 8 defines crime (CR) as a function of police (POL), socio-economic (SOC) and demographic (DEM) characteristics. AS such the crime function is defined as in 8.

$$\begin{aligned} CR = f(CR, POL, SOC, DEM) \end{aligned}$$
(8)

In the dataset adopted for simulation purposes, crime consists of the number of drug (\(C_1\)), theft (\(C_2\)) and violence (\(C_3\)) related cases in the Belgian province of Antwerp. The data set contains 31 four-monthly observations, starting in the year 2006. Compared to other time series used in literature, the small nature of the data set provides an added level of complexity.

5.2 Methodology

The results from the experiments are obtained using a 80-20 division between training and test. This results in the 25 first observations to be used to learn the model, while the last six are used for validation.

All available data is normalized linearly in the [0, 1] range, with 0 representing the effective theoretical minimum of 0, and 1 representing the maximum observed value for the entire Belgian area, plus a small margin. Although this paper does not intend to make long-term predictions, this margin gives the models a larger range of error to operate in.

The results compare predictions for different FCM-related techniques and are obtained after 20 independent runs for each configuration. Model M1 uses Eq. 3. In Eq. 4 used in M2, activation values are used for concepts, \(C_1\), \(C_2\) and \(C_3\), while actual values are used for the other concept. M3 uses actual values for all concepts, also using 4. The model introducing the ARIMA concepts is M4, using Eq. 5, with only activation values to evolve the model.

A real-valued Genetic Algorithm is used to determine the weight matrices for each of the different settings. The algorithm is implemented in the package GA, available for RFootnote 2. The size of the population is 49, with a maximum number of iterations equal to 500. The crossover probability is 0.7, while mutation probability is 0.2. All values in the weight matrix are restricted to the \([-1,1]\) interval. The goal function to be optimized is a standardized form of the mean absolute error (MAE) and can be seen in Eq. 9.

$$\begin{aligned} fitness = \Bigg (1 + \dfrac{\sum \limits _{c=1}^{C^*}\sum \limits _{t=1}^T |A_c^i - R_d^i|}{C^* \times T}\Bigg )^{-1} \end{aligned}$$
(9)

5.3 Results

Figure 1 displays the values computed by each forecasting method, using the weights that yield the lowest MAE on the test set. Predictions are shown for \(C_1\), \(C_2\) and \(C_3\), which are the concepts of interest in the dataset. The line graph depicts the predicted values according to the model, while the data points display the actual values from the data set.

From this numerical simulation we can notice that M1 converges quite early in the time series. Convergence is not achieved in M2 and M3, each showing varying degrees of fluctuations in the predictions. However, both need actual values from a data set to do a next-step prediction. Lacking this input data, they are not capable of making predictions, as can be seen for the last observations in the time series. The M4 method does not suffer from a converged series while also being capable of predicting multiple steps ahead.

According to the prediction accuracy - as MAE - of 20 independent runs in the boxplots in Table 1, M4 causes a drop in both accuracy and robustness compared to M1 and M3. This is noticeable on both the training and the test set. As expected, the one-step ahead prediction of M3 produces the highest accuracy results. Furthermore, the robustness of M1 seems noteworthy. Its boxplot is dwarfed by the large range of M2, which occasionally outperforms M1, but does not seem to produce stable results.

Fig. 1.
figure 1

Predictions for the models with the best validation fitness for each method.

Full size image
Table 1. Mean absolute error and standard deviations.
Full size table

The relatively worse MAE results attached to the M4 method can be explained by the fact that its model is quite complex, compared to the others, with the weights not having a direct effect but rather being modified by correlations of previous predictions. As such, there is a higher degree of freedom as well as less predictability in the behavior the model.

The facts that the weights are amplified based on correlations between previous predictions, the model has become less transparent. The weight matrix can only be interpreted by combining it with those correlations, which are dynamically changing throughout the iterations. As a result, the impact of the causal relations cannot be completely understood from the weight matrix.

6 Conclusions

In this paper, we try to remedy some of the inherent drawbacks of FCMs when applied to time series analysis. By introducing concepts familiar from ARIMA models, the goal is to enable an FCM to (1) predict a fluctuating time series, (2) predict multiple steps ahead in the future, (3) maintain the prediction accuracy and (4) maintain the transparency of the weight matrix.

The results seem to suggest that the introduction of the ARIMA components does allow the FCM to predict multiple steps ahead in the future, without converging to a single set of values.

However, this has come at the expense of decreased accuracy scores. More importantly though, the transparency of the weight matrix has been blurred by the weight amplification function.

Despite some promising results, the method needs some optimization in order to achieve all goals set out in this paper.

Other unsolved issues regarding time series prediction remain a topic for future research. First of all, in the FCM model proposed by Kosko, an iteration has no meaning. An FCM is a type of recurrent neural network, representing a set of complex interactions within a system. When using the technique for analysis and predictions of time series, it is thus not self-evident that an iteration corresponds to a time interval.

Clarification of the relation between an observation at time k and an activation value at iteration t, will also provide insights into the issue of lagging effects in a multivariate time series. Ideally, the model should be able to deal with effects that have varying lags in a [0, T] range, in which case both contemporary and historic causality can be taken into account.

Addressing iterations and time intervals also inevitably leads to the topic of convergence. Convergence is sought after in the area of cognitive mapping, as it represents a stable state of the system. Without that stable state, it is not obvious to extract decision-making rules from the results. In contrast, in a time series, convergence is less likely to be desirable. This paper already exposes a possible path towards a solution. However, further research is needed to develop a model that exhibits all strengths of an FCM, while also boasting the strong time series prediction capabilities.