Hybrid Algorithms Based on Integer Programming for the Search of Prioritized Test Data in Software Product Lines

Abstract

In Software Product Lines (SPLs) it is not possible, in general, to test all products of the family. The number of products denoted by a SPL is very high due to the combinatorial explosion of features. For this reason, some coverage criteria have been proposed which try to test at least all feature interactions without the necessity to test all products, e.g., all pairs of features (pairwise coverage). In addition, it is desirable to first test products composed by a set of priority features. This problem is known as the Prioritized Pairwise Test Data Generation Problem. In this work we propose two hybrid algorithms using Integer Programming (IP) to generate a prioritized test suite. The first one is based on an integer linear formulation and the second one is based on a integer quadratic (nonlinear) formulation. We compare these techniques with two state-of-the-art algorithms, the Parallel Prioritized Genetic Solver (PPGS) and a greedy algorithm called prioritized-ICPL. Our study reveals that our hybrid nonlinear approach is clearly the best in both, solution quality and computation time. Moreover, the nonlinear variant (the fastest one) is 27 and 42 times faster than PPGS in the two groups of instances analyzed in this work.

This research is partially funded by the Spanish Ministry of Economy and Competitiveness and FEDER under contract TIN2014-57341-R, the University of Málaga, Andalucía Tech and the Spanish Network TIN2015-71841-REDT (SEBASENet).

1 Introduction

A Software Product Line (SPL) is a set of related software systems, which share a common set of features providing different products [1]. The effective management of variability can lead to substantial benefits such as increased software reuse, faster product customization, and reduced time to market. Systems are being built, more and more frequently, as SPLs rather than individual products because of several technological and marketing trends. This fact has created an increasing need for testing approaches that are capable of coping with large numbers of feature combinations that characterize SPLs. Many testing alternatives have been put forward [2,3,4,5]. Salient among them are those that support pairwise testing [6,7,8,9,10,11,12]. The pairwise coverage criterion requires that all pairs of feature combinations should be present in at least one test product. Some feature combinations can be more important than others (e.g., they can be more frequent in the products). In this case, a weight is assigned to each feature combination (usually based on product weights). In this context, the optimization problem that arises consists in finding a set of products with minimum cardinality reaching a given accumulated weight. This problem has been solved in the literature using only approximated algorithms.

The use of exact methods, like Mathematical Programming solvers, has the drawback of a poor scalability. Solving integer linear programs (ILP) is NP-hard in general. Actual solvers, like CPLEX¹ and Gurobi², include modern search strategies which allow them to solve relatively large instances in a few seconds. However, the size of the real instances of the problem we solve in this paper is too large to be exactly solved using ILP solvers. For this reason, we propose a combination of a high level heuristic (greedy) strategy and a low level exact strategy. The combination of heuristics and mathematical programming tools, also called matheuristics, is gaining popularity in the last years due to its great success [13].

In this paper we present two novel proposals: a Hybrid algorithm based on Integer Linear Programming (HILP) and another Hybrid algorithm based on Integer Nonlinear Programming (HINLP). We compare our proposals with two state-of-the-art algorithms: a greedy algorithm that generates competitive solutions in a short time, called prioritized-ICPL (pICPL) [14] and a hybrid algorithm based on a genetic algorithm, called Prioritized Pairwise Genetic Solver (PPGS) [15], which obtains higher quality solutions than pICPL but generally using more time. Our comparison covers a total of 235 feature models with a wide range of features and products, using three different priority assignments and five product prioritization selection strategies. Our main contributions in this paper are as follows:

• Two novel hybrid algorithms based on Integer Programming. One models the problem using linear functions (HILP) and the other one using nonlinear functions (HINLP).

• A comprehensive evaluation of the performance of HILP and HINLP. In the experimental evaluation 235 feature models and different prioritization schemes were used. We also compared the new approaches with those of state-of-the-art methods: PPGS and pICPL.

The remainder of the article is organized as follows. The next section presents some background on SPLs and feature models. In Sect. 3 the Prioritized Pairwise Test Data Generation Problem in SPL is formalized. Next, Sect. 4 details our algorithmic proposals. In Sect. 5 we briefly present the other algorithms of the comparison, the priority assignments and experimental corpus used in the experiments. Section 6 is devoted to the statistical analysis of the results and Sect. 7 describes possible threats to the validity of this study. Finally, Sect. 8 outlines some concluding remarks and future work.

2 Background: Feature Models

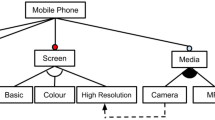
Feature models have become the de facto standard for modelling the common and variable features of an SPL and their relationships, collectively forming a tree-like structure. The nodes of the tree are the features which are depicted as labelled boxes, and the edges represent the relationships among them. Feature models denote the set of feature combinations that the products of an SPL can have [16].

Figure 1 shows the feature model of our running example for SPLs, the Graph Product Line (GPL) [17], a standard SPL of basic graph algorithms that has been widely used as a case study in the product line community. In GPL, a product is a collection of algorithms applied to directed or undirected graphs. In a feature model, each feature (except the root) has one parent feature and can have a set of child features. A child feature can only be included in a feature combination of a valid product if its parent is included as well. The root feature is always included. There are four kinds of feature relationships:

• Mandatory features are selected whenever their respective parent feature is selected. They are depicted with a filled circle. For example, features Driver and Algorithms.

• Optional features may or may not be selected if their respective parent feature is selected. An example is the feature Search.

• Exclusive-or relations indicate that exactly one of the features in the exclusive-or group must be selected whenever the parent feature is selected. They are depicted as empty arcs crossing over a set of lines connecting a parent feature with its child features. For instance, if feature Search is selected, then either feature DFS or feature BFS must be selected.

• Inclusive-or relations indicate that at least one of the features in the inclusive-or group must be selected if the parent is selected. They are depicted as filled arcs crossing over a set of lines connecting a parent feature with its child features. As an example, when feature Algorithms is selected then at least one of the features Num, CC, SCC, Cycle, Shortest, Prim, and Kruskal must be selected.

Fig. 1.

Graph Product Line feature model.

In addition to the parent-child relations, features can also relate across different branches of the feature model with the Cross-Tree Constraints (CTC). Figure 1 shows the CTCs of our feature model in textual form. For instance, Num requires Search means that whenever feature Num is selected, feature Search must also be selected. These constraints as well as those implied by the hierarchical relations between features are usually expressed and checked using propositional logic.

3 Problem Formalization: Prioritized Pairwise Test Data Generation

Combinatorial Interaction Testing (CIT) is a testing approach that constructs samples to drive the systematic testing of software system configurations [18, 19]. When applied to SPL testing, the idea is to select a representative subset of products where interaction errors are more likely to occur rather than testing the complete product family [18]. In the following we provide the basic terminology of CIT for SPLs³.

Definition 1 (Feature list)

A feature list FL is the list of features in a feature model.

Definition 2 (Feature set)

A feature set fs is a pair $(sel, \overline{sel})$ where the first and second components are respectively the set of selected and not-selected features of a SPL product. Let FL be a feature list, thus $sel, \overline{sel} \subseteq FL$, sel $\cap$ $\overline{sel}$ $=$ $\emptyset$, and sel $\cup$ $\overline{sel}$ $=$ FL. Wherever unambiguous we use the term product as a synonym of feature set.

Definition 3 (Valid feature set)

A feature set fs is valid with respect to a feature model fm iff fs.sel and fs.$\overline{sel}$ do not violate any constraints described by fm. The set of all valid feature sets represented by fm is denoted as $FS^{fm}$.

The focus of our study is pairwise testing, thus our concern is on the combinations between two features. The coming definitions are consequently presented with that perspective; however, the generalization to combinations of any number of features is straightforward.

Definition 4

(Pair⁴). A pair ps is a 2-tuple (sel, $\overline{sel}$) involving two features from a feature list FL, that is, ps.sel $\cup$ ps.$\overline{sel} \subseteq FL$ $\wedge$ ps.sel $\cap$ ps.$\overline{sel} = \emptyset$ $\wedge$ |ps.sel $\cup$ ps.$\overline{sel} |=2$. We say pair ps is covered by feature set fs iff ps.sel $\subseteq$ fs.sel $\wedge$ ps.$\overline{sel}\subseteq$ fs.$\overline{sel}$.

Definition 5 (Valid pair)

A pair ps is valid in a feature model fm if there exists a valid feature set fs that covers ps. The set of all valid pairs of a feature model fm is denoted with $VPS^{fm}$.

Let us illustrate pairwise testing with the GPL running example. Some samples of pairs are: GPL and Search selected, Weight and Undirected not selected, CC not selected and Driver selected. An example of invalid pair, i.e., not denoted by the feature model, is features Directed and Undirected both selected. Notice that this pair is not valid because they are part of an exclusive-or relation.

Definition 6 (Pairwise test suite)

A pairwise test suite pts for a feature model fm is a set of valid feature sets of fm. A pairwise test suite is complete if it covers all the valid pairs in $VPS^{fm}$, that is: $\{$fs|$\forall ps \in VPS^{fm}$ $\Rightarrow \exists fs \in FS^{fm}$ such that fs covers ps$\}$.

In GPL there is a total of 418 valid pairs, so a complete pairwise test suite for GPL must have all these pairs covered by at least one feature set. Henceforth, because of our focus and for the sake of brevity we will refer to pairwise test suites simply as test suites.

In the following we provide a formal definition of the priority scheme based on the sketched description provided in [14].

Definition 7 (Prioritized product)

A prioritized product pp is a 2-tuple (fs, w), where fs represents a valid feature set in feature model fm and $w \in \mathbb {R}$ represents its weight. Let $pp_{i}$ and $pp_{j}$ be two prioritized products. We say that $pp_{i}$ has higher priority than $pp_{j}$ for test-suite generation iff $pp_{i}$’s weight is greater than $pp_{j}$’s weight, that is $pp_{i}.w$ > $pp_{j}.w$.

As an example, let us say that we would like to prioritize product p0 with a weight of 17. This would be denoted as pp0 = (p1,17).

Definition 8 (Pairwise configuration)

A pairwise configuration pc is a 2-tuple ($sel, \overline{sel}$) representing a partially configured product, defining the selection of 2 features of feature list FL, i.e., pc.sel $\cup$ pc.$\overline{sel} \subseteq FL$ $\wedge$ pc.sel $\cap$ pc.$\overline{sel}=\emptyset$ $\wedge$ |pc.sel $\cup$ pc.$\overline{sel}| = 2$. We say a pairwise configuration pc is covered by feature set fs iff pc.sel $\subseteq$ fs.sel $\wedge$ pc.$\overline{sel} \subseteq$ fs.$\overline{sel}$.

Definition 9 (Weighted pairwise configuration)

A weighted pairwise configuration wpc is a 2-tuple (pc,w) where pc is a pairwise configuration and w $\in \mathbb {R}$ represents its weight computed as follows. Let PP be a set of prioritized products and PP$_{pc}$ be a subset, PP$_{pc}\subseteq$ PP, such that PP$_{pc}$ contains all prioritized products in PP that cover pc of wpc, i.e., PP$_{pc}$ $=\{pp \in PP | {pp.fs}$ covers ${wpc.pc}\}$. Then $w=\sum _{p\in PP_{pc}}{p.w}$

Definition 10 (Prioritized pairwise covering array)

A prioritized pairwise covering array ppCA for a feature model fm and a set of weighted pairwise configurations WPC is a set of valid feature sets FS that covers all weighted pairwise configurations in WPC whose weight is greater than zero: $\forall wpc \in WPC$ $({wpc.w}>0 \Rightarrow \exists fs \in ppCA$ such that fs covers wpc.pc).

Given a prioritized pairwise covering array ppCA and a set of weighted pairwise configurations WPC, we define coverage of ppCA, denoted by cov(ppCA), as the sum of all weighted pairwise configurations in WPC covered by any configuration in ppCA divided by the sum of all weighted configurations in WPC, that is:

$$\begin{aligned} cov(ppCA) = \frac{\sum _{wpc\in WPC \atop \exists cc \in ppCA, cc \text { covers } {wpc.pc}} {wpc.w}}{\sum _{wpc\in WPC} {wpc.w}}. \end{aligned}$$

(1)

The optimization problem we are interested in consists of finding a prioritized pairwise covering array, ppCA, with the minimum number of feature sets |ppCA| maximizing the coverage, cov(ppCA).

4 Hybrid Algorithms Based on Integer Programming

In this work we propose two different hybrid algorithms combining a heuristic and Integer Programming. The first one is based on an integer linear formulation (HILP) and the second is based on a quadratic (nonlinear) integer formulation (HINLP). Throughout this section we highlight the commonalities and differences between the proposals.

The two algorithms proposed in this work use the same high level greedy strategy. In each iteration they try to find a product that maximizes the weighted coverage. This could be expressed by the following objective function h:

$$\begin{aligned} h(x) = \sum _{wpc\in I(x) \cap U} {wpc.w} \end{aligned}$$

(2)

where x is a product, U the set of not covered pairwise configurations and I(x) the set of pairwise configurations covered by x.

Once the algorithm found the best possible product, it is added to the set of products, the pairs covered are removed from the set of all weighted pairs, and then it seeks for the next product. The algorithms stop when it is not possible to add more products to increase the weighted coverage. This happens when all pairs of features with weight greater than zero are covered.

Let us first describe the common part related to the integer program which is the base of the computation of the best product in each iteration. The transformation of the given feature model is common in the two algorithms. However, the expressions used for dealing with pairwise coverage are different in the linear and nonlinear approaches.

Let $f$ be the number of features in a model fm, we use decision variables $x_{j} \in \{0,1\}$ and $j \in \{1,2,\ldots ,f\}$ to indicate if we should include feature j in the next product ($x_j=1$) or not ($x_j=0$). Not all the combinations of features form valid products. According to Benavides et al. [20] we can use propositional logic to express the validity of a product with respect to a FM. These Boolean formulas can be expressed in Conjunctive Normal Form (CNF) as a conjunction of clauses, which in turn can be expressed as constraints in an integer program. The way to do it is by adding one constraint for each clause in the CNF. Let us focus on one clause and let us define the Boolean vectors v and u as follows [22]:

$$\begin{aligned}&v_j = \left\{ \begin{array}{ll} 1 &{} \text {if feature}\, { j}\, \text {appears in the clause}, \nonumber \\ 0 &{} \text {otherwise}, \end{array} \right. \\&u_j = \left\{ \begin{array}{ll} 1 &{} \text {if feature}\, { j} \,\text {appears negated in the clause}, \nonumber \\ 0 &{} \text {otherwise}. \end{array} \right. \end{aligned}$$

With the help of u and v we can write the constraint that corresponds to one CNF clause for the i-th product as:

$$\begin{aligned} \sum _{j=1}^{f} v_j (u_j (1-x_{j}) + (1-u_j) x_{j}) \ge 1 . \end{aligned}$$

(3)

Finally, Algorithm 1 represents the general scheme used by our algorithmic proposals based on integer programming. In Line 1 the list of products ppCA is initialized to the empty list. Then, the execution enters the loop (Line 2) that tries to find the best product maximizing the coverage with respect to the configurations not covered yet, U (Line 3). The new product is added to the list of products ppCA (Line 4) and the covered pairs are removed from the set U (Line 5).

4.1 Linear Approach

In the linear approach we need decision variables to model the pairwise configurations that are covered by a product. These variables are denoted by $c_{j,k}$, $c_{j,\overline{k}}$, $c_{\overline{j},k}$ o $c_{\overline{j},\overline{k}}$, depending on the presence/absence of the features j, k in a configuration. They will take value 1 if the product covers a configuration and 0 otherwise. The values of variables c depends on the values of the x variables. To reflect this dependency in our linear program, we need to add the following constraints for all pairs of features $1\le j < k \le f$:

$$\begin{aligned}&2 c_{\overline{j},\overline{k}} \le (1-x_{j}) + (1-x_{k}),\end{aligned}$$

(4)

$$\begin{aligned}&2 c_{\overline{j},k} \le (1-x_{j}) + x_{k},\end{aligned}$$

(5)

$$\begin{aligned}&2 c_{j,\overline{k}} \le x_{j} + (1-x_{k}),\end{aligned}$$

(6)

$$\begin{aligned}&2 c_{j,k} \le x_{j} + x_{k}. \end{aligned}$$

(7)

It is not necessary to add all possible variables c, but only those corresponding to a pair not yet covered. Finally, the goal of our program is to maximize the weighted pairwise coverage, which is given by the sum of variables $c_{j,k}$ weighted with $w_{j,k}$. Let us denote with U the set of configurations not covered yet. The expression to maximize is, thus:

$$\begin{aligned} \sum _{(j,k) \in U} w_{j,k} c_{j,k}, \end{aligned}$$

(8)

where (abusing notation) j and k are used to represent the presence/absence of features.

4.2 Nonlinear Approach

In the nonlinear approach we avoid using the decision variables that represent the presence/absence of particular pairs in a product, reducing the number of variables and constraints compared to the linear approach. As a counter part we need to use nonlinear functions to represent the objective function. In this case the objective function to maximize is as follows:

$$\begin{aligned}&\sum _{(j,k) \in U} w_{j,k} x_j x_k + \sum _{(\overline{j},k) \in U} w_{\overline{j},k} (1-x_j) x_k + \end{aligned}$$

(9)

$$\begin{aligned}&\sum _{(j,\overline{k}) \in U} w_{j,\overline{k}} x_j (1-x_k) + \sum _{(\overline{j},\overline{k}) \in U} w_{\overline{j}, \overline{k}} (1-x_j) (1-x_k). \end{aligned}$$

(10)

This problem formulation results in a more concise problem representation because the objective function is smaller and the inequalities (4)–(7) are not required.

5 Experimental Setup

This section describes how the evaluation was performed. First, we describe the PPGS and pICPL algorithms, object of the comparison. Next, we present the methods used to assign priorities, the feature models used as experimental corpus, and the experiments configuration.

5.1 Prioritized Pairwise Genetic Solver

Prioritized Pairwise Genetic Solver (PPGS) is a constructive genetic algorithm that follows a master-slave model to parallelize the individuals’ evaluation. In each iteration, the algorithm adds the best product to the test suite until all weighted pairs are covered. The best product to be added is the product that adds more weighted coverage (only pairs not covered yet) to the set of products.

The parameter settings used by PPGS are the same of the reference paper for the algorithm [15]. It uses binary tournament selection and a one-point crossover with a probability 0.8. The population size of 10 individuals implies a more exploitation than exploration behaviour of the search with a termination condition of 1,000 fitness evaluations. The mutation operator iterates over all selected features of an individual and randomly replaces a feature by another one with a probability 0.1. The algorithm stops when all the weighted pairs have been covered. For further details on PPGS see [15].

5.2 Prioritized-ICPL (pICPL) Algorithm

Prioritized-ICPL is a greedy algorithm to generate n-wise covering arrays proposed by Johansen et al. [14]. pICPL does not compute covering arrays with full coverage but rather covers only those n-wise combinations among features that are present in at least one of the prioritized products, as was described in the formalization of the problem in Sect. 3. We must highlight here that the pICPL algorithm uses data parallel execution, supporting any number of processors. Their parallelism comes from simultaneous operations across large sets of data. For further details on prioritized-ICPL please refer to [14].

5.3 Priority Assignment Methods

We considered three methods to assign weight values to prioritized products: rank-based values, random values, and measured values.

Rank-based Values. In the rank-based weight assignment, the products are sorted according to how dissimilar they are. More dissimilar products appear first in the ranking and have a lower rank. Then, they are assigned priority weights based on their rank values, low ranked products are assigned higher priorities. Giving the same weight value to two of the most SPL-wide dissimilar products, the weight values will be more likely spread among a larger number of pairwise configurations making the covering array harder to compute. In addition, this enables us to select different percentages of the number of products for prioritization. The selected percentages used are: 5$\%$, 10$\%$, 20$\%$, 30$\%$ and 50$\%$.

Random Values. In the random weight assignment, the weights are randomly generated from a uniform distribution between the minimum and maximum values obtained with the rank-based assignment. A percentage of the products denoted by each individual feature model was used for product prioritization. The selected percentages are: 5$\%$, 10$\%$, 20$\%$, 30$\%$, and 50$\%$.

Table 1. Measured values benchmark

Measured Values. For this third method, the weights are derived from non-functional properties values obtained from 16 real SPL systems, that were measured with the SPL Conqueror approach [23]. This approach aims at providing reliable estimates of measurable non-functional properties such as performance, main memory consumption, and footprint. These estimations are then used to emulate more realistic scenarios whereby software testers need to schedule their testing effort giving priority, for instance, to products or feature combinations that exhibit higher footprint or performance. In this work, we use the actual values taken on the measured products considering pairwise feature interactions. Table 1 summarizes the SPL systems evaluated, their measured property (Prop), number of features (NF), number of products (NP), number of configurations measured (NC), and the percentage of prioritized products (PP$\%$) used in our comparison.

5.4 Benchmark of Feature Models

In this work we use two different groups of feature models. The first one (G1) is composed of 219 feature models which represent between 16 and 80,000 products using rank-based and random weight priority assignments. The second group (G2) is composed of 16 real feature models which represent between 16 and $\approx$3E20 products for which the measured values strategy for weight assignment was used. In total, we used 235 distinct feature models: 16 feature models from SPL Conqueror, 5 from Johansen et al. [14], and 201 from the SPLOT website [24]. Note that for G1, two priority assignment methods are used with five different prioritization selection percentages. For feature models which denote less than 1,000 products we use 20%, 30% and 50% of the prioritized products. For feature models which denote between 1,000 and 80,000 products we use 5%, 10% and 20%. This yields a grand total of 1,330 instances analyzed with the four algorithms in our comparison (Table 2).

Table 2. Benchmark summary

5.5 Hardware

PPGS and pICPL are non-deterministic algorithms, so we performed 30 independent runs for a fair comparison between them. As performance measures we analyzed both the number of products required to test the SPL and the time required to run the algorithm. In both cases, the lower the value the better the performance, since we want a small number of products to test the SPL and we want the algorithm to be as fast as possible. All the executions were run in a cluster of 16 machines with Intel Core2 Quad processors Q9400 (4 cores per processor) at 2.66 GHz and 4 GB memory running Ubuntu 12.04.1 LTS and managed by the HT Condor 7.8.4 cluster manager. Since we have four cores available per processor, we have executed only one task per single processor, so we have used four parallel threads in each independent execution of the analyzed algorithms. HILP and HINLP were executed once per instance and weight assignment, because they are deterministic algorithms. Four cores were used as in the other algorithms.

6 Results Analysis

In this section, we study the behaviour of the proposed approaches using statistical techniques with the aim of analyzing the computed best solutions and highlighting the algorithm that performs the best.

6.1 Quality Analysis

In Table 3 we summarize the results obtained for group G1, feature models with up to 80,000 products. Each column corresponds to one algorithm and in the rows we show the number of products required to reach 50% up to 100% of total weighted coverage. The data shown in each cell is the mean and the standard deviation of the independent runs of 219 feature models. We highlight the best value for each percentage of weighted coverage.

At first glance we observe that the algorithms based on integer programming are the best in solution quality for all percentages of weighted coverage. Between HILP and HINLP the differences are almost insignificant except for 100% coverage, so it is difficult to claim that one algorithm is better than the other. It is also noteworthy that PPGS is the worst algorithm for 100% coverage while pICPL is the worst for the rest of percentages of coverage.

Table 3. Mean and standard deviation for G1 instances (219 FMs).

In order to check if the differences between the algorithms are statistically significant or just a matter of chance, we applied the non-parametric Kruskal-Wallis test with a confidence level of 95% (p-value under 0.05). In summary the number of times that one algorithm is statistically better than the other algorithms is as follows: HILP in 11 out of 21 comparisons (7% and 3 other algorithms), HINLP in 10 out of 21, PPGS in 7 out of 21, and pICPL 1 out of 21. These results confirm that for G1 the algorithms based on integer programming are statistically better than the other proposals, so they are able to compute better sets of prioritized test data than PPGS and pICPL.

Let us now focus on group G2, feature models with measured weight values. In Table 4 we show the results for this group of real instances. Here, pICPL and PPGS are the best algorithms in one percentage of coverage, 50% and 80% respectively. Nevertheless HILP and HINLP are able to compute better test suites for most percentages of coverage, so the conclusions extracted are similar than those extracted from the experiments with G1 instances. For 50% and 100% coverage there are no significant differences among the four algorithms, but in the rest of scenarios there are significant differences with respect to pICPL. Therefore, it is clear that pICPL is the worst algorithm for G2 instances. We want to highlight that there is no difference again between HILP and HINLP.

Table 4. Mean and standard deviation for G2 instances (16 FMs).

6.2 Performance Analysis

In Fig. 2 we show the boxplots of the execution time (logarithmic scale) required by each algorithm in the two group of instances to reach 100% of weighted coverage. The median is also shown in text. Regarding the computation time, pICPL is clearly the fastest algorithm with statistically significant differences with the rest of algorithms in G1. Actually, in G1 all algorithms are significantly different from each other. In a closer look at the data, we observe that pICPL has a first and second quartiles lower than HINLP’s, nevertheless the third pICPL’s quartile is far from HINLP’s. This means that the performance of pICPL decreases as the instance increases in size. In contrast, HINLP has a smaller inter-quartile range, then HINLP seems to scale better than pICPL.

Besides, in the comparison between HILP and HINLP, all quartiles are lower for HINLP, so from these results, it is clear that HINLP produce a boost in computation time due to the reduction of clauses in comparison with the linear variant of the algorithm (HILP).

With regard to the G2 group of instances, HINLP is the fastest with significant differences with the rest of algorithms. In this group of instances, there are not significant differences between HILP and pICPL. Again, pICPL’s third quartile is far from the values of HILP and HINLP, then it scales worse than the integer programming approaches. Although PPGS is not the worst algorithm in solution quality, in computation time is the worst of the comparison in the two groups of instances.

Fig. 2.

Comparison of algorithms’ execution time in logarithmic scale.

As a general conclusion we can say that the two proposed hybrid algorithms obtain good quality solutions while they are also very competitive in runtime. Between them, the variant using nonlinear functions is the best in the comparison with statistical significant differences. For the benchmark of feature models analyzed here our proposals do not have scalability problems. Note that some of the feature models denote ${\approx }1E20$ products. Part of our future work is to verify if this trend holds for feature models with a larger number of products.

7 Threats to Validity

There are two main threats to validity in our work. The first one is related to the parameters values of the genetic algorithm (PPGS). A change in the values of these parameters could have an impact in the results of the algorithm. Thus, we can only claim that the conclusions are valid for the combination of parameter values that we used, which are quite standard in the field. Second, the selection of feature models for the experimental corpus can indeed bias the results obtained. In order to mitigate this threat, we used three different priority assignment methods, five percentages of prioritized products, and different sources for our feature models. From them we selected a number of feature models as large as possible, with the widest ranges in both, number of features and number of products.

8 Conclusions and Final Remarks

In this paper we have studied the Prioritized Pairwise Test Data Generation Problem in the context of SPL with the aim of proposing two novel hybrid algorithms. The first one is based on an integer linear formulation (HILP) and the second is based on a integer quadratic (nonlinear) formulation (HINLP). We have performed a comparison using 235 feature models of different sizes, different priority assignment methods and four different algorithms, the two proposed algorithms and two algorithms of the state-of-the-art (pICLP and PPGS). Overall, the proposed hybrid algorithms are better in solution quality. In computation time HINLP is the best with significant difference, except for pICPL in G1.

Regarding the comparison between HILP and HINLP, there is no significant difference in solution quality. The slight existing differences are due to the different solvers used for dealing with linear and nonlinear functions. In contrast, concerning the execution time, there are significant differences between them. The nonlinear variant outperformed the linear variant. The reason behind this improvement in performance could be the number of clauses (constraints) not needed by the nonlinear variant to represent the covered pairs. Then, we can avoid considering a maximum of $f*(f-1)*2$ constraints⁵ (total number of valid pairs). Moreover, the nonlinear technique has no scalability issues computing the feature models analyzed here. Therefore, with no doubt the best algorithm in our comparison is HINLP.

There are two promising future lines possible after the work contained in this paper. Broadly speaking, these lines are search for the limits of the nonlinear approach applying this technique to larger feature models and the test suites computation using the whole test suite approach [25]. In this last regard, the hybrid approaches do not assure the optimum because they are constructive algorithms that only deal with one product at a time. Obtaining the Pareto front would require the computation of several products at a time and multiple executions of the algorithm with different upper bounds in number of products. Preliminary results suggest that the number of variables and constraints grow very fast with the number of products computed, what could be an issue for the integer programming solver. Further research will be needed in that direction.