Abstract
Based on the Unifying Theories of Programming (UTP) semantic framework, Hoare and He have defined (a means for constructing) a high-level language with labels and jumps, using the concept of continuations. The language permits placing labels at given points within a program and making jumps to these labels when desired. In their work, Hoare and He have limited themselves to the definition of continuations for sequential programs. This paper is concerned with the extension of that work to reactive programs. We first extend their results to include parallelism and Higher Order programs. This is achieved by designing a new control variable \(\mathcal {L}\) whose value follows the parallel structure of programs. We then proceed to define reactive (CSP) processes that contain the new control variable \(\mathcal {L}\), resulting in the theory of Reactive (Process) Blocks. The encapsulation operator defined by Hoare and He and which may also be used for hiding the control variable \(\mathcal {L}\) does readily provide a (functional) link between both UTP theories of Reactive Processes and of Reactive Blocks. The semantics are denotational.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Implementing a program consists of adding details related to the program’s execution on a given platform: the result is called an implementation. A detail of particular importance relates to control flow, or the order of the execution of the instructions in the program. A device called the program counter normally computes and stores the value of the address of the next instruction to be executed. When executing a program, the processor always refers to the program counter.
The method of continuations [10, 11] has been devised for giving semantics to programming languages with labels and jumps. As it also allows giving semantics to other programming constructs than jumps, it has resulted in a programming paradigm called continuation-passing style or CPS.
Continuations naturally permit to localise the instructions of a program amongst other instructions. Locations are unique and are ordered according to the order of execution within a given program. Since locations are explicit, a program must always provide the location of the next program, which is properly called the continuations of its predecessor. High-level programs do not rely on continuations for defining control flow, which is rather associated with the order of evaluation of the instructions of the program.
Process mobility [7] refers to any model or theory that describes the movement of a process from its initial computational environment (or source) to another computational environment (or target). It has two variants: weak mobility, in which only the code of the process moves; and strong mobility, in which a program is first interrupted, then its code and interrupt state are migrated to a remote target where its execution is to be resumed. Denotational semantics for weak mobility have been defined on the basis of UTP-CSP by Tang and Woodcock [5, 6]. We plan to extend their results with semantics for strong mobility.
The resume operation on the remote machine requires the capacity to tell what instruction to execute next, and also to jump to that instruction. However, UTP-CSP [1, 4]may rightly be called a high-level language and hence does not provide any jump instruction. The concept of continuations naturally comes to mind for reasoning about control flow in process algebra, and we are not aware of any other model for achieving that. Although some may argue that jumps are a harmful feature at an implementation level, such is not the case as far as semantics are concerned, given that simple elegant models are to be preferred. In sum, we need to extend UTP-CSP with jump features in order to define strong mobility, and we propose using continuations as a solution.
Much work is dedicated to continuation-passing style, e.g. [12,13,14,15,16]. However their approach is not directly relevant to our work. In [9], Jahnig et al. provide a denotational semantics for a CSP-like language. Hence, they do not deal directly with CSP either. In the context of UTP, two pieces of work deal with continuations. [1, Chap. 6] provides semantics for sequential programs in general. This work may be used for giving semantics to UTP-CSP processes that have no parallel operator, only. In [8], the authors also use continuations, although they are interested in verifying shared-memory programs. It is not clear from their work why they use continuations. Notwithstanding, their semantics deal with parallel programs in general, hence their work may be used for giving semantics to all UTP-CSP processes. Unfortunately this latter extension is not straightforward and leads us to design a new control variable.
In Sect. 2 we present the UTP semantics for continuations defined in [1, Chap. 6]. They will notably serve as a basis for the formalisation of continuations for parallel programs in general (including the design of the new control variable), discussed in Sect. 3. The corresponding denotational semantics are then presented in Sect. 4. The continuations semantics for UTP-CSP processes are then obtained by applying CSP healthiness conditions to parallel programs (with continuations), thus yielding reactive process blocks, presented in Sect. 5. We then conclude.
2 UTP Background - Continuations for Sequential Programs
2.1 An Overview of UTP
UTP [1] is a formal semantics framework for reasoning about programs, programming theories and the links between theories. The semantics of a program are given by a relation between the initial (undecorated) and final (decorated) observations that can be made of the variables that characterise the program behaviour. Relations are themselves represented as alphabetised predicates, i.e. predicates of the form \((\alpha P, P)\). \(\alpha P\) is called the alphabet of the predicate P, and determines what variables P may mention. \(\alpha P\) may be partitioned into two subsets: \(in \alpha P\), which represents the initial observations, and \(out \alpha P\), which represents the final observations.
Programming languages and paradigms are formalised as UTP theories. A UTP theory is just a collection of predicates, and consists of three elements: an alphabet, containing only those variables that the predicates of the theory may mention; a signature, which contains the operators of the theory, and healthiness conditions which are laws constricting the set of legal predicates to those that obey the properties expressed by the conditions.
Healthiness conditions generally have the form: \({\varvec{NAME}} \quad P = f(P)\), for some idempotent function f (i.e. \(f \circ f(x) = f(x)\)). \({\varvec{NAME}}\) stands for the name of the healthiness condition and is also used as an alias for f i.e. we write \(P = {\varvec{NAME}}(P)\) and we say that P is \({\varvec{NAME}}\)-healthy.
Specifications are also expressible in UTP, and a theory of refinement permits us to ensure the correctness of a program with regard to a given specification.
The most basic of all UTP theories is the theory of Relations, on top of which every other UTP is built. We define below some program constructs.
Assignment. \(x :=_{\mathsf {A}} e\) denotes the assignment of an expression e to a variable x. The meaning of assignment is thus equality: that between x and e after the assignment.

Skip. \(II_{A}\) denotes the command that does nothing; it is equivalent to the assignment \(x := x\).

Conditional.  stands for ‘if b then P else Q’, where b is some testable condition. Formally, a condition is defined as a predicate not containing dashed variables.
stands for ‘if b then P else Q’, where b is some testable condition. Formally, a condition is defined as a predicate not containing dashed variables.

Variable Declaration, Undeclaration. \(\mathbf {var}~x\) denotes the declaration of a new program variable x and \(\mathbf {end}~x\) its undeclaration. Let \(\mathsf {A}\) be an alphabet which includes x and \(x'\). Then:

Alphabet Extension. The scope of x lies between \(\mathbf {var}\, x\) and \(\mathbf {end}\, x\); beyond, the variable is undefined and cannot be observed. Let \(x, x' \in \alpha R\), then:

Floyd Assertion and Assumption. An assertion is the statement that a condition, c say, is expected to be true at the point at which it is written; otherwise, the program behaves in a totally unpredictable, chaotic way, i.e. like \(\bot \). We also say that the failure is caused by the programmer. An assertion captures the intent of the programmer, that something is meant to be true.

On the other hand, an assumption is the statement that a condition is true at the point at which it is written; otherwise the program behaves in an impossible, miraculous way, i.e. like \(\top \). We also say that the failure is caused by the program. An assumption captures the confidence of the programmer, that something is true.

Reactive Processes
The theory of Relations is too general and may be restricted accordingly by means of healthiness conditions. Here, we give a brief overview of the theory of reactive processes, which permits reasoning about communicating programs.
The alphabet of a reactive process consists of the following:
-
\(\mathcal {A}\), the set of authorised events; \(tr, tr': \mathcal {A}^{*}\), the trace;
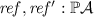 , the refusal set
, the refusal set -
 , stability and termination;
, stability and termination;  , waiting states
, waiting states -
\(v, v'\), other variables
The above alphabet alone is not enough to characterise reactive processes. Predicates with such an alphabet must also satisfy the following healthiness conditions.

where  .
.
\({\varvec{R1}}\) states that the occurrence of an event cannot be undone viz. the trace can only get longer. \({\varvec{R2}}\) states that the initial value of tr may not affect the current observation. \({\varvec{R3}}\) states that a process behaves like  when its predecessor has not yet terminated.
when its predecessor has not yet terminated.
Alternatively, we may use the single healthiness condition \({\varvec{R}} = {\varvec{R1}} \circ {\varvec{R2}} \circ {\varvec{R3}} \).
A particular model of reactive processes is provided by the CSP process algebra ([2, 3]) whose semantics in UTP are presented subsequently. CSP processes are reactive processes that obey the following additional healthiness conditions:

where 
\({\varvec{CSP1}}\) states that if a process has not started (\(ok = false\)) then nothing except for trace expansion can be said about its behaviour. Otherwise the behaviour of the process is determined by its definition. \({\varvec{CSP2}}\) states that a process may always terminate. It characterises the fact that divergence may never be enforced.
Alternatively, we may use the single healthiness condition \( {\varvec{CSP}} = {\varvec{R}} \circ {\varvec{CSP1}} \circ {\varvec{CSP2}} \).
We present the semantics of some CSP processes subsequently. Some definitions are similar to the ones presented earlier, with some changes. For example, the definitions mention new alphabet elements, and certain healthiness conditions are applied directly, as in assignment below.
Assignment (2). Denoted by \(x := e\), is the process that sets the value of the variable x to e on termination, but does not modify the other variables. It does not interact with the environment, always terminates, and never diverges.

A particular kind of assignment is one that leaves everything unchanged, and has already been seen above viz.  .
.
Skip (2). Denoted by SKIP, is the process that refuses to engage in any event, terminates immediately and does not diverge. It is a special instance of  .
.

Parallel Composition. Denoted by \(P \parallel Q\), is the process that behaves like both P and Q and terminates when both have terminated. P and Q may not share any variable other than the observational variables (ok, wait, ...). P andQ modify separate copies of the shared observational variables which are then merged at the end using the merge predicate M, as defined below.

2.2 Continuations in UTP
In UTP [1, Chap. 6], the program counter is represented by a variable, denoted l, and referred to as the control variable. The set of possible values which l can take is called continuations set or simply continuations, and is denoted by \(\alpha l\) (\(\alpha lP\), the continuations of a predicate P). The instructions of the program are represented by steps, which are themselves predicates. An implementation may consist of a ‘single’ step or of an assembly of such steps.
First, we define programs that may be represented as the sequential repetition of a single step. The value of l is tested before each repetition of the step and determines if the execution of the step starts, continues or ends. Hence, l does also specify termination.
Definition 1
(Continuations and execution).

\(\alpha lP\) denotes the set of continuations of P; \(l \in \alpha lP\) denotes the control variable for its execution; and \(P^{*}\) denotes the execution of P, defined as a loop, which iterates the step as long as l remains in the continuations set.
For a step P, the value of l determines the start and termination of its execution. When l is outside the continuations of P, P may not be started. Although the behaviour of P in such case may be anything, it is safe to assume that it does nothing, i.e. that its behaviour is II. This is a sound assumption when we consider the execution of P in conjunction with that of other steps.
Definition 2
(Step). A predicate P is a step if \(l \in \alpha lP\) and

As a consequence,

The following theorem gives the closure property of some operators.
Theorem 1
(Step closure). If P and Q are steps, then
-
1.
 is a step.
is a step. -
2.
 and
and  are also steps whenever \(\alpha lP = \alpha lQ\).
are also steps whenever \(\alpha lP = \alpha lQ\). -
3.
The set of steps is a complete lattice.
Programs may occupy disjoint storage areas, in which case they are said to be disjoint. This means that two steps which have disjoint continuations are disjoint. It is possible to assemble them into a single program, by using the assembly operator defined below.
Definition 3
(Assembly). Let P and Q be disjoint steps, i.e. \(\alpha lP\, \cap \,\alpha lQ = \{\}\).

There are two known ways of implementing a program: compilation and interpretation. In what follows we present the former only.
Compilation. Compilation is the transformation of the program into a target program expressed in the machine code of the processor that is to execute it. Compilation conserves the meaning of the source program. The semantics of the target language (or machine code) may equally be given in UTP. Each instruction in the language may be given a meaning as a step.
A single instruction is a step with a single continuation given by the singleton set \(\{m\}\).
Definition 4
(Single instruction). If INST is a machine code instruction then

is a single instruction.
Single instructions may be assembled together using the assembly operator ( ).
).
Definition 5
(Machine code block). A machine code block is a program expressed as an assembly of single instructions.

Using the preceding definition, it is possible to enter a machine code block at any of its constituent continuation points. In practice, it is common to define a normal starting point, denoted by s, and a normal finishing point, denoted by f. They relate respectively to the first and last single instructions of the program. s is the value of l when control enters sequentially into the program; any other point should be entered by a jump. f is the value of l when control leaves sequentially through the last instruction. Respectively in each case, we will also talk about normal start or entry and normal termination or exit. The assumption of normal entry is expressed by the predicate \((l = s)_{\top }\). The obligation to terminate normally is expressed by the predicate \((l = f)_{\bot }\). Machine code blocks that have these pre- and post-condition are called structured.
Definition 6
(Structured block). A structured block is a program of the form

where P is a machine code block. The value of s is called its starting point and the value of f its finishing point.
Let \( \hat{P} \) denote the target program into which a source program P has been compiled by a compiler. \( \hat{P} \) should have the same effect (or behaviour) as P. \( l \in \alpha \hat{P}\) but \(l \notin \alpha P\) (since P is not a step).

Definition 7
(Target code). A program is in target code if it is expressed in the form

where P is a machine code block. An equivalent formulation is:

According to the fundamental theorem of compilation [1, Chap. 6, Theorem 6.2.10], every program can be expressed in target code.
Theorem 2
(Fundamental theorem of compilation). Every program can be expressed in target code.
It is possible to combine low-level language features, such as jumps and labels, with high-level language features. Such a facility was provided by many early programming languages.
High-Level Language with Jumps and Labels. For the combination of a high-level language with jumps and labels to be possible, it is necessary to consider, in addition to s and f, other continuation points viz. those corresponding to entry and exit by a jump. A special value, denoted by \(\mathbf {n}\), will be used for both s and f. \(\alpha l_{0}P\) will denote the set of all entry points; \(\alpha l'P\) will denote the set of all exit points; and neither may contain \(\mathbf {n}\). If l takes its value in either of these sets, it will signify that the program has been entered or exited by a jump respectively, in contrast to normal entry and exit through \(\mathbf {n}\).
Definition 8
(Blocks and proper blocks). Let S and F be sets of labels (continuation points), and \(\mathbf {n} \notin S\), and \(\mathbf {n} \notin F\).

A program is a block if it satisfies \(P: \alpha l_{0}P \implies \alpha l'P\); a block is called a proper block if \(\alpha l_{0}P \cap \alpha l'P = \{\}\).
The construction \(\mathbf {label}~s\) permits placing a label within the program at the point intended to be the destination of a jump. \(\mathbf {label}~s\) may be entered normally or by a jump, but it always exits normally. The construction \(\mathbf {jump}~f\) permits jump-ing to the location indicated by the label f. \(\mathbf {jump}~f\) may be entered normally or by a jump, but it always exits by a jump.
Definition 9
(Labels and jumps).

The following theorem gives the permitted operators for blocks having the same alphabets of entry and exit points.
Theorem 3
(Block closure) The set of blocks \(\{P \,\, | \,\, P: S \implies F\} \) is a complete lattice, and closed with respect to non-deterministic choice and conditional. The same applies to proper blocks.
Before giving the closure for sequential composition, we first give its continuations. A sequential composition  may be entered normally through \(\mathbf {n}\), or by a jump. In the second case, the entry point may belong to either P or Q. Similarly, it may be exited normally through \(\mathbf {n}\), or by a jump from either P or Q.
may be entered normally through \(\mathbf {n}\), or by a jump. In the second case, the entry point may belong to either P or Q. Similarly, it may be exited normally through \(\mathbf {n}\), or by a jump from either P or Q.
Definition 10
(Continuations for sequential composition).

Theorem 4
(Sequential composition closure) If \(P: S \implies F\) and \(Q: T \implies G\), then

3 Concepts and Formalisation
Note. For ease, we will refer to the work presented in the previous section as HH98 steps or simply HH98. Similarly, we will refer to the work in [8] as WH02 steps or simply WH02.
The CPS transformation (or compiler) is inherently sequential [10, 11]. UTP-CSP processes also permit the representation of sequential programs, which form a subset of the class of reactive programs. This suggests that HH98 may be applied at least to sequential UTP-CSP. All that is needed is to extend the alphabet of UTP-CSP sequential processes, and point-wise extend the definition of sequential composition to the control variable l, as suggested in HH98. However, l is not expressive enough for reasoning about control flow in the presence of parallelism.
The problem actually lies with the design of the control variable as single-valued. We need a mathematical model that follows more tightly the computation model. For example, using l in the presence of interrupt, it would be as if a single program was interrupted at a time whereas we should be able to say that many programs may be interrupted at a time. The solution is to design a value of the control variable that follows more tightly the structure of processes. This is what is done in [8].
In [8] (hereafter also WH02), Woodcock and Hughes use a set-valued control variable, denoted ls instead, and that contains the continuations of all the steps that may be executed in parallel next. Using WH02, we may point-wise extend the UTP-CSP parallel composition operator. However, a number of changes must first be considered. Unlike HH98 steps, a WH02 step may now exit at many points at any one time, implying that a step may be entered simultaneously at multiple entry points. This is a little counter-intuitive but poses no great difficulties. Yet, ls is not sufficient for our purpose. To see this, consider the following illustration.
Let  , and let \(ls = \{s, h\}\). The value of ls is valid, but does not reflect the structure of P. If the programmer was expecting parallel composition, sequential composition will be performed instead, which is an error and will not be detected. Let \(Q = \langle s, Q_{1}, f \rangle \parallel \langle t, Q_{2}, g \rangle \), and let \(ls = \{s\}\). Then Q will behave like \(Q_{1}\), since \(Q_{2}\) behaves like SKIP (by definition). Again, if parallel composition was expected then only one step will be executed instead of two in parallel, which is an error and will not be detected.
, and let \(ls = \{s, h\}\). The value of ls is valid, but does not reflect the structure of P. If the programmer was expecting parallel composition, sequential composition will be performed instead, which is an error and will not be detected. Let \(Q = \langle s, Q_{1}, f \rangle \parallel \langle t, Q_{2}, g \rangle \), and let \(ls = \{s\}\). Then Q will behave like \(Q_{1}\), since \(Q_{2}\) behaves like SKIP (by definition). Again, if parallel composition was expected then only one step will be executed instead of two in parallel, which is an error and will not be detected.
In sum, we have to design a new value for the control variable seeing that neither HH98 variable l nor WH02 variable ls are adequate. \(\mathcal {L}\) will denote the new control variable, and we discuss its formalisation subsequently.
Design of the Control Variable \(\varvec{\mathcal {L}}\)
Parallel composition may be seen as a single block such that when entered sequentially, the steps that compose the block are executed in parallel, and when they have all exited, then the block is also exited. That is, entry into (resp. exit from) a block of parallel steps is identical to entry into (resp. exit from) a sequential block. Sequential and parallel blocks would hence differ in their respective execution order: for the first, only one step may be executed at a single (observation) time, whilst multiple steps may be executed at a single time for the second. In other words, parallel composition acts as an envelop w.r.t. its components. It has its own continuations, that differ from those of its constituents. Let \(P = P_{1} \parallel P_{2}\), then the block denoted by P differs from its component blocks \(P_{1}\) and \(P_{2}\). P has its own entry and exit points that differ from those of \(P_{1}\) and \(P_{2}\).
A control flow graph (CFG) is a standard representation of programs with no parallel constructs, using a graph. A CFG and related concepts are appropriate for discussing the structure of UTP-CSP processes. Note that we are not interested in a graphical formalism, but only to use graphs as an adequate means for discussion. In what follows, we sketch what such a graph might look like.
A CFG for Reactive Processes. Figure 1(a) shows an example of such a graph read in a left-right, then top-down, iterative manner, thus indicating the flow of control. \(P_{i}\) nodes may denote either single instructions, sequential blocks, or nested (parallel) blocks. Both the root node (P) and initial nodes (e.g. \(P_{31}\), \(P_{32}\), \(P_{33}\)) are indicated by empty circles. A nesting node (e.g. \(P_{3}\)) is indicated by a vertical line starting from the node downwards, as shown in (b). An empty square indicates termination for a horizontal line, whereas it simply serves as a visual aid to indicate the end of a vertical line. A flattened graph (c) shows how control goes through \(P_{3}\), and then again through \(P_{312}\). More information could have been added for loops, and jumps, and bigger graphs may be conceived, but such are not our main interest. Rather, we may also annotate nodes with their continuations. The annotation procedure would then show how to evaluate the control variable.
Value of \(\varvec{\mathcal {L}}\)
Let \(\mathcal {L}\) denote the control variable whose value we will be discussing. Then \(\alpha \mathcal {L}P\) denotes the continuations of a step P.
To formalise the nesting relation between a parent and its children, we may partition the continuations set of every node into two subsets: \(\alpha l\), the continuations of the parent, and \(\alpha ls\), the continuations of its children. We make the following restriction: the parent-child relation does not extend beyond two adjacent levels. Hence, \(\alpha ls\) contains the continuations of nodes at the lower adjacent level only; e.g. for sequential blocks, \(\alpha ls = \{\}\). In what follows, we describe in detail the procedure for attributing continuations to nodes. That is also the procedure for computing the value of \(\alpha \mathcal {L}\) for a given block.
Continuations may be attributed hierarchically, in a bottom-up fashion.
-
1.
We make no difference between nodes denoting either single instructions or sequential blocks, and we will refer to them commonly as \(\mathbf {lv_{0}}\) (read level-0) nodes. Such nodes do not introduce nesting, hence they have no children, i.e. \(\alpha ls = \{\}\).
-
2.
We then put in parallel \(\mathbf {lv_{0}}\) nodes, exclusively, to form \(\mathbf {lv1}\) nodes. Such nodes correspond to the nesting nodes mentioned earlier. The value of \(\alpha ls\) is given by the union of continuations \(\alpha l\) of its constituents. e.g. \(\alpha lsP_{3} = \{\alpha lP_{31}, \alpha lP_{32}, \alpha lP_{33}\}\).
-
3.
Again, putting exclusively \(\mathbf {lv_{1}}\) nodes in parallel, or together with \(\mathbf {lv_{0}}\) nodes, we obtain \(\mathbf {lv_{2}}\) nodes. \(\alpha ls\) is the union of all the continuations of adjacent \(\mathbf {lv_{1}}\) (and \(\mathbf {lv_{0}}\)) nodes, only. Hence the value of \(\alpha ls\) for a \(\mathbf {lv_{2}}\) node does not contain the continuations of those \(\mathbf {lv_{0}}\) nodes that are nested to \(\mathbf {lv_{1}}\) nodes. e.g. \(\alpha lP_{312x} \nsubseteq \alpha lsP_{3}\), although \( \alpha lP_{312} \subseteq \alpha lP_{31} \subset \alpha lsP_{3} ~ \& ~ \alpha lsP_{312} = \{..., \alpha lP_{312x}, ...\}\). This illustrates what we said earlier about \(\alpha ls\): it contains only the continuations of the lower adjacent levels. We reiterate this construction procedure for higher-levelled nodes.
The value of \(\alpha \mathcal {L}\) may be obtained by iteration on the level of a node considered as the root (of the graph), as follows:
-
\(\mathbf {lv_{0}}\) root, no children: \( \alpha lP \, \& \, \alpha lsP = \{\}\, \& ~ \alpha \mathcal {L}P = \alpha lP \)
-
\(\mathbf {lv_{1}}\) root or parent, \(\mathbf {lv_{0}}\) children only: \( \alpha lsP = \bigcup _{i} \alpha lP_{i}\, \& ~ \alpha \mathcal {L}P = \alpha lP \cup \alpha lsP \)
-
\(\mathbf {lv_{2}}\) root or parent, at least one \(\mathbf {lv_{1}}\) child: \( \alpha lsP = \bigcup _{i} \alpha lP_{i}\, \& ~ \alpha \mathcal {L}P = \alpha lP \cup (\bigcup _{i} \alpha \mathcal {L}P_{i}) \)
-
\(\mathbf {lv_{n}}\) root or parent, at least one \(\mathbf {lv_{n-1}}\) child: \( \alpha lsP = \bigcup _{i} \alpha lP_{i} \, \& ~ \alpha \mathcal {L}P = \alpha lP \cup (\bigcup _{i} \alpha \mathcal {L}P_{i}) \)
Note. The introduction of a nesting step is what distinguishes the value of \(\mathcal {L}\) from that of WH02’ control variable ls [8]. Its effect is to delegate the instantiation of parallel (nested) nodes to the nesting node, which is a dummy. Thanks to that, control flows as in sequential programs, since the dummy node hides away the parallel structure of programs. It is also thanks to the nesting node that we solve the limitations of ls discussed earlier. Indeed, using WH02 steps, it is possible to jump to a step without care for its nesting level. The presence of the dummy step resolves this by imposing that control must enter into the dummy step first before it can then enter into the parallel steps.
In what follows we describe the semantics of \(\mathcal {L}\) formally.
4 Continuations for Programs with Nested Parallelism
HH98 steps (Sect. 2) are programs that compute the control variable l. By analogy, we present programs that compute the control variable \(\mathcal {L}\) instead. We follow the same methodology of Hoare and He [1, Chap. 6] that consists of starting with unstructured predicates (i.e. steps) and then adding more structure to obtain in turn target code programs, and then program blocks. In our case, after (re)defining steps, we shall restrict our programs to Reactive Processes and obtain, as a result, the theory of Reactive Process Blocks (Sect. 5) i.e. reactive processes that contain the control variable \(\mathcal {L}\).
We now describe predicates whose alphabet include a set of continuations denoted by \(\alpha \mathcal {L}\). \(\alpha \mathcal {L}\) is partitioned into two subsets: \(\alpha l\), which contains the continuations at the current level of execution, and \(\alpha ls\), which contains the continuations at the adjacent lower level of execution, w.r.t. nesting.
At first, each level of execution may be considered without regard for nesting. Then, every step is entered horizontally, and exits horizontally. In a graph, a level corresponds to a single horizontal line that links nodes arranged from left to right, according to their execution order. There is a node which has no horizontal predecessor, called the root of the level. Each node on a line is adjoined a continuation. We say that a node is entered horizontally if we can draw a line from the root leading to it viz. the value of \(\mathcal {L}\) corresponds to the node’s continuation.
In the case of nesting, in a graph, there is a vertical line linking the higher level, at the top, with its adjacent lower levels, all arranged as parallel horizontal lines. The root of the graph has neither vertical nor horizontal predecessors (i.e. there is no vertical/horizontal line leading to the graph-root); the root of a lower level has no horizontal predecessor and should have at least one vertical predecessor. A lower level (or child) node may be entered only if its parent has been entered first. That is, we can draw a vertical line from the parent node to the lower level line that contains the given child node, when traversing the graph of the step from its root to the given node. In other words, the value of \(\mathcal {L}\) must hold both the parent and the child nodes continuations.
Definition 11
Let P be a predicate describing a step. Let \(\alpha \mathcal {L}P\) denote its set of continuations, and let \(\mathcal {L}\) be the control variable for its execution. We may partition the set \(\alpha \mathcal {L}P\) into two subsets \(\alpha lP\) and \(\alpha lsP\) such that:
-
\(\alpha lP\) denotes the set of all the continuations of P at a single level of execution.
-
\(\alpha lsP\) denotes the set of all the continuations of P at the adjacent lower level of execution.
Control may enter into a step horizontally with regard to its own execution level, or vertically with regard to nesting. In either case, a step may be entered only when the value of \(\mathcal {L}\) coincides with one of the step’s entry points. Otherwise the step does nothing. Formally,

Some operators induce/embed a nesting relation (cf. below, e.g. parallel assembly) whilst others do not.
Definition 12
(Nesting relation). Let P be a step, and \(\mathbf {op}\) an operator on steps and which is closed.
\(\mathbf {op}\) is said to induce nesting if, and only if, \(\alpha l~\mathbf {op}(P) \ne \alpha lP\) and \(\alpha lP \subset \alpha ls~\mathbf {op}(P)\): then, we say that \(\mathbf {op}(P)\) is the parent of P, and is called a nesting step; or equivalently, we say that P is nested into \(\mathbf {op}(P)\), and is called a nested step.
Otherwise, i.e. if \(\alpha l~\mathbf {op}(P) = \alpha lP\), then \(\mathbf {op}\) does not induce nesting.
The value of \(\alpha \mathcal {L}P\) may only be given by recursion over the nesting level of P.
Definition 13
( \(\mathbf {lv_{k}}\) -steps, \(\varvec{\alpha \mathcal {L}}\) ). Let P be a step, then

where both \(\alpha lP\) and \(\alpha lsP\) are specified according to the level of the nested programs in the expression of P, as described subsequently.
We say that a program P is a \(\mathbf {lv_{0}}\)-step, denoted by \(P = \mathbf {lv_{0}}(P)\), if, and only if, P has neither parent nor children, i.e. \(\alpha lsP = \{\}\). Then

Let \(\mathbf {op}\) be a binary operator that induces nesting. Then:
-
if P and Q are both \(\mathbf {lv_{0}}\)-steps, then we say that \(\mathbf {op}(P, Q)\) is a \(\mathbf {lv_{1}}\)-step and

-
if either P or Q is a \(\mathbf {lv_{1}}\)-step, or both are, then we say that \(\mathbf {op}(P, Q)\) is a \(\mathbf {lv_{2}}\)-step and

-
if either P or Q is a \(\mathbf {lv_{k}}\)-step, or both are, then we say that \(\mathbf {op}(P, Q)\) is a \(\mathbf {lv_{k+1}}\)-step and

where \(\mathbf {op}(P, Q)\) is a nesting step and may have only one entry point, and only one exit point, both denoted by \(\mathbf {nn}\) for convenience.
Consequence 1
-
1.
\(\mathbf {lv_{0}}\)-steps do not induce a nesting relation.
-
2.
\(\mathbf {lv_{0}}\)-steps are
 -closed. Hence, every operator that may be defined in terms of
-closed. Hence, every operator that may be defined in terms of  (such as
(such as  ) does not induce a nesting relation.
) does not induce a nesting relation.
The relation with HH98 steps is obvious:
Theorem 5
HH98 steps are \(\mathbf {lv_{0}}\)-steps.
Sequential Assembly (2). The sequential assembly is as defined by HH98. We simply redefine it here to account for the changes introduced.

Parallel Assembly. Traditionally, control enters sequentially into a single step at any one time. However, when dealing with parallelism, control may enter sequentially into many steps at any one time. It is therefore possible for a step, upon exit, to indicate that many steps may be executed in parallel next (cf. WH02 [8]).
The selection of next parallel steps may be delegated to a dummy step, or nesting step, which is hence responsible of splitting control. In particular, thanks to the nesting step, we are able to ‘guarantee by construction’ that none of the component steps may be jumped into at random, and that all the component steps are always entered at the same time — it is necessary to enter the nesting step first.
We define below the parallel composition of steps, called parallel assembly and denoted by / /. It states that the parallel assembly of two steps yields a third, nesting step. Such a step may have only one entry point, and only one exit point, both denoted by \(\mathbf {nn}\).
Definition 14
(Parallel assembly).

Instructions, Blocks, Program Blocks. In this section, we principally add more structure to the steps defined in the previous section.
First, we redefine the notion of single instruction.
Definition 15
(Single instruction(2)). Let INST be a \(\mathbf {lv_{0}}\)-step, i.e. \(\alpha lsINST = \{\}\), then

is a single instruction.
We may distinguish two types of machine code blocks, according to the assembly operator used for their composition: (purely) sequential blocks (which we also call proper blocks) are the sequential assembly of single instructions (called machine code block in HH98 [1]); and parallel blocks (or nesting blocks) are the parallel assembly of single instructions.
Definition 16
(Proper-, nesting- block). A proper block, say SeqB, is a program expressible as a sequential assembly of single instructions i.e.

A nesting block, say ParB, is a program expressible as a parallel assembly of single instructions i.e.

We expect any instruction to always pass control via a single exit point that may lead either to a proper instruction or to a nesting one. The definition of target code below reflects that expectation.
Definition 17
(Proper-, nesting- target code). Let P be a step. Let S below denote the set of entry points of all the steps that will be executed in parallel next, and let F denote the corresponding set of exit points.
If \(\alpha lsP \ne \{\}\), then we say that any step of the form \(\langle (s, S), P, (F, f) \rangle \) is in nesting target code, and defined by

However, if P is a \(\mathbf {lv_{0}}\)-step i.e. \(\alpha lsP = \{\}\), then \(S = \{\} = F\); we say that the step is in proper target code and we may write simply \(\langle s, P, f \rangle \).
Notice above that the entry and exit points of the nesting step are independent of those of the steps supposed to execute in parallel. Upon entry, \(\mathcal {L}\) is updated with the continuation s to ensure normal entry into the nesting step itself, and also with the set S so that the parallel steps may be entered conjointly afterwards. Upon exit, the value of \(\mathcal {L}\) is first determined by a given merge function (cf. parallel assembly Definition 14) that ensures that \(\mathcal {L}' \in F\) upon exiting the parallel assembly, and then \(\mathcal {L}\) should be updated with the continuation f to provide normal exit out of the nesting step itself.
In what follows, we define the target code for the parallel composition operator \(\parallel \) only.
The parallel composition of two steps simply yields a third, nesting step, which has its own distinct entry and exit points from those of the steps that are to be run in parallel. Each component step may start only when its continuation has been provided by the nesting step.
Definition 18
(Target code for parallel composition).

We expect the possibility of jumping into nested parallel steps. However, such jumps may not be left unguarded. The least requirement we can impose is that the continuation of the parent must figure in the definition of the jump statement together with the continuations of the children nodes to jump into.
Definition 19
(Vertical jump).

Placing a label to multiple steps at the same time for the purpose of running them in parallel may seem like an interesting feature at first, but it would only add pointless complications. It is sufficient for us to place labels in each program individually and then run the result (of each labelling procedure) in parallel.
In sum, in this section, we have defined the semantics of programs which may contain the control variable \(\mathcal {L}\), thus extending the range of programs expressible using HH98 and WH02 to nested parallel programs. We have not discussed the case of Higher-order (HO) programs and this should be done, given that the theory of mobile processes for which we have built the continuations above relies on HO programming. We postpone such a discussion to Sect. 5.
5 Reactive Process Blocks
In this section we present the construction and semantics of Reactive Process Blocks (or RPB), based on the results obtained previously. RPB processes are meant to extend UTP-CSP processes with continuations. Since we are also interested in Higher-order programming, i.e. the possibility of calling a program within another program, we shall consider the extension of UTP-CSP with HO programming defined by Tang and Woodcock [6].
Alphabet. First, let us consider UTP-CSP processes as defined in [6]. The alphabet of a UTP-CSP process P is defined by

where \(Obs = \{\mathbf {o, o'} | \mathbf {o} \in \{ok, tr, ref\}\}\) is the set of observational variables; \(\mathcal {A}\) the set of events that P may perform (including communications), and VarP the set of variables that P may use. We may extend such an alphabet with both \(\alpha \mathcal {L}P\), the continuations of P, and \(\mathcal {L}\), the control variable. This yields the following alphabet for P

Such an extension poses no difficulty at all, remembering that the alphabet of a predicate is simply a collection of symbols (otherwise meaningless on their own). We will refer to processes with such an alphabet as reactive steps.
Healthiness Conditions. UTP-CSP processes are characterised by a monotonic and idempotent healthiness condition \( {\varvec{CSP}} ~=~ {\varvec{R}} \circ {\varvec{CSP1}} \circ {\varvec{CSP2}} \).
The latter healthiness condition trivially holds under the extension of the alphabet proposed precedently. Nonetheless, that is not enough for characterising reactive steps. In order to achieve such a characterisation, it is necessary to regard the definition of steps given earlier as an additional healthiness condition that applies to UTP-CSP processes with \(\{\mathcal {L}\}\) in their alphabet. We denote that healthiness condition by \({\varvec{RPB1}}\), i.e.  .
.
The following law trivially holds:
Both the control variable \(\mathcal {L}\) and the observational variables ok and wait allow reasoning about termination; in addition, \(\mathcal {L}\) permits reasoning about control, while ok and wait permit reasoning about intermediate stable states. We need to ensure that no contradiction arises from the definitions of each of these variables. Thus, we may define the following laws to ensure the consistency of the definitions of \(\mathcal {L}\), ok and wait variables.
Laws 1
(Consistency between \(\varvec{\mathcal {L}}\) , ok and wait ). The variables wait and \(\mathcal {L}\) must agree on the behaviour of a Step prior to its execution.

The variables ok and \(\mathcal {L}\) must agree on the start of the execution.

The variables ok and wait, and \(\mathcal {L}\) must agree on valid intermediate states.

The variables ok and wait, and \(\mathcal {L}\) must agree on the termination.

Definition 20

We may also define  .
.
We may now define reactive steps formally:
Definition 21
(Reactive steps). Any predicate whose alphabet includes that for reactive processes, and, additionally, both \(\alpha \mathcal {L}\), and \(\mathcal {L}\), and that is \({\varvec{RPB}}\)-healthy is called a reactive step.
Basic Predicates and Operators. We now give the semantics of some basic predicates and operators. Since we are building a target language for high-level UTP-CSP processes viz. that do not contain \(\mathcal {L}\), we need to specify our basic instructions. The definition of target code earlier makes it possible of defining arbitrarily complex predicates even as single instructions. In what follows, we will consider a language with only two single instructions: assignment and action prefix.
The notation m : INST may be considered as a predicate transformer, a function that takes a constant value m and a UTP-CSP process INST, and returns a reactive step with continuations \(\{m\}\).
Assignment Instruction.

Simple Action Prefix Instruction.

where  , and
, and  , and X denotes any predicate of a given UTP theory.
, and X denotes any predicate of a given UTP theory.
We may then define, in an analogue way to HH98, basic (sequential) blocks, basic parallel blocks, and proper blocks (or reactive process blocks).
Assuming that every other operator is well-defined, we now turn to the case of higher-order (HO) programming. A HO program or procedure is one that may be assigned as the value of a HO process variable. \(\{| P |\}\) denotes the procedure that, when executed, behaves like process P.
HO Variable Declaration. In UTP-CSP, the declaration of a HO variable h supposes that h may only contain as values procedures that have the same actions set \(\mathcal {A}\). We may follow this idea for continuations too. We assume that any HO variable h may only receive for value procedures that have the same continuations. Thus, besides the latter assumption about continuations, there is no need for modifying the existing definition of variable declaration that was given for UTP-CSP processes in [6].
6 Conclusion
We have presented continuations for reactive processes, with an emphasis on the semantics for the parallel composition operator, and we have also defined continuations for HO programs. These results find an immediate application in the semantics for strong mobility for UTP-CSP which we aim to publish in the near future. The model presented in this paper does apply to all programs that may contain parallel operators, and not only to UTP-CSP. An interesting ongoing work is the study of the healthiness conditions \({\varvec{A1}}\) to \({\varvec{A4}}\), in view of their eventual simplification.
References
Hoare, C.A.R., He, J.: Unifying Theories of Programming. Prentice-Hall, Upper Saddle River (1998)
Hoare, C.A.R.: Communicating Sequential Processes. Prentice-Hall, Upper Saddle River (1985)
Roscoe, A.W.: The Theory and Practice of Concurrency. Prentice-Hall, Upper Saddle River (1998)
Cavalcanti, A., Woodcock, J.: A tutorial introduction to CSP in unifying theories of programming. In: Cavalcanti, A., Sampaio, A., Woodcock, J. (eds.) PSSE 2004. LNCS, vol. 3167, pp. 220–268. Springer, Heidelberg (2006). doi:10.1007/11889229_6
Tang, X., Woodcock, J.: Travelling processes. In: Kozen, D. (ed.) MPC 2004. LNCS, vol. 3125, pp. 381–399. Springer, Heidelberg (2004). doi:10.1007/978-3-540-27764-4_20
Tang, X., Woodcock, J.: Towards mobile processes in UTP. In: SEFM 2004, pp. 44–53. IEEE (2004)
Fuggetta, A., Picco, G.P., Vigna, G.: Understanding code mobility. In: TSE 1998, vol. 24, pp. 342–361. IEEE (1998)
Woodcock, J., Hughes, A.: Unifying theories of parallel programming. In: George, C., Miao, H. (eds.) ICFEM 2002. LNCS, vol. 2495, pp. 24–37. Springer, Heidelberg (2002). doi:10.1007/3-540-36103-0_5
Jahnig, N., Gothel, T., Glesner, S.: A denotational semantics for communicating unstructured code. In: FESCA 2015, EPTCS, vol. 178, pp. 9–21 (2015)
Reynolds, J.C.: The discoveries of continuations. LISP Symbolic Comput. 6, 233–247 (1993)
Strachey, C., Wadsworth, C.P.: Continuations: a mathematical semantics for handling full jumps. Higher-Order Symbolic Comput. 13, 135–152 (2000)
Danvy, O., Filinski, A.: Representing control: a study of the CPS transformation. Math. Struct. Comp. Sci. 2, 361–391 (1992)
Felleisen, M., Friedman, D.P., Duba, B.F., Merrill, J.: Beyond continuations. Technical report, Indiana University Computer Science Department (1987)
Giorgi, J.F., LeMetayer, D.: Continuation-based parallel implementations of functional languages. In: LFP 1990, pp. 209–217. ACM (1990)
Moreau, L., Queinnec, C.: Partial continuations as the difference of continuations a duumvirate of control operators. In: Hermenegildo, M., Penjam, J. (eds.) PLILP 1994. LNCS, vol. 844, pp. 182–197. Springer, Heidelberg (1994). doi:10.1007/3-540-58402-1_14
Todoran, E., Papaspyrou, N.S.: Continuations for parallel logic programming. In: PPDP 2000, pp. 257–267. ACM (2000)
Acknowledgments
We are grateful to the anonymous reviewers for their useful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Ngondi, G.E., Woodcock, J. (2017). UTP Semantics of Reactive Processes with Continuations. In: Bowen, J., Zhu, H. (eds) Unifying Theories of Programming. UTP 2016. Lecture Notes in Computer Science(), vol 10134. Springer, Cham. https://doi.org/10.1007/978-3-319-52228-9_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-52228-9_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-52227-2
Online ISBN: 978-3-319-52228-9
eBook Packages: Computer ScienceComputer Science (R0)





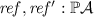 , the refusal set
, the refusal set , stability and termination;
, stability and termination;  , waiting states
, waiting states is a step.
is a step. and
and  are also steps whenever
are also steps whenever 



 -closed. Hence, every operator that may be defined in terms of
-closed. Hence, every operator that may be defined in terms of  (such as
(such as  ) does not induce a nesting relation.
) does not induce a nesting relation.