Abstract
I present a branching time model of CSP that is finer than all other models of CSP proposed thus far. It is obtained by taking a semantic equivalence from the linear time – branching time spectrum, namely divergence-preserving coupled similarity, and showing that it is a congruence for the operators of CSP. This equivalence belongs to the bisimulation family of semantic equivalences, in the sense that on transition systems without internal actions it coincides with strong bisimilarity. Nevertheless, enough of the equational laws of CSP remain to obtain a complete axiomatisation for closed, recursion-free terms.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
- Internal Action
- Operational Semantic
- Parallel Composition
- Label Transition System
- Communicate Sequential Process
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
The process algebra CSP—Communicating Sequential Processes—was presented in Brookes, Hoare & Roscoe [4]. It is sometimes called theoretical CSP, to distinguish it from the earlier language CSP of Hoare [10]. It is equipped with a denotational semantics, mapping each CSP process to an element of the failures-divergences model [4, 5]. The same semantics can also be presented operationally, by mapping CSP processes to states in a labelled transition system (LTS), and then mapping LTSs to the failures-divergences model. Olderog & Hoare [13] shows that this yields the same result. Hence, the failures-divergences model of CSP can alternatively be seen as a semantic equivalence on LTSs, namely by calling two states in an LTS equivalent iff they map to the same element of the failures-divergences model.
Several other models of CSP are presented in the literature, and each can be cast as a semantic equivalence on LTSs, which is a congruence for the operators of CSP. One such model is called finer than another if its associated equivalence relation is finer, i.e., included in the other one, or more discriminating. The resulting hierarchy of models of CSP has two pillars: the divergence-strict models, most of which refine the standard failures-divergences model, and the stable models, such as the model based on stable failures equivalence from Bergstra, Klop & Olderog [2], or the stable revivals model of Roscoe [16].
Here I present a new model, which can be seen as the first branching time model of CSP, and the first that refines all earlier models, i.e. both pillars mentioned above. It is based on the notion of coupled similarity from Parrow & Sjödin [14]. What makes it an interesting model of CSP—as opposed to, say, strong or divergence-preserving weak bisimilarity—is that it allows a complete equational axiomatisation for closed recursion-free CSP processes that fits within the existing syntax of that language.
2 CSP
CSP [4, 5, 11] is parametrised with a set \(\varSigma \) of communications. In this paper I use the subset of CSP given by the following grammar.

Here P and Q are CSP expressions, \(a\in \varSigma \), \(A\subseteq \varSigma \) and \(f:\varSigma \rightarrow \varSigma \). Furthermore, \(p\) ranges over a set of process identifiers. A CSP process is a CSP expression in which each occurrence of a process identifier \(p\) lays within a recursion construct \(\mu p.P\). The operators in the above grammar are inaction, divergence, action prefixing, internal, external and sliding choice, parallel composition, concealment, renaming, interrupt and throw. Compared to [15, 17], this leaves out
-
successful termination (
 ) and sequential composition (;),
) and sequential composition (;), -
infinitary guarded choice,
-
prefixing operators with name binding, conditional choice,
-
relational renaming, and
-
the version of internal choice that takes a possibly infinite set of arguments.
The operators  , \(a\rightarrow \),
, \(a\rightarrow \),  , \(\backslash A\), \(f(\_)\) and recursion stem from [4], and \(\mathbf {div} \) and \(\Vert _A\) from [13], whereas
, \(\backslash A\), \(f(\_)\) and recursion stem from [4], and \(\mathbf {div} \) and \(\Vert _A\) from [13], whereas  and \(\mathbin {\varTheta \!_A}\) were added to CSP by Roscoe [15, 17].
and \(\mathbin {\varTheta \!_A}\) were added to CSP by Roscoe [15, 17].
The operational semantics of CSP is given by the binary transition relations \(\mathop {\longrightarrow }\limits ^{\alpha }\) between CSP processes. The transitions \(P \mathop {\longrightarrow }\limits ^{\alpha } Q\) are derived by the rules in Table 1. Here a, b range over \(\varSigma \) and \(\alpha \), \(\beta \) over  , and relabelling operators f are extended to
, and relabelling operators f are extended to  by \(f(\tau )=\tau \). The transition labels \(\alpha \) are called actions, and \(\tau \) is the internal action.
by \(f(\tau )=\tau \). The transition labels \(\alpha \) are called actions, and \(\tau \) is the internal action.
3 The Failures-Divergences Model of CSP
The process algebra CSP stems from Brookes, Hoare & Roscoe [4]. It is also called theoretical CSP, to distinguish it from the language CSP of Hoare [10]. Its semantics [5] associates to each CSP process a pair \(\langle F, D\rangle \) of failures \(F \subseteq \varSigma ^* \times \mathscr {P}(\varSigma )\) and divergences \(D \subseteq \varSigma ^*\), subject to the conditions:

Here \(\varepsilon \in \varSigma ^*\) is the empty sequence of communications and st denotes the concatenation of sequences s and \(t\in \varSigma ^*\). If \(\langle F, D\rangle \) is the semantics of a process P, \(( s,\emptyset )\in F\), with \(s\not \in D\), tells that P can perform the sequence of communications s, possibly interspersed with internal actions. Such a sequence is called a trace of P, and Conditions N1 and N2 say that the set of traces of any processes is non-empty and prefix-closed. A failure \(( s,X )\in F\), with \(s\notin D\), says that after performing the trace s, P may reach a state in which it can perform none of the actions in X, nor the internal action. A communication \(x\in \varSigma \) is thought to occur in cooperation between a process and its environment. Thus \(( s,X )\in F\) indicates that deadlock can occur if after performing s the process runs in an environment that allows the execution of actions in X only. From this perspective, Conditions N3 and N4 are obvious.
A divergence \(s \in D\) is a trace after which an infinite sequence of internal actions is possible. In the failures-divergences model of CSP divergence is regarded catastrophic: all further information about the process’ behaviour past a divergence trace is erased. This is accomplished by flooding: all conceivable failures \(( st,X )\) and divergences st that have s as a prefix are added to the model (regardless whether P actually has a trace st).
A CSP process P from the syntax of Sect. 2 has the property that for any trace s of P, with \(s\notin D\), the set \({ next}(s)\) of actions c such that sc is also a trace of P is finite. By (N3–4), \(( s,X )\in F\) iff \(( s,X\cap { next}(s) )\in F\). It follows that if \(( s,X )\notin F\), then there is a finite subset Y of X, namely \(X \cap { next}(s)\), such that \(( s,Y )\notin F\). This explains Condition (N5).
In Brookes & Roscoe [5] the semantics of CSP is defined denotationally: for each n-ary CSP operator Op, a function is defined that extracts the failures and divergences of \(Op(P_1,\dots ,P_n)\) out of the failures and divergences of the argument processes \(P_1,\dots ,P_n\). The meaning of a recursively defined CSP process \(\mu p.P\) is obtained by means of fixed-point theory. Alternatively, the failures and divergences of a CSP process can be extracted from its operational semantics:
Definition 1
Write  if there are processes \(P_0,\dots ,P_n\), with \(n\ge 0\), such that \(P=P_0\), \(P_i \mathop {\longrightarrow }\limits ^{\tau } P_{i+1}\) for all \(0\le i < n\), and \(P_n=Q\).
if there are processes \(P_0,\dots ,P_n\), with \(n\ge 0\), such that \(P=P_0\), \(P_i \mathop {\longrightarrow }\limits ^{\tau } P_{i+1}\) for all \(0\le i < n\), and \(P_n=Q\).
Write  if there are processes \(P',Q'\) with
if there are processes \(P',Q'\) with  .
.
Write  if either \(\alpha \in \varSigma \) and
if either \(\alpha \in \varSigma \) and  , or \(\alpha =\tau \) and
, or \(\alpha =\tau \) and  .
.
Write  , for \(s=a_1a_2 \dots a_n \in \varSigma ^*\) with \(n\ge 0\), if there are processes \(P_0,\dots ,P_n\) such that \(P=P_0\),
, for \(s=a_1a_2 \dots a_n \in \varSigma ^*\) with \(n\ge 0\), if there are processes \(P_0,\dots ,P_n\) such that \(P=P_0\),  for all \(0\le i < n\), and \(P_n=Q\).
for all \(0\le i < n\), and \(P_n=Q\).
Let \(I(P)=\{\alpha \in \varSigma \cup \{\tau \} \mid \exists Q.\, P \mathop {\longrightarrow }\limits ^{\alpha } Q\}\).
Write \(P{\Uparrow }\) if there are processes \(P_i\) for all \(i\mathbin \ge 0\) with  .
.
\(s\in \varSigma ^*\) is a divergence trace of a process P if there is a Q with  .
.
The divergence set of P is \(\mathscr {D}(P):=\{st\mid s\,\text{ is } \text{ a } \text{ divergence } \text{ trace } \text{ of } P\}\).
A stable failure of a process P is a pair \(( s,X ) \in \varSigma ^*\times \mathscr {P}(\varSigma )\) such that  for some Q with \(I(Q)\cap (X\cup \{\tau \}) = \emptyset \). The failure set of a process P is \(\mathscr {F}(p) = \{( s,X ) \mid s \in \mathscr {D}(P) \text { or }( s,X )\,\text{ is } \text{ a } \text{ stable } \text{ failure } \text{ of } P\}\).
for some Q with \(I(Q)\cap (X\cup \{\tau \}) = \emptyset \). The failure set of a process P is \(\mathscr {F}(p) = \{( s,X ) \mid s \in \mathscr {D}(P) \text { or }( s,X )\,\text{ is } \text{ a } \text{ stable } \text{ failure } \text{ of } P\}\).
The semantics \([\![ {P}]\!]_{\mathscr {F}\mathscr {D}}\) of a CSP process P is the pair \(\langle \mathscr {F}(P), \mathscr {D}(P) \rangle \).
Processes P and Q are failures-divergences equivalent, notation \(P \equiv _{FD} Q\), iff \([\![ {P}]\!]_{\mathscr {F}\mathscr {D}}=[\![ {Q}]\!]_{\mathscr {F}\mathscr {D}}\). Process P is a failures-divergences refinement of Q, notation \(P \sqsupseteq _{FD} Q\), iff \(\mathscr {F}(P) \subseteq \mathscr {F}(Q) \wedge \mathscr {D}(P) \subseteq \mathscr {D}(Q)\).
The operational semantics of Sect. 2 (then without the operators \(\rhd \),  and \(\mathbin {\varTheta \!_A}\)) appears, for instance, in [13], and was created after the denotational semantics. In Olderog & Hoare [13] it is shown that the semantics \([\![ {P}]\!]\) of a CSP process defined operationally through Definition 1 equals the denotational semantics given in [5]. The argument extends smoothly to the new operators \(\rhd \),
and \(\mathbin {\varTheta \!_A}\)) appears, for instance, in [13], and was created after the denotational semantics. In Olderog & Hoare [13] it is shown that the semantics \([\![ {P}]\!]\) of a CSP process defined operationally through Definition 1 equals the denotational semantics given in [5]. The argument extends smoothly to the new operators \(\rhd \),  and \(\mathbin {\varTheta \!_A}\) [17]. This can be seen as a justification of the operational semantics of Sect. 2.
and \(\mathbin {\varTheta \!_A}\) [17]. This can be seen as a justification of the operational semantics of Sect. 2.
In Brookes, Hoare & Roscoe [4] a denotational semantics of CSP was given involving failures only. Divergences were included only implicitly, namely by thinking of a trace s as a divergence of a process P iff P has all failures \(( st,X )\). So the semantics of \(\mathbf {div} \) or \(\mu X.X\) is simply the set of all failure pairs. As observed in De Nicola [6], this approach invalidates a number of intuitively valid laws, such as  . The improved semantics of [5] solves this problem.
. The improved semantics of [5] solves this problem.
In Hoare [11] a slightly different semantics of CSP is given, in which a process is determined by its failures, divergences, as well as its alphabet. The latter is a superset of the set of communications the process can ever perform. Rather than a parallel composition \(\Vert _A\) for each set of synchronising actions \(A \subseteq \varSigma \), this approach has an operator \(\Vert \) where the set of synchronising actions is taken to be the intersection of the alphabets of its arguments. Additionally, there is an operator \(|||\), corresponding to \(\Vert _\emptyset \). This approach is equally expressive as the one of [5], in the sense that there are semantics preserving translations in both directions. The work reported in this paper could just as well have been carried out in this typed version of CSP.
4 A Complete Axiomatisation
In [4,5,6, 11, 15, 17] many algebraic laws \(P=Q\), resp. \(P \sqsubseteq Q\), are stated that are valid w.r.t. the failures-divergences semantics of CSP, meaning that \(P \equiv _{FD} Q\), resp. \(P \sqsubseteq _{FD} Q\). If \({ Th}\) is a collection of equational laws \(P=Q\) then \({ Th}\vdash R=S\) denotes that the equation \(R=S\) is derivable from the equations in \({ Th}\) using reflexivity, symmetry, transitivity and the rule of congruence, saying that if Op is an n-ary CSP operator and \(P_i = Q_i\) for \(i=1,\dots ,n\) then \(Op(P_1,\dots ,P_n)=Op(Q_1,\dots ,Q_n)\). Likewise, if \({ Th}\) is a collection of inequational laws \(P\sqsubseteq Q\) then \({ Th}\vdash R\sqsubseteq S\) denotes that the inequation \(R\sqsubseteq S\) is derivable from the inequations in \({ Th}\) using reflexivity, transitivity and the rule saying that if Op is an n-ary CSP operator and \(P_i \sqsubseteq Q_i\) for \(i=1,\dots ,n\) then \(Op(P_1,\dots ,P_n)\sqsubseteq Op(Q_1,\dots ,Q_n)\).
Definition 2
An equivalence \(\sim \) on process expressions is called a congruence for an n-ary operator Op if \(P_i \sim Q_i\) for \(i=1,\dots ,n\) implies \(Op(P_1,\dots ,P_n)\sim Op(Q_1,\dots ,Q_n)\). A preorder \(\preceq \) is a precongruence for Op, or Op is monotone for \(\preceq \), if \(P_i \preceq Q_i\) for \(i=1,\dots ,n\) implies \(Op(P_1,\dots ,P_n)\preceq Op(Q_1,\dots ,Q_n)\).
If \(\sim \) is a congruence for all operators of CSP (resp. \(\preceq \) is a precongruence for all operators of CSP) and \({ Th}\) is a set of (in)equational laws that are valid for \(\sim \) (resp. \(\preceq \)) then any (in)equation \(R=S\) with \({ Th}\vdash R=S\) (resp. \(R\sqsubseteq S\) with \({ Th}\vdash R\sqsubseteq S\)) is valid for \(\sim \) (resp. \(\preceq \)).
\(\equiv _{FD}\) is a congruence for all operators of CSP. This follows immediately from the existence of the denotational failures-divergences semantics. Likewise, \(\sqsubseteq _{FD}\) is a precongruence for all operators of CSP [4,5,6, 11, 13, 15, 17].
Definition 3
A set \({ Th}\) of (in)equational laws—an axiomatisation—is sound and complete for an equivalence \(\sim \) (or a preorder \(\preceq \)) if \({ Th}\vdash R=S\) iff \(R \sim S\) (resp. \({ Th}\vdash R\sqsubseteq S\) iff \(R \preceq S\)). Here “\(\Rightarrow \)” is soundness and “\(\Leftarrow \)” completeness.
In De Nicola [6] a sound and complete axiomatisation of \(\sqsubseteq _{FD}\) for recursion-free CSP, and no process identifiers or variables, is presented. It is quoted in Table 2. As this axiomatisation consist of a mix of equations and inequations, formally it is an inequational axiomatisation, where an equation \(P=Q\) is understood as the conjunction of \(P \sqsubseteq Q\) and \(Q \sqsubseteq P\). This mixed use is justified because \(\equiv _{FD}\) is the kernel of \(\sqsubseteq _{FD}\): one has \(P \equiv _{FD} Q\) iff \(P \sqsubseteq _{FD} Q \wedge Q \sqsubseteq _{FD} P\).
In [6], following [4, 5], two parallel composition operators \(\Vert \) and \(|||\) were considered, instead of the parametrised operator \(\Vert _A\). Here \(\Vert =\Vert _\varSigma \) and \(|||= \Vert _\emptyset \). In Table 2 the axioms for these two operators are unified into an axiomatisation of \(\Vert _A\). Additionally, I added axioms for sliding choice, renaming, interrupt and throw—these operators were not considered in [6]. The associativity of parallel composition (Axiom \(\mathbf {P0}\)) is not included in [6] and is not needed for completeness. I added it anyway, because of its importance in equational reasoning.
The soundness of the axiomatisation of Table 2 follows from \(\sqsubseteq _{FD}\) being a precongruence, and the validity of the axioms—a fairly easy inspection using the denotational characterisation of \([\![ {\_}]\!]\). To obtain completeness, write  , with \(I\mathbin =\{i_1,\ldots ,i_n\}\) any finite index set, for
, with \(I\mathbin =\{i_1,\ldots ,i_n\}\) any finite index set, for  , where
, where  represents
represents  . This notation is justified by Axioms E2–4. Furthermore,
. This notation is justified by Axioms E2–4. Furthermore,  , with \(J\mathbin =\{j_1,..,j_m\}\) any finite, nonempty index set, denotes
, with \(J\mathbin =\{j_1,..,j_m\}\) any finite, nonempty index set, denotes  . This notation is justified by Axioms \(\mathbf {I2}\) and \(\mathbf {I3}\). Now a normal form is a defined as a CSP expression of the form \(\mathbf {div} \) or
. This notation is justified by Axioms \(\mathbf {I2}\) and \(\mathbf {I3}\). Now a normal form is a defined as a CSP expression of the form \(\mathbf {div} \) or  , with
, with  for \(j\in J\), where the subexpressions \(R_{kj}\) are again in normal form. Here J and the \(K_j\) are finite index sets, J nonempty.
for \(j\in J\), where the subexpressions \(R_{kj}\) are again in normal form. Here J and the \(K_j\) are finite index sets, J nonempty.
Axioms \(\mathbf {\bot }\) and \(\mathbf {I4}\) derive  . Together with Axioms \(\mathbf {D1}\), \(\mathbf {SC}\), P1–4, H1–4, R1–5, T1–6 and U1–5 this allows any recursion-free CSP expression to be rewritten into normal form. In [6] it is shown that for any two normal forms P and Q with \(P \sqsubseteq _{FD} Q\), Axioms \(\mathbf {\bot }\), I1–4, E1–5 and D1–4 derive \(\vdash P=Q\). Together, this yields the completeness of the axiomatisation of Table 2.
. Together with Axioms \(\mathbf {D1}\), \(\mathbf {SC}\), P1–4, H1–4, R1–5, T1–6 and U1–5 this allows any recursion-free CSP expression to be rewritten into normal form. In [6] it is shown that for any two normal forms P and Q with \(P \sqsubseteq _{FD} Q\), Axioms \(\mathbf {\bot }\), I1–4, E1–5 and D1–4 derive \(\vdash P=Q\). Together, this yields the completeness of the axiomatisation of Table 2.
5 Other Models of CSP
Several alternative models of CSP have been proposed in the literature, including the readiness-divergences model of Olderog & Hoare [13] and the stable revivals model of Roscoe [16]. A hierarchy of such models is surveyed in Roscoe [17]. Each of these models corresponds with a preorder (and associated semantic equivalence) on labelled transition systems. In [7] I presented a survey of semantic equivalences and preorders on labelled transition systems, ordered by inclusion in a lattice. Each model occurring in [17] correspond exactly with with one of the equivalences of [7], or—like the stable revivals model—arises as the meet or join of two such equivalences.
In the other direction, not every semantic equivalence or preorder from [7] yields a sensible model of CSP. First of all, one would want to ensure that it is a (pre)congruence for the operators of CSP. Additionally, one might impose sanity requirements on the treatment of recursion.
The hierarchy of models in [17] roughly consist of two hierarchies: the stable models, and the divergence-strict ones. The failures-divergences model could be seen as the centre piece in the divergence-strict hierarchy, and the stable failures model [15], which outside CSP stems from Bergstra, Klop & Olderog [2], plays the same role in the stable hierarchy. Each of these hierarchies has a maximal (least discriminating) element, called \(\mathcal {FL}^\Downarrow \) and \(\mathcal {FL}\) in [17]. These correspond to the ready trace models \({ RT}^\downarrow \) and \({ RT}\) of [7].
The goal of the present paper is to propose a sensible model of CSP that is strictly finer than all models thus far considered, and thus unites the two hierarchies mentioned above. As all models of CSP considered so far have a distinctly linear time flavour, I here propose a branching time model, thereby showing that the syntax of CSP is not predisposed towards linear time models. My model can be given as an equivalence relation on labelled transition system, provided I show that it is a congruence for the operators of CSP. I aim for an equivalence that allows a complete axiomatisation in the style of Table 2, obtained by replacing axioms that are no longer valid by weaker ones.
One choice could be to base a model on strong bisimulation equivalence [12]. Strong bisimilarity is a congruence for all CSP operators, because their operational semantics fits the tyft/tyxt format of [9]. However, this is an unsuitable equivalence for CSP, because it fails to abstract from internal actions. Even the axiom \(\mathbf {I1}\) would not be valid, as the two sides differ by an internal action.
A second proposal could be based on weak bisimilarity [12]. This equivalence abstracts from internal activity, and validates \(\mathbf {I1}\). The default incarnation of weak bisimilarity is not finer than failures-divergences equivalence, because it satisfies  . Therefore, one would take a divergence-preserving variant of this notion: the weak bisimulation with explicit divergence of Bergstra, Klop & Olderog [2]. Yet, some crucial CSP laws are invalidated, such as \(\mathbf {I3}\) and \(\mathbf {D1}\). This destroys any hope of a complete axiomatisation along the lines of Table 2.
. Therefore, one would take a divergence-preserving variant of this notion: the weak bisimulation with explicit divergence of Bergstra, Klop & Olderog [2]. Yet, some crucial CSP laws are invalidated, such as \(\mathbf {I3}\) and \(\mathbf {D1}\). This destroys any hope of a complete axiomatisation along the lines of Table 2.
My final choice is divergence-preserving coupled similarity [7], based on coupled similarity for divergence-free processes from Parrow & Sjödin [14]. This is the finest equivalence in [7] that satisfies \(\mathbf {I3}\) and \(\mathbf {D1}\). In fact, it satisfies all of the axioms of Table 2, except for the ones marked red: \(\mathbf {\bot }\), \(\mathbf {I4}\), \(\mathbf {E1}\), \(\mathbf {E5}\), D2–4, \(\mathbf {SC}\), \(\mathbf {P2}\), \(\mathbf {P3}\), \(\mathbf {H2}\), \(\mathbf {U2}\), \(\mathbf {U3}\) and \(\mathbf {U5}\).
Divergence-preserving coupled similarity belongs to the bisimulation family of semantic equivalences, in the sense that on transition systems without internal actions it coincides with strong bisimilarity.
In Sect. 6 I present divergence-preserving coupled similarity. In Sect. 7 I prove that it is a congruence for the operators of CSP, and in Sect. 8 I present a complete axiomatisation for recursion-free CSP processes without interrupts.
6 Divergence-Preserving Coupled Similarity
Definition 4
A coupled simulation is a binary relation \(\mathscr {{\,}R{\,}}\) on CSP processes, such that, for all \(\alpha \in \varSigma \cup \{\tau \}\),
-
if \(P \mathscr {{\,}R{\,}}Q\) and \(P \mathop {\longrightarrow }\limits ^{\alpha } P'\) then there exists a \(Q'\) with
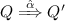 and \(P' \mathscr {{\,}R{\,}}Q'\),
and \(P' \mathscr {{\,}R{\,}}Q'\), -
and if \(P \mathscr {{\,}R{\,}}Q\) then there exists a \(Q'\) with
 and \(Q' \mathscr {{\,}R{\,}}P\).
and \(Q' \mathscr {{\,}R{\,}}P\).
It is divergence-preserving if \(P \mathscr {{\,}R{\,}}Q\) and \(P {\Uparrow }\) implies \(Q {\Uparrow }\). Write  if there exists a divergence-preserving coupled simulation \(\mathscr {{\,}R{\,}}\) with \(P \mathscr {{\,}R{\,}}Q\). Two processes P and Q are divergence-preserving coupled similar, notation
if there exists a divergence-preserving coupled simulation \(\mathscr {{\,}R{\,}}\) with \(P \mathscr {{\,}R{\,}}Q\). Two processes P and Q are divergence-preserving coupled similar, notation  , if \(P \sqsupseteq _{CS}^\varDelta Q\) and \(Q \sqsupseteq _{CS}^\varDelta P\).
, if \(P \sqsupseteq _{CS}^\varDelta Q\) and \(Q \sqsupseteq _{CS}^\varDelta P\).
Note that the union of any collection of divergence-preserving coupled simulations is itself a divergence-preserving coupled simulation. In particular, \(\sqsupseteq _{CS}^\varDelta \) is a divergence-preserving coupled simulation. Also note that in the absence of the internal action \(\tau \), coupled simulations are symmetric, and coupled similarity coincides with strong bisimilarity (as defined in [12]).
Intuitively,  says that P is “ahead” of a state matching Q, where \(P'\) is ahead of P if
says that P is “ahead” of a state matching Q, where \(P'\) is ahead of P if  . The first clause says that if P is ahead of a state matching Q, then any transition performed by P can be matched by Q—possibly after Q “caught up” with P by performing some internal transitions. The second clause says that if P is ahead of Q, then Q can always catch up, so that it is ahead of P. Thus, if P and Q are in stable states—where no internal actions are possible—then \(P \sqsubseteq _{CS}^\varDelta Q\) implies \(Q \sqsubseteq _{CS}^\varDelta P\). In all other situations, P and Q do not need to be matched exactly, but there do exists under- and overapproximations of a match. The result is that the relation behaves like a weak bisimulation w.r.t. visible actions, but is not so pedantic in matching internal actions.
. The first clause says that if P is ahead of a state matching Q, then any transition performed by P can be matched by Q—possibly after Q “caught up” with P by performing some internal transitions. The second clause says that if P is ahead of Q, then Q can always catch up, so that it is ahead of P. Thus, if P and Q are in stable states—where no internal actions are possible—then \(P \sqsubseteq _{CS}^\varDelta Q\) implies \(Q \sqsubseteq _{CS}^\varDelta P\). In all other situations, P and Q do not need to be matched exactly, but there do exists under- and overapproximations of a match. The result is that the relation behaves like a weak bisimulation w.r.t. visible actions, but is not so pedantic in matching internal actions.
Proposition 1
\(\sqsupseteq _{CS}^\varDelta \) is reflexive and transitive, and thus a preorder.
Proof
The identity relation \({ Id}\) is a divergence-preserving coupled simulation, and if \(\mathscr {{\,}R{\,}}\), \(\mathscr {{\,}R{\,}}'\) are divergence-preserving coupled simulations, then so is \(\mathscr {{\,}R{\,}};\mathscr {{\,}R{\,}}' \cup \mathscr {{\,}R{\,}}';\mathscr {{\,}R{\,}}\). Here \({\mathscr {{\,}R{\,}}};{\mathscr {{\,}R{\,}}'}\) is defined by \(P \mathrel {{\mathscr {{\,}R{\,}}};{\mathscr {{\,}R{\,}}'}} R\) iff there is a Q with \(P \mathscr {{\,}R{\,}}Q \mathscr {{\,}R{\,}}' R\).
\(\mathscr {{\,}R{\,}}{;}\mathscr {{\,}R{\,}}'\) is divergence-preserving: if \(P {\mathscr {{\,}R{\,}}} Q {\mathscr {{\,}R{\,}}'} R\) and \(P {\Uparrow }\), then \(Q {\Uparrow }\), and thus \(R {\Uparrow }\!\). The same holds for \(\mathscr {{\,}R{\,}}';\mathscr {{\,}R{\,}}\), and thus for \(\mathscr {{\,}R{\,}};\mathscr {{\,}R{\,}}' \cup \mathscr {{\,}R{\,}}';\mathscr {{\,}R{\,}}\).
To check that \(\mathscr {{\,}R{\,}};\mathscr {{\,}R{\,}}' \cup \mathscr {{\,}R{\,}}';\mathscr {{\,}R{\,}}\) satisfies the first clause of Definition 4, note that if \(Q \mathscr {{\,}R{\,}}' R\) and  , then, by repeated application of the first clause of Definition 4, there is an \(R'\) with
, then, by repeated application of the first clause of Definition 4, there is an \(R'\) with  and \(Q' \mathscr {{\,}R{\,}}' R'\).
and \(Q' \mathscr {{\,}R{\,}}' R'\).
Towards the second clause, if \(P \mathscr {{\,}R{\,}}Q \mathscr {{\,}R{\,}}' R\), then, using the second clause for \(\mathscr {{\,}R{\,}}\), there is a \(Q'\) with  and \(Q' \mathscr {{\,}R{\,}}P\). Hence, using the first clause for \(\mathscr {{\,}R{\,}}'\), there is an \(R'\) with
and \(Q' \mathscr {{\,}R{\,}}P\). Hence, using the first clause for \(\mathscr {{\,}R{\,}}'\), there is an \(R'\) with  and \(Q' \mathscr {{\,}R{\,}}' R'\). Thus, using the second clause for \(\mathscr {{\,}R{\,}}'\), there is an \(R''\) with
and \(Q' \mathscr {{\,}R{\,}}' R'\). Thus, using the second clause for \(\mathscr {{\,}R{\,}}'\), there is an \(R''\) with  and \(R'' \mathscr {{\,}R{\,}}' Q'\), and hence \(R'' \mathrel {{\mathscr {{\,}R{\,}}'};{\mathscr {{\,}R{\,}}}} P'\). \(\square \)
and \(R'' \mathscr {{\,}R{\,}}' Q'\), and hence \(R'' \mathrel {{\mathscr {{\,}R{\,}}'};{\mathscr {{\,}R{\,}}}} P'\). \(\square \)
Proposition 2
If  then \(P \sqsubseteq _{CS}^\varDelta Q\).
then \(P \sqsubseteq _{CS}^\varDelta Q\).
Proof
I show that \({ Id}\cup \{(Q,P)\}\), with \({ Id}\) the identity relation, is a coupled simulation. Namely if  then surely
then surely  . The second clause of Definition 4 is satisfied because
. The second clause of Definition 4 is satisfied because  . Furthermore, if \(Q {\Uparrow }\) then certainly \(P {\Uparrow }\), so the relation is divergence-preserving. \(\square \)
. Furthermore, if \(Q {\Uparrow }\) then certainly \(P {\Uparrow }\), so the relation is divergence-preserving. \(\square \)
Proposition 3
\(P \sqsupseteq _{CS}^\varDelta Q\) iff  .
.
Proof
“\(\Rightarrow \)”: Let \(\mathscr {{\,}R{\,}}\) be the smallest relation such that, for any P and Q, \(P \sqsupseteq _{CS}^\varDelta Q\) implies \(P \mathscr {{\,}R{\,}}Q\),  and
and  . It suffices to show that \(\mathscr {{\,}R{\,}}\) is a divergence-preserving coupled simulation.
. It suffices to show that \(\mathscr {{\,}R{\,}}\) is a divergence-preserving coupled simulation.
That \(\mathscr {{\,}R{\,}}\) is divergence-preserving is trivial, using that  iff \(P{\Uparrow } \vee Q{\Uparrow }\).
iff \(P{\Uparrow } \vee Q{\Uparrow }\).
Suppose \(P^* \mathscr {{\,}R{\,}}Q\) and \(P^* \mathop {\longrightarrow }\limits ^{\alpha } P'\). The case that \(P^*=P\) with \(P \sqsupseteq _{CS}^\varDelta Q\) is trivial. Now let Q be  . Since
. Since  , surely
, surely  , and \(P' \mathscr {{\,}R{\,}}P'\). Finally, let
, and \(P' \mathscr {{\,}R{\,}}P'\). Finally, let  with
with  . Then \(\alpha =\tau \) and \(P'\) is either P or Q. Both cases are trivial, taking \(Q'=Q\).
. Then \(\alpha =\tau \) and \(P'\) is either P or Q. Both cases are trivial, taking \(Q'=Q\).
Towards the second clause of Definition 4, suppose \(P^* \mathscr {{\,}R{\,}}Q\). The case \(P^*=P\) with  is trivial. Now let Q be
is trivial. Now let Q be  . Then
. Then  and \(P^* \mathscr {{\,}R{\,}}P^*\). Finally, let
and \(P^* \mathscr {{\,}R{\,}}P^*\). Finally, let  with
with  . Then
. Then  and
and  .
.
“\(\Leftarrow \)”: Suppose  . Since
. Since  there exists a \(Q'\) with
there exists a \(Q'\) with  and \(P \sqsupseteq _{CS}^\varDelta Q'\). By Proposition 2
and \(P \sqsupseteq _{CS}^\varDelta Q'\). By Proposition 2  and by Proposition 1 \(P \sqsupseteq _{CS}^\varDelta Q\). \(\square \)
and by Proposition 1 \(P \sqsupseteq _{CS}^\varDelta Q\). \(\square \)
7 Congruence Properties
Proposition 4
\(\equiv _{CS}^\varDelta \) is a congruence for action prefixing.
Proof
I have to show that \(P \equiv _{CS}^\varDelta Q\) implies \((a\rightarrow P) \equiv _{CS}^\varDelta (a\rightarrow Q)\).
Let \(\mathscr {{\,}R{\,}}\) be the smallest relation such that, for any P and Q, \(P \sqsubseteq _{CS}^\varDelta Q\) implies \(P \mathscr {{\,}R{\,}}Q\), and \(P \equiv _{CS}^\varDelta Q\) implies \((a\rightarrow P) \mathscr {{\,}R{\,}}(a\rightarrow Q)\). It suffices to show that \(\mathscr {{\,}R{\,}}\) is a divergence-preserving coupled simulation.
Checking the conditions of Definition 4 for the case \(P \mathscr {{\,}R{\,}}Q\) with \(P \sqsubseteq _{CS}^\varDelta Q\) is trivial. So I examine the case \((a\rightarrow P) \mathscr {{\,}R{\,}}(a\rightarrow Q)\) with \(P \equiv _{CS}^\varDelta Q\).
Suppose \((a\rightarrow P) \mathop {\longrightarrow }\limits ^{\alpha } P'\). Then \(\alpha =a\) and \(P'=P\). Now \((a\rightarrow Q)\mathop {\longrightarrow }\limits ^{\alpha } Q\) and \(P \mathscr {{\,}R{\,}}Q\), so the first condition of Definition 4 is satisfied.
For the second condition,  , and, since \(Q \equiv _{CS}^\varDelta P\), \((a\rightarrow Q) \mathscr {{\,}R{\,}}(a\rightarrow P)\). Thus, \(\mathscr {{\,}R{\,}}\) is a coupled simulation.
, and, since \(Q \equiv _{CS}^\varDelta P\), \((a\rightarrow Q) \mathscr {{\,}R{\,}}(a\rightarrow P)\). Thus, \(\mathscr {{\,}R{\,}}\) is a coupled simulation.
As \(a\rightarrow P\) does not diverge, \(\mathscr {{\,}R{\,}}\) moreover is divergence-preserving. \(\square \)
Since  but
but  , and thus
, and thus  , the relation
, the relation  is not a precongruence for action prefixing.
is not a precongruence for action prefixing.
It is possible to express action prefixing in terms of the throw operator: \(a \rightarrow P\) is strongly bisimilar with  . Consequently,
. Consequently,  is not a precongruence for the throw operator.
is not a precongruence for the throw operator.
Proposition 5
\(\equiv _{CS}^\varDelta \) is a congruence for the throw operator.
Proof
Let \(A\subseteq \varSigma \). Let \(\mathscr {{\,}R{\,}}\) be the smallest relation such that, for any \(P_1,P_2,Q_1\), \(Q_2\), \(P_1 \sqsupseteq _{CS}^\varDelta Q_1\) and \(P_2 \equiv _{CS}^\varDelta Q_2\) implies \(P_1 \mathscr {{\,}R{\,}}Q_1\) and \((P_1\mathbin {\varTheta \!_A}P_2) \mathscr {{\,}R{\,}}(Q_1\mathbin {\varTheta \!_A}Q_2)\). It suffices to show that \(\mathscr {{\,}R{\,}}\) is a divergence-preserving coupled simulation.
So let \(P_1 \sqsupseteq _{CS}^\varDelta Q_1\), \(P_2 \equiv _{CS}^\varDelta Q_2\) and \((P_1\mathbin {\varTheta \!_A}P_2) \mathop {\longrightarrow }\limits ^{\alpha } P'\). Then  for some \(P_2'\), and either \(\alpha \notin A\) and \(P'=P_1' \mathbin {\varTheta \!_A}P_2\), or \(\alpha \in A\) and \(P'=P_2\). So there is a \(Q_1'\) with
for some \(P_2'\), and either \(\alpha \notin A\) and \(P'=P_1' \mathbin {\varTheta \!_A}P_2\), or \(\alpha \in A\) and \(P'=P_2\). So there is a \(Q_1'\) with  and \(P_1' \sqsupseteq _{CS}^\varDelta Q_1'\). If \(\alpha \notin A\) it follows that
and \(P_1' \sqsupseteq _{CS}^\varDelta Q_1'\). If \(\alpha \notin A\) it follows that  and \((P'_1\mathbin {\varTheta \!_A}P_2) \mathscr {{\,}R{\,}}(Q'_1\mathbin {\varTheta \!_A}Q_2)\). If \(\alpha \in A\) it follows that
and \((P'_1\mathbin {\varTheta \!_A}P_2) \mathscr {{\,}R{\,}}(Q'_1\mathbin {\varTheta \!_A}Q_2)\). If \(\alpha \in A\) it follows that  and \(P_2 \mathscr {{\,}R{\,}}Q_2\).
and \(P_2 \mathscr {{\,}R{\,}}Q_2\).
Now let \(P_1 \sqsupseteq _{CS}^\varDelta Q_1\) and \(P_2 \equiv _{CS}^\varDelta Q_2\). Then there is a \(Q_1'\) with  and
and  . Hence
. Hence  and \((Q_1'\mathbin {\varTheta \!_A}Q_2) \mathscr {{\,}R{\,}}(P_1\mathbin {\varTheta \!_A}P_2)\).
and \((Q_1'\mathbin {\varTheta \!_A}Q_2) \mathscr {{\,}R{\,}}(P_1\mathbin {\varTheta \!_A}P_2)\).
The same two conditions for the case \(P \mathscr {{\,}R{\,}}Q\) because \(P \sqsupseteq _{CS}^\varDelta Q\) are trivial. Thus \(\mathscr {{\,}R{\,}}\) is a coupled simulation. That \(\mathscr {{\,}R{\,}}\) is divergence-preserving follows because \(P_1 \mathbin {\varTheta \!_A}P_2 {\Uparrow }\) iff \(P_1 {\Uparrow }\). \(\square \)
I proceed to show that  is a precongruence for all the other operators of CSP. This implies that
is a precongruence for all the other operators of CSP. This implies that  is a congruence for all the operators of CSP.
is a congruence for all the operators of CSP.
Proposition 6
\(\sqsupseteq _{CS}^\varDelta \) is a precongruence for internal choice.
Proof
Let \(\mathscr {{\,}R{\,}}\) be the smallest relation such that, for any \(P_i\) and \(Q_i\), \(P_i \sqsupseteq _{CS}^\varDelta Q_i\) for \(i=1,2\) implies \(P_i \mathscr {{\,}R{\,}}Q_i\) (\(i=1,2\)) and  . It suffices to show that \(\mathscr {{\,}R{\,}}\) is a divergence-preserving coupled simulation.
. It suffices to show that \(\mathscr {{\,}R{\,}}\) is a divergence-preserving coupled simulation.
So let  for \(i=1,2\) and
for \(i=1,2\) and  . Then \(\alpha =\tau \) and \(P'=P_i\) for \(i=1\) or 2. Now
. Then \(\alpha =\tau \) and \(P'=P_i\) for \(i=1\) or 2. Now  and \(P_i \mathscr {{\,}R{\,}}Q_i\).
and \(P_i \mathscr {{\,}R{\,}}Q_i\).
Now let  for \(i=1,2\). Then there is a \(Q_1'\) with
for \(i=1,2\). Then there is a \(Q_1'\) with  and
and  . By Proposition 2
. By Proposition 2  and by Proposition 1
and by Proposition 1  .
.
The same two conditions for the case \(P \mathscr {{\,}R{\,}}Q\) because \(P \sqsupseteq _{CS}^\varDelta Q\) are trivial. Thus \(\mathscr {{\,}R{\,}}\) is a coupled simulation. That \(\mathscr {{\,}R{\,}}\) is divergence-preserving follows because  iff \(P_1 {\Uparrow } \vee P_2 {\Uparrow }\). \(\square \)
iff \(P_1 {\Uparrow } \vee P_2 {\Uparrow }\). \(\square \)
Proposition 7
\(\sqsupseteq _{CS}^\varDelta \) is a precongruence for external choice.
Proof
Let \(\mathscr {{\,}R{\,}}\) be the smallest relation such that, for any \(P_i\) and \(Q_i\), \(P_i \sqsupseteq _{CS}^\varDelta Q_i\) for \(i=1,2\) implies \(P_i \mathscr {{\,}R{\,}}Q_i\) (\(i=1,2\)) and  . It suffices to show that \(\mathscr {{\,}R{\,}}\) is a divergence-preserving coupled simulation.
. It suffices to show that \(\mathscr {{\,}R{\,}}\) is a divergence-preserving coupled simulation.
So let \(P_i \sqsupseteq _{CS}^\varDelta Q_i\) for \(i=1,2\) and  . If \(\alpha \in \varSigma \) then \(P_i \mathop {\longrightarrow }\limits ^{\alpha } P'\) for \(i=1\) or 2, and there exists a \(Q'\) with
. If \(\alpha \in \varSigma \) then \(P_i \mathop {\longrightarrow }\limits ^{\alpha } P'\) for \(i=1\) or 2, and there exists a \(Q'\) with  and
and  . Hence
. Hence  and \(P'\mathscr {{\,}R{\,}}Q'\). If \(\alpha =\tau \) then either
and \(P'\mathscr {{\,}R{\,}}Q'\). If \(\alpha =\tau \) then either  for some \(P_1'\) with
for some \(P_1'\) with  , or
, or  for some \(P_2'\) with
for some \(P_2'\) with  . I pursue only the first case, as the other follows by symmetry. Here
. I pursue only the first case, as the other follows by symmetry. Here  for some \(Q_1'\) with
for some \(Q_1'\) with  . Thus
. Thus  and
and  .
.
Now let  for \(i=1,2\). Then, for \(i=1,2\), there is a \(Q_i'\) with
for \(i=1,2\). Then, for \(i=1,2\), there is a \(Q_i'\) with  and
and  . Hence
. Hence  and
and  .
.
Thus \(\mathscr {{\,}R{\,}}\) is a coupled simulation. That \(\mathscr {{\,}R{\,}}\) is divergence-preserving follows because  iff \(P_1 {\Uparrow } \vee P_2 {\Uparrow }\). \(\square \)
iff \(P_1 {\Uparrow } \vee P_2 {\Uparrow }\). \(\square \)
Proposition 8
\(\sqsupseteq _{CS}^\varDelta \) is a precongruence for sliding choice.
Proof
Let \(\mathscr {{\,}R{\,}}\) be the smallest relation such that, for any \(P_i\) and \(Q_i\), \(P_i \sqsupseteq _{CS}^\varDelta Q_i\) for \(i=1,2\) implies \(P_i \mathscr {{\,}R{\,}}Q_i\) (\(i=1,2\)) and \((P_1\rhd P_2) \mathscr {{\,}R{\,}}(Q_1\rhd Q_2)\). It suffices to show that \(\mathscr {{\,}R{\,}}\) is a divergence-preserving coupled simulation.
So let \(P_i \sqsupseteq _{CS}^\varDelta Q_i\) for \(i=1,2\) and \((P_1\rhd P_2) \mathop {\longrightarrow }\limits ^{\alpha } P'\). If \(\alpha \in \varSigma \) then \(P_1 \mathop {\longrightarrow }\limits ^{\alpha } P'\), and there exists a \(Q'\) with  and
and  . Hence
. Hence  and \(P'\mathscr {{\,}R{\,}}Q'\). If \(\alpha \mathbin =\tau \) then either \(P'\mathbin =P_2\) or
and \(P'\mathscr {{\,}R{\,}}Q'\). If \(\alpha \mathbin =\tau \) then either \(P'\mathbin =P_2\) or  for some \(P_1'\) with \(P'\mathbin =P_1'\rhd P_2\). In the former case
for some \(P_1'\) with \(P'\mathbin =P_1'\rhd P_2\). In the former case  and \(P_2 \mathscr {{\,}R{\,}}Q_2\). In the latter case
and \(P_2 \mathscr {{\,}R{\,}}Q_2\). In the latter case  for some \(Q_1'\) with
for some \(Q_1'\) with  . Thus
. Thus  and \((P_1'\rhd P_2) \mathscr {{\,}R{\,}}(Q_1'\rhd Q_2)\).
and \((P_1'\rhd P_2) \mathscr {{\,}R{\,}}(Q_1'\rhd Q_2)\).
Now let  for \(i=1,2\). Then there is a \(Q_2'\) with
for \(i=1,2\). Then there is a \(Q_2'\) with  and
and  . By Proposition 2
. By Proposition 2  and by Proposition 1 \(Q_2' \sqsupseteq _{CS}^\varDelta P_1\rhd P_2\).
and by Proposition 1 \(Q_2' \sqsupseteq _{CS}^\varDelta P_1\rhd P_2\).
Thus \(\mathscr {{\,}R{\,}}\) is a coupled simulation. That \(\mathscr {{\,}R{\,}}\) is divergence-preserving follows because \(P_1 \rhd P_2 {\Uparrow }\) iff \(P_1 {\Uparrow } \vee P_2 {\Uparrow }\). \(\square \)
Proposition 9
\(\sqsupseteq _{CS}^\varDelta \) is a precongruence for parallel composition.
Proof
Let \(A\subseteq \varSigma \). Let \(\mathscr {{\,}R{\,}}\) be the smallest relation such that, for any \(P_i\) and \(Q_i\), \(P_i \sqsupseteq _{CS}^\varDelta Q_i\) for \(i=1,2\) implies \((P_1\Vert _A P_2) \mathscr {{\,}R{\,}}(Q_1\Vert _A Q_2)\). It suffices to show that \(\mathscr {{\,}R{\,}}\) is a divergence-preserving coupled simulation.
So let \(P_i \sqsupseteq _{CS}^\varDelta Q_i\) for \(i=1,2\) and \((P_1\Vert _A P_2) \mathop {\longrightarrow }\limits ^{\alpha } P'\). If \(\alpha \notin A\) then \(P_i \mathop {\longrightarrow }\limits ^{\alpha } P_i'\) for \(i=1\) or 2, and \(P'=P_1'\Vert _A P_2'\), where \(P_{3-i}':=P_{3-i}\). Hence there exists a \(Q_i'\) with  and
and  . Let \(Q_{3-i}':=Q_{3-i}\). Then
. Let \(Q_{3-i}':=Q_{3-i}\). Then  and \((P_1'\Vert P'_2)\mathscr {{\,}R{\,}}(Q_1'\Vert Q'_2)\). If \(\alpha \in A\) then
and \((P_1'\Vert P'_2)\mathscr {{\,}R{\,}}(Q_1'\Vert Q'_2)\). If \(\alpha \in A\) then  for \(i=1\) and 2. Hence, for \(i=1,2\),
for \(i=1\) and 2. Hence, for \(i=1,2\),  for some \(Q_i'\) with
for some \(Q_i'\) with  . Thus
. Thus  and \((P_1'\Vert _A P'_2) \mathscr {{\,}R{\,}}(Q_1'\Vert _A Q'_2)\).
and \((P_1'\Vert _A P'_2) \mathscr {{\,}R{\,}}(Q_1'\Vert _A Q'_2)\).
Now let  for \(i=1,2\). Then, for \(i=1,2\), there is a \(Q_i'\) with
for \(i=1,2\). Then, for \(i=1,2\), there is a \(Q_i'\) with  and
and  . Hence
. Hence  and \((Q_1'\Vert _A Q_2') \mathscr {{\,}R{\,}}(P_1\Vert _A P_2)\).
and \((Q_1'\Vert _A Q_2') \mathscr {{\,}R{\,}}(P_1\Vert _A P_2)\).
Thus \(\mathscr {{\,}R{\,}}\) is a coupled simulation. That \(\mathscr {{\,}R{\,}}\) is divergence-preserving follows because \(P_1 \Vert _A P_2 {\Uparrow }\) iff \(P_1 {\Uparrow } \vee P_2 {\Uparrow }\). \(\square \)
Proposition 10
\(\sqsupseteq _{CS}^\varDelta \) is a precongruence for concealment.
Proof
Let \(A\subseteq \varSigma \). Let \(\mathscr {{\,}R{\,}}\) be the smallest relation such that, for any P and Q, \(P \sqsubseteq _{CS}^\varDelta Q\) implies \((P\backslash A) \mathscr {{\,}R{\,}}(Q \backslash A)\). It suffices to show that \(\mathscr {{\,}R{\,}}\) is a divergence-preserving coupled simulation.
So let \(P \sqsubseteq _{CS}^\varDelta Q\) and \(P\backslash A \mathop {\longrightarrow }\limits ^{\alpha } P^*\). Then \(P^*=P'\backslash A\) for some \(P'\) with  , and either \(\beta \in A\) and \(\alpha =\tau \), or \(\beta =\alpha \notin A\). Hence
, and either \(\beta \in A\) and \(\alpha =\tau \), or \(\beta =\alpha \notin A\). Hence  for some \(Q'\) with \(P' \sqsubseteq _{CS}^\varDelta Q'\). Therefore
for some \(Q'\) with \(P' \sqsubseteq _{CS}^\varDelta Q'\). Therefore  and \((P'\backslash A) \mathscr {{\,}R{\,}}(Q'\backslash A)\).
and \((P'\backslash A) \mathscr {{\,}R{\,}}(Q'\backslash A)\).
Now let \(P \sqsubseteq _{CS}^\varDelta Q\). Then there is a \(Q'\) with  and
and  . Hence
. Hence  and
and  .
.
To check that \(\mathscr {{\,}R{\,}}\) is divergence-preserving, suppose \((P\backslash A) {\Uparrow }\). Then there are \(P_i\) and \(\alpha _i \in A\cup \{\tau \}\) for all \(i>0\) such that  . By the first condition of Definition 4, there are \(Q_i\) for all \(i>0\) such that \(P_i \mathscr {{\,}R{\,}}Q_i\) and
. By the first condition of Definition 4, there are \(Q_i\) for all \(i>0\) such that \(P_i \mathscr {{\,}R{\,}}Q_i\) and  . This implies
. This implies  .
.
In case \(\alpha _i \in \varSigma \) for infinitely many i, then for infinitely many i one has  and thus
and thus  . This implies that \((Q\backslash A) {\Uparrow }\).
. This implies that \((Q\backslash A) {\Uparrow }\).
Otherwise there is an \(n>0\) such that \(\alpha _i=\tau \) for all \(i \ge n\). In that case \(P_n {\Uparrow }\) and thus \(Q_n {\Uparrow }\). Hence \((Q_n\backslash A) {\Uparrow }\) and thus \((Q\backslash A) {\Uparrow }\). \(\square \)
Proposition 11
\(\sqsupseteq _{CS}^\varDelta \) is a precongruence for renaming.
Proof
Let \(f:\varSigma \rightarrow \varSigma \). Let \(\mathscr {{\,}R{\,}}\) be the smallest relation such that, for any P and Q, \(P \sqsubseteq _{CS}^\varDelta Q\) implies \(f(P) \mathscr {{\,}R{\,}}\, f(Q)\). It suffices to show that \(\mathscr {{\,}R{\,}}\) is a divergence-preserving coupled simulation.
So let \(P \sqsubseteq _{CS}^\varDelta Q\) and \(f(P) \mathop {\longrightarrow }\limits ^{\alpha } P^*\). Then \(P^*=f(P')\) for some \(P'\) with  and \(f(\beta )=\alpha \). Hence
and \(f(\beta )=\alpha \). Hence  for some \(Q'\) with \(P' \sqsubseteq _{CS}^\varDelta Q'\). Therefore
for some \(Q'\) with \(P' \sqsubseteq _{CS}^\varDelta Q'\). Therefore  and \(f(P') \mathscr {{\,}R{\,}}\, f(Q')\).
and \(f(P') \mathscr {{\,}R{\,}}\, f(Q')\).
Now let \(P \sqsubseteq _{CS}^\varDelta Q\). Then there is a \(Q'\) with  and
and  . Hence
. Hence  and
and  .
.
To check that \(\mathscr {{\,}R{\,}}\) is divergence-preserving, suppose \(f(P) {\Uparrow }\). Then \(P {\Uparrow }\), so \(Q {\Uparrow }\) and \(f(Q) {\Uparrow }\). \(\square \)
Proposition 12
\(\sqsupseteq _{CS}^\varDelta \) is a precongruence for the interrupt operator.
Proof
Let \(\mathscr {{\,}R{\,}}\) be the smallest relation such that, for any \(P_i\) and \(Q_i\), \(P_i \sqsupseteq _{CS}^\varDelta Q_i\) for \(i=1,2\) implies \(P_2 \mathscr {{\,}R{\,}}Q_2\) and  . It suffices to show that \(\mathscr {{\,}R{\,}}\) is a divergence-preserving coupled simulation.
. It suffices to show that \(\mathscr {{\,}R{\,}}\) is a divergence-preserving coupled simulation.
So let \(P_i \sqsupseteq _{CS}^\varDelta Q_i\) for \(i=1,2\) and  . Then either
. Then either  for some \(P_1'\) with
for some \(P_1'\) with  , or \(\alpha =\tau \) and
, or \(\alpha =\tau \) and  for some \(P_2'\) with
for some \(P_2'\) with  , or \(\alpha \in \varSigma \) and
, or \(\alpha \in \varSigma \) and  .
.
In the first case there is a \(Q_1'\) with  and \(P_1' \sqsupseteq _{CS}^\varDelta Q_1'\). It follows that
and \(P_1' \sqsupseteq _{CS}^\varDelta Q_1'\). It follows that  and
and  .
.
In the second case there is a \(Q_2'\) with  and \(P_2' \sqsupseteq _{CS}^\varDelta Q_2'\). It follows that
and \(P_2' \sqsupseteq _{CS}^\varDelta Q_2'\). It follows that  and
and  .
.
In the last case there is a \(Q_2'\) with  and \(P_2' \sqsupseteq _{CS}^\varDelta Q_2'\). It follows that
and \(P_2' \sqsupseteq _{CS}^\varDelta Q_2'\). It follows that  and \(P_2' \mathscr {{\,}R{\,}}Q_2'\).
and \(P_2' \mathscr {{\,}R{\,}}Q_2'\).
Now let  for \(i=1,2\). Then, for \(i=1,2\), there is a \(Q_i'\) with
for \(i=1,2\). Then, for \(i=1,2\), there is a \(Q_i'\) with  and
and  . Hence
. Hence  and
and  .
.
Thus \(\mathscr {{\,}R{\,}}\) is a coupled simulation. That \(\mathscr {{\,}R{\,}}\) is divergence-preserving follows because  iff \(P_1 {\Uparrow } \vee P_2 {\Uparrow }\). \(\square \)
iff \(P_1 {\Uparrow } \vee P_2 {\Uparrow }\). \(\square \)
8 A Complete Axiomatisation of \(\equiv _{CS}^\varDelta \)
A set of equational laws valid for \(\equiv _{CS}^\varDelta \) is presented in Table 3. It includes the laws from Table 2 that are still valid for \(\equiv _{CS}^\varDelta \). I will show that this axiomatisation is sound and complete for \(\equiv _{CS}^\varDelta \) for recursion-free CSP without the interrupt operator. The axioms \(\mathbf {U2}\) and \(\mathbf {U3}\), which are not valid for \(\equiv _{CS}^\varDelta \), played a crucial rôle in reducing CSP expressions with interrupt into normal form. It is not trivial to find valid replacements, and due to lack of space and time I do not tackle this problem here.
The axiom \(\mathbf {H5}\) replaces the fallen axiom \(\mathbf {H2}\), and is due to [17]. Here the result of hiding actions results in a process that cannot be expressed as a normal form built up from \(a \rightarrow \),  and
and  . For this reason, one needs a richer normal form, involving the sliding choice operator. It is given by the context-free grammar
. For this reason, one needs a richer normal form, involving the sliding choice operator. It is given by the context-free grammar

Definition 5
A CSP expression is in head normal form if it is of the form  , with
, with  for \(j\in J\). Here I, J and the \(K_j\) are finite index sets, and the parts between square brackets are optional. Here, although
for \(j\in J\). Here I, J and the \(K_j\) are finite index sets, and the parts between square brackets are optional. Here, although  is undefined, I use
is undefined, I use  to represent P. An expression is in normal form if it has this form and also the subexpressions \(R_i\) and \(R_{kj}\) are in normal form.
to represent P. An expression is in normal form if it has this form and also the subexpressions \(R_i\) and \(R_{kj}\) are in normal form.
A head normal form is saturated if the \(\mathbf {div} \)-summand on the left is present whenever any of the \(R_j\) has a \(\mathbf {div} \)-summand, and for any \(j\mathbin \in J\) and any \(k\mathbin \in K_j\) there is an \(i\mathbin \in I\) with \(a_i\mathbin =a_{kj}\) and \(R_i \mathbin = R_{kj}\).
My proof strategy is to ensure that there are enough axioms to transform any CSP process without recursion and interrupt operators into normal form, and to make these forms saturated; then to equate saturated normal forms that are divergence-preserving coupled simulation equivalent.
Due to the optional presence in head normal forms of a \(\mathbf {div} \)-summand and a sliding choice, I need four variants of the axiom \(\mathbf {H5}\); so far I have not seen a way around this. Likewise, there are \(4\times 4\) variants of the axiom \(\mathbf {P4}\) from Table 2, of which 6 could be suppressed by symmetry (P4–P13). There are also 3 axioms replacing \(\mathbf {P2}\) (P14–P16).
9 Soundness
Since divergence-preserving coupled similarity is a congruence for all CSP operators, to establish the soundness of the axiomatisation of Table 3 it suffices to show the validity w.r.t. \(\equiv _{CS}^\varDelta \) of all axioms. When possible, I show validity w.r.t. strong bisimilarity, which is a strictly finer equivalence.
Definition 6
Two processes are strongly bisimilar [12] if they are related by a binary relation \(\mathscr {{\,}R{\,}}\) on processes such that, for all \(\alpha \in \varSigma \cup \{\tau \}\),
-
if \(P \mathscr {{\,}R{\,}}Q\) and \(P \mathop {\longrightarrow }\limits ^{\alpha } P'\) then there exists a \(Q'\) with \(Q \mathop {\longrightarrow }\limits ^{\alpha } Q'\) and \(P' \mathscr {{\,}R{\,}}Q'\),
-
if \(P \mathscr {{\,}R{\,}}Q\) and \(Q \mathop {\longrightarrow }\limits ^{\alpha } Q'\) then there exists a \(P'\) with \(P \mathop {\longrightarrow }\limits ^{\alpha } P'\) and \(P' \mathscr {{\,}R{\,}}Q'\).
Proposition 13
Axiom \(\mathbf {I1}\) is valid for \(\equiv _{CS}^\varDelta \).
Proof
 is a divergence-preserving coupled simulation. \(\square \)
is a divergence-preserving coupled simulation. \(\square \)
Proposition 14
Axiom \(\mathbf {I2}\) is valid even for strong bisimilarity.
Proof
 is a strong bisimulation. \(\square \)
is a strong bisimulation. \(\square \)
Proposition 15
Axiom \(\mathbf {I3}\) is valid for \(\equiv _{CS}^\varDelta \).
Proof
The relation  is a divergence-preserving coupled simulation. \(\square \)
is a divergence-preserving coupled simulation. \(\square \)
Proposition 16
Axioms E2–4 are valid for strong bisimilarity.
Proof
The relation  is a strong bisimulation. So is
is a strong bisimulation. So is  , as well as
, as well as  . \(\square \)
. \(\square \)
Proposition 17
Axiom \(\mathbf {S1}\) is valid for \(\equiv _{CS}^\varDelta \).
Proof
\(\{(P' \rhd P, P),(P,P' \rhd P) \mid P' \sqsupseteq _{CS}^\varDelta P\} \cup { Id}\) is a divergence-preserving coupled simulation. This follows from Proposition 2. \(\square \)
Proposition 18
Axiom \(\mathbf {S2}\) is valid for \(\equiv _{CS}^\varDelta \).
Proof
\(\{\big ( P \rhd (Q \rhd R) , (P \rhd Q) \rhd R \big ), \big ((P \rhd Q) \rhd R , P \rhd (Q \rhd R) \big ) \mid P,Q,R \, \text{ processes }\} \cup { Id}\) is a divergence-preserving coupled simulation. \(\square \)
Proposition 19
Axiom \(\mathbf {S3}\) is valid for \(\equiv _{CS}^\varDelta \).
Proof
 is a divergence-preserving coupled simulation. \(\square \)
is a divergence-preserving coupled simulation. \(\square \)
Proposition 20
Axiom \(\mathbf {S4}\) is valid for \(\equiv _{CS}^\varDelta \).
Proof
 is a divergence-preserving coupled simulation. Checking this involves Proposition 2. \(\square \)
is a divergence-preserving coupled simulation. Checking this involves Proposition 2. \(\square \)
Proposition 21
Axiom \(\mathbf {S5}\) is valid for \(\equiv _{CS}^\varDelta \).
Proof
The relation  is a divergence-preserving coupled simulation.
is a divergence-preserving coupled simulation.
\(\square \)
Proposition 22
Axiom \(\mathbf {S6}\) is valid for \(\equiv _{CS}^\varDelta \).
Proof
 is a divergence-preserving coupled simulation. \(\square \)
is a divergence-preserving coupled simulation. \(\square \)
Proposition 23
Axiom \(\mathbf {S7}\) is valid for \(\equiv _{CS}^\varDelta \).
Proof
 is a divergence-preserving coupled simulation. \(\square \)
is a divergence-preserving coupled simulation. \(\square \)
Proposition 24
Axiom \(\mathbf {D1}\) is valid for \(\equiv _{CS}^\varDelta \).
Proof
 is a divergence-preserving coupled simulation. \(\square \)
is a divergence-preserving coupled simulation. \(\square \)
Proposition 25
Axiom \(\mathbf {Prune}\) is valid for \(\equiv _{CS}^\varDelta \).
Proof
 is a divergence-preserving coupled simulation. \(\square \)
is a divergence-preserving coupled simulation. \(\square \)
Proposition 26
Axioms P0–1 and P4–10 are valid for strong bisimilarity.
Axioms P11–16 are valid for \(\equiv _{CS}^\varDelta \).
Proof
Straightforward. \(\square \)
Proposition 27
Axioms \(\mathbf {U4}\), \(\mathbf {H1}\), R0–5 and T0–6 are valid for strong bisimilarity. Axioms H5–8 are valid for \(\equiv _{CS}^\varDelta \).
Proof
Straightforward. \(\square \)
Proposition 28
Axiom \(\mathbf {U1}\) is valid for \(\equiv _{CS}^\varDelta \).
Proof
 is a divergence-preserving coupled simulation. \(\square \)
is a divergence-preserving coupled simulation. \(\square \)
10 Completeness
Let \({ Th}\) be the axiomatisation of Table 3.
Proposition 29
For each recursion-free CSP process P without interrupt operators there is a CSP process Q in normal form such that \({ Th}\vdash P=Q\).
Proof
By structural induction on P it suffices to show that for each n-ary CSP operator Op, and all CSP processes \(P_1,...,P_n\) in normal form, also \(Op(P_1,...,P_n)\) can be converted to normal form. This I do with structural induction on the arguments \(P_i\).
-
Let
 or \(\mathbf {div} \). Then P is already in normal form. Take \(Q:=P\).
or \(\mathbf {div} \). Then P is already in normal form. Take \(Q:=P\). -
Let \(P=a \rightarrow P'\). By assumption \(P'\) is in normal form; therefore so is P.
-
Let
 . By assumption \(P_1\) and \(P_2\) are in normal form. So
. By assumption \(P_1\) and \(P_2\) are in normal form. So  with
with  for \(j\in J\cup M\). With Axiom \(\mathbf {S5}\) I may assume that \(J,M\ne \emptyset \). Now Axiom \(\mathbf {S6}\) converts P to normal form.
for \(j\in J\cup M\). With Axiom \(\mathbf {S5}\) I may assume that \(J,M\ne \emptyset \). Now Axiom \(\mathbf {S6}\) converts P to normal form. -
Let
 . By assumption \(P_1\) and \(P_2\) are in normal form. So
. By assumption \(P_1\) and \(P_2\) are in normal form. So  with
with  for \(j\in J\cup M\). With \(\mathbf {S5}\) I may assume that \(J,M\ne \emptyset \). Now Axioms \(\mathbf {S7}\) and \(\mathbf {D1}\) convert P to normal form.
for \(j\in J\cup M\). With \(\mathbf {S5}\) I may assume that \(J,M\ne \emptyset \). Now Axioms \(\mathbf {S7}\) and \(\mathbf {D1}\) convert P to normal form. -
Let \(P=P_1 \rhd P_2\). Axioms S2–4 and \(\mathbf {D1}\) convert P to normal form.
-
Let \(P=P_1 \Vert _A P_2\). Axioms \(\mathbf {P1}\) and P4–16, together with the induction hypothesis, convert P to normal form.
-
Let \(P=P\backslash A\). Axioms \(\mathbf {H1}\) and H5–8, together with the induction hypothesis, convert P to normal form.
-
Let \(P=f(P)\). Axioms R0–5, together with the induction hypothesis, convert P to normal form.
-
Let \(P=P_1 \mathbin {\varTheta \!_A}P_2\). Axioms T0–6, together with the induction hypothesis, convert P to normal form.
Lemma 1
For any CSP expression P in head normal form there exists a saturated CSP expression Q in head normal form.
Proof
Let  . Then P has the form \(S \rhd R\). By Axioms S1–3
. Then P has the form \(S \rhd R\). By Axioms S1–3  . By means of Axioms \(\mathbf {D1}\) and \(\mathbf {S4}\) the subexpression
. By means of Axioms \(\mathbf {D1}\) and \(\mathbf {S4}\) the subexpression  can be brought in the form
can be brought in the form  . The resulting term is saturated. \(\square \)
. The resulting term is saturated. \(\square \)
Definition 7
A CSP expression  is pruned if, for all \(i,h\in I\), \(b_i\mathbin =b_h \wedge P_i \sqsupseteq _{CS}^\varDelta P_h \Rightarrow i=h\).
is pruned if, for all \(i,h\in I\), \(b_i\mathbin =b_h \wedge P_i \sqsupseteq _{CS}^\varDelta P_h \Rightarrow i=h\).
Theorem 1
Let P and Q be recursion-free CSP processes without interrupt operators. Then \(P \equiv _{CS}^\varDelta Q\) iff \({ Th}\vdash P = Q\).
Proof
“\(\Leftarrow \)” is an immediate consequence of the soundness of the axioms of \({ Th}\), and the fact that \(\equiv _{CS}^\varDelta \) is a congruence for all operators of CSP.
“\(\Rightarrow \)”: Let \({ depth}(P)\) be the length of the longest trace of P—well-defined for recursion-free processes P. If \(P \equiv _{CS}^\varDelta Q\) then \({ depth}(P)={ depth}(Q)\). Given \(P \equiv _{CS}^\varDelta Q\), I establish \({ Th}\vdash P = Q\) with induction on \({ depth}(P)\).
By Proposition 29 I may assume, without loss of generality, that P and Q are in normal form. By Lemma 1 I furthermore assume that P and Q are saturated. Let  and
and  with
with  for \(j\mathbin \in J\cup M\), where \(R_i\), \(R_l\) and \(R_{kj}\) are again in normal form.
for \(j\mathbin \in J\cup M\), where \(R_i\), \(R_l\) and \(R_{kj}\) are again in normal form.
Suppose that there are \(i,h\in I\) with \(i\ne h\), \(a_i=a_h\) and \(R_i \sqsupseteq _{CS}^\varDelta R_h\). Then  by Proposition 3. Since
by Proposition 3. Since  , the induction hypothesis yields
, the induction hypothesis yields  . Hence Axiom \(\mathbf {Prune}\) allows me to prune the summand \(a_i \rightarrow R_i\) from
. Hence Axiom \(\mathbf {Prune}\) allows me to prune the summand \(a_i \rightarrow R_i\) from  . Doing this repeatedly makes
. Doing this repeatedly makes  pruned. By the same reasoning I may assume that
pruned. By the same reasoning I may assume that  is pruned.
is pruned.
Since \(P{\Uparrow } \Leftrightarrow Q{\Uparrow }\) and P and Q are saturated, P has the \(\mathbf {div} \)-summand iff Q does. I now define a function \(f:I\rightarrow L\) such that \(a_{f(i)}=a_i\) and \(R_i \sqsupseteq _{CS}^\varDelta R_{f(i)}\) for all \(i \in I\).
Let \(i \in I\). Since \(P \mathop {\longrightarrow }\limits ^{a_i} R_i\), by Definition 4  for some \(Q'\) with
for some \(Q'\) with  . Hence either there is an \(l\in L\) such that \(a_l=a_i\) and
. Hence either there is an \(l\in L\) such that \(a_l=a_i\) and  , or there is a \(j\in M\) and \(k\in K_j\) such that \(a_{kj}=a_i\) and
, or there is a \(j\in M\) and \(k\in K_j\) such that \(a_{kj}=a_i\) and  . Since P is saturated, the first of these alternatives must apply. By Proposition 2
. Since P is saturated, the first of these alternatives must apply. By Proposition 2  and by Proposition 1 \(R_i \sqsupseteq _{CS}^\varDelta R_l\). Take \(f(i):=l\).
and by Proposition 1 \(R_i \sqsupseteq _{CS}^\varDelta R_l\). Take \(f(i):=l\).
By the same reasoning there is a function \(g:L\rightarrow I\) such that \(a_{g(l)}=a_l\) and  for all \(l \in L\). Since
for all \(l \in L\). Since  and
and  are pruned, there are no different \(i,h \in I\) (or in L) with \(a_i=a_h\) and \(R_i \sqsupseteq _{CS}^\varDelta R_h\). Hence the functions f and g must be inverses of each other. It follows that
are pruned, there are no different \(i,h \in I\) (or in L) with \(a_i=a_h\) and \(R_i \sqsupseteq _{CS}^\varDelta R_h\). Hence the functions f and g must be inverses of each other. It follows that  with \(R_i \equiv _{CS}^\varDelta R_{f(i)}\) for all \(i \in I\). By induction \({ Th}\vdash R_i = R_{f(i)}\) for all \(i\in I\).
with \(R_i \equiv _{CS}^\varDelta R_{f(i)}\) for all \(i \in I\). By induction \({ Th}\vdash R_i = R_{f(i)}\) for all \(i\in I\).
So in the special case that \(I=M=\emptyset \) I obtain \({ Th}\vdash P = Q\). (*)
Next consider the case \(J=\emptyset \) but \(M \ne \emptyset \). Let \(j \in M\). Since  , there is a \(P'\) with
, there is a \(P'\) with  and
and  . Moreover, there is a \(P''\) with
. Moreover, there is a \(P''\) with  and
and  . Since \(J=\emptyset \), \(P''=P'=P\), so \(P \equiv _{CS}^\varDelta R_j\). By (*) above \({ Th}\vdash P \mathbin = R_j\). This holds for all \(j \in J\), so by Axiom \(\mathbf {I1}\)
. Since \(J=\emptyset \), \(P''=P'=P\), so \(P \equiv _{CS}^\varDelta R_j\). By (*) above \({ Th}\vdash P \mathbin = R_j\). This holds for all \(j \in J\), so by Axiom \(\mathbf {I1}\)  . By Axiom \(\mathbf {S1}\) one obtains \({ Th}\vdash P=Q\).
. By Axiom \(\mathbf {S1}\) one obtains \({ Th}\vdash P=Q\).
The same reasoning applies when \(M\mathbin =\emptyset \) but \(J\mathbin {\ne }\emptyset \). So henceforth I assume \(J,M \mathbin {\ne }\emptyset \). I now define a function \(h\mathop {:}J\mathbin \rightarrow M\) with \({ Th}\mathbin \vdash R_j \mathbin =R_{h(j)}\) for all \(j \mathbin \in J\).
Let \(j \in J\). Since  , by Definition 4
, by Definition 4  for some \(Q'\) with
for some \(Q'\) with  , and
, and  for some \(Q''\) with
for some \(Q''\) with  . There must be an \(m\in M\) with
. There must be an \(m\in M\) with  . By Definition 4
. By Definition 4  for some \(R'\) with
for some \(R'\) with  , and
, and  for some \(R''\) with
for some \(R''\) with  . By the shape of \(R_j\) one has \(R''=R'=R_j\), so \(R_j \equiv _{CS}^\varDelta R_m\). By (*) above \({ Th}\vdash R_j = R_m\). Take \(h(j):=m\).
. By the shape of \(R_j\) one has \(R''=R'=R_j\), so \(R_j \equiv _{CS}^\varDelta R_m\). By (*) above \({ Th}\vdash R_j = R_m\). Take \(h(j):=m\).
By the same reasoning there is a function \(e\mathop :M\rightarrow J\) with \({ Th}\mathbin \vdash R_m \mathbin =R_{e(m)}\) for all \(m \mathbin \in M\). Using Axioms I1–3 one obtains \({ Th}\vdash P=Q\). \(\square \)
11 Conclusion
This paper contributed a new model of CSP, presented as a semantic equivalence on labelled transition systems that is a congruence for the operators of CSP. It is the finest I could find that allows a complete equational axiomatisation for closed recursion-free CSP processes that fits within the existing syntax of the language. For \(\tau \)-free system, my model coincides with strong bisimilarity, but in matching internal transitions it is less pedantic than weak bisimilarity.
It is left for future work to show that recursion is treated well in this model, and also to extend my complete axiomatisation with the interrupt operator of Roscoe [15, 17].
An annoying feature of my complete axiomatisation is the enormous collections of heavy-duty axioms needed to bring parallel compositions of CSP processes in head normal form. These are based on the expansion law of Milner [12], but a multitude of them is needed due to the optional presence of divergence-summands and sliding choices in head normal forms. In the process algebra ACP the expansion law could be avoided through the addition of two auxiliary operators: the left merge and the communication merge [3]. Unfortunately, failures-divergences equivalence fails to be a congruence for the left-merge, and the same problems exists for any other models of CSP [8, Sect. 3.2.1]. In [1] an alternative left-merge is proposed, for which failures-divergences equivalence, and also \(\equiv _{CS}^\varDelta \), is a congruence. It might be used to eliminate the expansion law \(\mathbf {P4}\) from the axiomatisation of Table 2. Unfortunately, the axiom that splits a parallel composition between a left-, right- and communication merge (Axiom CM1 in [3]), although valid in the failures-divergences model, is not valid for \(\equiv _{CS}^\varDelta \). This leaves the question of how to better manage the axiomatisation of parallel composition entirely open.
References
Aceto, L., Ingólfsdóttir, A.: A theory of testing for ACP. In: Baeten, J.C.M., Groote, J.F. (eds.) CONCUR 1991. LNCS, vol. 527, pp. 78–95. Springer, Heidelberg (1991). doi:10.1007/3-540-54430-5_82
Bergstra, J.A., Klop, J.W., Olderog, E.-R.: Failures withoutchaos: a new process semantics for fair abstraction. In: Wirsing, M. (ed.) Formal Description of Programming Concepts - III, Proceedings of the 3th IFIP WG 2.2 working conference, Ebberup 1986, North-Holland, Amsterdam, pp. 77–103 (1987)
Bergstra, J.A., Klop, J.W.: Process algebra for synchronous communication. Inform. Control 60, 109–137 (1984). doi:10.1016/S0019-9958(84)80025-X
Brookes, S.D., Hoare, C.A.R., Roscoe, A.W.: A theory of communicating sequential processes. J. ACM 31(3), 560–599 (1984). doi:10.1145/828.833
Brookes, S.D., Roscoe, A.W.: An improved failures model for communicating processes. In: Brookes, S.D., Roscoe, A.W., Winskel, G. (eds.) CONCURRENCY 1984. LNCS, vol. 197, pp. 281–305. Springer, Heidelberg (1985). doi:10.1007/3-540-15670-4_14
De Nicola, R.: Two complete Axiom systems for a theory of communicating sequential processes. Inf. Control 64(1–3), 136–172 (1985). doi:10.1016/S0019-9958(85)80048-6
Glabbeek, R.J.: The linear time — branching time spectrum II. In: Best, E. (ed.) CONCUR 1993. LNCS, vol. 715, pp. 66–81. Springer, Heidelberg (1993). doi:10.1007/3-540-57208-2_6
van Glabbeek, R.J., Vaandrager, F.W.: Modular specification of process algebras. Theor. Comput. Sci. 113(2), 293–348 (1993). doi:10.1016/0304-3975(93)90006-F
Groote, J.F., Vaandrager, F.W.: Structured operational semantics and bisimulation as a congruence. Inf. Comput. 100(2), 202–260 (1992). doi:10.1016/0890-5401(92)90013-6
Hoare, C.A.R.: Communicating sequential processes. Commun. ACM 21(8), 666–677 (1978). doi:10.1145/359576.359585
Hoare, C.A.R.: Communicating Sequential Processes. Prentice-Hall, Upper Saddle River (1985)
Milner, R.: Operational and algebraic semantics of concurrent processes. In: van Leeuwen, J. (ed.) Handbook of Theoretical Computer Science, Chap. 19, pp. 1201–1242. Elsevier Science Publishers B.V., North-Holland (1990). Alternatively see Communication and Concurrency. Prentice-Hall (1989), of which an earlier version appeared as A Calculus of Communicating Systems. LNCS, vol. 92. Springer (1980)
Olderog, E.-R., Hoare, C.A.R.: Specification-oriented semantics for communicating processes. Acta Informatica 23, 9–66 (1986). doi:10.1007/BF00268075
Parrow, J., Sjödin, P.: Multiway synchronization verified with coupled simulation. In: Cleaveland, W.R. (ed.) CONCUR 1992. LNCS, vol. 630, pp. 518–533. Springer Berlin Heidelberg, Berlin, Heidelberg (1992). doi:10.1007/BFb0084813
Roscoe, A.W.: The Theory and Practice of Concurrency. Prentice-Hall, Upper Saddle River (1997). http://www.comlab.ox.ac.uk/bill.roscoe/publications/68b.pdf.
Roscoe, A.W.: Revivals, stuckness and the hierarchy of CSP models. J. Logic Algebraic Program. 78(3), 163–190 (2009). doi:10.1016/j.jlap.2008.10.002
Roscoe, A.W.: Understanding Concurrent Systems. Springer, London (2010). doi:10.1007/978-1-84882-258-0
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
van Glabbeek, R. (2017). A Branching Time Model of CSP. In: Gibson-Robinson, T., Hopcroft, P., Lazić, R. (eds) Concurrency, Security, and Puzzles. Lecture Notes in Computer Science(), vol 10160. Springer, Cham. https://doi.org/10.1007/978-3-319-51046-0_14
Download citation
DOI: https://doi.org/10.1007/978-3-319-51046-0_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-51045-3
Online ISBN: 978-3-319-51046-0
eBook Packages: Computer ScienceComputer Science (R0)





 ) and sequential composition (;),
) and sequential composition (;),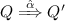 and
and  and
and  or
or  . By assumption
. By assumption  with
with  for
for  . By assumption
. By assumption  with
with  for
for