Abstract
Error detection, localization and correction are time-intensive tasks in software development, but crucial to deliver functionally correct products. Thus, automated approaches to these tasks have been intensively studied for standard software systems. For model-based software systems, the situation is different. While error detection is still well-studied, error localization and correction is a less-studied domain. In this paper, we examine error localization and correction for models of service compositions. Based on formal definitions of error and correction in this context, we show that the classical approach of error localization and correction, i.e. first determining a set of suspicious statements and then proposing changes to these statements, is ineffective in our context. In fact, it lessens the chance to succeed in finding a correction at all.
In this paper, we introduce correction proposal as a novel approach on error correction in service compositions integrating error localization and correction in one combined step. In addition, we provide an algorithm to compute such correction proposals automatically.
This work was partially supported by the German Research Foundation (DFG) within the Collaborative Research Centre “On-The-Fly Computing” (SFB 901).
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
In modern software development, Service-Oriented Architectures (SOA) emphasize the construction of software out of existing services to facilitate the construction of large software system. Such software systems then consist of service calls, which are assembled to contribute to a specific task, using standard operators from workflow construction like sequential composition, decisions and repetitions. A very important assumption in the SOA setting is that all information, which is available about a single service, is its interface, i.e. its input and output variables and its pre- and postcondition. SOA favor a model-based development because at design time, only a model of the service composition under construction is developed.
Debugging, i.e. the detection, localization and correction of faults, is one of the most important tasks to deliver functionally correct products. While these tasks are well-studied for standard software systems (and especially imperative programs), the situation is different for models of service compositions.
Models of software in general typically abstract from details of the final systems, which facilitates error detection in terms of verification, leading to the existence of a broad range of verification approaches for models of software (and of services), e.g. [10, 11, 22].
In contrast, error localization becomes more difficult for models of service compositions, because most standard approaches for standard software systems cannot be applied to models of software. The reason is that almost all error localization techniques for standard software rely on the availability of a larger number of test cases or the ability to executed the system under consideration at will. Techniques like Delta Debugging [5, 25,26,27], Tarantula [13], Pinpoint [3] and AMPLE [7] inspect test cases and compare, for instance, how often a statement is executed in a failing and how often in a successful test cases. Slicing [17, 24, 28] and trace formula approaches to error localization [4, 9, 14,15,16, 19], which encode single executions of the programs, examine dependence information between single statements to find errors. Unfortunately, models of software usually fail to provide a larger number of test cases and – being models and not software – cannot be executed arbitrarily. For a detailed discussion, see [18].
Similarly, for standard software, several effective error correction approaches exist (see [20] for a detailed survey). However, most of them make assumption about their domain of application not valid for models of software, and service compositions in particular (cf. Section 2).
Providing effective error localization and correction methods for models of service composition remains an open challenge. In this paper, we provide a novel and formally rigorous approach that combines the computation of error localization and correction in one step. As we will argue, the standard approach to error localization and correction, i.e. the computation of suspicious statements, followed by attempts to correct the errors within these statements, appears to be unrewarding for models of service composition in general.
Organization of the Paper. We present our definition of service compositions in 2. In 3, we formally define error localization and correction. Our automated approach to the computation of corrections is presented in Sect. 4. Section 5 discusses why both error localization and correction need to be combined into a single step for service compositions. We conclude the paper with discussion and future work in Sect. 6.
2 Services and Service Compositions
In this section, we introduce service compositions and their formal semantics. Service compositions consist of single services assembled together to finally assure a given postcondition for the outputs. While we still use standard concepts of workflow modeling like sequential composition, decisions and repetitions, we use a textual representation inspired by service effect specifications (SEFFs) [2] to denote service compositions. Various other graphical and structural notations, for instance, WS-BPEL [21], exist.
In the following, we associate each service and service composition with a domain \(\mathsf {D}=(\mathcal {T}_\mathsf {D},\mathcal {P}_\mathsf {D},\mathcal {R}_\mathsf {D})\), which consists of a set \(\mathcal {T}_\mathsf {D}\) of types, a set \(\mathcal {P}_\mathsf {D}\) of predicates and a set \(\mathcal {R}_\mathsf {D}\) of rules to reason within the domain. In our context, predicates are functions \(p:\bigotimes _{i \in I} T_i \rightarrow \mathbb {B}\) where \(\mathbb {B}= \{ true , false \}\), I is a finite index set and \(T_i\) denotes a type for all \(i \in I\). The set \(\mathcal {P}_\mathsf {D}\) of a domain must always satisfy \({\bigcup _{p\in \mathcal {P}_\mathsf {D}} \mathsf {use}_\mathcal {T}(p)\subseteq \mathcal {T}_\mathsf {D}}\), where \(\mathsf {use}_\mathcal {T}(p)\) denotes the set \(\{T_i \mid i \in I\}\) of all types occurring in the specification of predicate p.
Service providers offer services in a service market. A service market \(\mathsf {SM(D)}\) on a domain \(\mathsf {D}\) is a set of services, which operate in \(\mathsf {D}\).
Definition 1
(Service Composition). Let \(\mathsf {D}=(\mathcal {T}_\mathsf {D},\mathcal {P}_\mathsf {D},\mathcal {R}_\mathsf {D})\) be an abstract domain. The set of all service compositions \(\mathcal {SC}\) is given by the following grammar in Backus-Naur-form:

where \(m,n\in \mathbb {N}\), \( B \in \mathcal {P}_\mathsf {D}\), \(\ell \) is a label, \(T_1, \cdots , T_n \in \mathcal {T}_\mathsf {D}\) and \(\mathsf {S}\) has m input and n output variables.
In the following, \(\mathsf {def}(\mathsf {SC})\) denotes the set of variables assigned to in a service composition \(\mathsf {SC}\). Each statement \( st \) of a service composition has a special label \(\ell \) in order to identify the statement. As in Definition 1, we write \([ st ]^\ell \) if \(\ell \) is the label of \( st \). We assume that different statements have different labels and use natural numbers as labels in the following. If a service composition \(\mathsf {SC}\) is not in this form, we can rename all occurring statements by traversing the control-flow graph s.t. \(\mathsf {SC}\) complies to this criterion.
Figure 1 shows a simple service composition example. The input to the service composition is the painter \( painter \) and a painting \( painting \). The aim of the composition is to frame the painting and then, to sell the resulting image at the highest price possible. As advertising is costly, we assume that the highest price with an unknown artist is achieved only if the image is not advertised at all. In contrast, if the artist is famous, the highest price is achieved if the image is advertised before. The output of the service composition is the money gained ( ).
).
A service composition calls a service according to its specification, i.e. its name, its input and output variables as well as its pre- and postconditions (also called effects).Footnote 1 While this information is not part of our syntax, we annotated Fig. 1 accordingly for the convenience of the reader.
Formally, the domain of our example comprises the types \( Painting \), \( Image \), \( Money \), \( Gain \) and the predicates  and
and  . In addition, we assume the following rules to be known:
. In addition, we assume the following rules to be known:

In its current state, however, the service composition is faulty. The condition in the if-statement leads to a call of service \(\mathsf {advertise}\) when the painter is not well-known and not – as intended – when the painter is famous.
Definition 2
(Service). Let \(\mathsf {D}=(\mathcal {T}_\mathsf {D},\mathcal {P}_\mathsf {D},\mathcal {R}_\mathsf {D})\) be a domain. A service specification (or short, service) consists of a name together with an interface. An interface \(\mathrm {I}\) over the domain \(\mathsf {D}\) is a tuple \(\mathrm {I}_{} = (\mathsf {In}_{}, \mathsf {Out}_{}, \mathsf {pre}_{}, \mathsf {post}_{})\) such that
-
\(\mathsf {In}\), \(\mathsf {Out}\) are sets of typed input and output variables such that \(\mathsf {In}\cap \mathsf {Out}= \emptyset \), \(\mathsf {use}_\mathcal {T}(\mathsf {In})\subseteq \mathcal {T}_\mathsf {D}\) and \(\mathsf {use}_\mathcal {T}(\mathsf {Out})\subseteq \mathcal {T}_\mathsf {D}\),
-
and pre and post are logical formulas build over the predicates in \(\mathsf {D}\) using \(\lnot ,\vee ,\wedge \) and are called the pre- and postcondition of the service, respectively. We have \(\mathsf {var}(\mathsf {pre}) \subseteq \mathsf {In}\) and \(\mathsf {var}(\mathsf {post}) \subseteq \mathsf {In}\cup \mathsf {Out}\).
In addition, we assume that services do not modify their input variables, i.e. if the precondition holds before a service call, then it also holds afterwards.
If a service \(\mathsf {S}\) changes its inputs, we replace every call  with two assignments service
with two assignments service  such that the actual input variables are not changed.
such that the actual input variables are not changed.
We write \(\mathsf {Out}_\mathsf {S}\), \(\mathsf {In}_\mathsf {S}\), \(\mathsf {pre}_\mathsf {S}\), \(\mathsf {post}_\mathsf {S}\) for the components of a service \(\mathsf {S}\). In the following, we say that a service with interface \(\mathrm {I}_{1} = (\mathsf {In}_{1}, \mathsf {Out}_{1}, \mathsf {pre}_{1}, \mathsf {post}_{1})\) refines a service with interface \(\mathrm {I}_{2} = (\mathsf {In}_{2}, \mathsf {Out}_{2}, \mathsf {pre}_{2}, \mathsf {post}_{2})\), denoted by \(\mathrm {I}_1 \sqsubseteq \mathrm {I}_2\), if \(In_1 \subseteq In_2\), \(Out_1 \supseteq Out_2\) and additionally, \(\mathsf {pre}_2 \Rightarrow \mathsf {pre}_1\) and \(\mathsf {post}_1 \Rightarrow \mathsf {post}_2\).
Remark 1
From a logical perspective, services are implications because they do not modify their input variables, i.e. services guarantee that whenever the precondition holds, the postcondition can be established for the output variables.
Remark 2
Note that Definition 2 can be generalized to service compositions immediately, as from an abstract perspective, service compositions can be considered services themselves. For instance, the service composition in Fig. 1 has the input variables  and
and  , the output variables
, the output variables  , the precondition \( true \) and the postcondition
, the precondition \( true \) and the postcondition  .
.
Strongest Postcondition Semantics. In this section, we define a partial-correctness strongest postcondition semantics for service compositions [1, 8]. Partial correctness here refers to that we do not consider termination as correctness criterion. W.l.o.g., we assume all service compositions to be in single static assignment form (SSA)Footnote 2.
In addition, we assume loops to be annotated with invariants. We consider this assumption practically feasible. Even if not every loop is annotated with an invariant by its developer in practice, various existing automated invariant generation methods can be applied to overcome this (e.g. [12]).
Strongest postconditions for service compositions and for programs mainly differ in the treatment of service calls. The postcondition of a service does not uniquely determine the values of outputs. Due to SSA form, services never change values of variables (especially not the inputs of the service), but only make assignments to previously unused, fresh variables. Therefore, all properties, which hold before a certain statement, also hold afterwards. Note that in a service call \((u_1, \cdots , u_n):=S(v_1, \cdots , v_m)\), the inputs and outputs are thus disjoint, i.e., \(\{u_1, \cdots , u_n\} \cap \{v_1, \cdots , v_m\} = \emptyset \). In the following, we write \(\bar{x} = (x_1, \cdots , x_n)\) for a tuple of variables. The  -semantics of service calls is
-semantics of service calls is

Strongest postcondition definitions for the remaining cases can be found in Fig. 2. Please note that we abstract the loop by its invariant and therefore, only know that the invariant holds at the end of the loop and the loop predicate does not. Due to variable renaming in SSA form, we need to rename the variables occurring in the invariant and in the predicate of the loop to the variable names introduced by the transformation to SSA form (variable names of join-nodes). For branches, it suffices to treat join-nodes as special service calls, which assign the correct value to variables occurring in both branches.
3 Errors and Corrections
In this section, we discuss all three steps of debugging of service compositions. First, we shortly present how to detect errors in service compositions using verification. Second, we formally define the types of errors, which we consider here. Finally, we define corrections for service compositions.
Please note that we still only consider services compositions in SSA form. Services are in general well-tested pieces of code, thus, we assume that single services are correct, i.e. services used in a service compositions always correctly implement their interface. Moreover, we assume that all loops are annotated with loop invariants capturing the complete loop behavior. In Sect. 4, we shortly discuss how to correct faulty loops.
Correct Service Compositions. Service compositions are specified using interfaces (cf. Definition 2), where pre- and postconditions describe the expected behavior in terms of predicates over input and output variables. Intuitively, a service composition is correct if the output satisfies the postcondition whenever the input meets the precondition. Formally, we say that a service composition is correct, if it can be proven (for instance, using the approach in [23]), that the service compositions complies to its interface. Otherwise, we call the service composition faulty. If we apply [23] to our example (Fig. 1), we see that the service composition fails to establish the precondition of the service \(\mathsf {sellAtPrice}\).
Error and Correction. We restrict ourselves to the localization and correction of errors, which can be detected as follows:
-
1.
the correctness requirement is not met, i.e., when started in a state satisfying \(\mathsf {pre}_{\mathsf {SC}}\) we might reach a state outside \(\mathsf {post}_{\mathsf {SC}}\),
-
2.
the execution of a service composition blocks at some service call because the precondition of the service is not satisfied, and
-
3.
during an execution a loop is reached but the loop invariant does not hold.
In Definiton 3, the first case corresponds to a global error, whereas the second and the third case are subsumed by local errors. The first type of error mainly occurs if the service composition does not make enough progress towards the postcondition, whereas the second type of error is mainly caused by calling the wrong service, which invalidates the precondition of the next service or the invariant of a succeeding loop.
Definition 3
(Error). Let \(\mathsf {SC}\) be a service composition, \(\ell \) one of its labels, and \((\mathsf {pre},\mathsf {post})\) the requirement on \(\mathsf {SC}\). An error in \(\mathsf {SC}\) occurs at \(\ell \) if one of the following conditions hold:
-
1.
\(\ell = {\ell _\bot }\) and
 (a global error),
(a global error), -
2.
\(\ell \notin \{{\ell _\bot }, {\ell _\top }\}\) and \(\ell \) is not inside an if or while statement, and
 (a local error).
(a local error).
Please note that \(\mathsf {pre}_\ell \) denotes the precondition of a statement \(\ell \). If the statement is a service call \(\mathsf {S}\), it holds \(\mathsf {pre}_\ell =\mathsf {pre}_\mathsf {S}\). We use the invariant of a loop as its precondition and for all remaining cases, the precondition is \( true \).
Our example has a local error as it fails to establish the precondition of the service at label 4.
A correction serves as a replacement of a part of the service composition. Therefore, a correction consists of two labels, which specify the part the correction might eventually replace and an interface, which specifies the service, which should be inserted between the two labels.
Definition 4
(Correction). Let \(\mathsf {SC}\) be a service composition. A correction  for \(\mathsf {SC}\) is a triple \((\ell ,\bar{u}:=\mathsf {S}(\bar{v}),\ell '))\) such that \(\mathsf {SC}\) can be divided into \({ \mathsf {SC}_{\rightarrow _\ell }; {\mathsf {SC}';\mathsf {SC}_{\ell '}}}\). Applying
for \(\mathsf {SC}\) is a triple \((\ell ,\bar{u}:=\mathsf {S}(\bar{v}),\ell '))\) such that \(\mathsf {SC}\) can be divided into \({ \mathsf {SC}_{\rightarrow _\ell }; {\mathsf {SC}';\mathsf {SC}_{\ell '}}}\). Applying  to \(\mathsf {SC}\) (by replacing \(\mathsf {SC}'\)) yields
to \(\mathsf {SC}\) (by replacing \(\mathsf {SC}'\)) yields 
The key difference between imperative programs and service compositions w.r.t. error correction is now the fact that not all services we like to use in a correction are available in the service market. It is essential to note that markets cannot and do not offer every possible service operating in the domain. Hence, we call a correction realizable in a service market \(\mathsf {SM}{(\mathsf {D})}\) if every service \(\mathsf {S}\) occurring in the correction, is contained in \(\mathsf {SM}{(\mathsf {D})}\). Error localization for service compositions can thus only propose corrections, which afterwards needs to be checked for their realizability.
4 Correction Proposals
In this section, we present an automatic approach to compute corrections for service compositions. The aim is to provide small correction proposals first. Small here refers to the number of statements, which are replaced by the correction. Nonetheless, the easiest correction of a faulty service composition with requirement \((\mathsf {pre},\mathsf {post})\) is to replace the entire composition by a single service call of a service \(\mathsf {S}\) with \(\mathsf {pre}_\mathsf {S}= \mathsf {pre}\) and \(\mathsf {post}_\mathsf {S}= \mathsf {post}\). Quite likely this is not a realizable correction (since otherwise one would not have bothered to construct the service composition at first hand).
Corrections for Global Errors. We assume service compositions to be in SSA form. Thus, we have at most one assignment to every output variable of the service composition. Most likely, this output is determined at the end of the service composition (otherwise, the statements behind that can be discarded because they do not affect the output anymore). Hence, we start the correction of global errors, i.e. when the service composition in its entirety has failed to establish the postcondition, at the end of the service composition.
The key to the correction of global errors is to determine the functionally missing in the current service composition. We specify the missing part in terms of so-called bridges.
Definition 5
(Bridge). A bridge between two logic formulas \(\varphi \) and \(\psi \) is a formula \(\rho \) such that \(\varphi \wedge \rho \Rightarrow \psi \) holds. The set of bridges between \(\varphi \) and \(\psi \) is defined as  .
.
As an example: \(\varphi := p(x)\), \(\psi := p(x) \wedge q(z)\). Then \(\psi \setminus \varphi \) contains for instance \( false , q(z)\) and \(\psi \). We use the notation \(\setminus \) here since a bridge can easily be computed as set difference when both \(\varphi \) and \(\psi \) are given as conjunctions (sets) of literals – as for our strongest postconditions. As the  -semantics does not introduce quantifiers, it is sufficient to consider propositional logic formulae \(\varphi \) and \(\psi \).
-semantics does not introduce quantifiers, it is sufficient to consider propositional logic formulae \(\varphi \) and \(\psi \).
Proposition 1
For arbitrary formulae \(\varphi \) and \(\psi \), it holds that \(\psi \setminus \varphi \) is infinite.
Proof
The set always contains \( false \) as \(\varphi \wedge ~ false \equiv false \) and \( false \) implies everything. The set is non-finite as \( false \) can be expressed with infinitely many formulae.
While there always exists a bridge, there does not necessarily exist a service, which has the bridge as postcondition. Thus, the corrections which we propose below, might not be realizable.
Computing Corrections for Global Errors. Corrections for global errors need to range from some label \(\ell \) of the service composition (not contained in a branch or a loop) to the end of the service composition denoted by \({\ell _\bot }\). Thus, we need to construct a bridge between the strongest postcondition, which can be guaranteed at \(\ell \) and the postcondition \(\mathsf {post}\).
The correction from \(\ell \) to \({\ell _\bot }\) thus proposed to add a service call using the service  of the following form
of the following form  where
where
-
\(\{o_1, \cdots , o_l\} = \mathsf {Out}\setminus (\mathsf {def}(\mathsf {SC}_{\rightarrow \ell }) \cup \mathsf {In}_{\mathsf {SC}})\),
-
\(\{x_1, \cdots , x_k\} = \mathsf {def}(\mathsf {SC}_{\rightarrow \ell }) \cup \mathsf {In}_{\mathsf {SC}}\),
-
 and
and -

and  . The bridge, which we take here, needs to be chosen such that \(\mathsf {var}(\rho ) \subseteq \{o_1, \cdots , o_l,x_1, \cdots , x_k\}\). One candidate is \(\mathsf {post}\) itself. It is, however, preferable to use smaller (in terms of variables used) \(\rho \)’s since this increases the chances of proposing a realizable correction. We do not need to rename the variables of the service calls as the service
. The bridge, which we take here, needs to be chosen such that \(\mathsf {var}(\rho ) \subseteq \{o_1, \cdots , o_l,x_1, \cdots , x_k\}\). One candidate is \(\mathsf {post}\) itself. It is, however, preferable to use smaller (in terms of variables used) \(\rho \)’s since this increases the chances of proposing a realizable correction. We do not need to rename the variables of the service calls as the service  takes the variables defined so far as inputs and must provide all output variables of the service composition.
takes the variables defined so far as inputs and must provide all output variables of the service composition.
Theorem 1
Let \(\mathsf {SC}\) be a service composition with requirement \((\mathsf {pre},\mathsf {post})\) and let \(\mathsf {SC}\) have a global error (and no local errors). Let \(\ell \ne {\ell _\bot }\) be a label of \(\mathsf {SC}\). Then, the correction \((\ell ,\bar{u} := \mathsf {S}(\bar{v}),{\ell _\bot })\), where  , is a refinement of
, is a refinement of  as given above, corrects the error.
as given above, corrects the error.
Proof
We have to prove that \((\ell ,\bar{u}:=S(\bar{v}),{\ell _\bot })\) is a correction, i.e. we have to prove that the service composition
satisfies the postcondition \(\mathsf {post}_{\mathsf {SC}}\) for every input, which satisfies the precondition.
Formally, we thus need to show the following:

-
(A)
First, we show that there does not exist a local error in the corrected service composition:
-
\(\mathsf {SC}_{\rightarrow \ell }\) does not contain a local error by assumption.
-
The following holds:

By definition,
 and the service S refines
and the service S refines  , i.e.
, i.e.  . Thus, it holds that
. Thus, it holds that  , and \(\mathsf {S}\) is applicable and does not block.
, and \(\mathsf {S}\) is applicable and does not block. -
\(\mathsf {SC}_{{\ell _\bot }}\) is the empty program and therefore, cannot contain a local error.
-
-
(B)
Second, we prove that there does not exist a global error. The strongest postcondition of the service call is given by
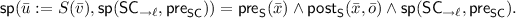
By definition, it holds that
 as the postcondition of the service
as the postcondition of the service  is defined as a bridge between
is defined as a bridge between  and \(\mathsf {post}_{\mathsf {SC}}\). As
and \(\mathsf {post}_{\mathsf {SC}}\). As  , it holds that
, it holds that  .
.The service composition \(\mathsf {SC}_{\ell _\bot }\) denotes the empty program as \({\ell _\bot }\) does not correspond to any program label. Therefore, the following holds:

Thus, the service composition \({\mathsf {SC}_{\rightarrow \ell };{\bar{u}:=S(\bar{v}); \mathsf {SC}_{{\ell _\bot }}}}\) is correct wrt. the sp-semantics and \((\ell ,\bar{u}:=S(\bar{v}),{\ell _\bot }))\) is indeed a correction. \(\square \)
The theorem does not consider realizability of the proposed correction. If the pre- and postcondition of a service composition are incompatible or even \( false \), or the proposed service cannot be found in the market, the proposed correction cannot be applied. Then, another proposal has to be computed and checked for realizability.
Correction of Local Errors. A local error occurs when the precondition of a service (or the invariant of a loop) is not established upon the call of the service (start of the loop). Every local error can be rephrased as a global error in the following way. If \(\ell \) is the location of the local error, we only consider the service composition up to \(\ell \), and use the precondition of \(\ell \) as postcondition of the subcomposition.
Proposition 2
Let \(\mathsf {SC}\) be a service composition with a local error at \(\ell \) and requirement \((\mathsf {pre},\mathsf {post})\). Then the following holds: \(\mathsf {SC}\) has a local error at \(\ell \) iff \(\mathsf {SC}_{\rightarrow \ell }\) has a global error with respect to \((\mathsf {pre},\mathsf {pre}_\ell )\).
Hence, we can reuse the algorithm to compute correction proposals for global errors also for local errors by simply modifying the considered service composition and pre- and postconditions. An alternative correction proposal for local errors is \((\ell ,\bar{u}:=\mathsf {S}(\bar{v}),{{\ell _\bot }})\), where the precondition of \(\mathsf {S}\) is the strongest postcondition of \(\mathsf {SC}_{\rightarrow \ell }\) and the postcondition of \(\mathsf {S}\) is the postcondition of \(\mathsf {SC}\).
We have already seen that our service composition has a local error at label 4. As one correction, we propose to replace the block before 4 (the if-statement) by a new service call. As input, it gets all the variables used so far, i.e.,  ,
,  and
and  . As output variable, it gets
. As output variable, it gets  . Its precondition is
. Its precondition is  and the postcondition is
and the postcondition is  . Thus, We need to check whether this service is available in the service market and if yes, can use it at the place of the if-statement. This correction also leads to an error-free service composition as the strongest postcondition of
. Thus, We need to check whether this service is available in the service market and if yes, can use it at the place of the if-statement. This correction also leads to an error-free service composition as the strongest postcondition of  wrt. \(\mathsf {pre}\) together with the rules of the ontology now imply the overall postcondition \(\mathsf {post}\).
wrt. \(\mathsf {pre}\) together with the rules of the ontology now imply the overall postcondition \(\mathsf {post}\).
Correction of Loops and Branches. We treat loops and branches as a single block in the above approach and do not allow to correct errors, which occur inside of loops and branches. Nevertheless, we can also correct errors in loops and branches using the same approach as above.
Let  be a loop and \( Inv \) its invariant. We say that the loop has a while-global error if
be a loop and \( Inv \) its invariant. We say that the loop has a while-global error if  . We then consider \(S_1\) as a complete service composition with precondition \( Inv \wedge B \) and postcondition \( Inv \) and apply the correction proposal algorithm for global errors.
. We then consider \(S_1\) as a complete service composition with precondition \( Inv \wedge B \) and postcondition \( Inv \) and apply the correction proposal algorithm for global errors.
Similarly, we can correct local errors in loops and branches. We say a loop  has a local error at label \(\ell '\) if
has a local error at label \(\ell '\) if  and
and

Analogously, we say that a branch  has a local error at label \(\ell '\) if either
has a local error at label \(\ell '\) if either  and
and  or
or  and
and  Also for local errors in branches or loops, we first propose corrections in \(\mathsf {S}_1\) and \(\mathsf {S}_2\), respectively, by considering both of them as single service composition and then, applying the algorithm given above. Afterwards, we again treat loops and branches as single blocks and try to replace them with new services.
Also for local errors in branches or loops, we first propose corrections in \(\mathsf {S}_1\) and \(\mathsf {S}_2\), respectively, by considering both of them as single service composition and then, applying the algorithm given above. Afterwards, we again treat loops and branches as single blocks and try to replace them with new services.
5 Discussion
In this section, we discuss why existing error localization methods are not helpful w.r.t. to error correction in service compositions. We start with the following artificial service compositions, which illustrates that considering only a subset of statements (i.e. only a set of suspicious statements) of the service composition in fact lessens the chance to find a realizable correction.

The requirement on this service composition is  using the services \(\mathsf {makeA}\), which has precondition
using the services \(\mathsf {makeA}\), which has precondition  and postcondition
and postcondition  , \(\mathsf {makeB}\), which has precondition
, \(\mathsf {makeB}\), which has precondition  and postcondition
and postcondition  and \(\mathsf {makeD}\), which has precondition
and \(\mathsf {makeD}\), which has precondition  and postcondition
and postcondition  .
.
The local error (precondition of service \(\mathsf {makeD}\) not met) can be corrected in various ways, for example,
-
it can be considered as a missing code problem – the service with precondition
 and postcondition
and postcondition  (whereas both the input and the output variable have type \( C \)) needs to be inserted or
(whereas both the input and the output variable have type \( C \)) needs to be inserted or -
it can be solved by exchanging the service \(\mathsf {makeB}\) with a service with the same precondition, but the postcondition \(\lnot isC(c)\) or
-
it is also possible to replace both the service calls \(\mathsf {makeA}\) and \(\mathsf {makeB}\) by, for example, services with precondition
 and postcondition
and postcondition  and precondition \(\lnot isB(b)\) and postcondition
and precondition \(\lnot isB(b)\) and postcondition  , respectively.
, respectively.
This construction can be repeated arbitrarily often and we do not know, which correction to prefer unless we know the available service markets, and thus, which alternative services exist.
The previous example shows why errors in service compositions can be at any places. The next example shows why reducing the set of statements does not help with error localization. Assume that the requirement on the service composition given below is  .
.

The service \(\mathsf {makeE}\) has the precondition  and the postcondition
and the postcondition  , the service \(\mathsf {makeF}\) has the precondition
, the service \(\mathsf {makeF}\) has the precondition  and the postcondition
and the postcondition  and the service \(\mathsf {makeNotC}\) has precondition
and the service \(\mathsf {makeNotC}\) has precondition  and the postcondition
and the postcondition  . The pre- and postcondition of all other services remain unchanged. For any input, the service composition already guarantees
. The pre- and postcondition of all other services remain unchanged. For any input, the service composition already guarantees  , but not
, but not  . Thus, we could apply slicing to only correct the part of the service composition, which is responsible for the error
. Thus, we could apply slicing to only correct the part of the service composition, which is responsible for the error  , i.e. we only correct the service composition
, i.e. we only correct the service composition  . Nevertheless, this may obliterate the only existing correction. For example, the service composition can be fixed with a service
. Nevertheless, this may obliterate the only existing correction. For example, the service composition can be fixed with a service  , which has the precondition
, which has the precondition  and the desired postcondition
and the desired postcondition  . As the variable f is not in the slice, slicing cannot propose this correction.
. As the variable f is not in the slice, slicing cannot propose this correction.
6 Conclusion
In this paper, we addressed the problem of automated error localization and correction for models of service compositions. We therefore needed to find a way to overcome the lack of executability of single services, which makes most error localization and correction methods for standard software inapplicable. Thus, we proposed correction proposals, which state where and how to modify existing service compositions in terms of alternative services. Correction proposals can be statically computed based on the strongest postcondition semantics of our service compositions and thus, are completely independent from test cases or executability. Hence, the computation of correction proposals is a good way to the localization and correction of errors in model-driven design approaches in general. Moreover, the computation of correction proposals can easily be generalized to every setting, which has a formal semantics in terms of strongest postconditions. Hence, even automated correction of imperative programs might benefit from our approach.
As future work, we want to practically evaluate the effectiveness of correction proposals for existing service markets w.r.t. to the existence of alternative markets. Moreover, we want to examine whether existing approaches to error localization and correction might be reused for more specific classes of errors (for instance, errors caused by a missing negation in conditions of loops or branches). Finally, we want to study the generalization of our approach to software systems.
Notes
- 1.
In WSDL (https://www.w3.org/TR/wsdl), all four components together are called IOPE.
- 2.
Using [6], SSA form can be established for all service compositions.
References
Apt, K.R., Olderog, E.-R.: Verification of Sequential and Concurrent Programs: Graduate Texts in Computer Science, 2nd edn. Springer, Heidelberg (1997)
Becker, S., Koziolek, H., Reussner, R.: The palladio component model for model-driven performance prediction. J. Syst. Softw. 82, 3–22 (2009). Special Issue: Software Performance - Modeling and Analysis
Chen, M.Y., Kiciman, E., Fratkin, E., Fox, A., Brewer, E., Pinpoint: problem determination in large, dynamic internet services. In: International Conference on Dependable Systems and Networks (2002)
Christ, J., Ermis, E., Schäf, M., Wies, T.: Flow-sensitive fault localization. In: Giacobazzi, R., Berdine, J., Mastroeni, I. (eds.) VMCAI 2013. LNCS, vol. 7737, pp. 189–208. Springer, Heidelberg (2013). doi:10.1007/978-3-642-35873-9_13
Cleve, H., Zeller, A.: Locating causes of program failures. In: Proceedings of 27th International Conference on Software Engineering, ICSE 2005. ACM (2005)
Cytron, R., Ferrante, J., Rosen, B.K., Wegman, M.N., Zadeck, F.K.: Efficiently computing static single assignment form and the control dependence graph. ACM Trans. Program. Lang. Syst. 13(4), 451–490 (1991)
Dallmeier, V., Lindig, C., Zeller, A.: Lightweight defect localization for java. In: Black, A.P. (ed.) ECOOP 2005. LNCS, vol. 3586, pp. 528–550. Springer, Heidelberg (2005). doi:10.1007/11531142_23
Dijkstra, E.W., Scholten, C.S.: Predicate Calculus and Program Semantics: Texts and Monographs in Computer Science. Springer, New York (1990)
Ermis, E., Schäf, M., Wies, T.: Error invariants. In: Giannakopoulou, D., Méry, D. (eds.) FM 2012. LNCS, vol. 7436, pp. 187–201. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32759-9_17
Fahrenberg, U., Larsen, K.G., Legay, A.: Model-based verification, optimization, synthesis and performance evaluation of real-time systems. In: Liu, Z., Woodcock, J., Zhu, H. (eds.) Unifying Theories of Programming and Formal Engineering Methods. LNCS, vol. 8050, pp. 67–108. Springer, Heidelberg (2013). doi:10.1007/978-3-642-39721-9_2
Güdemann, M., Poizat, P., Salaün, G., Dumont, A.: VerChor: a framework for verifying choreographies. In: Cortellessa, V., Varró, D. (eds.) FASE 2013. LNCS, vol. 7793, pp. 226–230. Springer, Heidelberg (2013). doi:10.1007/978-3-642-37057-1_16
Gupta, A., Rybalchenko, A.: InvGen: an efficient invariant generator. In: Bouajjani, A., Maler, O. (eds.) CAV 2009. LNCS, vol. 5643, pp. 634–640. Springer, Heidelberg (2009). doi:10.1007/978-3-642-02658-4_48
Jones, J.A., Harrold, M.J.: Empirical evaluation of the tarantula automatic fault-localization technique. In: Proceedings of 20th IEEE/ACM International Conference on Automated Software Engineering, ASE 2005. ACM (2005)
Jose, M., Majumdar, R.: Cause clue clauses: error localization using maximum satisfiability. ACM SIGPLAN Not. 46(6), 437–446 (2011)
Jose, M., Majumdar, R.: Cause clue clauses: error localization using maximum satisfiability. In: Proceedings of 32nd ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2011. ACM (2011)
önighofer, R.K., Bloem, R.: Automated error localization and correction for imperative programs, FMCAD 2011. FMCAD Inc. (2011)
Korel, B., Laski, J.: Dynamic program slicing. Inf. Process. Lett. 29(3), 155–163 (1988)
Krämer, J., Wehrheim, H.: A short survey on using software error localization for service compositions. In: Aiello, M., Johnsen, E.B., Georgievski, I., Dustdar, S. (eds.) Service Oriented and Cloud Computing, ESOCC 2016 (2016). (to appear)
Lamraoui, S.-M., Nakajima, S.: A formula-based approach for automatic fault localization of imperative programs. In: Merz, S., Pang, J. (eds.) ICFEM 2014. LNCS, vol. 8829, pp. 251–266. Springer, Heidelberg (2014). doi:10.1007/978-3-319-11737-9_17
Monperrus, M., Automatic software repair: a bibliography. Technical report hal-01206501, University of Lille (2015)
OASIS. Web Services Business Process Execution Language v2.0. http://docs.oasis-open.org/wsbpel/2.0/OS/wsbpel-v2.0-OS.pdf
Schäfer, W.: Model driven development with mechatronic UML. In: Stapleton, G., Howse, J., Lee, J. (eds.) Diagrams 2008. LNCS (LNAI), vol. 5223, p. 4. Springer, Heidelberg (2008). doi:10.1007/978-3-540-87730-1_3
Walther, S., Wehrheim, H.: Knowledge-based verification of service compositions - an SMT approach. In: Engineering of Complex Computer Systems (ICECCS) (2013)
Weiser, M.: Program slicing. In: Proceedings of 5th International Conference on Software Engineering, ICSE 1981. IEEE Press, Piscataway (1981)
Zeller, A.: Yesterday, my program worked. today, it does not. why? In: Nierstrasz, O., Lemoine, M. (eds.) ESEC/SIGSOFT FSE -1999. LNCS, vol. 1687, pp. 253–267. Springer, Heidelberg (1999). doi:10.1007/3-540-48166-4_16
Zeller, A.: Isolating cause-effect chains from computer programs. In: Proceedings of 10th ACM SIGSOFT Symposium on Foundations of Software Engineering, SIGSOFT 2002/FSE-10. ACM (2002)
Zeller, A., Hildebrandt, R.: Simplifying and isolating failure-inducing input. IEEE Trans. Softw. Eng. 28(2), 183–200 (2002)
Zhang, X., He, H., Gupta, N., Gupta, R.: Experimental evaluation of using dynamic slices for fault location. In: Proceedings of Sixth International Symposium on Automated Analysis-driven Debugging, AADEBUG 2005. ACM (2005)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Krämer, J., Wehrheim, H. (2016). A Formal Approach to Error Localization and Correction in Service Compositions. In: Milazzo, P., Varró, D., Wimmer, M. (eds) Software Technologies: Applications and Foundations. STAF 2016. Lecture Notes in Computer Science(), vol 9946. Springer, Cham. https://doi.org/10.1007/978-3-319-50230-4_35
Download citation
DOI: https://doi.org/10.1007/978-3-319-50230-4_35
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-50229-8
Online ISBN: 978-3-319-50230-4
eBook Packages: Computer ScienceComputer Science (R0)







 (a global error),
(a global error), (a local error).
(a local error). and
and

 and the service S refines
and the service S refines  , i.e.
, i.e.  . Thus, it holds that
. Thus, it holds that  , and
, and 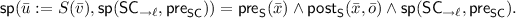
 as the postcondition of the service
as the postcondition of the service  is defined as a bridge between
is defined as a bridge between  and
and  , it holds that
, it holds that  .
.
 and postcondition
and postcondition  (whereas both the input and the output variable have type
(whereas both the input and the output variable have type  and postcondition
and postcondition  and precondition
and precondition  , respectively.
, respectively.