Abstract
Hybrid Communicating Sequential Processes (HCSP) is a powerful formal modeling language for hybrid systems, which is an extension of CSP by introducing differential equations for modeling continuous evolution and interrupts for modeling interaction between continuous and discrete dynamics. In this paper, we investigate the semantic foundation for HCSP from an operational point of view by proposing the notion of approximate bisimulation, which provides an appropriate criterion to characterize the equivalence between HCSP processes with continuous and discrete behaviour. We give an algorithm to determine whether two HCSP processes are approximately bisimilar. In addition, based on which, we propose an approach on how to discretize HCSP, i.e., given an HCSP process A, we construct another HCSP process B which does not contain any continuous dynamics such that A and B are approximately bisimilar with given precisions. This provides a rigorous way to transform a verified control model to a correct program model, which fills the gap in the design of embedded systems.
This work is supported partly by “973 Program” under grant No. 2014CB340701, by NSFC under grants 91418204 and 61502467, by CDZ project CAP (GZ 1023), and by the CAS/SAFEA International Partnership Program for Creative Research Teams.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Embedded Systems (ESs) make use of computer units to control physical processes so that the behavior of the controlled processes meets expected requirements. They have become ubiquitous in our daily life, e.g., automotive, aerospace, consumer electronics, communications, medical, manufacturing and so on. ESs are used to carry out highly complex and often critical functions such as to monitor and control industrial plants, complex transportation equipments, communication infrastructure, etc. The development process of ESs is widely recognized as a highly complex and challenging task. Model-Based Engineering (MBE) is considered as an effective way of developing correct complex ESs, and has been successfully applied in industry [16, 21]. In the framework of MBE, a model of the system to be developed is defined at the beginning; then extensive analysis and verification are conducted based on the model so that errors can be detected and corrected at early stages of design of the system. Afterwards, model transformation techniques are applied to transform abstract formal models into more concrete models, even into source code.
To improve the efficiency and reliability of MBE, it is absolutely necessary to automate the system design process as much as possible. This requires that all models at different abstraction levels have a precise mathematical semantics. Transformation between models at different abstraction levels should preserve semantics, which can be done automatically with tool support.
Thus, the first challenge in model-based formal design of ESs is to have a powerful modelling language which can model all kinds of features of ESs such as communication, synchronization, concurrency, continuous and discrete dynamics and their interaction, real-time, and so on, in an easy way. To address this issue, Hybrid Communicating Sequential Processes (HCSP) was proposed in [14, 36], which is an extension of CSP by introducing differential equations for modeling continuous evolutions and interrupts for modeling interaction between continuous and discrete dynamics. Comparing with other formalisms, e.g., hybrid automata [17], hybrid programs [24], etc., HCSP is more expressive and much easier to be used, as it provides a rich set of constructors. Through which a complicated ES with different behaviours can be easily modeled in a compositional way. The semantic foundation of HCSP has been investigated in the literature, e.g., in He’s original work on HCSP [14], an algebraic semantics of HCSP was given by defining a set of algebraic laws for the constructors of HCSP. Subsequently, a DC-based semantics for HCSP was presented in [36] due to Zhou et al. These two original formal semantics of HCSP are very restrictive and incomplete, for example, it is unclear whether the set of algebraic rules defined in [14] is complete, and super-dense computation and recursion are not well handled in [36]. In [8, 13, 22, 33, 35], the axiomatic, operational, and the DC-based and UTP-based denotational semantics for HCSP are proposed, and the relations among them are discussed. However, regarding operational semantics, just a set of transition rules was proposed in [35]. It is unclear in what sense two HCSP processes are equivalent from an operational point of view, which is the cornerstone of operational semantics, also the basis of refinement theory for a process algebra. So, it absolutely deserves to investigate the semantic foundation of HCSP from an operational point of view.
Another challenge in the model-based formal design of ESs is how to transform higher level abstract models (control models) to lower level program models (algorithm models), even to C code, seamlessly in a rigorous way. Although huge volume of model-based development approaches targeting embedded systems has been proposed and used in industry and academia, e.g., Simulink/Stateflow [1, 2], SCADE [9], Modelica [31], SysML [3], MARTE [28], Ptolemy [10], hybrid automata [17], CHARON [5], HCSP [14, 36], Differential Dynamic Logic [24], and Hybrid Hoare Logic [22], the gap between higher-level control models and lower-level algorithm models still remains.
Approximate bisimulation [12] is a popular method for analyzing and verifying complex hybrid systems. Instead of requiring observational behaviors of two systems to be exactly identical, it allows errors but requires the “distance” between two systems remain bounded by some precisions. In [11], with the use of simulation functions, a characterization of approximate simulation relations between hybrid systems is developed. A new approximate bisimulation relation with two parameters as precisions, which is very similar to the notion defined in this paper, is introduced in [18]. For control systems with inputs, the method for constructing a symbolic model which is approximately bisimilar with the original continuous system is studied in [26]. Moreover, [23] discusses the problem for building an approximately bisimilar symbolic model of a digital control system. Also, there are some works on building symbolic models for networks of control systems [27]. But for all the above works, either discrete dynamics is not considered, or it is assumed to be atomic actions independent of the continuous variables. In [15, 20, 32], the abstraction of hybrid automata is considered, but it is only guaranteed that the abstract system is an approximate simulation of the original system. In [25], a discretization of hybrid programs is presented for a proof-theoretical purpose, i.e., it aims to have a sound and complete axiomatization relative to properties of discrete programs. Differently from all the above works, we aim to have a discretization of HCSP, for which discrete and continuous dynamics, communications, and so on, are entangled with each other tightly, to guarantee that the discretized process has the approximate equivalence with the original process.
The main contributions of this paper include:
-
First of all, we propose the notion of approximate bisimulation, which provides a criterion to characterize in what sense two HCSP processes with differential kinds of behaviours are equivalent from an operational point of view. Based on which, a refinement theory for HCSP could be developed.
-
Then, we show that whether two HCSP processes are approximately bisimilar or not is decidable if all ordinary differential equations (ODEs) occurring in them satisfy globally asymptotical stability (GAS) condition (the definition will be given later). This is achieved by proposing an algorithm to compute an approximate bisimulation relation for the two HCSP processes.
-
Most importantly, we present how to discretize an HCSP process (a control model) by a discrete HCSP process (an algorithm model), and prove they are approximately bisimilar, if the original HCSP process satisfies the GAS condition and is robustly safe with respect to some given precisions.
The rest of this paper is organized as follows: In Sect. 2, we introduce some preliminary notions on dynamical systems. Sect. 3 defines transition systems and the approximate bisimulation relation between transition systems. The syntax and the transition semantics of HCSP, and the approximately bisimilar of HCSP processes are presented in Sect. 4. The discretization of HCSP is presented in Sect. 5. Throughout the paper, and in Sect. 6, a case study on the water tank system [4] is shown to illustrate our method. At the end, Sect. 7 concludes the paper and discusses the future work. For space limitation, the proofs for all the lemmas and theorems are omitted, but can be found in [34].
2 Preliminary
In this section, we briefly review some notions in dynamical systems, that can be found at [19, 29]. In what follows, \(\mathbb {N}\), \(\mathbb {R}\), \(\mathbb {R}^+\), \(\mathbb {R}^+_0\) denote the natural, real, positive and nonnegative real numbers, respectively. Given a vector \(\mathbf {x}\in \mathbb {R}^n\), \(\Vert \mathbf {x}\Vert \) denotes the infinity norm of \(\mathbf {x}\in \mathbb {R}^n\), i.e., \(\Vert \mathbf {x}\Vert =\max \{|x_1|,|x_2|,...,|x_n|\}\). A continuous function \(\gamma :\mathbb {R}^+_0 \rightarrow \mathbb {R}^+_0\), is said in class \(\mathcal {K}\) if it is strictly increasing and \(\gamma (0)=0\); \(\gamma \) is said in class \(\mathcal {K}_\infty \) if \(\gamma \in \mathcal {K}\) and \(\gamma (r) \rightarrow \infty \) as \(r \rightarrow \infty \). A continuous function \(\beta :\mathbb {R}^+_0 \times \mathbb {R}^+_0 \rightarrow \mathbb {R}^+_0\) is said in class \(\mathcal {K\!L}\) if for each fixed s, the map \(\beta (r,s) \in \mathcal {K}_\infty \) with respect to r and, for each fixed r, \(\beta (r,s)\) is decreasing with respect to s and \(\beta (r,s) \rightarrow 0\) as \(s \rightarrow \infty \).
A dynamical system is of the following form
where \(\mathbf {x}\in \mathbb {R}^n\) is the state and \(\mathbf {x}(t_0)=\mathbf {x}_0\) is the initial condition.
Suppose \(a<t_0<b\). A function \(X(.):(a,b)\rightarrow \mathbb {R}^n\) is said to be a trajectory (solution) of (1) on (a, b), if \(X(t_0)=\mathbf {x}_0\) and \(\dot{X}(t)=\mathbf {f}(X(t))\) for all \(t \ge t_0\). In order to ensure the existence and uniqueness of trajectories, we assume \(\mathbf {f}\) satisfying the local Lipschitz condition, i.e., for every compact set \(S\subset \mathbb {R}^n\), there exists a constant \(L>0\) s.t. \(\Vert \mathbf {f}(\mathbf {x})-\mathbf {f}(\mathbf {y})\Vert \le L\Vert \mathbf {x}-\mathbf {y}\Vert \), for all \(\mathbf {x},\mathbf {y}\in S\). Then, we write \(X(t,\mathbf {x}_0)\) to denote the point reached at time \(t \in (a,b)\) from initial condition \(\mathbf {x}_0\), which should be uniquely determined. In addition, we assume (1) is forward complete [7], i.e., it is solvable on an open interval \((a,+\infty )\). An equilibrium point of (1) is a point \(\bar{\mathbf {x}}\in \mathbb {R}^n\) s.t. \(\mathbf {f}(\bar{\mathbf {x}})=0\).
Definition 1
A dynamical system of form (1) is said to be globally asymptotically stable (\(\mathrm {GAS}\)) if there exists a point \(\mathbf {x}_0\) and a function \(\beta \) of class \(\mathcal {K\!L}\) s.t.
It is easy to see that the point \(\mathbf {x}_0\) is actually the unique equilibrium point of the system. When this point is previously known or can be easily computed, one can prove the system to be GAS by constructing a corresponding Lyapunov function. However, \(\mathbf {x}_0\) cannot be found sometimes, for example, when the dynamics \(\mathbf {f}\) of the system depends on external inputs and thus is not completely known. The concept of \(\delta \)-\(\mathrm {GAS}\) would be useful in this case.
Definition 2
A dynamical system of (1) is said to be incrementally globally asymptotically stable (\(\delta \)-\(\mathrm {GAS}\)) if it is forward complete and there is a \(\mathcal {K\!L}\) function \(\beta \) s.t.
In [6], the relationship between \(\mathrm {GAS}\) and \(\delta \)-\(\mathrm {GAS}\) was established, restated by the following proposition.
Proposition 1
-
If (1) is \(\delta \)-\(\mathrm {GAS}\), then it is \(\mathrm {GAS}\).
-
If there exist two strictly positive reals M and \(\varepsilon \), and a differentiable function \(V(\mathbf {x},\mathbf {y})\) with \(\alpha _1(\Vert \mathbf {x}-\mathbf {y}\Vert ) \le V(\mathbf {x},\mathbf {y}) \le \alpha _2(\Vert \mathbf {x}-\mathbf {y}\Vert )\) for some \(\alpha _1\), \(\alpha _2\) and \(\rho \) of class \(\mathcal {K}_\infty \), s.t.
$$\begin{aligned} \forall \mathbf {x},\mathbf {y}\in \mathbb {R}^n. \left( \begin{array}{cl} &{} \Vert \mathbf {x}-\mathbf {y}\Vert \le \varepsilon \wedge \Vert \mathbf {x}\Vert \ge M \wedge \Vert \mathbf {y}\Vert \ge M \\ \Rightarrow &{} \frac{\partial V}{\partial \mathbf {x}}\mathbf {f}(\mathbf {x}) + \frac{\partial V}{\partial \mathbf {y}}\mathbf {f}(\mathbf {y}) \le -\rho (\Vert \mathbf {x}-\mathbf {y}\Vert ) \end{array} \right) , \end{aligned}$$then the system (1) is \(\delta \)-\(\mathrm {GAS}\).
A function \(V(\mathbf {x},\mathbf {y})\) satisfying the condition in Proposition 1 is called a \(\delta \)-\(\mathrm {GAS}\) Lyapunov function of (1). Proposition 1 tells us that (1) is \(\delta \)-\(\mathrm {GAS}\) if and only if it admits a \(\delta \)-\(\mathrm {GAS}\) Lyapunov function. In general, checking the inequality in Definition 2 is difficult, one may construct \(\delta \)-\(\mathrm {GAS}\) Lyapunov functions as an alternative.
3 Transition Systems and Approximate Bisimulation
In the following, the set of actions, denoted by Act, is assumed to consist of a set of discrete actions which take no time (written as \(\mathcal {E}\)), \(\mathbb {R}^+_0\) the set of delay actions which just take time delay, and a special internal action \(\tau \). Actions are ranged over \(l_1,\ldots , l_n, \ldots \).
Definition 3
(Transition system). A labeled transition system with observations is a tuple \(T=\langle Q,L,\rightarrow ,Q^{0},Y,H\rangle \), where Q is a set of states, \(L\subseteq \textit{Act}\) is a set of labels, \(Q^{0}\subseteq Q\) is a set of initial states, Y is a set of observations, and H is an observation function \(H:Q\rightarrow Y\), \(\rightarrow \subseteq Q\times L\times Q\) is a transition relation, satisfying
-
1,
identity: \(q\overset{0}{\longrightarrow } q\) always holds;
-
2,
delay determinism: if \(q\overset{d}{\longrightarrow } q'\) and \(q\overset{d}{\longrightarrow } q''\), then \(q'=q''\); and
-
3,
delay additivity: if \(q\overset{d_{1}}{\longrightarrow } q'\) and \(q'\overset{d_{2}}{\longrightarrow } q''\) then \(q\overset{d_{1}+d_{2}}{\longrightarrow } q''\), where \(d,d_1,d_2\in \mathbb {R}^+_0\).
A transition system T is said to be symbolic if Q and \(L\cap \mathcal {E}\) are finite, and \(L\cap \mathbb {R}^+_0\) is bounded, and metric if the output set Y is equipped with a metric \(\mathbf d :Y\times Y\rightarrow \mathbb {R}^{+}_{0}\). In this paper, we regard Y as being equipped with the metric \(\mathbf d (\mathbf {y}_1,\mathbf {y}_2)=\Vert \mathbf {y}_1-\mathbf {y}_2 \Vert \).
A state trajectory of a transition system T is a (possibly infinite) sequence of transitions \(\mathbf {q}^0 \xrightarrow {l^{0}} \mathbf {q}^1 \xrightarrow {l^{1}}\cdots \xrightarrow {l^{i-1}} \mathbf {q}^{i}\xrightarrow {l^{i}} \cdots \), denoted by \(\{\mathbf {q}^i\xrightarrow {l^i}\mathbf {q}^{i+1}\}_{i\in \mathbb {N}}\), s.t. \(\mathbf {q}^{0}\in Q^0\) and for any i, \(\mathbf {q}^{i} \xrightarrow {l^{i}} \mathbf {q}^{i+1}\). An observation trajectory is a (possibly infinite) sequence \(\mathbf {y}^0 \xrightarrow {l^{0}} \mathbf {y}^1 \xrightarrow {l^{1}}\cdots \xrightarrow {l^{i-1}} \mathbf {y}^{i}\xrightarrow {l^{i}} \cdots \), denoted by \(\{\mathbf {y}^i\xrightarrow {l^i}\mathbf {y}^{i+1}\}_{i\in \mathbb {N}}\), and it is accepted by T if there exists a corresponding state trajectory of T s.t. \(\mathbf {y}^{i}=H(\mathbf {q}^{i})\) for any \(i\in \mathbb {N}\). The set of observation trajectories accepted by T is called the language of T, and is denoted by L(T). The reachable set of T is a subset of Y defined by
We can verify the safety property of T by computing \(Reach(T)\cap Y_{U}\), in which \(Y_{U}\subseteq Y\) is the set of unsafe observations. If it is empty, then T is safe, otherwise, unsafe.
For a maximum sequence of \(\tau \) actions \(\mathbf {q}^{i} \xrightarrow {\tau } \mathbf {q}^{i+1} \xrightarrow {\tau } \cdots \xrightarrow {\tau }\mathbf {q}^{i+k}\), we remove the intermediate states and define the \(\tau \)
-compressed transition \(\mathbf {q}^{i}\mathop {\twoheadrightarrow }\limits ^{\tau }\mathbf {q}^{i+k}\) instead. For unification, for a non-\(\tau \) transition \(\mathbf {q}^{i}\xrightarrow {l^i}\mathbf {q}^{i+1}\) where \(l^i \ne \tau \), we define \(\mathbf {q}^{i}\mathop {\twoheadrightarrow }\limits ^{l^i}\mathbf {q}^{i+1}\). In what follows, we will denote \(\langle Q,L,\twoheadrightarrow ,Q^{0},Y,H\rangle \) the resulting labeled transition system from \(\langle Q,L,\rightarrow ,Q^{0},Y,H\rangle \) by replacing each label transition with its \(\tau \)-compressed version. As a common convention in process algebra, we use  to denote the closure of \(\tau \) transitions, i.e., \(\mathbf {p}(\mathop {\twoheadrightarrow }\limits ^{\tau })^{\{0,1\}} \mathop {\twoheadrightarrow }\limits ^{l}( \mathop {\twoheadrightarrow }\limits ^{\tau })^{\{0,1\}}\mathbf {p}^{\prime }\), for any \(l\in L\) in the sequel.
to denote the closure of \(\tau \) transitions, i.e., \(\mathbf {p}(\mathop {\twoheadrightarrow }\limits ^{\tau })^{\{0,1\}} \mathop {\twoheadrightarrow }\limits ^{l}( \mathop {\twoheadrightarrow }\limits ^{\tau })^{\{0,1\}}\mathbf {p}^{\prime }\), for any \(l\in L\) in the sequel.
Given \(l_1, l_2\in L\cup \{\tau \}\), we define the distance \(\textit{dis}(l_1, l_2)\) between them as follows:
Definition 4
(Approximate bisimulation). Let \(T_{i}=\langle Q_i,L_i,\twoheadrightarrow _i,Q^{0}_i,Y_i,H_i\rangle \), \((i=1,2)\) be two metric transition systems with the same output set Y and metric \(\mathbf d \). Let h and \(\varepsilon \) be the time and value precision respectively. A relation \(\mathcal {B}_{h, \varepsilon }\subseteq Q_{1}\times Q_{2}\) is called a \((h, \varepsilon )\)-approximate bisimulation relation between \(T_{1}\) and \(T_{2}\), if for all \((\mathbf {q}_{1},\mathbf {q}_{2})\in \mathcal {B}_{h,\varepsilon }\),
-
1.
\(\mathbf {d}(H_{1}(\mathbf {q}_{1}),H_{2}(\mathbf {q}_{2}))\le \varepsilon \),
-
2.
\(\forall \mathbf {q}_{1}\mathop {\twoheadrightarrow }\limits ^{l}_1 \mathbf {q}^{\prime }_{1}\),
 s.t. \(\textit{dis}(l, l') \le h\) and \((\mathbf {q}^{\prime }_{1},\mathbf {q}^{\prime }_{2})\in \mathcal {B}_{h, \varepsilon }\), for \(l\in L_1\) and \(l'\in L_2\)
s.t. \(\textit{dis}(l, l') \le h\) and \((\mathbf {q}^{\prime }_{1},\mathbf {q}^{\prime }_{2})\in \mathcal {B}_{h, \varepsilon }\), for \(l\in L_1\) and \(l'\in L_2\)
-
3.
\(\forall \mathbf {q}_{2}\mathop {\twoheadrightarrow }\limits ^{l}_2 \mathbf {q}^{\prime }_{2}\),
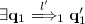 s.t. \(\textit{dis}(l, l') \le h\) and \((\mathbf {q}^{\prime }_{1},\mathbf {q}^{\prime }_{2})\in \mathcal {B}_{h, \varepsilon }\), for \(l\in L_2\) and \(l'\in L_1\).
s.t. \(\textit{dis}(l, l') \le h\) and \((\mathbf {q}^{\prime }_{1},\mathbf {q}^{\prime }_{2})\in \mathcal {B}_{h, \varepsilon }\), for \(l\in L_2\) and \(l'\in L_1\).
Definition 5
\(T_{1}\) and \(T_{2}\) are approximately bisimilar with the precision h and \(\varepsilon \) (denoted \(T_{1}\cong _{h, \varepsilon }T_{2}\)), if there exists a \((h, \varepsilon )\)-approximate bisimulation relation \(\mathcal {B}_{h,\varepsilon }\) between \(T_{1}\) and \(T_{2}\) s.t. for all \(\mathbf {q}_{1}\in Q^{0}_{1}\), there exists \(\mathbf {q}_{2}\in Q^{0}_{2}\) s.t. \((\mathbf {q}_{1},\mathbf {q}_{2})\in \mathcal {B}_{h,\varepsilon }\), and vice versa.
The following result ensures that the set of \((h,\varepsilon )\)-approximate bisimulation relations has a maximal element.
Lemma 1
Let\(\{\mathcal {B}^i_{h, \varepsilon }\}_{i\in I}\) be a family of \((h,\varepsilon )\)-approximate bisimulation relations between \(T_1\) and \(T_2\). Then, \(\bigcup _{i\in I}\mathcal {B}^i_{h, \varepsilon }\) is a \((h,\varepsilon )\)-approximate bisimulation relation between \(T_1\) and \(T_2\).
By Lemma 1, given the precision parameters h and \(\varepsilon \), let \(\{\mathcal {B}^i_{h, \varepsilon }\}_{i\in I}\) be the set of all \((h,\varepsilon )\)-approximate bisimulation relations between \(T_1\) and \(T_2\), then the maximal \((h,\varepsilon )\)-approximate bisimulation relation between \(T_1\) and \(T_2\) is defined by \(\mathcal {B}^{max}_{h, \varepsilon }=\bigcup \limits _{i\in I}\mathcal {B}^i_{h, \varepsilon }\). For two transition systems that are approximately bisimilar, the reachable sets have the following relationship:
Theorem 1
If \(T_{1}\cong _{h, \varepsilon }T_{2}\), then \( \textit{Reach}(T_1)\subseteq N(\textit{Reach}(T_2),\varepsilon ) \), where \(N(Y,\varepsilon )\) denotes the \(\varepsilon \) neighborhood of Y, i.e. \(\{x \mid \exists y. y \in Y \wedge \Vert x-y \Vert < \varepsilon \}\).
Thus, if the distance between \(\textit{Reach}(T_2)\) and the unsafe set \(Y_U\) is greater than \(\varepsilon \), then the intersection of \(\textit{Reach}(T_1)\) and \(Y_U\) is empty and hence \(T_1\) is safe, whenever \(T_{1}\cong _{h, \varepsilon }T_{2}\).
4 Hybrid CSP (HCSP)
In this section, we present a brief introduction to HCSP and define the transition system of HCSP from an operational point of view. An example is given for better understanding. Finally, we investigate the approximate bisimilarity for HCSP processes.
4.1 HCSP
Hybrid Communicating Sequential Process (HCSP) is a formal language for describing hybrid systems, which extends CSP by introducing differential equations for modelling continuous evolutions and interrupts for modeling the arbitrary interaction between continuous evolutions and discrete jumps. The syntax of HCSP can be described as follows:

where \(x,\mathbf {s}\) for variables and vectors of variables, respectively, B and e are boolean and arithmetic expressions, d is a non-negative real constant, ch is the channel name, \(io_{i}\) stands for a communication event, i.e., either \(ch_{i}?x\) or \(ch_{i}!e\), \(P,Q,Q_{i}\) are sequential process terms, and S stands for an HCSP process term. Given an HCSP process S, we define \(\textit{Var}(S)\) for the set of variables in S, and \(\varSigma (S)\) the set of channels occurring in S, respectively. The informal meanings of the individual constructors are as follows:
-
\(\mathrm{skip}\), \(x := e\), \(\text {wait}\ d\), ch?x, ch!e, P; Q, \(P \sqcap Q\), and
 are defined as usual. \(B \rightarrow P\) behaves as P if B is true, otherwise terminates.
are defined as usual. \(B \rightarrow P\) behaves as P if B is true, otherwise terminates. -
For repetition \(P^*\), P executes for an arbitrary finite number of times. We assume an oracle \(\textit{num}\), s.t. for a given \(P^*\) in the context process S, \(\textit{num}(P^*, S)\) returns the upper bound of the number of times that P is repeated in the context.
-
\( \langle {F}(\dot{\mathbf {s}},\mathbf {s})=0 \& B\rangle \) is the continuous evolution statement. It forces the vector \(\mathbf {s}\) of real variables to obey the differential equations F as long as B, which defines the domain of \(\mathbf {s}\), holds, and terminates when B turns false. Without loss of generality, we assume that the set of B is open, thus the escaping point will be at the boundary of B. The communication interrupt
 behaves like \( \langle {F}(\dot{\mathbf {s}},\mathbf {s})=0 \& B\rangle \), except that the continuous evolution is preempted as soon as one of the communications \(io_{i}\) takes place, which is followed by the respective \(Q_{i}\). These two statements are the main extension of HCSP for describing continuous behavior.
behaves like \( \langle {F}(\dot{\mathbf {s}},\mathbf {s})=0 \& B\rangle \), except that the continuous evolution is preempted as soon as one of the communications \(io_{i}\) takes place, which is followed by the respective \(Q_{i}\). These two statements are the main extension of HCSP for describing continuous behavior. -
\(S_1\Vert S_2\) behaves as if \(S_{1}\) and \(S_{2}\) run independently except that all communications along the common channels connecting \(S_{1}\) and \(S_{2}\) are to be synchronized. \(S_{1}\) and \(S_{2}\) in parallel can neither share variables, nor input or output channels.
For better understanding of the HCSP syntax, we model the water tank system [4], for which two components Watertank and Controller, are composed in parallel. The HCSP model of the system is given by WTS as follows:
where \(Q_{max}\), \(\pi \), r and g are system parameters, v is the control variable which takes 1 or 0, depending on whether the valve is open or not, d is the water level of the \(\textit{Watertank}\) and its dynamics depends on the value of v. \(v_0\) and \(d_0\) are the initial values of controller variable and water level, respectively. Two channels, wl and cv, are used to transfer the water level (d in \(\textit{Watertank}\)) and control variable (y in \(\textit{Controller}\)) between \(\textit{Watertank}\) and \(\textit{Controller}\), respectively. The control value is computed by the Controller with a period of p. When the water level is less than or equal to lb, the control value is assigned to 1, and when the water level is greater than or equal to ub, the control value is assigned to 0, otherwise, it keeps unchanged. Basically, based on the current value of v, \(\textit{Watertank}\) and \(\textit{Controller}\) run independently for p time, then \(\textit{Watertank}\) sends the current water level to \(\textit{Controller}\), according to which a new value of the control variable is generated and sent back to \(\textit{Watertank}\), after that, a new period repeats.
4.2 Transition System of HCSP
Given an HCSP process S, we can derive a transition system \(T(S)=\langle Q,L,\rightarrow ,Q^{0},Y,H\rangle \) from S by the following procedure:
-
the set of states \(Q=(\textit{subp}(S)\cup \{\epsilon \})\times V(S)\), where \(\textit{subp}(S)\) is the set of sub-processes of S, e.g., \(\textit{subp}(S)=\{S, \text {wait}\ d,B \rightarrow P\} \cup \textit{subp}(P)\) for \(S{:}{:=}\text {wait}\ d;B \rightarrow P\), \(\epsilon \) is introduced to represent the terminal process, meaning that the process has terminated, and \(V(S) = \{v| v\in \textit{Var}(S) \rightarrow \textit{Val}\}\) is the set of evaluations of the variables in S, with \(\textit{Val}\) representing the value space of variables. Without confusion in the context, we often call an evaluation v a (process) state. Given a state \(q\in Q\), we will use \(\textit{fst}(q)\) and \(\textit{snd}(q)\) to return the first and second component of q, respectively.
-
The label set L corresponds to the actions of HCSP, defined as \(L= \mathbb {R}^+_0 \cup \varSigma (S)\centerdot \{?,!\}\centerdot \mathbb {R}\cup \{\tau \}\), where \(d\in \mathbb {R}^+_0\) stands for the time progress, \(ch?c, ch!c \in \varSigma (S)\centerdot \{?,!\}\centerdot \mathbb {R}\) means that an input along channel ch with value c being received, an output along ch with value c being sent, respectively. Besides, the silent action \(\tau \) represents a discrete non-communication action of HCSP, such as assignment, evaluation of boolean expressions, and so on.
-
\(Q^{0}=\{(S, v) | v \in V(S)\}\), representing that S has not started to execute, and v is the initial process state of S.
-
\(Y=\overline{\textit{Val}}\), represents the set of value vectors corresponding to \(\textit{Var}(S)\).
-
Given \(q \in Q\), \(H(q)=\textit{vec}(\textit{snd}(q))\), where function \(\textit{vec}\) returns the value vector corresponding to the process state of q.
-
\(\rightarrow \) is the transition relation of S, which is given next.
Sequential Processes. A transition relation of a sequential HCSP process takes the form \((P,v)\xrightarrow {l}(P^{\prime },v^{\prime })\), indicating that starting from state v, P executes to \(P'\) by performing action l, with the resulting state \(v'\). Here we present the transition rules for continuous evolution as an illustration. Readers are referred to [35] for the full details of the transition semantics, for both sequential and parallel HCSP processes.
For \( \langle {F}(\dot{\mathbf {s}},\mathbf {s})=0 \& B\rangle \), for any \(d\ge 0\), it evolves for d time units according to F if B evaluates to true within this period (the right end exclusive). In the rule, \(S(\cdot ): [0, d] \rightarrow \mathbb {R}^n\) defines the trajectory of the ODE F with initial value \(v(\mathbf {s})\). Otherwise, by performing a \(\tau \) action, the continuous evolution terminates if B evaluates to false.
Parallel Composition. Given two sequential processes \(P_{1}\), \(P_{2}\) and their transition systems \(T(P_{1})=\langle Q_{1},L_{1},\rightarrow _{1},Q^{0}_{1},Y_{1},H_{1}\rangle \) and \(T(P_{2})=\langle Q_{2},L_{2},\rightarrow _{2},Q^{0}_{2},Y_{2},H_{2}\rangle \), we can define the transition system of \(P_{1}\Vert P_{2}\) as \(T(P_{1}\Vert P_{2})=\langle Q,L,\rightarrow ,Q,Y,H\rangle \), where:
-
\(Q=((\textit{subp}(P_1)\cup \{\epsilon \}) \Vert (\textit{subp}(P_2)\cup \{\epsilon \}))\times \{v_1 \uplus v_2 | v_1 \in V(P_1), v_2 \in V(P_2)\}\), where given two sets of processes \(PS_1\) and \(PS_2\), \(PS_1 \Vert PS_2\) is defined as \(\{\alpha \Vert \beta | \alpha \in PS_1 \wedge \beta \in PS_2\}\); \(v_1 \uplus v_2\) represents the disjoint union, i.e. \(v_1 \uplus v_2 (x)\) is \(v_1(x)\) if \(x \in \textit{Var}(P_1)\), otherwise \(v_2(x)\).
-
\(L=L_{1}\cup L_{2}\).
-
\(Q^{0}=\{(P_{1}\Vert P_{2}, v^{0}_{1}\uplus v^{0}_{2}) | (P_i, v^{0}_{i}) \in Q^{0}_{i} \text{ for } i=1, 2\}\).
-
\(Y=Y_{1}\times Y_{2}\), the observation space of the parallel composition is obviously the Cartesian product of \(Y_1\) and \(Y_2\).
-
\(H(q)= H_1(q) \times H_2(q)\), the observation function is the Cartesian product of the two component observation functions correspondingly.
-
\(\rightarrow \) is defined based on the parallel composition of transitions of \(L_1\) and \(L_2\).
Suppose two transitions \((P_{1},u)\xrightarrow {\alpha }(P^{\prime }_{1},u^{\prime })\) and \((P_{2},v)\xrightarrow {\beta }(P^{\prime }_{2},v^{\prime })\) occur for \(P_1\) and \(P_2\), respectively. The rule for synchronization is given below:
4.3 Approximate Bisimulation Between HCSP Processes
Let \(P_1\) and \(P_2\) be two HCSP processes, and \(h, \varepsilon \) the time and value precisions. Let \(v_0\) be an arbitrary initial state. \(P_1\) and \(P_2\) are \((h, \varepsilon )\)-approximately bisimilar, denoted by \(P_1\cong _{h, \varepsilon }P_2\), if \(T(P_1)\cong _{h, \varepsilon }T(P_2)\), in which \(T(P_1)\) and \(T(P_2)\) are the \(\tau \)-compressed transition systems of \(P_1\) and \(P_2\) with the same initial state \(v_0\), respectively.

In Algorithm 1, we consider the \((h, \varepsilon )\)-approximate bisimilation between \(P_1\) and \(P_2\) for which all the ODEs occurring in \(P_1\) and \(P_2\) are \(\mathrm {GAS}\). Suppose the set of ODEs occurring in \(P_i\) is \(\{F^i_1, \cdots , F^i_{ki}\}\), and the equilibrium points for them are \(x^i_1, \cdots , x^i_{ki}\) for \(i=1, 2\) respectively. As a result, for each ODE, there must exist a sufficiently large time, called equilibrium time, s.t. after the time, the distance between the trajectory and the equilibrium point is less than \(\varepsilon \). We denote the equilibrium time for each \(F^i_{j}\) for \(j=1, \cdots , ki\) by \(T^i_j\), respectively. Furthermore, in order to record the execution time of ODEs, for each ODE \(F^i_{j}\), we introduce an auxiliary time variable \(t^i_{j}\) and add \(t^i_{j}:=0; \dot{t^i_{j}}=1\) to \(F^i_{j}\) correspondingly.
Algorithm 1 decides whether \(P_1\) and \(P_2\) are \((h, \varepsilon )\)-approximately bisimilar. When \(P_{1}\cong _{h, \varepsilon }P_{2}\), it returns true, otherwise, it returns false. Let d be the discretized time step. The algorithm is then taken in two steps. The first step (lines 1–6) constructs the transition systems for \(P_1\) and \(P_2\) with time step d. For \(m=1, 2\), \(T(P_m).Q\) and \(T(P_m).T\) represent the reachable set of states and transitions of \(P_m\), respectively, which are initialized as empty sets and then constructed iteratively. At each step i, a new transition can be a d time progress, a \(\tau \) event, or a communication event. Besides, a transition can be a time progress less than d, which might be caused by the occurrence of a boundary interrupt or a communication interrupt during a continuous evolution. The new transition will be added only when the running time for each ODE \(F^m_j\), denoted by \(t^m_j\), is less than the corresponding equilibrium time. Therefore, for either process \(P_m\), whenever some ODE runs beyond its equilibrium time, the set of reachable transitions reaches a fixpoint by allowing precision \(\varepsilon \) and will not be extended any more. The set of reachable states can be obtained by collecting the post states of reachable transitions. Based on Definition 4, the second step (lines 7–17) decides whether the transition systems for \(P_1\) and \(P_2\) are approximately bisimilar with the given precisions.
The first part (lines 1–6) of the algorithm computes the transitions of processes. For each process \(P_m\), its complexity is \(O(|T(P_m).T|)\), which is \(O(\lceil \frac{T_m}{d}\rceil + N_m)\), where \(T_m\) represents the execution time of \(P_m\) till termination or reaching the equilibrium time of some ODE, and \(N_m\) the number of atomic statements of \(P_m\). The second part (lines 7–17) checks for \(P_1\) and \(P_2\) each pair of the states whose distance is within \(\varepsilon \) by traversing the outgoing transitions, to see if they are truly approximate bisimilar, till the fixpoint \(\mathcal {B}_{h, \varepsilon }\) is reached. We can compute the time complexity to be \(O(Q_1^2Q_2^2T_1T_2)\), where \(Q_m\) and \(T_m\) represent \(O(|T(P_m).Q|)\) and \(O(|T(P_m).T|)\) for \(m=1, 2\) respectively.
Theorem 2
(Correctness). Algorithm 1 terminates, and for any \(v_0\), \(P_1 \cong _{h, \varepsilon } P_2\) iff \(((P_1, v_0), (P_2, v_0))\in \mathcal {B}_{h, \varepsilon }\).
5 Discretization of HCSP
In this section, we consider the discretization of HCSP processes, by which the continuous dynamics is represented by discrete approximation. Let P be an HCSP process and \((h,\varepsilon \)) be the precisions, our goal is to construct a discrete process D from P, s.t. P is \((h,\varepsilon )\)-bisimilar with D, i.e., \(P\cong _{h,\varepsilon }D\) holds.
5.1 Discretization of Continuous Dynamics
Since most differential equations do not have explicit solutions, the discretization of the dynamics is normally given by discrete approximation. Consider the ODE \(\dot{\mathbf {x}} = \mathbf {f}(\mathbf {x})\) with the initial value \(\widetilde{\mathbf {x}}_0 \in \mathbb {R}^n\), and assume \(X(t, \widetilde{\mathbf {x}}_0)\) is the trajectory of the initial value problem along the time interval \([t_0, \infty )\). In the following discretization, assume h and \(\xi \) represent the time step size and the precision of the discretization, respectively. Our strategy is as follows:
-
First, from the fact that \(\dot{\mathbf {x}} = \mathbf {f}(\mathbf {x})\) is GAS, there must exist a sufficiently large T s.t. \(\Vert X(t, \widetilde{\mathbf {x}}_0)-\bar{\mathbf {x}}\Vert < \xi \) holds when \(t > T\), where \(\bar{\mathbf {x}}\) is an equilibrium point. As a result, after time T, the value of \(\mathbf {x}\) can be approximated by the equilibrium point \(\bar{\mathbf {x}}\) and the distance between the actual value of \(\mathbf {x}\) and \(\bar{\mathbf {x}}\) is always within \(\xi \).
-
Then, for the bounded time interval \([t_0, T]\), we apply Euler method to discretize the continuous dynamics.
There are a range of different discretization methods for ODEs [30] and the Euler method is an effective one among them. According to the Euler method, the ODE \(\dot{\mathbf {x}} = \mathbf {f}(\mathbf {x}) \) is discretized as
A sequence of approximate solutions \(\{\mathbf {x}_i\}\) at time stamps \(\{h_i\}\) for \(i=1, 2, \cdots , N\) with \( N= \lceil \frac{T-t_0}{h}\rceil \) are obtained, satisfying (define \(\mathbf {x}_0 = \widetilde{\mathbf {x}}_0\)):
\(\Vert X(h_i, \widetilde{\mathbf {x}}_0) - \mathbf {x}_i\Vert \) represents the discretization error at time \(h_i\). To estimate the global error of the approximation, by Theorem 3 in [25], we can prove the following theorem:
Theorem 3
(Global error with an initial error). Let \(X(t, \widetilde{\mathbf {x}}_0)\) be a solution on \([t_0, T]\) of the initial value problem \(\dot{\mathbf {x}} = \mathbf {f}(\mathbf {x}), \mathbf {x}(t_0)=\widetilde{\mathbf {x}}_0\), and L the Lipschitz constant s.t. for any compact set S of \(\mathbb {R}^n\), \(\Vert \mathbf {f}(\mathbf {y}_1) - \mathbf {f}(\mathbf {y}_2)\Vert \le L\Vert \mathbf {y}_1 - \mathbf {y}_2\Vert \) for all \(\mathbf {y}_1, \mathbf {y}_2 \in S\). Let \(\mathbf {x}_0 \in \mathbb {R}^n\) satisfy \(\Vert \mathbf {x}_0 - \widetilde{\mathbf {x}}_0\Vert \le \xi _1\). Then there exists an \(h_0 > 0\), s.t. for all h satisfying \(0<h\le h_0\), and for all n satisfying \(nh \le (T-t_0)\), the sequence \(\mathbf {x}_n = \mathbf {x}_{n-1} + h\mathbf {f}(\mathbf {x}_{n-1})\) satisfies:
By Theorem 3 and the property of GAS, we can prove the following main theorem.
Theorem 4
(Approximation of an ODE). Let \(X(t, \widetilde{\mathbf {x}}_0)\) be a solution on \([t_0, \infty ]\) of the initial value problem \(\dot{\mathbf {x}} = \mathbf {f}(\mathbf {x}), \mathbf {x}(t_0)=\widetilde{\mathbf {x}}_0\), and L the Lipschitz constant. Assume \(\dot{\mathbf {x}} = \mathbf {f}(\mathbf {x})\) is GAS with the equilibrium point \(\bar{\mathbf {x}}\). Then for any precision \(\xi >0\), there exist \(h>0, T>0\) and \(\xi _1 >0\) s.t. \(\dot{\mathbf {x}} = \mathbf {f}(\mathbf {x}), \mathbf {x}(t_0)=\widetilde{\mathbf {x}}_0\) and \(\mathbf {x}:=\mathbf {x}_0; (\mathbf {x}:= \mathbf {x}+h\mathbf {f}(\mathbf {x}); \text {wait}\ h)^N; \mathbf {x}:=\bar{\mathbf {x}}; \mathbf{stop}\) with \(N=\lceil \frac{T-t_0}{h}\rceil \) are \((h,\xi )\)-approximately bisimilar, in which \(\Vert \mathbf {x}_0 - \widetilde{\mathbf {x}}_0\Vert < \xi _1\) holds, i.e., there is an error between the initial values.
5.2 Discretization of HCSP
We continue to consider the discretization of HCSP processes, among which any arbitrary number of ODEs, the discrete dynamics, and communications are involved. Below, given an HCSP process P, we use \(\textit{D}_{h, \varepsilon }(P)\) to represent the discretized process of P, with parameters h and \(\varepsilon \) to denote the step size and the precision (i.e. the maximal “distance” between states in P and \(\textit{D}_{h, \varepsilon }(P)\)), respectively.
Before giving the discretization of HCSP processes, we need to introduce the notion of readiness variables. In order to express the readiness information of communication events, for each channel ch, we introduce two boolean variables ch? and ch!, to represent whether the input and output events along ch are ready to occur. We will see that in the discretization, the readiness information of partner events is necessary to specify the behavior of communication interrupt.
Table 1 lists the definition of \(\textit{D}_{h, \varepsilon }(P)\). For each rule, the original process is listed above the line, while the discretized process is defined below the line. For \(\mathrm{skip}, x:=e\) and \(\text {wait}\ d\), they are kept unchanged in the discretization. For input ch?x, it is discretized as itself, and furthermore, before ch?x occurs, ch? is assigned to 1 to represent that ch?x becomes ready, and in contrary, after ch?x occurs, ch? is reset to 0. The output ch!e is handled similarly. The compound constructs, P; Q, \(P \sqcap Q\), \(P^*\) and \(P \Vert Q\) are discretized inductively according to their structure. For \(B \rightarrow P\), B is still approximated to B and P is discretized inductively. For external choice  , the readiness variables \(io_i\) for all \(i\in I\) are set to 1 at first, and after the choice is taken, all of them are reset to 0 and the corresponding process is discretized. Notice that because I is finite, the \(\forall \) operator is defined as an abbreviation of the conjunction over I.
, the readiness variables \(io_i\) for all \(i\in I\) are set to 1 at first, and after the choice is taken, all of them are reset to 0 and the corresponding process is discretized. Notice that because I is finite, the \(\forall \) operator is defined as an abbreviation of the conjunction over I.
Given a boolean expression B and a precision \(\varepsilon \), we define \(N(B, \varepsilon )\) to be a boolean expression which holds in the \(\varepsilon \)-neighbourhood of B. For instance, if B is \(x>2\), then \(N(B, \varepsilon )\) is \(x>2-\varepsilon \). For a continuous evolution \( \langle \dot{\mathbf {x}}=\mathbf {f}(\mathbf {x}) \& B\rangle \), under the premise that \(\dot{\mathbf {x}}=\mathbf {f}(\mathbf {x})\) is GAS, there must exists time T such that when the time is larger than T, the distance between the actual state of \(\mathbf {x}\) and the equilibrium point, denoted by \(\bar{\mathbf {x}}\), is less than \(\varepsilon \). Then according to Theorem 3, \( \langle \dot{\mathbf {x}}=\mathbf {f}(\mathbf {x}) \& B\rangle \) is discretized as follows: First, it is a repetition of the assignment to \(\mathbf {x}\) according to the Euler method for at most \(\lceil \frac{T}{h}\rceil \) number of times, and then followed by the assignment of \(\mathbf {x}\) to the equilibrium point and stop forever. Both of them are guarded by the condition \(N(B, \varepsilon )\). For a communication interrupt  , suppose T is sufficiently large s.t. when the time is larger than T, the distance between the actual state of \(\mathbf {x}\) and the equilibrium point, denoted by \(\bar{\mathbf {x}}\), is less than \(\varepsilon \), and furthermore, if the interruption occurs, it must occur before T, and let \(\overline{ch*}\) be the dual of \(ch*\), e.g., if \(ch*=ch?\), then \(\overline{ch*}=ch!\) and vice versa. After all the readiness variables corresponding to \(\{io_i\}_I\) are set to 1 at the beginning, the discretization is taken by the following steps: first, if \(N(B, \varepsilon )\) holds and no communication among \(\{io_i\}_{i \in I}\) is ready, it executes following the discretization of continuous evolution, for at most \(\lceil \frac{T}{h}\rceil \) number of steps; then if \(N(B, \varepsilon )\) turns false without any communication occurring, the whole process terminates and meanwhile the readiness variables are reset to 0; otherwise if some communications get ready, an external choice between these ready communications is taken, and then, the readiness variables are reset to 0 and the corresponding \(Q_i\) is followed; finally, if the communications never occur and the continuous evolution never terminates, the continuous variable is assigned to the equilibrium point and the time progresses forever. It should be noticed that, the readiness variables of the partner processes will be used to decide whether a communication is able to occur. They are shared between parallel processes, but will always be written by one side.
, suppose T is sufficiently large s.t. when the time is larger than T, the distance between the actual state of \(\mathbf {x}\) and the equilibrium point, denoted by \(\bar{\mathbf {x}}\), is less than \(\varepsilon \), and furthermore, if the interruption occurs, it must occur before T, and let \(\overline{ch*}\) be the dual of \(ch*\), e.g., if \(ch*=ch?\), then \(\overline{ch*}=ch!\) and vice versa. After all the readiness variables corresponding to \(\{io_i\}_I\) are set to 1 at the beginning, the discretization is taken by the following steps: first, if \(N(B, \varepsilon )\) holds and no communication among \(\{io_i\}_{i \in I}\) is ready, it executes following the discretization of continuous evolution, for at most \(\lceil \frac{T}{h}\rceil \) number of steps; then if \(N(B, \varepsilon )\) turns false without any communication occurring, the whole process terminates and meanwhile the readiness variables are reset to 0; otherwise if some communications get ready, an external choice between these ready communications is taken, and then, the readiness variables are reset to 0 and the corresponding \(Q_i\) is followed; finally, if the communications never occur and the continuous evolution never terminates, the continuous variable is assigned to the equilibrium point and the time progresses forever. It should be noticed that, the readiness variables of the partner processes will be used to decide whether a communication is able to occur. They are shared between parallel processes, but will always be written by one side.
Consider the water tank system introduced in Sect. 4, by using the rules in Table 1, a discretized system \(\textit{WTS}_{h,\varepsilon }\) is obtained as follows:
5.3 Properties
Before giving the main theorem, we introduce some notations. In order to keep the consistency between the behavior of an HCSP process and its discretized process, we introduce the notion of \((\delta , \epsilon )\)-robustly safe. First, let \(\phi \) denote a formula and \(\epsilon \) a precision, define \(N(\phi , -\epsilon )\) as the set \(\{ \mathbf {x}| \mathbf {x}\in \phi \wedge \forall \mathbf {y}\in \lnot \phi . \Vert \mathbf {x}-\mathbf {y}\Vert > \epsilon \}\). Intuitively, when \(\mathbf {x}\in N(\phi , -\epsilon )\), then \(\mathbf {x}\) is inside \(\phi \) and moreover the distance between it and the boundary of \(\phi \) is greater than \(\epsilon \).
Definition 6
( \((\delta , \epsilon )\) -robustly safe). An HCSP process P is \((\delta , \epsilon )\)-robustly safe, for a given initial state \(v_0\), a time precision \(\delta >0\) and a value precision \(\epsilon >0\), if the following two conditions hold:
-
for every continuous evolution \( \langle \dot{\mathbf {x}}=\mathbf {f}(\mathbf {x}) \& B\rangle \) occurring in P, when P executes up to \( \langle \dot{\mathbf {x}}=\mathbf {f}(\mathbf {x}) \& B\rangle \) at time t with state v, if \(v(B) = false\), then there exists \(\widehat{t} > t\) with \(\widehat{t} -t < \delta \) s.t. for any \(\sigma \) satisfying \(\mathbf {d}(\sigma , v[\mathbf {x}\mapsto X(\widehat{t}, \widetilde{\mathbf {x}}_0)]) < \epsilon \), \(\sigma \in N(\lnot B, -\epsilon )\), where \(X(t, \widetilde{\mathbf {x}}_0)])\) is the solution of \(\dot{\mathbf {x}}=\mathbf {f}(\mathbf {x})\) with initial value \(\widetilde{\mathbf {x}}_0 = v_0(\mathbf {x})\);
-
for every alternative process \(B \rightarrow P\) occurring in S, if B depends on continuous variables of P, then when P executes up to \(B \rightarrow P\) at state v, \(v \in N(B, -\epsilon )\) or \(v\in N(\lnot B, -\epsilon )\).
As a result, when P is discretized with a time error less than \(\delta \) and a value error less than \(\epsilon \), then P and its discretized process have the same control flow. The main theorem is given below.
Theorem 5
Let P be an HCSP process and \(v_0\) is the initial state. Assume P is \((\delta , \epsilon )\)-robustly safe with respect to \(v_0\). Let \(0< \varepsilon < \epsilon \) be a precision. If for any ODE \(\dot{\mathbf {x}}=\mathbf {f}(\mathbf {x})\) occurring in P, \(\mathbf {f}\) is Lipschitz continuous and \(\dot{\mathbf {x}}=\mathbf {f}(\mathbf {x})\) is GAS with \(\mathbf {f}(\bar{\mathbf {x}})=0\) for some \(\bar{\mathbf {x}}\), then there exist \(h >0\) and the equilibrium time for each ODE F in P, \(T_F>0\), s.t. \(P\cong _{h,\varepsilon }\textit{D}_{h, \varepsilon }(P)\).
We can compute that, the relation \(\mathcal {L} \delta + Mh \le \varepsilon \) holds for some constants \(\mathcal {L}\) and M. Especially, \(\mathcal {L}\) is the maximum value of the first derivative of \(\mathbf {x}\) with respect to t. More details can be found in [34].
6 Case Study
In this section, we illustrate our method through the safety verification of the water tank system, \(\textit{WTS}\), that is introduced in Sect. 4. The safety property is to maintain the value of d within [low, high], which needs to compute the reachable set of \(\textit{WTS}\). However, it is usually difficult because of the complexity of the system. Fortunately, the reachable set of the discretized \(\textit{WTS}_{h,\varepsilon }\) in Sect. 5 could be easily obtained. Therefore, we can verify the original system \(\textit{WTS}\) through the discretized one, \(\textit{WTS}_{h,\varepsilon }\), as follows.
In order to analyze the system, first of all, we set the values of parameters to \(Q_{max}=2.0\), \(\pi =3.14\), \(r=0.18\), \(g=9.8\), \(p=1\), \(lb=4.1\), \(ub=5.9\), \(low = 3.3\), \(high=6.6\), \(v_0=1\), and \(d_0=4.5\) (units are omitted here). Then, by simulation, we compute the values of \(\delta \) and \(\epsilon \) as 0.5 and 0.24, s.t. \(\textit{WTS}\) is \((\delta , \epsilon )\)-robustly safe. By Theorem 5, for a given \(\varepsilon \) with \(0< \varepsilon < \epsilon \), since \(\dot{d}\) and d are monotonic for both ODEs, we can compute a \(h>0\) s.t. \(\textit{WTS}\cong _{h,\varepsilon }{} \textit{WTS}_{h,\varepsilon }\). For different values of \(\varepsilon \) and h, \(\textit{Reach}(\textit{WTS}_{h,\varepsilon })\) could be computed, and then based on Theorem 1, we can obtain \(\textit{Reach}(\textit{WTS})\). Table 2 shows the results for different choices of \(\varepsilon \) and h. As seen from the results, when the values of precisions become smaller, \(\textit{Reach}(\textit{WTS}_{h,\varepsilon })\) and \(\textit{Reach}(\textit{WTS})\) get closer and tighter. For the smaller precisions, i.e., \((\varepsilon =0.1,h=0.05)\) and \((\varepsilon =0.05,h=0.01)\), the safety property of the system is proved to be true. However, for \((\varepsilon =0.2,h=0.2)\), the safety property of the system can not be promised.
7 Conclusion
Approximate bisimulation is a useful notion for analyzing complex dynamic systems via simpler abstract systems. In this paper, we define the approximate bisimulation of hybrid systems modelled by HCSP, and present an algorithm for deciding whether two HCSP processes are approximately bisimilar. We have proved that if all the ODEs are \(\mathrm {GAS}\), then the algorithm terminates in a finite number of steps. Furthermore, we define the discretization of HCSP processes, by representing the continuous dynamics by Euler approximation. We have proved for an HCSP process that, if the process is robustly safe, and if each ODE occurring in the process is Lipschitz continuous and \(\mathrm {GAS}\), then there must exist a discretization of the original HCSP process such that they are approximate bisimilar with the given precisions. Thus, the results of analysis performed on the discrete system can be carried over into the original dynamic system, and vice versa. At the end, we illustrate our method by presenting the discretization of a water tank example. Note that \(\mathrm {GAS}\) and robust safety are very restrictive from a theoretical point of view, but most of real applications satisfy these conditions in practice.
Regarding future work, we will focus on the implementation, in particular, the transformation from HCSP to ANSI-C. Moreover, it could be interesting to investigate approximate bisimularity with time bounds so that the assumptions of GAS and robust safety can be dropped. In addition, it deserves to investigate richer refinement theories for HCSP based on the notion of approximately bisimulation, although itself can be seen as a refinement relation as discussed in process algebra.
References
Simulink User’s Guide (2013). http://www.mathworks.com/help/pdf_doc/simulink/sl_using.pdf
Stateflow User’s Guide (2013). http://www.mathworks.com/help/pdf_doc/stateflow/sf_using.pdf
SysML V 1.4 Beta Specification (2013). http://www.omg.org/spec/SysML
Ahmad, E., Dong, Y., Wang, S., Zhan, N., Zou, L.: Adding formal meanings to AADL with hybrid annex. In: Lanese, I., Madelaine, E. (eds.) FACS 2014. LNCS, vol. 8997, pp. 228–247. Springer, Heidelberg (2015). doi:10.1007/978-3-319-15317-9_15
Alur, R., Dang, T., Esposito, J., Hur, Y., Ivancic, F., Kumar, V., Mishra, P., Pappas, G., Sokolsky, O.: Hierarchical modeling and analysis of embedded systems. Proc. IEEE 91(1), 11–28 (2003)
Angeli, D., et al.: A Lyapunov approach to incremental stability properties. IEEE Trans. Autom. Control 47(3), 410–421 (2002)
Angeli, D., Sontag, E.: Forward completeness, unboundedness observability, and their Lyapunov characterizations. Syst. Control Lett. 38(4), 209–217 (1999)
Chen, M., Ravn, A., Wang, S., Yang, M., Zhan, N.: A two-way path between formal and informal design of embedded systems. In: UTP 2016. LNCS (2016)
Dormoy, F.: Scade 6: a model based solution for safety critical software development. ERTS 08, 1–9 (2008)
Eker, J., Janneck, J., et al.: Taming heterogeneity - the Ptolemy approach. Proc. IEEE 91(1), 127–144 (2003)
Girard, A., Julius, A., Pappas, G.: Approximate simulation relations for hybrid systems. Discrete Event Dyn. Syst. 18(2), 163–179 (2008)
Girard, A., Pappas, G.: Approximation metrics for discrete and continuous systems. IEEE Trans. Autom. Control 52(5), 782–798 (2007)
Guelev, D., Wang, S., Zhan, N.: Hoare-style reasoning about hybrid CSP in the duration calculus. Technical report ISCAS-SKLCS-13-01, Institute of Software, Chinese Academy of Sciences (2013)
He, J.: From CSP to hybrid systems. In: A Classical Mind, Essays in Honour of C.A.R. Hoare, pp. 171–189. Prentice Hall International (UK) Ltd. (1994)
Henzinger, T., Ho, P., Wong-Toi, H.: Algorithmic analysis of nonlinear hybrid systems. IEEE Trans. Autom. Control 43(4), 540–554 (1998)
Henzinger, T.A., Sifakis, J.: The embedded systems design challenge. In: Misra, J., Nipkow, T., Sekerinski, E. (eds.) FM 2006. LNCS, vol. 4085, pp. 1–15. Springer, Heidelberg (2006). doi:10.1007/11813040_1
Henzinger, T.A.: The theory of hybrid automata. In: LICS 1996, pp. 278–292 (1996)
Julius, A., D’Innocenzo, A., Di Benedetto, M., Pappas, G.: Approximate equivalence and synchronization of metric transition systems. Syst. Control Lett. 58(2), 94–101 (2009)
Khalil, H.K., Grizzle, J.W.: Nonlinear Systems, vol. 3. Prentice Hall, New Jersey (1996)
Lanotte, R., Tini, S.: Taylor approximation for hybrid systems. In: Morari, M., Thiele, L. (eds.) HSCC 2005. LNCS, vol. 3414, pp. 402–416. Springer, Heidelberg (2005). doi:10.1007/978-3-540-31954-2_26
Lee, E.A.: What’s ahead for embedded software? Computer 33(9), 18–26 (2000)
Liu, J., Lv, J., Quan, Z., Zhan, N., Zhao, H., Zhou, C., Zou, L.: A calculus for hybrid CSP. In: Ueda, K. (ed.) APLAS 2010. LNCS, vol. 6461, pp. 1–15. Springer, Heidelberg (2010). doi:10.1007/978-3-642-17164-2_1
Majumdar, R., Zamani, M.: Approximately bisimilar symbolic models for digital control systems. In: Madhusudan, P., Seshia, S.A. (eds.) CAV 2012. LNCS, vol. 7358, pp. 362–377. Springer, Heidelberg (2012). doi:10.1007/978-3-642-31424-7_28
Platzer, A.: Differential-algebraic dynamic logic for differential-algebraic programs. J. Logic Comput. 20(1), 309–352 (2010)
Platzer, A.: The complete proof theory of hybrid systems. In: LICS, pp. 541–550. IEEE (2012)
Pola, G., Girard, A., Tabuada, P.: Approximately bisimilar symbolic models for nonlinear control systems. Automatica 44(10), 2508–2516 (2008)
Pola, G., Pepe, P., Di Benedetto, M.: Symbolic models for networks of discrete-time nonlinear control systems. In: ACC, pp. 1787–1792. IEEE (2014)
Selic, B., Gérard, S.: Modeling and Analysis of Real-Time and Embedded Systems with UML and MARTE: Developing Cyber-Physical Systems. Elsevier, Amsterdam (2013)
Sontag, E.D.: Mathematical Control Theory: Deterministic Finite Dimensional Systems, vol. 6. Springer, Heidelberg (2013)
Stoer, J., Bulirsch, R.: Introduction to Numerical Analysis, vol. 12. Springer, Heidelberg (2013)
Tiller, M.: Introduction to Physical Modeling with Modelica, vol. 615. Springer, Heidelberg (2012)
Tiwari, A.: Abstractions for hybrid systems. Formal Methods Syst. Des. 32(1), 57–83 (2008)
Wang, S., Zhan, N., Guelev, D.: An assume/guarantee based compositional calculus for hybrid CSP. In: Agrawal, M., Cooper, S.B., Li, A. (eds.) TAMC 2012. LNCS, vol. 7287, pp. 72–83. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29952-0_13
Yan, G., Jiao, L., Li, Y., Wang, S., Zhan, N.: Approximate Bisimulation and Discretization of Hybrid CSP. CoRR, abs/1609.00091, August 2016
Zhan, N., Wang, S., Zhao, H.: Formal modelling, analysis and verification of hybrid systems. In: Liu, Z., Woodcock, J., Zhu, H. (eds.) Unifying Theories of Programming and Formal Engineering Methods. LNCS, vol. 8050, pp. 207–281. Springer, Heidelberg (2013). doi:10.1007/978-3-642-39721-9_5
Chaochen, Z., Ji, W., Ravn, A.P.: A formal description of hybrid systems. In: Alur, R., Henzinger, T.A., Sontag, E.D. (eds.) HS 1995. LNCS, vol. 1066, pp. 511–530. Springer, Heidelberg (1996). doi:10.1007/BFb0020972
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Yan, G., Jiao, L., Li, Y., Wang, S., Zhan, N. (2016). Approximate Bisimulation and Discretization of Hybrid CSP. In: Fitzgerald, J., Heitmeyer, C., Gnesi, S., Philippou, A. (eds) FM 2016: Formal Methods. FM 2016. Lecture Notes in Computer Science(), vol 9995. Springer, Cham. https://doi.org/10.1007/978-3-319-48989-6_43
Download citation
DOI: https://doi.org/10.1007/978-3-319-48989-6_43
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-48988-9
Online ISBN: 978-3-319-48989-6
eBook Packages: Computer ScienceComputer Science (R0)





 s.t.
s.t. 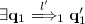 s.t.
s.t.  are defined as usual.
are defined as usual.  behaves like
behaves like