Data Access Based on Faceted Queries over Ontologies

Abstract

We propose a method for generating and evaluating faceted queries over ontology-enhanced distributed graph databases. A user, who only vaguely knows the domain ontology, starts with a set of keywords. Then, an initial faceted query is automatically generated and the user is guided in interactive modification and refinement of successively created faceted queries. We provide the theoretical foundation for this way of faceted query construction and translation into first order monadic positive existential queries.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In recent years, there is an increasing interest in developing database systems enriched with ontologies. The terminological component of the ontology can be used as a global schema providing an integrated global view over a set of local databases. A crucial issue is then a query language and a query paradigm. A standard way for querying graph databases (including RDF repositories) is SPARQL [13]. However, it is not a suitable language for end-users. Moreover, in order to formulate structural queries (e.g., in SPARQL or SQL), users have to know both the structure of the underlying ontology and the query language. In order to gain knowledge about the ontology, there is a need to query metadata. Only then, the metadata can be used to formulate queries concerning data. It can be expected that in order to progressively improve queries, the process of querying data and metadata can be iterative, can make a lot of trouble and be time consuming.

To avoid the aforementioned inconveniences, another query paradigms have been proposed, such as keyword search [10, 17], and faceted search [14]. Keyword search is the most popular in information retrieval systems, but lately we observe also a widespread application of keyword search paradigm to structured and semistructured data sources [3]. Faceted search has emerged as a foundation for interactive information browsing and retrieval and has become increasingly prevalent in online information access systems, particularly for e-commerce and site search [14]. Especially significant in the faceted search is implementation of the browsing paradigm, allowing for exploring and expressing information needs in interactive and iterative ways [7, 16]. Most importantly, the browsing and exploring concerns both the data and metadata.

In this paper, we follow both the keyword and the faceted search paradigms proposing a method of creating faceted queries starting from a keyword query. As a keyword query we assume a partially ordered set consisting of keywords being ontology concepts (unary predicates) and constants. The partial ordering is induced by the order of keywords in the query. The response to a keyword query is a subgraph of the ontology graph covering the given set of keywords and preserving partial ordering of keywords in the keyword query. The subgraph is used to generate an initial faceted query, which is presented to the user in a form of a faceted interface. A user can interactively modify and refine the faceted query browsing and exploring the ontology by means of the faceted interface. The final faceted query is translated into a first order (FO) query which is evaluated in local databases storing the extensional component of the ontology (in a form of graph databases).

Besides providing a global schema, an ontology is used for: (a) guiding the creation of faceted queries, (b) supporting translation of faceted queries into FO queries, (c) query rewriting, (d) dealing with labeled nulls, (e) deciding about query propagation, and to (f) control consistency [11]. It can be shown, that a faceted query is equivalent to a FO monadic positive existential query in a tree-shaped form. This allows for very efficient execution with polynomial combined complexity (considering the size of ontology rules, sizes of local graph databases and size of queries) [1, 11].

Related work: The faceted search has been surveyed in [5, 14]. This paradigm was used for querying documents, databases and semantic data, e.g., [4, 7, 12, 18]. Our work mostly relates to the results reported in [16] and [1]. In [16], the authors focused on browsing-oriented semantic faceted search supporting users in addressing their imprecise (fuzzy) needs. To this order, an extended facet tree has been proposed, which compactly captures both facets and facet values. In this case, faceted queries are equivalent to a subclass of FO conjunctive queries. Our formalization of faceted queries is rooted in [1], where faceted queries are equivalent to a subclass of FO positive existential queries. In [11], we proposed a way of answering faceted queries in a multiagent system. We discussed, how local agents consult with each other while evaluating queries, and we have shown that it is enough to propagate only boolean queries during this cooperation. The efficiency of query execution can be increased by asynchronous and parallel processing.

Contribution: The main novelties of the paper are: (1) we propose a method of generating faceted queries starting from a keyword query, and (2) we define semantics of faceted queries by translating them into FO faceted queries (FOFQ).

Paper outline: The paper is organized as follows. In Sect. 2, we review preliminaries and define the class of ontology under interest. A motivating running example and architecture of the system are presented in Sect. 3. In Sect. 4, we propose the way of defining faceted queries. Formal syntax and semantics of faceted queries are studied and illustrated in Sect. 5. In Sect. 6, we summarize the paper.

2 Preliminaries

Let $\mathsf{UP}$, $\mathsf{BP}$ and $\mathsf{Const}$ be countably infinite sets of, respectively, unary predicates (denoted by A, B, C), binary predicates (denoted by R, S, T) and constants (denoted by a, b, c). In $\mathsf{BP}$ we distinguish $\mathsf{type}$ (to denote the relation “type of”) and $=$ (to denote equality relation between constants). In $\mathsf{Const}$ we distinguish a subset $\mathsf{LabNull}$ of labeled nulls. For constants, which are not in $\mathsf{LabNull}$, the Unique Name Assumption (UNA) holds, i.e., different constants in $\mathsf{Const}\setminus \mathsf{LabNull}$ represent different values (nodes). For labeled nulls the UNA is not required, i.e., different labeled nulls may represent the same value (node) [6].

A graph database is a finite edge-labeled and directed graph ${\mathcal G}=({\mathcal N},{\mathcal E})$, where ${\mathcal N}\subseteq \mathsf{Const}\cup \mathsf{UP}$ is a finite set of nodes, and ${\mathcal E}\subseteq {\mathcal N}\times \mathsf{BP}\times {\mathcal N}$ is a finite set of labeled edges (or facts) , such that: if $(n_1,R,n_2)\in {\mathcal E}$ and $R\in \mathsf{BP}\setminus \{\mathsf{type}\}$, then $n_1,n_2\in \mathsf{Const}$, if $(n_1,\mathsf{type},n_2)\in {\mathcal E}$ then $n_1\in \mathsf{Const}$, and $n_2\in \mathsf{UP}$. In first order (FO) logic, we use the following notation: A(n) for $(n,\mathsf{type},A)\in {\mathcal E}$; $n_1= n_2$ for $(n_1,=,n_2)\in {\mathcal E}$, and $R(n_1,n_2)$, for $(n_1,R,n_2)\in {\mathcal E}$.

Let $\varSigma =\varSigma _E\cup \varSigma _I$ be a finite subset of $\mathsf{UP}\cup \mathsf{BP}$. An ontology with signature $\varSigma$ is a triple ${\mathcal O}=(\varSigma ,{\mathcal R},{\mathcal G})$, where ${\mathcal R}$ and ${\mathcal G}$ are, respectively, a finite set of rules and a finite database graph, over $\varSigma$ and $\mathsf{Const}$. The pair $(\varSigma ,{\mathcal R})$ is called the terminological component (or a TBox) of the ontology, while ${\mathcal G}$ is called the assertional component (or the ABox) of the ontology [2]. Predicates occurring in ${\mathcal G}$ are referred to as extensional predicates, and are denoted by $\varSigma _E$. The set $\varSigma _I=\varSigma \setminus \varSigma _E$ of predicates which are not in ${\mathcal G}$ are called intentional predicates. In practice, an ontology conforms to one of OWL 2 profiles [9]. In this paper, we restrict ourselves to rules of categories (1)–(11) listed in Table 1, last category, (12), is the category of integrity constraints [8].

Table 1. Categories of ontology rules

A FO formula is a monadic positive existential query (MPEQ), if it has exactly one free variable and is constructed only out of: (a) atoms of the form A(v), $R(v_1,v_2)$ and $v=a$; (b) conjunction $(\wedge )$, disjunction $(\vee )$, and existential quantification $(\exists )$. A query $Q(\mathbf{x})$, where $\mathbf{x}$ is a tuple of free variables (empty for boolean queries), is satisfiable in ${\mathcal O}=(\varSigma ,{\mathcal R},{\mathcal G})$, denoted ${\mathcal O}\models Q(\mathbf{x})$ if there is a tuple $\mathbf{a}$ (empty for boolean queries) from $\mathsf{Const}$, such that ${\mathcal G}\cup {\mathcal R}\models Q(\mathbf{a})$, where ${\mathcal G}\cup {\mathcal R}$ denotes all facts deduced from ${\mathcal G}$ using rules from ${\mathcal R}$. Then $\mathbf{a}$ is an answer to $Q(\mathbf{x})$ with respect to ${\mathcal O}$ (the empty tuple $\mathbf{a}$ denotes $\mathtt{TRUE}$).

3 Running Example and Architecture

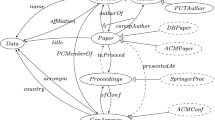
Let ${\mathcal O}=(\varSigma ,{\mathcal R},{\mathcal G})$, where: (1) ${\mathcal G}={\mathcal G}_1\cup {\mathcal G}_2\cup {\mathcal G}_3$ (Fig. 1); (2) rules in ${\mathcal R}$ are of categories listed in Table 1, some of them are given in Table 2; (3) $\varSigma =\varSigma _E\cup \varSigma _I$ is clear from the context.

Fig. 1.

A sample graph database consisting of three graphs

Fig. 2.

Architecture of DAFO system

Table 2. Sample rules in ${\mathcal O}$ conforming to categories from Table 1

A system providing data access based on faceted queries over ontologies (DAFO) (Fig. 2) belongs to a class of Ontology-Based Data Access (OBDA) systems [15], and follows so called single ontology approach. Data in different local DAFO databases complement each other, can overlap but do not contradict one another. The union of all local databases is a consistent database.

A user interacts with the system using a faceted query interface (FQ Interface) (step 1) and is guided by an ontology ${\mathcal O}=(\varSigma ,{\mathcal R},{\mathcal G})$, stored in part in the global schema, $Sch=(\varSigma ,{\mathcal R})$, and partly in local databases, $DB_i$, $1\le i\le k$. As a result of the interaction, a faceted query is created. The query is translated into FOFQ query Q, and rewritten into $Q'$ (step 2).

Then, $Q'$ is sent to all server agents (step 3). An agent do some local database specific rewritings and evaluations (step 4), propagates (if necessary) some boolean requests to partner agents (step 5), and gathers local answers (step 6). Finally, answers obtained from server agents are collected by the manager agent and returned to the user (step 7). Each server agent $S_i$ has its local database $DB_i=(\varSigma _i,{\mathcal R}_i,{\mathcal G}_i)$, where $\varSigma _i\subseteq \varSigma$, and ${\mathcal R}_i\subseteq {\mathcal R}$, $1\le i\le k$.

4 Defining Faceted Queries

In the process of defining queries in DAFO, a user starts from specifying a keyword query, which is understood as an ordered set of keywords. In response, a faceted interface and a first approximation of the expected faceted query, are generated. The user can interactively refine the query using information provided by the interface. Finally, the resulting faceted query is translated into a first order faceted query (FOFQ), which is a monadic PEQ.

Keyword Queries. A keyword query KQ over an ontology ${\mathcal O}$ is a partially ordered (by means of the preceding relation $\prec$) set $KQ=(K_0,K_1,\dots ,K_q)$, $q\ge 0$, of keywords, where $K_0\in \mathsf{UP}$, $K_i\in \mathsf{UP}\cup \mathsf{Const}$, $1\le i\le q$. For example, the following keyword query asks about ACM authors who presented a paper in 2014 at a DEXA conference.

$$\begin{aligned} KQ=(ACMAuthor, Paper, 2014, \textit{DEXAConf}). \end{aligned}$$

(1)

A keyword K subsumes a keyword $K'$ in ${\mathcal O}$, denoted ${\mathcal O}\models K'\sqsubseteq K$, iff: (1) if K and $K'$ are constants, then $K=K'$; (2) if $K',K\in \mathsf{UP}$, then: (a) $K=K'$, or (b) ${\mathcal O}\models sub(K',K)$ (rule (1) Table 1), or (c) there is $A\in \mathsf{UP}$ such that ${\mathcal O}\models K'\sqsubseteq A$ and ${\mathcal O}\models A\sqsubseteq K$.

A sequence $s=(K_1,R_1,K_2,\dots ,R_{m-1},K_m)$ is a path in ${\mathcal O}$ from $K_1$ to $K_m$, denoted $s\in path_{{\mathcal O}}(K_1,K_m)$, if: (1) $m=1$; (2) if $K_i\in \mathsf{UP}$ then $K_i$ is a domain of $R_i$, and a range of $R_{i-1}$; (3) if $K_i=a_i\in \mathsf{Const}$, then $\exists x R_i(a_i,x)$ and $\exists x R_{i-1}(x,a_i)$ are satisfied in ${\mathcal O}$.

We assume, that if $s\in path_{{\mathcal O}}(K_1,K_m)$, then also $s\in path_{{\mathcal O}}(K'_1,K'_m)$, for each $K'_1$ and $K'_m$, such that $K_1$ and $K_m$ subsume $K'_1$ and $K'_m$, respectively, in ${\mathcal O}$. A sequence s preserves the ordering $K_i\prec K_j$ if $K_i$ precedes $K_j$ in s, and violates this ordering if $K_j$ precedes $K_i$ in s.

Definition 1

The answer to KQ in ${\mathcal O}$ is a set PSet of paths in ${\mathcal O}$ such that:

• any path starts with $K_0$ and ends with some $K\in KQ$,

• any path preserves ordering of keywords induced by KQ.

Example 1

For the keyword query (1), PSet can have five paths:

$s_1=(ACMAuthor)$, $s_2=(ACMAuthor,authorOf,Paper)$,

$s_3=(ACMAuthor,authorOf,Paper,atConf,DEXAConf)$,

$s_4=(ACMAuthor,authorOf,Paper,pyear,2014)$,

$s_5=(ACMAuthor,authorOf,Paper,atConf,Conf,cyear,2014)$.

$s_5$ violates the preceding $2014\prec DEXAConf$, and is removed from PSet.

From a given PSet, a set TSet representing PSet is created. Each path from PSet, longer than 1, is represented by a set of triples, and a path with length 1, with itself:

$$TSet=\cup \{tset(s)\ \vert \ s\in PSet'\},$$

$$tset(s)=\{A\vert \ s=(A)\}\cup \{(A,R,B)\ \vert \ (A,R,B)\in s\}\cup \{(A,R,a)\ \vert \ (A,R,a)\in s\}.$$

For example, $TSet=\{ACMAuthor,(ACMAuthor,authorOf,Paper),$

$(Paper,atConf,DEXAConf),(Paper,pyear,2014),\dots \}$.

Creating Faceted Interface and Faceted Queries. Now, we discuss the way of creating faceted interfaces (FIs) and faceted queries (FQs) from a set TSet of triples representing the answer to a keyword query KQ. A FQ arises from a FI by selecting among alternatives offered by the FI.

Algorithm 1 specifies creation of FI (the upper part (FI)) and a selection procedure constituting a FQ (the bottom part (FQ)). In result, both FI and FQ are represented by the labeled tree T defined as the output of the algorithm.

A labeled tree in Fig. 3 represents a FI, and its underlined (selected) elements represent a FQ. The selection is done either by default (e.g., $\vee$) or is determined by the content of the underlying keyword query.

Fig. 3.

FI and initial FQ generated by Algorithm 1 for the keyword query KQ (1)

In Fig. 4, there is the interface implemented in DAFO system. First, a keyword query is defined. Next, a FI and a FQ are generated as the answer to the keyword query. The query can be interactively modified by a user. For example, the labeled tree viewed in Fig. 4, represents the faceted query presented in Fig. 3 after some modifications (refinement).

Fig. 4.

A sample graphical form of a faceted query in DAFO

The textual form of FQ in Fig. 4 is:

$$\begin{aligned} \begin{array}{c} \varGamma =T_1[B_1\wedge B_2/T_2[B_3/T_3\wedge B_4]], \end{array} \end{aligned}$$

(2)

where: $T_1=\{{ ACMAuthor}\}$, $B_1=(univ,\wedge \{NY,LA\})$, $B_2=(authorOf,\{\mathsf{any}\})$, $T_2=\{Paper\}$, $B_3=(atConf,\{\mathsf{any}\})$, $T_3=\vee \{{ ACMConf,DEXAConf}\}$, $B_4=(pyear,\{2014\})$.

Intuitively, $\vee \{{ ACMConf,DAXAConf}\}$ denotes conferences, classified either as ACM or DEXA conferences; $(atConf,\{\mathsf{any}\})$ denotes papers which have been presented at any conference; $(univ,\wedge \{NY,LA\})$ denotes authors representing both universities, i.e., NY and LA university.

5 Formal Syntax and Semantics of Faceted Queries

Complex faceted queries, like (2), are built of simple faceted queries defined by Definition 3, which in turn refer to simple faceted interfaces.

Definition 2

Simple faceted interfaces over an ontology ${\mathcal O}$ are:

• 1. $F=(\mathsf{type}, \{\vee ,\wedge \}X)$, where $X\subseteq \mathsf{UP}$ – a simple $\mathsf{type}$-based faceted interface,

• 2. $F=(R,(\{\vee ,\wedge \}\{\mathsf{any}\}\cup X)$, where $R\in \mathsf{BP}$, and $X\subseteq \{a\ \vert \ {\mathcal O}\models \exists x R(x,a)\}$ – a simple BP-based faceted interface.

Definition 3

Simple faceted queries over simple faceted interfaces are:

• 1. $\circ L$, where $L\subseteq X$ – over $F=(\mathsf{type}, \{\vee ,\wedge \}X)$, $\circ \in \{\vee ,\wedge \}$ denotes disjunctive ($\vee$) and conjunctive ($\wedge$) query;

• 2. $(R,\{\mathsf{any}\})$ and $(R,\circ L)$, where $L\subseteq X$ – over $F=(R,(\{\vee ,\wedge \}\{\mathsf{any}\}\cup X)$.

Definition 4

Let T and B be simple $\mathsf{type}$- and BP-based FQs, respectively. A (complex) FQ is an expression conforming to the syntax:

$$\begin{array}{rl} \varGamma &{} {:}{:}= T\ \vert \ T[\varDelta ]\\ \varDelta &{} {:}{:}= B\ \vert \ B/\varGamma \ \vert \ \varDelta \wedge \varDelta \end{array}$$

Note, that the FQ $\varGamma$ in (2) conforms to the above definition. A FQ in a tree form generated by means of Algorithm 1, can be translated into a FQ in the textual form defined by the grammar given in Definition 4. The translation is specified in Definition 5.

Definition 5

Let $T=r((v_1,T_1),\dots ,(v_k,T_k))$ be a tree form of FQ, where $T_i$ is a subtree with a root $v_i$. Translation $\tau (T)$ is defined recursively as follows:

$$\begin{aligned} \kappa (e,T) = \left\{ \begin{array}{ll} \lambda _E(e) &{} {if}\, \lambda _V(T)=\varepsilon \,\mathrm{,}\\ \lambda _E(e)/\tau (T) &{} {otherwise.} \end{array} \right. \end{aligned}$$

In order to define semantics, the faceted queries will be represented by means of atomic faceted queries.

Definition 6

An atomic faceted query is an unary predicate $A\in \mathsf{UP}$, a pair $(R,\mathsf{any})$, and a pair (R, a), where $R\in \mathsf{BP}$.

Any simple faceted query can be translated into a disjunction or a conjunction of atomic faceted queries. For example:

• $tr(\vee \{ACMConf,DAXAConf\})=ACMConf\vee DAXAConf$,

• $tr((atConf,\{\mathsf{any}\}))=(atConf,\mathsf{any})$,

• $tr((univ,\wedge \{NY,LA\}))=(univ,NY)\wedge (univ,LA)$.

Definition 7

Let t and b be atomic $\mathsf{type}$- and BP-based FQs, respectively. A (complex) FQ in the atomic normal form is defined by the grammar ($\circ \in \{\vee ,\wedge \}$):

$$\begin{array}{rl} \alpha &{} {:}{:}= t\ \vert \ t[\beta ]\ \vert \ \alpha \circ \alpha \ \vert \ (\alpha )\\ \beta &{} {:}{:}= b\ \vert \ b/\alpha \ \vert \ \beta \circ \beta \ \vert \ (\beta ) \end{array}$$

The translation $tr(\varGamma )$ of (2) into the atomic normal form results in:

$$\begin{aligned} \begin{array}{c} \sigma =t_1[b_1\wedge b_2\wedge b_3/t_2[b_4/(t_3\vee t_4)\wedge b_5]], \end{array} \end{aligned}$$

(3)

where: $t_1={ ACMAuthor}$, $b_1=(univ,NY)$, $b_2=(univ,LA)$, $b_3=(authorOf,\mathsf{any})$, $t_2=Paper$, $b_4=(atConf,\mathsf{any})$, $t_3={ ACMConf}$, $t_4={ DEXAConf}$, $b_5=(pyear,2014)$,.

Semantics for FQs is defined by means of the semantic function $\llbracket \alpha \rrbracket _x$ that assigns to a FQ in the atomic normal form a first order monadic positive existential query, referred to as FOFQ. x is then the only free variable in FOFQ.

Definition 8

The semantic function $\llbracket \alpha \rrbracket _x$ for FQs conforming to the grammar given in Definition 7, is as follows ($\circ \in \{\vee , \wedge \}$):

Fig. 5.

Syntactic tree of FOFQ $\llbracket \sigma \rrbracket _x$, where $\sigma$ is defined in (3)

In general, a FQ $\sigma$ in atomic normal form, can be expressed as a FOFQ $\llbracket \sigma \rrbracket _x$ of the form $A(x)\wedge \varphi (x)$, where $\varphi (x)$ is referred to as the qualifier of the query. For $\sigma$ in (3), $\llbracket \sigma \rrbracket _x=ACMAuthor(x)\wedge \varphi (x)$, with the syntactic tree presented in Fig. 5.

In [11], we proposed a method for evaluating FOFQs in a multiagent system. Then a set of server agents (see Fig. 2) cooperate in answering the query.

6 Summary and Conclusions

We proposed a method of creating and evaluating faceted queries in an ontology-enhanced database. The ontology under consideration belongs to the class determined by OWL 2 RL profile, and serves many purposes (mainly, as the global schema, to query rewriting and to decide about query propagation). A user formulates a request starting from a keyword query which is used to generate an initial faceted query. The faceted query can be next modified and refined in interactive and iterative way. Finally, the query is translated into a first ordered query and answered by cooperating local agents. The main issue for future work concerns the way of presenting and browsing the information content in the process of faceted query creation. In particular, there is a need for: (1) creating hierarchies of value clusters, (2) inventing a way of presenting objects represented by null values, (3) adopting a method of compact representation of complex structures or complex contents. We are also planning to verify our approach in real-world applications. This research has been supported by Polish Ministry of Science and Higher Education under grant 04/45/DSPB/0149.