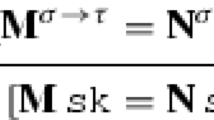AUTO2, A Saturation-Based Heuristic Prover for Higher-Order Logic

Abstract

We introduce a new theorem prover for classical higher-order logic named auto2. The prover is designed to make use of human-specified heuristics when searching for proofs. The core algorithm is a best-first search through the space of propositions derivable from the initial assumptions, where new propositions are added by user-defined functions called proof steps. We implemented the prover in Isabelle/HOL, and applied it to several formalization projects in mathematics and computer science, demonstrating the high level of automation it can provide in a variety of possible proof tasks.

1 Introduction

The use of automation is a very important part of interactive theorem proving. As the theories to be formalized become deeper and more complex, having a good automatic tool becomes increasingly indispensable. Such tools free users from the tedious task of specifying low level arguments, allowing them to focus instead on the high level outline of the proof.

There is a large variety of existing automatic proof tools. We will be content to list some of the representative ones. Some tools emulate human reasoning by attempting, at any stage of the proof, to apply a move that humans are also likely to make. These include the grind tactic in PVS [15], and the “waterfall” algorithm in ACL2 [10]. A large class of automatic provers are classical first-order logic solvers, based on methods such as tableau, satisfiability-modulo-theories (SMT), and superposition calculus. Sledgehammer in Isabelle [3] is a representative example of the integration of such solvers into proof assistants. Finally, most native tools in Isabelle and Coq are based on tactics, and their compositions to realize a search procedure. Examples for these include the auto tactic in Isabelle and Coq. The blast tactic in Isabelle [13] can also be placed in this category, although it has some characteristics of classical first-order solvers.

All these automatic tools have greatly improved the experience of formalization using proof assistants. However, it is clear that much work still needs to be done. Ideally, formalizing a proof on the computer should be very much like writing a proof in a textbook, with automatic provers taking the place of human readers in filling in any “routine” intermediate steps that are left out in the proof. Hence, one reasonable goal for the near future would be to develop an automatic prover that is strongly enough to consistently fill in such intermediate steps.

In this paper, we describe an alternative approach toward automation in proof assistants. It is designed to combine various desirable features of existing approaches. On the one hand it is able to work with human-like heuristics, classical higher-order logic, and simple type theory. On the other hand it has a robost, saturation-based search mechanism. We discuss these features and their motivations in Sect. 2.

As a first approximation, the algorithm in our approach consists of a best-first search through the space of propositions derivable from the initial assumptions, looking for a contradiction (any task is first converted into contradiction form). New propositions are generated by proof steps: user provided functions that match one or two existing propositions, and produce new propositions that logically follow from the matched ones. The order in which new propositions are added is dictated by a scoring function, as in a best-first search framework. There are several elaborations to this basic picture, in order to support case analysis, rewriting, skolemization, and induction. The algorithm will be described in detail, along with a simple example, in Sect. 3.

We implemented our approach in Isabelle/HOL, and used it to develop several theories in mathematics and computer science. In these case studies, we aim to use auto2 to prove all major theorems, either on its own or using a proof outline at a level of detail comparable to that of human exposition. We believe this aim is largely achieved in all the case studies. As a result, the level of automation provided by auto2 in our examples compares favorably with, and in some cases greatly exceeds that of existing tools provided in Isabelle. We give some examples from the case studies in Sect. 4.

The implementation, as well as the case studies, are available at https://github.com/bzhan/auto2. We choose the name auto2 for two reasons: first, we intend it to be a general purpose prover capable of serving as the main automatic tool of a system, as auto in Isabelle and Coq had been. Second, it relates to one of the main features of the algorithm, which is that any proof step matches at most two items in the state.

In Sect. 5, we compare our approach with other major approaches toward automation, as well as list some related work. We conclude in Sect. 6, and discuss possible improvements and future directions of research.

2 Objectives

In this section, we list the main features our approach is designed to have, and the motivations behind these features.

Use of human-like heuristics: The prover should make use of heuristics that humans employ when searching for proofs. Roughly speaking, such heuristics come in two levels. At the lower level, there are heuristics about when to apply a single theorem. For example, a theorem of the form $A\implies B\implies C$ can be applied in three ways: deriving C from A and B, deriving $\lnot A$ from B and $\lnot C$, and deriving $\lnot B$ from A and $\lnot C$. Some of these directions may be more fruitful than others, and humans often instinctively apply the theorem in some of the directions but not in others. At the higher level, there are heuristics concerning induction, algebraic manipulations, procedures for solving certain problems, and so on. Both levels of heuristics are essential for humans to work with any sufficiently deep theory. Hence we believe it is important for the automatic prover to be able to take these into account.

Extensibility: The system should be extensible in the sense that users can easily add new heuristics. At the same time, such additions should not jeopardize the soundness of the prover. This can be guaranteed by making sure that every step taken by the user-added heuristics is verified, following the LCF framework.

Use of higher-order logic and types: The prover should be able to work with higher-order logic, and any type information (in the Isabelle sense) that is present. In particular, we want to avoid translations to and from untyped first-order logic that are characteristic of the use of classical first-order solvers. Avoiding these has several benefits: many heuristics that humans use are best stated in higher-order logic. Also, the statement to be proved is kept short and close to what humans work with, which facilitates printing an informative trace when a proof fails.

Saturation-based search mechanism: Most heuristics are fallible in the sense that they are not appropriate in every situation, and can lead to dead ends when applied in the wrong situations. Moreover, when several mutually-exclusive heuristics are applicable, we would like to consider all of them in turn. Some kind of search is necessary to deal with both of these problems. We follow a saturation-based search strategy in order to obtain the following desirable property: all steps taken by the prover are both permanent and “non-committal”. That is, the result of any step is available for use throughout the remainder of the search, but there is never a requirement for it to be used, to allow for the possibility that the step is not appropriate for the proof at hand. The choice of E-matching over simplification to deal with equality reasoning is also chosen with this property in mind.

Having listed the principles motivating our approach, we also want to clarify what are not our main concerns. First, our focus is on proof tasks that occur naturally as intermediate steps during proofs of theorems in mathematics and computer science. We do not intend the prover to be competitive against more specialized algorithms when faced with large tasks that would also be difficult for humans. Second, the prover is not fully automated in the sense that it requires no human intervention – the user still needs to provide heuristics to the prover, including how to use each of the previously proved theorems. Finally, we do not intend to make the prover complete. For more difficult theorems, it expects hints in the form of intermediate steps.

3 Description of the System

In this section, we describe the auto2 prover in detail, followed by a simple example, and a discussion of how the system is used in practice. We begin with a high-level description of the algorithm, leaving the details to the following subsections.

The algorithm follows a saturation-based strategy, maintaining and successively adding to a list of items. We will call this list the main list in the remainder of this section. For a first pass, we can think of items as propositions that follow from the initial assumptions, and possibly additional assumptions. Later on (Sect. 3.2) we will see that it can also contain other kinds of information, in addition to or instead of a proposition. Each item is placed in a box, which specifies what additional assumptions the item depends on. We discuss boxes in more detail in Sect. 3.1.

New items that may be added to the list are created by proof steps, which are user-provided functions that accept as input one or two existing items, and derive a list of new items from the inputs. With a few exceptions (Sect. 3.3), the new items must logically follow from the input items. One common kind of proof steps matches the input items to the one or two assumptions of a theorem, and when there is a match, return the conclusion of the theorem. However, as proof steps are arbitrary functions, they can have more complex behavior.

Reasoning with equalities is achieved by matching up to equivalence (E-matching) using a rewritetable. The rewrite table is a data structure that maintains the list of currently known equalities (not containing schematic variables). It provides a matching function that, given a pattern p and a term t, returns all matches of t against p, up to rewriting t using the known equalities. The rewrite table automatically uses transitivity of equality, as well as the congruence property (that is, $a_1=b_1,\dots ,a_n=b_n$ implies $f(a_1,\dots ,a_n)=f(b_1,\dots ,b_n)$). See [11] for a modern introduction to E-matching. In our implementation, E-matching is essentially a first-order process (we only make use of equalities between terms not in function position), but we also allow matching of certain higher-order patterns, and extend it in other ways (Sect. 3.4). Matching using the rewrite table is used as the first step of nearly all proof steps.

New items produced by proof steps are collected into updates, and each update is assigned a score, which indicates its priority in the best-first search. All new updates are first inserted into a priority queue. At each iteration of the algorithm, the update with the lowest score is pulled from the queue. The items contained in the update are then added to the main list and processed one-by-one. Scoring is discussed in Sect. 3.5.

With these in mind, we can give a first sketch of the main loop of the algorithm. We assume that the statement to be proved is written in contradiction form (that is, $[A_1,\dots ,A_n]\implies C$ is written as $[A_1,\dots ,A_n,\lnot C]\implies \texttt {False}$), so the goal is to derive a contradiction from a list of assumptions $A_1,\dots ,A_n$.

• The algorithm begins by inserting a single update to the priority queue, containing the propositions $A_1,\dots , A_n$.

• At each iteration, the update with the lowest score is pulled from the priority queue. Items within the update are added one-by-one to the main list.

• Upon adding a non-equality item, all proof steps taking one input item are invoked on the item. All proof steps taking two input items are invoked on all pairs of items consisting of the new item and another item in the main list. All updates produced are added to the priority queue.

• Upon adding an equality item (without schematic variables), the equality is added to the rewrite table. Then the procedure in the previous step is redone with the new rewrite table on all items containing up to equivalence either side of the equality (this is called incremental matching). All new updates (those that depend on the new equality) are added to the priority queue.

• The loop continues until a contradiction (depending only on the initial assumptions) are derived by some proof step, or if there are no more updates in the queue, or if some timeout condition is reached.

In the current implementation, we use the following timeout condition: the loop stops after pulling N updates from the priority queue, where N is set to 2000 (in particular, all invocations of auto2 in the given examples involve less than 2000 steps).

3.1 Box Lattice

Boxes are used to keep track of what assumptions each item depends on. Each primitive or composite box represents a list of assumptions. They are defined recursively as follows: a composite box is a set of primitive boxes, representing the union of their assumptions. The primitive boxes are indexed by integers starting at 0. Each primitive box inherits from a composite box consisting of primitive boxes with smaller index, and contains an additional list of assumptions. It represents the result of adding those assumptions to the parent box. The primitive box 0 (inheriting from {}) contains the list of assumptions in the statement to be proved. Other primitive boxes usually inherit, directly or indirectly, from {0}. The primitive boxes also keep track of introduced variables. From now on we will simply call a composite box as a box.

If a contradiction is derived in a box (that is, if False is derived from the assumptions in that box), the box is called resolved, and appropriate propositions (negations of the assumptions) are added to each of its immediate parent boxes. The overall goal of the search is then to resolve the box {0}, which contains exactly the assumptions for the statement to be proved.

There is a natural partial order on the boxes given by inclusion, and a merge operation given by taking unions, making the set of boxes into a semilattice. New primitive boxes are created by proof steps, and are packaged into updates and added to the queue with a score just like new items. Creating a new primitive box effectively starts a case analysis, as we will explain in the example in Sect. 3.6.

3.2 Item Types

In this section we clarify what information may be contained in an item. In general, we think of an item in a box b as any kind of information that is available under the assumptions in b. One important class of items that are not propositions are the term items. A term item t in box b means t appears as a subterm of some proposition (or another kind of item) in b. The term items can be matched by proof steps just like propositions. This allows the following implementation of directed rewrite rules: given a theorem $P = Q$, where any schematic variable appearing in Q also appears in P, we can add a proof step that matches P against any term item t, and produces the equality $P(\sigma ) = Q(\sigma )$ for any match with instantiation $\sigma$. This realizes the forward rewrite rule from P to Q.

In general, each item consists of the following information: a string called item type that specifies how to interpret the item; a term called tname that specifies the content of the item; a theorem that justifies the item if necessary, and an integer score which specifies its priority in the best-first search. The most basic item type is PROP for propositions, for which tname is the statement of the theorem, and is justified by the theorem itself. Another basic type is TERM for terms items, for which tname is the term itself, and requires no justifying theorems.

The additional information contained in items can affect the behavior of proof steps, and by outputting an item with additional information, a proof step can affect how the output is used in the future. This makes it possible to realize higher level controls necessary to implement more complex heuristics. To give a simple example, in the current implementation, disjunctions are stored under two different item types: DISJ and DISJ_ACTIVE. The latter type induces case analysis on the disjunction, while the former does not. By outputting disjunctions in the appropriate type, a proof step can control whether case analysis will be invoked on the result.

3.3 Skolemization and Induction

Usually, when a proof step outputs a proposition, it must derive the justifying theorem for that proposition, using the justifying theorems of the input items. There are two main exceptions to this. First, given an input proposition $\exists x. P(x)$, a proof step can output the proposition P(x), where x is a previously unused constant. This realizes skolemization, which in our framework is just one of the proof steps.

The second example concerns the use of certain induction theorems. For example, induction on natural numbers can be written as:

$$\begin{aligned} P(0) \implies \forall n. P (n - 1) \longrightarrow P(n) \implies P(n). \end{aligned}$$

This form of the induction theorem suggests the following method of application: suppose n is an initial variable in a primitive boxi, and proposition $n\ne 0$ is known in (the composite) box $\{i\}$. Then we may insert $P(n-1)$ into box $\{i\}$, where P is obtained from the list of assumptions in i containing n. This corresponds to the intuition that once the zero case is proved, one may assume $P(n-1)$ while proving P(n).

In both cases, any contradiction that depends on the new proposition can be transformed into one that does not. In this first case, this involves applying a particular theorem about existence (exE in Isabelle). In the second case, it involves applying the induction theorem.

3.4 Matching

In this section, we provide more details about the matching process. First, the presence of box information introduces additional complexities to E-matching. In the rewrite table, each equality is stored under a box, and each match is associated to a box, indicating which assumptions are necessary for that match. When new items are produced by a proof step, the items are placed in the box that is the merge of boxes containing the input items, and the boxes associated to all matches performed by that proof step.

We also support the following additional features in matching:

• Matching of associative-commutative (AC) functions: the matching makes limited use of properties of AC functions. For example, if $x= y \star z$ is known, where $\cdot \star \cdot$ is AC, then the pattern $y \star ?a$ can match the term $p \star x$, with instantiation $?a := p \star z$ (since $y \star (p \star z) = p \star (y \star z) = p \star x$). The exact policy used in AC-matching is rather involved, as it needs to balance efficiency and not missing important matches.

• Matching of higher-order patterns: we support second-order matching, with the following restriction on patterns: it is possible to traverse the pattern in such a way that any schematic variable in function position is applied to distinct bound variables in its first appearance. For example, in the following theorem:

  $$\begin{aligned} \forall (n\,{:}{:}\,\text {nat}). f(n) \le f (n + 1) \implies m \le n\implies f(m) \le f(n), \end{aligned}$$

  one can match its first assumption and conclusion against two items, since the left side of the inequality in the first assumption can be matched to give a unique instantiation for f. The condition given here is slightly more general than the condition given by Nipkow [12], where all appearances of a schematic variable in function position must be applied to distinct bound variables.

• Schematic variables for numeric constants: one can restrict a schematic variable to match only to numeric constants (in the current implementation, this is achieved by a special name $?\mathtt {NUMC}_i$). For example, one can write proof steps that perform arithmetic operations, by matching terms to patterns such as $?\mathtt {NUMC}_1 + ?\mathtt {NUMC}_2$.

• Custom matching functions: one can write custom functions for matching a pattern against an item. This is especially important for items of type other than PROP. But it is also useful for the PROPs themselves. For example, if the pattern is $\lnot (p < q)$, one can choose to match $q \le p$ instead, and convert any resulting theorem using the equivalence to $\lnot (p <q)$.

3.5 Scoring

The scoring function, which ranks future updates, is crucial for the efficiency of the algorithm as it determines which updates will be explored first in the search. It tries to guess which reasoning steps are more likely to be relevant to the proof at hand. In the current implementation, we choose a very simple strategy. Finding a better scoring strategy will certainly be a major focus in the future.

The current scoring strategy is as follows: the score of any update equals the maximum of the scores of the dependent items, plus an increment depending on the content of the update. The increment is bigger (i.e. the update is discouraged) if the terms in the update are longer, or if the update depends on many additional assumptions.

3.6 A Simple Example

We now give a sample run of auto2 on a simple theorem. Note this example is for illustration only. The actual implementation contains different proof steps, especially for handling disjunctions. Moreover, we ignore scoring and the priority queue, instead adding items directly to the list. We also ignore items that do not contribute to the eventual proof.

The statement to be proved is

$$\begin{aligned} \text {prime }p \implies p > 2 \implies \text {odd } p. \end{aligned}$$

Converting to contradiction form (and noting that odd p is an abbreviation for $\lnot \text {even } p$), our task is to derive a contradiction from assumptions $\text {prime }p$, $p > 2$, and $\text {even } p$. The steps are:

• 1. Add primitive box 0, with variable p, and assumptions $\text {prime }p$, $p > 2$, and $\text {even } p$.

• 2. Add subterms of the propositions, including $\texttt {TERM}\,\text {prime }p$ and $\texttt {TERM}\,\text {even } p$.

• 3. The proof step for applying the definition of prime adds equality

  $$\begin{aligned} \text {prime }p = (p > 1 \wedge \forall m. m \text { dvd }p\longrightarrow m = 1 \vee m = p) \end{aligned}$$

  from $\texttt {TERM}\,\text {prime }p$. Likewise, the proof step for applying the definition of even adds equality $\text {even } p = 2 \text { dvd }p$ from $\texttt {TERM}\,\text {even } p$.

• 4. When the first equality in the previous step is applied, incremental matching is performed on the proposition $\text {prime }p$. It now matches the pattern $?A \wedge ?B$, so the proof step for splitting conjunctions produces $p > 1$ and $\forall m. m \text { dvd }p\longrightarrow m = 1 \vee m = p$.

• 5. A proof step matches the propositions $\forall m. m \text { dvd }p \longrightarrow m = 1 \vee m = p$ and $\text {even } p$ (the second item, when rewritten as $2 \text { dvd }p$, matches the antecedent of the implication), producing $2 = 1 \vee 2 = p$.

• 6. The proof step for invoking case analysis matches $2 = 1 \vee 2 = p$ with pattern $?A \vee ?B$. It creates primitive box 1, with assumption $2 = 1$ (see Fig. 1).

• 7. A proof step matches $2 = 1$ (in box $\{1\}$) with pattern $?\mathtt {NUMC}_1 =\, ?\mathtt {NUMC}_2$. The proof step examines the constants on the two sides, finds they are not equal, and outputs a contradiction. This resolves box $\{1\}$, adding $2\ne 1$ into box $\{0\}$.

• 8. A proof step matches $2 = 1 \vee 2 = p$ with $2\ne 1$, producing $2 = p$.

• 9. When the equality in the previous step is added, incremental matching is performed on the proposition $p > 2$ (one of the initial assumptions). This proposition matches pattern $?n >\, ?n$ (when rewritten as $p > p$ or $2 > 2$), giving a contradiction. This resolves box $\{0\}$ and finishes the proof.

Fig. 1.

State of proof after step 6. Arrow indicates inheritance relation on boxes.

3.7 Proof Scripts

For the case studies, we designed our own language of proof scripts for specifying intermediate steps in the proof of a more difficult theorem. The proof scripts are provided as an argument to the auto2 tactic, and are interpreted within the tactic. This requires some straightforward modifications to the main loop and the scoring mechanism, which we will not discuss. The benefit of using an internally interpreted script (instead of Isar) is that the entire state of the proof is maintained between lines of the script, and all previously proved statements are available for use at any given point.

The proof script consists of atomic commands joined together with two connectors: THEN and WITH. Each atomic command specifies an intermediate statement to prove, and what update to add once that statement is proved. The meanings of the two connectors are as follows. The command A THEN B means first process A, and after A is finished, process B. The command A WITH B (with A atomic) means attempt to prove the intermediate statement specified in A, processing B as a part of the attempt.

The simplest atomic commands are OBTAIN and CASE. The command OBTAIN p means attempt to prove p and add it to the list. The command CASE p means attempt to prove that p results in a contradiction, and add $\lnot p$ to the list. It is equivalent to OBTAIN $\lnot p$.

The command CHOOSE $x,\, p(x)$ specifies $\exists x. p(x)$ as an intermediate statement. After it is proved, the resulting existence fact is instantiated with variable x (the command fixes variable x so it is not used in other places).

Finally, there are various flavors of induction commands, which specify applications of various kinds of induction theorems. We designed the script system to be extensible: it is possible for the user to add new types of atomic commands.

3.8 Practical Usage

We end this section with a discussion of practical issues concerning the use of the auto2 system.

First, we describe the process of constructing the collection of proof steps. The collection of proof steps specifies exactly what steps of reasoning auto2 may take. With the exception of equality reasoning, which relies on the rewrite table and E-matching, all other forms of reasoning are encoded as proof steps. This includes basic deductions in logic and arithmetic, and the simplification of terms. In particular, auto2 does not invoke any of the other Isabelle commands such as simp and arith, except within the implementation of individual proof steps, for carrying out very specific tasks.

Each proof step is intended to represent a single step of reasoning, and has a clearly-defined behavior. The simplest proof steps apply a single theorem. For example, a theorem of the form $A\implies B\implies C$ can be added for use in either the forward or one of the two backward directions. More complex proof steps are implemented as ML functions. The implementation can make full use of the existing conversion and tactics facility in Isabelle/ML.

In theories developed using auto2, each proof step using theorems in that theory is added right after all required theorems are proved. Once the proof step is added, it is used in all ensuing proofs, both in the current theory and in all descendent theories. For theorems proved in the Isabelle library, “wrapper” theories are created to add proof steps using them. The case studies, for example, use shared wrapper theories for theorems concerning logic, arithmetic, sets, and lists.

There are some circumstances where removing a proof step after using it in a few proofs is acceptable. For example, if a theory introduces constructions, or proves lemmas that are used only within the theory, it is acceptable to remove proof steps related to those constructions and lemmas once they are no longer used. The guiding principle is as follows: by the end of the development of a theory, the collection of proof steps from that theory should form a coherent system of heuristics on how to use the results in that theory. In subsequent theories, auto2 should have a basic competence in using results from that theory, and it should always be possible to specify more involved applications in proof scripts. In particular, the user should never need to add proof steps for using theorems from a previous theory, nor temporarily remove a proof step from a previous theory (to avoid exploding the search space). Realizing this principle means more work is needed when building each theory, to specify the right set of proof steps, but it should pay off in the long run, as it frees the user from having to refer back to the theory in subsequent developments.

Second, we describe the usual interaction loop when proving a theorem or which applying auto2 directly fails. One begins by working out an informal proof of the theorem, listing those steps that appear to require some creativity. One can then try auto2 with these intermediate steps added. If it still does not work, the output trace shows the first intermediate step that auto2 cannot prove, and what steps of reasoning are taken in the attempt to prove that step. If there is some step of reasoning that should be taken automatically but is not, it is an indication that some proof step is missing. The missing proof step should be added, either to a wrapper theory if the relevant theorem is proved in the Isabelle library, or right after the theorem if it is proved in a theory developed using auto2. On the other hand, if one feels the missing step should not be taken automatically, but is a non-obvious step to take in the proof of the current theorem, one should add that step to the proof script instead. The process of adding to the collection of proof steps or to the proof script continues until auto2 succeeds.

4 Case Studies

In this section, we give some examples from the case studies conducted using auto2. We will cover two of the six case studies. Descriptions for the other four (functional data structures, Hoare logic, construction of real numbers, and Arrow’s impossibility theorem) can be found in the repository. In writing the case studies, we aim to achieve the following goal: all major theorems are proved using auto2, either directly or using proof scripts at a level of detail comparable to human exposition. When a case study parallels an existing Isabelle theory, there may be some differences in the definitions, organization, and method of proof used. The content of the theorems, however, are essentially the same. In the examples below, we will sometimes compare the length of our scripts with the length of Isar scripts for the same theorem in the Isabelle library. We emphasize that this is not intended to be a rigorous comparison, due to the differences just mentioned, and since auto2 is provided additional information in the form of the set of proof steps, and takes longer to verify the script. The intent is rather to demonstrate the level of automation that can be expected from auto2.

Besides the examples given below, we also make a special note of the case study on Arrow’s impossibility theorem. The corresponding theory in the Isabelle AFP is one of the seven test theories used in a series of benchmarks on Sledgehammer, starting in [4].

4.1 Elementary Theory of Prime Numbers

The development of the elementary theory of prime numbers is one of the favourites for testing theorem provers [5, 14]. We developed this theory starting from the definition of prime numbers, up to the proof of the infinitude of primes and the unique factorization theorem, following HOL/Number_Theory in the Isabelle library. For the infinitude of primes, the main lemma is that there always exists a larger prime:

auto2 is able to prove this theorem when provided with the following proof script:

This corresponds to the following proof of next_prime_bound in the Isabelle theory HOL/Number_Theory/Primes (18 lines).

Likewise, we formalized the unique factorization theorem. The uniqueness part of the theorem is as follows (note M and N are multisets, and ${\text {set}}M$ and ${\text {set}}N$ are the sets corresponding to M and N, eliminating duplicates).

The script needed for the proof is:

This can be compared to the proof of multiset_prime_factorization_unique_aux in the Isabelle theory HOL/Number_Theory/UniqueFactorization (39 lines).

4.2 Verification of Imperative Programs

A much larger project is the verification of imperative programs, building on the Imperative HOL library, which describes imperative programs involving pointers using a Heap Monad [6]. The algorithms and data structures verified are:

• Reverse and quicksort on arrays.

• Reverse, insert, delete, and merge on linked lists.

• Insert and delete on binary search trees.

The proofs are mostly automatic, which is in sharp contrast with the corresponding examples in the Isabelle distribution (in Imperative_HOL/ex). We give one example here. The merge function on two linked lists is defined as:

To prove the main properties of the merge function, we used the following two lemmas (commands adding their proof steps are omitted):

The statements of the theorems are:

Each of these theorems is proved (in 30–40 s on a laptop) using the same proof script, specifying the induction scheme:

In the Isabelle library the proof of the three corresponding theorems, including that of two induction lemmas proved specifically for these theorems, takes 166 lines in total. These theorems also appear to be well beyond the ability of the Sledgehammer tools. It is important to note that this automation is not based on Hoare logic or separation logic (the development here is separate from the case study on Hoare logic), but the proofs here use directly the semantics of commands like in the original examples.

5 Related Work

The author is particularly inspired by the work of Ganesalingam and Gowers [9], which describes a theorem prover that can output proofs in a form extremely similar to human exposition. Our terminology of “box” is taken from there (although the meaning here is slightly different).

There are two ways in which our approach resembles some of the classical first-order solvers. The first is the use of a“blackboard” maintaining a list of propositions, with many“modules” acting on them, as in a Nelson-Oppen architecture [2]. The second is the use of matching up to equivalence (E-matching), which forms a basic part of most SMT solvers. The main differences are explained in the first three items in Sect. 2: our focus on the use of human-like heuristics, and our lack of translation to and from untyped first-order logic.

There have been extensive studies on heuristics that humans use when proving theorems, and their applications to automation. Ganesalingam and Gowers [9] give a nice overview of the history of such efforts. Some of the more recent approaches include the concept of proof plans introduced by Bundy [7, 8]. Among proof tools implemented in major proof assistants, the grind tactic [15] and the “waterfall” algorithm in ACL2 [10] both attempt to emulate human reasoning processes. Compared to these studies, we place a bigger emphasis on search, in order to be tolerant to mistaken steps, and to try different heuristics in parallel. We also focus more on heuristics for applying single theorems, although the system is designed with the possibility of higher-level heuristics in mind (in particular with the use of item types).

Finally, tactic-based automation such as auto, simp, and fast in Isabelle also use heuristics in the sense that they apply theorems directionally, and are able to carry out procedures. The main difference with our approach is the search mechanism used. In tactic-based automation, the search is conducted over the space of proof states, which consists of the current goal and a list of subgoals. For blast and other tableau-based methods, the search is over the space of possible tableaux. In our approach, the search is saturation-based, and performed over the space of propositions derivable from the initial assumptions.

A similar “blackboard” approach is used for heuristic theorem proving by Avigad et al. [1], where the focus is on proving real inequalities. The portion of our system concerning inequalities is not as sophisticated as what is implemented there. Instead, our work can be viewed as applying a similar technique to all forms of reasoning.

6 Conclusion

In this paper, we described an approach to automation in interactive theorem proving that can be viewed as a mix of the currently prevailing approaches. While the ideas behind the prover are mostly straightforward, we believe the combination of these ideas is underexplored and, given the examples above, holds significant promise that warrants further exploration.

There are many aspects of auto2 that can be improved in the future. Two immediate points are performance and debugging. The E-matching process is far from optimized, in the sense of [11]. For debugging, the program currently outputs the list of updates applied to the state. One might instead want to view and traverse the dependency graph of updates. One would also like to query the rewrite table at any point in the proof.

There are also many directions of future research. I will just list three main points:

• The scoring function is currently very simple. Except for a few cases, there is currently no attempt at take into account during scoring the proof step used. Instead, one would like to distinguish between proof steps that “clearly should be applied”, and those that should be applied “with reluctance”. There is also the possibility of using various machine learning techniques to automatically adjust the scoring function for individual proof steps.

• Several aspects of elementary reasoning, such as dealing with associative-commutative functions, and with ordered rings and fields, pose special challenges for computers. While the current implementation is sufficient in these aspects for the examples at hand, more will need to be done to improve in both completeness and efficiency.

• Finally, one would like to improve auto2’s ability to reason in other, diverse areas of mathematics and computer science. On the verification of imperative programs front, one would like to know how well auto2 can work with separation logic, or perhaps a framework based on a mix of separation logic and“natural” reasoning used in the given examples will be ideal. On the mathematical front, each field of mathematics offers a distinctive system of heuristics and language features. One would like to expand the collection of proof steps, as well as proof script syntax, to reflect these features.