Abstract
This paper presents the first formalization of three classic confluence criteria for first-order term rewrite systems by Huet and Toyama. We have formalized proofs, showing that (1) linear strongly closed systems, (2) left-linear parallel closed systems, and (3) left-linear almost parallel closed systems are confluent. The third result is extended to commutation. The proofs were carried out in the proof assistant Isabelle/HOL as part of the library IsaFoR and integrated into the certifier CeTA, significantly increasing the number of certifiable proofs produced by automatic confluence tools.
This work is supported by FWF (Austrian Science Fund) project P27528.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Confluence of rewrite systems is an important property, which is intimately connected to uniqueness of normal forms, and hence to determinism of programs. In recent years there has been tremendous progress in establishing confluence or non-confluence of TRSs automatically, with a number of tools under active development, like ACP [2], Saigawa [8, 11], CoLL [18], and our own tool, CSI [23].
The recent achievements in confluence research have enabled a competitionFootnote 1 where such automated tools try to establish/refute confluence. As the proofs produced by these tools are often complicated and large, there is interest in checking them with trustable certifiers like CeTA [21]. (CeTA is a certifier for termination, confluence and complexity proofs for TRSs. Other certifiers exist for termination proofs, notably Rainbow [4] and CiME3 [5].) Given a certificate in CPF (certification problem format) [19], CeTA will either answer CERTIFIED or return a detailed error message why the proof was REJECTED. Its correctness is formally proven as part of IsaFoR, the Isabelle Formalization of Rewriting. IsaFoR contains executable “check”-functions for each formalized proof technique together with formal proofs that whenever such a check succeeds, the technique was indeed applied correctly. Isabelle ’s code-generation facility is used to obtain a trusted Haskell program from these check functions: the certifier CeTA.Footnote 2
In the recent past, several confluence results have been formalized, starting from the fundamental result by Knuth and Bendix [12] that a terminating rewrite system is confluent if and only if all its critical pairs are joinable. For non-terminating rewrite systems, weak orthogonality as well as sufficient conditions for non-joinability of critical pairs based on unification, discrimination pairs [1], interpretations, and tree automata [6] have been formalized. These results are described in [14]. More recently, redundant rules [13] and rule labeling [15] increased the number of certifiable confluence proofs significantly.
In this paper we report on the formalization of three classical confluence results. Two of these are due to Huet [10] and presented in full detail in the textbook of Baader and Nipkow [3, Lemma 6.3 and Sect. 6.4]. The third result is due to Toyama [22].
The remainder of this paper is organized as follows. After recalling basic notions of term rewriting in the next section, in Sect. 3 we report on the formalization of the result that linear strongly closed rewrite systems are confluent. Linearity is an important limitation, but the result does have its uses [7]. Section 4 is devoted to the formalization of the result of Huet that a left-linear rewrite system is confluent if its critical pairs are parallel closed. In Sect. 5 we consider Toyama’s generalization of the previous result. Apart from a weaker joinability requirement on overlays, the result is extended to the commutation of two rewrite systems. Our formalization is an important first step for the certification of confluence proofs produced by CoLL [18], which is based on commutation. In Sect. 6 we explain what is needed for the automatic certification of confluence proofs that employ the formalized techniques and we present experimental results. In the final section we conclude with an outlook on future work, in particular the challenges that need to be overcome when extending the results from parallel closed rewrite systems to development closed higher-order rewrite systems [17]. The main Isabelle theories developed and integrated into IsaFoR are Strongly_Closed.thy , for the result on strongly closed rewrite systems, Parallel_Closed.thy for results on (almost) parallel closed systems (where we make heavy use of multihole contexts, cf. Multihole_Context.thy ), and Critical_Pair_Closure_Impl.thy for the executable check functions.
2 Preliminaries
We assume familiarity with the basics of rewriting [3, 20]. Knowledge of Isabelle [16] is not essential but experience with an interactive theorem prover might be helpful.
Let \(\mathcal {F}\) be a signature and \(\mathcal {V}\) a set of variables disjoint from \(\mathcal {F}\). By \(\mathcal {T(F,V)}\) we denote the set of terms over \(\mathcal {F}\) and \(\mathcal {V}\). Positions are strings of positive natural numbers, i.e., elements of \(\mathbb {N}_+^*\). We write \(q \leqslant p\) if \(qq' = p\) for some position \(q'\), in which case \(p \backslash q\) is defined to be \(q'\). Furthermore \(q < p\) if \(q \leqslant p\) and \(q \ne p\). Finally, positions q and p are parallel, written as \(q \parallel p\), if neither \(q \leqslant p\) nor \(p < q\). Positions are used to address subterm occurrences. The set of positions of a term t is defined as \(\mathcal {P}\textsf {os}(t) = \{ \epsilon \}\) if t is a variable and as \(\mathcal {P}\textsf {os}(t) = \{ \epsilon \} \cup \{ iq \mid 1 \leqslant ~{i}~\leqslant ~{n}~\text {and}~q \in \mathcal {P}\textsf {os}(t_i) \}\) if \(t = f({t_1},\ldots ,{t_{n}})\). The subterm of t at position \(p \in \mathcal {P}\textsf {os}(t)\) is defined as \({t|_{p}} = t\) if \(p = {\epsilon }\) and as \({t|_{p}} = {t_{i}|_{q}}\) if \(p = iq\) and \(t = f({t_1},\ldots ,{t_{n}})\). We write \({s[t]_{p}}\) for the result of replacing the subterm at position p of s with t. The size of a term t, i.e., the size of \(\mathcal {P}\textsf {os}(t)\), is denoted by |t|. We write \(\mathcal {V}\textsf {ar}(t)\) for the set of variables occurring in the term t. A term t is linear if every variable occurs at most once in it. A substitution is a mapping \({\sigma }\) from \(\mathcal {V}\) to \(\mathcal {T(F,V)}\) such that its domain \(\{ x \in {\mathcal {V}} \mid {\sigma }(x) \ne x \}\) is finite. We write \(t{\sigma }\) for the result of applying \({\sigma }\) to the term t.
Assume a fresh symbol \({\Box }\), called hole. A multihole context is a term that may contain an arbitrary number of holes. Filling the holes in a multihole context C with terms \({t_1},\ldots ,{t_{n}}\) is written as \(C[{t_1},\ldots ,{t_{n}}]\). (At this point we mention that in the formalization we of course have to make sure that the number of terms n matches the number of holes in C. To ease readability we usually do not make this explicit.) A term with exactly one hole is just called context and we also write \(s[]_p\) for the context obtained by replacing position p in s by the hole. If \(C[s] = t\) for some context C then s is called a subterm of t and we write \(s \unlhd t\). If additionally \(C \not = \Box \) then s is a proper subterm of t, which is denoted by \(s \lhd t\).
A rewrite rule is a pair of terms \((\ell ,r)\), written \(\ell \rightarrow r\).Footnote 3 A rewrite rule \(\ell \rightarrow r\) is left-linear if \(\ell \) is linear, right-linear if r is linear, and linear if it is both left- and right-linear. A variant of a rewrite rule is obtained by renaming its variables. A term rewrite system (TRS) is set of rewrite rules over a signature. In the sequel, signatures are left implicit. A TRS is (left-)linear if all its rules are (left-)linear. A rewrite relation is a binary relation on terms that is closed under contexts and substitutions. For a TRS \(\mathcal {R}\) we define \(\rightarrow _\mathcal {R}\) (often written as \(\rightarrow \)) to be the smallest rewrite relation that contains \(\mathcal {R}\). As usual \(\rightarrow ^=\) and \(\rightarrow ^*\) denote the reflexive, and reflexive and transitive closure of \(\rightarrow \), respectively.
A relation \(\rightarrow \) is said to have the diamond property if \({\leftarrow \cdot \rightarrow } \subseteq {\rightarrow \cdot \leftarrow }\) and is called confluent if its reflexive transitive closure has the diamond property. It is strongly confluent if \({\leftarrow \cdot \rightarrow } \subseteq {\rightarrow ^= \cdot \mathrel {{{}^{*}}{\leftarrow }}}\). The results in Sect. 5 will be proved in the more general setting of commutation. Two relations \(\rightarrow _1\) and \(\rightarrow _2\) commute if  , they strongly commute if
, they strongly commute if  . The following lemma captures the well-known connections between the diamond property, (strong) confluence and (strong) commutation.
. The following lemma captures the well-known connections between the diamond property, (strong) confluence and (strong) commutation.
Lemma 1
Let \(\rightarrow \), \(\rightarrow _1\), \(\rightarrow _2\), \(\rightarrow _{1'}\), and \(\rightarrow _{2'}\) be binary relations.
-
1.
If \(\rightarrow \) has the diamond property then it is confluent.
-
2.
If \(\rightarrow \) is strongly confluent then it is confluent.
-
3.
If \(\rightarrow _1\) and \(\rightarrow _2\) strongly commute then they commute.
-
4.
If \(\rightarrow \) commutes with itself then it is confluent.
-
5.
If \({\rightarrow _1} \subseteq {\rightarrow _{1'}} \subseteq {\rightarrow _1^*}\) and \(\rightarrow _{1'}\) is confluent then \(\rightarrow _1\) is confluent.
-
6.
If \({\rightarrow _1} \subseteq {\rightarrow _{1'}} \subseteq {\rightarrow _1^*}\) and \({\rightarrow _2} \subseteq {\rightarrow _{2'}} \subseteq {\rightarrow _2^*}\) and \(\rightarrow _{1'}\) and \(\rightarrow _{2'}\) commute then \(\rightarrow _1\) and \(\rightarrow _2\) commute.
Later, when applying the last two statements, the relations \(\rightarrow _{1'}\) and \(\rightarrow _{2'}\) between one and many step rewriting that we will use is parallel rewriting.
Definition 1
For a TRS \(\mathcal {R}\), the parallel rewrite relation  is defined inductively by
is defined inductively by
-
 if x is a variable,
if x is a variable, -
 if \(\ell \rightarrow r \in \mathcal {R}\), and
if \(\ell \rightarrow r \in \mathcal {R}\), and -
 if f is a function symbol of arity n and
if f is a function symbol of arity n and  for all \(1 \leqslant i \leqslant n\).
for all \(1 \leqslant i \leqslant n\).
The following properties of parallel rewriting are well-known and follow by straight-forward induction proofs.
Lemma 2
The following properties of  hold:
hold:
-
 ,
, -
 for all terms s,
for all terms s, -
if
 for all \(x \in \mathcal {V}\textsf {ar}(s)\) then
for all \(x \in \mathcal {V}\textsf {ar}(s)\) then  .
.
The confluence results formalized in this work are based on (left-)linearity and restricted joinability of critical pairs. Critical pairs arise from situations where two redexes overlap with each other. The definition we use here is slightly non-standard in two regards. First we consider critical pairs for two rewrite systems to use them in a commutation setting later on. Second we do not exclude root overlaps of a rule with (a variant of) itself as is commonly done. This allows us to dispense with the variable condition that all variables in the right-hand side of a rule must also occur on the left. Moreover, if a TRS does satisfy the condition then all extra critical pairs that would normally be excluded are trivial.
A critical overlap \((\ell _1 \rightarrow r_1,C,\ell _2 \rightarrow r_2)_\mu \) of two TRSs \(\mathcal {R}_1\) and \(\mathcal {R}_2\) consists of variants \(\ell _1 \rightarrow r_1\) and \(\ell _2 \rightarrow r_2\) of rewrite rules in \(\mathcal {R}_1\) and \(\mathcal {R}_2\) without common variables, a context C, such that \(\ell _2 = C[\ell ']\) with \(\ell ' \notin \mathcal {V}\) and a most general unifier \(\mu \) of \(\ell _1\) and \(\ell '\). From a critical overlap \((\ell _1 \rightarrow r_1,C,\ell _2 \rightarrow r_2)_\mu \) we obtain a critical peak \(C\mu [r_1\mu ] \mathrel {{{}_{\mathcal {R}_1}}{\leftarrow }} C\mu [\ell _1\mu ] \rightarrow _{\mathcal {R}_2} r_2\mu \) and the corresponding critical pair \(C\mu [r_1\mu ] \mathrel {\mathrel {{{}_{\mathcal {R}_1}}{\leftarrow }}\rtimes \rightarrow _{\mathcal {R}_2}} r_2\mu \). If \(C = \Box \), the corresponding critical pair is called an overlay and written as  , otherwise it is called an inner critical pair, and denoted using \(\mathrel {\mathrel {{{}_{\mathcal {R}_1}}{\leftarrow }}{\cdot \rtimes }\rightarrow _{\mathcal {R}_2}}\). When considering the critical pairs of a TRS \(\mathcal {R}\) with itself we drop the subscripts and write \(\mathrel {\leftarrow \rtimes \rightarrow }\) instead of \(\mathrel {\mathrel {{{}_{\mathcal {R}}}{\leftarrow }}\rtimes \rightarrow _{\mathcal {R}}}\).
, otherwise it is called an inner critical pair, and denoted using \(\mathrel {\mathrel {{{}_{\mathcal {R}_1}}{\leftarrow }}{\cdot \rtimes }\rightarrow _{\mathcal {R}_2}}\). When considering the critical pairs of a TRS \(\mathcal {R}\) with itself we drop the subscripts and write \(\mathrel {\leftarrow \rtimes \rightarrow }\) instead of \(\mathrel {\mathrel {{{}_{\mathcal {R}}}{\leftarrow }}\rtimes \rightarrow _{\mathcal {R}}}\).
3 Strongly Closed Critical Pairs
The first confluence criterion we consider is due to Huet [10] and based on the observation that in a linear rewrite system it suffices to have strong-confluence like joins for all critical pairs in order to guarantee strong confluence of the rewrite system. A preliminary version of the formalization described in this section was reported in [14].
Definition 2
A TRS \(\mathcal {R}\) is strongly closed if every critical pair \(s \mathrel {\leftarrow \rtimes \rightarrow }t\) of \(\mathcal {R}\) satisfies both \(s \rightarrow ^= \cdot \mathrel {{{}^{*}}{\leftarrow }} t\) and \(s \rightarrow ^* \cdot \mathrel {{{}^{=}}{\leftarrow }} t\).
The following folklore lemma tells us that in a linear term applying a substitution can be done by replacing the one subterm where the variable occurs and applying the remainder of the substitution.
Lemma 3
Let t be a linear term and let \(p \in \mathcal {P}\textsf {os}(t)\) be a position with \(t|_p = x\). Then for substitutions \({\sigma }\) and \(\tau \) with \(\sigma (y) = \tau (y)\) for all \(y \in \mathcal {V}\textsf {ar}(t)\) different from x we have \(t\tau = t\sigma [\tau (x)]_p\).
The proof that linear strongly closed systems are strongly confluent is very similar to the one of the famous critical pair lemma, by analyzing the relative positions of the rewrite steps in a peak. The next lemma, which appears implicitly in Huet’s proof of Corollary 1, takes care of the case where one position is above the other.
Lemma 4
Let \(\mathcal {R}\) be a linear, strongly closed TRS and assume \(s \rightarrow _\mathcal {R}t\) with rule \(\ell _1 \rightarrow r_1\) and substitution \(\sigma _1\) at position \(p_1\) and let \(s \rightarrow _\mathcal {R}u\) with rule \(\ell _2 \rightarrow r_2\) and substitution \(\sigma _2\) at position \(p_2\) with \(p_1 \leqslant p_2\). Then there are terms v and w with  and
and  .
.
Proof
(Sketch). Since the proof is standard and the formalization closely follows the paper proof, we only sketch the idea and refer to the formalization for full details. We distinguish whether the step from s to u overlaps with the one from s to t or takes place in the substitution. If there is a critical pair, we can close it by the assumption that the system is strongly closed. If the step from s to u happens in the substitution we can join in the required shape due to linearity of \(\mathcal {R}\), which avoids duplication of the redex, by using Lemma 3.
Now the main result of this section follows easily.
Corollary 1
(Huet [10]). If a TRS \(\mathcal {R}\) is linear and strongly closed then \(\rightarrow _\mathcal {R}\) is strongly confluent.
Proof
Assume \(s \rightarrow _\mathcal {R}t\) and \(s \rightarrow _\mathcal {R}u\). Then there are positions \(p_1, p_2 \in \mathcal {P}\textsf {os}(s)\), substitutions \(\sigma _1\), \(\sigma _2\) and rules \(\ell _1 \rightarrow r_1\), \(\ell _2 \rightarrow r_2\) in \(\mathcal {R}\) with \(s|_{p_1} = \ell _1\sigma _1\), \(s|_{p_2} = \ell _2\sigma _2\) and \(t = s[r_1\sigma _1]_{p_1}\), \(u = s[r_2\sigma _2]_{p_2}\). We show existence of a term v with \(t \rightarrow ^* v\) and \(u \rightarrow ^= v\) by analyzing the positions \(p_1\) and \(p_2\). If they are parallel then \(t \rightarrow t[r_2\sigma _2]_{p_2} = u[r_1\sigma _1]_{p_1} \leftarrow u\). If they are not parallel then one is above the other. In both cases we conclude by Lemma 4.
Then by Lemma 1 \(\mathcal {R}\) is also confluent.
Example 1
Consider the TRS \(\mathcal {R}\) consisting of the two rewrite rules

There are four non-trivial critical pairs

Since \(\mathcal {R}\) is linear and all critical pairs are strongly closed, \(\mathcal {R}\) is confluent.
The next example shows how to apply the criterion to a TRS that does not fulfill the variable conditions.
Example 2
Consider the linear TRS \(\mathcal {R}\) consisting of the following three rules:

There are five critical pairs modulo symmetry:

Using the second rule it is easy to see that all of them are strongly closed. Hence \(\mathcal {R}\) is confluent.
The next example shows that, if the variable condition is not satisfied, critical pairs that arise from overlapping a rule with itself at the root are essential.
Example 3
Consider the linear rewrite system \(\mathcal {R}\) consisting of the rule \(\textsf {a} \rightarrow y\). Because of the peak \(x \leftarrow \textsf {a} \rightarrow y\), \(\mathcal {R}\) is not confluent and indeed \(x \mathrel {\leftarrow \rtimes \rightarrow }y\) is a non-joinable critical pair according to our definition.
In the next section we consider a criterion that drops the condition on \(\mathcal {R}\) to be right-linear.
4 Parallel Closed Critical Pairs
The criterion from the previous section requires the TRS to be linear and while left-linearity is a common restriction, right-linearity is a rather unnatural one. Thus we turn our attention to criteria for left-linear systems that change the restriction on the joinability of critical pairs. The crucial observation is that in a non-right-linear system executing the upper step in variable overlap can duplicate the redex below. Thus to join such a situation multiple steps might be necessary, all of which take place at parallel positions. Consequently we consider parallel rewriting. The following definition describes the new joinability condition.
Definition 3
A TRS \(\mathcal {R}\) is parallel closed if every critical pair \(s \mathrel {\leftarrow \rtimes \rightarrow }t\) of \(\mathcal {R}\) satisfies  .
.
Together with left-linearity this guarantees the diamond property of the parallel rewrite relation.
Theorem 1
(Huet [10]). If a TRS \(\mathcal {R}\) is left-linear and parallel closed then  has the diamond property.
has the diamond property.
Overview of the proof of Theorem 1.
The proof of this theorem is much more involved than the one for strongly closed systems. The first observation is that we will now have to consider a peak of parallel steps, in order to show the diamond property of  . In case the two parallel steps are orthogonal to each other, they simply commute by the well-known Parallel Moves Lemma. However, if they do interfere the assumption of the theorem only allows us to close a single critical pair to reduce the amount of interference. Thus we will have to use some form of induction on how much the patterns of the two parallel steps overlap. Figure 1 shows the setting for the overlapping case. The horizontal parallel step, described by the horizontally striped redexes, and the vertical step, described by the vertically striped redexes, overlap. Hence there is a critical pair, say the one obtained from overlapping the leftmost vertical redex with the leftmost horizontal redex. Then, by assumption there is a closing parallel step, which, since it takes place inside the critical pair, can be combined with the remaining horizontal redexes to obtain a new peak with less overlap, which can be closed by the induction hypothesis. When making this formal we identified two crucial choices. First the representation of the parallel rewrite relation and second the way to measure the amount of overlap between two parallel steps with the same source. Huet in his original proof heavily uses positions. That is, a parallel step is defined as multiple single steps that happen at parallel positions and for measuring overlap he takes the sum of the sizes of the subterms that are affected by both steps. More precisely, writing
. In case the two parallel steps are orthogonal to each other, they simply commute by the well-known Parallel Moves Lemma. However, if they do interfere the assumption of the theorem only allows us to close a single critical pair to reduce the amount of interference. Thus we will have to use some form of induction on how much the patterns of the two parallel steps overlap. Figure 1 shows the setting for the overlapping case. The horizontal parallel step, described by the horizontally striped redexes, and the vertical step, described by the vertically striped redexes, overlap. Hence there is a critical pair, say the one obtained from overlapping the leftmost vertical redex with the leftmost horizontal redex. Then, by assumption there is a closing parallel step, which, since it takes place inside the critical pair, can be combined with the remaining horizontal redexes to obtain a new peak with less overlap, which can be closed by the induction hypothesis. When making this formal we identified two crucial choices. First the representation of the parallel rewrite relation and second the way to measure the amount of overlap between two parallel steps with the same source. Huet in his original proof heavily uses positions. That is, a parallel step is defined as multiple single steps that happen at parallel positions and for measuring overlap he takes the sum of the sizes of the subterms that are affected by both steps. More precisely, writing  for a parallel step that takes place at positions in a set P, for a peak
for a parallel step that takes place at positions in a set P, for a peak  he uses
he uses
where \(Q = \{ p_1 \in P_1 \mid p_2 \leqslant ~p_1~\text {for~some}~p_2\, \in \, P_2 \} \cup \{ p_2 \in P_2 \mid ~p_1~\leqslant ~p_2 \text { for~some} p_1 \in P_1 \}\). This formulation is also adopted in the text book by Baader and Nipkow [3]. Consequently, when starting the present formalization, we also adopted this definition. However, the book keeping required by working with sets of positions as well as formally reasoning about this measure in Isabelle became so convoluted that it very much obscured the ingenuity and elegance of Huet’s original idea while at the same time defeating our formalization efforts. Hence in the end we had to adopt a different approach.
Toyama [22], in the proof of his extension of Huet’s result, does not use positions at all and instead relies on (multihole) contexts, which means a parallel step is then described by a context and a list of root steps that happen in the holes. To measure overlap he collects those redexes that are subterms of some redex in the other step, i.e., decorating the parallel rewrite relation with the redexes contracted in the step, for a peak  Toyama’s measure is
Toyama’s measure is
where \(S = \{ u_i \mid u_i \unlhd t_j~\text{ for } \text{ some }~t_j \} \cup \{ t_j \mid t_j \unlhd u_i~\text{ for } \text{ some }~u_i \}\). However, this measure turns out to be problematic as shown in the following example.
Example 4
Consider the TRS consisting of the following five rewrite rules:

Then we have the peak  . The measure of this peak according to the definition above is 2, since \(S = \{ \textsf {a}, \textsf {b} \} \cup \varnothing \). Now after splitting of one of the four critical steps—it does not matter which one—and closing the corresponding critical pair, we arrive at
. The measure of this peak according to the definition above is 2, since \(S = \{ \textsf {a}, \textsf {b} \} \cup \varnothing \). Now after splitting of one of the four critical steps—it does not matter which one—and closing the corresponding critical pair, we arrive at

The measure of the new peak  is still 2 since \(S = \{ \textsf {a}, \textsf {b} \} \cup \{ \textsf {a}, \textsf {b} \}\).
is still 2 since \(S = \{ \textsf {a}, \textsf {b} \} \cup \{ \textsf {a}, \textsf {b} \}\).
Note that using multisets instead of sets does not help, since then the measure of the initial peak is 4 (\(S = \{ \textsf {a}, \textsf {a}, \textsf {b}, \textsf {b} \}\)) and of the new peak, after closing the critical pair, it is 7 since \(S = \{ \textsf {a}, \textsf {b}, \textsf {b} \} \uplus \{ \textsf {b}, \textsf {a}, \textsf {b}, \textsf {b} \}\) (and even if we take into account that three of the redexes are counted twice we still get 4). The problem is that in the new peak the redex at position 1 of the closing step is counted again, because \(\textsf {b}\) is a subterm of one the redexes of the other step. Hence it is crucial to only count redexes at overlapping positions.
To remedy this situation we will collect all overlapping redexes of a peak in a multiset. These multisets will then be compared by \(\mathrel {\rhd _\textsf {mul}}\), the multiset extension of the proper superterm relation. We start by characterizing parallel rewrite steps using multihole contexts.
Definition 4
We write  if \(s = C[{a_1},\ldots ,{a_{n}}]\) and \(t = C[{b_1},\ldots ,{b_{n}}]\) for some \({b_1},\ldots ,{b_{n}}\) with \(a_i \rightarrow ^\epsilon _\mathcal {R}b_i\) for all \(1 \leqslant i \leqslant n\).
if \(s = C[{a_1},\ldots ,{a_{n}}]\) and \(t = C[{b_1},\ldots ,{b_{n}}]\) for some \({b_1},\ldots ,{b_{n}}\) with \(a_i \rightarrow ^\epsilon _\mathcal {R}b_i\) for all \(1 \leqslant i \leqslant n\).
To save space we sometimes abbreviate a list of terms \({{a_1},\ldots ,{a_{n}}}\) by \({\overline{a}}\) and write  leaving length implicit. The following expected correspondence is easily shown by induction.
leaving length implicit. The following expected correspondence is easily shown by induction.
Lemma 5
We have  if and only if
if and only if  for some C and \(\overline{s}\).
for some C and \(\overline{s}\).
Now we can formally measure the overlap between two parallel rewrite steps by collecting those redexes that are below some redex in the other step.
Definition 5
The overlap between two co-initial parallel rewrite steps is defined by the following equations

where \({\overline{a}_1},\ldots ,{\overline{a}_{n}} = \overline{a}\) and \({\overline{b}_1},\ldots ,{\overline{b}_{n}} = \overline{b}\) are partitions of \({\overline{a}}\) and \({\overline{b}}\) such that the length of \({\overline{a}_{i}}\) and \({\overline{b}_{i}}\) matches the number of holes in \(C_i\) and \(D_i\), for all \(1 \leqslant i \leqslant n\).
Example 5
Applying this definition for the two peaks from Example 4 yields

and \(\{ \textsf {a},\textsf {a},\textsf {b},\textsf {b} \} \mathrel {\rhd _\textsf {mul}} \{ \textsf {a},\textsf {b},\textsf {b} \}\) as desired.
Note that our definition of  is in fact an over-approximation of the actual overlap between the steps. That is because we do not split redexes into the left-hand side of the applied rule and a substitution but take the redex as a whole. The following example illustrates the effect.
is in fact an over-approximation of the actual overlap between the steps. That is because we do not split redexes into the left-hand side of the applied rule and a substitution but take the redex as a whole. The following example illustrates the effect.
Example 6
Consider the rewrite system consisting of the two rules

and the peak \({\textsf {a}} \leftarrow {\textsf {f}}({\textsf {a}}) \rightarrow {\textsf {f}}({\textsf {b}})\). We have

although the two steps do not overlap—the step to the right takes place completely in the substitution of the one to the left (in fact the rewrite system in question is orthogonal).
However, since we are dealing with parallel rewriting, no problems arise from this over-approximation. This changes when extending the results to development steps, see Sect. 7 for further discussion.
The following properties of  turned out to be crucial in our proof of Theorem 1.
turned out to be crucial in our proof of Theorem 1.
Lemma 6
For a peak  the following properties of
the following properties of  hold.
hold.
-
If \(s = f({s_1},\ldots ,{s_{n}})\) with \(C = f({C_1},\ldots ,{C_{n}})\) and \(D = f({D_1},\ldots ,{D_{n}})\) then

for all \(1 \leqslant i \leqslant n\).
-
The overlap is bounded by \({\overline{a}}\), i.e.,
 .
. -
The overlap is symmetric, i.e.,
 .
.
There is one more high-level difference between the formalization and the paper proof. In the original proof one needs to combine the closing step for the critical pair with the remainder of the original step in order to obtain a new peak, to which the induction hypothesis can then be applied. This reasoning can be avoided, by using an additional induction on the source of the peak. Then the case where neither of the two parallel steps is a root step (and thus a single step) can be discharged by the induction hypothesis of that induction.
The following technical lemma tells us that a parallel rewrite step starting from \(s\sigma \) is either inside s, i.e., we can split off a critical pair, or we can do the step completely inside \({\sigma }\).
Lemma 7
Let s be a linear term. If  then either \(t = s\tau \) for some substitution \(\tau \) such that
then either \(t = s\tau \) for some substitution \(\tau \) such that  or there exist a context D, a non-variable term \(s'\), a rule \(\ell \rightarrow r \in \mathcal {R}\), a substitution \(\tau \), and a multihole context \(C'\) such that \(s = D[s']\), \(s'\sigma = \ell \tau \), \(D\sigma [r\tau ] = C'[s_1,\ldots ,s_{i-1},s_{i+1},\ldots ,s_n]\) and \(t = C'[t_1,\ldots ,t_{i-1},t_{i+1},\ldots ,t_n]\) for some \(1 \leqslant i \leqslant n\).
or there exist a context D, a non-variable term \(s'\), a rule \(\ell \rightarrow r \in \mathcal {R}\), a substitution \(\tau \), and a multihole context \(C'\) such that \(s = D[s']\), \(s'\sigma = \ell \tau \), \(D\sigma [r\tau ] = C'[s_1,\ldots ,s_{i-1},s_{i+1},\ldots ,s_n]\) and \(t = C'[t_1,\ldots ,t_{i-1},t_{i+1},\ldots ,t_n]\) for some \(1 \leqslant i \leqslant n\).
We are now ready to prove the main result of this section. To ease presentation, the following proof does use the condition that the left-hand sides of rewrite rules are not variables. By employing additional technical case analyses this restriction can be easily dropped. We refer to the formalization for details.
Proof
(of Theorem 1
). Assume  . We show
. We show  for some term v by well-founded induction on the overlap between the two parallel steps using the order \(\mathrel {\rhd _\textsf {mul}}\) and continue by induction on s with respect to \(\rhd \). If \(s = x\) for some variable x then \(t = u = x\). So let \(s = f({s_1},\ldots ,{s_{n}})\). We distinguish four cases.
for some term v by well-founded induction on the overlap between the two parallel steps using the order \(\mathrel {\rhd _\textsf {mul}}\) and continue by induction on s with respect to \(\rhd \). If \(s = x\) for some variable x then \(t = u = x\). So let \(s = f({s_1},\ldots ,{s_{n}})\). We distinguish four cases.
-
1.
If \(C = f({C_1},\ldots ,{C_{n}})\) and \(D = f({D_1},\ldots ,{D_{n}})\) then \(t = f({t_1},\ldots ,{t_{n}})\) and \(u = f({u_1},\ldots ,{u_{n}})\) and we obtain partitions \({{\overline{a}_1},\ldots ,{\overline{a}_{n}}} = {\overline{a}}\) and \({{\overline{b}}_1},\ldots ,{{\overline{b}}_{n}} = {\overline{b}}\) of \({\overline{a}}\) and \({\overline{b}}\) with
 for all \(1 \leqslant i \leqslant n\). Then, since we have
for all \(1 \leqslant i \leqslant n\). Then, since we have 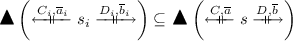
by Lemma 6 and thus also

we can apply the inner induction hypothesis and obtain terms \(v_i\) with
 for all \(1 \leqslant i \leqslant n\) and thus we have
for all \(1 \leqslant i \leqslant n\) and thus we have  .
. -
2.
If \(C = D = \Box \) then both steps are root steps and thus single rewrite steps and we can write \(t = r_1\sigma _1 \xleftarrow {\epsilon } \ell _1\sigma _1 = s = \ell _2\sigma _2 \xrightarrow {\epsilon } r_2\sigma _2 = u\). Hence, since \(\ell _1\sigma _1 = \ell _2\sigma _2\), there is a critical pair
 for variable disjoint variants \(\ell _{1}' \rightarrow r_{1}'\), \(\ell _{2}' \rightarrow r_{2}'\) of \(\ell _1 \rightarrow r_1\), \(\ell _2 \rightarrow r_2\) with \(\mu \) a most general unifier of \(\ell _1'\) and \(\ell _2'\). Then by assumption
for variable disjoint variants \(\ell _{1}' \rightarrow r_{1}'\), \(\ell _{2}' \rightarrow r_{2}'\) of \(\ell _1 \rightarrow r_1\), \(\ell _2 \rightarrow r_2\) with \(\mu \) a most general unifier of \(\ell _1'\) and \(\ell _2'\). Then by assumption 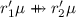 and by closure under substitution also
and by closure under substitution also  .
. -
3.
If \(C = f({C_1},\ldots ,{C_{n}})\) and \(D = \Box \) then the step to the right is a single root step and we write
 . Since \(\ell \) is linear by assumption, we can apply Lemma 7 and either obtain \(\tau \) with \(t = \ell \tau \) and
. Since \(\ell \) is linear by assumption, we can apply Lemma 7 and either obtain \(\tau \) with \(t = \ell \tau \) and  for all \(x \in \mathcal {V}\textsf {ar}(\ell )\) or a critical pair.
for all \(x \in \mathcal {V}\textsf {ar}(\ell )\) or a critical pair.-
In the first case define
$$ \delta (x) = {\left\{ \begin{array}{ll} \tau (x) &{} \text {if}~x \in \mathcal {V}\textsf {ar}(\ell ) \\ \sigma (x) &{} \text {otherwise} \end{array}\right. } $$We have \(t = \ell \tau = \ell \delta \) by definition of \(\delta \) and hence
 by a single root step. Moreover we have
by a single root step. Moreover we have  since
since  for all variables \(x \in \mathcal {V}\textsf {ar}(r)\). This holds because either \(x \in \mathcal {V}\textsf {ar}(\ell )\) and then
for all variables \(x \in \mathcal {V}\textsf {ar}(r)\). This holds because either \(x \in \mathcal {V}\textsf {ar}(\ell )\) and then  or \(x \notin \mathcal {V}\textsf {ar}(\ell )\) and then \(x\sigma = x\delta \).
or \(x \notin \mathcal {V}\textsf {ar}(\ell )\) and then \(x\sigma = x\delta \). -
In the second case Lemma 7 yields a context E, a non-variable term \(\ell ''\), a rule \(\ell ' \rightarrow r' \in \mathcal {R}\), a substitution \(\tau \), and a multihole context \(C'\) such that \(\ell = E[\ell '']\), \(\ell ''\sigma = \ell '\tau \), \(E\sigma [r'\tau ] = C'[a_1,\ldots ,a_{i-1},a_{i+1},\ldots ,a_c]\) and \(t = C'[a'_1,\ldots ,a'_{i-1},a'_{i+1},\ldots ,a'_c]\) for some \(1 \leqslant i \leqslant c\). Since \(\ell ''\sigma = \ell '\tau \) there is a critical pair \(E\mu [r'\mu ] \mathrel {\leftarrow \rtimes \rightarrow }r\mu \) and by assumption
 and thus also
and thus also  . That is, we obtain a new peak
. That is, we obtain a new peak 
with \({\overline{a}}' = a_1,\ldots ,a_{i-1},a_{i+1},\ldots ,a_c\). Since

by Lemma 6, we can apply the induction hypothesis and obtain v with
 .
.
-
-
4.
The final case, \(D = f({D_1},\ldots ,{D_{n}})\) and \(C = \Box \), is completely symmetric.
Finally, by Lemmas 1 and 2 we obtain confluence of \(\rightarrow _\mathcal {R}\).
Example 7
Consider the TRS \(\mathcal {R}\) consisting of the following three rewrite rules:

Since the four critical pairs of \(\mathcal {R}\)

are parallel closed, \(\mathcal {R}\) is confluent.
5 Almost Parallel Closed Critical Pairs and Commutation
In this section we consider two extensions to Huet’s result due to Toyama [22]. The first one allows us to weaken the joining condition for some critical pairs.
When carefully examining the proof of Theorem 1 one realizes that in the case where both steps of the peak are single root steps, i.e., the case where \(C = D =~\Box \), the induction hypothesis does not need to be applied, since closing the critical pair immediately closes the whole peak. This suggests that the joining condition can be weakened for overlays. A first idea could be to take  since then we would still have the diamond property in the overlay case. However Toyama realized that one can do even better by weakening the diamond property to strong confluence. The following definition captures the new conditions.
since then we would still have the diamond property in the overlay case. However Toyama realized that one can do even better by weakening the diamond property to strong confluence. The following definition captures the new conditions.
Definition 6
A TRS \(\mathcal {R}\) is almost parallel closed if  for all overlays
for all overlays  and
and  for all inner critical pairs \(s \mathrel {\leftarrow {\cdot \rtimes }\rightarrow }t\).
for all inner critical pairs \(s \mathrel {\leftarrow {\cdot \rtimes }\rightarrow }t\).
Using exactly the same proof structure as before we could now prove strong confluence of  for left-linear almost parallel closed systems. However, considering Toyama’s second extension of Theorem 1, we will prove the theorem in the more general setting of commutation.
for left-linear almost parallel closed systems. However, considering Toyama’s second extension of Theorem 1, we will prove the theorem in the more general setting of commutation.
Theorem 2
(Toyama [22]). Let \(\mathcal {R}_1\) and \(\mathcal {R}_2\) be left-linear TRSs. If  for all critical pairs \(s \mathrel {\mathrel {{{}_{1}}{\leftarrow }}\rtimes \rightarrow _{2}} t\) and additionally
for all critical pairs \(s \mathrel {\mathrel {{{}_{1}}{\leftarrow }}\rtimes \rightarrow _{2}} t\) and additionally  for all inner critical pairs \(s \mathrel {\mathrel {{{}_{2}}{\leftarrow }}{\cdot \rtimes }\rightarrow _{1}} t\) then
for all inner critical pairs \(s \mathrel {\mathrel {{{}_{2}}{\leftarrow }}{\cdot \rtimes }\rightarrow _{1}} t\) then  and
and  strongly commute.
strongly commute.
Proof
(Adaptations). We only highlight the differences to the proof of Theorem 1 and refer to the formalization for the full proof details. Assume

We show  for some term v. We apply the same inductions and case analyses as before. The cases \(C = f({C_1},\ldots ,{C_{n}})\), \(D = f({D_1},\ldots ,{D_{n}})\) and \(C = D = \Box \) require no noteworthy adaptation. The main difference is that now the cases \(D = f({D_1},\ldots ,{D_{n}})\), \(C = \Box \) and \(C = f({C_1},\ldots ,{C_{n}})\), \(D = \Box \) become asymmetric for the critical pair case—the corresponding diagrams are shown in Fig. 2.
for some term v. We apply the same inductions and case analyses as before. The cases \(C = f({C_1},\ldots ,{C_{n}})\), \(D = f({D_1},\ldots ,{D_{n}})\) and \(C = D = \Box \) require no noteworthy adaptation. The main difference is that now the cases \(D = f({D_1},\ldots ,{D_{n}})\), \(C = \Box \) and \(C = f({C_1},\ldots ,{C_{n}})\), \(D = \Box \) become asymmetric for the critical pair case—the corresponding diagrams are shown in Fig. 2.
Asymmetry in the proof of Theorem 2.
First, suppose \(C = f({C_1},\ldots ,{C_{n}})\) and \(D = \Box \), write  , and assume there is a critical pair according to Lemma 7. That is, we obtain
, and assume there is a critical pair according to Lemma 7. That is, we obtain  with
with  and by assumption we obtain a v such that
and by assumption we obtain a v such that  . Then using the same reasoning as before, for the new peak
. Then using the same reasoning as before, for the new peak

we have

and can apply the induction hypothesis to obtain a \(v'\) with  , which combined with \(u = r\sigma \rightarrow ^*_1 v\) concludes this case.
, which combined with \(u = r\sigma \rightarrow ^*_1 v\) concludes this case.
In the second case, i.e., when \(D = f({D_1},\ldots ,{D_{n}})\) and \(C = \Box \), observe that the critical pair we obtain is an inner critical pair between \(\mathcal {R}_2\) and \(\mathcal {R}_1\), since \(D \not = \Box \). Thus, after applying the assumption for critical pairs \(\mathrel {\mathrel {{{}_{2}}{\leftarrow }}{\cdot \rtimes }\rightarrow _{1}}\), the proof is the same as for Theorem 1.
Instantiating \(\mathcal {R}_1\) and \(\mathcal {R}_2\) with the same TRS \(\mathcal {R}\) yields the corresponding result for confluence.
Corollary 2
(Toyama [22]). If the TRS \(\mathcal {R}\) is left-linear and almost parallel closed then  is strongly confluent.
is strongly confluent.
Proof
Immediate from the definition of almost parallel closed, Theorem 2 and the fact that \(s \mathrel {\leftarrow \rtimes \rightarrow }t\) if and only if  .
.
Example 8
Recall the rewrite system from Example 4. One easily verifies that all its critical pairs are almost parallel closed, and hence it is confluent.
6 Certification and Experiments
To facilitate checking of confluence proofs generated by automatic tools based on Corollarys 1 and 2 we extended the CPF to represent such proofs. Since in order to check that a given TRS is strongly or almost parallel closed, CeTA has to compute all critical pairs anyway, in the certificate we just require the claim that the system is strongly or almost parallel closed, together with a bound on the length of the rewrite sequences to join the critical pairs.Footnote 4 Certificates for commutation are not yet supported, since currently no tool produces them, and CPF does not contain a specification for commutation proofs.
For experiments we considered all 277 TRSs in the CopsFootnote 5 database and used the confluence tool CSI to obtain certificates in CPF for confluence proofs. All generated certificates have been certified by CeTA. Table 1 shows the results of running CSI with different strategies. The first and second column show the results of applying just Corollarys 1 and 2 respectively, the third column is the combination. In the fourth column we show the result when additionally adding and removing redundant rewrite rules [13], which yields a considerable boost in power. The idea of that technique is to add and remove rules that can be simulated by other rules, which consequently does not change confluence of the system, but often makes other criteria, like the ones we consider here, applicable. Column “full” shows the results for the full certified strategy of CSI, which additionally includes Knuth and Bendix’ criterion, weak orthogonality (which is subsumed by Corollary 2, however) and the rule labeling heuristic [15] as well as several criteria for non-confluence. The last column shows the difference to last year’s version of CSI ’s certified strategy, which already included Corollary 1, but not Corollary 2. In addition to the new certifiable proofs, several existing proofs of CSI 2015 could be simplified and no longer require complicated reasoning via decreasing diagrams.
7 Conclusion
In this paper we presented the first formalization of three classical criteria for confluence and commutation of (left-)linear rewrite systems. Building on top of IsaFoR—which provided invaluable support on the one hand, e.g. by its theories on critical pairs and multihole contexts, and on the other hand, as expected, was also extended with new basic facts about lists, multisets, multihole contexts etc.—we formalized proofs that linear strongly closed systems, and left-linear (almost) parallel closed systems are confluent (commute). The major difference to the paper proof is our definition of the overlap between two parallel steps that are represented via multihole contexts.
Concerning future work, another important extension of the results of Huet and Toyama due to van Oostrom [17] is using multisteps (also called development steps)  which allow nested non-overlapping redexes. This extension not only strengthens Huet’s criterion in the first-order world but also makes it applicable to higher-order rewriting, where using parallel steps fails due to \(\beta \)-reduction.
which allow nested non-overlapping redexes. This extension not only strengthens Huet’s criterion in the first-order world but also makes it applicable to higher-order rewriting, where using parallel steps fails due to \(\beta \)-reduction.
However, although the paper proofs superficially look very similar, and do employ similar ideas, obtaining a formalized proof will require serious effort. In fact neither our representation of (parallel) rewrite steps, nor our definition of  , nor the idea of using an induction on the source of the peak to avoid reasoning about combining steps, carry over. To make the concepts that are hard to formalize in a proof assistant, e.g. measuring the amount of overlap between two multisteps or the descendants of a multistep, Hirokawa and Middeldorp [9] suggested to use proof terms to obtain a rigorous proof (and at the same time extended the result to commutation). This is a step forward but more is needed to obtain a formalized proof, also for the extension to higher-order systems. In particular, we anticipate the extensive use of sets of positions (in [9]) to be problematic without alternative notions. We plan to employ residual theory [20, Sect. 8.7] and to develop a notion of overlap for multisteps similar to Definition 5 to close the gap.
, nor the idea of using an induction on the source of the peak to avoid reasoning about combining steps, carry over. To make the concepts that are hard to formalize in a proof assistant, e.g. measuring the amount of overlap between two multisteps or the descendants of a multistep, Hirokawa and Middeldorp [9] suggested to use proof terms to obtain a rigorous proof (and at the same time extended the result to commutation). This is a step forward but more is needed to obtain a formalized proof, also for the extension to higher-order systems. In particular, we anticipate the extensive use of sets of positions (in [9]) to be problematic without alternative notions. We plan to employ residual theory [20, Sect. 8.7] and to develop a notion of overlap for multisteps similar to Definition 5 to close the gap.
Notes
- 1.
- 2.
IsaFoR/CeTA and CPF are available at http://cl-informatik.uibk.ac.at/software/ceta/.
- 3.
We do not impose the common variable conditions, i.e., the restriction that \(\ell \) is not a variable and all variables in r are contained in \(\ell \).
- 4.
This bound is necessary to ensure termination of the certifier.
- 5.
References
Aoto, T.: Disproving confluence of term rewriting systems by interpretation and ordering. In: Fontaine, P., Ringeissen, C., Schmidt, R.A. (eds.) FroCoS 2013. LNCS, vol. 8152, pp. 311–326. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40885-4_22
Aoto, T., Yoshida, J., Toyama, Y.: Proving confluence of term rewriting systems automatically. In: Treinen, R. (ed.) RTA 2009. LNCS, vol. 5595, pp. 93–102. Springer, Heidelberg (2009). doi:10.1007/978-3-642-02348-4_7
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, Cambridge (1998)
Blanqui, F., Koprowski, A.: CoLoR, a Coq library on well-founded rewrite relations and its application to the automated verification of termination certificates. Math. Struct. Comput. Sci. 21(4), 827–859 (2011). doi:10.1017/S0960129511000120
Contejean, E., Courtieu, P., Forest, J., Pons, O., Urbain, X.: Automated certified proofs with CiME3. In: Schmidt-Schauß, M. (ed.) RTA 2011. LIPIcs, vol. 10. pp. 21–30. Schloss Dagstuhl–Leibniz-Zentrum für Informatik (2011). doi:10.4230/LIPIcs.RTA.2011.21
Felgenhauer, B., Thiemann, R.: Reachability analysis with state-compatible automata. In: Dediu, A.-H., Martín-Vide, C., Sierra-Rodríguez, J.-L., Truthe, B. (eds.) LATA 2014. LNCS, vol. 8370, pp. 347–359. Springer, Heidelberg (2014). doi:10.1007/978-3-319-04921-2_28
Geser, A., Middeldorp, A., Ohlebusch, E., Zantema, H.: Relative undecidability in the term rewriting, part 2: The confluence hierarchy. Inf. Comput. 178(1), 132–148 (2002). doi:10.1006/inco.2002.3150
Hirokawa, N., Klein, D.: Saigawa: a confluence tool. In: Hirokawa, N., Middeldorp, A. (eds.) IWC 2012, p. 49 (2012). http://cl-informatik.uibk.ac.at/events/iwc-2012/
Hirokawa, N., Middeldorp, A.: Commutation via relative termination. In: Hirokawa, N., van Oostrom, V. (eds.) IWC 2013, pp. 29–33 (2013). http://www.jaist.ac.jp/~hirokawa/iwc2013/
Huet, G.: Confluent reductions: abstract properties and applications to term rewriting systems. J. ACM 27(4), 797–821 (1980). doi:10.1145/322217.322230
Klein, D., Hirokawa, N.: Confluence of non-left-linear TRSs via relative termination. In: Bjørner, N., Voronkov, A. (eds.) LPAR-18 2012. LNCS, vol. 7180, pp. 258–273. Springer, Heidelberg (2012). doi:10.1007/978-3-642-28717-6_21
Knuth, D., Bendix, P.: Simple word problems in universal algebras. In: Leech, J. (ed.) Computational Problems in Abstract Algebra, pp. 263–297. Pergamon Press (1970)
Nagele, J., Felgenhauer, B., Middeldorp, A.: Improving automatic confluence analysis of rewrite systems by redundant rules. In: Fernández, M. (ed.) RTA 2015. LIPIcs, vol. 36, pp. 257–268. Schloss Dagstuhl–Leibniz-Zentrum für Informatik (2015). doi:10.4230/LIPIcs.RTA.2015.257
Nagele, J., Thiemann, R.: Certification of confluence proofs using CeTA. In: Aoto, T., Kesner, D. (eds.) IWC 2014, pp. 19–23 (2014). http://www.nue.riec.tohoku.ac.jp/iwc2014/
Nagele, J., Zankl, H.: Certified rule labeling. In: Fernández, M. (ed.) RTA 2015. LIPIcs, vol. 36, pp. 269–284. Schloss Dagstuhl–Leibniz-Zentrum für Informatik (2015). doi:10.4230/LIPIcs.RTA.2015.269
Nipkow, T., Paulson, L., Wenzel, M.: Isabelle/HOL - A Proof Assistant for Higher-Order Logic. LNCS, vol. 2283. Springer, Heidelberg (2002)
van Oostrom, V.: Developing developments. Theoret. Comput. Sci. 175(1), 159–181 (1997). doi:10.1016/S0304-3975(96)00173-9
Shintani, K., Hirokawa, N.: CoLL: A confluence tool for left-linear term rewrite systems. In: Felty, A., Middeldorp, A. (eds.) CADE 2015. LNCS, vol. 9195, pp. 127–136. Springer, Heidelberg (2015). doi:10.1007/978-3-319-21401-6_8
Sternagel, C., Thiemann, R.: The certification problem format. In: Benzmüller, C., Woltzenlogel Paleo, B. (eds.) UITP 2014. EPTCS, vol. 167, pp. 61–72. Open Publishing Association (2014). doi:10.4204/EPTCS.167.8
Terese: Term Rewriting Systems. Cambridge Tracts in Theoretical ComputerScience, vol. 55. Cambridge University Press, Cambridge (2003)
Thiemann, R., Sternagel, C.: Certification of termination proofs using CeTA. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 452–468. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03359-9_31
Toyama, Y.: Commutativity of term rewriting systems. In: Fuchi, K., Kott, L. (eds.) Programming of Future Generation Computers II, pp. 393–407. North-Holland (1988)
Zankl, H., Felgenhauer, B., Middeldorp, A.: CSI – a confluence tool. In: Bjørner, N., Sofronie-Stokkermans, V. (eds.) CADE 2011. LNCS, vol. 6803, pp. 499–505. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22438-6_38
Acknowledgments
We thank Nao Hirokawa for suggesting Lemma 6 and Bertram Felgenhauer and Christian Sternagel for insightful discussion.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Nagele, J., Middeldorp, A. (2016). Certification of Classical Confluence Results for Left-Linear Term Rewrite Systems. In: Blanchette, J., Merz, S. (eds) Interactive Theorem Proving. ITP 2016. Lecture Notes in Computer Science(), vol 9807. Springer, Cham. https://doi.org/10.1007/978-3-319-43144-4_18
Download citation
DOI: https://doi.org/10.1007/978-3-319-43144-4_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-43143-7
Online ISBN: 978-3-319-43144-4
eBook Packages: Computer ScienceComputer Science (R0)





 if x is a variable,
if x is a variable, if
if  if f is a function symbol of arity n and
if f is a function symbol of arity n and  for all
for all  ,
, for all terms s,
for all terms s, for all
for all  .
.

 .
. .
. for all
for all 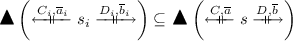

 for all
for all  .
. for variable disjoint variants
for variable disjoint variants 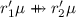 and by closure under substitution also
and by closure under substitution also  .
. . Since
. Since  for all
for all  by a single root step. Moreover we have
by a single root step. Moreover we have  since
since  for all variables
for all variables  or
or  and thus also
and thus also  . That is, we obtain a new peak
. That is, we obtain a new peak 

 .
.