Keywords

1 Introduction

The idea of learning algorithms can be traced back to the early 1960s. The main stream of research then was (and ut still is) learning classifiers or more generally, learning the Bayes decision rules when underlying probability distributions are unknown and the learning is based on a sequence of examples – called the learning sequence. At the first stage of development of this theory the learning was reduced to estimating unknown parameters of unknown distributions. Then, the so called nonparametric approach emerged, which is based on estimating completely unknown probability density functions (p.d.f.’s) either by Parzen-Rosenblatt kernel methods (see [9]) or by expanding it into a complete and orthonormal bases with estimated coefficients (see [12]). Up to now, these kinds of classifiers have been further developed [17, 28], the support vector machines being the most popular. All these approaches have a common feature, namely, after the learning phase they are applied as follows: when a new vector of features appears, then it is classified without taking into account neither earlier nor future decisions. Furthermore, the result of a classification does not depend on time, i.e., a vector of features is classified in the same way independently of a time instant when it appears. Rutkowski [25, 26] developed the theory of learning when an environment is non-stationary. Recently, such approaches are called: learning when a concept drift is present.

A parallel stream of research (see [15, 16]) extended the bayesian decision theory by considering that the next decision should take into account our previous decisions as a local context, as it happens in recognizing letters in a word. In [21, 22] an outer context approach in learning decisions is proposed.

However, none of the above sketched approaches to learning do not takes into account future consequences of earlier decisions. In the framework of learning, an approach that explicitly incorporates a system dynamics into a decision process has been proposed by Feldbaum (see [2, 3] and the bibliography cited therein). His theory, although pleasing from the methodological point of view, occurred to be too demanding for data, which are necessary for learning. Therefore, many approaches, known under a common name adaptive control, have been proposed [3]. Their common feature is gaining information about unknown parameters of a system (or its model) during a decision process, which is split into consecutive steps. In adaptive control approaches usually only one, but sufficiently long, decision process is considered and the emphasis of researchers is on the stability of the adaptation process [27].

However, a large number of control processes in industry and in robotics is repetitive in the sense that they are repeated many times in similar circumstances. Repetitions of passes of a process provide additional opportunities for learning and they are in the main focus of this paper. This class contains strictly periodic processes (see [29]), which are not discussed here. We shall also leave outside the scope of this paper the so called run-to-run control approach, since it concentrates mainly on statistical, but static models of processes.

As a motivating example consider a laser cladding process. The laser head moves back and forth, pouring and melting a metal powder. The temperature of the melting lake is observed by an infrared camera. This temperature has to be precisely controlled by changing the power emitted by the laser. The main difficulty is at the end points, in which the laser head changes its direction it stays longer than at other points. This results in an unwanted additional dropping of a material. One can design a desirable trajectory of changing (decreasing) the lake temperature near end points. However, the optimal control signal cannot be calculated once and repeated without changes because of changes of the powder properties when different parts are produced. These changes are rather slow and we can improve the control signal, using information gained from earlier passes. Almost the same general pattern arises in a 3D printing process. Similar control problems arise also in the chemical industry when a batch type chemical reactors are used. Later on we shall call a pass: one run of the laser or a robot arm movement from place to place, or one full batch reaction etc.

In this paper we put an emphasis on learning from pass-to-pass, which is called an iterative learning control (ILC). ILC is a common name for a large number of algorithms (see [31] for a recent survey paper). ILC theory puts emphasis on designing control systems for repetitive processes – see [5, 20]. They should be designed in such a way that the stability of the control process is ensured. The stability notions for repetitive processes and ILC are nontrivial (see [7]). A number of approaches to the control problems for such systems has been proposed (see [11, 13, 14]). In a number of papers the authors optimized ILC procedures (see [1, 24]). ILC for optimal control of processes is much less developed, although some results in this direction have been obtained – see [10, 19, 23] – as close to the problem statement considered in this paper. However, our approach is different, namely, we propose an iterative learning of optimal control that is based on functional analog of the gradient search procedure. We shall provide theorems on its convergence and robustness to small changes of unknown parameters, but the proofs are omitted due to page limitations. They will be published elsewhere.

The paper is organized as follows. In Sect. 2 we state the problem of iterative learning of optimal control (ILOC). Then, in Sect. 3 we provide the algorithm of learning for nominal system parameters. Finally, its on-line version is presented, which is able to work when parameters are uncertain, since it collects information from pass-to-pass behavior of the system. Notice that there is no explicit parameters estimation in our approach. Finally, we provide an example of how the laser power control behaves under the proposed ILOC algorithm.

2 Problem Statement

As the first step toward the problem statement we consider the well known problem of minimization of a quadratic cost function for finding the optimal control of the linear, time-invariant (LTI) dynamic system (LQ problem), but with uncertain parameters. Assumptions concerning their uncertainty will be imposed later.

Generic LQ Optimal Control Problem. The dependence of the system state \(x(t)\in R^d\) at time \(t\in [0,\, T]\) on a scalar input signal u(t) is given by

$$\begin{aligned} \dot{x}(t)=A(\theta ^0)\, x(t) + b\, u(t), \quad x(0)=x_0, \end{aligned}$$
(1)

where \(A(\theta )\) is a \(d\times d\) matrix that depends on a vector of uncertain parameters \(\theta \in R^m\), while \(\theta =\theta ^0\) are their nominal values. In (1) \(b\in R^d\) is a vector of knownFootnote 1 amplifications. In the above, \(\dot{x}(t)\) stands for \(\frac{d\, x(t)}{dt}\), \(x_0\) is the initial state and T is the control horizon, which is finite and this assumption is important. We confine ourselves to scalar input signals to keep the notation simple. It will be clear that the results can be generalized to the multi-input case.

In the standard setting (see, e.g., [4, 18]) the problem is to find a control signal \(u^*\in L_2(0,\, T)\) for which the following cost functional J(u) attains its minimal value:

$$\begin{aligned} J(u)=\int _0^T \left[ (x_{ref}(t)-x(t))^{tr}\, (x_{ref}(t)-x(t)) + r\, u^2(t) \right] \, dt , \end{aligned}$$
(2)

subject to (1) as constraints, where \(x_{ref}\) is the known reference signal to follow, but with not too excessive use of the control signal energy, which is tuned by selecting a weighting factor \(r>0\).

One can consider also a more general criterion

$$\begin{aligned} J(u)=\int _0^T \left[ (x_{ref}(t)-x(t))^{tr}\, Q\, (x_{ref}(t)-x(t)) + r\, u^2(t) \right] \, dt , \end{aligned}$$
(3)

where Q is a \(d\times d\) symmetric and positive definite matrix of known weights, but it can be reduced to (2) by transforming the state variables using \(Q^{1/2}\).

Assuming that there is no uncertainty in parameters, i.e., \(\theta \) assumes nominal value \(\theta ^0\) that are known, then also the solution of this problem is well known (see, e.g., [4]), but we summarize it for further references. Define the Hamiltonian

$$\begin{aligned} H(x(t),\, u(t), \psi (t))&= (x_{ref}(t)-x(t))^{tr}\, (x_{ref}(t)-x(t)) + r\, u^2(t)+{} \\&{}+ \psi ^{tr}(t)\,\left[ A\left( \theta ^0 \right) \, x(t)+b\, u(t) \right] , \nonumber \end{aligned}$$
(4)

where \(\psi (t)\in R^d\) is a vector of the adjoint variables, for which the following ordinary differential equations (ODE) hold

$$\begin{aligned} \dot{\psi }(t)=-A^{tr}(\theta ^0)\,\psi (t) + 2\, (x_{ref}(t)-x(t)), \quad \psi (T)=0. \end{aligned}$$
(5)

According to the Pontriagin’s minimum principle, if \(u^*(.)\) and \(x^*(.)\) solves the problem (2) and (1), then there exists \(\psi ^*(.)\) for which the following equations hold:

$$\begin{aligned} \dot{\psi }^*(t)=-A^{tr}(\theta ^0)\,\psi ^*(t) + 2\, (x_{ref}(t)-x^*(t)), \quad \psi (T)=0, \end{aligned}$$
(6)
$$\begin{aligned} \dot{x}^*(t) \, =\, A\left( \theta ^0 \right) \, x^*(t) +b\, u^*(t), \quad x^*(0)=x_0 \end{aligned}$$
(7)

and for each \(t\in [0,\, T]\) the following condition holds

$$\begin{aligned} \frac{d}{d\, v}\, H(x^*(t),\, v, \psi ^*(t))\Big |_{v=u^*(t)}\,=\, 0. \end{aligned}$$
(8)

For LTI systems with criterion (2) it can be proved that condition (8) is also sufficient for the optimality of \(u^*(.)\). Furthermore, \(u^*(.)\) is the unique solution of this problem and (8) yields

$$\begin{aligned} 2\, r\, u^*(t) + b^{tr}\,\psi ^{*}(t)\, = 0, \quad t\in [0,\, T] . \end{aligned}$$
(9)

Thus, \(u^*(t)=P(t)\, (x_{ref}(t)-x(t))\) where P(t) is a \(d\times d\) matrix that solves the well known matrix Riccati quadratic differential equations. Notice that both P(t) and \(\psi ^{*}(t)\) in (9) depend on \(\theta ^0\). When d is large, then finding a numerical solution of the Riccati equations is not easy task and one can consider the approach proposed in this paper as an alternative to the classic approach based on solving these equations. We shall not develop this idea here in order to concentrate on the main topic.

The following facts are crucial for further considerations.

  • Fact 1. The Gateaux differential (see, e.g., [18]) of J at \(u\in L_2(0,\, T)\) in the direction \(\underline{U}\in L_2(0,\, T)\) has the following form:

    $$\begin{aligned} \frac{d\, J(u+\epsilon \, \underline{U})}{d\, \epsilon }\Big |_{\epsilon =0}= \int _0^T F(x(t),\, u(t),\, \psi (t))\, \underline{U}(t)\, dt. \end{aligned}$$
    (10)

    If the Frechet derivative of J exists (see, e.g., [18]) then F is equal to it and – in our case – it is given by

    $$\begin{aligned}&F(x(t),\, u(t),\, \psi (t))= \frac{d}{d\, v}\, H(x(t),\, v, \psi (t))\Big |_{v=u(t)}= {} \\&\qquad \qquad \qquad \;\; {}= 2\, r\, u(t) + b^{tr}\,\psi (t), \nonumber \end{aligned}$$
    (11)

    where \(\psi (.)\) solves (5).

  • Fact 2. Direction \(\underline{U}(t)=-F(x(t),\, u(t),\, \psi (t))\) is locally the steepest descent direction oh J at u(.). Furthermore, \(F(x^*(t),\, u^*(t),\, \psi ^*(t)) \equiv 0\). As one can notice, when searching the minimum of J the Frechet derivative F can play the same role as the gradient in searching for the minimum of a multivariate function.

The problem of iterative learning of the optimal control for repetitive processes. When \(\theta \) in (1) is the uncertain vector of parameters, then it is customary to invoke one of the following two approaches:

  • Plug-in approach – firstly estimate (identify) unknown parameters, then plug them into (1) instead of \(\theta ^0\) and consider it as certain,

  • Adaptive control approach – estimate \(\theta \) on-line and substitute it into the control law.

Both approaches have been historically developed without taking into account that a large number of processes to be controlled are repetitive (see the Introduction section for examples). In the proposed approach we consider repetitive processes and uncertainty of parameters is taken into account by feedback between the passes of a repetitive process that bears information about the uncertain parameters, which is then used for iterative learning approach, without explicitly estimating them.

For n-th pass the system is described by

$$\begin{aligned} \dot{x}_n(t)=A(\theta ^0)\, x_n(t) + b\, u_n(t), \; \; x_n(0)=x_0,\;\; n=1,\, 2,\ldots , \end{aligned}$$
(12)

where \( x_n(t)\in R^d\) and \( u_n(t)\), \(t\in [0,\, T]\) are the system state vector and the control signal along n-th pass, respectively. Equation (12) are seemingly unrelated between passes, but our aim is to design a learning procedure that improves \(u_n(.)\), taking into account \(u_{n-1}(.)\) and \(x_{n-1}(.)\) and introduces links between passes. In other words, we are looking for an operator \(\varPsi \)

$$\begin{aligned} u_n(.)=\varPsi (x_{n-1}(.),\, u_{n-1}(.)), \quad n=1,\, 2,\ldots \end{aligned}$$
(13)

such that

(a) \(\lim _{n\rightarrow \infty } J(u_n)=J(u^*)\), when \(\theta =\theta ^0\),

(b) \(\lim _{n\rightarrow \infty } J(u_n)\) convergent to a value not far from \(J(u^*)\), when \(\theta =\theta ^1\) and \(\delta \theta \mathop {=}\limits ^{def}||\theta ^1-\theta ^1||_m\) is sufficiently small, where \(||.||_m\) is the Euclidean norm in \(R^m\). Our reference point is the solution of the generic problem described in the previous subsection.

3 Iterative Learning Algorithm

In this section we derive an iterative learning algorithm for a repetitive process, assuming that its parameters take nominal values \(\theta ^0\). Then, we shall prove its convergence and local robustness against uncertainty of parameters.

Derivation of the Learning Algorithm. According to Facts 1, 2, one can expect that the following updates of \(u_n(.)\) will lead to improvements of J

$$\begin{aligned} u_{n+1}(t)=u_n(t)-\gamma \, F_n(t),\quad t\in [0,\, T], \end{aligned}$$
(14)

where \(\gamma >0\) is the step size,

$$\begin{aligned} F_n(t)\mathop {=}\limits ^{def} F(x_n(t),\, u_{(t)},\, \psi _n(t)) =\left( 2\, r\, u_n(t)+ b^{tr}\, \psi _n(t) \right) \end{aligned}$$
(15)

while \(\psi _n(.)\) is defined as a solution of the following adjoint equations:

$$\begin{aligned} \dot{\psi }_n(t)=-A^{tr}(\theta ^0)\,\psi _n(t) + 2\, (x_{ref}(t)-x_n(t)), \quad \psi _n(T)=0. \end{aligned}$$
(16)

Their solution can be expressed as

$$\begin{aligned} \psi _n(t)=\exp (-A^{tr}(\theta ^0)\,t)\psi _n^0+\int _0^t \exp (-A^{tr}(\theta ^0)\, (t-\tau ))\, e_n(\tau )\, d\tau , \end{aligned}$$
(17)

where \(e_n(\tau )\mathop {=}\limits ^{def} 2\, (x_{ref}(\tau )-x_n(\tau ))\) and \(\psi _n^0\) is selected so as to ensure \(\psi _n(T)=0\). After finding such \(\psi _n^0\) and substituting it into (17), we obtain

$$\begin{aligned} \psi _n(t)=-\int _t^T \exp \left[ -A^{tr}(\theta ^0)\, (t-\tau )\right] \, e_n(\tau )\, d\tau . \end{aligned}$$
(18)

Substitution of this expression into (14) leads to the following learning procedure: for \(t\in [0,\, T]\) and \(n=0,\, 1,\ldots \) iterate

$$\begin{aligned} u_{n+1}(t)=(1-\gamma \, 2\, r)\,u_n(t) + \gamma \, b^{tr} \int _t^T \!\! \exp \left[ -A^{tr}(\theta ^0)\, (t-\tau )\right] \, e_n(\tau )\, d\tau . \end{aligned}$$
(19)

At this stage, it is worth comparing (19) with the structure of a typical ILC algorithm that for LTI systems has (in our notation) the following form

$$\begin{aligned} u_{n+1}(t) = \alpha \,u_n(t) + \bar{\beta }^1\, e_n(t) + \bar{\beta }^2\, (x_{n}(t)-x_{n-1}(t), \quad t\in [0,\, T] , \end{aligned}$$
(20)

where \(\alpha \in R\), \(\bar{\beta }^1,\, \bar{\beta }^2\in R^d\) are selected in such a way that the repetitive system with such a control law is asymptotically stable.

The similarities between (20) and (19) are apparent, but there are also important differences: (1) the term \((x_{n}(t)-x_{n-1}(t))\) is not present in (19) and it seems that its presence may slow down the rate of convergence of learning algorithms, but – on the other hand – it may stabilize them, (2) the main updating component \( e_n(t)\) is present in the both cases, but in (19) it is integrated (with the weighting matrix) from t to T, which can be interpreted as the integrated prediction error from now to the end of n-th pass, (3) the structure of (19) has been derived as the descent direction of J at \(u_n(.)\) and all the weights, except \(\gamma \), are specified by the system description and J.

Convergence of the Learning Process. In order to select \(\gamma >0\) that locally speeds up the learning process let us \(J(u_n-\gamma \, F_n)\) into the Taylor series, which is exact in this case,

$$\begin{aligned} J(u_{n+1})=J(u_n-\gamma \, F_n)= J(u_n)-\gamma \, ||F_n(.)||^2 +(2\, r)\,\frac{\gamma ^2}{2}\, ||F_n(.)||^2 . \end{aligned}$$
(21)

A proper selection of \(\gamma >0\) requires \((1-r\,\gamma )<0\), i.e., \(\gamma <1/r\) in order to ensure \(J(u_{n+1}) < J(u_n)\). Indeed, then we have

$$\begin{aligned} J(u_{n+1})= J(u_n) - \frac{1}{(r+\nu )}\, ||F_n(.)||^2 \end{aligned}$$
(22)

for arbitrary \(\nu >0\).

Theorem 1

The learning process

$$\begin{aligned} u_{n+1}(t)=u_n(t)- \frac{1}{r+\nu }\,\left( 2\, r\, u_n(t)+ b^{tr}\, \psi _n(t) \right) ,\quad t\in [0,\, T], \end{aligned}$$
(23)

where \(\nu >0\) and \(\psi _n(.)\) solves

$$\begin{aligned} \dot{\psi }_n(t)=-A^{tr}(\theta ^0)\,\psi _n(t) +2\, (x_{ref}(t)-x_n(t)), \quad \psi _n(T)=0. \end{aligned}$$
(24)

designed for the following repetitive process

$$\begin{aligned} \dot{x}_n(t)=A(\theta ^0)\, x_n(t) + b\, u_n(t), \; \; x_n(0)=x_0,\;\; n=1,\, 2,\ldots , \end{aligned}$$
(25)

is convergent to the solution of the optimal control problem for one pass in the following sense: (a) \(\lim _{n\rightarrow \infty } J(u_n)=J(u^*)\), (b) \(\lim _{n\rightarrow \infty } ||u_n(.) - u^*(.)||=0\), (c) \(\lim _{n\rightarrow \infty } ||x_n(.) - x^*(.)||=0\).

Pass-to-pass on-line Learning. In Theorem 1 it was assumed that \(\theta ^0\) is known, hence we can calculate \( x_n(.)\) as a solution of (25). In this section we present an on-line version of the learning process that uses observations of the system state instead in order to cope with possible inaccuracies in knowledge of \(\theta ^0\) and/or with from pass to pass fluctuations of these parameters, assuming that they are not too far from \(\theta ^0\).

Algorithm 1

(Pass-to-pass Learning (PPL)) 

  • Step 0. Select \(\hat{u}_0(.)\in L_2(0,\, T)\) (preferably obtained by running off-line several iterations of (23), (24) and (25)). Set \(n=0\). Select \(\varepsilon >0\) as the level when a desired accuracy is obtained.

  • Step 1. Apply \(\hat{u}_n(.)\) along the pass to a real system, then observe and store \(\hat{x}_n(.)\).

  • Step 2. Calculate the adjoint states \(\hat{\psi }_n(.)\) along the pass by solving the following equations:

    $$\begin{aligned} \dot{\hat{\psi }}_n(t)=-A^{tr}(\theta ^0)\,\hat{\psi }_n(t) + 2\,(x_{ref}(t)-\hat{x}_n(t)), \quad \hat{\psi }_n(T)=0. \end{aligned}$$
    (26)

    Adjoint states contain information on the system behavior in the future and therefore they cannot be observed. Hence, we are forced to calculate them using the nominal parameter values \(\theta ^0\) as the only available.

  • Step 3. Calculate \(\hat{F}_n(t)\mathop {=}\limits ^{def} (2\, r\, \hat{u}_n(t)+ b^{tr}\, \hat{\psi }_n(t)\), \(t\in [0,\, T]\). If

    $$\begin{aligned} \max _{t\in [0,\, T]} |\hat{F}_n(t)| > \varepsilon , \end{aligned}$$
    (27)

    then skip updating \(\hat{u}_n(.)\) and use it in the next iteration. Set \(n:=n+1\) and go to Step 1. Otherwise, go to Step 4

  • Step 4. Update \(\hat{u}_n(.)\) as follows:

    $$\begin{aligned} \hat{u}_{n+1}(t)=\hat{u}_n(t) - \gamma \, \hat{F}_n(t) ,\quad t\in [0,\, T], \end{aligned}$$
    (28)

    where \(\gamma \le {1}/{(r+\nu )}\), \(\nu >0\). Set \(n:=n+1\) and go to Step 1.

When uncertainties in parameters are allowed, we can not be sure that the step length in (28) is properly selected to ensure the monotonicity of the criterion. If it does not decrease, than one should decrease \(\gamma \).

Condition (27) is usually used as the stopping condition. Here, it is used to temporarily skip updating \(u_n(.)\), but the algorithm is not halted, since we allow small fluctuations of the parameters between passes. In this version the PPL algorithm is able to detect them and reduce their influence by updating \(u_n(.)\) again.

A Limiting Point of the PPL Algorithm. For theoretical considerations we assume that:

(a) the parameters can change to a certain \(\theta ^1\ne \theta ^0\) and these values are kept for a long (infinite) time,

(b) \(\theta ^1\) is not too far from \(\theta ^0\) in the following sense: \(||\theta ^1 - \theta ^0||_d \le C \gamma \), where \(\gamma >0\) is the step size of the PPL algorithm, while \(C>0\) is a certain constant,

(c) Step 3 is omitted in order to have an infinite sequence of passes with updates.

When assumptions (a), (b), (c) hold, then the PPL algorithm can stop updating \(\hat{u}_n\) only when there exists a triple \(\hat{x}(.),\, \hat{u}(.),\, \hat{\psi }(.))\) such that

$$\begin{aligned} \left( 2\, r\, \hat{u}(t)+ b^{tr}\, \hat{\psi }(t) \right) =0,\quad t\in [0,\, T], \end{aligned}$$
(29)
$$\begin{aligned} \dot{\hat{\psi }}(t)=-A^{tr}(\theta ^0)\,\hat{\psi }(t) + 2\, (x_{ref}(t)-\hat{x}(t)), \quad \hat{\psi }(T)=0, \end{aligned}$$
(30)
$$\begin{aligned} \dot{\hat{x}}(t)=A(\theta ^1)\, \hat{x}(t)+b\, \hat{u}(t),\quad \hat{x}(0)=x_0. \end{aligned}$$
(31)

Existence of such a triple is further assumed. Notice that in (31) we have \(\theta ^1\) instead of \(\theta ^0\). Thus, we cannot check these conditions, but we can do it in a certain vicinity of \(\theta ^0\).

Theorem 2

If \(||\theta ^1-\theta ^0||\le \gamma \), then for the PPL algorithm we have

$$\begin{aligned} \lim _{n\rightarrow \infty } J(\hat{u}_n)=J(\hat{u}), \end{aligned}$$

where \(\hat{u}\) is defined through (29), (30) and (31). Furthermore,

$$\begin{aligned} \lim _{n\rightarrow 0} ||\hat{F}_n(.)||=||\hat{F}(.)||=0. \end{aligned}$$
(32)

In order to prove the convergence of \(\hat{u}_n\) to \(\hat{u}\) we have to specify more precisely the dependence of \(\mathcal {A}(\theta )\) on perturbations of \(\theta \).

Assumption 1

We shall assume that a perturbation from \(\theta ^0\) to \(\theta ^1\) for sufficiently small \(||\theta ^1 - \theta ^0||\le C_0\,\gamma \) invokes the following change

$$\begin{aligned} \mathcal {A}(\theta ^1)=(1+\varsigma )\,\mathcal {A}(\theta ^0) \end{aligned}$$
(33)

where \(\varsigma \in R\) is a parameter dependent on \(\theta ^1\) and \(\theta ^0\).

We sketch the rational arguments in favor of the above assumption. Let us suppose that a perturbation can be expressed as follows: \(A(\theta ^1)=A(\theta ^0) + \varDelta A\). Notice that \(\mathcal {A}(\theta ^1)\varDelta u_n(t)=\int _0^T \exp (\mathcal {A}(\theta ^1)\,\tau )\, \varDelta u_n(t-\tau )\, d\tau \). It is well known that \(||\exp (\mathcal {A}(\theta ^0\, t))||_{d\times d} \le \exp (\omega \, t)\) for a certain \(\omega \), where \(||.||_{d\times d}\) is the matrix norm. Furthermore, from the theory of perturbations of semigroups (see, e.g., [6, 8]) it is also known that

$$\begin{aligned}&||\exp (\mathcal {A}(\theta ^0\, t + \varDelta A\, t))||_{d\times d} \le \exp ((\omega + ||\varDelta A||_{d\times d})\, t) \\&\qquad \qquad \qquad \approx 1 + \omega \, t + ||\varDelta A||_{d\times d})\, t. \nonumber \end{aligned}$$
(34)

Convergence of Learning under Perturbations. If Assumption 1 holds and a perturbation is such that \((2\, r + (1+\varsigma )\,\lambda _{min})>0\), then for the sequence generated by Algorithm PPL we have: \( \lim _{n\rightarrow \infty } ||\hat{u}(.)-\hat{u}_n(.) ||=0\).

4 ILOC for Laser Cladding Process

In this section we summarize simulation experiments of ILOC applied to the laser cladding process described in the Introduction.

Fig. 1.
figure 1

The starting point \(U_{start}(.)\) (panel A) and \(y_{start}(.)\) (panel B). Approximately optimal input signal (panel C) and the resulting approximately optimal system state (panel D).

Full size image

Lake Temperature – Laser Power Model. Our starting point is a model that links the laser power U(t) [W], which is our input signal and the temperature of the lake induced by the laser, which is simultaneously our state and output variable and therefore it is denoted as y(t) [K] Using [30] as a guideline, assume the following model:

$$\begin{aligned} \tau \, \dot{y}(t)+y(t)= K\, (U(t))^\beta , \quad y(0)=\tilde{y} \end{aligned}$$
(35)

where \(\tilde{y}\) - given initial temperature. The parameters are explained below, following [30] with small changes. Overall system gain (amplification) \(K = K_1\, (V^\alpha )\, (M^\vartheta )= 1418.9\), where \(K_1 = 1.42*10^3\) is the system amplification, \(\alpha = -7.1\, 10^{-3}\), \( \beta = 6.25\, 10^{-2}\), \(\vartheta = 3.0\, 10^{-3}\), where \(V = 2\) [mm/sec] is the laser traverse speed. \(M = 4.0\) [g/min] is the cladding powder supply rate, while \(\tau =2\, 10^{-2}\) [sec.] is the system time constant.

Results of simulations. We have developed ILOC procedures for linear systems, while (35) is a nonlinear system, but a simple substitution \(u(t)=U^{\beta }(t)\) converts it into the following linear system:

$$\begin{aligned} \tau \, \dot{x}(t)+y(t)= K\, u(t), \quad x(0)=x_0 . \end{aligned}$$
(36)

It suffices to run ILOC algorithms for (36), since rising to a positive power is the invertible transformation and at each iteration we can calculate \(U_n(t)=u_n^{1/\beta }(t)\) and apply it to the real system.

Notice that the adjoint equation for n-th pass has the form

$$\begin{aligned} \dot{\psi }_n(t) = 2\, ({x}_{ref}(t) - x_n(t)) + \tau ^{-1}\,\psi _n(t), \quad \psi _n(T)=0., \end{aligned}$$
(37)

while the Frechet derivative of J is given by

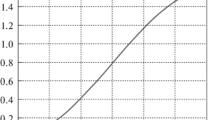
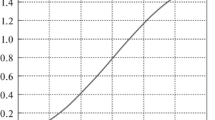
$$\begin{aligned} F(x_n(.),\, u_n(.),\, \psi _n(.))(t) = (K\, \tau ^{-1})\,\psi _n(t)\, + 2\, r\, u_n(t). \end{aligned}$$
(38)

In the simulations reported below \(\gamma =152\) has been used. As a starting point a signal that is shown in Fig. 1 (upper left panel) has been selected. The response of the system (35) to this signal is shown in Fig. 1 (upper right panel).

Our aim is to simulate the learning process, which provides the temperature shape that is close to the profile shown in Fig. 1 by the dashed line. The learning process converges quickly at the first several passes. Then, it slows down, which is typical for gradient improvement procedures. It is however crucial that the learning process provides quick improvements at the first phase and it is sufficiently simple to be learnt from pass-to-pass observations. The shape of the approximately optimal input signal is shown in Fig. 1 (lower left panel), while the system response is sketched in Fig. 1 (lower right panel) by the solid line. As one can notice, the lake temperature differs from the desired one by no more than 5 [K], which is sufficient in practice. It can be further reduced by setting less penalty for the usage of the laser energy.