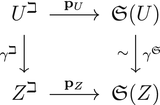Skeletons and Fans of Logarithmic Structures

Abstract

We survey a collection of closely related methods for generalizing fans of toric varieties, include skeletons, Kato fans, Artin fans, and polyhedral cone complexes, all of which apply in the wider context of logarithmic geometry. Under appropriate assumptions these structures are equivalent, but their different realizations have provided for surprisingly disparate uses. We highlight several current applications and suggest some future possibilities.

1 Introduction

1.1 Toric Varieties, Toroidal Embeddings, and Logarithmic Structures

Toric varieties were introduced in [21] and studied in many sources, see, for instance, [19, 20, 23, 35, 43, 44]. They are the quintessence of combinatorial algebraic geometry: there is a category of combinatorial objects called fans, which is equivalent to the category of toric varieties with torus-equivariant morphisms between them. Further, classical tropical geometry probes the combinatorial structure of subvarieties of toric varieties. We review this theory in utmost brevity in Sect. 2 below.

In [35] some of this picture was generalized to toroidal embeddings, especially toroidal embeddings without self-intersections, and their corresponding polyhedral cone complexes (Sect. 2.7). Following Kato [34] we argue that the correct generality is that of fine and saturated logarithmic structures. Working over perfect fields, toroidal embeddings can be identified as logarithmically regular varieties. Since logarithmic structures might not be familiar to the reader, we provide a brief review of the necessary definitions in Sect. 3. To keep matters as simple as possible, all the logarithmic structures we use below are fine and saturated (Definition 3.12). These are the logarithmic structures closest to toroidal embeddings which still allow us to pass to arbitrary subschemes.

The purpose of this text is to survey a number of ways one can think of generalizing fans of toric varieties to the realm of logarithmic structures: Kato fans, Artin fans, polyhedral cone complexes, and skeletons. These are all closely related and, under appropriate assumptions, equivalent. But the different ways they are realized provide for entirely different applications. We do not address skeletons of logarithmic structures over non-trivially valued non-Archimedean fields—see Werner’s contribution [63]. Nor do we address the general theory of skeletons of Berkovich spaces and their generalizations [13, 28, 40].

1.2 Kato Fans

In [34], Kato associated a combinatorial structure F _X , which has since been called the Kato fan of X, to a logarithmically regular scheme X (with Zariski-local charts), see Sect. 4. This is a reformulation of the polyhedral cone complexes of [35] which realizes them within the category of monoidal spaces. In [59], one further generalizes the construction of the associated Kato fan to logarithmic structures without monodromy. As in [35], Kato fans provide a satisfying theory encoding logarithmically smooth birational modifications in terms of subdivisions of Kato fans. Procedures for resolution of singularities of polyhedral cone complexes of Kato fans are given in [35] and [34]. As an outcome, we obtain a combinatorial procedure for resolution of singularities of logarithmically smooth structures without self-intersections.

Kato fans, or generalizations of them, can be constructed for more general logarithmic structures. We briefly discuss such a construction using sheaves on the category of Kato fans. A different, and possibly more natural approach, is obtained using Artin fans.

1.3 Artin Fans and Olsson’s Stack of Logarithmic Structures

In order to import notions and structures from scheme theory to logarithmic geometry, Olsson [46] showed that a logarithmic structure X on a given underlying scheme $\underline{X}$ is equivalent to a morphism $\underline{X} \rightarrow \underline{\mathsf{Log}}$, where $\underline{\mathsf{Log}}$ is a rather large, zero-dimensional Artin stack—the moduli stack of logarithmic structures. It carries a universal logarithmic structure whose associated logarithmic algebraic stack we denote by Log—providing a universal family of logarithmic structures $\mathsf{Log} \rightarrow \underline{\mathsf{Log}}$.

Being universal, the logarithmic stack Log cannot reflect the combinatorics of X. In Sect. 5 we define, following [3, 8], the notion of Artin fans, and show that the morphism X → Log factors through an initial morphism $X \rightarrow \mathcal{A}_{X}$, where $\mathcal{A}_{X}$ is an Artin fan and $\mathcal{A}_{X} \rightarrow \mathsf{Log}$ is étale and representable.

We argue that, unlike Log, the Artin fan $\mathcal{A}_{X}$ is a combinatorial object which encodes the combinatorial structure of X. Indeed, when X is without monodromy, the underlying topological space of $\mathcal{A}_{X}$ is simply the Kato fan F _X . In other words, $\mathcal{A}_{X}$ combines the advantages of the Kato fan F _X , being combinatorial, and of Log, being algebraic.

In addition $\mathcal{A}_{X}$ exists in greater generality, when X is allowed to have self-intersections and monodromy—even not to be logarithmically smooth; in a roundabout way, it provides a definition of F _X in this generality, by taking the underlying “monoidal space”—or more properly, “monoidal stack”—of $\mathcal{A}_{X}$.

The theory of Artin fans is not perfect. Its current foundations lack full functoriality of the construction of $X \rightarrow \mathcal{A}_{X}$, just as Olsson’s characteristic morphism X → Log is functorial only for strict morphisms Y → X of logarithmic schemes. In Sect. 5.4.2 we provide a patch for this problem, again following Olsson’s ideas.

1.4 Artin Fans and Unobstructed Deformations

Artin fans were developed in [3, 8] and the forthcoming [6] in order to study logarithmic Gromov–Witten theory. The idea is that since an Artin fan $\mathcal{A}$ is logarithmically étale, a map $f: C \rightarrow \mathcal{A}_{X}$ from a curve to $\mathcal{A}_{X}$ is logarithmically unobstructed. Precursors to this result for specific X were obtained in [4, 5, 7, 16]. In [5] an approach to Jun Li’s expanded degenerations was provided using what in hindsight we might call the Artin fan of the affine line $\mathcal{A} = \mathcal{A}_{\mathbb{A}^{1}}$. The papers [4, 7, 16] use this formalism to prove comparison results in relative Gromov–Witten theory. For logarithmically smooth X, the map $X \rightarrow \mathcal{A}_{X}$ was used in [3] to prove that logarithmic Gromov–Witten invariants are invariant under logarithmic blowings up; in [8], it was used for general X to complete a proof of boundedness of the space of logarithmic stable maps. We review these results, for which both the combinatorial and algebraic features of $\mathcal{A}_{X}$ are essential, in Sect. 6. They serve as evidence that the algebraic structure of Artin fans is an advantage over the purely combinatorial structure of their associated Kato fans.

1.5 Skeletons and Tropicalization

In Sect. 7 we follow Thuillier [58] and associate to a Zariski-logarithmically smooth scheme X its extended cone complex $\overline{\varSigma }_{X}$. This is a variant of the cone complex Σ _X of [35], and is related to the Kato fan in an intriguing manner:

$$\displaystyle{\overline{\varSigma }_{X} = F_{X}(\mathbb{R}_{\geq 0} \sqcup \{\infty \}).}$$

The complex $\overline{\varSigma }_{X}$ is canonically homeomorphic to the skeleton $\mathfrak{S}(X)$ of the non-Archimedean space $X^{\beth }$ associated to the logarithmic scheme X, when viewing the base field as a valued field with trivial valuation, as developed by Thuillier [58]. In this case there is a continuous map $X^{\beth } \rightarrow \overline{\varSigma } _{X}$, and $\overline{\varSigma }_{X} \subset X^{\beth }$ is a strong deformation retract. Thuillier used this formalism to prove a compelling result independent of logarithmic or non-Archimedean considerations: the homotopy type of the dual complex of a logarithmic resolution of singularities does not depend on the choice of resolution.

For a general fine and saturated logarithmic scheme X, we still have a continuous mapping $X^{\beth } \rightarrow \overline{\varSigma } _{X}$, although we do not have a continuous section $\overline{\varSigma }_{X} \subset X$. It is argued in [59] that the image of $X^{\beth } \rightarrow \overline{\varSigma } _{X}$ can be viewed as the tropicalization of X.

Note that in this discussion we have limited the base field of X to have a trivial absolute value. A truly satisfactory theory must apply to subvarieties defined over valued-field extensions, in particular with nontrivial valuation.

1.6 Analytification of Artin Fans

Artin fans can be tied into the skeleton picture via their analytifications, as we indicate in Sect. 8. We again consider our base field as a trivially valued field. The analytification of the morphism $\phi _{X}: X \rightarrow \mathcal{A}_{X}$ is a morphism $\phi _{X}^{\beth }: X^{\beth } \rightarrow \mathcal{A}_{X}^{\beth }$ into an analytic Artin stack $\mathcal{A}_{X}^{\beth }$. The whole structure sits in a commutative diagram

On the left side of the diagram the horizontal arrows remain in their respective categories—algebraic on the bottom, analytic on top—but discard all geometric data of X and $X^{\beth }$ except the combinatorics of the logarithmic structure. On the right side the arrows $\mathcal{A}_{X}^{\beth } \rightarrow \overline{\varSigma } _{X}$ and $\mathcal{A}_{X} \rightarrow F_{X}$ discard the analytic and algebraic data and preserve topological and monoidal structures. In particular $\mathcal{A}_{X}^{\beth } \rightarrow \overline{\varSigma } _{X}$ is a homeomorphism, endowing the familiar complex $\overline{\varSigma }_{X}$ with an analytic stack structure.

1.7 Into the Future

While we have provided evidence that the algebraic structure of $\mathcal{A}_{X}$ has advantages over the underlying monoidal structure F _X , at this point we can only hope that the analytic structure $\mathcal{A}_{X}^{\beth }$ would have significant advantages over the underlying piecewise-linear structure $\overline{\varSigma }_{X}$, as applications are only starting to emerge, see [55].

We discuss some questions that might usher further applications in Sect. 9.

2 Toric Varieties and Toroidal Embeddings

Mostly for convenience, we work here over an algebraically closed field k. We recall, in briefest terms, the standard setup of toric varieties and toroidal embeddings.

2.1 Toric Varieties

Consider a torus $T \simeq \mathbb{G}_{m}^{n}$ and a normal variety X on which T acts with a dense orbit isomorphic to T—and fix such isomorphism. Write M for the character group of T and write N for the co-character group. Then M and N are both isomorphic to $\mathbb{Z}^{n}$ and are canonically dual to each other. We write $M_{\mathbb{R}} = M \otimes \mathbb{R}$ and $N_{\mathbb{R}} = N \otimes \mathbb{R}$ for the associated real vector spaces.

2.2 Affine Toric Varieties and Cones

If X is affine, it is canonically isomorphic to $X_{\sigma } =\mathop{ \mathrm{Spec}}\nolimits k[S_{\sigma }]$, where $\sigma \subset N_{\mathbb{R}}$ is a strictly convex rational polyhedral cone, and $S_{\sigma } = M \cap \sigma ^{\vee }$ is the monoid of lattice points in the n-dimensional cone $\sigma ^{\vee }\subset M_{\mathbb{R}}$ dual to σ. Such affine X _σ contains a unique closed orbit $\mathcal{O}_{\sigma }$, which is itself isomorphic to a suitable quotient torus of T.

2.3 Invariant Opens

A nonempty torus-invariant affine open subset of X _σ is always of the form X _τ where $\tau \prec \sigma$ is a face of σ—either σ itself or the intersection of σ with a supporting hyperplane. For instance, the torus T itself corresponds to the vertex {0} of σ.

2.4 Fans

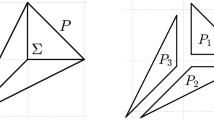
Any toric variety X is covered by invariant affine opens of the form $X_{\sigma _{i}}$, and the intersection of $X_{\sigma _{i}}$ with $X_{\sigma _{j}}$ is of the form $X_{\tau _{ij}}$ for a common face $\tau _{ij} =\sigma _{i} \cap \sigma _{j}$. It follows that the cones σ _i form a fan $\Delta _{X}$ in N. This means precisely that $\Delta _{X}$ is a collection of strictly convex rational polyhedral cones in N, that any face of a cone in $\Delta _{X}$ is a member of $\Delta _{X}$, and the intersection of any two cones in $\Delta _{X}$ is a common face (see Fig. 1).

Fig. 1

The fan of $\mathbb{P}^{2}$

And vice versa: given a fan $\Delta$ in N one can glue together the associated affine toric varieties X _σ along the affine opens X _τ to form a toric variety $X(\Delta )$.

2.5 Categorical Equivalence

One defines a morphism from a toric variety T ₁ ⊂ X ₁ to another T ₂ ⊂ X ₂ to be an equivariant morphism X ₁ → X ₂ extending a homomorphism of tori T ₁ → T ₂. On the other hand one defines a morphism from a fan $\Delta _{1}$ in $(N_{1})_{\mathbb{R}}$ to a fan $\Delta _{2}$ in $(N_{2})_{\mathbb{R}}$ to be a group homomorphism N ₁ → N ₂ sending each cone $\sigma \in \Delta _{1}$ into some cone $\tau \in \Delta _{2}$.

A fundamental theorem says

Theorem 2.1.

The correspondence above extends to an equivalence of categories between the category of toric varieties over k and the category of fans.

Under this equivalence, toric birational modifications X ₁ → X ₂ of X ₂ correspond to subdivisions $\Delta _{X_{1}} \rightarrow \Delta _{X_{2}}$ of $\Delta _{X_{2}}$.

2.6 Extended Fans

The closure $\overline{\mathcal{O}}_{\sigma }\subset X$ of a T-orbit $\mathcal{O}_{\sigma }$, which is itself a toric variety, is encoded in $\Delta _{X}$, but in a somewhat cryptic manner. Thuillier [58] provided a way to add all the fans of these loci $\overline{\mathcal{O}}_{\sigma }$ and obtain a compactification $\Delta _{X} \subset \overline{\Delta }_{X}$: instead of gluing together the cones σ along their faces, one replaces σ with a natural compactification, the extended cone

$$\displaystyle{\overline{\sigma }:=\mathop{ \mathrm{Hom}}\nolimits _{\mathbf{Mon}}(S_{\sigma }, \mathbb{R}_{\geq 0} \cup \{\infty \}),}$$

where the notation Hom _Mon stands for the set of monoid homomorphisms. This has the effect of adding, in one step, lower dimensional cones isomorphic to $\sigma /\mathop{\mathrm{Span}}\nolimits \tau$ at infinity corresponding to the closure of $\mathcal{O}_{\tau }$ in X _σ , for all $\tau \prec \sigma$. We still have that $\overline{\tau }_{ij} = \overline{\sigma } _{i} \cap \overline{\sigma } _{j}$, and one can glue together these extended cones to obtain the extended fan $\overline{\Delta }_{X}$ (Fig. 2).

Fig. 2

The extended fan of $\mathbb{P}^{2}$

2.7 Toroidal Embeddings

The theory of toroidal embedding was developed in [35] in order to describe varieties that look locally like toric varieties. A toroidal embedding U ⊂ X is a dense open subset of a normal variety X such that, for any closed point x, the completion $\widehat{U } _{x} \subset \widehat{X} _{x}$ is isomorphic to the completion of an affine toric variety $T_{x} \subset X_{\sigma _{x}}$. Equivalently, each x ∈ X should admit an étale neighborhood $\phi _{x}: V _{x} \rightarrow X$ and an étale morphism $\psi _{x}: V _{x} \rightarrow X_{\sigma _{x}}$ such that $\psi _{x}^{-1}T_{x} =\phi _{ x}^{-1}U$. Note that the open set U ⊂ X serves as a global structure connecting the local pictures $T_{x} \subset X_{\sigma _{x}}$.

2.8 The Cone Complex of a Toroidal Embedding Without Self-Intersections

If the morphisms ϕ _x : V _x  → X are assumed to be Zariski open embeddings, then the toroidal embedding is a toroidal embedding without self-intersections. In this case the book [35] provides a polyhedral cone complex Σ _X replacing the fan of a toric variety. The main difference is that the cones of the complex Σ _X do not lie linearly inside an ambient space of the form $N_{\mathbb{R}}$.

For a toroidal embedding without self-intersections, the strata of $X_{\sigma _{x}}$ glue together to form a stratification $\{\mathcal{O}_{i}\}$ of X. For $x \in \mathcal{O}_{i}$ the cone σ _x , along with its sublattice $\sigma _{x} \cap N$, is independent of x. It can be described canonically as follows. Let X _i be the star of $\mathcal{O}_{i}$, namely the union of strata containing $\mathcal{O}_{i}$ in their closures. It is an open subset of X. Let $\overline{M}_{i}$ be the monoid of effective Cartier divisors on X _i supported on X _i ∖ U. Let $N_{\sigma } =\mathop{ \mathrm{Hom}}\nolimits _{\mathbf{Mon}}( \overline{M}_{i}, \mathbb{N})$ be the dual monoid. Then $\sigma _{x} = (N_{\sigma })_{\mathbb{R}}$ is the associated cone. When one passes to another stratum contained in X _i one obtains a face τ ≺ σ, and $N_{\tau } =\tau \cap N_{\sigma }$. These cones glue together naturally, in a manner compatible with the sublattices, to form a cone complex Σ _X with integral structure. Unlike the case of fans, the intersection $\sigma _{i} \cap \sigma _{j}$ could be a whole common subfan of σ _i and σ _j , and not necessarily one cone (Fig. 3).

Fig. 3

The complex of $\mathbb{P}^{2}$ with the divisor consisting of a line and a transverse conic: the cones associated to the zero-dimensional strata meet along both their edges

2.9 Extended Complexes

Just as in the case of toric varieties, these complexes canonically admit compactifications $\varSigma _{X} \subset \overline{\varSigma } _{X}$, obtained by replacing each cone σ _x by the associated extended cone $\overline{\sigma }_{x}$. This structure was introduced in Thuillier’s [58].

2.10 Functoriality

Let U ₁ ⊂ X ₁ and U ₂ ⊂ X ₂ be toroidal embeddings without self-intersections and f: X ₁ → X ₂ a dominant morphism such that f(U ₁) ⊂ U ₂. Then one canonically obtains a mapping $\varSigma _{X_{1}} \rightarrow \varSigma _{X_{2}}$, simply because Cartier divisors supported away from U ₂ pull back to Cartier divisors supported away from U ₁. This mapping is continuous, sends cones into cones linearly, and sends lattice points to lattice points. Declaring such mappings to be mappings of polyhedral cone complexes with integral structure, we obtain a functor from toroidal embeddings to polyhedral cone complexes. This functor is far from being an equivalence.

In [35] one focuses on toroidal modifications f: X ₁ → X ₂, namely those birational modifications described on charts of X ₂ by toric modifications of the toric varieties $X_{\sigma _{x}}$. Then one shows

Theorem 2.2.

The correspondence $X_{1}\mapsto \varSigma _{X_{1}}$ extends to an equivalence of categories between toroidal modifications of U ₂ ⊂ X ₂ , and subdivisions of $\varSigma _{X_{2}}$.

3 Logarithmic Structures

We briefly review the theory of logarithmic structures [33].

3.1 Notation for Monoids

Definition 3.1.

A monoid is a commutative semi-group with a unit. A morphism of monoids is required to preserve the unit element.

We denote the category of monoids by the symbol Mon.

Given a monoid P, we can associate a group

$$\displaystyle{ P^{gp}:=\{ (a,b)\vert (a,b) \sim (c,d)\ \mbox{ if}\ \exists s \in P\ \mbox{ such that}\ s + a + d = s + b + c\}. }$$

Note that any morphism from P to an abelian group factors through P ^gp uniquely.

Definition 3.2.

A monoid P is called integral if $P \rightarrow P^{gp}$ is injective. It is called fine if it is integral and finitely generated.

An integral monoid P is said to be saturated if whenever p ∈ P ^gp and n is a positive integer such that np ∈ P then p ∈ P.

As has become customary, we abbreviate the combined condition “fine and saturated” to fs.

3.2 Logarithmic Structures

Definition 3.3.

Let $\underline{X}$ be a scheme. A pre-logarithmic structure on $\underline{X}$ is a sheaf of monoids M _X on the small étale site $\mathrm{\acute{e}t}(\underline{X})$ combined with a morphism of sheaves of monoids: $\alpha: M_{X}\longrightarrow \mathcal{O}_{\underline{X}}$, called the structure morphism, where we view $\mathcal{O}_{\underline{X}}$ as a monoid under multiplication. A pre-logarithmic structure is called a logarithmic structure if $\alpha ^{-1}(\mathcal{O}_{\underline{X}}^{{\ast}})\mathop{\cong}\mathcal{O}_{\underline{X}}^{{\ast}}$ via α. The pair $(\underline{X},M_{X})$ is called a logarithmic scheme, and will be denoted by X.

The structure morphism α is frequently denoted exp and an inverse $\mathcal{O}_{X}^{{\ast}}\rightarrow M_{X}$ is denoted log.

Definition 3.4.

Given a logarithmic scheme X, the quotient sheaf $\overline{M}_{X} = M_{X}/\mathcal{O}_{\underline{X}}^{{\ast}}$ is called the characteristic monoid, or just the characteristic, of the logarithmic structure M _X .

Definition 3.5.

Let M and N be pre-logarithmic structures on $\underline{X}$. A morphism between them is a morphism $M \rightarrow N$ of sheaves of monoids which is compatible with the structure morphisms.

Definition 3.6.

Let $\alpha: M \rightarrow \mathcal{O}_{\underline{X}}$ be a pre-logarithmic structure on $\underline{X}$. We define the associated logarithmic structure M ^a to be the push-out of

in the category of sheaves of monoids on $\mathrm{\acute{e}t}(\underline{X})$, endowed with

$$\displaystyle{M^{a} \rightarrow \mathcal{O}_{\underline{ X}}\qquad (a,b)\mapsto \alpha (a)b\qquad \qquad (a \in M,b \in \mathcal{O}_{\underline{X}}^{{\ast}}).}$$

The following are two standard examples from [33, (1.5)]:

Example 3.7.

Let $\underline{X}$ be a smooth scheme with an effective divisor $D \subset \underline{ X}$. Then we have a standard logarithmic structure M on $\underline{X}$ associated to the pair $(\underline{X},D)$, where

$$\displaystyle{M_{X}:=\{ f \in \mathcal{O}_{\underline{X}}\ \vert \ f\vert _{\underline{X}\setminus D} \in \mathcal{O}_{\underline{X}}^{{\ast}}\}}$$

with the structure morphism $M_{X} \rightarrow \mathcal{O}_{\underline{X}}$ given by the canonical inclusion. This is already a logarithmic structure, as any section of $\mathcal{O}_{\underline{X}}^{{\ast}}$ is already in M _X .

Example 3.8.

Let P be an fs monoid, and $\underline{X} =\mathop{ \mathrm{Spec}}\nolimits \mathbb{Z}[P]$ be the associated affine toric scheme. Then we have a standard logarithmic structure M _X on $\underline{X}$ associated to the pre-logarithmic structure

$$\displaystyle{P \rightarrow \mathbb{Z}[P]}$$

defined by the obvious inclusion.

We denote by $\mathop{\mathrm{Spec}}\nolimits (P \rightarrow \mathbb{Z}[P])$ the log scheme $(\underline{X},M_{X})$.

3.3 Inverse Images

Let $f:\underline{ X} \rightarrow \underline{ Y }$ be a morphism of schemes. Given a logarithmic structure M _Y on $\underline{Y }$, we can define a logarithmic structure on $\underline{X}$, called the inverse image of M _Y , to be the logarithmic structure associated to the pre-logarithmic structure $f^{-1}(M_{Y }) \rightarrow f^{-1}(\mathcal{O}_{\underline{Y }}) \rightarrow \mathcal{O}_{\underline{X}}$. This is usually denoted by f ^∗(M _Y ). Using the inverse image of logarithmic structures, we can give the following definition.

Definition 3.9.

A morphism of logarithmic schemes $X \rightarrow Y$ consists of a morphism of underlying schemes $f:\underline{ X} \rightarrow \underline{ Y }$, and a morphism $f^{\flat }: f^{{\ast}}M_{Y } \rightarrow M_{X}$ of logarithmic structures on $\underline{X}$. The morphism is said to be strict if $f^{\flat }$ is an isomorphism.

We denote by LogSch the category of logarithmic schemes.

3.4 Charts of Logarithmic Structures

Definition 3.10.

Let X be a logarithmic scheme, and P a monoid. A chart for M _X is a morphism $P \rightarrow \Gamma (X,M_{X})$, such that the induced map of logarithmic structures P ^a → M _X is an isomorphism, where P ^a is the logarithmic structure associated to the pre-logarithmic structure given by $P \rightarrow \Gamma (X,M_{X}) \rightarrow \Gamma (X,\mathcal{O}_{\underline{X}})$.

In fact, a chart of M _X is equivalent to a morphism

$$\displaystyle{f: X \rightarrow \mathop{\mathrm{Spec}}\nolimits (P \rightarrow \mathbb{Z}[P])}$$

such that f ^♭ is an isomorphism. In general, we have the following:

Lemma 3.11 ([45, 1.1.9]).

The mapping

$$\displaystyle{\mathop{\mathrm{Hom}}\nolimits _{\mathbf{LogSch}}(X,\mathop{\mathrm{Spec}}\nolimits (P \rightarrow \mathbb{Z}[P]))\ \rightarrow \ \mathop{\mathrm{Hom}}\nolimits _{\mathbf{Mon}}(P,\Gamma (X,M_{X}))}$$

associating to f the composition

$$\displaystyle{P \rightarrow \Gamma (\underline{X},P_{X})\mathop{\longrightarrow}\limits_{}^{\Gamma (f^{b})}\Gamma (\underline{X},M_{ X})}$$

is a bijection.

We will see in Example 5.2 that Artin cones have a similar universal property on the level of characteristic monoids.

Definition 3.12.

A logarithmic scheme X is said to be fine, if étale locally there is a chart $P \rightarrow M_{X}$ with P a fine monoid. If moreover P can be chosen to be saturated, then X is called a fine and saturated (or fs) logarithmic structure. Finally, if P can be chosen isomorphic to $\mathbb{N}^{k}$, we say that the logarithmic structure is locally free.

Lemma 3.13.

Let X be a fine and saturated logarithmic scheme. Then for any geometric point $\bar{x} \in X$ , there exists an étale neighborhood U → X of $\bar{x}$ with a chart $\overline{M}_{\bar{x},X} \rightarrow M_{U}$ , such that the composition $\overline{M}_{\bar{x},X} \rightarrow M_{U} \rightarrow \overline{M}_{\bar{x},X}$ is the identity.

Proof.

This is a special case of [46, Proposition 2.1]. □ 

3.5 Logarithmic Differentials

To form sheaves of logarithmic differentials, we add to the sheaf $\Omega _{\underline{X}/\underline{Y }}$ symbols of the form dlog(α(m)) for all elements m ∈ M _X , as follows:

Definition 3.14.

Let f: X → Y be a morphism of fine logarithmic schemes. We introduce the sheaf of relative logarithmic differentials $\Omega _{X/Y }^{1}$ given by

$$\displaystyle{\Omega _{X/Y }^{1} ={\Bigl ( \Omega _{\underline{ X}/\underline{Y }} \oplus (\mathcal{O}_{\underline{X}} \otimes _{\mathbb{Z}}M_{X}^{gp})\Bigr )}\big/\mathcal{K}}$$

where $\mathcal{K}$ is the $\mathcal{O}_{\underline{X}}$-module generated by local sections of the following forms:

• (1) (d α(a), 0) − (0, α(a) ⊗ a) with a ∈ M _X and

• (2) (0, 1 ⊗ a) with $a \in \mathop{\mathrm{im}}\nolimits (f^{-1}(M_{Y }) \rightarrow M_{X})$.

The universal derivation (∂, D) is given by $\partial: \mathcal{O}_{\underline{X}}\stackrel{d}{\rightarrow }\Omega _{\underline{X}/\underline{Y }} \rightarrow \Omega _{X/Y }^{1}$ and $D: M_{X} \rightarrow \mathcal{O}_{\underline{X}} \otimes _{\mathbb{Z}}M_{X}^{gp} \rightarrow \Omega _{X/Y }^{1}$.

Example 3.15.

Let $h: Q \rightarrow P$ be a morphism of fine monoids. Denote $X =\mathop{ \mathrm{Spec}}\nolimits (P \rightarrow \mathbb{Z}[P])$ and $Y =\mathop{ \mathrm{Spec}}\nolimits (Q \rightarrow \mathbb{Z}[Q])$. Then we have a morphism $f: X \rightarrow Y$ induced by h. A direct calculation shows that $\Omega _{f}^{1} = \mathcal{O}_{\underline{X}} \otimes _{\mathbb{Z}}\mathop{ \mathrm{coker}}\nolimits (h^{gp})$. The free generators correspond to the logarithmic differentials dlog(α(p)) for p ∈ P, which are regular on the torus $\mathop{\mathrm{Spec}}\nolimits \mathbb{Z}[P^{gp}]$, modulo those coming from Q. This can also be seen from the universal property of the sheaf of logarithmic differentials.

3.6 Logarithmic Smoothness

Consider the following commutative diagram of logarithmic schemes illustrated with solid arrows:

(1)

where j is a strict closed immersion (Definition 3.9) defined by the ideal J with J ² = 0. We define logarithmic smoothness by the infinitesimal lifting property:

Definition 3.16.

A morphism $f: X \rightarrow Y$ of fine logarithmic schemes is called logarithmically smooth (resp., logarithmically étale) if the underlying morphism $\underline{X} \rightarrow \underline{ Y }$ is locally of finite presentation and for any commutative diagram (1), étale locally on T ₁ there exists a (resp., there exists a unique) morphism $g: T_{1} \rightarrow X$ such that $\phi = g \circ j$ and ψ = f ∘ g.

We have the following useful criterion for smoothness from [33, Theorem 3.5].

Theorem 3.17 (K. Kato).

Let $f: X \rightarrow Y$ be a morphism of fine logarithmic schemes. Assume we have a chart $Q \rightarrow M_{Y }$ , where Q is a finitely generated integral monoid. Then the following are equivalent:

• (1) f is logarithmically smooth (resp., logarithmically étale) and

• (2) étale locally on X, there exists a chart $(P_{X} \rightarrow M_{X},Q_{Y } \rightarrow M_{Y },Q \rightarrow P)$ extending the chart $Q_{Y } \rightarrow M_{Y }$ , satisfying the following properties:

  • (a) The kernel and the torsion part of the cokernel (resp., the kernel and the cokernel) of $Q^{gp} \rightarrow P^{gp}$ are finite groups of orders invertible on X.

  • (b) The induced morphism from $\underline{X} \rightarrow \underline{ Y } \times _{\mathop{\mathrm{Spec}}\nolimits \mathbb{Z}[Q]}\mathop{ \mathrm{Spec}}\nolimits \mathbb{Z}[P]$ is étale in the usual sense.

Remark 3.18.

• (1) We can require $Q^{gp} \rightarrow P^{gp}$ in (a) to be injective, and replace the requirement that $\underline{X} \rightarrow \underline{ Y } \times _{\mathop{\mathrm{Spec}}\nolimits \mathbb{Z}[Q]}\mathop{ \mathrm{Spec}}\nolimits \mathbb{Z}[P]$ be étale in (b) by requiring it to be smooth without changing the conclusion of Theorem 3.17.

• (2) In this theorem something wonderful happens, which Kato calls “the magic of log.” The arrow in (b) shows that a logarithmically smooth morphism is “locally toric” relative to the base. Consider the case where Y is a logarithmic scheme with underlying space given by $\mathop{\mathrm{Spec}}\nolimits \mathbb{C}$ with the trivial logarithmic structure, and $X =\mathop{ \mathrm{Spec}}\nolimits (P \rightarrow \mathbb{C}[P])$ where P is a fine, saturated, and torsion free monoid. Then $\underline{X}$ is a toric variety with the action of $\mathop{\mathrm{Spec}}\nolimits \mathbb{C}[P^{gp}]$. According to the theorem, X is logarithmically smooth relative to Y, though the underlying space might be singular. These singularities are called toric singularities in [34]. This is closely related to the classical notion of toroidal embeddings [35].

Logarithmic differentials behave somewhat analogously to differentials:

Proposition 3.19.

Let $X\stackrel{f}{\rightarrow }Y \stackrel{g}{\rightarrow }Z$ be a sequence of morphisms of fine logarithmic schemes.

• (1) There is a natural exact sequence $f^{{\ast}}\Omega _{g}^{1} \rightarrow \Omega _{fg}^{1} \rightarrow \Omega _{f}^{1} \rightarrow 0$.

• (2) If f is logarithmically smooth, then $\Omega _{f}^{1}$ is a locally free $\mathcal{O}_{X}$ -module, and we have the following exact sequence: $0 \rightarrow f^{{\ast}}\Omega _{g}^{1} \rightarrow \Omega _{gf}^{1} \rightarrow \Omega _{f}^{1} \rightarrow 0$.

• (3) If gf is logarithmically smooth and the sequence in (2) is exact and splits locally, then f is logarithmically smooth.

A proof can be found in [45, Chap. IV].

4 Kato Fans and Resolution of Singularities

4.1 The Monoidal Analogues of Schemes

In parallel to the theory of schemes, Kato developed a theory of fans, with the role of commutative rings played by monoids. As with schemes, the theory begins with the spectrum of a monoid:

Definition 4.1 ([34, Definition (5.1)]).

Let M be a monoid. A subset I ⊂ M is called an ideal of M if M + I ⊂ I. If M ∖ I is a submonoid of M, then I is called a prime ideal of M. The set of prime ideals of M is denoted SpecM and called the spectrum of M.

If $f: M \rightarrow N$ is a homomorphism of monoids and P ⊂ N is a prime ideal, then f ⁻¹ P ⊂ M is a prime ideal as well. Therefore f induces a morphism of spectra: $\mathop{\mathrm{Spec}}\nolimits N \rightarrow \mathop{\mathrm{Spec}}\nolimits M$.

Definition 4.2 ([34, Definition (5.2)]).

Suppose that M is a monoid and S is a subset of M. We write M[−S] for the initial object among the monoids N equipped a morphism $f: M \rightarrow N$ such that f(S) is invertible. When S consists of a single element s, we also write M[−s] in lieu of M[−{s}].

It is not difficult to construct M[−S] with the familiar Grothendieck group construction M ↦ M ^gp of Definition 3.1. Certainly M[−S] coincides with M[−S′] where S′ is the submonoid of M generated by S. One may therefore assume that S is a submonoid of M. Then for M[−S] one may take the set of formal differences m − s with m ∈ M and s ∈ S, subject to the familiar equivalence relation:

$$\displaystyle{ m - s \sim m' - s'\qquad \;\Longleftrightarrow\;\qquad \exists \:t \in S,\:t + m + s' = t + m' + s }$$

If M is integral, then one may construct M[−S] as a submonoid of M ^gp.

The topology of the spectrum of a monoid is defined exactly as for schemes:

Definition 4.3 ([34, Definition (9.2)]).

Let M be a monoid. For any f ∈ M, let $D(f) \subset \mathop{\mathrm{Spec}}\nolimits M$ be the set of prime ideals P ⊂ M such that f ∉ P. A subset of $\mathop{\mathrm{Spec}}\nolimits M$ is called open if it is open in the minimal topology in which the D(f) are open subsets.

Equivalently D(f) is the image of the map $\mathop{\mathrm{Spec}}\nolimits (M[-f]) \rightarrow \mathop{\mathrm{Spec}}\nolimits M$. The intersection of D(f) and D(g) is D(f + g) so the sets D(f) form a basis for the topology of $\mathop{\mathrm{Spec}}\nolimits M$ (Fig. 4).

Fig. 4

Points and topology of $\mathop{\mathrm{Spec}}\nolimits \mathbb{N}^{2}.$ The big point corresponds to the ideal $\varnothing$, the intermediate points are the primes $\mathbb{N} \times \mathbb{N}_{>0}$ and $\mathbb{N}_{>0} \times \mathbb{N}$, and the small closed point is the maximal ideal $\mathbb{N}_{>0}^{2}$. The arrows indicate specialization, thus determining the topology

We equip $\mathop{\mathrm{Spec}}\nolimits M$ with a sheaf of monoids $\mathcal{M}_{\mathop{\mathrm{Spec}}\nolimits M}$ where

$$\displaystyle{ \mathcal{M}_{\mathop{\mathrm{Spec}}\nolimits M}(D(f)) = M[-f]/M[-f]^{{\ast}} }$$

where M[−f]^∗ is the set of invertible elements of M. This is a sharply monoidal space:

Definition 4.4 ([34, Definition (9.1)]).

Recall that a monoid is called sharp if its only invertible element is the identity element 0. If M and N are sharp monoids, then a sharp homomorphism $f: M \rightarrow N$ is a homomorphism of monoids such that $f^{-1}\{0\} =\{ 0\}$.

A sharply monoidal space is a pair $(S,\mathcal{M}_{S})$, where S is a topological space and $\mathcal{M}_{S}$ is a sheaf of sharp monoids on S. A morphism of sharply monoidal spaces $f: (S,\mathcal{M}_{S}) \rightarrow (T,\mathcal{M}_{T})$ consists of a continuous function $f: S \rightarrow T$ and a sharp homomorphism of sheaves of sharp monoids $f^{-1}\mathcal{M}_{T} \rightarrow \mathcal{M}_{S}$.

A sharply monoidal space is called an affine Kato fan or a Kato cone if it is isomorphic to $(\mathop{\mathrm{Spec}}\nolimits M,\mathcal{M}_{\mathop{\mathrm{Spec}}\nolimits M})$. A sharply monoidal space is called a Kato fan if it admits an open cover by Kato cones.

We call a Kato fan integral or saturated if it admits a cover by the spectra of monoids with the respective properties (Definition 3.2). A Kato fan is called locally of finite type if it admits a cover by spectra of finitely generated monoids. We use fine as a synonym for integral and locally of finite type.

A large collection of examples of Kato fans is obtained from fans of toric varieties (see Sect. 4.3) or logarithmically smooth schemes (Sect. 4.5). In particular, any toric singularity is manifested in a Kato fan.

Any Kato cone $\mathop{\mathrm{Spec}}\nolimits M$ of a finitely generated integral monoid M contains an open point corresponding to the ideal $\varnothing \subset M$, carrying the trivial stalk $M^{\mathop{\mathrm{gp}}\nolimits }/M^{\mathop{\mathrm{gp}}\nolimits } = 0$. We can always glue an arbitrary collection of such Kato cones along their open points. If the collection is infinite, this gives examples of connected Kato fans which are not quasi-compact.

4.2 Points and Kato Cones

Definition 4.5.

Let $F' \rightarrow F$ be a morphism of fine, saturated Kato fans. The morphism is said to be quasi-compact if the preimage of any open subcone of F is quasi-compact.

Lemma 4.6.

Let F be a Kato fan. There is a bijection between the open Kato subcones of F and the points of F.

Proof.

Suppose that $U =\mathop{ \mathrm{Spec}}\nolimits M$ is an open subcone of F. Let P ⊂ M be the complement of 0 ∈ M. Then P is a prime ideal, hence corresponds to a point of F.

To give the inverse, we show that every point of F has a minimal open affine neighborhood. Indeed, suppose that U is an open affine neighborhood of p ∈ F. Then the underlying topological space of U is finite, so there is a smallest open subset of U containing p. Replace U with this open subset. It must be affine, since affine open subsets form a basis for the topology of U.

It is straightforward to see that these constructions are inverse to one another. □ 

Lemma 4.7.

A morphism of fine, saturated Kato fans is quasi-compact if and only if it has finite fibers. In particular, a Kato fan is quasi-compact if and only if its underlying set is finite.

4.3 From Fans to Kato Fans

If $\Delta$ is a fan in $N_{\mathbb{R}}$ in the sense of toric geometry, it gives rise to a Kato fan $F_{\Delta }$. The underlying topological space of $F_{\Delta }$ is the set of cones of $\Delta$ and a subset is open if and only if it contains all the faces of its elements. In particular, if σ is one of the cones of $\Delta$, then the set of faces of σ is an open subset F _σ of K and these open subsets form a basis. We set $\mathcal{M}(F_{\sigma }) = (M \cap \sigma ^{\vee })/(M \cap \sigma ^{\vee })^{{\ast}}$ where M is the dual lattice of N and σ ^∨ is the dual cone of σ. With this sheaf of monoids, $F_{\sigma } \simeq \mathop{\mathrm{Spec}}\nolimits (M \cap \sigma ^{\vee })/(M \cap \sigma ^{\vee })^{{\ast}}$, so $F_{\Delta }$ has an open cover by Kato cones, hence is a Kato fan.

4.4 Resolution of Singularities of Kato Fans

Kato introduced the following monoidal space analogue of subdivisions of fans of toric varieties, in such a way that a subdivision of a fan Σ gives rise to a subdivision of the Kato fan F _Σ . A morphism of fans Σ ₁ → Σ ₂ is a subdivision if and only if it induces a bijection on the set of lattice points $\cup _{\sigma }N_{\sigma }$. The Kato fan notion is the direct analogue:

Definition 4.8.

A morphism $p: F' \rightarrow F$ of fine, saturated Kato fans is called a proper subdivision if it is quasi-compact and the morphism

$$\displaystyle{ \mathop{\mathrm{Hom}}\nolimits (\mathop{\mathrm{Spec}}\nolimits \mathbb{N},F') \rightarrow \mathop{\mathrm{Hom}}\nolimits (\mathop{\mathrm{Spec}}\nolimits \mathbb{N},F) }$$

is a bijection.

Remark 4.9.

This definition has an appealing resemblance to the valuative criterion for properness.

Explicitly subdividing Kato fans is necessarily less intuitive than subdividing fans. The following examples, which are in direct analogy to subdivisions of fans, may help in developing intuition:

Example 4.10.

• (i) Suppose that F is a fine, saturated Kato fan and $v:\mathop{ \mathrm{Spec}}\nolimits \mathbb{N} \rightarrow F$ is a morphism. The star subdivision of F along v is constructed as follows: If $U =\mathop{ \mathrm{Spec}}\nolimits M$ is an open Kato subcone of F not containing v, then U is included as an open Kato subcone of F′; if U does contain v, then for each face $V =\mathop{ \mathrm{Spec}}\nolimits N$ contained in U that does not contain v, we include the face $v + V =\mathop{ \mathrm{Spec}}\nolimits M_{v+V }$, where

  $$\displaystyle{M_{v+V } = \left \{\alpha \in M^{\mathrm{gp}}\:\ \alpha \big \vert _{ V } \in N\text{ and }v^{{\ast}}\alpha \in \mathbb{N}\right \}.}$$

• (ii) Let F =  SpecM be a fine, saturated Kato cone. There is a canonical morphism $\mathop{\mathrm{Spec}}\nolimits \mathbb{N} \rightarrow F$ by regarding $\mathop{\mathrm{Hom}}\nolimits (\mathop{\mathrm{Spec}}\nolimits \mathbb{N},F) =\mathop{ \mathrm{Hom}}\nolimits (M, \mathbb{N})$ as a monoid and taking the sum of the generators of the 1-dimensional faces of F. This morphism is called the barycenter of F.

  If F is a fine, saturated Kato fan, we obtain a subdivision $F' \rightarrow F$ by performing star subdivision of F along the barycenters of its open subcones, in decreasing order of dimension. A priori this is well defined if cones of F have bounded dimension, but as the procedure is compatible with restriction to subfans, this works for arbitrary F. This subdivision is called the barycentric subdivision.

Definition 4.11.

A fine, saturated Kato fan F is said to be smooth if it has an open cover by Kato cones $U \simeq \mathop{\mathrm{Spec}}\nolimits \mathbb{N}^{r}$.

Theorem 4.12 ([35, Theorem I.11], [23, Sect. 2.6], [34, Proposition (9.8)]).

Let F be a fine, saturated Kato fan. Then there is a proper subdivision $F' \rightarrow F$ such that F′ is smooth.

The classical combinatorial proofs start by first using star or barycentric subdivisions to make the fan simplicial, and then repeatedly reducing the index by further star subdivisions.

4.5 Logarithmic Regularity and Associated Kato Fans

In this section we will work only with logarithmic structures admitting charts Zariski locally.

Let X be a logarithmic scheme and x a schematic point of X. Let I(x, M _X ) be the ideal of the local ring $\mathcal{O}_{X,x}$ generated by the maximal prime ideal of M _X, x .

Definition 4.13 ([34, Definition (2.1)]).

A locally noetherian logarithmic scheme X admitting Zariski-local charts is called logarithmically regular at a schematic point x if it satisfies the following two conditions:

• (i) the local ring $\mathcal{O}_{X,x}/I(x,M_{X})$ is regular and

• (ii) $\dim \mathcal{O}_{X,x} =\dim \mathcal{O}_{X,x}/I(x,M) +\mathop{ \mathrm{rank}}\nolimits \overline{M}_{X,x}^{\mathrm{gp}}$.

Example 4.14 ([34, Example (2.2)]).

A toric variety with its toric logarithmic structure is logarithmically regular.

If X is a logarithmic scheme, then the Zariski topological space of X is equipped with a sheaf of sharp monoids $\overline{M}_{X}$. Thus $(X, \overline{M}_{X})$ is a sharply monoidal space. Moreover, morphisms of logarithmic schemes induce morphisms of sharply monoidal spaces. We therefore obtain a functor from the category of logarithmic schemes to the category of sharply monoidal spaces. We may speak in particular about morphisms from logarithmic schemes to Kato fans.

Theorem 4.15 (cf. [34, (10.2)]).

Let X be a fine, saturated locally noetherian, logarithmically regular logarithmic scheme that admits charts Zariski locally . Then there is an initial strict morphism X → F _X to a Kato fan.

We call the Kato fan F _X the Kato fan associated to X.

Kato constructs the Kato fan F _X as a skeleton of the logarithmic strata of X. Let $\underline{F}_{X} \subset X$ be the set of points x ∈ X such that I(x, M _X ) coincides with the maximal ideal of $\mathcal{O}_{X,x}$. As we indicate below these are the generic points of the logarithmic strata of X. Let $M_{F_{X}}$ be the restriction of $\overline{M}_{X}$ to $\underline{F}_{X}$. We denote the resulting monoidal space by F _X .

Lemma 4.16 ([34, Proposition (10.1)]).

If X is a fine, saturated, locally noetherian, logarithmically regular scheme admitting a chart Zariski locally, then the sharply monoidal space constructed above is a fine, saturated Kato fan.

Lemma 4.17 ([34, (10.2)]).

There is a canonical continuous retraction of X onto its Kato fan F _X.

We briefly summarize the definition of the map and omit the rest of the proof. Let x be a point of X. The quotient $\mathcal{O}_{X,x}/I(x,M_{X})$ is regular, hence in particular a domain, so it has a unique minimal prime corresponding to a point y of F _X  ⊂ X. We define π(x) = y.

Lemma 4.18.

The Kato fan of X is the initial Kato fan admitting a morphism from X.

Proof.

Let $\varphi: X \rightarrow F$ be another morphism to a Kato fan. By composition with the inclusion F _X  ⊂ X we get a map $F_{X} \rightarrow F$. We need to show that $\varphi$ factors through $\pi: X \rightarrow F_{X}$.

Let x be a point of X and let A be the local ring of x in X. Let $P = \overline{M}_{X,x}$. Let y = π(x). Then y is the generic point of the vanishing locus of I(x, M _X ). We would like to show $\varphi (y) =\varphi (x)$. We can replace X with $\mathop{\mathrm{Spec}}\nolimits A$, replace F _X with $F_{X} \cap \mathop{\mathrm{Spec}}\nolimits A$, and replace F with an open Kato cone in F containing $\varphi (x)$. Then $F =\mathop{ \mathrm{Spec}}\nolimits Q$ for some fine, saturated, sharp monoid Q and we get a map $Q \rightarrow P$. Since $X \rightarrow F$ is a morphism of sharply monoidal spaces, $X \rightarrow F$ factors through the open subset defined by the kernel of $Q \rightarrow P$, so we can replace F by this open subset and assume that $Q \rightarrow P$ is sharp. But then $X \rightarrow F$ factors through no smaller open subset, so $\varphi (x)$ is the closed point of F. Moreover, we have $\overline{M}_{X,y} = \overline{M}_{X,x}$ so the same reasoning applies to y and shows that $\varphi (y) =\varphi (x)$, as desired. □ 

This completes the proof of Theorem 4.15.

4.6 Towards the Monoidal Analogues of Algebraic Spaces

4.6.1 The Need for a More General Approach: The Nodal Cubic

Not every logarithmically smooth scheme has a Kato fan. For example, the divisorial logarithmic structure on $\mathbb{A}^{2}$ associated to a nodal cubic curve does not have a chart in any Zariski neighborhood of the node of the cubic. The Kato fan of this logarithmic structure wants to be the Kato fan of the plane with the open subsets corresponding to the complements of the axes glued together (Fig. 5).

Fig. 5

The fan of the nodal cubic, drawn as a cone with the two edges glued to each other

This cannot be a Kato fan, because there is no open neighborhood of the closed point that is a Kato cone. Indeed, the closed point has two different generizations to the codimension 1 point.

Clearly, the solution here is to allow more general types of gluing (colimits) into the definition of a Kato fan. The purpose of this section is to outline what this might entail. Our favorite solution will only come in the next section, where we discuss Artin fans.

The theory of algebraic spaces provides a blueprint for how to proceed. The universal way to add colimits to a category is to pass to its category of presheaves. In order to retain the Kato fans as colimits of their open Kato subcones, we look instead at the category of sheaves. Finally, we restrict attention to those sheaves that resemble Kato cones étale locally.

4.6.2 The Need for a More General Approach: The Whitney Umbrella

These cone spaces are general enough to include a fan for the divisorial logarithmic structure of the nodal cubic. However, one cannot obtain a fan for the punctured Whitney umbrella this way:

Working over $\mathbb{C}$, let $X = \mathbb{A}^{2} \times \mathbb{G}_{m}$ with the logarithmic structure pulled back from the standard logarithmic structure on $\mathbb{A}^{2}$, associated to the divisor xy = 0 as in Example 3.7. Let $G = \mathbb{Z}/2\mathbb{Z}$ act by $t.(x,y,z) = (y,x,-z)$. Since the divisor is G stable, the action lifts to the logarithmic structure, so the logarithmic structure descends to the quotient $Y = X/G$.

There is a projection $\pi: Y \rightarrow \mathbb{G}_{m}$, and traversing the nontrivial loop in $\mathbb{G}_{m}$ results in the automorphism of $\mathbb{A}^{2}$ exchanging the axes. Thus the logarithmic structure of Y has monodromy.

If there is a map from Y to a cone space Z, then it is not possible for $\overline{M}_{Y }$ to be pulled back from M _Z . Just as in a Kato fan, the strata of Z on which M _Z is locally constant are discrete and therefore cannot have monodromy.

However, Deligne–Mumford stacks can have monodromy at points. By enlarging our perspective to include cone stacks, the analogues of Deligne–Mumford stacks for Kato fans, we are able to construct fans that record the combinatorics of the logarithmic strata for any locally connected logarithmic scheme (logarithmic smoothness is not required). The construction proceeds circuitously, by showing that cone stacks form a full subcategory of Artin fans (defined in Sect. 5) and then constructing an Artin fan associated to any logarithmically smooth scheme (Fig. 6).

Fig. 6

The fan of the Whitney umbrella drawn as a cone—the first quadrant—folded over itself via the involution (x, y) ↦ (y, x)

5 Artin Fans

In order to simplify the discussion we work over an algebraically closed field k.

5.1 Definition and Basic Properties

Definition 5.1.

An Artin fan is a logarithmic algebraic stack that is logarithmically étale over $\mathop{\mathrm{Spec}}\nolimits \mathbf{k}$. A morphism of Artin fans is a morphism of logarithmic algebraic stacks. We denote the 2-category of Artin fans by the symbol AF.

Olsson showed that there is an algebraic stack $\underline{\mathsf{Log}}$ over the category of schemes such that morphisms $\underline{S} \rightarrow \underline{\mathsf{Log}}$ correspond to logarithmic structures S on $\underline{S}$ [46, Theorem 1.1].¹ Equipping $\underline{\mathsf{Log}}$ with its universal logarithmic structure yields the logarithmic algebraic stack Log. If $\mathcal{X}$ is an Artin fan, then the morphism $\underline{\mathcal{X}}\rightarrow \underline{\mathsf{Log}}$ induced by the logarithmic structure of $\mathcal{X}$ is étale, and conversely: any logarithmic algebraic stack whose structural morphism to $\underline{\mathsf{Log}}$ is étale is an Artin fan.

Example 5.2.

Let V be a toric variety with dense torus T. The toric logarithmic structure of V is T-equivariant, hence descends to a logarithmic structure on [V∕T], making [V∕T] into an Artin fan.

If $V =\mathop{ \mathrm{Spec}}\nolimits \mathbf{k}[M]$ for some fine, saturated, sharp monoid M, then [V∕T] represents the following functor on logarithmic schemes [46, Proposition 5.17]:

$$\displaystyle{ (X,M_{X})\mapsto \mathop{\mathrm{Hom}}\nolimits {\bigl (M,\Gamma (X, \overline{M}_{X})\bigr )}. }$$

As $\overline{M}_{X}$ is an étale sheaf over X, it is immediate that [V∕T] is logarithmically étale over a point.

Definition 5.3.

An Artin cone is an Artin fan isomorphic to $\mathcal{A}_{M} = [V/T]$, where $V =\mathop{ \mathrm{Spec}}\nolimits \mathbf{k}[M]$ and M is a fine, saturated, sharp monoid (Fig. 7).

Fig. 7

$\mathcal{A}_{\mathbb{N}^{2}}.$ The small closed point is $B\mathbb{G}_{m}^{2}$, the intermediate points are $B\mathbb{G}_{m}$, and the big point is just a point

If $\mathcal{X} \rightarrow \mathsf{Log}$ is étale and representable, then $\mathcal{X}$ is determined by its étale stack of sections over Log. Moreover, any étale stack on Log corresponds to an Artin fan by passage to the espace (champ) étalé. The following lemma characterizes the étale site of Log as a category of presheaves:

Lemma 5.4.

• (i) The Artin cones are an étale cover of Log.

• (ii) An Artin cone has no nontrivial representable étale covers.

• (iii) If M and N are fine, saturated, sharp monoids, then

  $$\displaystyle{ \mathop{\mathrm{Hom}}\nolimits _{\mathbf{AF}}(\mathcal{A}_{M},\mathcal{A}_{N}) =\mathop{ \mathrm{Hom}}\nolimits _{\mathbf{Mon}}(N,M). }$$

Proof.

Statement (i) was proved in [46, Corollary 5.25]. It follows from the fact that every logarithmic scheme admits a chart étale locally.

Statement (ii) follows from [3, Corollary 2.4.3]. Concretely, étale covers of Artin cones correspond to equivariant étale covers of toric varieties, which restrict to equivariant étale covers of tori, of which there are none other than the trivial ones [3, Proposition 2.4.1].

Statement (iii) follows from $\Gamma (\mathcal{A}_{M}, \overline{M}_{\mathcal{A}_{M}}) = M$ and consideration of the functor represented by $\mathcal{A}_{N}$ (Example 5.2). □ 

5.2 Categorical Context

Lemma 5.4 (iii) enables us to relate the 2-category of Artin fans to the notions surrounding Kato fans. Let us write RPC for the category of rational polyhedral cones. The category RPC is equivalent to the opposite of the category of fine, saturated, sharp monoids.² Therefore RPC is equivalent to the category of Kato cones and, by Lemma 5.4 (iii), to the category of Artin cones. Furthermore, we obtain

Corollary 5.5.

The 2-category of Artin fans with faithful monodromy is fully faithfully embedded in the 2-category of fibered categories over RPC .

Proof.

Lemma 5.4 gives an embedding of AF in the 2-category of fibered categories on the category of Artin cones and identifies the category of Artin cones with RPC. □ 

This enables us to relate the 2-category AF with the framework proposed in Sects. 4.6.1 and 4.6.2: the 2-category of cone stacks suggested in Sect. 4.6.2 is necessarily equivalent to a full subcategory the 2-category AF. The key to proving this is the fact that the diagonal of an Artin fan is represented by algebraic spaces, which enables one to relate it to a morphism of “cone spaces” as suggested in Sect. 4.6.1.

In particular, we have a fully faithful embedding KF → AF of the category of Kato fans in the 2-category of Artin fans.

5.3 The Artin Fan of a Logarithmic Scheme

Definition 5.6.

A Zariski logarithmic scheme X is said to be small with respect to a point x ∈ X, if the restriction morphism $\Gamma (X, \overline{M}) \rightarrow \overline{M}_{X,x}$ is an isomorphism and the closed logarithmic stratum

$$\displaystyle{ \big\{y \in X\big\vert \overline{M}_{X,y} \simeq \overline{M}_{X,x}\big\} }$$

is connected. We say X is small if it is small with respect to some point.

Let $N = \Gamma (X, \overline{M}_{X})$. There is a canonical morphism

$$\displaystyle{ X \rightarrow \mathcal{A}_{N} }$$

corresponding to the morphism $N \rightarrow \Gamma (X, \overline{M}_{X})$. It is shown in [8] that if X is small this morphism is initial among all morphisms from X to Artin fans. We therefore call $\mathcal{A}_{N}$ the Artin fan of such small X. By the construction, the Artin fan of X is functorial with respect to strict morphisms.

Now consider a logarithmic algebraic stack X with a groupoid presentation

$$\displaystyle{ V \rightrightarrows U \rightarrow X }$$

in which U and V are disjoint unions of small Zariski logarithmic schemes. Then V and U have Artin fans $\mathcal{V}$ and $\mathcal{U}$ and we obtain strict morphisms of Artin fans $\mathcal{V}\rightarrow \mathcal{U}$. Strict morphisms of Artin fans are étale, so this is a diagram of étale spaces over Log. It therefore has a colimit, also an étale space over Log, which we call the Artin fan of X.

5.4 Functoriality of Artin Fans: Problem and Fix

The universal property of the Artin fan implies immediately that Artin fans are functorial with respect to strict morphisms of logarithmic schemes. They are not functorial in general, but we will be able to salvage a weak replacement for functoriality in which morphisms of logarithmic schemes induce correspondences of Artin fans.

5.4.1 The Failure of Functoriality

We use the notation for the punctured Whitney umbrella introduced in Sect. 4.6.2. As X has a global chart, its Artin fan $\mathcal{X}$ is easily seen to be $\mathcal{A}^{2}$. The Artin fan $\mathcal{Y}$ of Y is the quotient of $\mathcal{A}^{2}$ by the action of $\mathbb{Z}/2\mathbb{Z}$ exchanging the components, as a representable étale space over Log. In other words, the group action induces an étale equivalence relative to Log by taking the image of the action map

$$\displaystyle{ \mathbb{Z}/2\mathbb{Z} \times \mathcal{A}^{2} \rightarrow \mathcal{A}^{2}\mathop{ \times }_{\mathsf{ Log}}\mathcal{A}^{2}. }$$

A logarithmic morphism from a logarithmic scheme S into $\mathcal{A}^{2}\mathop{ \times }_{\mathsf{Log}}\mathcal{A}^{2}$ consists of two maps $\mathbf{N}^{2} \rightarrow \Gamma (S, \overline{M}_{S})$ and an isomorphism between the induced logarithmic structures M ₁ and M ₂ commuting with the projection to M _S . This implies that

$$\displaystyle{ \mathcal{A}^{2}\mathop{ \times }_{\mathsf{ Log}}\mathcal{A}^{2} = \mathcal{A}^{2}\mathop{ \coprod }_{ \mathcal{A}^{0}}\mathcal{A}^{2} }$$

where by $\mathcal{A}^{0}$ we mean the open point of $\mathcal{A}^{2}$. The nontrivial projection in

$$\displaystyle{ \mathcal{A}^{2}\mathop{ \coprod }_{ \mathcal{A}^{0}}\mathcal{A}^{2} = \mathcal{A}^{2}\mathop{ \times }_{\mathsf{ Log}}\mathcal{A}^{2} \rightrightarrows \mathcal{A}^{2} }$$

is given by the identity map on one component and the exchange of coordinates on the other component. (The trivial projection is the identity on both components.)

It is now easy to see that $\mathbb{Z}/2\mathbb{Z} \times \mathcal{A}^{2}$ surjects onto $\mathcal{A}^{2}\mathop{ \coprod }_{\mathcal{A}^{0}}\mathcal{A}^{2}$, so the Artin fan of Y is the image of $\mathcal{A}^{2}$ in Log. We will write $\mathcal{A}^{[2]}$ for this open substack and observe that it represents the functor sending a logarithmic scheme S to the category of pairs $( \overline{M},\varphi )$ where $\overline{M}$ is an étale sheaf of monoids on S and $\varphi: \overline{M} \rightarrow \overline{M}_{S}$ is a strict morphism that can be presented étale locally by a map $\mathbf{N}^{2} \rightarrow \overline{M}_{S}$. Equivalently, it is a logarithmic structure over M _S that has étale-local charts by N ².

Of course, there is a map $\mathcal{X} \rightarrow \mathcal{Y}$ consistent with the maps $X \rightarrow Y$: it is the canonical projection $\mathcal{A}^{2} \rightarrow \mathcal{A}^{[2]}$. However, we take $\widetilde{X}$ to be the logarithmic blowup of X at $\{0\} \times \mathbb{G}_{m}$ and let $\widetilde{Y }$ be the logarithmic blowup of Y at the image of this locus. Then we have a Cartesian diagram, since X is flat over Y:

We will compute the Artin fans of $\widetilde{X}$ and $\widetilde{Y }$.

Since X and Y are flat over their Artin fans, the blowups $\widetilde{X}$ and $\widetilde{Y }$ are pulled back from the blowups $\widetilde{\mathcal{X}}$ and $\widetilde{\mathcal{Y}}$ of $\mathcal{X}$ and $\mathcal{Y}$. Furthermore, the square in the diagram below is Cartesian:

We have written $\mathcal{Z}$ for the Artin fan of $\widetilde{Y }$. Since $\widetilde{Y } \rightarrow \widetilde{\mathcal{Y}}$ is strict and smooth with connected fibers, the map $\widetilde{Y } \rightarrow \mathcal{Z}$ factors through $\widetilde{\mathcal{Y}}$. We will see in a moment that there is no dashed arrow making the triangle on the right above commutative, thus witnessing the failure of the functoriality of the Artin fan construction with respect to the morphism $\widetilde{Y } \rightarrow Y$.³

The reason no map $\mathcal{Z}\rightarrow \mathcal{Y}$ can exist making the diagram above commutative is that $\widetilde{\mathcal{Y}}$ has monodromy at the generic point of its exceptional divisor, pulled back from the monodromy at the closed point of $\mathcal{Y}$. However, the image of the exceptional divisor of $\widetilde{\mathcal{Y}}$ in $\mathcal{Z}$ is a divisor, and $\mathcal{Z}\rightarrow \mathsf{Log}$ is representable by algebraic spaces. No rank 1 logarithmic structure can have monodromy, so there is no monodromy at the image of the exceptional divisor in $\mathcal{Z}$.

A variant of the last paragraph shows that there is no commutative diagram

We can find a loop γ in the exceptional divisor E of $\widetilde{Y }$ that projects to a nontrivial loop in Y, around which the logarithmic structure of Y has nontrivial monodromy. Even though the logarithmic structure of $\widetilde{Y }$ has no monodromy around γ, the image of γ in $\mathcal{Y}$ is nontrivial. But all of the exceptional divisor E is collapsed to a point in $\mathcal{Z}$, so the image of γ in $\mathcal{Y}$ must act trivially.⁴

5.4.2 The Patch

There seem to be two ways to get around this failure of functoriality. The first is to allow the Artin fan to include more information about the fundamental group of the original logarithmic scheme X. However, the most naive application of this principle would introduce the entire étale homotopy type of X into the Artin fan, sacrificing Artin fans’ essentially combinatorial nature.

Another approach draws inspiration from Olsson’s stacks of diagrams of logarithmic structures [47]. Let Log ^[1] be the stack whose S-points are morphisms of logarithmic structures $M_{1} \rightarrow M_{2}$ on S. A morphism of logarithmic schemes $X \rightarrow Y$ induces a commutative diagram

where $\mathsf{Log}^{[1]} \rightarrow \mathsf{Log}$ sends $M_{1} \rightarrow M_{2}$ to M ₁. If Log ^[1] is given M ₂ as its logarithmic structure, this is a commutative diagram of logarithmic algebraic stacks. The construction of the Artin fan works in a relative situation, and we take $\mathcal{Y} =\pi _{0}(Y/\mathsf{Log})$ and $\mathcal{X} =\pi _{0}(X/\mathsf{Log}^{[1]})$. Note that $\mathcal{Y}\mathop{\times }_{\mathsf{Log}}\mathsf{Log}^{[1]}$ is étale over Log ^[1], so we get a map

$$\displaystyle{ \mathcal{X} \rightarrow \mathcal{Y}\mathop{\times }_{\mathsf{Log}}\mathsf{Log}^{[1]} \rightarrow \mathcal{Y} }$$

salvaging a commutative diagram:

Theorem 5.7 ([3, Corollary 3.3.5]).

For any morphism of logarithmic schemes $X \rightarrow Y$ with étale-locally connected logarithmic strata there is an initial commutative diagram

in which the horizontal arrows are strict and both $\mathcal{X}$ and $\mathcal{Y}$ are Artin fans representable by algebraic spaces relative to Log ^[1] and Log, respectively.

6 Algebraic Applications of Artin Fans

6.1 Gromov–Witten Theory and Relative Gromov–Witten Theory

Algebraic Gromov–Witten theory is the study of the virtually enumerative invariants, known as Gromov–Witten invariants, of algebraic curves on a smooth target variety X. In Gromov–Witten theory one integrates cohomology classes on X against the virtual fundamental class $[ \overline{\mathcal{M} }_{\Gamma }(X)]^{\mathrm{vir}}$ of the moduli space $\overline{\mathcal{M} }_{\Gamma }(X)$ of stable maps with target X. The subscript $\Gamma$ indicates fixed numerical invariants, including the genus of the domain curve, the number of marked points on it, and the homology class of its image.

Relative Gromov–Witten theory comes from efforts to define Gromov–Witten invariants for degenerations of complicated targets that, while singular, are still geometrically simple. In the mild setting of two smooth varieties meeting along a smooth divisor, such a theory has been developed by Li [37, 38], following work in symplectic geometry by Li–Ruan [39] and Ionel–Parker [30, 31].

Working over $\mathbb{C}$, one considers a degeneration

(2)

where π: X → B is a flat, projective morphism from a smooth variety to a smooth curve, and where the singular fiber $X_{0} = Y _{1} \sqcup _{D}Y _{2}$ consists of two smooth varieties meeting along a smooth divisor.

Jun Li proved an algebro-geometric degeneration formula through which one can recover Gromov–Witten invariants of the possibly complicated but smooth general fiber of X from relative Gromov–Witten invariants determined by a space $\overline{\mathcal{M} }_{\Gamma _{i}}(Y _{i})$ of relative stable maps to each of the two smooth components Y _i of X ₀. Here, in addition to the genus, the number of markings, and homology class, one must fix the contact orders of the curve with the given divisor.

6.1.1 Expanded Degenerations and Pairs

In order to define Gromov–Witten invariants of the singular degenerate fiber X ₀, Jun Li constructed a whole family of expansions X ₀′ → X ₀, where

$$\displaystyle{X_{0}' = Y _{1} \sqcup _{D}P \sqcup _{D}\cdots \sqcup _{D}P \sqcup _{D}Y _{2}.}$$

Here P is the projective completion of $N_{D/Y _{1}} \simeq N_{D/Y _{2}}^{\vee }$ (explicitly, it is $\mathbb{P}(\mathcal{O}\oplus N_{D/Y _{1}})$) and the gluing over D attaches 0-sections to ∞-sections.

Similarly, in order to guarantee that contact orders of maps in each Y _i are maintained, Jun Li constructed a family of expansions Y _i ′ → Y _i where

$$\displaystyle{Y _{i}' = Y _{i} \sqcup _{D}P \sqcup _{D}\cdots \sqcup _{D}P.}$$

Here is the first point where Artin fans, in their simplest form and even without logarithmic structures, become of use:

In Jun Li’s construction, not every deformation of an expansion Y _i ′ → Y _i is itself an expansion. For instance, the expansion $Y _{i} \sqcup _{D}P$ can deform to $Y _{i} \sqcup _{D}P'$, where $P'' = \mathbb{P}(\mathcal{O}\oplus N'')$ with N″ a deformation of $N_{D/Y _{1}}$. Precisely the same problem occurs with deformation of an expansion X ₀′ → X ₀.

6.1.2 The Artin Fan as the Universal Target, and Its Expansions

In [5], following ideas in [14], it was noted that the Y _i has a canonical map $Y _{i} \rightarrow \mathcal{A}:= [\mathbb{A}^{1}/\mathbb{G}_{m}]$. From the point of view of the present text, $\mathcal{A} = \mathcal{A}_{Y _{i}}$, the Artin fan associated to the divisorial logarithmic structure (Y _i , D), and its divisor $\mathcal{D} = B\mathbb{G}_{m} \subset \mathcal{A}$ is the universal divisor. Next, if $\mathcal{A}'\rightarrow \mathcal{A}$ is an expansion, then all deformations of $\mathcal{A}'\rightarrow \mathcal{A}$ are expansions of $\mathcal{A}$ in the sense of Jun Li. And finally, any expansion Y _i ′ → Y _i is obtained as the pullback $Y _{i}' = \mathcal{A}'\times _{\mathcal{A}}Y _{i}$ of some expansion $\mathcal{A}'\rightarrow \mathcal{A}$.

This means that the moduli space of expansions of any pair (Y _i , D) is identical to the moduli space of expansions of $(\mathcal{A},\mathcal{D})$, and the expansions themselves are obtained by pullback.

A similar picture occurs for degenerations: the Artin fan of X → B is the morphism $\mathcal{A}\times \mathcal{A}\rightarrow \mathcal{A}$ induced by the multiplication morphism $\mathbb{A}^{2} \rightarrow \mathbb{A}^{1}$:

There is again a stack of universal expansions of $\mathcal{A}\times \mathcal{A}\rightarrow \mathcal{A}$, and every expansion X ₀′ → X ₀ is the pullback of a fiber of the universal expansion:

From the point of view of logarithmic geometry this is not surprising: expansions are always stable under logarithmic deformations. But the approach through Artin fans provides us with further results, which we outline below.

6.1.3 Redefining Obstructions

Using expanded degenerations and expanded pairs, Jun Li defined moduli spaces of degenerate stable maps $\overline{\mathcal{M} }_{\Gamma }(X/B)$ and of relative stable maps $\overline{\mathcal{M} }_{\Gamma _{i}}(Y _{i},D)$. Jun Li had an additional challenge in defining the virtual fundamental classes of these spaces, which he constructed by bare hands. With a little bit of hindsight, we now know that Li’s virtual fundamental classes are associated to the natural relative obstruction theories of the morphisms $\overline{\mathcal{M} }_{\Gamma }(X/B) \rightarrow \mathfrak{M}_{\Gamma }(\mathcal{A}^{2}/\mathcal{A})$ and $\overline{\mathcal{M} }_{\Gamma _{i}}(Y _{i},D) \rightarrow \mathfrak{M}_{\Gamma _{i}}(\mathcal{A},\mathcal{D})$, where $\mathfrak{M}_{\Gamma }(\mathcal{A}^{2}/\mathcal{A})$ and $\mathfrak{M}_{\Gamma _{i}}(\mathcal{A},\mathcal{D})$ are the associated moduli spaces of prestable maps. Moreover, the virtual fundamental classes can be understood with machinery available off the shelf of any deformation theory emporium. This observation from [7] made it possible to prove a number of comparison results, including those described below.

6.1.4 Other Approaches and Comparison Theorems

Denote by (Y, D) a smooth pair, consisting of a smooth projective variety Y with a smooth and irreducible divisor D. Jun Li’s moduli space $\overline{\mathcal{M} }_{\Gamma }(Y,D)$ of relative stable maps to (Y, D) provides an algebraic setting for relative Gromov–Witten theory. Only recently have efforts to generalize the theory to more complicated singular targets come to fruition [1, 24, 29, 48, 49]. Because of the technical difficulty of Jun Li’s approach, several alternate approaches to the relative Gromov–Witten invariants of (Y, D) have been developed:

• $\mathsf{Li}_{\Gamma }^{\mathrm{stab}}(Y,D):$ Li’s original moduli space of relative stable maps;

• $\mathsf{AF}_{\Gamma }^{\mathrm{stab}}(Y,D):$ Abramovich–Fantechi’s stable orbifold maps with expansions [2];

• $\mathsf{Kim}_{\Gamma }^{\mathrm{stab}}(Y,D):$ Kim’s stable logarithmic maps with expansions [36]; and

• $\mathsf{ACGS}_{\Gamma }^{\mathrm{stab}}(Y,D):$ Abramovich–Chen and Gross–Siebert’s stable logarithmic maps without expansions [1, 17, 24].

There are analogous constructions

$$\displaystyle{ \mathsf{Li}_{\Gamma }^{\mathrm{stab}}(X/B)\qquad \mathsf{AF}_{ \Gamma }^{\mathrm{stab}}(X/B)\qquad \mathsf{Kim}_{ \Gamma }^{\mathrm{stab}}(X/B)\qquad \mathsf{ACGS}_{ \Gamma }^{\mathrm{stab}}(X/B) }$$

for a degeneration.

This poses a new conundrum: how do these approaches compare? The answer, which depends on the Artin fan $\mathcal{A}$, is as follows:

Theorem 6.1 ([7, Theorem 1.1]).

There are maps

such that

$$\displaystyle\begin{array}{rcl} \Psi _{{\ast}}[\mathsf{AF}]^{\mathrm{vir}} = [\mathsf{Li}]^{\mathrm{vir}}& \Theta _{ {\ast}}[\mathsf{Kim}]^{\mathrm{vir}} = [\mathsf{Li}]^{\mathrm{vir}}& \Upsilon _{ {\ast}}[\mathsf{Kim}]^{\mathrm{vir}} = [\mathsf{ACGS}]^{\mathrm{vir}}. {}\\ \end{array}$$

In particular, the Gromov–Witten invariants associated to these four theories coincide.

The principle behind this comparison for each of the three maps $\Psi,\Theta$, and $\Upsilon$ is the same, and we illustrate it on $\Psi$: there are algebraic stacks parametrizing orbifold and relative stable maps to the Artin fan $(\mathcal{A},\mathcal{D})$, which we denote here by $\mathsf{AF}_{\Gamma }(\mathcal{A},\mathcal{D})$ and $\mathsf{Li}_{\Gamma }(\mathcal{A},\mathcal{D})$. These stacks sit in a Cartesian diagram

such that

• (1) The virtual fundamental classes of the spaces $\mathsf{AF}_{\Gamma }^{\mathrm{stab}}(Y,D)$ and $\mathsf{Li}_{\Gamma }^{\mathrm{stab}}(Y,D)$ may be computed using the natural obstruction theory relative to the vertical arrows π _AF and π _Li .

• (2) The obstruction theory for π _AF is the pullback of the obstruction theory of π _Li .

• (3) The morphism $\Psi _{\mathcal{A}}$ is birational.

One then applies a general comparison result of Costello [18, Theorem 5.0.1] to obtain the theorem.

What makes all this possible is the fact that the virtual fundamental classes of $\mathsf{AF}_{\Gamma }(\mathcal{A},\mathcal{D})$ and $\mathsf{Li}_{\Gamma }(\mathcal{A},\mathcal{D})$ agree with their fundamental classes. This in turn results from the fact that the Artin fan $(\mathcal{A},\mathcal{D})$ of (X, D) discards all the complicated geometry of (X, D), retaining just enough algebraic structure to afford stacks of maps such as $\mathsf{AF}_{\Gamma }(\mathcal{A},\mathcal{D})$ and $\mathsf{Li}_{\Gamma }(\mathcal{A},\mathcal{D})$. In effect, the virtual birationality of $\Psi$ is due to the genuine birationality of $\Psi _{\mathcal{A}}$.

Similar results were obtained by similar methods in [16] and [4].

6.2 Birational Invariance for Logarithmic Stable Maps

More general Artin fans have found applications in the logarithmic approach to Gromov–Witten theory.

Let X be a projective logarithmically smooth variety over $\mathbb{C}$, and denote by $\overline{\mathcal{M} }(X)$ the moduli space of logarithmic stable maps to X, as defined in [1, 17, 24]. Fix a logarithmically étale morphism h: Y → X of projective logarithmically smooth varieties. There is a natural morphism $\overline{\mathcal{M} }(h): \overline{\mathcal{M} }(Y ) \rightarrow \overline{\mathcal{M} }(X)$ induced by h, and the central result of [3] is the following pushforward statement for virtual classes.

Theorem 6.2.

$\overline{\mathcal{M} }(h)_{{\ast}}\left ([ \overline{\mathcal{M} }(Y )]^{\mathrm{vir}}\right ) = [ \overline{\mathcal{M} }(X)]^{\mathrm{vir}}.$ In particular the logarithmic Gromov–Witten invariants of X and Y coincide.

This theorem is proven by working relative to the underlying morphism of Artin fans $\mathcal{Y}\rightarrow \mathcal{X}$ provided by Theorem 5.7. This morphism and h fit into a Cartesian diagram

(3)

One carefully constructs a Cartesian diagram of moduli spaces

(4)

to which principles (1), (2), and (3) in the proof of Theorem 6.1 apply. Costello’s comparison theorem [18, Theorem 5.0.1] again gives the result.

6.3 Boundedness of Logarithmic Stable Maps

A recent application of both Theorem 6.2 and the theory of Artin fans can be found in [8], where a general statement for the boundedness of logarithmic stable maps to projective logarithmic schemes is proven.

Theorem 6.3 ([8, Theorem 1.1.1]).

Let X be a projective logarithmic scheme. Then the stack $\overline{\mathcal{M} }_{\Gamma }(X)$ of stable logarithmic maps to X with discrete data $\Gamma$ is of finite type.

The boundedness of $\overline{\mathcal{M} }_{\Gamma }(X)$ has been established when the characteristic monoid $\overline{M}_{X}$ is globally generated in [1, 17], and more generally when the associated group $\overline{M}_{X}^{\mathrm{gp}}$ is globally generated in [24]. The strategy used in [8] for the general setting is to reduce to the case of a globally generated sheaf of monoids $\overline{M}_{X}$ by studying the behavior of stable logarithmic maps under an appropriate modification of X. This is accomplished by modifying the Artin fan $\mathcal{X} = \mathcal{A}_{X}$ constructed in Sect. 5.3, lifting this modification to the level of logarithmic schemes, and applying a virtual birationality result refining Theorem 6.2.

A key step is the modification of $\mathcal{X}$:

Proposition 6.4 ([8, Proposition 1.3.1]).

Let $\mathcal{X}$ be an Artin fan. Then there exists a projective, birational, and logarithmically étale morphism $\mathcal{Y}\rightarrow \mathcal{X}$ such that $\mathcal{Y}$ is a smooth Artin fan, and the characteristic sheaf $\overline{M}_{\mathcal{Y}}$ is globally generated and locally free.

The proof of this Proposition is analogous to [35, I.11]: successive star subdivisions are applied until each cone is smooth (see Example 4.10), and barycentric subdivisions guarantee that the resulting logarithmic structure has no monodromy.

7 Skeletons and Tropicalization

7.1 Berkovich Spaces

Ever since [56] it has been known that affinoid algebras are the correct coordinate rings for defining non-Archimedean analogues of complex analytic spaces. Working just with affinoid algebras as coordinate rings, we have enough information to build an intricate theory with many applications. The work of Berkovich [11] and [12] beautifully enriches this theory by providing us with an alternative definition of non-Archimedean analytic spaces, which naturally come with underlying topological spaces that have many of the favorable properties of complex analytic spaces, such as being locally path-connected and locally compact.

Let k be a non-Archimedean field, i.e., suppose that k is complete with respect to a non-Archimedean absolute value $\vert.\vert$. We explicitly allow k to carry the trivial absolute value. If U =  SpecA is an affine scheme of finite type over k, as a set the analytic space U ^an associated to U is equal to the set of multiplicative seminorms on A that restrict to the given absolute value on k. We usually write x for a point in U ^an and $\vert.\vert _{x}$, if we want to emphasize that x is thought of as a multiplicative seminorm on A. The topology on U ^an is the coarsest that makes the maps

$$\displaystyle{ \begin{array}{rl} U^{an}&\longrightarrow \mathbb{R}\\ x &\longmapsto \vert f\vert _{ x} \end{array} }$$

continuous for all f ∈ A. There is a natural continuous structure morphism $\rho \mathop{:} U^{an} \rightarrow U$ given by sending x ∈ U ^an to the preimage of zero $\big\{f \in A\big\vert \vert f\vert _{x} = 0\big\}$. A morphism $f \mathop{:} U \rightarrow V$ between affine schemes U =  SpecA and V =  SpecB of finite type over k, given by a k-algebra homomorphism $f^{\#} \mathop{:} B \rightarrow A$, induces a natural continuous map $f^{an} \mathop{:} U^{an} \rightarrow V ^{an}$ given by associating to x ∈ U ^an the point f(x) ∈ V ^an given as the multiplicative seminorm

$$\displaystyle{ \vert.\vert _{f(x)} =\vert.\vert _{x} \circ f^{\#} }$$

on B. The association f ↦ f ^an is functorial in f.

Let X be a scheme that is locally of finite type over k. Choose a covering $U_{i} =\mathop{ \mathrm{Spec}}\nolimits A_{i}$ of X by open affines. Then the analytic space X ^an associated to X is defined by glueing the U _i ^an over the open subsets $\rho ^{-1}(U_{i} \cap U_{j})$. It is easy to see that this construction does not depend on the choice of a covering and that it is functorial with respect to morphisms of schemes over k. We refrain from describing the structure sheaf on X ^an, since we are only going to be interested in the topological properties of X ^an, and refer the reader to [11, 12, 57] for further details.

Example 7.1.

Suppose that k is algebraically closed and endowed with the trivial absolute value. Let t be a coordinate on the affine line $\mathbb{A}^{1} =\mathop{ \mathrm{Spec}}\nolimits \mathbf{k}[t]$. One can classify the points in $(\mathbb{A}^{1})^{an}$ as follows:

• For every a ∈ k and r ∈ [0, 1) we have the seminorm $\vert.\vert _{a,r}$ on k[t] that is uniquely determined by

  $$\displaystyle{ \vert t - a\vert _{a,r} = r, }$$

  and

• for r ∈ [1, ∞) we have the seminorm $\vert.\vert _{\infty,r}$ that is uniquely determined by

  $$\displaystyle{ \vert t - a\vert _{\infty,r} = r }$$

  for all a ∈ k.

Noting that

$$\displaystyle{ \lim _{r\rightarrow 1}\vert.\vert _{a,r} =\vert.\vert _{\infty,1} }$$

for all a ∈ k we can visualize $(\mathbb{A}^{1})^{an}$ as follows:

In particular, we can embed the closed points of $\mathbb{A}^{1}(\mathbf{k})$ into $(\mathbb{A}^{1})^{an}$ by the association $a\mapsto \vert.\vert _{a,0}$ for a ∈ k.

One can give an alternative description of X ^an as the set of equivalence classes of non-Archimedean points of X. A non-Archimedean point of X consists of a pair (K, ϕ) where K is a non-Archimedean extension of k and $\phi \mathop{:}\mathop{ \mathrm{Spec}}\nolimits K \rightarrow X$. Two non-Archimedean points (K, ϕ) and (L, ψ) of X are equivalent, if there is a common non-Archimedean extension $\Omega$ of both K and L such that the diagram commutes.

Proposition 7.2.

The analytic space X ^an is equal to the set of non-Archimedean points modulo equivalence.

Proof.

We may assume that X =  SpecA is affine. A non-Archimedean point (K, ϕ) of X naturally induces a multiplicative seminorm

$$\displaystyle{ A\mathop{\longrightarrow}\limits_{}^{\phi ^{\#}}K\mathop{\longrightarrow}\limits_{}^{\vert.\vert }\mathbb{R} }$$

on A. Conversely, given x ∈ X ^an, we can consider the integral domain $A/\ker \vert.\vert _{x}$ and form the completion $\mathcal{H}(x)$ of its field of fractions. The natural homomorphism $A \rightarrow \mathcal{H}(x)$ defines a non-Archimedean point on X and these two constructions are inverse up to equivalence. □ 

Now suppose that k is endowed with the trivial absolute value. In [58, Sect. 1] Thuillier introduces a slight variant of the analytification functor that functorially associates to a scheme locally of finite type over k a non-Archimedean analytic space $X^{\beth }$. Its points are pairs (R, ϕ) consisting of a valuation ring R extending k together with a morphism $\phi \mathop{:}\mathop{ \mathrm{Spec}}\nolimits R \rightarrow X$ modulo an equivalence relation as above: two pairs (R, ϕ) and (S, ψ) are equivalent, if there is a common valuation ring $\mathcal{O}$ extending both R and S such that the diagram commutes.

So, if U =  SpecA is affine, then $U^{\beth }$ is nothing but the set of multiplicative seminorms $\vert.\vert _{x}$ on A that are bounded, i.e., that fulfill $\vert f\vert _{x} \leq 1$ for all f ∈ A. The topology on $U^{\beth }$ is the one induced from U ^an and there is a natural anti-continuous reduction map $r \mathop{:} U^{\beth } \rightarrow U$ that sends $x \in U^{\beth }$ to the prime ideal $\big\{f \in A\big\vert \vert f\vert _{x} < 1\big\}$. For a general scheme X locally of finite type over k, we again choose a covering U _i by open affine subsets, and now glue the $U_{i}^{\beth }$ over the closed subsets $r^{-1}(U_{i} \cap U_{j})$ in order to obtain $X^{\beth }$.

As an immediate application of the valuative criteria for separatedness and properness, we obtain that, if X is separated, then $X^{\beth }$ is naturally a locally closed subspace of X ^an, and, if X is complete, then $X^{\beth } = X^{an}$.

Example 7.3.

The space $(\mathbb{A}^{1})^{\beth }$ is precisely the subspace of $(\mathbb{A}^{1})^{an}$ consisting of the points $\vert.\vert _{a,r}$ for a ∈ k and r ∈ [0, 1) as well as the Gauss point $\vert.\vert _{\infty,1}$.

7.2 The Case of Toric Varieties

Let k be a non-Archimedean field. As observed in [10, 22, 25, 26], there is an intricate relationship between non-Archimedean analytic geometry and tropical geometry. In particular, in many interesting situations the tropicalization of an algebraic variety X over k can be regarded as a natural deformation retract of X ^an, a so-called skeleton of X ^an. In this section we are going to give a detailed explanation of this relationship in the simplest possible case, that of toric varieties.

Let T be a split algebraic torus with character lattice M and co-character lattice N, and $X = X(\Delta )$ a T-toric variety that is defined by a rational polyhedral fan $\Delta$ in $N_{\mathbb{R}}$. We refer the reader to Sect. 2 for a brief summary of this beautiful theory, and to [23] and [19] for a more thorough account.

In [32] and [50] Kajiwara and Payne independently construct a tropicalization map

$$\displaystyle{ \mathop{\mathrm{trop}}\nolimits _{\Delta } \mathop{:} X^{an}\longrightarrow N_{ \mathbb{R}}(\Delta ) }$$

associated to X, whose codomain is a partial compactification of $N_{\mathbb{R}}$, uniquely determined by $\Delta$ (also see [51, Sect. 4] and [53, Sect. 3]).

For a cone σ in $\Delta$ set $N_{\mathbb{R}}(\sigma ) =\mathop{ \mathrm{Hom}}\nolimits (S_{\sigma },\overline{\mathbb{R}})$, where S _σ denotes the toric monoid $\sigma ^{\vee }\cap M$ and write $\overline{\mathbb{R}}$ for the additive monoid $(\mathbb{R} \sqcup \{\infty \},+)$. Endow $N_{\mathbb{R}}(\sigma )$ with the topology of pointwise convergence.

Lemma 7.4 ([53, Proposition 3.4]).

• (i) The space $N_{\mathbb{R}}(\sigma )$ has a stratification by locally closed subsets isomorphic to the vector spaces $N_{\mathbb{R}}/\mathop{\mathrm{Span}}\nolimits (\tau )$ for all faces τ of σ.

• (ii) For a face τ of σ the natural map $S_{\sigma } \rightarrow S_{\tau }$ induces the open embedding

  $$\displaystyle{ N_{\mathbb{R}}(\tau ) `\longrightarrow N_{\mathbb{R}}(\sigma ) }$$

  that identifies $N_{\mathbb{R}}(\tau )$ with the union of strata in $N_{\mathbb{R}}(\sigma )$ corresponding to faces of τ in N _R (σ).

So one can think of $N_{\mathbb{R}}(\sigma )$ as a partial compactification of $N_{\mathbb{R}}$ given by adding a vector space $N_{\mathbb{R}}/\mathop{\mathrm{Span}}\nolimits (\tau )$ at infinity for every face τ ≠ 0 of σ. The partial compactification $N_{\mathbb{R}}(\Delta )$ of $N_{\mathbb{R}}$ is defined to be the colimit of the $N_{\mathbb{R}}(\sigma )$ for all cones σ in $\Delta$. Since the stratifications on the $N_{\mathbb{R}}(\sigma )$ are compatible, the space $N_{\mathbb{R}}(\Delta )$ is a partial compactification of $N_{\mathbb{R}}$ that carries a stratification by locally closed subsets isomorphic to $N_{\mathbb{R}}/\mathop{\mathrm{Span}}\nolimits (\sigma )$ for every cone σ in $\Delta$.

On the T-invariant open affine subset $X_{\sigma } =\mathop{ \mathrm{Spec}}\nolimits \mathbf{k}[S_{\sigma }]$ the tropicalization map

$$\displaystyle{ \mathop{\mathrm{trop}}\nolimits _{\sigma } \mathop{:} X_{\sigma }^{an}\longrightarrow N_{ \mathbb{R}}(\sigma ) }$$

is defined by associating to an element x ∈ X ^an the homomorphism $s\mapsto -\log \vert \chi ^{s}\vert _{x}$ in $N_{\mathbb{R}}(\sigma ) =\mathop{ \mathrm{Hom}}\nolimits (S_{\sigma },\overline{\mathbb{R}})$.

Lemma 7.5.

The tropicalization map trop_σ is continuous and, for a face τ of σ, the natural diagram

commutes and is Cartesian.

Therefore we can glue the trop _σ on local T-invariant patches X _σ and obtain a global continuous tropicalization map

$$\displaystyle{ \mathop{\mathrm{trop}}\nolimits _{\Delta } \mathop{:} X^{an}\longrightarrow N_{ \mathbb{R}}(\Delta ) }$$

that restricts to trop _σ on T-invariant open affine subsets X _σ . Its restriction to T-orbits is the usual tropicalization map in the sense of [26, Sect. 3].

The following Proposition 7.6 is well-known among experts and can be found in [58, Sect. 2] in the constant coefficient case, i.e., the case that k is trivially valued.

Proposition 7.6.

The tropicalization map $\mathop{\mathrm{trop}}\nolimits _{\Delta } \mathop{:} X^{an} \rightarrow N_{\mathbb{R}}(\Delta )$ has a continuous section $J_{\Delta }$ and the composition

$$\displaystyle{ \mathbf{p}_{\Delta } = J_{\Delta } \circ \mathop{\mathrm{trop}}\nolimits _{\Delta } \mathop{:} X^{an} \rightarrow X^{an} }$$

defines a strong deformation retraction.

The deformation retract

$$\displaystyle{ \mathfrak{S}(X) = J_{\Delta }\big(N_{\mathbb{R}}(\Delta )\big) = \mathbf{p}_{\Delta }(X^{an}) }$$

is said to be the non-Archimedean skeleton of X ^an.

Proof Sketch of Proposition 7.6.

Consider a T-invariant open affine subset $X_{\sigma } =\mathop{ \mathrm{Spec}}\nolimits \mathbf{k}[S_{\sigma }]$. We may construct the section $J_{\sigma } \mathop{:} N_{\mathbb{R}}(\sigma ) \rightarrow X_{\sigma }^{an}$ by associating to $u \in N_{\mathbb{R}}(\sigma ) =\mathop{ \mathrm{Hom}}\nolimits (S_{\sigma },\overline{\mathbb{R}})$ the seminorm J _σ (u) defined by

$$\displaystyle{ J_{\sigma }(u)(f) =\max _{s\in S_{\sigma }}\:{\Bigl \{\vert a_{s}\vert \:\exp \big(\!-\!u(s)\big)\Bigr \}} }$$

for $f =\sum _{s}a_{s}\chi ^{s} \in \mathbf{k}[S_{\sigma }]$. A direct verification shows that J _σ is continuous and fulfills $\mathop{\mathrm{trop}}\nolimits _{\sigma } \circ J_{\sigma } =\mathop{ \mathrm{id}}\nolimits _{N_{\mathbb{R}}(\sigma )}$.

The construction of J _σ is compatible with restrictions to T-invariant affine open subsets and we obtain a global section $J_{\Delta } \mathop{:} N_{\mathbb{R}}(\Delta ) \rightarrow X^{an}$ of the tropicalization map $\mathop{\mathrm{trop}}\nolimits _{\Delta } \mathop{:} X^{an} \rightarrow N_{\mathbb{R}}(\Delta )$.

Since $J_{\Delta }$ is a section of $\mathop{\mathrm{trop}}\nolimits _{\Delta }$, the continuous map

$$\displaystyle{ \mathbf{p}_{\Delta } = J_{\Delta } \circ \mathop{\mathrm{trop}}\nolimits _{\Delta } \mathop{:} X^{an}\longrightarrow X^{an} }$$

is a retraction map. On X _σ the image p _σ (x) of $x \in X_{\sigma }^{an}$ is the seminorm given by

$$\displaystyle{ \mathbf{p}_{\sigma }(x)(f) =\max _{s\in S_{\sigma }}\:{\bigl \{\vert a_{s}\vert \:\vert \chi ^{s}\vert _{ x}\bigr \}} }$$

for $f =\sum _{s}a_{s}\chi ^{s} \in \mathbf{k}[S_{\sigma }]$. The arguments in [58, Sect. 2.2] generalize to this situation and show that $\mathbf{p}_{\Delta }$ is, in fact, a strong deformation retraction (see in particular [58, Lemma 2.8(1)]). □ 

Example 7.7.

The skeleton of $\mathbb{A}^{1}$ is given by the half open line connecting 0 to ∞, i.e., for trivially valued k we have

$$\displaystyle{ \mathfrak{S}(X) ={\Bigl \{\:\:\vert \cdot \vert _{0,r}\:\:\Big\vert \:\:r \in [0,1)\Bigr \}} \cup {\Bigl \{\:\:\vert \cdot \vert _{\infty,r}\:\:\Big\vert \:\:r \in [1,\infty )\Bigr \}} }$$

in the notation of Example 7.1.

Let k now be endowed with the trivial absolute value. As seen in [58, Sect. 2.1] the deformation retraction $\mathbf{p}_{\Delta } \mathop{:} X^{an} \rightarrow X^{an}$ restricts to a deformation retraction $\mathbf{p}_{X} \mathop{:} X^{\beth } \rightarrow X^{\beth }$, whose image is homeomorphic to the closure $\overline{\Delta }$ of $\Delta$ in $N_{\mathbb{R}}(\Delta )$. On T-invariant open affine subsets $X_{\sigma } =\mathop{ \mathrm{Spec}}\nolimits \mathbf{k}[S_{\sigma }]$ this homeomorphism is induced by the tropicalization map

$$\displaystyle{ \begin{array}{rl} \mathop{\mathrm{trop}}\nolimits _{X} \mathop{:} X^{\beth } & \longrightarrow \mathop{ \mathrm{Hom}}\nolimits (S_{\sigma },\overline{\mathbb{R}}_{\geq 0}) \\ x&\longrightarrow \big(s\mapsto -\log \vert \chi ^{s}\vert _{x}\big)\end{array} }$$

into the extended cone $\overline{\sigma } =\mathop{ \mathrm{Hom}}\nolimits (S_{\sigma },\overline{\mathbb{R}}_{\geq 0})$.

7.3 The Case of Logarithmic Schemes

7.3.1 Zariski Logarithmic Schemes

Suppose that k is endowed with the trivial absolute value and let X be logarithmically smooth over k. In [58] Thuillier constructs a strong deformation retraction $\mathbf{p}_{X} \mathop{:} X^{\beth } \rightarrow X^{\beth }$ onto a closed subset $\mathfrak{S}(X)$ of $X^{\beth }$, the skeleton of $X^{\beth }$. We summarize the basic properties of this construction in the following Proposition 7.8. We refer to Definition 5.6 for the notion of small Zariski logarithmic schemes.

Proposition 7.8.

• (i) The construction of p _X is functorial with respect to logarithmic morphisms, i.e., given a logarithmic morphism $f \mathop{:} X \rightarrow Y$ , there is a continuous map $f^{\mathfrak{S}} \mathop{:} \mathfrak{S}(X) \rightarrow \mathfrak{S}(Y )$ that makes the diagram

  

  commute. Moreover, if f is logarithmically smooth, then $f^{\mathfrak{S}}$ is the restriction of $f^{\beth }$ to $\mathfrak{S}(X)$.

• (ii) For every strict étale neighborhood $U \rightarrow X$ that is small with respect to x ∈ U and for every strict étale morphism $\gamma \mathop{:} U \rightarrow Z$ into a γ(x)-small toric variety Z the analytic map $\gamma ^{\beth }$ induces a homeomorphism $\gamma ^{\mathfrak{S}} \mathop{:} \mathfrak{S}(U)\mathop{\longrightarrow}\limits_{}^{ \sim } \mathfrak{S}(Z)$ that makes the diagram commute.

  

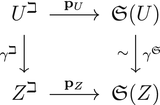
• (iii) The skeleton $\mathfrak{S}(X)$ is the colimit of all skeletons $\mathfrak{S}(U)$ associated to strict étale morphisms $U \rightarrow X$ from a Zariski logarithmic scheme U that is small and the deformation retraction $\mathbf{p}_{X} \mathop{:} X^{\beth } \rightarrow X^{\beth }$ is induced by the universal property of colimits.

Suppose now that the logarithmic structure on X is defined in the Zariski topology. In this case, following [59], one can use the theory of Kato fans in order to define a tropicalization map $\mathop{\mathrm{trop}}\nolimits _{X} \mathop{:} X^{\beth } \rightarrow \overline{\varSigma } _{X}$ generalizing the map defined for toric varieties.

Let F be a fine and saturated Kato fan and consider the cone complex

$$\displaystyle{ \varSigma _{F} = F(\mathbb{R}_{\geq 0}) =\mathop{ \mathrm{Hom}}\nolimits \big(\mathop{\mathrm{Spec}}\nolimits \mathbb{R}_{\geq 0},F\big) }$$

and the extended cone complex

$$\displaystyle{ \overline{\varSigma } _{F} = F(\overline{\mathbb{R}}_{\geq 0}) =\mathop{ \mathrm{Hom}}\nolimits \big(\mathop{\mathrm{Spec}}\nolimits \overline{\mathbb{R}}_{\geq 0},F\big) \supseteq \overline{\varSigma } _{F} }$$

associated to F. In order to describe the structure of $\overline{\varSigma }_{F}$ and $\overline{\varSigma }_{F}$ one can use the structure map

$$\displaystyle{ \begin{array}{rl} \rho \mathop{:} \overline{\varSigma } _{F}&\longrightarrow F \\ u&\longmapsto u\big(\{\infty \}\big) \end{array} }$$

and the reduction map

$$\displaystyle{ \begin{array}{rl} r \mathop{:} \overline{\varSigma } _{F}&\longrightarrow F \\ u&\longmapsto u(\overline{\mathbb{R}}_{>0})\ . \end{array} }$$

Proposition 7.9 ([61] Proposition 3.1).

The inverse image r ⁻¹ (U) of an open affine subset $U =\mathop{ \mathrm{Spec}}\nolimits P$ in $\overline{\varSigma }_{F}$ is the canonical compactification $\overline{\sigma }_{U} =\mathop{ \mathrm{Hom}}\nolimits (P,\overline{\mathbb{R}}_{\geq 0})$ of a rational polyhedral cone $\sigma _{U} =\mathop{ \mathrm{Hom}}\nolimits (P, \mathbb{R}_{\geq 0})$ and its relative interior $\mathring{\sigma} _{U}$ is given by r ⁻¹ (x) for the unique closed point x in U.

• (i) If V ⊆ U for open affine subsets U,V ⊆ F, then σ _V is a face of σ _U.

• (ii) For two open affine subsets U and V of F the intersection $\sigma _{U} \cap \sigma _{V }$ is a union of finitely many common faces.

So the cone complex Σ _F is a rational polyhedral cone complex in the sense of [35]. It naturally carries the weak topology, in which a subset $A \subseteq \varSigma _{F}$ is closed if and only if the intersections $A \cap \sigma _{U}$ for all open affine subsets $U =\mathop{ \mathrm{Spec}}\nolimits P$ of F are closed. The extended cone complex $\overline{\varSigma }_{F}$ is a canonical compactification of Σ _F , carrying the weak topology with the topology of pointwise convergence on $\sigma _{U} =\mathop{ \mathrm{Hom}}\nolimits (P,\overline{\mathbb{R}}_{\geq 0})$ as local models.

Proposition 7.10.

• (i) The reduction map $r \mathop{:} \overline{\varSigma } _{F} \rightarrow F$ is anti-continuous.

• (ii) The structure map $\rho \mathop{:} \overline{\varSigma } _{F} \rightarrow F$ is continuous.

• (iii) There is a natural stratification

  $$\displaystyle{ \bigsqcup _{x\in \mathop{\mathrm{Spec}}\nolimits F}\rho ^{-1}(x) \simeq \overline{\varSigma } _{ F} }$$

  of $\overline{\varSigma }_{F}$ by locally closed subsets.

Let X be a Zariski logarithmic scheme that is logarithmically smooth over k and denote by $\phi _{X} \mathop{:} (X,\overline{\mathcal{O}}_{X}) \rightarrow F_{X}$ the characteristic morphism into its Kato fan F _X . We write Σ _X and $\overline{\varSigma }_{X}$ for the cone complex and the extended cone complex of F _X , respectively.

Following [59, Sect. 6.1] one can define the tropicalization map $\mathop{\mathrm{trop}}\nolimits _{X} \rightarrow \overline{\varSigma }_{X}$ as follows: a point $x \in X^{\beth }$ can be represented by a morphism $\underline{x} \mathop{:}\mathop{ \mathrm{Spec}}\nolimits R \rightarrow (X,\overline{\mathcal{O}}_{X})$ for a valuation ring R extending k. Its image $\mathop{\mathrm{trop}}\nolimits _{X}(x)$ in $\overline{\varSigma }_{X} =\mathop{ \mathrm{Hom}}\nolimits (\mathop{\mathrm{Spec}}\nolimits \overline{\mathbb{R}}_{\geq 0},F_{X})$ is defined to be the composition

$$\displaystyle{ \mathop{\mathrm{Spec}}\nolimits \overline{\mathbb{R}}_{\geq 0}\mathop{\longrightarrow}\limits_{}^{\ \mathrm{val^{\#}}\ }\mathop{ \mathrm{Spec}}\nolimits R\mathop{\longrightarrow}\limits_{}^{\ \underline{x}\ }(X,\overline{\mathcal{O}}_{ X})\mathop{\longrightarrow}\limits_{}^{\ \phi _{X}\ }F_{X}, }$$

where $\mathop{\mathrm{val}}\nolimits ^{\#}$ is the morphism $\mathop{\mathrm{Spec}}\nolimits \overline{\mathbb{R}}_{\geq 0} \rightarrow \mathop{\mathrm{Spec}}\nolimits R$ induced by the valuation $\mathop{\mathrm{val}}\nolimits \mathop{:} R \rightarrow \overline{\mathbb{R}}_{\geq 0}$ on R.

Proposition 7.11 ([59] Proposition 6.2).

• (i) The tropicalization map is well-defined and continuous. It makes the diagrams

  

  commute.

• (ii) A morphism $f \mathop{:} X \rightarrow X'$ of Zariski logarithmic schemes, both logarithmically smooth and of finite type over k , induces a continuous map $\overline{\varSigma }(f) \mathop{:} \overline{\varSigma } _{X} \rightarrow \overline{\varSigma } _{X'}$ such that the diagram commutes. The association $f\mapsto \overline{\varSigma }(f)$ is functorial in f.

  

Corollary 7.12 (Strata-Cone Correspondence, [61] Corollary 3.5).

There is an order-reversing one-to-one correspondence between the cones in Σ _X and the strata of X. Explicitly it is given by

$$\displaystyle{\mathring{\sigma }\longmapsto r\big(\mathop{\mathrm{trop}}\nolimits _{X}^{-1}(\mathring{\sigma} )\big) }$$

for a relatively open cone $\mathring{\sigma} \subseteq \varSigma _{X}$ and

$$\displaystyle{ E\longmapsto \mathop{\mathrm{trop}}\nolimits _{X}\big(r^{-1}(E) \cap X_{ 0}^{an}\big) }$$

for a stratum E of X.

Proof.

This is an immediate consequence of the commutativity of

from Propositions 7.11, 7.9, and the fact that ϕ _X sends every point in a stratum E = E(ξ) to its generic point ξ. □ 

Corollary 7.13 ([61] Corollary 3.6).

The tropicalization map induces a continuous map $X^{\beth } \cap X_{0}^{an} \rightarrow \varSigma _{F}$.

Proof.

This follows from the commutativity of

and the observations that $\rho ^{-1}(X_{0}) = X^{\beth } \cap X^{an}$ as well as $\rho ^{-1}(X_{0} \cap F_{X}) =\varSigma _{F}$. □ 

7.3.2 Étale Logarithmic Schemes

Let X be an étale logarithmic scheme that is logarithmically smooth over k. We can define the generalized extended cone complex associated to X as the colimit of all $\overline{\varSigma }_{X'}$ taken over all strict étale morphisms $X' \rightarrow X$ from a Zariski logarithmic scheme X′. The tropicalization map $\mathop{\mathrm{trop}}\nolimits _{X} \mathop{:} X^{\beth } \rightarrow \overline{\varSigma } _{X}$ is induced by the universal property of colimits.

In analogy with Proposition 7.6 we have the following compatibility result stating that p _X and $\mathop{\mathrm{trop}}\nolimits _{X}$ are equal up to a natural homeomorphism.

Theorem 7.14 ([59] Theorem 1.2).

Suppose that X is logarithmically smooth over k. There is a natural homeomorphism $J_{X} \mathop{:} \overline{\varSigma } _{X}\mathop{\longrightarrow}\limits_{}^{ \sim } \mathfrak{S}(X)$ making the diagram

commute.

Moreover, we obtain the following Corollary of Proposition 7.11 (ii).

Corollary 7.15 ([59] Theorem 1.1).

A morphism $f \mathop{:} X \rightarrow X'$ of logarithmic schemes, logarithmically smooth and of finite type over k , induces a continuous map $\overline{\varSigma }(f) \mathop{:} \overline{\varSigma } _{X} \rightarrow \overline{\varSigma } _{X'}$ such that the natural diagram

is commutative. The association $f\mapsto \overline{\varSigma }(f)$ is functorial in f.

8 Non-Archimedean Geometry of Artin Fans

8.1 Analytification of Artin Fans

In Sect. 7.3 we have seen that the extended cone complex $\overline{\varSigma }_{F}$ associated to a Kato fan F has topological properties analogous to the non-Archimedean analytic space $X^{\beth }$ associated to a scheme X of finite type over k. Moreover, if X is a Zariski logarithmic scheme that is logarithmically smooth over k, the tropicalization map $\mathop{\mathrm{trop}}\nolimits _{X} \mathop{:} X^{\beth } \rightarrow \overline{\varSigma } _{X}$ is the “analytification” of the characteristic morphism $\phi _{X} \mathop{:} (X,\mathcal{O}_{X}) \rightarrow F_{X}$. Using the theory of Artin fans we can make this analogy more precise, and even generalize the construction of trop _X to all logarithmic schemes.

Let k be endowed with the trivial absolute value. As explained in [62, Sect. V.3] the $(.)^{\beth }$-functor, originally constructed in [58], generalizes to a pseudofunctor from the 2-category of algebraic stacks locally of finite type over k into the category of non-Archimedean analytic stacks, such that whenever $[U/R] \simeq \mathcal{X}$ is a groupoid presentation of an algebraic stack $\mathcal{X}$ we have a natural equivalence $[U^{\beth }/R^{\beth }] \simeq \mathcal{X}^{\beth }$. We refer the reader to [52, 60], and [64, Sect. 6] for background on the theory of non-Archimedean analytic stacks.

Let $\mathcal{X}$ be an algebraic stack locally of finite type over k. Then the underlying topological space $\vert \mathcal{X}^{\beth }\vert$ of the analytic stack $\mathcal{X}$ can be identified with the set of equivalence classes of pairs (R, ϕ) consisting of a valuation ring R extending k and a morphism $\phi \mathop{:}\mathop{ \mathrm{Spec}}\nolimits R \rightarrow \mathcal{X}$. Two such pairs (ϕ, R) and (ψ, S) are said to be equivalent, if there is a valuation ring $\mathcal{O}$ extending both R and S such that the diagram

is 2-commutative. The topology on $\vert \mathcal{X}^{\beth }\vert$ is the coarsest making all maps $\vert U^{\beth }\vert \rightarrow \vert \mathcal{X}^{\beth }\vert$ induced by surjective flat morphisms $U \rightarrow \mathcal{X}$ from a scheme U locally of finite type over k onto X into a topological quotient map.

Suppose that X is a logarithmic scheme that is logarithmically smooth and of finite type over k. Consider the natural strict morphism $X \rightarrow \mathcal{A}_{X}$ into the Artin fan associated to X as constructed in Sect. 5.

Theorem 8.1 ([62]).

There is a natural homeomorphism

$$\displaystyle{ \mu _{X} \mathop{:}\big\vert \mathcal{A}_{X}^{\beth }\big\vert \mathop{\longrightarrow}\limits_{}^{ \sim }\overline{\varSigma } _{ X} }$$

that makes the diagram

commute.

So, by applying the functor $(.)^{\beth }$ to the morphism $X \rightarrow \mathcal{A}_{X}$ we obtain the tropicalization map on the underlying topological spaces. Note that this construction also works for étale logarithmic schemes and we do not have to take colimits as in Sect. 7.3.2 (they are already taken in the construction of $\mathcal{A}_{X}$). Theorem 7.14 immediately yields the following Corollary.

Corollary 8.2.

There is a natural homeomorphism

$$\displaystyle{ \tilde{\mu }_{X} \mathop{:}\big\vert \mathcal{A}_{X}^{\beth }\big\vert \mathop{\longrightarrow}\limits_{}^{ \sim } \mathfrak{S}(X) }$$

that makes the diagram

commute.

8.2 Stack Quotients and Tropicalization

Let X be a T-toric variety over k. In this case, Theorem 8.1 precisely says that on the underlying topological spaces the tropicalization map $\mathop{\mathrm{trop}}\nolimits _{X} \mathop{:} X^{\beth } \rightarrow \overline{\varSigma } _{X}$ is nothing but the analytic stack quotient map $X^{\beth } \rightarrow [X^{\beth }/T^{\beth }]$. Due to the favorable algebro-geometric properties of toric varieties we can generalize this interpretation to general ground fields.

Let k be any non-Archimedean field, and suppose that X is a T-toric variety defined by a rational polyhedral fan $\Delta \subseteq N_{\mathbb{R}}$ as in Sect. 7.2. Denote by $T^{\circ }$ the non-Archimedean analytic subgroup

$$\displaystyle{ \big\{x \in T^{an}\:\big\vert \:\vert \chi ^{m}\vert _{ x} = 1\text{ for all }m \in M\big\} }$$

of the analytic torus T ^an. Note that, if k is endowed with the trivial absolute value, then $T^{\circ } = T^{\beth }$. In general, we can think of $T^{\circ }$ as a non-Archimedean analogue of the real n-torus $N_{S^{1}} = N \otimes _{\mathbb{Z}}S^{1}$ naturally sitting in $N_{\mathbb{C}^{{\ast}}} = N \otimes _{\mathbb{Z}}\mathbb{C}^{{\ast}}$. The T-operation on X induces an operation of T ^∘ on X ^an.

Theorem 8.3 ([60] Theorem 1.1).

There is a natural homeomorphism

$$\displaystyle{\mu _{\Delta } \mathop{:}\big\vert [X^{an}/T^{\circ }]\big\vert \mathop{\longrightarrow}\limits_{}^{ \sim } N_{ \mathbb{R}}(\Delta )}$$

that makes the diagram

commute.

The proof Theorem 8.3 is based on establishing that the skeleton $\mathfrak{S}(X)$ of X is equal to the set of $T^{\circ }$-invariant points of X ^an. Then the statement follows, since by Ulirsch [60, Proposition 5.4 (ii)] the topological space $\big\vert [X^{an}/T^{\circ }]\big\vert$ is the colimit of the maps (Fig. 8)

$$\displaystyle{ T^{\circ }\times X^{an} \rightrightarrows X^{an}\ . }$$

Fig. 8

Consider the affine line $\mathbb{A}^{1}$ over a trivially valued field k. The non-Archimedean unit circle $\mathbb{G}_{m}^{\circ }$ is given as the subset of elements in $x \in (\mathbb{A}^{1})^{an}$ with $\vert t\vert _{x} = 1$, where t denotes a coordinate on $\mathbb{A}^{1}$. The skeleton $\mathfrak{S}(\mathbb{A}^{1})$ of $(\mathbb{A}^{1})^{an}$ is the line connecting 0 to ∞. It is precisely the set of “$\mathbb{G}_{m}^{\circ }$-invariant” points in $(\mathbb{A}^{1})^{an}$, and therefore naturally homeomorphic to the topological space underlying $\big[(\mathbb{A}^{1})^{an}\big/\mathbb{G}_{m}^{\circ }\big]$ (see [60, Example 6.2])

9 Where We Are, Where We Want to Go

9.1 Skeletons Fans and Tropicalization Over Non-Trivially Valued Fields

In almost all of our discussion, we have constructed Kato fans, Artin fans, and skeletons for a logarithmic variety over a trivially valued field k. One exception is the discussion of toric varieties in Sect. 7.2. This is quite useful and important: given a subvariety Y of a toric variety X, over a non-trivially valued field, the tropicalization $\mathop{\mathrm{trop}}\nolimits (Y )$ of Y is a polyhedral subcomplex of $N_{\mathbb{R}}(\Delta )$ which is not itself a fan. Much of the impact of tropical geometry relies on the way $\mathop{\mathrm{trop}}\nolimits (Y )$ reflects on the geometry of Y. So even though the toric variety X itself can be defined over a field with trivial valuation, the fact that Y —whose field of definition is non-trivially valued—has a combinatorial shadow is fundamental.

Can we define Artin fans over non-trivially valued fields? What should their structure be? In what generality can we canonically associate a skeleton with a logarithmic structure?

Some results in these directions are available in the recent paper of Gubler, Rabinoff, and Werner [27]. See also Werner’s contribution to this volume [63].

9.2 Improved Fans and Moduli Spaces

One of the primary applications of tropical geometry, and therefore of fans, is through moduli spaces. Mikhalkin’s correspondence theorem [41], Nishinou and Siebert’s vast extension [42], the work [15] of Cavalieri, Markwig, and Ranganathan, and the manuscript [6], all show that tropical moduli spaces $M^{\mathop{\mathrm{trop}}\nolimits }(X^{\mathop{\mathrm{trop}}\nolimits })$ of tropical curves in tropical varieties serve as good approximations of the tropicalization $\mathop{\mathrm{trop}}\nolimits (M(X))$ of moduli spaces M(X) of algebraic curves in algebraic varieties. But the picture is not perfect:

• 1. Apart from very basic cases of the moduli space of curves itself [9] and genus-0 maps with toric targets [54] the tropical moduli space does not coincide with the tropicalization of the algebraic moduli space

  $$\displaystyle{M^{\mathop{\mathrm{trop}}\nolimits }(X^{\mathop{\mathrm{trop}}\nolimits })\ \ \neq \ \ \ \mathop{\mathrm{trop}}\nolimits (M(X)).}$$

• 2. Even when it does, it is always a coarse moduli space, lacking the full power of universal families.

These seem to be two distinct challenges, but experience shows that they are closely intertwined. It also seems that the following problem is part of the puzzle:

• 3. The construction to the Artin fan $\mathcal{A}_{X}$ of a logarithmic scheme X is not functorial for all morphisms of logarithmic schemes.

The following program might inspire one to go some distance towards these challenges:

• 1. Good combinatorial moduli:

  • (a) Construct a satisfactory monoidal theory of cone spaces and cone stacks as described in Sects. 4.6.1 and 4.6.2.

  • (b) Construct a corresponding enhancement of $M_{g,n}^{\mathop{\mathrm{trop}}\nolimits }$ which is a fine moduli stack of tropical curves, with a universal family.

  This is part of current work of Cavalieri, Chan, Ulirsch, and Wise.

• 2. Stacky Artin fans:

  • (a) Find a way to relax the representability condition in the definition of $\mathcal{A}_{X}$ so that the enhanced moduli spaces above are canonically associated to the moduli stacks M _g, n

  • (b) Try to extend all of the above to moduli of maps.