Massively Parallel Cellular Matrix Model for Superpixel Adaptive Segmentation Map

Abstract

We propose the concept of superpixel adaptive segmentation map, to produce a perceptually meaningful representation of rigid pixel image, with higher resolution of more superpixels on interesting regions according to the density distribution of desired attributes. The solution is based on the self-organizing map (SOM) algorithm, for the benefits of SOM’s ability to generate a topological map according to a probability distribution and its potential to be a natural massive parallel algorithm. We also propose the concept of parallel cellular matrix which partitions the Euclidean plane defined by input image into an appropriate number of uniform cell units. Each cell is responsible of a certain part of the data and the cluster center network, and carries out massively parallel spiral searches based on the cellular matrix topology. Experimental results from our GPU implementation show that the proposed algorithm can generate adaptive segmentation map where the distribution of superpixels reflects the gradient distribution or the disparity distribution of input image, with respect to scene topology. When the input size augments, the running time increases in a linear way with a very weak increasing coefficient.

1 Introduction

Superpixels have become an essential tool to the vision community. As building blocks of many vision algorithms, superpixels divide raw image into perceptually meaningful atomic regions which can be employed to substitute the rigid structure of the pixel grid [1–3]. Therefore, these atomic regions should represent or reflect some local properties with respect to some attribute distributions of the raw image. However, most of the existing algorithms produce uniformly distributed superpixels. In this paper, we aim to generate adaptive segmentation, called superpixel adaptive segmentation map (SPASM), where the distribution (density) of superpixels coincides with the distribution of some desired attribute of input image, such as edges, textures, and depths. In order to implement the parallel level, on which parallel SPASM algorithm will take place, we also design a massively parallel computation model. Unlike most work of the general-purpose computing on graphics processing units (GPGPU) for image processing applications, where usually one thread deals with one pixel, we propose the concept of cellular matrix decomposition at different levels for (1) massive parallelism implementation under different topologies of the plane and (2) optimized load balancing computing with size-configurable cells. Each cell, assigned to one thread in our GPU implementation, is a basic parallel operation unit and performs spiral search [4] for closest point finding, e.g. from pixel to cluster center and vice versa. Then one important feature of the model is that it proceeds from a cellular decomposition of the input data in 2D space, such that each processing unit represents a constant and small part of data. Since the cellular matrix division is proportional to input data, and the processing units correspond one-to-one with the cells respectively, then, both the memory and the processing units needed are in linear correspondence of O(N) to the input image size N. Hence, as more and more multi-cores will be available in a single chip in the future, the approach should be more and more competitive, especially when dealing with very large size inputs. This property is what we call “massive parallelism”.

Numerous superpixel algorithms have been proposed in the literature and they could be roughly classified into graph-based methods and gradient ascent methods. Algorithms in the first category usually treat each pixel as a node in a graph where edge weights between two nodes are proportional to the similarity between neighboring pixels. Superpixels are then created by minimizing a cost function defined over the graph [5–8]. Gradient ascent approaches, on the other hand, usually start from a rough initial clustering of pixels and then iteratively refine the clusters until some convergence criterion is met to form superpixels. Examples in this category include mean shift [9], quick shift [10], watershed approach [11], and Turbopixel method [12]. Also, there exist some methods [13, 14] that use depth as an additional feature to perform segmentation on RGB-D images. A comprehensive survey and comparison study of superpixel algorithms can be found in [1], where a fast algorithm called simple linear iterative clustering (SLIC) is proposed to adapt k-means clustering to generate superpixels with good adherence to image boundaries. Our proposed algorithm extends the state-of-the-art SLIC algorithm, using our adaptive meshing tool to add compression abilities, with respect to the density distribution of image attributes and the topological relationship of cluster centers. Different from SLIC which performs a restricted nearest point search within a square region, through our cellular matrix model, we can conduct the true closest point finding in a massively parallel way, using the efficient spiral search algorithm under different topologies.

Fig. 1.

Flowchart of the SPASM algorithm.

2 SPASM Algorithm

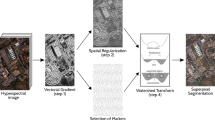
The superpixel adaptive segmentation map (SPASM) algorithm is a superpixel segmentation algorithm. By the word “adaptive” we mean in the final segmentation map of input image, (1) the distribution (density) of superpixels is adaptive and (2) the size of superpixel is adaptive. As illustrated in Fig. 1, at the beginning of the SPASM algorithm, we initialize a regular (uniformly distributed) 2-dimensional grid of nodes, in the Euclidean plane defined by input image. Each node is the cluster center of a superpixel. Then we apply the online version of the Kohonen’s self-organizing map [15] (SOM) algorithm on the grid of nodes, in order to deploy the nodes according to the distribution of some desired attribute of input image, such as edges, textures, and depths. Once the online SOM learning is finished, a projection procedure is carried out where each node searches its closest non-edge point (pixel) with spiral search under special conditions, and then all attributes (coordinates, color, density value, etc.) of nodes are copied from their closest points. After that, the batch version of SOM algorithm, using a new designed distance measure which considers the specific input image attribute, is applied to the deformed/adapted grid of nodes, for the final segmentation map. Meanwhile, a Voronoi color image is generated by filling the color of each point with the color of its cluster center node.

Now we give detailed explanations about how the online SOM and the batch SOM work in the SPASM algorithm. SOM deals with visual patterns that move and adapt themselves to brute distributed data in space. It is often presented as a non supervised learning procedure performing a non parametric regression that reflects topological information of the input data. The standard SOM works on a non directed graph $G=(V, E)$ of topological grid, where each vertex (node) $v\in V$ has a synaptic weight vector $w_v =(x,y)\in \mathfrak {R}^2$. Here a node corresponds to a superpixel cluster center.

When the online SOM is applied to the SPASM algorithm, the training procedure consists of a fixed amount of $t_{max}$ iterations that are applied to the grid, with the node coordinates being initialized according to a regular topology. At each iteration t, firstly, a point (pixel) $p(t)\in \mathfrak {R}^2$ is randomly extracted from the image (extraction step) according to a roulette wheel mechanism depending on different density values of different pixels. Then, a competition between nodes against the input point p(t) is performed to select the winner node $n^*$ (competition step). Usually, it is the closest node to p(t) in the Euclidean plane. Finally, the learning law (triggering step)

$$\begin{aligned} w_n(t+1)=w_n(t)+\alpha (t)\times h_t(n^*,n)\times (p(t)-w_n(t)) \end{aligned}$$

(1)

is applied to $n^*$ and to the nodes within a finite neighborhood of $n^*$ with radius $\sigma _t$, in the sense of the topological distance $d_G$, using learning rate $\alpha (t)$ and function profile $h_t$. The function profile is given by a Gaussian form of

$$\begin{aligned} h_t(n^*,n)=exp(- \frac{d_G^2(n^*,n)}{\sigma _t^2}) \end{aligned}$$

(2)

Here, the learning rate $\alpha (t)$ and radius $\sigma _t$ are geometric decreasing functions of time. To perform a decreasing run within $t_{max}$ iterations, at each iteration t, the coefficients $\alpha (t)$ and $\sigma _t$ are multiplied by $exp(ln(\chi _{final}/\chi _{init})/t_{max})$ with respectively $\chi = \alpha$ and $\chi =\sigma$, $\chi _{init}$ and $\chi _{final}$ being respectively the values at the starting and the final iteration.

The incremental-learning online SOM is a stochastic algorithm which updates the values of weight vectors sequentially iteration by iteration. Its deterministic batch equivalent, the batch SOM, uses all the data at each step. Instead of only one point being randomly extracted, at each iteration t of batch SOM, all points of the input image are taken into account, each of them being associated to its closest node according to a combined distance measure. The distance measure consists of spatial proximity, color, and density value, as

$$\begin{aligned} {\begin{matrix} D(i,j)=\tau _s \Vert \varvec{x}_{spa}(i) - \varvec{x}_{spa}(j) \Vert + \tau _c \Vert \varvec{x}_{rgb}(i) - \varvec{x}_{rgb}(j) \Vert + \tau _d \Vert \varvec{x}_{den}(i) - \varvec{x}_{den}(j) \Vert \end{matrix}} \end{aligned}$$

(3)

where $\varvec{x}_{spa}$, $\varvec{x}_{rgb}$, and $\varvec{x}_{den}$ respectively correspond to 2D coordinate, 3D RGB color, and 1D density value, while $\tau _s$, $\tau _c$, and $\tau _d$ are their corresponding normalized coefficients. Note that this distance measure is an extension to the SLIC distance measure [1] with a third component of density. Therefore our superpixel segmentation algorithm should have the same ability of boundary adherence as the SLIC algorithm [1], meanwhile considering the peculiar density attribute for distance computation between points and cluster centers. At the triggering step of the batch SOM, nodes update the three attributes according to the learning law of

$$\begin{aligned} w_n(t+1)=w_n(t)+\alpha (t)\times h_t(n^*,n)\times (\frac{\sum _{i=1}^{k} p_{n(i)}(t)}{k} -w_n(t)) \end{aligned}$$

(4)

where k is the number of points $p_{n(i)}$ which are associated to node $w_n$. Note that the batch SOM is a generalization of the k-means algorithm with topological relationship among cluster centers. If we set $\alpha _{init}=\alpha _{final}=1$ and $\sigma _{init}=\sigma _{final}=0$, then the batch SOM degenerates into the k-means algorithm.

3 Parallel Cellular Matrix Model

In order to implement the parallel level, on which parallel SPASM algorithm will take place, we design a massively parallel cellular matrix model which partitions data. The input image (low level), along with the two-dimensional grid (base level) of superpixel cluster centers, which is deployed in the Euclidean plane defined by the input image, are partitioned into uniformly sized cells with rigid topologies. The topology of the cellular matrix (dual level) and the grid could be quad, rhombus, and hexagonal, as shown in Fig. 2. The role of the cellular matrix is to memorize data in a distributed fashion and authorize massively parallel operations. Suppose the input image is with size $W\times H$, and suppose both the grid of cluster centers and the cellular matrix are with quad topology. Then the initial grid of cluster centers is with size $W/Rg\times H/Rg$, where the parameter Rg is the distance (measured by pixel) between two neighboring nodes on the base level. The cellular matrix is with size $W/2Rc\times H/2Rc$, where the parameter Rc is the radius (measured by pixel) of cell on the dual level. Hence, Rc controls the degree of parallelism, and we assume a linear association from input data to memory as the problem size increases. Each uniformly sized cell in the cellular matrix is a basic training unit and will be handled by one parallel processing unit, here a thread in our GPU implementation, during the iterations of the SOM processing. This is the level on which massive parallelism takes place. Since the cellular matrix division is proportional to the input image size, and the processing units correspond one-to-one with the cells respectively, then, the processing units are also in linear relationship to the input image size.

Fig. 2.

Parallel cellular matrix model with different topologies. Rows: (upper) quad; (middle) rhombus; (lower) hexagonal. Columns: (a) traversal sequence - the black nodes denote the anticlockwise spiral traversal sequence on the low level or the base level while the red nodes denote the clockwise spiral traversal sequence on the dual level; (b) base level grid; (c) dual level cellular matrix; (d) zoom in of the dual level cellular matrix (Color figure online).

Under the cellular matrix model, each cell, which is assigned to one parallel processing unit, performs in parallel the iterative online SOM training. At the beginning of every iteration, a particular cell activation formula

$$\begin{aligned} pra_i=\frac{S_i}{\max \{S_1, S_2, \ldots , S_{num} \}}\times \delta \end{aligned}$$

(5)

is employed to decide if the cell will execute or not at the considered iteration. Here $pra_i$ is the probability that the cell i will be activated, $S_i$ is the sum of density values of all the pixels in the cell i, and num is the number of cells. The empirical preset parameter $\delta$ is used to adjust the degree of activity of cells, in order to avoid too many memory access conflicts. Equation 5 allows many data points, extracted at the first step of the online SOM at a given parallel iteration, to reflect the input data density distribution. As a result, the higher density value a cell contains, the higher is the probability this cell to be activated to carry out the SOM execution at each parallel iteration. In this way, the cell activation depends on a random choice based on the input data density distribution. In the parallel extraction step of the online SOM, each activated cell performs a local roulette wheel mechanism in the cell itself, in order to get the extracted pixel.

In the closet node/point finding procedure of the SPASM algorithm, each parallel processing unit carries out the spiral search as stated in [16], based on the cellular matrix model. In Fig. 2(a) are illustrated the traversal sequences of spiral searches at different levels based on cellular matrices with different topologies. Note that a single spiral search process takes O(1) computation time on the average for a bounded distribution according to the instance size [4]. Then, one of the main interests of the cellular matrix model is to allow the execution of approximately N spiral searches in parallel, where N $(= W \times H$) is the input size, and thus transforming an O(N) sequential search algorithm into a parallel algorithm with theoretical constant time O(1) in the average case for bounded distributions. This is what we call “massive parallelism”, the theoretical possibility to reduce computation time by factor N, when solving a Euclidean NP-hard optimization problem.

4 Experimental Results

We use GPU to implement the cellular matrix model for parallel SPASM algorithm. With the compute unified device architecture (CUDA) programming interface, we employ GPU threads as processing units, to handle cells in parallel, and use CPU (host code) for flow control and the entire thread synchronization. The main CUDA algorithm is shown in Algorithm 1, where underscored lines are implemented with CUDA kernel functions that will be executed by GPU threads in parallel.

In line 4, of Algorithm 1, cells’ activation probabilities are computed according to the activation formula of Eq. 5. The three steps (extraction step, competition step, and triggering step) of the online SOM are implemented in the kernel function of line 9. In this kernel function, after the cell locates its position in the cellular matrix by threadId and blockId [17], it will firstly check if itself being activated or not. Only if being activated will the cell continue to perform local roulette wheel point extraction. Otherwise the cell finishes at this iteration. In the parallel batch SOM kernel function of line 15, there is no activation check and random extraction procedures. All cells perform spiral searches for all the points lie in them.

After the segmentation process is finished, a Voronoi color image is generated by filling the color of each pixel with the color of its cluster center node, through the kernel function of line 18.

Each cell has data structures where are deposited information of the number and indexes of the nodes this cell contains. This information may change during each iteration, but it appears that, during the online SOM learning phase, it can be sufficient to make the refreshing based on a refresh rate coefficient called CellRefreshRate. All the nodes’ locations are stored in GPU global memory which is accessible to all the threads. Like other multi-threaded applications, different threads may try to modify a same node’s location at the same time, which causes race conditions. In order to guarantee a coherent memory update in this situation, we use the CUDA atomic function which performs a read-modify-write atomic operation without interference from any other threads [17, 18].

In our experiments, the online SOM parameters are fixed as $(\alpha _{init}, \alpha _{final}, \sigma _{init}, \sigma _{final}, t_{max}) = (1,0.01,20,0.5,100)$, while the batch SOM parameters are fixed as $(\alpha _{init}, \alpha _{final}, \sigma _{init}, \sigma _{final}, t_{max}) = (1,0.1,1.5,0.5,5)$.

Fig. 3.

Results obtained with image gradient (upper row) and disparity (lower row): upper (a) image gradient, lower (a) disparity map, (b) online SOM training result, (c) superpixel segments, (d) Voronoi image. The Teddy image from [19] is used.

We utilize two kinds of image attributes, as the density distributions which the online SOM is trained with. The first attribute is image gradient. In this case, at the beginning of the algorithm, we initialize input density map with color gradient values. Here we compute gradient through Sobel operator, which gives us a fast approximation of the edge distribution of input image, as shown in Fig. 3 upper (a). The activation possibility of each cell is then computed according to Eq. 5, where $S_i$ is now the sum of gradient values of all the pixels inside the cell i. However in the point extraction step, we transfer the gradient g of each pixel into $1/(1+g^2)$ for the local roulette wheel extraction. The reason is to make edge points (with high gradient values) less likely to be extracted. Therefore, the image gradient distribution is preserved on the cell level, meanwhile inside activated cells, situations of nodes being moved onto edge points are reduced. In Fig. 3 upper (b) of the adapted grid after the online SOM learning phase, areas with high image gradient present high density of nodes, with respect to the topology of the scene. Then these areas generate more superpixels after the batch SOM phase, as shown in Fig. 3 upper (c), and hence in the Voronoi superpixel image they have higher resolution and their details are more finely represented, as the example in the red box of Fig. 3 upper (d).

The second image attribute we have tested as the density distribution is the disparity map. Figure 3 lower (a) gives an example of the disparity map for input image, where brighter regions are nearer to the camera view point and they have higher disparity values. As expected, these regions demonstrate higher density of superpixels in the segmentation result of Fig. 3 lower (c) and accordingly their details are better represented in the Voronoi image, such as the example in the yellow box of Fig. 3 lower (d). Our algorithm’s ability of generating adaptive superpixels with respect to user-specified density distribution can be proved through these two tests and the comparison of their results.

Fig. 4.

Comparison between SPASM (upper row) and SLIC (lower row). Upper (a) is input image and lower (a) is image gradient. The image size is $584 \times 388$. From (b1) to (b3), for both algorithms, the number of initial cluster centers is 2266, 566, 252. The Hydrangea image from [20] is used.

5 Comparison with SLIC Superpixel Algorithm

We compare the SPASM algorithm with the state-of-the-art SLIC superpixel algorithm [1] using publicly available source code¹. The image gradient, as shown in Fig. 4 lower (a), is used as density map. For SPASM, we respectively set $R_g$ to 10, 20, 30, which makes the initial superpixel size (with quad topology) is 100, 400, 900 and the number of initial cluster centers is N / 100, N / 400, N / 900 (N being the input image size). For SLIC we set the initial superpixel size accordingly, in order to make the two algorithms work with same number of initial cluster centers. As shown in the upper row of Fig. 4, in all cases the SPASM algorithm produces a high density of fine superpixels in the edge-dense area (the flower clump) while the background is covered with relatively coarse superpixels sparsely. On the other hand as illustrated in the lower row of Fig. 4, no matter how the initial superpixel size is set, the SLIC algorithm will always generate uniformly distributed segments. This is because the SLIC algorithm is a tailored k-means approach with no function of distribution learning like the SPASM algorithm. Therefore, the superpixel resolution of SLIC correlates with the number of initial cluster centers, while SPASM has the tendency of better matching the finer-resolution regions that are selected by the density map attribute, meanwhile obtaining finer segmentation results in such regions, regardless of the number of initial cluster centers. This property of the SPASM algorithm could be employed for many computer vision tasks, which usually need to treat different areas of input image differently according to some underlying attribute distribution, such as edges or textures.

Fig. 5.

(a) Comparison between SPASM and SLIC with different input sizes and different initial superpixel sizes. (b) Running time results of CPU SLIC (cSLIC), GPU SLIC (gSLIC), CPU SPASM (cSPASM), and GPU SPASM (gSPASM), with different input sizes. The Cones image from [19] is used. Experiment platform consists of an Intel Core 2 Duo CPU E8400 processor (only one core used) and a Nvidia GeForce GTX 570 Fermi graphics card endowed with 480 CUDA cores.

To provide a quantification of segmentation quality, we evaluate the results of these two algorithms according to the standard mean color distortion (MCD) as defined in

$$\begin{aligned} MCD=\frac{1}{N}{\sum _{i=1}^{N} (\Vert \varvec{x}_{rgb}(i) - \varvec{\bar{x}}_{rgb}(center(i)) \Vert )} \end{aligned}$$

(6)

where N is the input image size, $\varvec{x}_{rgb}(i)$ is the ground truth 3D RGB color of the $i^{th}$ pixel, and $\varvec{\bar{x}}_{rgb}(center(i))$ is the color of the $i^{th}$ pixel’s cluster center. We test input images of seven different sizes ($360 \times 300$, $450 \times 375$, $640 \times 480$, $720 \times 600$, $1080 \times 900$, $1440 \times 1200$, $1800 \times 1500$) and set different initial superpixel sizes ($20 \times 20$, $30 \times 30$, $40 \times 40$). For a good adherence to image boundaries, the distance parameters of SPASM are fixed as $(\tau _{spa}, \tau _{rgb}, \tau _{den}) = (1/2{Rg}^2,1/3,1/100)$ and the distance parameter (m parameter in [1]) of SLIC is set to 20. The iteration number of SLIC is set to the default of 10. Experimental results are depicted in Fig. 5(a). Note that all results are the mean values of 10 runs. Results from SPASM have smaller MCD values in all the tested cases when compared with results from SLIC. Also the MCD of SPASM results is steadier either with respect to different input image sizes, or with respect to different initial superpixel sizes. This shows the “adaptive” ability of our proposed SPASM which produces similar results regardless of the number of initial cluster centers and the input image size.

In order to make a running time comparison, we test four versions, the SLIC CPU implementation (cSLIC) with the raw public source code, the SLIC GPU implementation (gSLIC) in [21] with the raw public source code², the SPASM CPU implementation (cSPASM) which is a sequential simulation of parallel SPASM algorithm, and the SPASM GPU implementation (gSPASM). The initial superpixel size is set to $20 \times 20$ for the four versions. The running time results are reported in Fig. 5(b). For small size images ($360 \times 300$ and $450 \times 375$), the running time of cSLIC, gSLIC, and gSPASM is similar. For other larger size images, gSPASM runs faster than all the other three versions, especially for the largest image. cSPASM runs much slower than others for all images. This is because the sequential simulation of the iterative online SOM learning is time consuming. gSLIC runs slower than cSLIC for all images. This is because the gSLIC library we use is specifically optimized for high-end GPU cards, with a lot of shared memory employment, while the platform we use is a relatively out-dated GPU card. In spite of the absolute running time results of different implementations on different platforms (CPU and GPU), we think what is more important is that the running time of our GPU implementation of the parallel SPASM algorithm increases in a linear way with a very weak increasing coefficient. The results verify the “massive parallelism” characteristic of our proposed cellular matrix model, in a practical way by GPU implementation. We consider that such results are encouraging when solving very large scale problems.

6 Conclusion

The proposed SPASM algorithm extends the state-of-the-art SLIC superpixel algorithm, using our adaptive meshing tool to add compression abilities, with respect to the density distribution of image attributes while preserving the topological relationship of cluster centers. Experimental results support these merits, and they have better quality in the light of mean color distortion, when compared with the results of SLIC. This is attributed to (1) the “adaptive” ability of SPASM and (2) the true k-means clustering it employs by the efficient parallel spiral search under the cellular matrix model, rather than the restrained k-means that SLIC uses. The running time of our GPU implementation increases in a linear way with a very weak increasing coefficient according to the input size, which is encouraging to solve very large scale problems, under the proposed parallel cellular matrix model.

Future work should include comparisons with other state-of-the-art superpixel methods, by general benchmarks and standard quality evaluation criterions. Another important following work is to use the parallel SPASM algorithm based on the cellular matrix model, as a preprocessing tool and make possible fast and accurate visual correspondence applications such as stereo matching, optical flow, and scene flow.