Picture Array Generation Using Pure 2D Context-Free Grammar Rules

Abstract

Pure two-dimensional context-free grammar (P2DCFG) is a simple but effective non-isometric 2D grammar model to generate picture arrays. This 2D grammar uses only one kind of symbol as in a pure string grammar and rewrites in parallel all the symbols in a column or row by a set of context-free type rules. P2DCFG and a variant called (l / u)P2DCFG, which was recently introduced motivated by the “leftmost” rewriting mode in string context-free grammars, have been investigated for different properties. In this paper we introduce another variant of P2DCFG that corresponds to “rightmost” rewriting in string context-free grammars. The resulting grammar is called (r / d)P2DCFG and rewrites in parallel all the symbols only in the rightmost column or the lowermost row of a picture array by a set of context-free type rules. Unlike the case of string context-free grammars, the picture language families of P2DCFG and the two variants (l / u)P2DCFG and (r / d)P2DCFG are mutually incomparable, although they are not disjoint. We also examine the effect of regulating the rewriting in a (r / d)P2DCFG by suitably adapting two well-known control mechanisms in string grammars, namely, control words and matrix control.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

A variety of two-dimensional (2D) picture array generating grammars [5, 9–11, 18, 19] have been introduced and investigated by researchers, motivated by problems in different areas such as pattern generation and recognition, image description and analysis and others. These 2D grammars have been mainly developed based on the concepts and techniques of the well-investigated string grammar theory. They are basically of two varieties, namely, isometric array grammars in which geometric shape of the re-written portion of the array is preserved while non-isometric array grammars can alter the geometric shape. Here we consider a 2D picture grammar of the latter variety, called a pure 2D context-free grammar (P2DCFG) introduced in [17]. This 2D grammar represents a simple yet expressive non-isometric language generator of rectangular picture arrays, involving only terminal symbols as in a pure string grammar [7] and using tables of context-free (CF) type rules. All the symbols in a column or a row of a rectangular array are re-written in parallel by CF type rules in a P2DCFG and in order to maintain the rectangular form of the array, all the symbols rewritten are replaced by strings of equal length. A P2DCFG allows rewriting any column or any row of a picture array by the rules of an applicable column rule table or row rule table respectively. In [1, 2, 16], further properties of this 2D grammar model are investigated.

Motivated by the notion of leftmost derivation [14] in a context-free string grammar in which only leftmost nonterminal in a sentential form of a derivation is rewritten, a variant of P2DCFG, referred to as (l / u)P2DCFG was introduced in [6]. This variant considers a “leftmost rewriting mode” in terms of P2DCFG in the sense that only the leftmost column or the uppermost row of a rectangular picture array is rewritten in a derivation step. In the case of context-free string grammars, the notion of a rightmost derivation is also known [14] in which only the rightmost nonterminal in a sentential form of a derivation is rewritten. We recall that for an ordinary derivation of a terminal word in a context-free string grammar, there is an equivalent leftmost as well as rightmost derivation of the word. On the other hand, it has been shown in [6] that the picture language classes of P2DCFG (which correspond to “ordinary derivation mode”) and (l / u)P2DCFG (which correspond to “leftmost derivation mode”) are incomparable. Here we investigate another variant of P2DCFG by considering a “rightmost rewriting mode” in terms of P2DCFG in the sense that only the rightmost column or the lowermost row of a rectangular picture array is rewritten in a derivation step, with all the symbols being rewritten by “equal length” rules. We denote the resulting class of 2D grammars by (r / d)P2DCFG and the corresponding language class by (r / d)P2DCFL.

We show that this variant of (r / d)P2DCFL is also incomparable with both the picture language classes of P2DCFG and (l / u)P2DCFG. The effect of regulating the picture generation by controlling the application of rules with a regular control set on the labels of the tables of rules has been studied in [1, 2, 6, 16, 17] for the classes of P2DCFL and (l / u)P2DCFL. Besides examining the effect of this kind of a control on (r / d)P2DCFG, we also consider matrix type of control on the tables of rules for all the three classes, namely, P2DCFL and the two variants, (l / u)P2DCFL and (r / d)P2DCFL.

2 Preliminaries

For notions related to formal language theory we refer to [13, 14] and for array grammars and two-dimensional languages we refer to [5].

Given a finite alphabet $\varSigma$, a word or a string w is a sequence of symbols from $\varSigma$. The set of all words over $\varSigma$, including the empty word $\lambda$ with no symbols, is denoted by $\varSigma ^{*}$. The length of a word w is denoted by |w|. For any word $w = a_1a_2 \ldots a_n$, we denote by ${}^tw$, the word $w = a_1a_2 \ldots a_n \quad (n \ge 1)$ written vertically. For example, if $w = acbb$ over $\{a,b,c\}$, then ${}^tw =$ $\begin{array}{c} a\\ c\\ b\\ b \end{array}$. A two-dimensional $m \times n$ array (also called a picture array or a picture) p over an alphabet $\varSigma$ is a rectangular array with m rows and n columns and is of the form

$$\begin{aligned} p = \begin{array}{ccc} p(1,1) &{} \cdots &{} p(1,n) \\ \vdots &{} \ddots &{} \vdots \\ p(m,1) &{} \cdots &{} p(m,n) \\ \end{array} \end{aligned}$$

where each pixel $p(i,j) \in \varSigma , 1\le i \le m, \, 1 \le j \le n$. The uppermost row of p is considered as the first row and the leftmost column as the first column of p. Likewise, The lowermost row of p is the last row and the rightmost column, the last column of p. We denote the number of rows and the number of columns of p, respectively, by $|p|_{row}$ and $|p|_{col}$ and call the pair $(|p|_{row},|p|_{col})$ as the size of p. The set of all rectangular arrays over $\varSigma$ is denoted by $\varSigma ^{**}$, which includes the empty array $\lambda$. $\varSigma ^{++} = \varSigma ^{**}-\{\lambda \}$. A picture language is a subset of $\varSigma ^{**}$.

We now recall a pure 2D context-free grammar introduced in [16, 17].

Definition 1

A pure 2D context-free grammar (P2DCFG) is a 4-tuple

$$\begin{aligned}G = (\varSigma , P_1, P_2, \varGamma )\end{aligned}$$

where

• (i) $\varSigma$ is a finite alphabet of symbols;

• (ii) $P_1$ is a finite set of column rule tables $c_i, \, 1 \le i \le m$, for some $m \ge 1$, where each $c_i$ is a finite set of context-free rules of the form $a \rightarrow u, a \in \varSigma , u \in \varSigma ^*$ having the property that for any two rules $a \rightarrow u, b \rightarrow v$ in $c_i$, we have $|u| = |v|$ i.e. the words u and v have equal length;

• (iii) $P_2$ is a finite set of row rule tables $r_j, \, 1 \le j \le n$, for some $n \ge 1$, where each $r_j$ is a finite set of rules of the form $c \rightarrow {}^tx, c \in \varSigma , x \in \varSigma ^*$ such that for any two rules $c \rightarrow {}^tx, d \rightarrow {}^ty$ in $r_j$, we have $|x| = |y|$;

• (iv) $\varGamma \subseteq \varSigma ^{**} - \{ \lambda \}$ is a finite set of axiom arrays.

A derivation in a P2DCFG G is defined as follows: Let $p,q \in \varSigma ^{**}$. A picture q is derived in G from a picture p, denoted by $p \Rightarrow q$, either (i) by rewriting in parallel all the symbols in a column of p, each symbol by a rule in some column rule table or (ii) rewriting in parallel all the symbols in a row of p, each symbol by a rule in some row rule table. All the rules used to rewrite a column (or row) are taken from the same table.

The picture language generated by G is the set of picture arrays $L(G) = \{M \in \varSigma ^{**} |\ M_0 \Rightarrow ^* M$ for some $M_0 \in \varGamma \}$. The family of picture languages generated by P2DCFGs is denoted by P2DCFL.

Example 1

Consider the P2DCFG $G_1 = (\varSigma , P_1, P_2, \{M_0\})$ where $\varSigma = \{a,b,d \}$, $P_1 = \{c \}, P_2 = \{r \}$, where $c = \{a \rightarrow bab, d \rightarrow ada, e \rightarrow aea\}$, $r = \left\{ d \rightarrow \begin{array}{c} d\\ a \end{array}, a \rightarrow \begin{array}{c} a\\ b \end{array} \right\}$, and $M_{0} = \begin{array}{ccc} a&{}d&{}a \\ b&{}a&{}b \\ a&{}e&{}a \end{array}$.

$G_1$ generates a picture language $L_1$ consisting of picture arrays p of size $(m,2n+1)$, $m \ge 3$, $n \ge 1$ with $p(1,j) = p(1,j+n+1) = p(m,j) = p(m,j+n+1) = a$, for $1 \le j \le n$; $p(1,n+1) = d$; $p(m,n+1) = e$; $p(i,n+1) = a,$ for $2 \le i \le m-1$; $p(i,j) = b$, otherwise. We note that a derivation in $G_1$, starting from the axiom array $M_0$, generates a picture array of the form

$$\begin{aligned}\begin{array}{ccccccc} a&{}\cdots &{}a&{}d&{}a&{}\cdots &{}a \\ b&{}\cdots &{}b&{}a&{}b&{}\cdots &{}b \\ &{}\cdots &{}&{}&{}&{}\cdots &{} \\ &{}\cdots &{}&{}&{}&{}\cdots &{} \\ b&{}\cdots &{}b&{}a&{}b&{}\cdots &{}b \\ a&{}\cdots &{}a&{}e&{}a&{}\cdots &{}a \end{array}\end{aligned}$$

since the column rule table is applicable to only the “middle” column ${}^tda \cdots ae$, rewriting in parallel all the symbols d and a in that column, thereby adding the symbol a to the left and right of d as well as e, while adding the symbol b to the left and right of every a in that column. Likewise, the row rule table r is applicable to only the uppermost row and adds a row of the form $b \cdots bab \cdots b$ below it. Also note that the application of the column rule table c can take place independent of the row rule table r and hence the number of rows and the number of columns in the generated picture arrays of $L_1$ need not be related by any proportion. On the otherhand, due to the nature of rules in the column table c, every generated picture array has an equal number of columns to the left and right of the middle column ${}^t(da \ldots ae)$. A member of $L_1$ is shown in Fig. 1(a) and on interpreting the symbol b as blank, the corresponding picture representing the letter I is shown in Fig. 1(b).

Fig. 1.

(a) (on the left) A picture array in the language $L_1$ (b) (on the right) The interpreted picture representing letter I.

We now recall (l / u) mode of derivation in a P2DCFG introduced and investigated in [6].

Definition 2

Let $G = (\varSigma , P_1, P_2, \varGamma )$ be a P2DCFG with the components as in Definition 1. A picture array $M_2$ is derived from $M_1$ in G with (l / u) mode of derivation, denoted by $M_1 \Rightarrow _{(l/u)} M_2$, by rewriting all the symbols and only these symbols, either in the leftmost column or in the uppermost row of $M_1$ using respectively, the column rule tables or the row rule tables. All the rules used to rewrite a column (or row) are taken from the same table.

The picture language generated is defined as in the case of a P2DCFG but using $\Rightarrow _{(l/u)}$ derivations. The family of picture languages generated by P2DCFGs under $\Rightarrow _{(l/u)}$ derivations is denoted by (l / u)P2DCFL. For convenience, we write (l / u)P2DCFG to refer to P2DCFG with $\Rightarrow _{(l/u)}$ derivations.

We illustrate with an example.

Example 2

Consider an (l / u)P2DCFG $G_2 = (\varSigma , P_1, P_2, \{M_{0}\})$ where $\varSigma = \{a,b\}$, $P_1 = \{c\}$, $P_2 = \{r\}$ with $c = \{a \rightarrow ab, d \rightarrow da\}$, $r = \left\{ a \rightarrow \begin{array}{c} a\\ a \end{array}, b \rightarrow \begin{array}{c} b\\ b \end{array} \right\}$, and $M_{0} = \begin{array}{cc} a&{}b \\ d&{}a \end{array}$.

$G_2$ generates a picture language $L_2$ consisting of arrays p of size (m, n), $m \ge 2$, $n \ge 2$ with $p(m,1) = d$; $p(m,j) = a$, for $2 \le j \le n$; $p(i,1) = a$, for $1\le i \le m-1$; $p(i,j) = b$, otherwise. A member of $L_2$ is shown in Fig. 2. A member of $L_2$ is shown in Fig. 2(a) and on interpreting the symbol b as blank, the corresponding picture representing the letter L is shown in Fig. 2(b).

Fig. 2.

(a) (on the left) A picture array in the language $L_2$ (b) (on the right) The interpreted picture representing letter L.

3 Pure 2D Context-Free Grammar with (r / d) Mode of Derivations

We now introduce another variant of a P2DCFG. The leftmost and rightmost derivation modes in a context-free grammar (CFG) in string language theory, are well-known [13, 14], especially in the context of the study of parsers. It is also known that these derivation modes are equivalent to the “ordinary” derivations in a CFG in the sense of generating the same language class. Motivated to consider a corresponding notion of “leftmost kind” of derivation in pure 2D context-free grammars, the (l / u)P2DCFG with an (l / u) mode of derivation was introduced in [6]. Here we consider the dual idea of rewriting the rightmost column of a picture array by a column rule table or the lowermost row by a row rule table. This corresponds to the “rightmost kind” of derivation mode in a string CFG. The interesting aspect is that this results in a picture language family which neither contains nor is contained in P2DCFL or (l / u)P2DCFL.

Definition 3

Let $G = (\varSigma , P_1, P_2, \varGamma )$ be a P2DCFG with the components as in Definition 1. An (r / d) mode of derivation of a picture array $M_2$ from $M_1$ in G, denoted by $\Rightarrow _{(r/d)}$, is a derivation in G such that only the rightmost column or the lowermost row of $M_1$ is rewritten using respectively, the column rule tables or the row rule tables, to yield $M_2$. The generated picture language is defined as in the case of a P2DCFG but with $\Rightarrow _{(r/d)}$ derivations. The family of picture languages generated by P2DCFGs under $\Rightarrow _{(r/d)}$ derivations is denoted by (r / d)P2DCFL. For convenience, we write (r / d)P2DCFG to refer to P2DCFG with $\Rightarrow _{(r/d)}$ derivations.

We illustrate with an example.

Fig. 3.

A picture array in the language $L_3$

Example 3

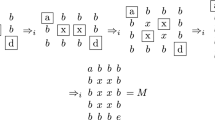
Consider an (r / d)P2DCFG $G_3 = (\varSigma , P_1, P_2, \{M_{0}\})$ where $\varSigma = \{a,b\}$, $P_1 = \{c\}$, $P_2 = \{r\}$ with $c = \{a \rightarrow ba, b \rightarrow ab\}$, $r = \left\{ a \rightarrow \begin{array}{c} b\\ a \end{array}, b \rightarrow \begin{array}{c} a\\ b \end{array} \right\}$, and $M_{0} = \begin{array}{cc} a&{}a \\ a&{}b \end{array}$.

$G_3$ generates a picture language $L_3$ consisting of arrays p of size (m, n), $m \ge 2$, $n \ge 2$ with $p(1,1) = a$; $p(m,n) = b$; $p(m,j) = a$, for $1 \le j \le n-1$; $p(i,n) = a$, for $1 \le i \le m-1$; $p(i,j) = b$, otherwise. A member of $L_3$ is shown in Fig. 3. A sample derivation in (r / d)P2DCFG $G_3$ starting from the axiom array $M_{0}$ and using the tables c, r, c, c in this order is shown in Fig. 4. The application of the column rule table c rewrites all symbols in the rightmost column in parallel and likewise, the application of the row rule table r rewrites all symbols in the lowermost row. We note that the application of a column table or a row table is independent of each other as in a P2DCFG and so cannot maintain any proportion between the number of columns and the number of rows in any generated picture array.

Fig. 4.

A sample derivation under (r / d) mode in Example 3

We now compare the generative power of (r / d)P2DCFL with (l / u)P2DCFL and P2DCFL.

Theorem 1

Each pair of the three families of P2DCFL, (l / u)P2DCFL and (r / d)P2DCFL is incomparable but not disjoint, when the alphabet contains at least two symbols. All the three families coincide if we restrict to only a unary alphabet.

Proof

The non-trivial picture language $L_{RECT}$ of all rectangular picture arrays over $\{a,b\}$ belongs to all the three families of P2DCFL, (l / u)P2DCFL and (r / d)P2DCFL. In fact the corresponding P2DCFG needs to have only two tables

$$\begin{aligned}c = \{a \rightarrow aa, a \rightarrow ab, b \rightarrow ba, b \rightarrow bb\}, r = \left\{ a \rightarrow \begin{array}{c} a\\ a \end{array}, a \rightarrow \begin{array}{c} a\\ b \end{array}, b \rightarrow \begin{array}{c} b\\ a \end{array}, b \rightarrow \begin{array}{c} b\\ b \end{array}\right\} \end{aligned}$$

and axiom pictures a, b, for all the three modes of derivations in the P2DCFG. This shows that the three families are mutually not disjoint.

The incomparability of the families P2DCFL and (l / u)P2DCFL has been established in [6]. The picture language $L_3$ in Example 3 which belongs to (r / d)P2DCFL cannot be generated by any P2DCFG since every column in the picture arrays of $L_3$ involves the two symbols a, b only and so in order to generate the picture arrays of $L_3$ starting from an axiom array, we have to specify column rules for both a, b. In the (r / d) mode of derivation, the rightmost column will require a column rule that will rewrite b into $a \cdots ab$ and a into $b \cdots ba$. But then the table with these rules can be applied to any other column in a P2DCFG, resulting in picture arrays not in the language $L_3$.

On the other hand the picture language $L_1$ in Example 1 belongs to P2DCFL but it cannot be generated by any (r / d)P2DCFG as there is an unique middle column in every picture array of $L_1$ and to the left and right of this middle column there are an equal number of identical columns. Since only the rightmost column can be rewritten in an (r / d)P2DCFG, it is not possible to maintain this feature of “equal number of identical columns” if rightmost column rewriting is done. We also note that the picture generated in any intermediate step also belongs to the language which prevents the use of any other symbol other than a and b. This proves the incomparability of the families P2DCFL and (r / d)P2DCFL.

Again, the picture language $L_3$ in Example 3, which belongs to $(r/d)P2DCFL$, cannot be generated by any (l / u)P2DCFG, since the leftmost column of every picture array in $L_3$ has the symbol a in the first row as well as the last row. The former will require a rule of the form $a \rightarrow ab \cdots b$ while the latter will require a rule of the form $a \rightarrow a \cdots ab$. But then the presence of these two rules in a column table gives a non-deterministic choice for rewriting a in the leftmost column in (l / u)mode of derivation, resulting in picture arrays not in the language $L_3$.

On the other hand, consider the picture language $L_3^\prime$ consisting of picture arrays p of size $(m,n),\, m \ge 2,\, n \ge 2$, with $p(1,1) = b$; $p(m,n) = a$; $p(1,j) = a$, for $2 \le j \le n$; $p(i,1) = a$, for $2 \le i \le m$; $p(i,j) = b$, otherwise. $L_3^\prime$ can be generated a (l / u)P2DCFG with axiom array $M_0 = \begin{array}{cc} b&{}a \\ a&{}a \end{array}$ and column table c and row table r given by

$$\begin{aligned}c = \{a \rightarrow ab, b \rightarrow ba\}, r = \left\{ a \rightarrow \begin{array}{c} a\\ b \end{array}, b \rightarrow \begin{array}{c} b\\ a \end{array}\right\} \end{aligned}$$

A member of $L_3^\prime$ is shown in Fig. 5. It can be seen that $L_3^\prime$ cannot be generated by any (r / d)P2DCFG. This proves the incomparability of the families (l / u)P2DCFL and (r / d)P2DCFL.

In the case of a unary alphabet with a single symbol, say, a, the column rules and the row rules can use only a and hence rewriting any column (or row) is equivalent to rewriting the leftmost or the rightmost column (or row) of a picture array. This shows that all the three families coincide in this case$.\quad \square$

Fig. 5.

A picture array in the language $L_3^\prime$.

Remark 1

In [2] (Proposition 3.14), the uniform membership problem (ump) for the class of P2DCFG with unary alphabet, namely, “does the picture p belong to the language L(G) generated by the P2DCFG G, given p as well as G as input?”, is shown to be in class P. As a consequence of the fact that in the case of an unary alphabet, rewriting any column (respectively row) of a picture array is equivalent to rewriting the leftmost or the rightmost column (respectively row), this result on ump holds for the classes of (l / u)P2DCFG and (r / d)P2DCFG.

4 Regulating Rewriting in (r / d)P2DCFG with Control Words

Based on the concept of regulating the rewriting in string and array grammars [3, 4, 14, 15] with different control mechanisms, as for example, grammars with control languages and matrix grammars, a P2DCFG with a control language on the labels of the column rule and row rule tables has been introduced in [17] and certain properties have been obtained. Further results on the effect of control have been established in [1, 2, 16]. This study on control language has been extended in [6] to the class (l / u)P2DCFG. Here we obtain corresponding results for the class (r / d)P2DCFG.

A (r / d)P2DCFG with a control language is $G^c = (G,Lab, \mathcal {C})$ where $G = (\varSigma$, $P_1$, $P_2$, $\varGamma )$ is a (r / d)P2DCFG, Lab is a set of labels of the tables of G, with each table in $P_1 \cup P_2$ being assigned a distinct label and $\mathcal {C} \subseteq Lab^*$ is a string language. The words in $Lab^*$ are called control words of G. Derivations $M_1 \Rightarrow _w M_2$ in $G^c$ are done as in G in (r / d) mode except that if $w \in Lab^*$ and $w = l_1l_2 \ldots l_m$, then the tables of rules with labels $l_1$, $l_2$, $\ldots$, and $l_m$ are successively applied starting with the picture array $M_1$ to finally yield the picture array $M_2$, which is collected in the language if $M_1$ is an axiom array. If any of the labels in a control word is such that the corresponding table of rules cannot be applied to the picture array on hand, the derivation is discarded and it does not yield any array. The picture array language generated by $G^c$ consists of all picture arrays obtained from axiom arrays of G with the derivations controlled as described above. We denote the family of picture languages generated by (r / d)P2DCFGs with a regular control language by (R)(r / d)P2DCFL and with a context-free control language by (CF)(l / u)P2DCFG.

Theorem 2

$(r/d)P2DCFL \subset (R)(r/d)P2DCFL \subset (CF)(r/d)P2DCFL$.

Proof

The inclusions follow by noting that a (r / d)P2DCFG is a $(R)(r/d)P2DCFG$ on setting the regular control language as $Lab^*$ where Lab is the set of labels of the tables of the (r / d)P2DCFG and the well-known fact [14] that the class of regular string languages is included in the class of context-free languages.

The proper inclusion in $(r/d)P2DCFL \subset (R)(r/d)P2DCFL$ can be seen by considering a picture language $L_4$ consisting of only square sized arrays p of the language $L_3$ given in the Example 3. This picture language can be generated by the (r / d)P2DCFG $G_3$ in Example 3 with a regular control language $(cr)^*$. But by definition, the application of the column rule and row rule tables are independent in a (r / d)P2DCFG and hence no (r / d)P2DCFG can generate $L_4$ which consists of square sized arrays.

The proper inclusion of (R)(r / d)P2DCFL in (CF)(r / d)P2DCFL can be shown by considering a picture language $L_5$ consisting of picture arrays p as in Example 1 but of sizes $(n+2,2n+1), n \ge 1$. The (CF)(r / d)P2DCFG $G^c = (G_5,Lab, \mathcal {C})$ generates $L_5$, where $G_5 = (\varSigma , P_1, P_2, \{M_{0}\})$, $\varSigma = \{a,b,d \}$, $P_1 = \{c_1, c_2, c_3 \}, P_2 = \{r\}$ with

$$\begin{aligned}c_1 = \{d \rightarrow ad, a \rightarrow ba\}, c_2 = \{d \rightarrow da, a \rightarrow ab\}, c_3 = \{a \rightarrow aa, b \rightarrow bb\},\end{aligned}$$

$$\begin{aligned}r = \left\{ d \rightarrow \begin{array}{c} a\\ d \end{array}, a \rightarrow \begin{array}{c} b\\ a\end{array} \right\} , \end{aligned}$$

$M_{0} = \begin{array}{cc} a&{}d \\ b&{}a \\ a&{}d \end{array}$ and $Lab = \{c_1, c_2, c_3, r \}$ with $c_1, c_2, c_3, r$ themselves being considered as the labels of the corresponding tables. The CF control language is $\mathcal {C} = \{(c_1r)^nc_2c_3^n |\ n \ge 0\}$. The grammar $G_5$ generates the picture arrays of $L_5$, in the (r / d) derivation mode according to the control words of $\mathcal {C}$. Starting from the axiom array $M_{0} = \begin{array}{cc} a&{}d \\ b&{}a \\ a&{}d \end{array}$ the rightmost column of $M_{0}$ is rewritten using the column rule table $c_1$ and this is immediately followed by the row rule table r which rewrites once, all the symbols in the lowermost row. This can be repeated n times (for some $n \ge 0$). Then the column rule table $c_2$ is applied once, followed by the application of the column rule table $c_3$, the same number of times as $c_1$ followed by r was done, thus yielding a picture array in $L_5$. But $L_5$ cannot be generated by any (r / d)P2DCFG with regular control. In fact if a generation of a picture array $p \in L_5$ makes use of a regular control, then there will be no information available on the number of columns generated once the derivation “crosses” the middle column (made of one d as the first symbol and another d as the last symbol with all other symbols in the column being a’s). Hence the columns to the left and right of this middle column cannot be generated in equal number. $\quad \square$

The notion of a control symbol or control character was considered in [2] while dealing with (R)P2DCFG. The idea is that In a (R)P2DCFG, the alphabet may contain some symbols called control symbols [2] which might not be ultimately involved in the picture arrays of the language generated. A picture language $L_d$ was considered in [2] given by $L_d = \{p \in \{a,b\}^{++} |\ \, |p|_{col} = |p|_{row}, p(i,j) = a,\, \text{ for } \, i = j, p(i,j) = b \, \text{ for } \, i \ne j \}$. It was shown in [2], that at least two control symbols are required to generate $L_d$ using (R)P2DCFG. In [6], it was proved that $L_d$ can be generated with a single control character using (R)(l / u)P2DCFG. We show here that an analogous result holds in the case of (R)(r / d)P2DCFG.

Lemma 1

The language $L_d$ can be generated by an (R)(r / d)P2DCFG using a single control character. Also, $L_d$ is not in (r / d)P2DCFL.

Proof

Consider the (R)(r / d)P2DCFG with the (r / d)P2DCFG given by

$(\{a,b,e\}, \{c\}, \{r\},\{\begin{array}{cc} a&{}b \\ b&{}a \end{array} \} )$ where

$$\begin{aligned}c = \{a \rightarrow ea, b \rightarrow bb\},r = \left\{ a \rightarrow \begin{array}{c} b\\ a \end{array}, e \rightarrow \begin{array}{c} a\\ b \end{array}, b \rightarrow \begin{array}{c} b\\ b \end{array} \right\} , \end{aligned}$$

and control language $(cr)^*$ generates $L_d$. The idea in the generation of the picture arrays of $L_d$ is that the symbol e in the alphabet acts as the control character. An application of the column table c produces e to the left of the only a in the last row and when this is followed by the application of the row table r (according to the control word), the symbol e “disappears”, yielding an array in $L_d$. It can be seen that $L_d$ cannot be generated by any (r / d)P2DCFG. $\quad \square$

In [2, p. 1730], a picture language $L_{2d}$ given by $L_{2d} = \{p \in \{a,b\}^{++} |\ \, |p|_{col} = |p|_{row}, p(i,j) = b,\, \text{ for } \, i = j \, \text{ and } \, i = j-1, p(i,j) = a \, \text{ otherwise } \}$ was shown to be generated by a (R)P2DCFG making use of four ([2] mentions three but the grammar actually involves four) control characters. We note that $L_{2d}$ can be generated by a (R)(r / d)P2DCFG $G_{2d}^c$ with three control characters. In fact the grammar is essentially as given in [2] with a slight modification. For completeness we give this grammar here. The P2DCFG in $G_{2d}^c$ is $(\{a,b,b_1,b_2,e\}, P_1, P_2, \{M_{0}\})$, $P_1 = \{c \}, P_2 = \{r_1, r_2\}$ with

$$\begin{aligned}c = \{a \rightarrow aa, b_2 \rightarrow b_2e\}, r_1 = \{a \rightarrow a, b_1 \rightarrow b,b_2 \rightarrow b \},\end{aligned}$$

$$\begin{aligned} r_2 = \left\{ a \rightarrow \begin{array}{c} a\\ a \end{array}, b_1 \rightarrow \begin{array}{c} b\\ a\end{array}, b_2 \rightarrow \begin{array}{c} b \\ b_1\end{array}, e \rightarrow \begin{array}{c} a\\ b_2\end{array} \right\} ,\end{aligned}$$

$M_{0} = \begin{array}{cc} b&{}a \\ b_1&{}b_2 \end{array}$ and the regular control language $(cr_2)^*r_1$. We can likewise construct a (R)(l / u)P2DCFG to generate $L_{2d}$. Also, in [2, p. 1728], it was shown that the family (R)P2DCFL has nonempty intersection with the class LOC [5] of local picture languages whose pictures are defined by means of tiles i.e. square pictures of size (2, 2) and another class of picture languages, which we call here as PL, defined by a class of picture grammars referred to as grammars [2]. This is done in [2] by showing that $L_{2d}$ is in all the three families $P2DCFL, \, LOC$ and PL. As a consequence of these remarks, we have the following Theorem 3.

Theorem 3

All the three families (R)P2DCFL, (R)(l / u)P2DCFL and

(R)(r / d)P2DCFL have non-empty intersection with the picture language families LOC and PL.

5 Matrix Control on P2DCFG

In another type of regulating the use of rules in derivations, known as matrix control, a pre-specified finite sequence of rules is applied constituting a single step of derivation in the grammar [3, 14]. Here we consider this kind of control in P2DCFG and the two variants (l / u)P2DCFG and (r / d)P2DCFG.

Definition 4

A matrix P2DCFG is a 3-tuple $G_m = (G,Lab,M)$ where $G = (\varSigma , P_1, P_2, \varGamma )$ is a P2DCFG, Lab is a set of labels of the tables of G, with each table in $P_1 \cup P_2$ being assigned a distinct label and M is a finite set of sequences, called matrices, of the form $m =[l_1, \cdots , l_n],\, n \ge 1$, where $l_i \in Lab$, for all $1 \le i \le n$.

Derivations in a matrix P2DCFG are defined as in a P2DCFG except that a single derivation step is done by the application of the tables of rules of a matrix m in M, in the order in which the labels of the tables are given in m. The family of picture languages generated by matrix P2DCFG is denoted by MP2DCFL.

We illustrate with an example.

Example 4

Consider the picture language $L_1^\prime$ consisting of arrays belonging to the picture language $L_1$ in Example 1 but of size $(n+2, 2n+1), \, n \ge 1$. Note that the arrays in $L_1^\prime$ maintain a proportion and hence $L_1^\prime$ cannot be generated by any P2DCFG since the column tables and row tables can be independently applied in a P2DCFG. But $L_1^\prime$ is generated by the matrix P2DCFG $G_{m1}^\prime = (G_1,Lab,M)$ where $G_1$ is as in Example 1. In fact the column table c and the row table r in $G_1$ are $c = \{a \rightarrow bab, d \rightarrow ada, e \rightarrow aea\}$, $r = \left\{ d \rightarrow \begin{array}{c} d\\ a \end{array}, a \rightarrow \begin{array}{c} a\\ b \end{array} \right\}$, and the axiom array is $M_{0} = \begin{array}{ccc} a&{}d&{}a \\ b&{}a&{}b \\ a&{}e&{}a \end{array}$. The label set $Lab = \{c,r\}$ and the set M consists of the only matrix $m = [c,r]$.

Note that in a derivation in $G_m^\prime$ that starts with the axiom array, an application of the matrix m amounts to rewriting by the rules of the table c followed by the rules of r to constitute one step of derivation yielding an array of size (4, 5) given by $\begin{array}{ccccc} a&{}a&{}d&{}a&{}a \\ b&{}b&{}a&{}b&{}b \\ b&{}b&{}a&{}b&{}b \\ a&{}a&{}d&{}a&{}a \end{array}$. The process can be repeated any number of times yielding the arrays of $L_1$.

Analogous to matrix P2DCFG, we can define matrix (l / u)P2DCFG and matrix (r / d)P2DCFG as in Definition 4, except that we replace P2DCFG by (l / u)P2DCFG or (r / d)P2DCFG. We denote the resulting families of picture languages by M(l / u)P2DCFL and M(r / d)P2DCFL.

We illustrate matrix (r / d)P2DCFG by an example.

Example 5

Consider the picture language $L_3^\prime$ consisting of arrays belonging to the picture language $L_3$ in Example 3 but of size $(n, n), \, n \ge 2$. The language $L_3^\prime$ cannot be generated by any (r / d)P2DCFG since the arrays in $L_3^\prime$ maintain a proportion. But $L_3^\prime$ is generated by the matrix (r / d)P2DCFG $G_{m3}^\prime = (G_3,Lab,M)$ where $G_3$ is as in Example 3. In fact the column table c and the row table r in $G_3$ are $c = \{a \rightarrow ba, b \rightarrow ab\}$, $r = \left\{ a \rightarrow \begin{array}{c} b\\ a \end{array}, b \rightarrow \begin{array}{c} a\\ b \end{array} \right\}$, and $M_{0} = \begin{array}{cc} a&{}a \\ a&{}b \end{array}$. The label set $Lab = \{c,r\}$ and the set M consists of the only matrix $m = [c,r]$.

Starting from the axiom array, one step of derivation on applying the matrix m yields the array $\begin{array}{ccc} a&{}b&{}a \\ b&{}b&{}a \\ a&{}a&{}b \end{array}$. On repeating the process, we obtain the arrays of $L_3^\prime$.

Lemma 2

• (i) $P2DCFL \subset MP2DCFL$

• (ii) $(l/u)P2DCFL \subset M(l/u)P2DCFL$

• (iii) $(r/d)P2DCFL \subset M(r/d)P2DCFL$

Proof

The proper inclusions in (i) and (iii) are a consequence of the Examples 4 and 5, while the inclusions are straightforward, noting that every table t of rules in a P2DCFG can be considered as a matrix $m = \{t\}$. The statement (ii) can be similarly shown.

Theorem 4

• (i) $P2DCFL \subset MP2DCFL \subset (R)P2DCFL$

• (ii) $(l/u)P2DCFL \subset M(l/u)P2DCFL \subset (R)(l/u)P2DCFL$

• (iii) $(r/d)P2DCFL \subset M(r/d)P2DCFL \subset (R)(r/d)P2DCFL$

Proof

The inclusions and proper inclusions in the first half of the statements (i), (ii) and (iii) follow from Lemma 2. We prove the second half of (i) and (iii). The second half of (ii) can be similarly shown. For every matrix of the form $m =[l_1, \cdots , l_n]$ in a given matrix P2DCFG $G_m$, where $l_i,\, 1 \le i \le n$, are the labels of the tables of rules, we associate a word $w = l_1 \cdots l_n$. If $w_1, \cdots , w_p$ are the words obtained in this way from the matrix P2DCFG $G_m$, then we form a (R)P2DCFG where the P2DCFG is the same as the one in the matrix P2DCFG but the set of control words is $\{w_1, \cdots , w_p\}^*$. It can be seen that the (R)P2DCFG constructed generates the picture language generated by $G_m$. This proves the inclusion $MP2DCFL \subseteq (R)P2DCFL$. The inclusion $M(r/d)P2DCFL \subseteq (R)(r/d)P2DCFL$ is similar.

Fig. 6.

A picture array in the language $L_{a,b}$

For the proper inclusion $MP2DCFL \subset (R)P2DCFL$, we consider the picture language $L_{a,b}$ generated by the P2DCFG $(\{a,b,d \}, \{c_1,c_2 \}, \{r \}, \{d \})$ where

$$\begin{aligned}c_1 = \{d \rightarrow adb\}, c_2 = \{d \rightarrow bda\}, r = \left\{ d \rightarrow \begin{array}{c} d\\ d \end{array}, a \rightarrow \begin{array}{c} a\\ a \end{array}, b \rightarrow \begin{array}{c} b\\ b \end{array} \right\} \end{aligned}$$

with a regular control language $\{(c_1r)^m(c_2r)^n | m,n \ge 1 \}$. We note that this regular language can be expressed as $(c_1r)^+(c_2r)^+$ in terms of the Kleene-plus operation [13] in string languages. The picture arrays generated are of size $(m+n,$ $2m+2n+1), \, m,n \ge 1$. A member of this language is shown in Fig. 6. We note that the first m columns are made of only a, the next n columns are made of only b and there is a middle column made of only d while to the right of this middle column, there are n columns made of only b followed by m columns only made of a. On the other hand no matrix P2DCFG can handle this feature. In fact, if there is a matrix with a column table that produces the columns of a and also a column table that produces the columns of b, then picture arrays which are not in the desired form will be generated. Likewise, if there are two independent matrices with one having a column table that produces the columns of a and another matrix having a column table that produces the columns of b, any of them can be applied again yielding pictures not in the language.

For the proper inclusion $M(r/d)P2DCFL \subset (R)P2DCFL$, we consider a similar picture language generated in the (r / d) mode, by the P2DCFG $(\{a,b,d \}, \{c_1,c_2 \}, \{r \}, \{d\})$ where

$$\begin{aligned}c_1 = \{d \rightarrow ad\}, c_2 = \{d \rightarrow bd\}, r = \left\{ d \rightarrow \begin{array}{c} d\\ d \end{array}, a \rightarrow \begin{array}{c} a\\ a \end{array}, b \rightarrow \begin{array}{c} b\\ b \end{array} \right\} \end{aligned}$$

with a regular control language $\{(c_1r)^m(c_2r)^n | m,n \ge 1$. It can be seen that matrix P2DCFG in (r / d) mode cannot generate this language.

6 Concluding Remarks

Another variant of P2DCFG [16, 17] rewriting only the rightmost column or the lowermost row of a picture array is considered and properties of the resulting family (r / d)P2DCFL of picture languages are obtained. We can also consider and examine other variants of P2DCFG having a mixed mode of derivation, as for example, rewriting the leftmost column along with the lowermost row or the rightmost column along with the uppermost row. In [2], membership problem and the effect of substitution rules of the form $a \rightarrow b$ have been elaborately explored for the class P2DCFL. These questions and other properties remain to be investigated in the (l / u)P2DCFG as well as (r / d)P2DCFG. Also we note that grammars are relevant to the problem of generation of fractals, as certain kind of Lindenmayer system (also called, L system) [8, 12], which uses context-free grammar (CFG) type of rules, has been used to generate fractals but the application of the CFG type of rules is done in parallel. The question of generation of fractals by the Pure 2D CF grammar models is a possible problem of investigation and we believe that this might require a different approach of applying the tables of rules of this 2D grammar.