Practical Stutter-Invariance Checks for $\omega$-Regular Languages

Abstract

An $\omega$-regular language is stutter-invariant if it is closed by the operation that duplicates some letter in a word or that removes some duplicate letter. Model checkers can use powerful reduction techniques when the specification is stutter-invariant.

We propose several automata-based constructions that check whether a specification is stutter-invariant. These constructions assume that a specification and its negation can be translated into Büchi automata, but aside from that, they are independent of the specification formalism. These transformations were inspired by a construction due to Holzmann and Kupferman, but that we broke down into two operations that can have different realizations, and that can be combined in different ways. As it turns out, implementing only one of these operations is needed to obtain a functional stutter-invariant check.

Finally we have implemented these techniques in a tool so that users can easily check whether an LTL or PSL formula is stutter-invariant.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The notion of stutter-invariance (to be defined formally later) stems from model checkers implementing partial-order reduction techniques (e.g., [6, Chap. 10] or [4, Chap. 8]). If a model checker knows that the property to verify is stutter-invariant, it is sufficient to check that property only on a selected subset of the executions of the model, often achieving a great speedup. Such partial-order reductions are implemented by explicit model checkers such as Spin [18, Chap. 9], LTSmin [21], or DiVinE [5], to cite a few. Detecting stutter-invariant properties has also usages beyond partial-order reductions; for instance it is used to optimize the determinization construction implemented in the tool ltl2dstar [20].

To activate these optimizations, tools must decide if a property is stutter-invariant. The range of available options for this check depends on how the property is specified.

Linear-time Temporal Logic (LTL) is a common specification formalism for verification tools. It is widely known that any LTL formula that does not use the next-step operator $\mathsf {X}$ (a.k.a. an LTL$\setminus \mathsf {X}$ formula) is stutter-invariant; this check is trivial to implement. Unfortunately there exist formulas using $\mathsf {X}$ that are stutter-invariant (for instance ‘$\mathsf {F}(a \wedge \mathsf {X}(\lnot a\wedge b))$’) and whose usage is desirable [23].

Dallien and MacCaull  [8] built a tool that recognizes a stuttering LTL formula if (and only if) it matches one of the patterns of Păun and Chechik  [23]. This syntactical approach is efficient, but incomplete, as not all stutter-invariant formulas follow the recognized patterns.

A more definite procedure was given by Peled and Wilke  [24] as a construction that inputs an LTL formula $\varphi$ with $|\varphi |$ symbols and n atomic propositions, and outputs an LTL$\setminus \mathsf {X}$ formula $\varphi '$ with $\mathrm {O}(4^n|\varphi |)$ symbols, such that $\varphi$ and $\varphi '$ are equivalent iff they represent a stutter-invariant property. This construction, which proves that any stutter-invariant formula can be expressed without $\mathsf {X}$, was later improved to $n^{\mathrm {O}(k)}|\varphi |$ symbols, where k is the $\mathsf {X}$-depth of $\varphi$, by Etessami  [13]. If a disjunctive normal form is desired, Tian and Duan [29] give a variant with size $\mathrm {O}(n2^n|\varphi |)$. To decide if an LTL formula $\varphi$ is stutter-invariant, we build $\varphi '$ using one of these constructions, and then check the equivalence of $\varphi$ and $\varphi '$. This equivalence check can be achieved by translating these formulas into automata. This approach, based on Etessami’s procedure, was implemented in our library Spot [10], but some practical performance issues prompted us to look into alternative directions.

Extending this principle to a more expressive logic is not necessarily easy. For instance, a generalization of the above procedure to the linear fragment of PSL (the Property Specification Language [1]) was proposed by Dax et al. [9], but we realized it was incorrect¹ when we recently implemented it in Spot. Still, Dax et al. [9] provide a syntactic characterization of a stutter-invariant subset of PSL (which is to PSL what LTL$\setminus \mathsf {X}$ is to LTL) that can be used to quickly classify some PSL formulas as stutter-invariant.

For most practical uses these linear-time temporal formulas are eventually converted into $\omega$-automata like Büchi automata, so one way to avoid the intricacies of the logic is to establish the stutter-invariance directly at the automaton level. This is the approach used for instance in ltl2dstar [20]. The property $\varphi$ and its negation are both translated into Büchi automata $A_\varphi$ and $A_{\lnot \varphi }$; then the automaton $A_\varphi$ is transformed (using a procedure inspired from Holzmann and Kupferman  [19]) into an automaton $A'_\varphi$ that accepts the smallest stutter-invariant language over-approximating the language of $\varphi$. The property $\varphi$ is stutter-invariant iff $A_\varphi$ and $A'_\varphi$ have the same language, which can be checked by ensuring that the product $A'_\varphi \otimes A_{\lnot \varphi }$ has an empty language. This procedure has the advantage of being independent of the specification formalism used (e.g., it can work with LTL or PSL, and will continue to work even if these logics are augmented with new operators).

In this paper, we present and compare several automata-based decision procedures for stutter-invariance, inspired from the one described above. We show that the transformation of $A_\varphi$ to $A'_\varphi$ is better seen as two operations: one that allows letters to be duplicated, and another that allows duplicate letters to be skipped. These two operations can then be recombined in many ways, giving seven decision procedures. Rather surprisingly, some of the proposed checks require only one of these two operations: as a consequence, they are easier to implement than the original technique.

We first define stutter-invariant languages, and some operations on those languages in Sect. 2. The main result of Sect. 2, Theorem 1, gives several characterizations of stutter-invariant languages. In Sect. 3, we introduce automata to realize the language transformations described in Sect. 2. This gives us seven decision procedures, as captured by Theorem 2. In Sect. 4 we describe in more details the similarities between one of the proposed checks and the aforementioned construction by Holzmann and Kupferman, and we also point to some other related constructions. Finally in Sect. 5 we benchmark our implementation of these procedures.

2 The Language View

We use the following notations. Let $\varSigma$ be an alphabet, and let $\varSigma ^\omega$ denote the set of infinite words over this alphabet. Since we only consider infinite words, we will simply write word from now on. Given a word $w\in \varSigma ^\omega$, we denote its individual letters by $w_0,w_1,w_2,\ldots$ and write $w=w_0w_1w_2\ldots$ using implicit concatenation. Given some letter $\ell \in \varSigma$ and a positive integer n, we use $\ell ^n$ as a shorthand for the concatenation $\ell \ell \ldots \ell$ of n copies of $\ell$, and $\ell ^\omega$ for the concatenation of an infinite number of instances of $\ell$. A language L over $\varSigma$ is a set of words, i.e., $L\subseteq \varSigma ^\omega$. Its complement language is $\overline{L}=\varSigma ^\omega \!\setminus \!L$.

Definition 1

(Stutter-Invariant Language). A language L is stutter-invariant iff it satisfies the following property:

$$\begin{aligned} \forall n_0\ge 1, \forall n_1\ge 1, \forall n_2\ge 1,\ldots , \left( w_0w_1w_2\ldots \in L \iff w_0^{n_0}w_1^{n_1}w_2^{n_2}\ldots \in L\right) \end{aligned}$$

In other words, in a stutter-invariant language L, duplicating any letter or removing any duplicate letter from a word of L will produce another word of L. When L is not stutter-invariant, we say that L is stutter-sensitive.

The following lemma restates the above definition for stutter-sensitive languages.

Lemma 1

A language L is stutter-sensitive iff there exists $n_0\ge 1, n_1\ge 1,$ $n_2\ge 1,\ldots$ such that either

• 1. there exists a word $w_0w_1w_2\ldots \in L$ such that $w_0^{n_0}w_1^{n_1}w_2^{n_2}\ldots \not \in L$

• 2. or there exists a word $w_0^{n_0}w_1^{n_1}w_2^{n_2}\ldots \in L$ such that $w_0w_1w_2\ldots \not \in L$.

Proposition 1

A language L is stutter-invariant iff $\overline{L}$ is stutter-invariant.

Proof

Assume by way of contradiction that L is stutter-invariant but $\overline{L}$ is not. Applying Lemma 1 to $\overline{L}$, there exists $n_0\ge 1, n_1\ge 1,\ldots$ such that either

• 1. there exists a word $w_0w_1\ldots \in \overline{L}$ such that $w_0^{n_0}w_1^{n_1}\ldots \not \in \overline{L}$; but this means $w_0^{n_0}w_1^{n_1}\ldots \in L$ and because L is stutter-invariant we must have $w_0w_1\ldots \in L$ which contradicts the fact that this word should be in $\overline{L}$;

• 2. or there exists a word $w_0^{n_0}w_1^{n_1}\ldots \in \overline{L}$ such that $w_0w_1\ldots \not \in \overline{L}$, but then $w_0w_1\ldots \in L$ implies that $w_0^{n_0}w_1^{n_1}\ldots$ should belong to L as well, which is also a contradiction.

The same argument can be done with L and $\overline{L}$ reversed.   $\square$

Proposition 2

If $L_1$ and $L_2$ are stutter-invariant then $L_1\cup L_2$ and $L_1\cap L_2$ are stutter-invariant.

Proof

Immediate from Definition 1.   $\square$

We now introduce new operations that we will combine to decide stutter-invariance.

Definition 2

For a word $w=w_0w_1w_2\ldots$, $\mathsf {Instut}(w)=\{w_0^{n_0}w_1^{n_1}w_2^{n_2}\ldots \mid \forall i,\, n_i\ge 1\}$ denotes the set of words built from w by allowing any letter of w to be duplicated (i.e., the stuttering of w can be increased).

Conversely, $\mathsf {Destut}(w)=\{u_0u_1u_2\ldots \in \varSigma ^\omega \mid \text {there exists }n_0\ge 1, n_1\ge 1, n_2\ge 1, \ldots \text {such that }w=u_0^{n_0}u_1^{n_1}u_2^{n_2}\ldots \}$ denotes the set of words built from w by allowing any duplicate letter to be removed (i.e., the stuttering of w can be decreased).

We extend these two definitions to languages straightforwardly using $\mathsf {Instut}(L)=\bigcup _{w\in L}\mathsf {Instut}(w)$ and $\mathsf {Destut}(L)=\bigcup _{w\in L}\mathsf {Destut}(w)$.

The following lemmas are immediate from the definition:

Lemma 2

For any two words u and v, $u\in \mathsf {Instut}(v)\iff v\in \mathsf {Destut}(u)$.

Lemma 3

For any language L, we have $L\subseteq \mathsf {Destut}(L) \subseteq \mathsf {Instut}(\mathsf {Destut}(L))$, $L\subseteq \mathsf {Instut}(L) \subseteq \mathsf {Destut}(\mathsf {Instut}(L))$, and $\mathsf {Instut}(\mathsf {Destut}(L))=\mathsf {Destut}(\mathsf {Instut}(L))$.

Lemma 4

For any language L, we have $L \subseteq \mathsf {Instut}(L) \cap \mathsf {Destut}(L)$.

To illustrate that Lemma 4 cannot be strengthened to $L=\mathsf {Instut}(L) \cap \mathsf {Destut}(L)$, consider the language $L=\{a^2b^\omega ,\,a^4b^\omega \}$. Then $\mathsf {Instut}(L)=\{a^ib^\omega \mid i\ge 2\}$, $\mathsf {Destut}(L)=\{a^ib^\omega \mid 1\le i\le 4\}$, and $\mathsf {Instut}(L) \cap \mathsf {Destut}(L)=\{a^i b^\omega \mid 2\le i\le 4\}\ne L$.

We now show that $L \ne \mathsf {Instut}(L) \cap \mathsf {Destut}(L)$ is only possible if L is stutter-sensitive.

Proposition 3

L is a stutter-invariant language iff $\mathsf {Instut}(L) = L = \mathsf {Destut}(L)$.

Proof

($\Longrightarrow$) If L is stutter-invariant, the words added to L by $\mathsf {Instut}(L)$ or $\mathsf {Destut}(L)$ are already in L by definition. ($\Longleftarrow$) If $L = \mathsf {Instut}(L)$ and $L = \mathsf {Destut}(L)$ there is no way to find a counterexample word for Lemma 1.    $\square$

Note that $\mathsf {Instut}(L) = \mathsf {Destut}(L)$ is not a sufficient condition for L to be stutter-invariant. For instance consider the stutter-sensitive language $L=\{a^ib^\omega \mid i\,\text {is odd}\}$ for which $\mathsf {Instut}(L) = \mathsf {Destut}(L) = \{a^ib^\omega \mid i > 0\}$.

Proposition 4

If a language L is stutter-sensitive, then either $\mathsf {Instut}(L)\cap \overline{L}\ne \emptyset$ or $\mathsf {Destut}(L)\cap \overline{L}\ne \emptyset$.

Proof

Applying Lemma 1 to L, there exists $n_0\ge 1, n_1\ge 1,\ldots$ such that either

• 1. there exists a word $w_0w_1\ldots \in L$ such that $w_0^{n_0}w_1^{n_1}\ldots \not \in L$, which implies that $\mathsf {Instut}(L)\cap \overline{L}\ne \emptyset$;

• 2. or there exists a word $w_0^{n_0}w_1^{n_1}\ldots \in L$ such that $w_0w_1\ldots \not \in L$, which implies that $\mathsf {Destut}(L)\cap \overline{L}\ne \emptyset$.

So one of $\mathsf {Instut}(L)$ or $\mathsf {Destut}(L)$ has to intersect $\overline{L}$.   $\square$

Proposition 5

If a language L is stutter-sensitive, then $\mathsf {Instut}(L) \cap \mathsf {Instut}(\overline{L}) \ne ~\emptyset$.

Proof

By Proposition 4, since L is stutter-sensitive we have either $\mathsf {Instut}(L)\cap \overline{L}\ne \emptyset$ or $\mathsf {Destut}(L)\cap \overline{L}\ne \emptyset$.

• If $\mathsf {Instut}(L)\cap \overline{L}\ne \emptyset$, then there exists a word $u\in \overline{L}$, and a word $v\in L$ such that $u\in \mathsf {Instut}(v)$. Since $u\in \overline{L}$ we have $u\in \mathsf {Instut}(\overline{L})$; however we also have $u\in \mathsf {Instut}(v)\subseteq \mathsf {Instut}(L)$. So $u \in \mathsf {Instut}(\overline{L})\cap \mathsf {Instut}(L)$.

• If $\mathsf {Destut}(L)\cap \overline{L}\ne \emptyset$, then there exists a word $u\in \overline{L}$ and a word v in L such that $u\in \mathsf {Destut}(v)$. By Lemma 2, we have $v\in \mathsf {Instut}(u)$. Therefore we have $v\in \mathsf {Instut}(u)\subseteq \mathsf {Instut}(\overline{L})$ and $v\in L\subseteq \mathsf {Instut}(L)$, so $v \in \mathsf {Instut}(\overline{L})\cap \mathsf {Instut}(L)$.

In both cases $\mathsf {Instut}(\overline{L})\cap \mathsf {Instut}(L)$ is non-empty.   $\square$

Proposition 6

If a language L is stutter-sensitive, then $\mathsf {Destut}(L) \cap \mathsf {Destut}(\overline{L}) \ne \emptyset$.

Proof

Similar to that of Proposition 5.   $\square$

Theorem 1

For any language L, the following statements are equivalent.

• (1) L is stutter-invariant

• (2) $L=\mathsf {Instut}(L)=\mathsf {Destut}(L)$

• (3) $\mathsf {Destut}(\mathsf {Instut}(L))\cap \overline{L} = \emptyset$

• (4) $\mathsf {Instut}(\mathsf {Destut}(L))\cap \overline{L} = \emptyset$

• (5) $\mathsf {Instut}(L)\cap \mathsf {Instut}(\overline{L}) = \emptyset$

• (6) $\mathsf {Destut}(L)\cap \mathsf {Destut}(\overline{L}) = \emptyset$.

Proof

$(1) \iff (2)$ is Proposition 3; $(2) \implies (3) \wedge (4)$ is immediate; $(2) \implies (5) \wedge (6)$ follows from Proposition 1 which means that the hypothesis (2) can be applied to $\overline{L}$ as well; $(3) \implies (1)$ and $(4) \implies (1)$ both follow from the contraposition of Proposition 4 and from Lemma 3; $(5) \implies (1)$ and $(6) \implies (1)$ are Propositions 5 and 6.   $\square$

The most interesting part of this theorem is the last two statements: it is possible to check the stutter-invariance of a language using only $\mathsf {Instut}$ or only $\mathsf {Destut}$. In the next section we show different implementations of these operations on automata.

3 The Automaton View

Specifications written in linear-time temporal logics like LTL or (the linear fragment of) PSL are typically converted into Büchi automata by model checkers (or specialized translators). Below we define the variant of Büchi automata we use in our tool: Transition-based Generalized Büchi Automata or TGBA for short.

The TGBA acronym was coined by [16], although similar automata have been used with different names before (e.g., [7, 14, 22]). As their name implies, these TGBAs have a generalized Büchi acceptance condition expressed in terms of transitions (instead of states). While these automata have the same expressiveness as Büchi automata (i.e., they can represent all $\omega$-regular languages), they can be more compact; furthermore they are the natural product of many LTL-to-automata translation algorithms [2, 7, 11, 14, 16].

The transformations we define on these automata should however not be difficult to adapt to other kinds of $\omega$-automata.

Definition 3

(TGBA [16]). A Transition-based Generalized Büchi Automaton (TGBA) is a tuple $A = \langle \varSigma , Q, q_0, \mathcal {F}, \delta \rangle$ where:

• $\varSigma$ is a finite alphabet,

• Q is a finite set of states,

• $q_0\in Q$ is the initial state,

• $\delta \subseteq Q\times \varSigma \times Q$ is a transition relation labeling each transition by a letter,

• $\mathcal {F}=\{F_1,F_2,\ldots ,F_n\}$ is a set of acceptance sets of transitions: $F_i\subseteq \delta$.

A sequence of transitions $\rho =(s_0,w_0,d_0)(s_1,w_1,d_1)\ldots \in \delta ^\omega$ is a run of A if $s_0=q_0$ and for all $i\ge 0$ we have $d_i=s_{i+1}$. We say that $\rho$ recognizes the word $w=w_0w_1\ldots \in \varSigma ^\omega$.

For a run $\rho$, let $\mathsf {Inf}(\rho )\subseteq \delta$ denote the set of transitions occurring infinitely often in this run. The run is accepting iff $F_i\cap \mathsf {Inf}(\rho )\ne \emptyset$ for all i, i.e., if $\rho$ visits all acceptance sets infinitely often.

Finally the language of A, denoted $\mathscr {L}(A)$, is the set of words recognized by the accepting runs of A.

Figure 1 shows some examples of TGBAs that illustrate the upcoming definitions. The membership of transitions to some acceptance sets is represented by numbered and colored circles. For instance, automaton $A_1$ in Fig. 1(a) has two acceptance sets $F_1$ and $F_2$ that respectively contain the transitions marked with

and

. This automaton accepts the word $(abba)^\omega$ but rejects $(aba)^\omega$, so its language is stutter-sensitive.

Fig. 1.

An example TGBA $A_1$, with its closure, self-loopization, complement, closed complement, and the product between the two closures. $\mathscr {L}(A_1)$ is stutter-sensitive.

We now propose some automata-based implementations of the operations from Definition 2. The next three constructions we define in the rest of this section, $\mathsf {cl}$ (Definition 4), $\mathsf {sl}$ (Definition 5), and $\mathsf {sl}_2$ (Definition 6), implement respectively $\mathsf {Destut}$, $\mathsf {Instut}$, and again $\mathsf {Instut}$.

Definition 4

(Closure). Given a TGBA $A = \langle \varSigma , Q, q_0, \{F_1,F_2,\ldots ,F_n\}, \delta \rangle$, let $\mathsf {cl}(A)=\langle \varSigma , Q, q_0, \{F'_1,F'_2,\ldots ,F'_n\}, \delta '\rangle$ be the closure of A defined as follows:

• $\delta '$ is the smallest subset of $Q\times \varSigma \times Q$ such that

  • $\delta \subseteq \delta '$,

  • if $(x,\ell ,y)\in \delta '$ and $(y,\ell ,z)\in \delta '$, then $(x,\ell ,z)\in \delta '$.

• each $F'_i$ is the smallest subset of $\delta '$ such that

  • $F_i\subseteq F'_i$,

  • if $(x,\ell ,y)\in \delta '$, $(y,\ell ,z)\in \delta '$, and either $(x,\ell ,y)\in F_i$ or $(y,\ell ,z)\in F_i$ then $(x,\ell ,z)\in F'_i$.

Figure 1(d) illustrates this construction which can be implemented by modifying the automaton in place: for every pair of transitions of the form

, add a shortcut transition

that allows to skip one of the duplicated letters on a run without affecting the acceptance of this run. When the transition

already exists, we just need to update its membership to acceptance sets. So in effect, these changes let the automaton accept all shorter words that can be constructed from an accepted words by removing a duplicate letter.

In the worst case (e.g., the states of A form a ring with transitions of the form $(x,\ell ,x+1\mod n)$ for all letters $\ell$), $\mathsf {cl}(A)$ ends up with $|Q^2|\times |\varSigma |$ transitions.

Definition 5

(Self-Loopization). Given a TGBA $A = \langle \varSigma , Q, q_0, \{F_1,F_2,\ldots ,F_n\}, \delta \rangle$, let $\mathsf {sl}(A)=\langle \varSigma , Q', q_0, \{F'_1,F'_2,\ldots ,F'_n\}, \delta '\rangle$ be the “self-loopization” of A defined by:

• $Q'=(Q\times \varSigma )\cup \{q_0\}$,

• $\displaystyle \begin{aligned}\delta '={}&\{((x,\ell _1),\ell _2,(y,\ell _2))\mid \ell _1\in \varSigma ,\,(x,\ell _2,y)\in \delta \}\\ {} \cup {}&\{((y,\ell ),\ell ,(y,\ell ))\mid (x,\ell ,y)\in \delta \} {}\cup {} \{(q_0,\ell ,(y,\ell ))\mid (x,\ell ,y)\in \delta , x=q_0 \}, \end{aligned}$

• $F'_i = \{ ((x,\ell _1),\ell _2,(y,\ell _2))\in \delta ' \mid (x,\ell _2,y)\in F_i \}$.

Figure 1(f) illustrates this construction. For each transition, letters are “pushed” in the identifier of the destination state, ensuring that all transitions entering this state have the same letter, and then a self-loop with this letter is added if it was not already present on the original state. Note that the only self-loop that belong to acceptance sets are those that already existed in the original automaton: this ensures that the stuttering we introduce can only duplicate letters a finite amount of times.

With this construction, a state is duplicated as many times as its number of different incoming letters. In the worst case the automaton size is therefore multiplied by $|\varSigma |$.

The following definition gives another automata-transformation that implements $\mathsf {Instut}$, but in such a way that is it easy to modify the automaton in place.

Definition 6

(Second Self-Loopization).  For a TGBA $A = \langle \varSigma , Q, q_0, \{F_1, F_2,\ldots ,F_n\}, \delta \rangle$, let $\mathsf {sl}_2(A)=\langle \varSigma , Q', q_0, \{F_1', F_2',\ldots ,F_n'\}, \delta '\rangle$ be another “self-loopization” of A with:

• $Q'=Q\cup (Q \times \varSigma )$,

• ,

• $F_i'=F_i \cup \{ (x,\ell ,(y,\ell )) \in \delta '\mid (x,\ell ,y)\in F_i \}$.

Figure 1(g) illustrates this construction. For each transition

such that x and y have no self-loop over $\ell$, we add

, therefore allowing $\ell$ to appear twice or more. Note again that the added self-loop does not belong to any accepting set, so that $\ell$ can only be stuttered a finite amount of times.

The number of transitions of $\mathsf {sl}_2(A)$ is at most 4 times the number of transitions in A. The number of states of the form $(y,\ell )$ that are added is obviously bounded by $|Q|\times |\varSigma |$ but also by $|\delta |$ since we may add at most one state per original transition. This implies $\mathsf {sl}_2(A)$ has $\mathrm {O}(|Q| + \min (|Q|\times |\varSigma |,|\delta |))$ reachable states. In automata with a lot of self-loops (which is frequent when they represent LTL formulas), it can happen that very few additions are necessary: for instance automaton $A_1$ from Fig. 1(a) requires no modification, while automaton $\overline{A_1}$ (Fig. 1(b) and (g)) requires only one extra state.

Table 1. Characteristics of automata constructed from $A= \langle \varSigma , Q, q_0, \mathcal {F}, \delta \rangle$.

Table 1 summarizes the characteristics of these three constructions, that satisfy the following proposition:

Proposition 7

For any TGBA A we have $\mathscr {L}(\mathsf {cl}(A))=\mathsf {Destut}(\mathscr {L}(A))$ and $\mathscr {L}(\mathsf {sl}(A))=\mathscr {L}(\mathsf {sl}_2(A))=\mathsf {Instut}(\mathscr {L}(A))$.

To fully implement cases (3)–(6) of Theorem 1 we now just need to discuss the product and emptiness check of TGBAs, which are well known operations.

The product of two TGBAs is a straightforward synchronized product in which acceptance sets from both sides have to be preserved, therefore ensuring that a word in the product is accepted if and only if it was accepted by each of the operands.

Definition 7

(Product of Two TGBAs). Let A and B be two TGBAs on the same alphabet: $A = \langle \varSigma , Q^A, q_0^A, \{F_1,F_2,\ldots ,F_n\}, \delta ^A\rangle$ and $B = \langle \varSigma , Q^B, q_0^B, \{G_1,G_2,\ldots ,G_m\}, \delta ^B\rangle$. The product of A and B, denoted $A\otimes B$, is the TGBA $\langle \varSigma , Q, \mathcal {F}, q_0,\delta \rangle$ where:

• $Q = Q^A \times Q^B$,

• $q_0=(q_0^A,q_0^B)$,

• $\delta =\{((x_1,x_2),\ell _1,(y_1,y_2))\mid (x_1,\ell _1,y_1)\in \delta ^A,\, (x_2,\ell _2,y_2)\in \delta ^B,\, \ell _1=\ell _2 \}$,

• $\mathcal {F}= \{F'_1,F_2',\ldots ,F'_n,G'_1,G_2',\ldots ,G'_m\}$ where $F'_i = \{ (x_1,x_2),\ell ,(y_1,y_2) \in \delta ' \mid (x_1,\ell ,y_1)\in F_i\}$ and $G'_i = \{ (x_1,x_2),\ell ,(y_1,y_2) \in \delta ' \mid (x_2,\ell ,y_2)\in G_i\}$.

Proposition 8

If A and B are two TGBAs, then $\mathscr {L}(A\otimes B)=\mathscr {L}(A)\cap \mathscr {L}(B)$.

Figure 1(e) shows an example of product.

Deciding whether a TGBA has an empty language can be done in linear time with respect to the size of the TGBA [7, 26, 28]. One way is to search for a strongly connected component that is reachable from the initial state, and whose transitions intersects all acceptance sets. The reader can verify that the product automaton from Fig. 1(e) has a non-empty language (for instance the word $a(ba)^\omega$ is accepted thanks to the cycle around

and

).

We can now state our main result:

Theorem 2

Let $\varphi$ be a property expressed as a TGBA A, and assume we know how to obtain $\overline{A}$. Testing $\varphi$ for stutter-invariance is equivalent to testing the emptiness of any of the following products:

• $\mathsf {cl}(\mathsf {sl}(A))\otimes \overline{A}$,

• $\mathsf {sl}(\mathsf {cl}(A))\otimes \overline{A}$,

• $\mathsf {cl}(\mathsf {sl}_2(A))\otimes \overline{A}$,

• $\mathsf {sl}_2(\mathsf {cl}(A))\otimes \overline{A}$,

• $\mathsf {sl}(A)\otimes \mathsf {sl}(\overline{A})$,

• $\mathsf {sl}_2(A)\otimes \mathsf {sl}_2(\overline{A})$,

• $\mathsf {cl}(A)\otimes \mathsf {cl}(\overline{A})$.

Proof

Consequence of Theorem 1 (3)–(6), and Propositions 7 and 8.   $\square$

In a typical scenario, $\varphi$ is a property specified as LTL or PSL, and from that we can obtain $A_\varphi$ and its negation $A_{\lnot \varphi }$ by just translating $\varphi$ and $\lnot \varphi$ using existing algorithms.

4 Comparison with Other Automata-Based Approaches

As mentioned in the introduction, an automata-based construction described by Holzmann and Kupferman [19] was used by Klein and Baier  [20] to implement a stutter-invariance check in ltl2dstar. Since our constructions have been heavily inspired by this construction, it makes sense that we discuss the similarities and differences.

Fig. 2.

Illustration of the similarities between the Holzmann and Kupferman’s construction (top row), and the composition of what we defined as $\mathsf {cl}$ and $\mathsf {sl}$ (bottom row).

Holzmann and Kupferman’s construction starts from a Büchi automaton (i.e., with state-based acceptance) such as $A_2$ in Fig. 2(a). This automaton is first converted into a Büchi automaton with labels on states and multiple initial states, such as the automaton $B_2$ pictured in Fig. 2(b). From $B_2$, they produce the stuttering over-approximation $B_2'$ in Fig. 2(c). This last step essentially consists in making two copies of the automaton: one non-accepting (the left part of $B_2'$), and one non-accepting (the right part of $B_2'$, in which we grayed out some states that are not reachable in this example and need not be constructed). The non-accepting part has self-loops on all its states, and is also closed in such a way that if there exists a path of states labeled by $\ell _1\ell _1\ldots \ell _1\ell _2$, there should exist a transition between the first and the last state. Additionally if this path visits an accepting state in the original automaton, there should be a transition to the accepting copy of the last state.

Now we can compare the transformation of $A_2$ into $B_2'$ and the transformation of the equivalent² TGBA $A_3$ into $\mathsf {cl}(\mathsf {sl}(A_3))$ presented at the bottom of Fig. 2. The transformation of $A_2$ into $B_2$ combined with the addition of self-loops later in $B_2'$ corresponds to the transformation of $A_3$ into $\mathsf {sl}(A_3)$. The only difference is that we keep a single initial state. Then, the closure of $B_2'$ corresponds to our $\mathsf {cl}$ operation, with two differences:

• First, using transition-based acceptance we do not have to duplicate states to keep track of paths that visit accepting states. The gain is not very important, since $B_2'$ can have at most twice the number of states of $B_2$. However one should keep in mind that the duplication of states between $B_2$ and $B_2'$ increases the non-determinism of the automaton, and this will be detrimental to any later product.

• Second, there is not an exact correspondence between the shortcuts added in $B_2'$ and those added by $\mathsf {cl}$ due to subtle semantic differences between automata with transition-labels and automata with state-labels. For instance in Fig. 2(f), there is a transition

  

  that is a shortcut for

  

  but that has no counterpart in Fig. 2(c) because

  

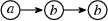
  is not labeled by a word of the form $\ell _1\ell _1\ldots \ell _1\ell _2$.

To conclude this informal comparison, $\mathsf {cl}(\mathsf {sl}(A))$ can be considered as an adaptation of the Holzmann and Kupferman  [19] construction to TGBA. Our contribution is the rest of Theorem 2: the fact that a different implementation of $\mathsf {sl}$ is possible (namely, $\mathsf {sl}_2$), and the fact that we can implement a stutter-invariance check using only one of the operators $\mathsf {cl}$, $\mathsf {sl}$, or $\mathsf {sl}_2$. Furthermore, our experiments in the next section will show that running $\mathsf {sl}(\mathsf {cl}(A))$ is more efficient than $\mathsf {cl}(\mathsf {sl}(A))$ (because the intermediate automaton is smaller).

The variant of Holzmann and Kupferman’s construction implemented in ltl2dstar 0.6 actually only checks stutter invariance one letter at a time. The problem addressed is therefore slightly different [20]: they want to know whether a language is invariant by repeating any occurrence of a given letter $\ell$, or removing any duplicate occurrence of $\ell$. In effect the automaton is cloned three times: the main copy is the original Büchi automaton, and every time a transition is labeled by $\ell$, the automaton makes non-deterministic jumps into the two other copies that behaves as in Holzmann and Kupferman’s construction.

Similar stuttering-checks for a single letter $\ell$ can be derived from any of the procedures we proposed. It suffices to modify $\mathsf {cl}$, $\mathsf {sl}$, or $\mathsf {sl}_2$ so that they add only self-loop or shortcuts for $\ell$.

Peled et al. [25, Thoerem 16] also presented an automaton-based check similar to $\mathsf {cl}(\mathsf {sl}(A))$, although in a framework that is less convenient from a developer’s point of view: the transformation of an automaton into its stutter-invariant over-approximation is achieved via multi-tape Büchi automata.

Finally, there is also a related construction proposed by Etessami  [12, Lemma 1] that provides a normal form for automata representing stutter-invariant properties. The construction could be implemented using $\mathsf {cl}(\mathsf {sl}(A))$ (or Holzmann and Kupferman’s construction) as a base, but the result is then fixed to ensure that one cannot arrive and depart from a state using the same letter. The latter fix (which is similar to some reduction performed while constructing testing automata [15, 17]) is only valid if the property is known to be stutter invariant: when applied to a non-stutter invariant property, the resulting automaton is not an over-approximation of the original one, so building a stutter-invariance check on that procedure would require a complete equivalence check instead of an inclusion check.

5 Evaluation

We evaluate the procedures of Theorem 2 in the context of deciding the stutter invariance of LTL formulas. LTL formulas are defined over a set ${ AP }$ of Boolean propositions (called Atomic Propositions), and the TGBAs that encode these formulas are labeled by valuations of all these propositions. In this context we therefore have $\varSigma =2^{ AP }$.

Our motivation is very practical. Since version 1.0, Spot distributes a tool called ltlfilt with an option --stutter-invariant to extract stutter-invariant formulas from a list of LTL formulas [10]. Our original implementation was based on Etessami’s rewriting function $\tau '$ [13]: if an LTL formula $\varphi$ uses the $\mathsf {X}$ operator, we compute $\tau '(\varphi )$ and test the equivalence between $\varphi$ and $\tau '(\varphi )$ by converting these formulas and their negations into TGBA and testing $\mathscr {L}(A_{\tau '(\varphi )}\otimes A_{\lnot \varphi })=\emptyset \wedge \mathscr {L}(A_{\lnot \tau '(\varphi )}\otimes A_{\varphi })=\emptyset$. However this equivalence³ test proved to be quite slow due to the translation of $\tau '(\varphi )$ and its negation, which are often very large formulas.

Furthermore Spot also supports PSL formulas for which we would also like to decide stutter invariance. The checks based on automata transformations discussed in this paper therefore solve our two problems: they are faster, and they are independent on the logic used.

In this section we show to which extent ltlfilt --stutter-invariant was improved by the use of automata-based checks, and compare the various checks suggested in Theorem 2 to reveal which one we decided to use by default.

It should be noted that those benchmarks are completely implemented in Spot (See Appendix A for tool support), in which transition-based generalized Büchi acceptance is the norm, so we did not implement any technique for automata with state-based acceptance. We also know of no other publicly available tool that would offer a similar service, and to which we could compare our results.⁴

We opted to implement $\mathsf {cl}$, $\mathsf {sl}$, $\mathsf {sl}_2$, and $\otimes$ as separate functions that take automata and produce new automata, the best as we could, using the TGBA data structure in the current development version of Spot. In the cases of $\mathsf {cl}$ and $\mathsf {sl}_2$ our implementation modifies the input automaton in place to save time. We use Couvreur’s algorithm [7] for emptiness check.

Table 2. Time to classify 500 random LTL formulas that all use the $\mathsf {X}$ operator and have the given number of atomic propositions.

Our first experiment is to compare the speed of the proposed automata-based checks to the speed achieved in our previous implementation. For Table 2 we prepared three files of 500 random formulas with a different number of atomic propositions, all using the $\mathsf {X}$ operator (otherwise they would be trivially stutter-invariant, and there is no point in running our algorithms), then we used our ltlfilt tool [10] with option --stutter-invariant to print only the stutter-invariant formulas of this list. The reported time is the user’s experience, i.e., it accounts for the complete run of ltlfilt (including parsing of input formulas, stutter-invariance check, and output of stutter-invariant formulas) and differs only by the stutter-invariance check performed. As the first line of this table demonstrates, testing the equivalence of $\varphi$ and $\tau '(\varphi )$ as we used to quickly becomes impractical: the experiment with $|{ AP }|=3$ aborted after 80 min with an out-of-memory error.⁵

It was recently pointed to us that Etessami  [13] does not suggest to test the equivalence of $\varphi$ and $\tau '(\varphi )$, but to test whether $\varphi \leftrightarrow \tau '(\varphi )$ is a tautology, i.e., whether $\lnot (\varphi \leftrightarrow \tau '(\varphi ))$ is satisfiable. This alternative approach is not practical in our implementation. The second line of Table 2 shows the cost of translating $\lnot (\varphi \leftrightarrow \tau '(\varphi ))$ into a TGBA and testing its emptiness⁶: the run-time is actually worse because in order to be translated into an automaton, the formula $\lnot (\varphi \leftrightarrow \tau '(\varphi ))$ has first to be put into negative normal form (i.e., rewriting the $\leftrightarrow$ operator and pushing negation operators down to the atomic propositions), which means the the resulting formula has a size that is the sum of the sizes of each of the formulas $\varphi$, $\lnot \varphi$, $\tau '(\varphi )$, and $\lnot \tau '(\varphi )$ used in the first line.

On the other hand, all the tests from Theorem 2 show comparable run times in Table 2: this is because most of the time is spent in the creation of $A_\varphi$ and $A_{\lnot \varphi }$, and the application of $\mathsf {cl}$, $\mathsf {sl}$, and $\mathsf {sl}_2$ only incurs a minor overhead.

We then conducted another evaluation, focused only on the checks from Theorem 2. In this evaluation, that involves 40000 unique LTL formulas (10000 formulas for each $|{ AP }|\in \{1,2,3,4\}$) using the $\mathsf {X}$ operator, we first translated $A_\varphi$ and $A_{\lnot \varphi }$, and then measured only the time spent by each of the checks (i.e., the run time of $\mathsf {cl}$, $\mathsf {sl}$, $\mathsf {sl}2$, the product, and the emptiness check). The resulting measurements allow to compare the 7 checks on each of the 40000 formulas, as summarized by Table 3.

Table 3. Cross-comparison of the checks of Theorem 2 on 40000 random LTL formulas with $\mathsf {X}$. A value v on line (x) and column (y) indicates that there are v cases where check (x) was more than $10\,\%$ slower than check (y). In other words, a line with many small numbers indicates a check that is usually faster than the others.

The benchmark data, as well as instructions to reproduce them can be found at http://www.lrde.epita.fr/~adl/spin15/. In addition to source code, this page contains CSV files with complete measurements, and a 16-page document with more analysis than we could do here.

Based on this evaluation, we decided to use $\mathscr {L}(\mathsf {cl}(A)\otimes \mathsf {cl}(A_{\lnot \varphi }))=\emptyset$, the last line in the table, as our default stutter-invariance check in ltlfilt. The operation $\mathsf {cl}$ seems to be more efficient than the other two because it can be performed in place without adding new states. The table also suggests that checks that involve the $\mathsf {sl}$ operation (i.e., the one that duplicates each state for each different incoming letter) should be avoided. $\mathsf {sl}_2$ seems to be a better replacement for $\mathsf {sl}$ as it can be implemented in place.

Different implementations of these checks could be imagined. For instance the composed constructions like $\mathsf {sl}_2(\mathsf {cl}(A))$ or $\mathsf {cl}(\mathsf {sl}_2(A))$ could be done in such a way that the outer operator is only considering the transitions and states that were already present in A. The product and emptiness check used for $\mathsf {cl}(A)\times \mathsf {cl}(\overline{A})$ could be avoided when it is detected that neither A nor $\overline{A}$ have been altered by $\mathsf {cl}$ (likewise with $\mathsf {sl}_2$). Also the $\mathsf {sl}$ and $\mathsf {sl}_2$ constructions, as well at the product, could be all computed on-the-fly as needed by the emptiness check, so that only the parts of $\mathsf {sl}(A)$ and $\mathsf {sl}(\overline{A})$ that is actually needed to prove the product empty (or not) is constructed.

6 Conclusion

We have presented seven decision procedures that can be used to check whether a property (for which we know an automaton and its complement) is stutter-invariant. A typical use case is to decide whether an LTL or PSL property is stutter-invariant, and we provide tools that implement these checks. The first variant of these procedures is essentially an adaptation of a construction by Holzmann and Kupferman [19] to the context of transition-based acceptance. But we have shown that this construction can actually be broken down into two operators: $\mathsf {cl}$ to allow longer words and $\mathsf {sl}$ to allow shorter words, that can accept different realizations (e.g., $\mathsf {sl}_2$), and that can be combined in different ways.

In particular, we have shown that it is possible to implement a stutter-invariance check by implementing only one operation among $\mathsf {cl}$, $\mathsf {sl}$, or $\mathsf {sl}_2$. This idea is new, and it makes any implementation easier. The implementation we decided to use in our tool because it had the best performance in our benchmark uses only the $\mathsf {cl}$ operation.

The definition of $\mathsf {cl}$, $\mathsf {sl}$ and $\mathsf {sl}_2$ we gave trivially adapt to $\omega$-automata with any kind of transition-based acceptance, such as those that can be expressed in the Hanoi Omega Automata format  babiak.15.cav, and that our implementation fully supports. Indeed, those three operations preserve the acceptance sets seen infinitely (and finitely) often along runs that are equivalent up to stuttering, so it is not be a problem if those acceptance sets are used by pairs in a Rabin or Streett acceptance condition, for instance. The acceptance condition used is relevant only to the emptiness check used.

To implement a check in a framework using state-based acceptance, we recommend using the $\mathsf {sl}_2(A)\otimes \mathsf {sl}_2(\overline{A})$ check, because the definition of $\mathsf {sl}_2(A)$ is trivial to adapt to state-based acceptance: the acceptance sets simply do not have to be changed. As we saw in Sect. 4, the operations $\mathsf {cl}$ and $\mathsf {sl}$ are less convenient to implement using state-based acceptance since one needs to add additional states to keep track of the accepting sets visited by some path fragments. Furthermore, $\mathsf {sl}_2(A)$ has the advantage that it can be implemented by modifying A in place.

A Tool Support

All the checks described in this article are implemented in Spot 1.99.1 which can be obtained from https://spot.lrde.epita.fr/.

Stutter-invariance of LTL or PSL formulas can be tested on-line without installing anything:

• 1. Load https://spot.lrde.epita.fr/trans.html.

• 2. Type an LTL or PSL formula.

• 3. Select “Desired Output: Formula” and then “property information”.

• 4. Scan the resulting properties for “syntactic stutter invariant” (this means the formula belongs to LTL$\setminus \mathsf {X}$or siPSL), “stutter invariant” or “stutter sensitive”. In the latter two cases, the automata-based check had to be performed.

If Spot is installed, the tool ltlfilt can be used from the command-line to make the same decision. For instance ltlfilt -f  ’$\varphi$’ --stutter-invariant will print $\varphi$ back iff $\varphi$ is stutter-invariant.

Similarly the tool autfilt can be used to apply the operations $\mathsf {cl}$, $\mathsf {sl}$, and $\mathsf {sl}_2$ to any automaton (with any acceptance condition). The corresponding options are --destut, --instut, and --instut=2 respectively.