Keywords

1 Introduction

Reduce is important and commonly used collective operation in the Message Passing Interface (MPI) [1]. A five-year profiling study [2] demonstrates that MPI reduction operations are the most used collective operations. In the reduce operation each node i owns a vector \(x_i\) of n elements. After completion of the operation all the vectors are reduced element-wise to a single n-element vector which is owned by a specified root process.

Optimization of MPI collective operations has been an active research topic since the advent of MPI in 1990s. Many general and architecture-specific collective algorithms have been proposed and implemented in the state-of-the-art MPI implementations. Hierarchical topology-oblivious transformation of existing communication algorithms has been recently proposed as a new promising approach to optimization of MPI collective communication algorithms and MPI-based applications [3, 5]. This approach has been successfully applied to the most popular parallel matrix multiplication algorithm, SUMMA [4], and the state-of-the-art MPI broadcast algorithms, demonstrating significant multi-fold performance gains, especially on large-scale HPC systems. In this paper, we apply this approach to optimization of the MPI reduce operation.

1.1 Contributions

We propose a hierarchical optimization of legacy MPI reduce algorithms without redesigning them. The approach is simple and general, allowing for application of the proposed optimization to any existing reduce algorithm. As by design the original algorithm is a particular case of its hierarchically transformed counterpart, the performance of the algorithm will either improve or stay the same in the worst case scenario. Theoretical study of the hierarchical transformation of six reduce algorithms, which are implemented in Open MPI [7], is presented. The theoretical results have been experimentally validated on a widely used Grid’5000 [8] infrastructure.

1.2 Outline

The rest of the paper is structured as follows. Section 2 discusses related work. The hierarchical optimization of MPI reduce algorithms is introduced in Sect. 3. The experimental results are presented in Sect. 4. Finally, Sect. 5 concludes the presented work and discusses future directions.

2 Related Work

In the early 1990s, the CCL library [9] implemented collective reduce operation as an inverse broadcast operation. Later collective algorithms for wide-area clusters were proposed [10], and automatic tuning for a given system by conducting a series of experiments on the system was discussed [11]. Design and high-performance implementation of collective communication operations and commonly used algorithms, such as minimum-spanning tree reduce algorithm, are discussed in [12]. Five reduction algorithms optimized for different message sizes and number of processes are proposed in [13]. Implementations of MPI collectives, including reduce, in MPICH [15] are discussed in [16]. Algorithms for MPI broadcast, reduce and scatter, where the communication happens concurrently over two binary trees, are presented in [14]. Cheetah framework [17] implements MPI reduction operations in a hierarchical way on multicore systems, which supports multiple communication mechanisms. Unlike that work, our optimization is topology-oblivious, and MPI reduce optimizations in this work do not design new algorithms from scratch, employing the existing reduce algorithms underneath. Therefore, our hierarchical design can be built on top of the algorithms from the Cheetah framework as well. This work focuses on reduce algorithms implemented in Open MPI such as flat, linear/chain, pipeline, binary, binomial and in-order binary tree algorithms.

We extend our previous studies on parallel matrix multiplication [3] and topology-oblivious optimization of MPI broadcast algorithms on large-scale distributed memory platforms [5, 6] to MPI reduce algorithms.

2.1 MPI Reduce Algorithms

We assume that the time to send a message of size m between any two MPI processes is modeled with Hockney model [18] as \(\alpha + m{\times }\beta \), where \(\alpha \) is the latency per message and \(\beta \) is the reciprocal bandwidth per byte. It is also assumed that the computation cost per byte in the reduction operation is \(\gamma \) on any MPI process. Unless otherwise noted, in the rest of the paper we will call MPI process just process.

  • Flat tree reduce algorithm.

    In this algorithm, the root process sequentially receives and reduces a message of size m from all the processes participating in the reduce operation in \(p-1\) steps:

    $$\begin{aligned} \left( p-1\right) {\times }\left( \alpha + m{\times }\beta + m{\times }\gamma \right) . \end{aligned}$$
    (1)

    In a segmented flat tree algorithm, a message of size m is split into X segments, in which case the number of steps is \(X{\times }(p-1)\). Thus, the total execution time will be as follows:

    $$\begin{aligned} X{\times }\left( p-1\right) {\times }\left( \alpha + \frac{m}{X}{\times }\beta + \frac{m}{X}{\times }\gamma \right) . \end{aligned}$$
    (2)

  • Linear tree reduce algorithm.

    Unlike the flat tree, here each process receives or sends at most one message. Theoretically, its cost is the same as the flat tree algorithm:

    $$\begin{aligned} \left( p-1\right) {\times }\left( \alpha + m{\times }\beta + m{\times }\gamma \right) . \end{aligned}$$
    (3)

  • Pipeline reduce algorithm.

    It is assumed that a message of size m is split into X segments and in one step of the algorithm a segment of size \(\frac{m}{X}\) is reduced between p processes. If we assume a logically reverse ordered linear array, in the first step of the algorithm the first segment of the message is sent to the next process in the array. Next, while the second process sends the first segment to the third process, the first process sends the second segment to the second process, and the algorithm continues in this way. The first segment takes \(p-1\) and the remaining segments take \(X-1\) steps to reach the end of the array. If we also consider the computation cost in each step, then overall execution time of the algorithm will be as follows:

    $$\begin{aligned} \left( p+X-2\right) {\times }\left( \alpha + \frac{m}{X}{\times }\beta + \frac{m}{X}{\times }\gamma \right) . \end{aligned}$$
    (4)

  • Binary tree reduce algorithms.

    If we take a full and complete binary tree of height h, its number of nodes will be \(2^{h+1}-1\). In the reduce operation, a node at the hight h will receive two messages from its children at the height \(h+1\). In addition, if we segment a message of size m into X segments, the overall run time will be as follows:

    $$\begin{aligned} 2\left( \log _2\left( p+1\right) + X -2\right) {\times }\left( \alpha + \frac{m}{X}{\times }\beta + \frac{m}{X}{\times }\gamma \right) . \end{aligned}$$
    (5)

    Open MPI uses the in-order binary tree algorithm for non-commutative operations. It works similarly to the binary tree algorithm but enforces order in the operations.

  • Binomial tree reduce algorithm.

    The binomial tree algorithm takes \(\log _2(p)\) steps and the message communicated at each step is m. If the message is divided into X segments, then the number of steps and the message communicated at each step will be \(X{\times }\log _2(p)\) and \(\frac{m}{X}\) respectively. Therefore, the overall run time will be as follows:

    $$\begin{aligned} \log _2\left( p\right) {\times }\left( \alpha + m{\times }\beta + m{\times }\gamma \right) . \end{aligned}$$
    (6)

  • Rabenseifner’s reduce algorithm.

    The Rabenseifner’s algorithm [13] is designed for large message sizes. The algorithm consists of reduce-scatter and gather phases. It has been implemented in MPICH [16] and used for message sizes greater than 2 KB. The reduce-scatter phase is implemented with recursive-halving, and the gather phase is implemented with binomial tree. Therefore, the run time of the algorithm is the sum of these two phases:

    $$\begin{aligned} 2\log _2\left( p\right) {\times }\alpha + 2\frac{p-1}{p}{\times }m{\times }\beta + \frac{p-1}{p}{\times }m{\times }\gamma . \end{aligned}$$
    (7)

The algorithm can be further optimized by recursive vector halving, recursive distance doubling, recursive distance halving, binary blocks, and ring algorithms for non-power-of-two number of processes. An interested reader can consult [13] for more detailed discussion of those algorithms.

3 Hierarchical Optimization of MPI Reduce Algorithms

This section introduces a topology-oblivious optimization of MPI reduce algorithms. The idea is inspired by our previous study on the optimization of the communication cost of parallel matrix multiplication [3] and MPI broadcast [5] on large-scale distributed memory platforms.

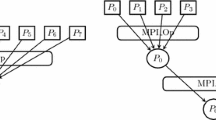
The proposed optimization technique is based on the arrangement of the p processes participating in the reduce into logical groups. For simplicity, it is assumed that the number of groups divides the number of MPI processes and can change between one and p. Let G be the number of groups. Then there will be \(\frac{p}{G}\) MPI processes per group. Figure 1 shows an arrangement of 8 processes in the original MPI reduce operation, and Fig. 2 shows the arrangement in a hierarchical reduce operation with 2 groups of 4 processes. The hierarchical optimization has two phases: in the first phase, a group leader is selected for each group and the leaders start reduce operation inside their own group in parallel (in this example between 4 processes). In the next phase, the reduce is performed between the group leaders (in this example between 2 processes). The grouping can be done by taking the topology into account as well. However, in this work the grouping is topology-oblivious and the first process in each group is selected as the group leader. In general, different algorithms can be used for reduce operations between group leaders and within each group. This work focuses on the case where the same algorithm is employed at both levels of hierarchy. Algorithm 1 shows the pseudocode of the hierarchically transformed MPI reduce operation. Line 4 calculates the root for the reduce between the groups. Then line 5 creates a sub-communicator of G processes between the groups, and line 6 creates a sub-communicator of \(\frac{p}{G}\) processes inside the groups. Our implementation uses the MPI_Comm_split MPI routine to create new sub-communicators.

Fig. 1.
figure 1

Logical arrangement of processes in MPI reduce.

Full size image
Fig. 2.
figure 2

Logical arrangement of processes in hierarchical MPI reduce.

Full size image
figure a

3.1 Hierarchical Transformation of Flat Tree Reduce Algorithm

After the hierarchical transformation, there will be two steps of the reduce operation: inside the groups and between the groups. The reduce operations inside the groups happen between \(\frac{p}{G}\) processes in parallel. Then, the operation continues between G groups. The cost of the reduce operations inside groups and between groups will be \((G-1){\times }(\alpha + m{\times }\beta + m{\times }\gamma )\) and \((\frac{p}{G}-1){\times }(\alpha + m{\times }\beta + m{\times }\gamma )\) respectively. Thus, the overall run time can be seen as a function of G:

$$\begin{aligned} F\left( G\right) =\left( G+\frac{p}{G}-2\right) {\times }\left( \alpha + m{\times }\beta + m{\times }\gamma \right) \end{aligned}$$
(8)

The derivative of the function is \((1-\frac{p}{G^2}){\times }(\alpha +m{\times }\beta + m{\times }\gamma )\), it can be shown that \(p=\sqrt{G}\) is the minimum point of the function in the interval (1, p). Then the optimal value of the function will be as follows:

$$\begin{aligned} F\left( \sqrt{p}\right) =\left( 2\sqrt{p}-2\right) {\times }\left( \alpha + m{\times }\beta + m{\times }\gamma \right) \end{aligned}$$
(9)

3.2 Hierarchical Transformation of Pipeline Reduce Algorithm

If we sum the costs of reduce inside and between groups with pipeline algorithm, the overall run time will be as follows:

$$\begin{aligned} F\left( G\right) =\left( 2X+G+\frac{p}{G}-4\right) {\times }\left( \alpha +\frac{m}{X}{\times }\beta + \frac{m}{X}{\times }\gamma \right) \end{aligned}$$
(10)

In the same way, it can be easily shown that the optimal value of the cost function is as follows:

$$\begin{aligned} F\left( \sqrt{p}\right) =\left( 2X+2\sqrt{p}-4\right) {\times }\left( \alpha +\frac{m}{X}{\times }\beta + \frac{m}{X}{\times }\gamma \right) \end{aligned}$$
(11)

3.3 Hierarchical Transformation of Binary Reduce Algorithm

For simplicity, we will take \(p+1{\approx }p\) in the formula 5. Then the cost of the reduce operations between the groups and inside the groups will be as follows respectively: \(2\log _2(G){\times }(\alpha +m{\times }\beta +m\gamma )\) and \(2\log _2(\frac{p}{G}){\times }(\alpha +m{\times }\beta +m\gamma )\). If we add these two terms, the overall cost of the hierarchical transformation of the binary tree algorithm will be equal to the cost of the original algorithm.

3.4 Hierarchical Transformation of Binomial Reduce Algorithm

Similarly to the binary reduce algorithm, the cost function of the binomial tree will not change after hierarchical transformation.

3.5 Hierarchical Transformation of Rabenseifner’s Reduce Algorithm

By applying the formula 7 between the groups with G processes and inside the groups with \(\frac{p}{G}\) processes, we can find the run time of hierarchical transformation of Rabenseifner’s algorithm. Unlike the previous algorithms, now the theoretical cost increases in comparison to the original Rabenseifner’s algorithm. Therefore, theoretically the hierarchical reduce implementation should use the number of groups equals to one, in which case the hierarchical algorithm retreats to the original algorithm.

$$\begin{aligned} 2\log _2(p){\times }\alpha +2m{\times }\beta {\times }\left( 2-\frac{G}{p}-\frac{1}{G}\right) +m\gamma \left( 2-\frac{G}{p}-\frac{1}{G}\right) \end{aligned}$$
(12)

3.6 Possible Overheads in the Hierarchical Design

Our implementation of the hierarchical reduce operation uses MPI_Comm_split operation to create groups of processes. The obvious questions would be to which extent the split operation can affect the scalability of the hierarchical algorithms. Recent research works show different approaches to improve the scalability of MPI communicator creation operations in terms of run time and memory footprint. The research in [20] introduces a new MPI_Comm_split algorithm, which scales well to millions of cores. The memory usage of the algorithm is \(O(\frac{p}{g})\) and the time is \(O(g\log _2(p) + \log ^2_2(p) + \frac{p}{g}\log _2(g))\), where p is the number of MPI processes, g is the number of processes in the group that perform sorting. More recent research work in [21] improves the previous algorithm with two variants. The first one, which uses a bitonic sort, needs \(O(\log _2(p))\) memory and \(O(\log ^2_2(p))\) time. The second one is a hash-based algorithm and requires O(1) memory and \(O(\log _2(p))\) time. Having these algorithms, we can utilize MPI_Comm_split operation in our hierarchical design with negligible overhead of creating MPI sub-communicators. There will not be any overhead at all for large messages as the split operation does not depend on the message size.

4 Experiments

The experiments were carried out on the Grid’5000 infrastructure in France. The platform consists of 24 clusters distributed over 9 sites in France and one in Luxembourg which includes 1006 nodes, 8014 cores. Almost all the sites are interconnected by 10 Gb/s high-speed network. We used the Graphene cluster from Nancy site of the infrastructure as our main testbed. The cluster is equipped with 144 nodes and each node has a disk of 320 GB storage, 16 GB of memory and 4-cores of CPU Intel Xeon X3440. The nodes in the Graphene cluster interconnected via 20 Gb/s Infiniband and Gigabyte Ethernet. More comprehensive information about the platform can be found on the Grid’5000 web site (http://www.grid5000.fr).

The experiments have been done with Open MPI 1.4.5, which provides a few reduce implementations. Among those implementations there are several reduce algorithms such as linear, chain, pipeline, binary, binomial, and in-order binary algorithms and platform/architecture specific algorithms, some of which are reduce algorithms for Infiniband networks, and the Cheetah framework for multicore architectures. In this work, we do not consider the platform specific reduce implementations. We used the same approach as described in MPIBlib [19] to benchmark our experiments. During the experiments, the mentioned reduce algorithms were selected by using Open MPI MCA (Modular Component Architecture) coll_tuned_use_dynamic_rules and coll_tuned_reduce_algorithm parameters. MPI_MAX operation has been used in the experiments. We have used Graphene cluster with two experimental settings, one process per core and one process per node with the Infiniband-20G network. A power-of-two number of processes have been used in the experiments.

4.1 Experiments: One Process per Core

The nodes in the Graphene cluster are organized into four groups and connected to four switches. The switches in turn are connected to the main Nancy router. We have used 10 patterns of process to core mappings, but we will show experimental results only with one such mappings where the processes are grouped by their rank in increasing order. The measurements with different groupings showed similar performance.

The theoretical and experimental results showed that the hierarchical approach mainly improves the algorithms which assume flat arrangements of the processes, such as linear, chain and pipeline. On the other hand the native Open MPI reduce operation selects different algorithms depending on the message size, the count and the number of processes sent to the MPI_Reduce function. This means the hierarchical transformation can improve the native reduce operation as well. The algorithms used in the Open MPI decision function are linear, chain, binomial, binary/in-order binary and pipeline reduce algorithms which can be used with different sizes of segmented messages.

Figure 3 shows experiments with default Open MPI reduce operation with a message of size 16 KB where the best performance is achieved when the group size is 1 or p, in which case the hierarchical reduce obviously turns into the original non-hierarchical reduce. Here for different numbers of groups the Open MPI decision function selected different reduce algorithms. Namely, if the number of groups is 8 or 64 then Open MPI selects the binary tree reduce algorithm between the groups and inside the groups respectively. In all other cases the binomial tree reduce algorithm is used. Figure 4 shows similar measurements with a message of size 16 MB where one can see a huge performance improvement up to 30 times. This improvement does not come solely from the hierarchical optimization itself, but also because of the number of groups in the hierarchical reduce resulted in Open MPI decision function to select the pipeline reduce algorithm with different segment sizes for each groups. The selection of the algorithms for different number of groups is described in Table 1.

Fig. 3.
figure 3

Hierarchical native reduce. m =16 KB and p = 512.

Full size image
Fig. 4.
figure 4

Hierarchical native reduce. m =16 MB and p = 512.

Full size image
Table 1. Open MPI algorithm selection in HReduce. m =16 MB, p = 512.
Full size table

As mentioned in Sect. 3.6, it is expected that the overhead from the MPI_Comm_split operation should affect only reduce operations with smaller message sizes. Figure 5 validates this with experimental results. The hierarchical reduce operation of 1 KB message with the underlying native reduce achieved its best performance when the number of groups was one as the overhead from the split operation itself was higher than the reduce.

It is interesting to study the pipeline algorithm with different segment sizes as it is used for large message sizes in Open MPI. Figure 6 presents experiments with the hierarchical pipeline reduce with a message size of 16 KB with 1 KB segmentation. We selected the segment sizes using coll_tuned_reduce_algorithm_segmentsize parameter provided by MCA. Figures 7 and 8 shows the performance of the pipeline algorithm with segment sizes of 32 KB and 64 KB respectively. In the first case, we see a 26.5 times improvement, while with the 64 KB the improvement is 18.5 times.

Figure 9 demonstrates speedup of the hierarchical transformation of native Open MPI reduce operation, linear, chain, pipeline, binary, binomial, and in-order binary reduce algorithms with message sizes starting from 16 KB up to 16 MB. Except binary, binomial and in-order binary reduce algorithms, there is a significant performance improvement. In the figure, NT is native Open MPI reduce operation, LN is linear, CH is chain, PL is pipeline with 32 KB segmentation, BR is binary, BL is binomial, and IBR denotes in-order binary tree reduce algorithm. We would like to highlight one important point that Fig. 9 does not compare the performance of different Open MPI reduce algorithms, it rather shows the speedup of their hierarchical transformations. Each of these algorithms can be better than the others in some specific settings depending on the message size, number of processes, underlying network and so on. At the same time, the hierarchical transformation of these algorithms will either improve their performance or be equally fast.

Fig. 5.
figure 5

Time spent on MPI_Comm_split and hierarchical native reduce. m = 1 KB, p = 512.

Full size image
Fig. 6.
figure 6

Hierarchical pipeline reduce. m = 16 KB, segment 1 KB and p = 512.

Full size image
Fig. 7.
figure 7

Hierarchical pipeline reduce. m = 16 MB, segment 32 KB and p = 512.

Full size image
Fig. 8.
figure 8

Hierarchical pipeline reduce. m = 16 MB, segment 64 KB and p = 512.

Full size image
Fig. 9.
figure 9

Speedup on 256 (left) and 512 (right) cores, one process per core.

Full size image

4.2 Experiments: One Process per Node

The experiments with one process per node showed a similar trend to that of with the one process per core setting. The performance of linear, chain, pipeline and native Open MPI reduce operations can be improved by the hierarchical approach. Figures 10 and 11 show experiments on 128 nodes with message sizes of 16 KB and 16 MB accordingly. In the first setting, the Open MPI decision function uses the binary tree algorithm when the number of processes is 8 between or inside groups, in all other cases the binomial tree is used.

Fig. 10.
figure 10

Hierarchical native reduce. m = 16 KB and p = 128.

Full size image
Fig. 11.
figure 11

Hierarchical native reduce. m = 16 MB and p = 128.

Full size image

The pipeline algorithm has similar performance improvement to that of with 512 processes, Fig. 12 shows experiments with a message of size 16 MB segmented by 32 KB and 64 KB sizes. The labels on the x axis has the same meaning as in the previous section.

Fig. 12.
figure 12

Hierarchical pipeline reduce. m = 16 MB, segment 32 KB (left) and 64 KB (right). p = 128.

Full size image

Figure 13 presents speedup of the hierarchical transformations of all the reduce algorihms from Open MPI “TUNED” component with message sizes from 16 KB up to 16 MB on 64 (left) and 128 (right) nodes. Again, the reduce algorithms wich has “flat” design and Open MPI default reduce operation have multi-fold performance improvement.

Fig. 13.
figure 13

Speedup on 64(left) and 128(right) cores. 1 process per node.

Full size image

5 Conclusion

Despite there has been a lot of research in MPI collective communications, this work shows that their performance is far from optimal and there is some room for improvement. Indeed, our simple hierarchical optimization, which transforms existing MPI reduce algorithms into two-level hierarchy, gives significant improvement on small and medium scale platforms. We believe that the idea can be incorporated into Open MPI decision function to improve the performance of reduce algorithms even further. It can also be used as a standalone software on top of MPI based applications.

The key feature of the optimization is that it can never be worse than any other optimized reduce operation. In the worst case, the algorithm can use one group and fall back to the native reduce operation.

As the future work, we plan to investigate if using different reduce algorithms in each phase and different number of processes per group can improve the performance. We would also like to generalize our optimization to other MPI collective operations.