Modified Orthogonal Neighborhood Preserving Projection for Face Recognition

Abstract

In recent times most of the face recognition algorithms are based on subspace analysis. High dimensional image data are being transformed into lower dimensional subspace thus leading towards recognition by embedding a new image into the lower dimensional space. Starting from Principle Component Analysis(PCA) many such dimensionality reduction procedures have been utilized for face recognition. Recent edition is Neighborhood Preserving Projection (NPP). All such methods lead towards creating an orthogonal transformation based on some criteria. Orthogonal NPP builds a linear relation within a small neighborhood of the data and then assumes its validity in the lower dimension space. However, the assumption of linearity could be invalid in some applications. With this aim in mind, current paper introduces an approximate non-linearity. In particular piecewise linearity, within the small neighborhood which gives rise to a more compact data representation that could be utilized for recognition. The proposed scheme is implemented on synthetic as well as real data. Suitability of the proposal is tested on a set of face images and a significant improvement in recognition is observed.

P. Koringa acknowledges Board of Research in Nuclear Science, BARC, India for supporting this research.

G. Shikkenawis is acknowledging Tata Consultancy Services for providing the financial support for carrying out this work.

1 Introduction

Subspace based methods are the recent trend for face recognition/identification problem. Face recognition appears as one of the most challenging problems in machine learning, and computer vision systems. Early recognition methods are based on the geometric features. Mostly local facial features, such as shape, size, structure and location of eyes, nose, mouth, chin, ears in each person’s face happened to be popular identification features in face recognition. On the contrary, subspace based methods use the intrinsic data manifold present in the face images.

Though, face image seems to be high dimensional data, it is observed that it lies in comparatively very low linear or non-linear manifold [1, 2]. This leads to develop face recognition systems based on subspace arising from data dimensionality reduction. The basic idea is to find a linear or non-linear transformation to map the image to a lower dimensional subspace which makes the same class of data more compact for the convenience of classification. Such underlying manifold learning based face recognition methods have attracted considerable interests in recent years. Some of the examples are Principal Component Analysis (PCA) [1], Linear Discriminant Analysis (LDA) [3], Locality Preserving Projection (LPP) [4, 5] and Neighborhood Preserving Embedding (NPE) [6]. Techniques such as PCA and LDA tend to preserve mostly global geometry of data (image in the present context). On the other hand, techniques such as LPP and NPE preserve local geometry by a graph structure, based on nearest neighborhood information.

The linear dimensionality reduction method Orthogonal Neighborhood Preserving Projection (ONPP) proposed in [2] preserves global geometry of data as well as captures intrinsic dependency of local neighborhood. ONPP is linear extension of Locally Linear Embedding (LLE) [7] which uses a weighted nearest neighborhood graph to preserve local geometry by representing each data point as linear combination of its neighbors. It simply embeds sample points into lower dimensional space without having any mechanism of reconstructing the data. ONPP uses the same philosophy as that of LLE and projects the sample data onto linear subspace but at the same time suggests a procedure to reconstruct data points. A variant of ONPP, Discriminative ONPP (DONPP) proposed in [8] takes into acount both, intraclass as well as interclass geometry. In this paper, a modified ONPP algorithm is proposed and its performance is compared with existing ONPP and DONPP algorithms. In particular, a z-shaped function based criterion is used to compute the coefficient of linear combination of neighbors of each data point. Note that, when the algorithm is applied to face recognition, face images are considered as data points. The modified algorithm is tested on synthetic as well as real data. To show its efficiency, the algorithm is tested on well-known face databases like AR [9], ORL [10], and UMIST [11]. Results of the proposed algorithm are comparable to that of the existing one in some cases and are significantly better in other cases.

The paper is organized in five sections. In the next section, ONPP and DONPP algorithms are explained in detail, followed by the modification on ONPP suggested in Sect. 3. Section 4 consists of experimental results and Sect. 5 concludes the performance of suggested algorithm on various types of databases.

2 Orthogonal Neighborhood Preserving Projection (ONPP)

ONPP [2] is a linear extension of Locally Linear Embedding. LLE is a nonlinear dimensionality reduction technique that embeds high dimension data samples on lower dimensional subspace. This mapping is not explicit in the sense that embedding is data dependent. In LLE, intrinsic data manifold changes with the inclusion or exclusion of data points. Hence, on inclusion of a new data point, embedding of all existing data points changes. This prevented subspace based recognition of unknown sample point, as this unknown sample point can not be embedded into the existing lower dimensional subspace. Lack of explicit mapping thus makes LLE not suitable for recognition. ONPP resolves this problem and finds the explicit mapping of the data in lower dimensional subspace through a linear orthogonal projection matrix. In presence of this orthogonal projection matrix, new data point can be embedded into lower dimensional subspace.

Let $\mathbf {x_{1},x_{2},....,x_{n}}$ be given data points form m-dimensional space $\mathbf {(x_{i}}\in {\mathbf {R}^{m}})$. So the data matrix is $\mathbf {X=[x_{1},x_{2},....,x_{n}]}\in {\mathbf {R}^{m\times n}}$. The basic task of subspace based methods is to find an orthogonal/non-orthogonal projection matrix $\mathbf {V}^{m\times d}$ such that $\mathbf {Y}=\mathbf {V}^{T}\mathbf {X}$, where $\mathbf {Y}\in {\mathbf {R}^{d \times n}}$ is the embedding of $\mathbf {X}$ in lower dimension as $d$ is assumed to be less than $m$.

ONPP is a two step algorithm where in the first step each data point is expressed as a linear combination of its neighbors. In the second step the data compactness is achieved through a minimization problem.

For, each data point $\mathbf {x_{i}}$, nearest neighbors are selected in two ways. In one way, $k$ neighbors are selected by Nearest Neighbor (NN) technique where $k$ is a suitably chosen parameter. In another way, neighbors could be selected which are within $\varepsilon$ distance apart from the data point. Let $\mathcal {N}_{x_{i}}$ be the set of $k$ neighbors. First, data point $\mathbf {x_{i}}$ is expressed as linear combination of its neighbors as $\sum _{j=1}^{k} w_{ij}\mathbf {x_{j}}$ where, $\mathbf {x_{j}}\in \mathcal {N}_{x_{i}}$. The weight $w_{ij}$ are calculated by minimizing the reconstruction errors i.e. error between $\mathbf {x_{i}}$ and linear combination of $\mathbf {x_{j}}\in \mathcal {N}_{x_{i}}$.

$$\begin{aligned} \arg \min \mathcal {E}(\mathbf {W})=\frac{1}{2}{\displaystyle {\displaystyle \sum _{i=1}^{n}}\parallel \mathbf {x_{i}}-\sum _{j=1}^{k}}w_{ij}\mathbf {x_{j}}\parallel ^{2} \end{aligned}$$

(1)

subject to $\sum _{j=1}^{k} w_{ij}=1$.

Corresponding to point $\mathbf {x_{i}}$, let $\mathbf {X}_{\mathbf{N}_{\mathbf{i}}}$ be a matrix having $\mathbf {x_{j}}$ as its columns, where $\mathbf {x_{j}}\in {{N}_{x_{i}}}$. Note that $\mathbf {X_{N_{i}}}$ includes $\mathbf {x_{i}}$ as its own neighbor. Hence, $\mathbf {X_{N_{i}}}$ is a $m\times k+1$ matrix. Now by solving the least square problem $(\mathbf {X_{N_{i}}-x_{i}e^{T})w_{i}}=\mathbf {0}$ with a constraint $\mathbf {e^{T}w_{i}}=\mathbf {1}$, a closed form solution, as shown in Eq.  (2) is evolved for $\mathbf {w_{i}}$. Here, $\mathbf {e}$ is a vector of ones having dimension $k\times 1$ same as $\mathbf {w_i}$.

$$\begin{aligned} \mathbf {w_{i}}=\frac{\mathbf {G}^{-1}\mathbf {e}}{{\mathbf {e}^{T}\mathbf {G}^{-1}\mathbf {e}}} \end{aligned}$$

(2)

where, $\mathbf {G}$ is Gramiam matrix of dimension $k\times k$. Each entry of $\mathbf {G}$ is calculated as $\mathbf {g_{pl}}=(\mathbf {x_{i}}-\mathbf {x_{p}})^{T}(\mathbf {x_{i}}-\mathbf {x_{l}}), \;for\,\forall \, \mathbf {x_{p}},\mathbf {x_{l}}\,\in \mathcal {N}_{x_{i}}$

Next step is dimensionality reduction or finding the projection matrix $V$ as stated earlier. The method basically seeks the lower dimensional projection $\mathbf {y_{i}}\in \mathbf {R}^{d}$ of data point $\mathbf {x_{i}} \in \mathbf {R}^{m}$ ($d<<m$) with some criteria. The criteria imposed here assumes that the linear combination of neighbors $\mathbf {x_{j}}$s which reconstruct the data point $\mathbf {x_{i}}$ in higher dimension would also reconstruct $\mathbf {y_{i}}$ in lower dimension with corresponding neighbors $\mathbf {y_{j}}$s along with same weight as in higher dimensional space. Such embedding is obtained by minimizing the sum of squares of reconstruction errors in the lower dimensional space. Hence, the objective function is given by

$$\begin{aligned} \arg \min \mathcal {F}(\mathbf {Y})=\sum _{i=1}^{n}\parallel \mathbf {y_{i}}-\sum _{j=1}^{n}w_{ij}\mathbf {y_{j}}\parallel ^{2} \end{aligned}$$

(3)

subject to, $\mathbf {V}^{T}\mathbf {V}=\mathbf {I}$ (orthogonality constraint).

This optimization problem results in computing eigen vectors corresponding to the smallest $d$ eigen values of matrix $\tilde{\mathbf {M}}=\mathbf {X}(\mathbf {I}-\mathbf {W})(\mathbf {I}-\mathbf {W}^{T})\mathbf {X}^{T}$. ONPP explicitly maps $\mathbf {X}$ to $\mathbf {Y}$, which is of the form $\mathbf {Y}=\mathbf {V}^{T}\mathbf {X}$, i.e. each new sample $\mathbf {x_{l}}$ can now be projected to lower dimension by just a matrix-vector product $\mathbf {y_{l}}=\mathbf {V}^{T}\mathbf {x_{l}}$.

ONPP can also be implemented in supervised mode where the class labels are known. Face recognition, character recognition etc. are problems where supervised mode is better suited. In supervised mode, data points $\mathbf {x_{i}}$ and $\mathbf {x_{j}}$ belonging to the same class are considered neighbors to each other thus $w_{ij}\ne 0$ and $w_{ij}=0$ otherwise. In supervised technique, the parameter $k$ (number of nearest neighbors) need not to be specified manually, it is automatically set to number of data samples in particular class.

Considering the undersampled size problem where the number of samples $n$ is less than dimension $m$, $m>n$. In such scenario, the matrix $\mathbf {\tilde{M}} \in \mathbf {R}^{m\times m}$ will have maximum rank $n - c$, where $c$ is number of classes. In order to ensure that the resulting matrix $\mathbf {\tilde{M}}$ will be non-singular, one may employ an initial PCA projection that reduces the dimensionality of the data vectors to $n - c$. If $\mathbf {V_{PCA}}$ is the dimensionality reduction matrix of PCA, then on performing the ONPP the resulting dimensionality reduction matrix is given by $\mathbf {V} = \mathbf {V_{PCA}V_{ONPP}}$.

ONPP considers only intraclass geometric information, a variant of ONPP proposed in [8], takes into account interclass information as well to improve classification performance, is known as Discriminative ONPP (DONPP). For a given sample $\mathbf {x_{i}}$, its $n_{i}-1$ neighbors having same class labels are denoted by $\mathbf {x_{i}, x_{i^{1}}, x_{i^{2}},..., x_{i^{n_{i}-1}}}$ and its k nearest neighbors having different class labels are denoted by $\mathbf {x_{i_{1}}, x_{i_{2}},..., x_{i_{k}}}$. Thus, neighbors of sample $\mathbf {x_{i}}$ can be described as $\mathbf {X_{i}}=[\mathbf {x_{i}, x_{i^{1}}, x_{i^{2}},..., x_{i^{n_{i}-1}}, x_{i_{1}}, x_{i_{2}},..., x_{i_{k}}}]$ and its low-dimensional projection can be denoted as $\mathbf {Y_{i}}=[\mathbf {y_{i}, y_{i^{1}}, y_{i^{2}},..., y_{i^{n_{i}-1}}, y_{i_{1}},..., y_{i_{k}}}]$.

In projected space, it is expected that the sample and its neighbors having same label preserve local geometry, while neighbors having different labels are projected as far as possible from the sample to increase interclass distance. This can be achieved by optimizing Eq. (3) in addition to Eq. (4).

$$\begin{aligned} \arg \max \mathcal {F}(\mathbf {Y_{i}})=\sum _{p=1}^{k}\parallel \mathbf {y_{i}}-\mathbf {y_{i_{p}}}\parallel ^{2} \end{aligned}$$

(4)

Considering Eqs. (3) and (4) simultaneously, the optimization problem for sample $x_{i}$ can be written as

$$\begin{aligned} \arg \min \mathcal {F}(\mathbf {Y_{i}})=(\parallel \mathbf {y_{i}}-\sum _{j=1}^{n_{i}-1}w_{ij}\mathbf {y_{j}} \parallel ^{2} -\beta \sum _{p=1}^{k}\parallel \mathbf {y_{i}}-\mathbf {y_{i_{p}}} \parallel ^{2}) \end{aligned}$$

(5)

where, $\beta$ is scaling factor between $[0,1]$. This minimization problem simplifies into an eigenvalue problem, and projection matrix $\mathbf {V_{DONPP}}$ can be achieved by eigenvectors corresponding to smallest d eigenvalues.

3 Modified Orthogonal Neighbourhood Preserving Projection (MONPP)

ONPP is based on two basic assumptions, first it assumes that a linear relation exists in a local neighborhood and hence any data point can be represented as a linear combination of its neighbors. Secondly it assumes that this linear relationship also exists in the projection space. The later assumption gives rise to a compact representation of the data that can enhance the classification performance. The data compactness would be more visible in the case when the first assumption is strongly valid. While experimenting with synthetic data, as shown in Fig. 2, it has been observed that data compactness is not clearly revealed. The main drawback could be the strict local linearity assumption. Focusing on this, we are trying to incorporate some kind of non-linear relationship of a data point with its neighbors. The proposed algorithm is termed as Modified ONPP.

In this proposed modification, a z-shaped function is used to assign weights to nearest neighbors in the first stage of ONPP. Note that in ONPP, the weight matrix $\mathbf {W}$ is calculated by minimizing the cost function in Eq. (1), which is a least square solution (2). In the least square solution, weights of neighbors are inversely proportional to the distance of the neighbors from the point of interest. We are looking for a situation where the neighbors closest to the point of interest would get maximum weight and there after the weights will be adjusted non-linearly (through Z-shaped function) as the distance increases. After a certain distance the weights will be very low. In particular, instead of assuming a linear relationship, a piecewise linear relationship is incorporated through the z-shaped function. This piecewise linear relationship is leading towards some kind of non-linear relationship.

$$\begin{aligned} \mathcal {Z}(x;a,b) = {\left\{ \begin{array}{ll} 1 &{} \text {if } x \le a \\ 1-2{\left( \frac{x-a}{a-b}\right) }^2 &{} \text {if }a \le x \le \frac{a+b}{2} \\ 2{\left( \frac{x-b}{a-b}\right) }^2 &{} \text {if }\frac{a+b}{2} \le x \le b \\ 0 &{} \text {Otherwise} \end{array}\right. } \end{aligned}$$

(6)

Fig. 1.

Z-shaped weight function for Range [0, Maximum within class distance], illustrated for max distance of 7000 unit

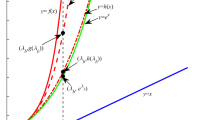
Parameters a and b locate the extremes of the sloped portion of the curve and can be set to 0 and maximum within class distance (i.e. maximum pair wise distance between data samples belonging to the same class) respectively, as shown in Fig. 1. In case of unsupervised mode, a $k$-NN algorithm could be implemented before assigning the weights and hence the parameters $a$ and $b$ of Eq. (6) can be adjusted.

Finally, Eq. (7) is used to assign weight to each neighbor $\mathbf {x}_{\mathbf{j}}$ corresponding to $\mathbf {x}_{\mathbf{i}}$. Note that this equation is same as Eq. (2), where $\mathbf {G}^{-1}$ is replaced by $\mathbf {Z}$. The new weights are

$$\begin{aligned} \mathbf {w}_{\mathbf{i}}=\frac{\mathbf {Ze}}{\mathbf {e}^{T}\mathbf {Ze}} \end{aligned}$$

(7)

where, elements of this $\mathbf {Z}$ matrix are defined as

$$\begin{aligned} Z_{pl}=\mathcal {Z}(d_{p};a,b)+\mathcal {Z}(d_{l};a,b)\;for,\,\forall \, \mathbf {x_{p},x_{l}}\,\in \mathbf {\mathcal {N}_{x_{i}}} \end{aligned}$$

(8)

here, $\mathcal {Z}(d_{k};a,b)$ is calculated using Eq. (6) where, $d_{k}$ is the Euclidean distance between $\mathbf {x_{i}}$ and it’s neighbor $\mathbf {x_{k}}$. Parameters $a$ and $b$ are obtained as discussed earlier.

Next step computes projection matrix $\mathbf {V}\in \mathbf {R}^{m\times d}$ whose column vectors are smallest $d$ eigen vectors of matrix $\mathbf {\tilde{M}}=\mathbf {X}(\mathbf {I}-\mathbf {W})(\mathbf {I}-\mathbf {W}^{T})\mathbf {X}^{T}$. Embedding of $\mathbf {X}$ on lower dimension $\mathbf {Y}$ is achieved by $\mathbf {Y}=\mathbf {V}^{T}\mathbf {X}$.

4 Experiments and Results

The suggested Modified ONPP is used for two well-known synthetic datasets along with a digit data [12], low dimensional projection of these data sets is compared with ONPP. MONPP has also been implemented extensively for various well-known face databases and the results are compared with that of the existing ONPP algorithm and a variant of ONPP, DONPP.

4.1 Synthetic Data

The modified algorithm is implemented on two synthetic datasets viz Swissroll (Fig. 2(a)) and S-curve (Fig. 2(e)) to visualize their two dimensional plot. These two datasets reveal a linear relationship within the class as well as between the classes when unfolded. Dimensionality reduction techniques such as PCA when applied to the data fail to capture this intrinsic linearity. However, dimensionality reduction techniques such as LPP [4], NPE [6] try to capture the local geometry and retain it into the projection space are expected to perform better. These algorithms give rise to a compact representation of the data without much distorting the shape of the data. To implement existing ONPP and proposed Modified ONPP, 1000 data points are randomly sampled from three dimensional manifold (Fig. 2(b) and (f)) to build the orthogonal transformation matrix($\mathbf {V}$). Note that similar experiment has been performed in [2] to show the suitability of ONPP over LPP. As suitability of ONPP over LPP has already been shown, we are not showing any results of LPP. From Fig. 2(c),(d) and (g),(h), it is clear that the 2D representations of both Swissroll and S-curve seem to be much better for MONPP. To explore how ONPP and MONPP work with varied values of $k$, experiments have been conducted and results are shown in Fig. 3. Note that repeated experiments with a fixed $k$ may not guarantee to generate same results. It is observed that projection using ONPP algorithm depends on $k$, variation in $k$ results in huge variation in its lower dimensional representation. However, projection using MONPP is more stable with varying values of $k$. Larger values of $k$ imply larger area of local neighborhood. It is possible that larger local area does not posses linearity. The linearity assumption of ONPP thus is invalid here. So the non-linearity present in moderately large local area is well-captured in MONPP and is reflected in the results.

Fig. 2.

Swissroll: original 3D data(a), sampled data(b), 2D projection obtained by ONPP(c) and MONPP(d). S-curve: original 3D data(e), sampled data(f), 2D projection obtained by ONPP(g) and MONPP(h). k(number of NN) is set to 6.

Fig. 3.

2D projection of S-curve(left) and Swissroll(right) with various k (number of NN) values with ONPP(top) and MONPP(bottom)

4.2 Digit Data

The MNIST database [12] of handwritten digits is used to compare data visualization of both the algorithms. Randomly 40 data samples from each class (digit) are taken and projected on 2-D plane using ONPP and proposed Modified ONPP. The results are shown in Fig. 4, it can be clearly observed that the data is compact and well separated when MONPP is applied. It seems that there is a wide range of variations in digit ‘1’ and that is reflected in Fig. 4(top-left). But the same digit ‘1’ is more compact in the 2-D representation of MONPP (Fig. 4(bottom-left)). Similar argument is true for digits ‘7’ and ‘9’. Overall, better compactness is evident for all digits in case of MONPP.

Fig. 4.

2D projection of digit data using ONPP and MONPP, top row shows performance of ONPP algorithm, Bottom row shows performance of MONPP algorithm, where, ‘$+$’ denotes 5, ‘$o$’ denotes 6, ‘$*$’ denotes 7, ‘$\varDelta$’ denotes 8, ‘$\diamond$’ denotes 9.

4.3 Face Data

The algorithm is also tested on three different face databases viz AR [9], ORL [10], and UMIST [11]. To maintain the uniformity, face images of all databases are resized to $38\times 31$ pixels, thus each image is considered as a point in $1178$ dimensional space. For each database, randomly $50\,\%$ of face images are selected as training samples and remaining are used for testing. The training samples are used to find the lower dimensional projection matrix $\mathbf {V}$. The test samples are then projected on this subspace and are recognized using a NN-classifier. The main intention of these experiments is to check the suitability of MONPP based image representation for face recognition and hence a simple classifier such as NN is used. To ensure that the results achieved are not biased to the randomized selection of training-testing data, the experiments are repeated twenty times with different randomization. Experiments are also conducted for different values of $d$ (dimension of reduced space) ranging from 10 to 160 (at an interval of 10). The best as well as average recognition rates are reported here for all databases.

Average recognition results for AR, UMIST and ORL databases using ONPP, DONPP and MONPP are shown in Fig. 5. It can be observed that MONPP performs better than ONPP and DONPP across almost all values of $d$. Average recognition accuracies and best recognition accuracies along with the corresponding dimensions using ONPP, DONPP and MONPP for all three databases are reported in Table 1.

Fig. 5.

Comparison of average performance of ONPP, DONPP and MONPP on AR database UMIST database ORL database

Table 1. Comparison of performance in the light of recognition score (in %) of ONPP, DONPP and MONPP

5 Conclusion

Subspace based methods for face recognition have been a major area of research and already proven to be more efficient. In this regard, Orthogonal Neighborhood Preserving Projection (ONPP) is assumed to handle the intrinsic non-linearity of the data manifold. The first step of ONPP deals with a linear model building within local neighborhoods. This linearity assumption may not be valid for a moderately large neighborhood. In the present work, this linear model is thus replaced by a notion of non-linearity where a piecewise linear model (z-shaped) is used instead. The suitability of the proposal is tested on non-linear synthetic data as well as a few benchmark face databases. Significant and consistent improvement in data compactness is observed for synthetic data where manifold is surely nonlinear. This signifies the suitability of the present proposal to handle non-linear manifold of the data. On the other hand, noticeable improvement is obtained for the face recognition problem. The modification suggested over existing ONPP though very simple but overall improvement in face recognition results is very encouraging.

Another way to handle non-linear manifold is to use kernel method of manifold learning. Kernel versions of subspace methods such as PCA [13], OLPP [14], ONPP [2] have already been proposed. A kernel version of the current Modified ONPP could be the possible future direction of work. Either the current form of the proposal associating with discriminating method [8] or its kernel version is expected to exploit the non-linear data manifold that is present in the face database in the sense of variations in facial expression. Recognizing facial expression along with faces would be a challenging task for future.