Performance Evaluation in Machine Learning

Abstract

Performance evaluation is an important aspect of the machine learning process. However, it is a complex task. It, therefore, needs to be conducted carefully in order for the application of machine learning to radiation oncology or other domains to be reliable. This chapter introduces the issue and discusses some of the most commonly used techniques that have been applied to it. The focus is on the three main subtasks of evaluation: measuring performance, resampling the data, and assessing the statistical significance of the results. In the context of the first subtask, the chapter discusses some of the confusion matrix-based measures (accuracy, precision, recall or sensitivity, and false alarm rate) as well as receiver operating characteristic (ROC) analysis; several error estimation or resampling techniques belonging to the cross-validation family as well as bootstrapping are involved in the context of the second subtask. Finally, a number of nonparametric statistical tests including McNemar’s test, Wilcoxon’s signed-rank test, and Friedman’s test are covered in the context of the third subtask. The chapter concludes with a discussion of the limitations of the evaluation process.

1 Introduction

While developing and applying machine learning tools to problems in radiation oncology or other domains are what will allow new advances to be made in these domains, it is important to realize that without proper means of evaluating the new methods, there is no way to know whether or not they are effective. While researchers and practitioners of machine learning have long known that and used general evaluation methods to judge the effectiveness of their algorithms, until recently, very little attention has been paid to the details of how this evaluation should be carried out. Instead, a uniform methodology was consistently applied without any concern regarding the appropriateness of that methodology for the particular cases considered. In this chapter, we begin by giving an overview of machine learning evaluation, pointing to some issues that may creep in if it is not conducted appropriately. We then follow with a discussion of evaluation metrics, resampling methods, and statistical testing. We conclude the chapter with a consideration of the limitations of the evaluation process. The discussion in this chapter is based on [1], which gives much more detail about the issue and its solution.

2 An Overview of Machine Learning Evaluation

While not as exciting a process as the design of machine learning algorithms or its application to difficult problems, the issue of machine learning evaluation needs to be considered very carefully. Indeed, there exist many approaches to evaluation and it remains unclear when or why certain approaches are more appropriate than others. In this chapter, we clarify these questions in at least a few cases that may be of interest to the radiation oncology research community.

To begin with, Fig. 4.1 presents the various steps of classifier evaluation along with the interaction between these steps. At each of these steps, choices must be made. In particular, the researcher must decide on which algorithms will be used in the study, which data sets they will be applied, and what performance measure, resampling technique, and statistical tests will be used. Each of these questions is quite complex because the choices made at one step may impact on the other steps. For example, if the data set on which the evaluation will be based contains very few instances of X-rays with malignant tumors and many instances of X-rays with benign tumors, then the performance measure (or metric) to be used cannot be the same as if there were as many instances of each cases. In addition, the choices to be made at each step depend on the purpose of the evaluation. Here are four common scenarios:

Fig. 4.1

The main steps of evaluation

• Comparison of a new algorithm to other (may be generic or application-specific) classifiers on a specific domain (e.g., when proposing a novel learning algorithm)

• Comparison of a new generic algorithm to other generic ones on a set of benchmark domains (e.g., to demonstrate general effectiveness of the new approach against other approaches)

• Characterization of generic classifiers on benchmarks domains (e.g., to study the algorithms’ behavior on general domains for subsequent use)

• Comparison of multiple classifiers on a specific domain (e.g., to find the best algorithm for a given application task)

To better illustrate the difficulties of making the appropriate choices at each step, we look at an example involving the choice of an appropriate performance measure. Table 4.1 shows the performance obtained by eight different classifiers (naive Bayes [NB], C4.5, three-nearest neighbor [3NN], ripper [Rip], support vector machines [SVM], bagging [Bagg], boosting [Boost], random forest [RF]) on a given data set (the UCI breast cancer data set [2]) using nine different performance measures (accuracy [Acc], root-mean-square error [RMSE], true positive rate [TPR], false positive rate [FPR], precision [Prec], recall [Rec], F-measure [F], area under the ROC curve [AUC], information score [Info S]). As can be seen from the table, each measure tells a different story. For example, accuracy ranks C4.5 as the best classifier for this domain, while according to the AUC, C4.5 is the worst classifier (along with SVM, which accuracy did not rank highly either). Similarly, the F-measure ranks naive Bayes in the first place, whereas it only reaches the 5th place as far as RMSE is concerned. This suggests that one may obtain very different conclusions depending on what performance measure is used. Generally speaking, this example points to the fact that classifier evaluation is not an easy task and that not taking it seriously may yield grave consequences.

Table 4.1 The performance of eight different classifiers according to nine different performance measures. There is clear disagreement among the evaluation measures

The next section looks at performance measures in more detail, while the next two sections will discuss resampling and statistical testing.

3 Performance Measures

Figure 4.2 presents an overview of the various performance measures commonly used in machine learning. This overview is not comprehensive, but touches upon the main measures. In the figure, the first line, below the “all measures” box indicates the kind of information used by the performance measure to calculate the value. All measures use the confusion matrix, which will be presented next, but some add additional information such as the classifier’s uncertainty or the cost ratio of the data set, while others also use other information such as how comprehensible the result of the classifier is or how generalizable it is, and so on. The next line in the figure indicates what kind of classifier the measure applies to deterministic classifiers, scoring classifiers, or continuous and probabilistic classifiers. Below this line comes information about the focus (e.g., multiclass with chance correction), format (e.g., summary statistics), and methodological basis (e.g., information theory) of the measures. The leaves of the tree list the measures themselves.

Fig. 4.2

An overview of performance measures

As just mentioned, all the measures of Fig. 4.2 are based on the confusion matrix. The template for a confusion matrix is given in Table 4.2:

Table 4.2 A generic confusion matrix

TP, FP, FN, and TN stand for true positive, false positive, false negative, and true negative, respectively. Some common performance measures calculated directly from the confusion matrix are:

• Accuracy = (TP + TN)/(P + N)

• Precision = TP/(TP + FP)

• Recall, sensitivity, or true positive rate = TP/P

• False alarm rate or false positive rate = FP/N

For a more comprehensive list of measures including sensitivity, specificity, likelihood ratios, positive and negative predictive values, and so on, please refer to [1].

We now illustrate some of the problems encountered with accuracy, precision, and recall since they represent important problems in evaluation. Consider the confusion matrices of Table 4.3. The accuracy for both matrices is 60 %. However, the two matrices t classifiers with the same accuracy account for two very different classifier behaviors. On the left, the classifier exhibits a weak positive recognition rate and a strong negative recognition rate. On the right, the classifier exhibits a strong positive recognition rate and a weak negative recognition rate. In fact, accuracy, while generally a good and robust measure, is extremely inappropriate in the case of class imbalance data, such as the example, mentioned in Sect. 4.2 where there were only very few instances of X-rays containing malignant tumors and many instances containing benign ones. For example, in the extreme case where, say, 99.9 % of all the images would not contain any malignant tumors and only 0.1 % would, the rough classifier consisting of predicting “benign” in all cases would produce an excellent accuracy rate of 99.9 %. Obviously, this is not representative of what the classifier is really doing because, as suggested by its 0 % recall, it is not an effective classifier at all, specifically if what it is trying to achieve is the recognition of rare, but potentially important, events. The problem of classifier evaluation in the case of class imbalance data is discussed in [3].

Table 4.3 The confusion matrices of two very different classifiers with the same accuracy

Table 4.4 illustrates the problem with precision and recall. Both classifiers represented by the table on the left and the table on the right obtain the same precision and recall values of 66.7 and 40 %. Yet, they exhibit very different behaviors: while they do show the same positive recognition rate, they show extremely different negative recognition rates; in the left confusion matrix, the negative recognition rate is strong, while in the right confusion matrix, it is nil! This certainly is information that is important to convey to a user, yet, precision and recall do not focus on this kind of information. Note, by the way, that accuracy which has a multiclass rather than a single-class focus has no problem catching this kind of behavior: the accuracy of the confusion matrix on the left is 60 %, while that of the confusion matrix on the right is 33 %!

Table 4.4 The confusion matrices of two very different classifiers with the same precision and recall

Because the class imbalance problem is very pervasive in machine learning, ROC analysis and its summary measure and the area under the ROC curve (AUC), which do not suffer from the problems encountered by accuracy, have become central to the issue of classifier evaluation. We now give a brief description of that approach. In the context of the class imbalance problem, the concept of ROC analysis can be interpreted as follows. Imagine that instead of training a classifier f only at a given class imbalance level, that classifier is trained at all possible imbalance levels. For each of these levels, two measurements are taken as a pair, the true positive rate (or sensitivity) and the false positive rate (FPR) (or false alarm rate). Many situations may yield the same measurement pairs, but that does not matter since duplicates are ignored. Once all the measurements have been made, the points represented by all the obtained pairs are plotted in what is called the ROC space, a graph that plots the true positive rate as a function of the false positive rate. The points are then joined in a smooth curve, which represents the ROC curve for that classifier. Figure 4.3 shows two ROC curves representing the performance of two classifiers f1 and f2 across all possible operating ranges.

Fig. 4.3

The ROC curves of two classifiers f1 and f2. f1 performs better than f2 in all parts of the ROC space

The closer a curve representing a classifier f is from the top-left corner of the ROC space (small false positive rate, large true positive rate), the better the performance of that classifier. For example, f 1 performs better than f 2 in the graph of Fig. 4.3. However, the ideal situation of Fig. 4.3 rarely occurs in practice. More often than not, one is faced with a situation such as that of Fig. 4.4, where one classifier dominates the other in some parts of the ROC space, but not in others.

Fig. 4.4

The ROC curves of two classifiers f1 and f2. f2 performs better than f1 on the left side of the ROC space. After the two curves, cross f1 performs better than f1

The reason why ROC analysis is well suited to the study of class imbalance domains is twofold. First, as in the case of the single-class focus metrics of the previous section, rather than being combined together into a single multiclass focus metric, performance on each class is decomposed into two distinct measures. Second, the imbalance ratio that truly applies in a domain is rarely precisely known. ROC analysis gives an evaluation of what may happen in diverse situations.

We now move on to discussing the question of data resampling.

3.1 Resampling

What is the purpose of resampling? Ideally, we would have access to the entire population or a lot of representative data from it. This, unfortunately, is usually not the case, and the limited data available has to be reused in clever ways in order to be able to estimate the error of our classifiers as reliably as possible. Resampling is divided into two categories: simple resampling (where each data point is used for testing only once) and multiple resampling (which allows the use of the same data point more than once for testing). In addition to discussing a few resampling approaches, this section will underline the issues that may arise when applying them. Figure 4.5 gives an overview of various resampling regimens. We will discuss a few of them. For a more detailed presentation, please see [1].

Fig. 4.5

Overview of resampling methods

When the data set is very large and all cases are well represented, then no resampling method is needed, and it is possible to use the holdout method where a portion of the data set is reserved for training while the rest of the data set is used for testing. Please note that the practice of training and testing on the same data set (re-substitution) is unacceptable when the goal of the study is to test the predictive capability of the learning tool. Such a practice gives an optimistic assessment of the tool’s capability. In general, the classifier will overfit the data it was trained on, which means that it will perform very well on that data and obtain much poorer results on data it has never seen before. To a certain extent and for many algorithms, the better the classifier performs on the known data, the worse it will perform on unknown data.

In most cases, there is not enough data to use the holdout method. The most commonly used resampling method then is k-fold cross validation and its variants, stratified k-fold cross validation, and leave-one-out, also known as the jackknife. 10 × 10-fold cross validation has also become quite common and the 0.632 bootstrap is sometimes used as well. We will present each of these schemes in turn and discuss the situations in which each scheme is believed to be most appropriate.

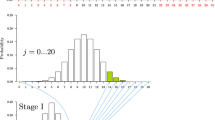
Figure 4.6 illustrates the k-fold cross-validation process in the following ways: each line of the graph symbolizes the entire data set. It is randomly divided into k subsets (on the graph, k = 10) as symbolized by the k = 10 rectangles that compose each line. The first line corresponds to Fold 1, the second to Fold 2, and so on. In Fold 1, the first rectangle is shaded differently from the others. This signifies that in this fold, the data represented by the first rectangle will be used as testing data while the data represented by the other k-1 rectangles will be used as training data. In Fold 2, it is the data of the second rectangle that is used as the testing set, while the data represented by the other rectangles are used as the training set. This goes on k times so that each of the rectangles is used as a testing set. This is an interesting scheme which guarantees that (1) at each fold, the training and the testing set are separate; (2) once the entire scheme has been executed, every data point has been used as a testing point; (3) no data point has been used more than once as a testing point; and (4) every data point has been used k-1 times as a training point. So in summary, there is no overlap in the testing sets, but there is overlap in the training set. The facts that there is no overlap in the testing set, that this scheme is very simple to implement, and that it is not very computer intensive make it a very popular approach believed to yield a good error estimate. Because of the high overlap in the training set, however, the method can yield a bias in the error estimate, but this is mitigated in the case of moderate to large data sets.

Fig. 4.6

The k-fold cross-validation process

When the data set is imbalanced, k-fold cross validation as just described can yield problems. In particular, the random division of the data into k subsets may yield situations where the data of the minority class is not at all represented in the subset. The performance of the classifier on such a data set would be misleading as it would be overly optimistic. Similarly, if the training data contained an even smaller proportion of minority examples than the actual data set, the classifier’s performance would be overly pessimistic. In order to avoid both problems, a process called stratified k-fold cross validation is used to ensure that the distribution is respected in the training and testing sets created at every fold. This would not necessarily be the case if a pure random process were used.

Another issue arises when the data set is quite small. In such cases, k-fold cross validation may cause the training portion of the data at each fold to be too small for effective learning to take place. In such cases, it is common to set k to the size of the data set, meaning that (1) there are as many folds as there are data points and, at each fold, (2) the testing set includes a single data point and (3) the classifier is trained on all the data but this particular point. This process is commonly called leave-one-out or the jackknife. It has the advantage of yielding a relatively unbiased classifier (since virtually all the data is used for training at each fold, although since the data set is small to begin with, the classifier is probably not unbiased); however, the error estimate is likely to show high variance since only one example is tested at every fold, resulting in a 0 or 100 % accuracy rate for each fold. In addition, it is a very time-consuming process since the number of folds equals the size of the data set.

A further issue with the family of k-fold cross-validation approaches just discussed concerns the stability of the estimate it produces. In order to improve the stability of that estimate, it has become commonplace to run the k-fold cross-validation process multiple times, each with different random partitions of the data into k-folds. The most common combination is the 10 × 10-fold cross validation [4], though 5 × 2-fold cross validation [5] had also been proposed early on as an alternative to tenfold cross validation.

We conclude this discussion with a presentation of bootstrapping, an alternative to the k-fold cross-validation schemes. Bootstrapping assumes that the available sample is representative and creates a large number of new samples by drawing from replacement from the available sample. Bootstrapping is useful in practice when the sample is too small for cross-validation or leave-one-out approaches to yield a good estimate. There are two bootstrap estimates that are useful in the context of classification: the Є0 and the e632 bootstraps. The Є0 bootstrap tends to be pessimistic because it is only trained on 63.2 % of the data in each run. The e632 attempts to correct for this. The listing below is an informal description of the algorithms for the Є0 and e632 bootstraps.

• Given a data set D of size m, we create k bootstrap samples B _i of size m, by sampling from D with replacement (k is typically ≥ 200).

• At each run, each of the k bootstraps represent the training set while the testing set is made up of a single copy of the examples from D that did not make it to B _i .

• At each run, a classifier is trained and tested and Єo_i represents the performance of the classifier at that run.

• Єo represents the average of all the Єo_i’s.

  e632 = 0.632 x Єo + 0.368 x err (f)

Where err(f) is the optimistically biased re-substitution error (error rate obtained when training and testing on D)

As previously mentioned, bootstrapping is a good estimator when the data set is too small to run k-fold cross validation or leave-one-out. In particular, it was shown to have low variance in such cases. On the other hand, bootstrapping is not a useful estimator in the case of classifiers that do not benefit from the presence of duplicate instances such as k-nearest neighbors.

4 Significance Testing

The performance metrics discussed in Sect. 4.2 allow us to make observations about different classifiers, and the resampling approaches discussed in Sect. 4.3 allow us to reuse the available data in order to obtain results believed to be more reliable. The question we ask in this section is related to the issue raised by resampling in Sect. 4.3. In particular, we ask to what extent the observed results are, indeed, reliable. More specifically, can the observed results be attributed to the real characteristics of the classifiers under scrutiny or are they observed by chance? The purpose of statistical significance testing is to help us gather evidence of the extent to which the results returned by an evaluation metric on the resampled data sets are representative of the general behavior of our classifiers.

Although some researchers have argued against the use of statistical tests mainly because it is often difficult to perform properly and its results are often overvalued and limit the search for new ideas [6, 7], statistical testing remains the norm in most experimental settings. Nonetheless, in line with the critics, it is important to conduct and interpret such tests properly. We will discuss basic aspects of the practice in what follows. In particular two issues arise:

• 1. Do we have enough information about the underlying distributions of the classifiers’ results to apply a parametric test?

• 2. What kind of problem are we considering?

  • The comparison of two algorithms on a single domain

  • The comparison of two algorithms on several domains

  • The comparison of multiple algorithms on multiple domains

Figure 4.7 overviews the various statistical tests in relation to these two problems. The first line in the figure differentiates between the kinds of problems considered. The next line lists the different statistical tests available in each situation. The tests in red boxes are parametric tests while those in green boxes represent nonparametric tests. Parametric tests have the advantage of being more powerful than nonparametric ones, but they apply in a more limited number of situations than the nonparametric ones since they require knowledge of the underlying distribution. Nonparametric tests are more flexible than the parametric ones since they do not take into account the underlying distribution. Instead, they use ranking information.

Fig. 4.7

Overview of statistical tests

A comprehensive discussion of all these tests can be found in [1]. In this chapter, we will focus on three versatile nonparametric tests: McNemar’s test, Wilcoxon’s signed-rank test for matched pairs, and Friedman’s test (followed by Nemenyi’s test). McNemar’s test applies in the case of two algorithms and one domain; Wilcoxon’s test applies in the case of two algorithms tested on multiple domains and Friedman’s test applies to the case of multiple algorithms executed over multiple domains.

McNemar’s test calculates four variables:

• The number of instances misclassified by both classifiers (C ₀₀)

• The number of instances misclassified by the first classifier but correctly classified by the second (C ₀₁)

• The number of instances misclassified by the second classifier but correctly classified by the first (C ₁₀)

• The number of instances correctly classified by both classifiers (C ₁₁)

McNemar’s χ ² statistics is given by

$$ {\chi^2}_{MC}={\left(\left|{C}_{01}\hbox{--} {C}_{10}\right|\hbox{--} 1\right)}^2/\left({C}_{01}+{C}_{10}\right) $$

If C ₀₁ + C ₁₀ < 20, then the test cannot be used.

Otherwise, the χ ² _MC statistics is compared to the χ² statistics. If χ ² _MC exceeds the χ² _{1, 1-α} statistic, then we can reject the null hypothesis that assumes that the first and second classifiers perform equally well with 1–α confidence.

Wilcoxon’s signed-rank test deals with two classifiers on multiple domains. It is also nonparametric. Here is its description:

• For each domain, we calculate the difference in the performance of the two classifiers.

• We rank the absolute values of these differences and graft the signs in front of the ranks.

• We calculate the sum of positive and negative ranks, respectively (W _S1 and W _S2).

• We compute T _Wilcox such that T _Wilcox = min (W _S1,W _S2).

• We compare T _Wilcox to critical value V _α . If V _α ≥T _Wilcox, we reject the null hypothesis that the performance of the two classifiers is the same at the α confidence level.

Wilcoxon’s signed-rank test is illustrated in Table 4.5 and in the discussion below the table. In this example, NB and SVM are compared on ten different domains.

Table 4.5 Wilcoxon’s signed-rank test for NB and SVM on 10 different domains

From the table, we find that W _S1 = 17 and W _S2 = 28, which means that T _Wilcox = min (17, 28) = 17. For n = 10–1 degrees of freedom and α = 0.005, V = 8 (see Table 4.5 in Appendix A of [1]) for the 1-sided test. V must be larger than T _Wilcox in order to reject the hypothesis. Since 17 >8, we cannot reject the hypothesis that NB’s performance is equal to that of SVM at the 0.005 level.

In the case where multiple algorithms are to be compared on multiple domains, Friedman’s test is a simple and good alternative. It is conducted as follows:

• All the classifiers are ranked on each domain separately. Ties are broken by adding the ranks of the tied algorithms and dividing them by the number of algorithms involved in the tie. The result is assigned to each of the algorithms involved in the tie.

• For each classifier, the sum of ranks obtained on all domains is calculated and labeled R. _j ² where j symbolizes the classifier.

• Friedman’s statistics is then calculated as follows:

$$ {\chi}_F=\left[12\raisebox{1ex}{}\!\left/ \!\raisebox{-1ex}{}\right.n.k.\left(k+1\right).\kern0.46em {\displaystyle \sum}_{j=1}^k\;R{.}_j\right]-3.\;n.\;\left(k+1\right) $$

where n represents the number of domains and k the number of classifiers

Table 4.6 illustrates Friedman’s test on a synthetic example. The table on the left lists the accuracies obtained by classifiers fA, fB, and fC on domains 1, 2, … 10. The table on the left calculates the rank of each classifier on each domain. These ranks in each column are then added yielding the R. _j ’s. Applying the formula, we find that χ _F ² = 15.05. From Table 7 in Appendix A of [1], we find that for a 2-tailed test at the 0.05 level of significance, the critical value is 7.8. Since χ _F ² >7.8, we can reject the null hypothesis that all three algorithms perform equally well.

Table 4.6 Friedman’s test applied to three classifiers fA, fB, and fC on ten different domains

Note that while Friedman’s test shows that there is a significant difference among the algorithms being tested, it does not say where that difference is. In such cases, Nemenyi’s test (or other post hoc tests) can be used to pinpoint where that difference lies. Here is how Nemenyi’s test works.

• Let R _ij be the rank of classifier f _j on data set S _i ; we compute the mean rank of classifier f _j on all data sets as

  $$ \overline{R{.}_j}=\kern1.34em \frac{1}{n}\;{\displaystyle \sum}_{i=1}^n{R}_{ij} $$

• Let q _yz be the statistic between classifier f_y and f _z . The formula is

  $$ {q}_{yz}=\frac{\overline{R{.}_y}-\overline{R{.}_z}}{\sqrt{\frac{k\left(k+1\right)}{6n}}} $$

  (n is the number of domains and k the number of classifiers).

• Nemenyi’s test proceeds by calculating all the q _yz statistics. Then, those that exceed a critical value q _α are said to indicate a significant difference between classifiers f_y and f _z at the α significance level.

To illustrate Nemenyi’s test, we calculate the following values from Friedman’s test we just ran¹:

$$ \overline{R{.}_A}=1.55,\overline{\mathrm{R}{.}_{\mathrm{B}}}=3,\;\mathrm{and}\;\overline{\mathrm{R}{.}_{\mathrm{C}}}=1.45 $$

• Replacing R _.y and R _.Z by the above values in

$$ {q}_{yz}=\frac{\overline{R.y}-\overline{R.z}}{\sqrt{\frac{k\left(k+1\right)}{6n}}} $$

we obtain q _AB  = −3.22, q _AC  = .222, and q _BC  = 3.44.

• q _α  = 2.55 for α = 0.05 [see [1]) (q _α must be larger than qyz for the hypothesis that y and z perform equally to be rejected).

• Therefore, we reject the null hypothesis in the case of classifiers A and B and B and C (please note that we consider the absolute value of the q _xy quantity), but not in the case of A and C.

5 Conclusion

This chapter presented the most common methods of evaluating the performance of classifiers on applied domains. Unfortunately, there is no preexisting recipe that satisfies every situation. In most cases, the user must reflect about what he or she is trying to verify, understand the restrictions of the experimental setting (e.g., too little data, data skews (or imbalances), and so on), and apply the best combination of evaluation methods that is available in these conditions. It is important to note that due to the fact that there is a lot of unknown in the data, certain assumptions about the data may end up being violated. It remains unknown to what extent this will invalidate the results. Last but not least, it is important to understand how to interpret the results one observes. These results should be thought of as support for a hypothesis or evidence about certain effects. They do not prove that a hypothesis is correct. Classifier evaluation thus remains an art rather than a perfect science.