Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Chaotic behaviour is an important feature, which is observed in some nonlinear dynamical systems. Chaotic behaviour was suspected well over hundred years ago in the study of three bodies problem, but it was established only a few decades ago in the study of 3-D weather models (Lorenz 1963).

A chaotic system is usually characterized by its extreme sensitivity of behavior to initial conditions. Small changes in an initial state will make a very large difference in the behavior of the system at future states.

The Lyapunov exponent is a measure of the divergence of phase points that are initially very close and can be used to quantify chaotic systems. It is common to refer to the largest Lyapunov exponent as the maximal Lyapunov exponent (MLE). A positive maximal Lyapunov exponent and phase space compactness are usually taken as defining conditions for a chaotic system.

In 1963, Lorenz found out that a very small difference in the initial conditions of his 3-D deterministic weather model led to large changes in the phase space (Lorenz 1963). This was followed by the discoveries of many well-known paradigms of 3-D chaotic systems in the literature (Rössler 1976; Arneodo et al. 1981; Sprott 1994; Chen and Ueta 1999; Lü and Chen 2002; Liu et al. 2004; Cai and Tan 2007; Chen and Lee 2004; Tigan and Opris 2008; Zhou et al. 2008; Sundarapandian and Pehlivan 2012; Vaidyanathan 2013a, b, 2014).

Chaotic systems have several applications in science and engineering. Some important applications can be mentioned as cryptosystems (Usama et al. 2010; Rhouma and Belghith 2011), secure communications (Murali and Lakshmanan 1998; Feki 2003; Zaher and Abu-Rezq 2011), chemical reactions (Petrov et al. 1993; Gaspard 1999), oscillators (Kengne et al. 2012; Sharma et al. 2012), lasers (Yuan et al. 2014; Li et al. 2014), biology (Das et al. 2014; Kyriazis 1991), ecology (Suérez 1999; Gibson and Wilson 2013), robotics (Nehmzow and Walker 2005; Volos et al. 2013; Mondal and Mahanta 2014), cardiology (Qu 2011; Witte and Witte 1991), neural networks (Kaslik and Sivasundaram 2012; Huang et al. 2012; Lian and Chen 2011), finance (Sprott 2004; Guégan 2009), etc.

Synchronization of chaotic systems is a phenomenon that occurs when two or more chaotic systems are coupled or when a chaotic system drives another chaotic system. Because of the butterfly effect which causes exponential divergence of the trajectories of two identical chaotic systems started with nearly the same initial conditions, the synchronization of chaotic systems is a challenging research problem in the chaos literature.

The master-slave or drive-response formalism is used in most of the chaos synchronization approaches. If a particular chaotic system is called the master or drive system and another chaotic system is called the slave or response system, then the goal of chaos synchronization is to use the output of the master system to control the slave system so that the output of the slave system tracks the output of the master system asymptotically.

Pecora and Carroll pioneered the research on synchronization of chaotic systems with their seminal papers in 1990s (Pecora and Carroll 1990; Carroll and Pecora 1991). The active control method (Ucar et al. 2007; Liu et al. 2007; Sundarapandian 2010; Vaidyanathan 2012c; Wang and Liu 2006; Rafikov and Balthazar 2007) is commonly used when the system parameters are available for measurement and the adaptive control method (Wu et al. 2008; Huang 2008; Lin 2008; Sarasu and Sundarapandian 2012a, b, c) is commonly used when some or all the system parameters are not available for measurement and estimates for unknown parameters of the systems.

Other popular methods for chaos synchronization are the sampled-data feedback method (Xiao et al. 2014; Zhang and Zhou 2012; Li et al. 2011; Gan and Liang 2012), time-delay feedback method (Shahverdiev and Shore 2009; Jiang et al. 2004; Chen et al. 2014; Shahverdiev et al. 2009), backstepping method (Njah et al. 2010; Tu et al. 2014; Zhang et al. 2004; Vaidyanathan 2012a), etc.

Complete synchronization (Vaidyanathan and Rajagopal 2011a; Rasappan and Vaidyanathan 2012a; Suresh and Sundarapandian 2013) is characterized by the equality of state variables evolving in time, while anti-synchronization (Vaidyanathan 2011; Vaidyanathan and Sampath 2012; Vaidyanathan 2012b) is characterized by the disappearance of the sum of relevant state variables evolving in time.

In hybrid synchronization of the master and slave systems, the odd numbered states of the two systems are completely synchronized while the even numbered states are anti-synchronized so that the complete synchronization (CS) and anti-synchronization (AS) co-exist in the synchronization process. Thus, the hybrid synchronization (Vaidyanathan and Rajagopal 2011b; Sundarapandian and Karthikeyan 2012; Karthikeyan and Sundarapandian 2014; Rasappan and Vaidyanathan 2012b) is an important type of synchronization of chaotic systems, which has applications in secure communication devices.

This research work is organized as follows. Section 2 gives a basic introduction into sliding mode control and chaos synchronization. Section 3 discusses the problem statement for the synchronization of two identical chaotic systems and our design methodology. Section 4 contains the main result of this work, namely, sliding controller design for the global chaos synchronization of identical chaotic systems. Section 5 summarizes the qualitative properties of the Vaidyanathan chaotic system (Vaidyanathan 2014). In Sect. 6, we describe the sliding mode controller design for the global chaos synchronization of identical Vaidyanathan systems. MATLAB simulations are shown to validate and illustrate the sliding mode controller design for the synchronization of the Vaidyanathan systems. Section 7 contains a summary of the main results derived in this research work.

2 Sliding Mode Control and Chaos Synchronization

In control theory, the sliding mode control approach is recognized as an efficient tool for designing robust controllers for linear or nonlinear control systems operating under uncertainty conditions (Perruquetti and Barbot 2002; Utkin 1992).

Sliding mode control method has a major advantage of low sensitivity to parameter variations in the plant and disturbances affecting the plant, which eliminates the necessity of exact modeling of the plant.

In the sliding mode control theory, the control dynamics has two sequential modes, viz. (i) the reaching mode, and (ii) the sliding mode. Basically, a sliding mode controller (SMC) design consists of two parts: hyperplane (or sliding surface) design and controller design.

A hyperplane is first designed via the pole-placement approach in the modern control theory and a controller is then designed based on the sliding condition. The stability of the overall control system is ensured by the sliding condition and by a stable hyperplane. Sliding mode control theory has been used to deal with many research problems of control literature (Feng et al. 2014; Ouyang et al. 2014; Bidarvatan et al. 2014; Lu et al. 2014; Zhang et al. 2014; Hamayun et al. 2013).

3 Problem Statement

This section gives a problem statement of global hybrid-phase synchronization of a pair of identical chaotic systems called the master and slave systems.

The master system is taken as the chaotic system

$$\begin{aligned} \dot{x} = A x + f(x), \end{aligned}$$
(1)

where \(x \in \mathbf{IR}^n\) is the state of the system, \(A\) is the \(n \times n\) matrix of system parameters and \(f\) is a vector field that contains the nonlinear parts of the system and satisfies \(f(0) = 0\).

The slave system is taken as the controlled chaotic system

$$\begin{aligned} \dot{y} = A y + f(y) + u, \end{aligned}$$
(2)

where \(y \in \mathbf{IR}^n\) is the state of the system, and \(u\) is the controller to be determined.

The hybrid synchronization error is defined by

$$\begin{aligned} e_i = \left\{ \begin{array}{cccl} y_i - x_i\quad \mathrm{{if}}\,i\,\mathrm{{is~odd}} \\[1mm] y_i + x_i\quad \mathrm{{if}}\,i\,\mathrm{{is~even}} \\[1mm] \end{array} \right. \end{aligned}$$
(3)

Differentiating (3) and simplifying, the error dynamics is obtained as

$$\begin{aligned} \dot{e} = A e + \eta (x, y) + u \end{aligned}$$
(4)

The design problem is to determine a feedback control \(u\) so that the error dynamics (4) is globally asymptotically stable at the origin for all initial conditions \(e(0) \in \mathbf{IR}^n\).

For the SMC design for the hybrid phase synchronization of the systems (1) and (2), the control \(u\) is taken as

$$\begin{aligned} u(t) = - \eta (x, y) + B v(t), \end{aligned}$$
(5)

where \(B\) is an \((n \times 1)\) column vector chosen such that \((A, B)\) is controllable.

Upon substituting (5) into (4), the closed-loop error system is obtained as

$$\begin{aligned} \dot{e}(t) = A e(t) + B v(t), \end{aligned}$$
(6)

which is a linear time-invariant control system with a single input \(v\).

Hence, by the use of the nonlinear control law (5), original problem of hybrid phase synchronization of identical chaotic systems (1) and (2) has been converted into an equivalent problem of globally stabilizing the error dynamics (6).

4 Sliding Controller Design for Hybrid Phase Synchronization

This section derives the main result, viz. sliding controller design for the hybrid phase synchronization of the identical chaotic systems (1) and (2). After applying the control (5) with \((A, B)\) a controllable pair, it is supposed that the nonlinear error dynamics (4) has been simplified as the linear error dynamics (6).

In the sliding controller design, the sliding variable is first defined as

$$\begin{aligned} s(e) = C e = c_1 e_1 + c_2 e_2 + \cdots + c_n e_n, \end{aligned}$$
(7)

where \(C\) is an \((1 \times n)\) row vector to be determined.

The sliding manifold \(S\) is defined as the hyperplane

$$\begin{aligned} S = \{ e \in \mathbf{IR}^n :\quad s(e) = C e = 0 \} \end{aligned}$$
(8)

If a sliding motion occurs on \(S\), then the sliding mode conditions must be satisfied, which are given by

$$\begin{aligned} s \equiv 0 ~ \mathrm{{and}} ~ \dot{s} = C A e + C B v = 0 \end{aligned}$$
(9)

It is assumed that the row vector \(C\) is chosen so that \(C B \ne 0\).

The sliding motion is affected by the so-called equivalent control given by

$$\begin{aligned} v_{\tiny \mathrm{eq}}(t) = - (C B)^{-1} C A e(t) \end{aligned}$$
(10)

As a consequence, the equivalent dynamics in the sliding phase is defined by

$$\begin{aligned} \dot{e} = \left[ I - B (C B)^{-1} C \right] A e = E e, \end{aligned}$$
(11)

where

$$\begin{aligned} E = \left[ I - B (C B)^{-1} C \right] A \end{aligned}$$
(12)

It can be easily verified that \(E\) is independent of the control and has at most \((n - 1)\) nonzero eigenvalues, depending on the chosen switching surface, while the associated eigenvectors belong to \(\mathrm{{ker}}(C)\).

Since \((A, B)\) is controllable, the matrices \(B\) and \(C\) can be chosen so that \(E\) has any desired \((n - 1)\) stable eigenvalues.

Thus, the dynamics in the sliding mode is globally asymptotically stable.

Finally, for the sliding mode controller (SMC) design, the constant plus proportional rate reaching law is used, which is given by

$$\begin{aligned} \dot{s} = - \beta \mathop {\mathrm {sgn}}(s) - \alpha s \end{aligned}$$
(13)

where \(\mathop {\mathrm {sgn}}(\cdot )\) denotes the sign function and the gains \(\alpha > 0, \beta > 0\) are found so that the sliding condition is satisfied and the sliding motion will occur.

From the equations (9) and (13), sliding control \(v\) is found as

$$\begin{aligned} C A e + C B v = - \beta \mathop {\mathrm {sgn}}(s) - \alpha s \end{aligned}$$
(14)

Since \(s = C e\), the equation (14) can be simplified to get

$$\begin{aligned} v = - (C B)^{-1} \left[ C (\alpha I + A) e + \beta \mathop {\mathrm {sgn}}(s) \right] \end{aligned}$$
(15)

Next, the main result of this section is established as follows.

Theorem 1

A sliding mode control law that achieves hybrid phase synchronization between the identical chaotic systems (1) and (2) for all initial conditions \(x(0), y(0) \in \mathbf{IR}^n\) is given by the equation

$$\begin{aligned} u(t) = - \eta (x(t), y(t)) + B v(t), \end{aligned}$$
(16)

where \(v\) is defined by (15), \(B\) is an \((n \times 1)\) vector such that \((A, B)\) is controllable, \(C\) is an \((1 \times n)\) vector such that \(C B \ne 0\) and that the matrix \(E\) defined by Eq. (12) has \((n - 1)\) stable eigenvalues.

Proof

\(\square \)The proof is carried out using Lyapunov stability theory (Khalil 2001).

Substituting the sliding control law (16) into the error dynamics (4) leads to

$$\begin{aligned} \dot{e} = A e + B v \end{aligned}$$
(17)

Substituting for \(v\) from (15) into (17), the error dynamics is obtained as

$$\begin{aligned} \dot{e} = A e - B (C B)^{-1} \left[ C (\alpha I + A) e + \beta \mathop {\mathrm {sgn}}(s) \right] \end{aligned}$$
(18)

The global asymptotic stability of the error system (18) is proved by taking the candidate Lyapunov function

$$\begin{aligned} V(e) = {1 \over 2} \ s^2(e), \end{aligned}$$
(19)

which is a non-negative definite function on \(\mathbf{IR}^n\).

It is noted that

$$\begin{aligned} V(e) = 0 \ \iff \ s(e) = 0 \end{aligned}$$
(20)

The sliding mode motion is characterized by the equations

$$\begin{aligned} s(e) = 0 \ \ \mathrm{{and}} \ \ \dot{s}(e) = 0 \end{aligned}$$
(21)

By the choice of \(E\), the dynamics in the sliding mode given by (11) is globally asymptotically stable.

When \(s(e) \ne 0\), \(V(e) > 0\).

Also, when \(s(e) \ne 0\), differentiating \(V\) along the error dynamics (18) or the equivalent dynamics (13), the following dynamics is obtained:

$$\begin{aligned} \dot{V} = s \dot{s} = - \beta s \, \mathop {\mathrm {sgn}}(s) - \alpha s^2 < 0 \end{aligned}$$
(22)

Hence, by Lyapunov stability theory (Khalil 2001), it is concluded that the error dynamics (18) is globally asymptotically stable for all initial conditions \(e(0) \in \mathbf{IR}^n\).

This completes the proof. \(\square \)

5 Analysis of the Vaidyanathan Chaotic System

This section gives details and qualitative properties of the Vaidyanathan chaotic system (Vaidyanathan 2014), which is a novel eight-term 3-D polynomial system with three quadratic nonlinearities.

The Vaidyanathan 3-D chaotic system is a polynomial system described by

$$\begin{aligned} \left. \begin{array}{ccl} \dot{x}_1 &{} = &{} a (x_2 - x_1) + x_2 x_3, \\ \dot{x}_2 &{} = &{} b x_1 + c x_2 - x_1 x_3, \\ \dot{x}_3 &{} = &{} - d x_3 + x_1^2, \\ \end{array} \right. \end{aligned}$$
(23)

where \(x_1, x_2, x_3\) are the states and \(a, b, c, d\) are constant, positive, parameters.

The Vaidyanathan system (23) depicts a strange chaotic attractor when the constant parameter values are taken as

$$\begin{aligned} a = 25, \quad b = 33, \quad c = 11, \quad d = 6. \end{aligned}$$
(24)

For simulations, the initial values of the Vaidyanathan system (23) are taken as

$$\begin{aligned} x_1(0) = 1.5, \quad x_2(0) = 3.2, \quad x_3(0) = 2.7 \end{aligned}$$
(25)

The Vaidyanathan 3-D chaotic system (23) exhibits a 3-scroll chaotic attractor. Figure 1 describes the 3-scroll chaotic attractor of the Vaidyanathan system (23) in 3-D view.

Fig. 1
figure 1

Strange attractor of the Vaidyanathan system in \(\mathbf{IR}^3\)

Full size image

Figure 2 describes the 2-D projection of the strange chaotic attractor of the novel system (23) in \((x_1, x_2)\)-plane. In the projection on the \((x_1, x_2)\)-plane, a 3-scroll chaotic attractor is clearly seen.

Fig. 2
figure 2

2-D projection of the Vaidyanathan system in \((x_1, x_2)\)-plane

Full size image
Fig. 3
figure 3

2-D projection of the Vaidyanathan system in \((x_2, x_3)\)-plane

Full size image

Figure 3 describes the 2-D projection of the strange chaotic attractor of the novel system (23) in \((x_2, x_3)\)-plane. In the projection on the \((x_2, x_3)\)-plane, a 3-scroll chaotic attractor is clearly seen.

Figure 4 describes the 2-D projection of the strange chaotic attractor of the novel system (23) in \((x_1, x_3)\)-plane. In the projection on the \((x_2, x_3)\)-plane, a 3-scroll chaotic attractor is clearly seen.

Fig. 4
figure 4

2-D projection of the Vaidyanathan system in \((x_1, x_3)\)-plane

Full size image

5.1 Symmetry and Invariance

The Vaidyanathan system (23) is invariant under the coordinates transformation

$$\begin{aligned} (x_1, x_2, x_3) \rightarrow (-x_1, -x_2, x_3). \end{aligned}$$
(26)

The transformation (26) persists for all values of the system parameters. Thus, the Vaidyanathan system (23) has rotation symmetry about the \(x_3\)-axis.

Hence, it follows that any non-trivial trajectory of the system (23) must have a twin trajectory.

It is easy to check that the \(x_3\)-axis is invariant for the flow of the Vaidyanathan system (23). Hence, all orbits of the system (23) starting from the \(x_3\) axis stay in the \(x_3\) axis for all values of time.

5.2 Equilibria

For the parameter values in (24), the Vaidyanathan system (23) has three equilibrium points given by

$$\begin{aligned} E_1 = \left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right] , \quad E_2 = \left[ \begin{array}{r} 14.9813 \\ 6.0015 \\ 37.4066 \\ \end{array} \right] \mathrm{{and}} \quad E_3 = \left[ \begin{array}{r} -14.9813 \\ -6.0015 \\ 37.4066 \end{array} \right] . \end{aligned}$$
(27)

The Jacobian matrix of the Vaidyanathan system (23) at \((x_1^\star , x_2^\star , x_3^\star )\) is obtained as

$$\begin{aligned} J(x^\star ) = \left[ \begin{array}{ccc} -25 &{} 25 + x_3^\star &{} x_2^\star \\[2mm] 33 - x_3^\star &{} 11 &{} -x_1^\star \\[2mm] 2 x_1^\star &{} 0 &{} -6 \\[2mm] \end{array} \right] \end{aligned}$$
(28)

The Jacobian matrix at \(E_1\) is obtained as

$$\begin{aligned} J_1 = J(E_1) = \left[ \begin{array}{rrr} -25 &{} 25 &{} 0 \\[2mm] 33 &{} 11 &{} 0 \\[2mm] 0 &{} 0 &{} -6 \\[2mm] \end{array} \right] \end{aligned}$$
(29)

The matrix \(J_1\) has the eigenvalues

$$\begin{aligned} \lambda _1 = -40.8969, \quad \lambda _2 = -6, \quad \lambda _3 = 26.8969 \end{aligned}$$
(30)

This shows that the equilibrium point \(E_1\) is a saddle-point.

The Jacobian matrix at \(E_2\) is obtained as

$$\begin{aligned} J_2 = J(E_2) = \left[ \begin{array}{ccc} -25 &{} 62.4066 &{} 6.0015 \\[2mm] -4.4066 &{} 11 &{} -14.9813 \\[2mm] 29.9626 &{} 0 &{} -6 \\[2mm] \end{array} \right] \end{aligned}$$
(31)

The matrix \(J_2\) has the eigenvalues

$$\begin{aligned} \lambda _1 = -40.5768, \quad \lambda _{2, 3} = 10.2884 \pm 25.1648 i \end{aligned}$$
(32)

This shows that the equilibrium point \(E_2\) is a saddle-focus.

The Jacobian matrix at \(E_3\) is obtained as

$$\begin{aligned} J_3 = J(E_3) = \left[ \begin{array}{ccc} -25 &{} 62.4066 &{} -6.0015 \\[2mm] -4.4066 &{} 11 &{} 14.9813 \\[2mm] -29.9626 &{} 0 &{} -6 \\[2mm] \end{array} \right] \end{aligned}$$
(33)

The matrix \(J_3\) has the eigenvalues

$$\begin{aligned} \lambda _1 = -40.5768, \quad \lambda _{2, 3} = 10.2884 \pm 25.1648 i \end{aligned}$$
(34)

This shows that the equilibrium point \(E_3\) is a saddle-focus.

Fig. 5
figure 5

Dynamics of the Lyapunov exponents of the Vaidyanathan system

Full size image

Hence, all the three equilibria of the Vaidyanathan system (23) are unstable.

5.3 Lyapunov Exponents and Lyapunov Dimension

For the parameter values as given by Eq. (24) and the initial state as given by Eq. (25), the Lyapunov exponents of the Vaidyanathan system (23) are numerically obtained as

$$\begin{aligned} L_1 = 6.5023, \quad L_2 = 0, \quad L_3 = -26.4352 \end{aligned}$$
(35)

Thus, the maximal Lyapunov exponent of the Vaidyanathan system (23) is \(L_1 = 6.5023\).

Since \(L_1 + L_2 + L_3 = -19.9329 < 0\), the system (23) is dissipative.

Also, the Lyapunov dimension of the Vaidyanathan system (23) is obtained as

$$\begin{aligned} D_L = 2 + {L_1 + L_2 \over | L_3 |} = 2.2467 \end{aligned}$$
(36)

which is fractional.

Figure 5 depicts the dynamics of the Lyapunov exponents of the Vaidyanathan system (23).

6 SMC Design of Synchronization of Vaidyanathan Chaotic Systems

This section details the construction of a hybrid synchronizer for identical Vaidyanathan chaotic systems via sliding mode control method.

The master system is taken as the Vaidyanathan system given by

$$\begin{aligned} \left. \begin{array}{ccl} \dot{x}_1 &{}=&{} a (x_2 - x_1) + x_2 x_3 \\[2mm] \dot{x}_2 &{}=&{} b x_1 + c x_2 - x_1 x_3 \\[2mm] \dot{x}_3 &{}=&{} - d x_3 + x_1^2 \\[2mm] \end{array} \right. \end{aligned}$$
(37)

where \(a, b, c, d\) are constant, positive parameters.

The slave system is also taken as the Vaidyanathan system with controllers attached and given by

$$\begin{aligned} \left. \begin{array}{ccl} \dot{y}_1 &{}=&{} a (y_2 - y_1) + y_2 y_3 + u_1 \\[2mm] \dot{y}_2 &{}=&{} b y_1 + c y_2 - y_1 y_3 + u_2 \\[2mm] \dot{y}_3 &{}=&{} - d y_3 + y_1^2 + u_3 \\[2mm] \end{array} \right. \end{aligned}$$
(38)

where \(u_1, u_2, u_3\) are sliding controllers to be found.

The hybrid phase synchronization error is defined by

$$\begin{aligned} \left. \begin{array}{ccl} e_1 ~ = ~y_1 - x_1 \\ e_2 ~ = ~y_2 + x_2 \\ e_3 ~ = ~y_3 - x_3 \\ \end{array} \right. \end{aligned}$$
(39)

Then the error dynamics is obtained as

$$\begin{aligned} \left. \begin{array}{ccl} \dot{e}_1 &{}=&{} a (e_2 - e_1) - 2 a x_2 + y_2 y_3 - x_2 x_3 + u_1 \\[1mm] \dot{e}_2 &{}=&{} b e_1 + c e_2 + 2 b x_1 - y_1 y_3 - x_1 x_3 + u_2 \\[1mm] \dot{e}_3 &{}=&{} -d e_3 + y_1^2 - x_1^2 + u_3 \\[1mm] \end{array} \right. \end{aligned}$$
(40)

The error dynamics (40) can be expressed in matrix form as

$$\begin{aligned} \dot{e} = A e + \eta (x, y) + u \end{aligned}$$
(41)

where

$$\begin{aligned} A = \left[ \begin{array}{ccc} -a &{} a &{} 0 \\[1mm] b &{} c &{} 0 \\[1mm] 0 &{} 0 &{} -d \\[1mm] \end{array} \right] , \quad \eta (x, y) = \left[ \begin{array}{c} -2 a x_2 + y_2 y_3 - x_2 x_3 \\[1mm] 2 b x_1 - y_1 y_3 + x_1 x_3 \\[1mm] y_1^2 - x_1^2 \\[1mm] \end{array} \right] , \quad u = \left[ \begin{array}{c} u_1 \\[1mm] u_2 \\[1mm] u_3 \\[1mm] \end{array} \right] \end{aligned}$$
(42)

A hybrid synchronizing sliding controller can be designed by the procedure outlined in Sect. 5.

The parameter values of \(a, b, c, d\) are taken as in the chaotic case, i.e.

$$\begin{aligned} a = 25, \quad b = 33, \quad c = 11, \quad d = 6. \end{aligned}$$
(43)

First, the control \(u\) is set as

$$\begin{aligned} u = - \eta (x, y) + B v, \end{aligned}$$
(44)

where \(B\) is chosen such that \((A, B)\) is controllable.

A simple choice for \(B\) is

$$\begin{aligned} B = \left[ \begin{matrix} 1 \\ 1 \\ 1 \\ \end{matrix} \right] \end{aligned}$$
(45)

The sliding variable is picked as

$$\begin{aligned} s = C e = \left[ \begin{matrix} 1 &{} 2 &{} -1 \\ \end{matrix} \right] e = e_1 + 2 e_2 - e_3 \end{aligned}$$
(46)

Then the matrix \(E\) defined by (12) has the eigenvalues

$$\begin{aligned} \lambda _1 = -47, \quad \lambda _2 = -20, \quad \lambda _3 = 0 \end{aligned}$$
(47)

The choice of the sliding variable indicated by (46) renders the sliding mode dynamics globally asymptotically stable.

Next, we choose the SMC gains as

$$\begin{aligned} \alpha = 6, \quad \beta = 0.2 \end{aligned}$$
(48)

Using the formula (15), the control \(v\) is obtained as

$$\begin{aligned} v(t) = - 23.5 e_1 - 29.5 e_2 - 0.1 \mathop {\mathrm {sgn}}(s) \end{aligned}$$
(49)

As a consequence of Theorem 1 (Sect. 4), the following result is obtained.

Theorem 2

The control law defined by (44), where \(v\) is defined by (49), renders the Vaidyanathan systems (37) and (38) globally and asymptotically hybrid phase synchronized for all values of the initial states \(x(0), y(0) \in \mathbf{IR}^3\). \(\square \)

For numerical simulations, the classical fourth-order Runge-Kutta method with step-size \(h = 10^{-8}\) is used in the MATLAB software.

The parameter values are taken as in the chaotic case of the Vaidyanathan systems (37) and (38), i.e.

$$ a = 25, \quad b = 33, \quad c = 11, \quad d = 6 $$

The sliding mode gains are taken as

$$ \alpha = 6 \ ~ \mathrm{{and}} ~ \beta = 0.2 $$

The initial values of the master system (37) are taken as

$$ x_1(0) = 2.5, \quad x_2(0) = -3.7, \quad x_3(0) = -3.2 $$

The initial values of the slave system (38) are taken as

$$ y_1(0) = 4.3, \quad y_2(0) = -1.6, \quad y_3(0) = 2.4 $$

Figures 6, 7 and 8 show the hybrid synchronization of the Vaidyanathan systems (37) and (38).

In Fig. 6, it is seen that the odd states \(x_1(t)\) and \(y_1(t)\) are completely synchronized in 0.5 s.

Fig. 6
figure 6

Hybrid synchronization of the states \(x_1\) and \(y_1\)

Full size image
Fig. 7
figure 7

Hybrid synchronization of the states \(x_2\) and \(y_2\)

Full size image
Fig. 8
figure 8

Hybrid synchronization of the states \(x_3\) and \(y_3\)

Full size image

In Fig. 7, it is seen that the even states \(x_2(t)\) and \(y_2(t)\) are anti-synchronized in 0.5 s.

In Fig. 8, it is seen that the odd states \(x_3(t)\) and \(y_3(t)\) are completely synchronized in 0.5 s.

Fig. 9
figure 9

Time-history of the hybrid synchronization errors \(e_1, e_2, e_3\)

Full size image

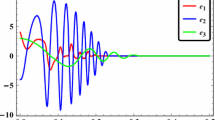
Figure 9 shows the time-history of the hybrid synchronization errors \(e_1, e_2\) and \(e_3\). It is seen that the hybrid synchronization errors converge to zero in 0.5 s. Thus, the sliding controller for hybrid synchronization of identical Vaidyanathan systems yields very fast convergence.

7 Conclusions

Hybrid phase synchronization is a new type of synchronization of a pair of chaotic systems called the master and slave systems, where the odd states are completely synchronized and the even states anti-synchronized. In this research work, a general theorem has been developed for the hybrid phase synchronization of identical chaotic systems via sliding mode controller. The main result was proved using Lyapunov stability theory. As an application of our general result, a sliding mode controller has been designed for the hybrid phase synchronization of identical Vaidyanathan chaotic systems (2014). MATLAB simulations were shown to illustrate the qualitative properties of the Vaidyanathan system and the hybrid synchronizer results for the identical Vaidyanathan systems. As future research, adaptive sliding mode controllers may be devised for the hybrid chaos synchronization of identical chaotic systems with unknown system parameters.