Canard Theory and Excitability

Abstract

An important feature of many physiological systems is that they evolve on multiple scales. From a mathematical point of view, these systems are modeled as singular perturbation problems. It is the interplay of the dynamics on different temporal and spatial scales that creates complicated patterns and rhythms. Many important physiological functions are linked to time-dependent changes in the forcing which leads to nonautonomous behaviour of the cells under consideration. Transient dynamics observed in models of excitability are a prime example.Recent developments in canard theory have provided a new direction for understanding these transient dynamics. The key observation is that canards are still well defined in nonautonomous multiple scales dynamical systems, while equilibria of an autonomous system do, in general, not persist in the corresponding driven, nonautonomous system. Thus canards have the potential to significantly shape the nature of solutions in nonautonomous multiple scales systems. In the context of neuronal excitability, we identify canards of folded saddle type as firing threshold manifolds. It is remarkable that dynamic information such as the temporal evolution of an external drive is encoded in the location of an invariant manifold—the canard.

1 Motivation

Physiological rhythms and patterns are central to life. Prominent examples are the beating of the heart, the activity patterns of neurons, and the release of the hormones that regulate growth and metabolism. Although many cells in the body display intrinsic, spontaneous rhythmicity, many physiological functions derive from the interaction of these cells, with each other and with external inputs, to generate these essential rhythms. Thus it is important to analyse both the origin of the intrinsic complex nonlinear processes and the effects of stimuli on these physiological rhythms.

Cell signalling is the result of a complex interaction of feedback loops that control and modify the cell behaviour via ionic flows and currents, proteins and receptor systems. The specific feedback loops differ from one cell to another and, from a physiological point of view, the signalling seems to be extremely cell specific. The respective mathematical cell models, however, have an amazingly similar structure. This suggests unifying mathematical mechanisms for cell signalling and its failure.

An important feature of most physiological systems is that they evolve on multiple scales. For example, the rhythm of the heart beat consists of a long interval of quasi steady-state followed by a short interval of rapid variation, which is the beat itself [34]. The same feature is observed for activity patterns of neurons [34, 55] and for calcium signalling in cells [34]. It is the interplay of the dynamics on different temporal or spatial scales that creates complicated rhythms and patterns.

Multiple scales problems of physiological systems are usually modelled by singularly perturbed systems [28, 34, 55]. The geometric theory of multiple scales dynamical systems—known as Fenichel theory [17, 32, 33, 49]—has provided powerful tools for studying singular perturbation problems. In conjunction with the innovative blow-up technique [15, 39, 57], geometric singular perturbation theory delivers rigorous results on global dynamics such as periodic and quasi-periodic relaxation oscillations in multiple time-scale problems [58]. When combined with results on Henon-like maps, this approach has the potential to explain chaotic dynamics in relaxation oscillators as observed in the periodically forced van der Pol relaxation oscillator [24].

This development within dynamical systems theory provides an excellent framework for addressing questions on how complex rhythms and patterns can be detected and controlled. The fact that equivalent stimulation can elicit qualitatively different spiking patterns in different neurons demonstrates that intrinsic coding properties differ significantly from one neuron to the next. Hodgkin recognized this and identified three basic types of neurons distinguished by their coding properties [29]. Pioneered by Rinzel and Ermentrout [31, 51, 52], bifurcation theory explains repetitive (tonic) firing patterns for adequate steady inputs (e.g. current step protocols) in integrator (type I) and resonator (type II) multiple time-scales neuronal models.

In contrast, the dynamic behaviour of differentiator (type III) neurons cannot be explained by standard (autonomous) dynamical systems theory. This third type of excitable neuron encodes a dynamic change in the input and hence they are well suited for temporal processing like phase-locking and coincidence detection [42, 53]. Auditory brain stem neurons are an important example of such neurons involved with precise timing computations. The nonautonomous (dynamic) nature of the signal is essential to determine the response of a type III neuron. A major aim of this chapter is to highlight the profound differences in the behaviour of all neuron types (I–III) when we apply a step current protocol compared to a smooth dynamic current protocol, either excitatory or inhibitory.

In a dynamical system that exhibits time-dependence in its forcing or parameters, one still expects convergence of the phase-space flow to some lower dimensional object; but this object, termed a pullback attractor [36, 37, 50], is now itself time-dependent. Identifying dynamic objects in phase-space that act effectively as separatrices is a major mathematical challenge. Such separatrices may influence the observed dynamics only on a certain (finite) time scale.

Recently, a canard mechanism was identified that leads to transient dynamics in multiple time-scales systems [26, 41, 44, 64]. Canards are exceptional solutions in singularly perturbed systems which occur on boundaries of regions corresponding to different dynamic behaviours. The theory on canards and their impact on transient dynamics of multiple scales dynamical systems is the main focus of this chapter. What makes canards so special for (driven) nonautonomous multiple scales dynamical systems? The key observation is that canard points (also known as folded singularities) are still well defined in nonautonomous multiple scales dynamical systems, while equilibria of an autonomous system will, in general, not persist in the corresponding driven, nonautonomous system. Thus canards have the potential to significantly shape the nature of solutions in nonautonomous multiple scales systems. We highlight this important point of view in Sect. 3.3.2.1.

Another class of complex oscillatory behaviour observed in neuroscience is mixed-mode oscillations (MMOs). These oscillations correspond to switching between small-amplitude oscillations and relaxation oscillations—patterns that have been frequently observed in experiments [1, 12, 25, 35, 47]. Recently, canard theory combined with an appropriate global return mechanism was used based on the multiple time-scale structure of the underlying models to explain these complicated dynamics [2, 3, 6, 22, 43, 57, 61, 63]. This is now one widely accepted explanation for MMOs; see, e.g., [5, 8, 14, 16, 27, 38, 54, 56, 60] and the current review [10].

The outline of the chapter is as follows: In Sect. 3.2 we review geometric singular perturbation theory in arbitrary dimensions with a particular emphasis on canard theory. In Sect. 3.3 we review excitable systems. We focus on external drives that are either piecewise constant or vary smoothly. The former models instantaneous (fast) changes while the later models smooth (slow) changes. We then outline the relationship between the theory of singularly perturbed systems and nonautonomous (multiple scales) systems. In particular, we show how canard theory can be used to explain excitability for smooth dynamic forcing protocols by identifying a canard of folded saddle type as the firing threshold manifold of an excitable neuron. The geometric theory is applied to neuronal and biophysical models. Finally, we conclude in Sect. 3.4.

Remark 3.1.

Section 3.2 provides a comprehensive review of geometric singular perturbation theory and assumes a solid background on dynamical systems theory such as found in [23]. While the basic ideas of geometric singular perturbation theory are well known to the mathematical biology/neuroscience community, the theory presented in this section might seem at certain points too technical and/or too rigorous for this peer group. We suggest that these readers skip (parts of) the section and explore the necessary theory after reading through Sect. 3.3 on excitability. Nevertheless, we hope that many readers will appreciate the rigor and generality of the presented material.

2 Geometric Singular Perturbation Theory

Our focus is on a system of differential equations that has an explicit time scale splitting of the form

$$\displaystyle{ \begin{array}{rcrcr} {w}^{{\prime}}& =& \epsilon \,g(w,v,\epsilon ) \\ {v}^{{\prime}}& =&f(w,v,\epsilon )\,, \end{array} }$$

(3.1)

where $(w,v) \in {\mathbb{R}}^{k} \times {\mathbb{R}}^{m}$ are state space variables and k, m ≥ 1. The variables v = (v ₁, …, v _m ) are denoted fast, the variables w = (w ₁, …, w _k ) are denoted slow, the prime denotes the time derivative d∕dt and ε ≪ 1 is a small positive parameter encoding the time scale separation between the slow and fast variables. The functions $f: {\mathbb{R}}^{k} \times {\mathbb{R}}^{m} \times \mathbb{R} \rightarrow {\mathbb{R}}^{m}$ and $g: {\mathbb{R}}^{k} \times {\mathbb{R}}^{m} \times \mathbb{R} \rightarrow {\mathbb{R}}^{k}$ are assumed to be C ^∞ smooth. By switching from the fast time scale t to the slow time scale τ = ε t, system (3.1) transforms to

$$\displaystyle{ \begin{array}{rcrcr} \dot{w}& =& g(w,v,\epsilon ) \\ \epsilon \,\dot{v}& =&f(w,v,\epsilon )\,. \end{array} }$$

(3.2)

where the overdot denotes the time derivative d∕dτ. System (3.1) respectively (3.2) are topologically equivalent and solutions often consist of a mix of slow and fast segments reflecting the dominance of one time scale or the other. We refer to (3.1) respectively (3.2) as a singularly perturbed system . As ε → 0, the trajectories of (3.1) converge during fast segments to solutions of the m-dimensional layer (or fast) problem

$$\displaystyle{ \begin{array}{rcl} {w}^{{\prime}}& =&0 \\ {v}^{{\prime}}& =&f(w,v,0) \end{array} }$$

(3.3)

while during slow segments, trajectories of (3.2) converge to solutions of

$$\displaystyle{ \begin{array}{rcl} \dot{w}& =&g(w,v,0) \\ 0& =&f(w,v,0)\end{array} }$$

(3.4)

which is a k-dimensional differential-algebraic problem called the reduced (or slow) problem . Geometric singular perturbation theory [17, 32] uses these lower-dimensional sub-systems (3.3) and (3.4) to predict the dynamics of the full (k + m)-dimensional system (3.1) or (3.2) for ε > 0.

2.1 The Layer Problem

First, we focus on the layer problem (3.3). Note that the slow variables w are parameters in this limiting system.

Definition 3.1.

The set

$$\displaystyle{ S:=\{ (w,v) \in {\mathbb{R}}^{k} \times {\mathbb{R}}^{m}\;\vert \;f(w,v,0) = 0\} }$$

(3.5)

is the set of equilibria of (3.3). In general, this set S defines a k-dimensional manifold, i.e. the Jacobian D _(w, v) f evaluated along S has full rank, and we refer to it as the critical manifold .

Remark 3.2.

The set S could be the union of finitely many k-dimensional manifolds. All definitions regarding the critical manifold hold also for such a set.

Since we assume that f is smooth, this implies that the critical manifold is a differentiable manifold. The basic classification of singularly perturbed systems is given by the properties of the critical manifold S of the layer problem (3.3).

Definition 3.2.

A subset S _h  ⊆ S is called normally hyperbolic if all (w, v) ∈ S _h are hyperbolic equilibria of the layer problem, that is, the Jacobian with respect to the fast variables v, denoted D _v f, has no eigenvalues with zero real part.

• We call a normally hyperbolic subset S _a  ⊆ S attracting if all eigenvalues of D _v f have negative real parts for (w, v) ∈ S _a ; the layer problem describes the flow towards this set.

• S _r  ⊆ S is called repelling if all eigenvalues of D _v f have positive real parts for (w, v) ∈ S _r ; the layer problem describes the flow away from this set.

• If S _s  ⊆ S is normally hyperbolic and neither attracting nor repelling we say it is of saddle type.

For a normally hyperbolic manifold S _h  ⊆ S, we have a uniform splitting of eigenvalues of D _v f along S _h into two groups, i.e. for each p ∈ S _h the Jacobian D _v f has m _u eigenvalues with positive real part and m _s eigenvalues with negative real part where $m_{u} + m_{s} = m$. This enables us to define local stable and unstable manifolds of the critical manifold S _h :

Definition 3.3.

The local stable and unstable manifolds of the critical manifold S _h denoted by $W_{loc}^{s}(S_{h})$ and $W_{loc}^{u}(S_{h})$, respectively, are the unions

$$\displaystyle{ W_{loc}^{s}(S_{ h}) =\bigcup _{p\in S_{h}}W_{loc}^{s}(p)\,,\quad W_{ loc}^{u}(S_{ h}) =\bigcup _{p\in S_{h}}W_{loc}^{u}(p)\,. }$$

(3.6)

The manifolds $W_{loc}^{s}(p)$ and $W_{loc}^{u}(p)$ form a family of fast fibers (called a fast fibration or foliation) for $W_{loc}^{s}(S_{h})$ and $W_{loc}^{u}(S_{h})$, respectively, with base points p ∈ S _h . The dimension of $W_{loc}^{s}(S_{h})$ is k + m _s and the dimension of $W_{loc}^{u}(S_{h,\epsilon })$ is k + m _u .

The geometric theory of singular perturbation problems with normally hyperbolic manifolds is referred to as Fenichel Theory [17, 32]. This theory guarantees the persistence of a normally hyperbolic manifold close to S _h  ⊆ S and corresponding local stable and unstable manifolds close to $W_{loc}^{s}(S_{h})$ and $W_{loc}^{u}(S_{h})$ as follows:

Theorem 3.1 (Fenichel’s Theorem 1, cf. [17, 32]).

Given system (3.1) with f,g ∈ C ^∞ . Suppose S _h ⊆ S is a compact normally hyperbolic manifold, possibly with boundary. Then for ε > 0 sufficiently small the following holds:

• (i) For any r < ∞, there exists a C ^r  smooth manifold S _h,ε , locally invariant under the flow (3.1) , that is C ^r  O(ε) close to S _h .

• (ii) For any r < ∞, there exist C ^r  smooth stable and unstable manifolds

  $$\displaystyle{ W_{loc}^{s}(S_{ h,\epsilon }) =\bigcup _{p_{\epsilon }\in S_{h,\epsilon }}W_{loc}^{s}(p_{\epsilon })\,,\quad W_{ loc}^{u}(S_{ h,\epsilon }) =\bigcup _{p_{\epsilon }\in S_{h,\epsilon }}W_{loc}^{u}(p_{\epsilon })\,, }$$

  (3.7)

  locally invariant under the flow (3.1) , that are C ^r  O(ε) close to $W_{loc}^{s}(S_{h})$ and $W_{loc}^{u}(S_{h,\epsilon })$ , respectively.

Remark 3.3.

S _h, ε is, in general, not unique but all representations of S _h, ε lie exponentially close in $\varepsilon$ from each other, i.e. all r-jets are uniquely determined.

Remark 3.4.

We assume that a compact, simply connected, k-dimensional smooth manifold with boundary implies that its boundary is a (k − 1)-dimensional smooth manifold. A compact manifold with boundary is called overflowing invariant , if the vector field inside the manifold is tangent to the manifold and along the boundary it points everywhere outward. The proof of Fenichel’s theorem is based on this definition.

2.1.1 Folded Critical Manifolds

Normal hyperbolicity fails at points on S where D _v f has (at least) one eigenvalue with zero real part, i.e. a bifurcation occurs in the layer problem under the variation of the parameter set w. Generically, such points are folds in the sense of singularity theory [59].

Definition 3.4.

The critical manifold S (3.5) of the singularly perturbed system (3.2) is (locally) folded if there exists a set F that forms a (k − 1)-dimensional manifold in the k-dimensional critical manifold S defined by

$$\displaystyle{ \begin{array}{rcl} F &:=&\{(w,v) \in {\mathbb{R}}^{k} \times {\mathbb{R}}^{m};\vert \;f(w,v,0) = 0\,,\mathrm{rk}(D_{v}f)(w,v,0) = m - 1\,, \\ & &l \cdot [(D_{vv}^{2}f)(w,v,0)\,(r,r)]\neq 0,\,l \cdot [(D_{w}f)(w,v,0)]\neq 0\} \end{array} }$$

(3.8)

with corresponding left and right null vectors l and r of the Jacobian D _v f. The set F denotes the fold points of the critical manifold.

A fold corresponds to a saddle-node bifurcation in the layer problem which is one of the generic codimension-one bifurcations in a dynamical system.

2.2 The Reduced Problem

The reduced problem (3.4) is a differential algebraic problem and describes the evolution of the slow variables w constrained to the critical manifold S. As a consequence, S defines an interface between the two sub-systems (3.3) and (3.4).

Definition 3.5.

Given the reduced problem (3.4). A vector field on the critical manifold S (3.5) is a C ¹-mapping $g: S \rightarrow {\mathbb{R}}^{k}$ such that g(w, v) ∈ T _(w, v) S for all (w, v) ∈ S.

In other words, the reduced vector field (3.4) has to be in the tangent bundle TS of the critical manifold S. The total (time) derivative of f(w, v, 0) = 0, i.e. $D_{v}f \cdot \dot{ v} + D_{w}f \cdot \dot{ w} = 0$ provides exactly the definition for a tangent vector $(\dot{w},\dot{v})$ of an integral curve $(w(\tau ),v(\tau )) \in {\mathbb{R}}^{k+m}$ to be constrained to the tangent bundle TS. This leads to the following representation of the reduced problem (3.4):

$$\displaystyle{ \begin{array}{rcl} \dot{w}& =&g(w,v,0) \\ - D_{v}f \cdot \dot{ v}& =&\left (D_{w}f \cdot g\right )(w,v,0)\\ \end{array} }$$

(3.9)

where (w, v) ∈ S. Let adj (D _v f) denote the adjoint of the matrix D _v f which is the transpose of the co-factor matrix of D _v f, i.e. $\mbox{ adj}\,(D_{v}f) \cdot D_{v}f = D_{v}f \cdot \mbox{ adj}\,(D_{v}f) =\det (D_{v}f)\,I$.

Remark 3.5.

In the case m = 1, $D_{v}f =\det D_{v}f = \frac{\partial f} {\partial v} = f_{v}$ is a scalar and adj (D _v f): = 1. Note that the adjoint of a square matrix is well defined for both regular and singular matrices. This is in contrast to the definition of the inverse of a square matrix which is only defined in the regular case.

We apply adj (D _v f) to both sides of the second equation in (3.9) to obtain

$$\displaystyle{ \begin{array}{rcl} \dot{w}& =&g(w,v,0) \\ -\det \left (D_{v}f\right )\dot{v}& =&\mbox{ adj}\,(D_{v}f) \cdot D_{w}f \cdot g\,(w,v,0)\\ \end{array} }$$

(3.10)

where (w, v) ∈ S. System (3.10) provides a representation of the original reduced problem (3.4) in any (local) coordinate chart on the manifold S.

Remark 3.6.

A coordinate chart on an n-dimensional smooth manifold S is a pair (U; ϕ), where U is an open subset of S and $\phi: U \rightarrow \tilde{ U}$ is a diffeomorphism from U to an open subset $\tilde{U} =\phi (U) \subset {\mathbb{R}}^{k}$. A well-known (and often used) example is the graph of a smooth function $F: U \rightarrow {\mathbb{R}}^{n}$ which is a subset of ${\mathbb{R}}^{n} \times {\mathbb{R}}^{k}$ defined by $\{(x;y) \in {\mathbb{R}}^{n} \times {\mathbb{R}}^{k}\,:\, x \in U\,,y = F(x)\}$.

Suppose that the critical manifold S is normally hyperbolic, i.e. D _v f has full rank for all (w, v) ∈ S. The implicit function theorem implies that S is given as a graph v = h(w). In other words, S can be represented in a single chart given by the slow variable base $w \in {\mathbb{R}}^{k}$. The reduced problem (3.10) on S _h is then given in this coordinate chart by

$$\displaystyle{ \dot{w} = g(w,h(w),0)\,. }$$

(3.11)

Fenichel theory [17, 32] guarantees the persistence of a slow flow on S _h, ε close to the reduced flow of S _h in the following way:

Theorem 3.2 (Fenichel’s Theorem 2, cf. [17, 32]).

Given system (3.1) with f,g ∈ C ^∞ . Suppose S _h ⊆ S is a compact normally hyperbolic manifold, possibly with boundary. Then for ε > 0 sufficiently small, Theorem  3.1 (i), holds and the following:

• (iii) The slow flow on S _h,ε converges to the reduced flow on S _h as ε → 0.

Since S _h is a graph v = h(w) it follows that S _h, ε is also a graph v _ε  = h(w, ε) for sufficiently small $\epsilon \ll 1$. Thus the slow flow on S _h, ε fulfills

$$\displaystyle{ \dot{w} = g(w,h(w,\epsilon ),\epsilon )\,, }$$

(3.12)

and we are dealing with a regular perturbation problem on S _h, ε which is a remarkable result. Consequently, we have

Corollary 3.1.

Hyperbolic equilibria of the reduced problem (3.11) persist as hyperbolic equilibria of the full problem (3.2) for sufficiently small $\epsilon \ll 1$ .

For ε > 0, the base points $p_{\epsilon } \in S_{h,\epsilon }$ of the fast fibers $W_{loc}^{s}(p_{\epsilon })$, respectively $W_{loc}^{u}(p_{\epsilon })$, evolve according to (3.12). Hence, the individual fast fibers $W_{loc}^{s}(p_{\epsilon })$, respectively $W_{loc}^{u}(p_{\epsilon })$, are not invariant, but the families of fibers (3.7) are invariant in the following sense:

Theorem 3.3 (Fenichel’s Theorem 3, cf. [17]).

Given system (3.1) with f,g ∈ C ^∞ . Suppose S _h ⊆ S is a compact normally hyperbolic manifold, possibly with boundary. Then for ε > 0 sufficiently small, Theorem  3.1 (ii) holds and the following:

• (iv) The foliation $\{W_{loc}^{s}(p_{\epsilon })\vert \,p_{\epsilon } \in S_{h,\epsilon }\}$ is (positively) invariant, i.e.

  $$\displaystyle{W_{loc}^{s}(p_{\epsilon }) \cdot t \subset W_{ loc}^{s}(p_{\epsilon } \cdot t)}$$

  for all t ≥ 0 such that $p_{\epsilon } \cdot t \in S_{h,\epsilon }$ , where ⋅ t denotes the solution operator of system (3.1) .

• (v) The foliation $\{W_{loc}^{u}(p_{\epsilon })\vert \,p_{\epsilon } \in S_{h,\epsilon }\}$ is (negatively) invariant, i.e.

  $$\displaystyle{W_{loc}^{u}(p_{\epsilon }) \cdot t \subset W_{ loc}^{u}(p_{\epsilon } \cdot t)}$$

  for all t ≤ 0 such that $p_{\epsilon } \cdot t \in S_{h,\epsilon }$ , where ⋅ t denotes the solution operator of system (3.1) .

This theorem implies that the exponential decay of a trajectory in the stable manifold ${W}^{s}(S_{h,\epsilon })$ towards its corresponding base point $p_{\epsilon } \in S_{h,\epsilon }$ is inherited from the unperturbed case. The same is true in backward time for a trajectory in the unstable manifold ${W}^{u}(S_{h,\epsilon })$ and summarized in the following:

Theorem 3.4 (Fenichel’s Theorem 4, cf. [17, 32]).

Let α _s < 0 be an upper bound $\mbox{ Re}\,\lambda _{i} <\alpha _{s} < 0$ , i = 1,…,m _s , for the stable eigenvalues of the critical manifold S _h . There exists a constant κ _s > 0, so that if $p_{\epsilon } \in S_{h,\epsilon }$ and $q_{\epsilon } \in W_{loc}^{s}(p_{\epsilon })$ then

$$\displaystyle{\|q_{\epsilon } \cdot t - p_{\epsilon } \cdot t\| \leq \kappa _{s}\exp (\alpha _{s}t)}$$

for all t ≥ 0 such that $p_{\epsilon } \cdot t \in S_{h,\epsilon }$ .

Similarly, let α _u > 0 be a lower bound $\mbox{ Re}\,\lambda _{j} >\alpha _{u} > 0$ , j = 1,…,m _u , for the unstable eigenvalues of the critical manifold S _h . There exists a constant κ _u > 0, so that if $p_{\epsilon } \in S_{h,\epsilon }$ and $q_{\epsilon } \in W_{loc}^{u}(p_{\epsilon })$ then

$$\displaystyle{\|q_{\epsilon } \cdot t - p_{\epsilon } \cdot t\| \leq \kappa _{u}\exp (\alpha _{u}t)}$$

for all t ≤ 0 such that $p_{\epsilon } \cdot t \in S_{h,\epsilon }$ .

If we assume that $S_{h} = S_{a}$ is an attracting normally hyperbolic manifold then Fenichel theory implies that the dynamics of system (3.2) are completely described (after some initial transient time) by the dynamics on the k-dimensional slow manifold S _a, ε which to leading order can be completely determined by the reduced flow on S _a . This result justifies certain model reduction techniques often found in the mathematical biology literature on biochemical reactions.

Example 3.1.

A classic biophysical example of a normally hyperbolic problem is given by Michaelis-Menten enzyme kinetics (see, e.g., [34] for details):

$$\displaystyle{ S + E\mathop{\mathop{ \rightleftharpoons }\limits_{ k_{-1}}}\limits^{k_{1}}C\mathop{ \rightharpoonup }\limits^{ k_{2}}P + E\,, }$$

(3.13)

which models an enzymatic reaction with substrate S, enzyme E, an intermediate complex C and product P. Using the law of mass action gives the following system of differential equations

$$\displaystyle{ \begin{array}{rcl} \frac{d[S]} {dt} & =&k_{-1}[C] - k_{1}[S][E], \\ \frac{d[C]} {dt} & =&k_{1}[S][E] - (k_{-1} + k_{2})[C], \\ \frac{d[E]} {dt} & =&(k_{-1} + k_{2})[C] - k_{1}[S][E], \\ \frac{d[P]} {dt} & =&k_{2}[C],\\ \end{array} }$$

(3.14)

where [X] denotes the concentration of X = S, C, E, P with initial concentrations

$$\displaystyle{[S](0) = S_{0},\quad [C](0) = 0,\quad [E](0) = E_{0},\quad [P](0) = 0.}$$

Notice that [P] can be found by direct integration, and there is a conserved quantity since $d[C]/dt + d[E]/dt = 0$, so that $[C] + [E] = E_{0}$. Hence it suffices to study the first two equations of system (3.14) with $[E] = E_{0} - [C]$. Using dimensional analysis gives the corresponding two-dimensional dimensionless system,

$$\displaystyle{ \begin{array}{rcrcl} \dfrac{ds} {d\tau } & =&\dot{s}& =&\alpha _{1}c - s(1 - c) = g(s,c) \\ \epsilon \dfrac{dc} {d\tau } & =& \epsilon \dot{c}& =&s(1 - c) - (\alpha _{1} +\alpha _{2})c = f(s,c)\,,\end{array} }$$

(3.15)

with (dimensionless) substrate and complex concentration $s = [S]/S_{0}$ and $c = [C]/E_{0}$, initial conditions s(0) = 1 and c(0) = 0, time $\tau = E_{0}k_{1}t$ and parameters $\alpha _{1} = k_{-1}/(S_{0}k_{1}) > 0$, $\alpha _{2} = k_{2}/(S_{0}k_{1}) > 0$, $\varepsilon = E_{0}/S_{0} \ll 1$. Here, the initial enzyme concentration E ₀ is considered significantly smaller than the initial substrate concentration S ₀ which is a realistic condition for enzyme reactions. Thus, the obtained dimensionless system is a singularly perturbed system with s slow and c fast.

Fig. 3.1

Michaelis-Menten kinetics: from the initial condition (s, c) = (1, 0), the complex c builds quickly up (along fast fibers ) until it reaches the normally hyperbolic manifold S _a . Then the slow uptake of the substrate s starts (slow flow along S _a towards the rest state (s, c) = (0, 0))

The critical manifold is given by f(s, c) = 0. The Jacobian of the layer problem is the derivative $f_{c} = -(s +\alpha _{1} +\alpha _{2}) < 0$ for all s ≥ 0. Hence, the critical manifold is an attracting normally hyperbolic manifold S _a for the biophysically relevant domain of s ≥ 0 and is given as a graph

$$\displaystyle{c = h(s) = \frac{s} {s +\alpha _{1} +\alpha _{2}}\,.}$$

The reduced problem is then given in the single coordinate chart $s \in \mathbb{R}$ by

$$\displaystyle{ \dot{s} = g(s,h(s)) = -\, \frac{\alpha _{2}s} {s +\alpha _{1} +\alpha _{2}} \leq 0\,,\quad \forall s \geq 0\,. }$$

(3.16)

This differential equation has a hyperbolic equilibrium at s = 0 which is stable. Since the initial condition (s(0), c(0)) = (1, 0) is not on the critical manifold S _a , we expect an initial fast transient behavior towards the slow manifold S _a, ε close to the stable fast fiber at s = 1. Then the slow dynamics will take over and the substrate concentration will slowly decay towards zero along the slow manifold S _a, ε as predicted by the reduced flow. Figure 3.1 confirms the predictions of Fenichel theory. The reduced problem (3.16) is indeed a good approximation of the substrate concentration dynamics after a transient initial time. The rate of uptake of the substrate s described by (3.16) is often referred to as the Michaelis-Menten law.

2.2.1 Reduced Problem on Folded Critical Manifolds

Similar to the normally hyperbolic case, a (local) graph representation of the critical manifold S is used to analyse the k-dimensional reduced problem (3.10) in the case of a folded critical manifold. From the definition (3.8) of the folded critical manifold follows that there exists (at least) one slow variable w _j , j ∈ { 1, …, k} with $l \cdot [(D_{w_{j}}f)(w,v,0)]\neq 0$. Without loss of generality, let w ₁ be this slow variable. One is then able to replace one column in D _v f (we assume, without loss of generality, that this column is $D_{v_{1}}f$) by the column of $D_{w_{1}}f$ such that $\mathrm{rk}D_{(w_{1},v_{2},\ldots,v_{m})}f = m$ along S (including F). In the case k = 1 respectively k ≥ 2, the implicit function theorem then implies that S is (locally) a graph y = h(v ₁) respectively $y = h(w_{2},\ldots,w_{k},v_{1})$ where $y = (w_{1},v_{2},\ldots,v_{m})$. In the case k = 1, incorporating this graph representation of S leads to the projection of the reduced problem (3.10) onto the coordinate chart $v_{1} \in \mathbb{R}$,

$$\displaystyle{ \begin{array}{rcl} -\det \left (D_{v}f\right )\dot{v}_{1} & =&\mbox{ adj}\,(D_{v}f)_{1} \cdot D_{w}f \cdot g\,(v_{1},0)\,,\\ \end{array} }$$

(3.17)

respectively in the case k ≥ 2 it leads to the projection of the reduced problem (3.10) onto the coordinate chart $(w_{2},\ldots,w_{k},v_{1}) \in {\mathbb{R}}^{k}$:

$$\displaystyle{ \begin{array}{rcl} \dot{w}_{j}& =&g_{j}(w_{2},\ldots,w_{k},v_{1},0)\,,\quad j = 2,\ldots k \\ -\det \left (D_{v}f\right )\dot{v}_{1} & =&\mbox{ adj}\,(D_{v}f)_{1} \cdot D_{w}f \cdot g\,(w_{2},\ldots,w_{k},v_{1},0)\,,\\ \end{array} }$$

(3.18)

where $\mbox{ adj}\,(D_{v}f)_{1}$ denotes the first row of the adjoint matrix adj (D _v f).

Remark 3.7.

This row vector $\mbox{ adj}\,(D_{v}f)_{1}$ represents the left null-vector l of the matrix D _v f. As mentioned before, the scalar $\mbox{ adj}\,(D_{v}f)_{1} \cdot D_{w_{1}}f\neq 0$ and, hence, the row vector $\mbox{ adj}\,(D_{v}f)_{1} \cdot D_{w}f$ is non-singular.

Looking at the reduced problem (3.17), respectively (3.18), we observe $\det \left (D_{v}f\right ) = 0$ along the fold F, i.e. (3.17), respectively (3.18), is singular along F.

Definition 3.6.

Regular fold points p ∈ F of the reduced flow (3.17) respectively (3.18) satisfy the transversality condition (normal switching condition)

$$\displaystyle{ \mbox{ adj}\,(D_{v}f)_{1} \cdot D_{w}f \cdot \, g\neq 0\,. }$$

(3.19)

The condition $l \cdot [(D_{vv}^{2}f)(w,v,0)\,(r,r)]\neq 0$ along F implies that $\det \left (D_{v}f\right )$ has different signs on adjacent subsets (branches) of the critical manifold S bounded by F. Hence, in the neighborhood of regular fold points p ∈ F the flow is directed either towards or away from the fold F. Solutions of the reduced problem will reach the fold F in finite (forward or backward) time where they cease to exist.

We can circumvent the problem of the singular nature of the reduced problem along the fold F by introducing a new time τ ₁ defined by $d\tau = -\det \left (D_{v}f\right )d\tau _{1}$, (this is a space dependent time rescaling and, hence, the differential form is needed), and rescaling time in system (3.17) respectively (3.18) which then gives the desingularized problem

$$\displaystyle{ \begin{array}{rcl} \dot{v}_{1} & =&\mbox{ adj}\,(D_{v}f)_{1} \cdot D_{w}f \cdot \, g\,(v_{1},0)\,,\\ \end{array} }$$

(3.20)

respectively

$$\displaystyle{ \begin{array}{rcl} \dot{w}_{j}& =& -\det \left (D_{v}f\right ) \cdot g_{j}(w_{2},\ldots,w_{k},v_{1},0)\,,\quad j = 2,\ldots k \\ \dot{v}_{1} & =&\mbox{ adj}\,(D_{v}f)_{1} \cdot D_{w}f \cdot \, g\,(w_{2},\ldots,w_{k},v_{1},0)\\ \end{array} }$$

(3.21)

where the overdot denotes now d∕dτ ₁. From the time rescaling it follows that the direction of the flow in (3.20) respectively (3.21) has to be reversed on branches where $\det \left (D_{v}f\right ) > 0$ to obtain the corresponding reduced flow (3.17), respectively (3.18). Otherwise, the flows of (3.17) and (3.20), respectively (3.18) and (3.21), are equivalent. Obviously, the analysis of the desingularized problem (3.20), respectively (3.21), is preferable.

2.3 Folded Singularities and Singular Canards

Our aim is to understand the properties of the reduced problem (3.17), respectively (3.18), based on properties of the desingularized problem (3.20), respectively (3.21). Keeping that in mind, we define the following:

Definition 3.7.

We distinguish between two possible types of singularities of the desingularized problem (3.20), respectively (3.21):

• Ordinary singularities which are defined by g = 0.

• Folded singularities which are defined by

  $$\displaystyle{ \det \left (D_{v}f\right ) = 0\,,\quad \mbox{ adj}\,(D_{v}f)_{1} \cdot D_{w}f \cdot \, g = 0\,. }$$

  (3.22)

Ordinary singularities correspond to equilibria of the reduced problem (3.17), respectively (3.18). Generically, they are positioned away from the fold F, i.e. $\det \left (D_{v}f\right )\neq 0$, and they are isolated singularities. In other words, these singularities correspond to equilibria in both the reduced and desingularized system.

Folded singularities are positioned on the fold F. There is a crucial difference between the case k = 1 and k ≥ 2 and we will study these two cases separately.

2.3.1 The Case k = 1

Recall from Remark 3.7 that the scalar $\mbox{ adj}\,(D_{v}f)_{1} \cdot D_{w}f\neq 0$. Hence, the folded singularity condition (3.22) can only be fulfilled for g = 0. This folded singularity is generically a hyperbolic equilibrium for the desingularized problem (3.20), but it does not correspond to an equilibrium of the reduced problem (3.17). In fact, the reduced problem has finite non zero speed at the folded singularity (due to a cancellation of a simple zero). This allows solutions of the reduced problem to cross (in forward or backward time) from one branch of S via the fold F to the other branch of S.

Definition 3.8.

Given a singularly perturbed system (3.2) with a (locally) folded critical manifold $S = S_{a} \cup F \cup S_{s/r}$ where S _a denotes an attracting branch and S _s∕r denotes a repelling branch (case m = 1) respectively a saddle type branch (case m ≥ 2). A trajectory of the reduced problem (3.17) that has the ability to cross in finite time from the S _a branch of the critical manifold to the S _r∕s branch via a folded singularity is called a singular canard .

Example 3.2.

The FitzHugh-Nagumo (FHN) model [20, 45] is a qualitative (dimensionless) description of action potential generation in a class of conductance based, Hodgkin-Huxley-type models [30], given by

$$\displaystyle{ \begin{array}{rcl} w\prime& =&\epsilon g(w,v) =\epsilon (v - cw) \\ v\prime& =&f(w,v) = v(v - a)(b - v) - w + I\,,\end{array} }$$

(3.23)

where we assume b > 0 > a. For I = 0, this system may have one, two or three equilibria depending on (a, b, c). We restrict the parameter set to $4/{(a - b)}^{2} > c > 0$ which guarantees only one equilibrium. Note, for sufficiently small c > 0 there will be only one equilibrium in system (3.23) for any choice of I.

Fig. 3.2

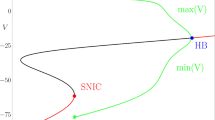
The FitzHugh-Nagumo (FHN) model (3.23) with $a = -\sqrt{3}$, $b = \sqrt{3}$, $c = 4/15$, $\epsilon = 8/100$: (a) singular canard cycles and relaxation oscillation cycles for $I = I_{f}^{-} = -7/4$ obtained through continuous concatenations of slow orbit segments (gray) and fast fibers (black); (b) the corresponding reduced flow projected onto coordinate chart $v \in \mathbb{R}$ indicates the crossing of a singular canard from $S_{a}^{-}$ to S _r ; (c) Bifurcation diagram includes a singular subcritical Andronov-Hopf bifurcation (HB) at $I = I_{H} \approx -1.632$, a branch of canard cycles and relaxation oscillation cycles and a saddle-node of limit cycles (SNLC) bifurcation at $I = I_{C} \approx -1.653$

The critical manifold S of system (3.23) is not normally hyperbolic since $f_{v} = -3{v}^{2} + 2(a + b)v - ab$ vanishes for ${v}^{\pm } = (a + b \pm \sqrt{{a}^{2 } - ab + {b}^{2}})/3$. At these values, $f_{vv}({v}^{\pm }) = \mp 2\sqrt{{a}^{2 } - ab + {a}^{2}}\neq 0$. Furthermore $f_{w} = -1\neq 0$ which shows that the FHN model has a cubic-shaped critical manifold $S = S_{a}^{-}\cup {F}^{-}\cup S_{r} \cup {F}^{+} \cup S_{a}^{+}$ with outer attracting branches $S_{a}^{\pm }$ and repelling middle branch S _r ; see Fig. 3.2a.

The critical manifold S is given as a graph $w = h(v) = v(v - a)(b - v) + I$. Thus we project the reduced problem on the single coordinate chart $v \in \mathbb{R}$,

$$\displaystyle{ \begin{array}{rcl} - (-3{v}^{2} + 2(a + b)v - ab)\dot{v}& =& - (v - c(v(v - a)(b - v) + I))\,.\end{array} }$$

(3.24)

The corresponding desingularized problem is given by

$$\displaystyle{ \begin{array}{rcl} \dot{v}& =& - (v - c(v(v - a)(b - v) + I))\,.\end{array} }$$

(3.25)

We have to reverse direction of the desingularized flow on S _r to obtain the corresponding reduced flow. Otherwise, the desingularized flow is equivalent to the reduced flow. There exist parameter values $I = I_{f}^{\pm }$ such that the right hand side of (3.25) evaluated at v = v ^± vanishes. These particular parameter values define folded singularities of the reduced problem (3.24). Figure 3.2a,b shows the case $I = I_{f}^{-}$ where the folded singularity exists at the lower fold F ⁻. We observe a singular canard crossing from $S_{a}^{-}$ to S _r .

This enables us to construct a whole family of singular limit cycles known as singular canard cycles that are formed through continuous concatenations of slow orbit segments including canard segments (gray segments, one arrowhead) and fast fibers (black segments, two arrowheads). We distinguish two types of canard cycles, known as canards without head and canards with head [2, 62]. Both are illustrated in Fig. 3.2a: a canard without head is a continuous concatenation of a singular canard segment from $S_{a}^{-}$ to S _r (grey) and a fast fiber segment connecting S _r with $S_{a}^{-}$ (black). Obviously, a jump back along a fast fiber segment from any base point on S _r works. This gives the family of canards without head.

Similarly, a canard with head is a continuous concatenation of a singular canard segment from $S_{a}^{-}$ to S _r (grey), a fast fiber segment connecting S _r to $S_{a}^{+}$ (black), a slow segment on $S_{a}^{+}$ connecting to the upper fold F ⁺ (grey) and, finally, a fast fiber segment connecting F ⁺ to $S_{a}^{-}$ (black). Again, a jump forward along a fast fiber segment from any base point on S _r works and we obtain a whole family of canards with head. All these singular canard cycles have O(1) amplitude and have a frequency on the order of the slow time scale. The canard cycles are bounded by a singular relaxation cycle, a continuous concatenation of a slow segment on S _a ⁻ connecting to F ⁻ (grey), a fast fiber segment connecting F ⁻ to $S_{a}^{+}$ (black), a slow segment on $S_{a}^{+}$ connecting to F ⁺ (grey) and, finally, a fast fiber segment connecting F ⁺ to $S_{a}^{-}$ (black).

2.3.2 The Case k ≥ 2

Here, the folded singularity condition (3.22) can be fulfilled for $g\neq 0$. Such generic folded singularities do not correspond to equilibria of the reduced problem (3.18). The set of these folded singularities, denoted M _f , forms a submanifold of codimension one in the (k − 1)-dimensional set of fold points F.

Remark 3.8.

In the case k = 2, the set M _f consists of isolated folded singularities. This makes the following description of associated geometric objects sometimes simpler or even trivial. The reader should keep that in mind since we do not distinguish between k = 2 and k > 2 throughout this section and Sect. 3.2.4.2.

Generically, the set M _f viewed as a set of equilibria of the desingularized system (3.21) has (k − 2) zero eigenvalues and two eigenvalues λ _1∕2 with nonzero real part. Thus for k ≥ 3, M _f represents a normally hyperbolic manifold of equilibria in system (3.21). The classification of folded singularities is based on these two nonzero eigenvalues λ _1∕2 and follows that of singularities in two-dimensional vector fields.

Definition 3.9.

Classification of generic folded singularities (3.22):

• In the case that λ _1∕2 are real, let us denote the eigenvalue ratio by

  $$\displaystyle{\mu:=\lambda _{1}/\lambda _{2}}$$

  where we assume without loss of generality that $\vert \lambda _{1}\vert \leq \vert \lambda _{2}\vert$. Then the corresponding singularity is either a folded saddle if μ < 0, or a folded node if 0 < μ ≤ 1.

• In the case that λ _1∕2 are complex conjugates and $\mbox{ Re}\,\lambda _{1/2}\neq 0$ then the corresponding singularity is a folded focus.

For a generic folded singularity, the algebraic multiplicity of the corresponding singularities on both sides of the last equation in the reduced problem (3.18) is the same (i.e. one). This leads in the case of a folded saddle or a folded node to a nonzero but finite speed of the reduced flow through a folded singularity. Hence, folded saddles and folded nodes create possibilities for the reduced flow to cross to different (normally hyperbolic) branches of the critical manifold S via such folded singularities. This is the hallmark of singular canards in systems with two or more slow variables. Definition 3.8 of singular canards applies here as well. We restate it here for convenience:

Definition 3.10.

Given a singularly perturbed system (3.2) with a folded critical manifold $S = S_{a} \cup F \cup S_{s/r}$ where S _a denotes an attracting branch and S _s∕r denotes a repelling branch (case m = 1) respectively a saddle type branch (case m ≥ 2). A trajectory of the reduced problem (3.18) that has the ability to cross in finite time from the S _a branch of the critical manifold to the S _r∕s branch via a folded singularity is called a singular canard .

Remark 3.9.

In the case of a folded focus there are no singular canards. Only the flow direction changes along the fold F at the folded focus. All solutions starting near a folded focus reach the set of fold-points F∕M _f in finite forward or backward time where they cease to exist due to finite time blow-up.

Fig. 3.3

A folded saddle singularity: (a) desingularized flow; (b) corresponding reduced flow and (c) reduced flow on the critical manifold S. There are two singular canards that cross the fold F at the folded singularity (black dot), one from S _a to S _r and the other (called faux canard) from S _r to S _a . The shaded region indicates a region of solutions on S _a that will reach the fold F in forward time

In the folded saddle case, μ < 0, there exists a (k − 1)-dimensional centre-stable manifold W _cs and a (k − 1)-dimensional centre-unstable manifold W _cu along the (k − 2)-dimensional normally hyperbolic manifold $W_{c} = W_{cs} \cap W_{cu} = M_{f}$. Both manifolds, W _cs and W _cu , are uniquely foliated by one-dimensional fast fibers W _s respectively W _u over the base M _f where the fibers are tangent to the stable respectively unstable eigenvector of the corresponding folded singularity $p_{f} \in M_{f}$, i.e. the corresponding base point.

Recall that the reduced flow is obtained from the desingularized flow by changing the direction of the flow on S _r∕s . Thus, trajectories that start in a stable fiber $W_{s} \subset W_{cs} \subset S_{a}$ approach M _f in finite time and cross tangent to the stable eigenvector of the corresponding folded singularity on M _f to the unstable branch $W_{cu} \subset S_{r/s}$. These are singular canards of folded saddle type.

All other trajectories of the reduced flow starting in S _a (close to F) reach either the set of fold-points F∕M _f in finite forward or backward time where they cease to exist due to finite time blow-up or they do not reach the set F∕M _f at all. Figure 3.3 shows the folded saddle case for k = 2 .

Remark 3.10.

Trajectories starting on an unstable fiber $W_{u} \subset W_{cu} \subset S_{r/s}$ approach M _f in finite time and cross tangent to the unstable eigenvector of the corresponding folded singularity on M _f to the stable branch $W_{cs} \subset S_{a}$. Such solutions are called singular faux canards .

In the folded node case μ > 0, assuming λ _1∕2 < 0 are both negative, the whole phase space S is equivalent to W _cs . Let us define $W_{ss} \subset W_{cs}$ as the (k − 1)-dimensional subset of unique fast fibers corresponding to the span of the strong stable eigenvectors along the base M _f . Again, the reduced flow is obtained from the desingularized flow by changing the direction of the flow on S _r .

Definition 3.11.

The set W _ss together with the (k − 1)-dimensional set of fold points F bounds a sector in S _a , called the singular funnel , with the property that every trajectory starting in the singular funnel reaches the set of folded node singularities M _f in finite time and subsequently crosses the set F transversely to the other branch S _r∕s in the direction that is tangent to the weak stable eigenvector of the corresponding folded node singularity on M _f .

Thus, every trajectory within a singular funnel is a singular canard. Trajectories that start on the boundary set $W_{ss} \subset S_{a}$ reach also the set M _f in finite time but cross tangent to the strong stable eigenvector of the corresponding folded node singularity (by definition). All other trajectories of the reduced flow starting in S _a (close to F) reach the set of fold-points F∕M _f in finite forward or backward time where they cease to exist due to finite time blow-up.

Remark 3.11.

In the folded node case μ > 0 with λ _1∕2 > 0, we are dealing with a whole family of faux canards.

2.4 Maximal Canards

Next, we are concerned with the persistence of singular canards as canards of the full system (3.1). We first provide a geometric definition of canards for ε > 0. Recall that the branches S _a and S _r∕s are normally hyperbolic away from the fold F. Thus, Fenichel theory implies the existence of (non-unique but exponentially close) invariant slow manifolds S _a, ε and S _r∕s, ε away from F. Fix a representative for each of these manifolds S _a, ε respectively S _r∕s, ε

Definition 3.12.

A maximal canard corresponds to the intersection of the manifolds S _a, ε and S _r∕s, ε extended by the flow of (3.1) into the neighborhood of the set M _f  ⊂ F.

Such a maximal canard defines a family of canards nearby which are exponentially close to the maximal canard, i.e. a family of solutions of (3.1) that follow an attracting branch S _a, ε of the slow manifold towards the neighbourhood of the set M _f  ⊂ F, pass close to M _f  ⊂ F and then follow, rather surprisingly, a repelling/saddle branch S _r∕s, ε of the slow manifold for a considerable amount of slow time. The existence of this family of canards is a consequence of the non-uniqueness of S _a, ε and S _r∕s, ε . However, in the singular limit ε → 0, such a family of canards is represented by a unique singular canard.

Remark 3.12.

The key to understanding the local dynamics near the set of folded singularities by means of geometric singular perturbation theory is the blow-up technique. The “blow-up” desingularizes degenerate singularities such as the set of folded singularities or the fold itself. With this procedure, one gains enough hyperbolicity on the blown-up locus B to apply standard tools from dynamical system theory. For a detailed description of the blow-up technique and its application to singularly perturbed systems we refer the interested reader to [15, 39, 40, 57, 58, 61, 63].

Remark 3.13.

A folded critical manifold S implies a single zero eigenvalue of the m-dimensional layer problem. Hence in system (3.1), there exist locally invariant manifolds W _cs (centre-stable) and W _cu (centre-unstable) near the fold F where $W_{cu} \cup W_{cs}$ spans the whole phase space and $W_{c} = W_{cu} \cap W_{cs}$ corresponds to a (k + 1)-dimensional centre-manifold. A centre manifold reduction of system (3.1) onto this (k + 1)-dimensional subspace W _c captures the local dynamics near the fold F. Note that the reduced problem (3.17) respectively (3.18) reflects already such a center manifold reduction (on the linear level) through the projection onto the nullvector $l = \mbox{ adj}\,(D_{v}f)_{1}$ corresponding to the zero eigenvalue of the Jacobian D _v f. In the following, we present results that are based on such a reduction. The interested reader is referred to, e.g. [6, 63, 65], for details.

2.4.1 Case k = 1: Singular Hopf Bifurcation and Canard Explosion

Recall from the FHN model that a folded singularity and associated singular canards exist only for a specific parameter value I = I _f . In the case k = 1, this shows that a folded singularity is degenerate, i.e. a codimension-one phenomenon. Furthermore, the condition for the folded singularity coincides with the equilibrium condition g = 0. This indicates a bifurcation of the equilibrium state in the full system under the variation of I. This can be easily seen when looking at a planar slow-fast system

$$\displaystyle{ \begin{array}{rcl} w\prime& =&\epsilon g(w,v) \\ v\prime& =&f(w,v,I)\,.\end{array} }$$

(3.26)

The trace and the determinant of the Jacobian are given by

$$\displaystyle{ \mathrm{tr} J = f_{v} +\epsilon g_{w}\,,\qquad \det J =\epsilon (f_{v}g_{w} - f_{w}g_{v})\,. }$$

(3.27)

Close to the fold F, a bifurcation of equilibria defined by $f = g = 0$ happens for $0 <\epsilon \ll 1$ when trJ = 0. This implies $f_{v} = -\epsilon g_{w} = O(\epsilon )$ and, in the singular limit, this gives the fold condition f _v  = 0. The existence of singular canards is given if the equilibrium g = 0 of the desingularized problem (3.20) is stable. This implies that $f_{w}g_{v} < 0$ evaluated at g = 0 and, hence, detJ = O(ε) > 0. So, we are expecting a singular Andronov-Hopf bifurcation for I = I _H that creates small $O(\sqrt{\epsilon })$ amplitude limit cycles with nonzero frequencies of order $O(\sqrt{\epsilon })$ [39]. Hence, the singular nature of the Andronov-Hopf bifurcation is encoded in both, amplitude and frequency. Figure 3.2c shows an example of a singular subcritical Andronov-Hopf bifurcation.

Note in Fig. 3.2c that the $O(\sqrt{\epsilon })$ branch of the Andronov-Hopf bifurcation suddenly changes dramatically near I = I _c . This almost vertical branch marks the unfolding of the canard cycles within an exponentially small parameter interval of the bifurcation parameter I. This is often referred to as a canard explosion [2, 15, 39]. The following summarizes these observations:

Theorem 3.5 (cf. [39]).

Given a planar slow-fast system

$$\displaystyle{ \begin{array}{rcl} w\prime& =&\epsilon g(w,v) \\ v\prime& =&f(w,v,I)\,, \end{array} }$$

(3.28)

with a (locally) folded critical manifold $S = S_{a} \cup F \cup S_{r}$ . Assume there exists a folded singularity for I = I _f that also allows for the existence of singular canards. Then a singular Andronov-Hopf bifurcation and a canard explosion occur at

$$\displaystyle\begin{array}{rcl} I_{H}& =& I_{f} + H_{1}\,\epsilon + O{(\epsilon }^{3/2})\qquad \mbox{ and}{}\end{array}$$

(3.29)

$$\displaystyle\begin{array}{rcl} I_{c}& =& I_{f} + (H_{1} + K_{1})\,\epsilon + O{(\epsilon }^{3/2}).{}\end{array}$$

(3.30)

The coefficients H ₁ and K ₁ can be calculated explicitly and, hence, the type of Andronov-Hopf bifurcation (super- or subcritical).

In the singular limit, we have $I_{H} = I_{c} = I_{f}$. By definition, we associate one maximal canard with the canard explosion. In Fig. 3.2a, this maximal canard is represented by the singular canard that moves along the middle branch S _r right up to the upper fold F ⁺. It delineates between jump back canards that form small amplitude canard cycles—canards without head—and jump away canards that form large amplitude canard cycles—canards with head.

In Fig. 3.2c, the branch of canard cycles then connects to the branch of stable relaxation oscillation cycles with large amplitude. Note, there is also a saddle-node of limit cycles bifurcation of the canard cycles where the stability property changes. Since canards are exponentially sensitive to parameter variations, they are hard to detect. In reality, this makes canard cycles rather exceptional.

2.4.2 Case k ≥ 2: Folded Saddle and Folded Node Canards

Here, folded singularities are generic, i.e. they persist under small parameter variations. This makes these canards robust creatures, i.e. their impact on the dynamics of a singularly perturbed system is observable. In the following, we present persistence results of canards.

Theorem 3.6 (cf. [57, 63]).

In the folded saddle case (μ < 0) of a singularly perturbed system (3.1) , the (k − 1)-dimensional set W _cs of singular canards perturb to a (k − 1)-dimensional set of maximal canards for sufficiently small $\epsilon \ll 1$ .

Thus, there is a one-to-one correspondence between singular and maximal canards in the case of folded saddles. Note that these canards form a separatrix set for solutions that either reach the fold F locally near the set M _f or not. This separatrix set of folded saddles will play an important role in the analysis of neural excitability (see Sect. 3.3).

Theorem 3.7 (cf. [6, 57, 61, 63]).

In the folded node case 0 < μ ≤ 1 of a singularly perturbed system (3.1) , we have the following results:

• (i) The (k − 1)-dimensional set W _ss of singular strong canards perturb to a (k − 1)-dimensional set of maximal strong canards called primary strong canards for sufficiently small $\epsilon \ll 1$ .

• (ii) If $1/\mu \notin \mathbb{N}$ then the (k − 1)-dimensional set of singular weak canards perturb to a (k − 1)-dimensional set of maximal weak canards called primary weak canards for sufficiently small $\epsilon \ll 1$ .

• (iii) If $2l + 1 {<\mu }^{-1} < 2l + 3$, $l \in \mathbb{N}$ and ${\mu }^{-1}\neq 2l + 2$ , then there exist l additional sets of maximal canards, all (k − 1)-dimensional, called secondary canards for sufficiently small $\epsilon \ll 1$ . These l sets of secondary canards are $O{(\epsilon }^{(1-\mu )/2})$ close to the set of primary strong canards in an O(1) distance from the fold F.

Note the difference to the folded saddle case. In the folded node case, only a finite number of maximal canards persists under small perturbations $0 <\epsilon \ll 1$ out of the continuum of singular canards given in the singular limit ε = 0. Furthermore, these maximal canards create some counter-intuitive geometric properties of the invariant manifolds S _a, ε and S _r∕s, ε near the set of folded singularities M _f . In particular, the (k − 1)-dimensional set of primary weak canards forms locally an “axis of rotation” for the k-dimensional sets S _a, ε and S _r∕s, ε and hence also for the set of primary strong canards and the set of secondary canards; this follows from [61], case k = 2. These rotations happen in an $O(\sqrt{\epsilon })$ neighbourhood of F. The rotational properties of maximal canards are summarized in the following result:

Theorem 3.8 (cf. [6, 57, 61, 63]).

In the folded node case of a singularly perturbed system (3.1) with $2l + 1 {<\mu }^{-1} < 2l + 3$, $l \in \mathbb{N}$ and ${\mu }^{-1}\neq 2l + 2$,

• (i) the set of primary strong canards twists once around the set of primary weak canards in an $O(\sqrt{\epsilon })$ neighbourhood of F,

• (ii) the j-th set of secondary canards, 1 ≤ j ≤ l, twists (2j + 1)-times around the set of primary weak canards in an $O(\sqrt{\epsilon })$ neighbourhood of F,

where a twist corresponds to a half rotation. Thus each set of maximal canards has a distinct rotation number.

As a geometric consequence, the funnel region of the set of folded nodes M _f in S _a is split by the secondary canards into (l + 1) sub-sectors I _j , $j = 1,\ldots,l + 1$, with distinct rotational properties. I ₁ is the sub-sector bounded by the primary strong canard and the first secondary canard, I ₂ is the sub-sector bounded by the first and second secondary canard, I _l is the sub-sector bounded by the (l − 1)-th and the l-th secondary canard and finally, I _l+1 is bounded by the l-th secondary canard and the set of fold points F. Trajectories with initial conditions in the interior of I _j , 1 ≤ j < l + 1, make $(2j + 1/2)$ twists around the set of primary weak canards, while trajectories with initial conditions in the interior of I _l+1 make at least $[2(l + 1) - 1/2]$ twists around the set of primary weak canards. All these solutions are forced to follow the funnel created by the manifolds $S_{a,\sqrt{\epsilon }}$ and $S_{r/s,\sqrt{\epsilon }}$. After solutions leave the funnel in an $O(\sqrt{\epsilon })$ neighbourhood of F they get repelled by the manifold $S_{r/s,\sqrt{\epsilon }}$ and will follow close to a fast fiber of system (3.1). Hence, folded node type canards form separatrix sets in the phase space for different rotational properties near folded critical manifolds. Canard induced mixed mode oscillations (MMOs) are a prominent example of a complex rhythm that can be traced to folded node singularities. We refer the interested reader to, e.g., [5, 6, 10, 43, 61].

3 Excitable Systems

The notion of excitability was first introduced in an attempt to understand firing behaviors of neurons. Neural action potentials are responsible for transmitting information through the nervous system. Most neurons are excitable, i.e. they are typically silent but can fire an action potential or produce a firing pattern in response to certain forms of stimulation. While the biophysical basis of action potential generation per se is well established, the coding properties of single neurons are less well understood. A first answer to the question of the neuron’s computational properties was given by Hodgkin [29] who identified three basic types (classes) of excitable axons distinguished by their different responses to injected steps of currents of various amplitudes.

Type I (class I) axons are able to integrate the input strength of an injected current step, i.e. the corresponding frequency-current (f-I) curve is continuous.

Type II (class II) axons have a discontinuous f-I curve because of their inability to maintain spiking below a certain frequency. The frequency band of a type II neuron is very limited and, hence, relatively insensitive to the strength of the injected current. It appears that type II neurons resonate with a preferred frequency input.

Type III (class III) axons will only fire a single or a few action potentials at the onset of the injected current step, but are not able to fire repetitive action potentials like type I and type II neurons (besides for extremely strong injected currents). Type III neurons are able to differentiate, i.e. they are able to encode the occurrence of a “change” in the stimulus. Such phasic firing (versus tonic or repetitive firing) identifies these type III neurons as slope detectors . Obviously, the f-I curve is not defined for type III neurons.

Rinzel and Ermentrout [52] pioneered a mathematical framework based on bifurcation theory that distinguishes type I and type II neural models. In Sect. 3.3.1, we will briefly review this approach but with a slight twist. We will emphasise the inherent multiple time-scales structure found in many neuronal models and apply geometric singular perturbation theory together with bifurcation theory to define the different types of excitability.

In Sect. 3.3.2 we will go a step further and ask more general questions about excitability. In particular, we want to focus on dynamic inputs beyond (current) step protocols (that are usually applied in laboratory settings). For example, synapses produce excitatory or inhibitory inputs and these synaptic inputs may be activated (resp. inactivated) fast or slow. We will model sufficiently smooth dynamic inputs and apply these inputs to the 2D slow-fast excitable system models introduced in Sect. 3.3.1. The geometric key to the understanding of excitability will be to identify threshold manifolds (aka separatrices). This is very much in the spirit of FitzHugh’s work on excitability [18–20] (see also Izhikevich [31], Chap. 7), but it extends FitzHugh’s ideas to the dynamic, nonautonomous case.

3.1 Slow-Fast Excitable Systems with Step Protocols

We focus on a class of 2D excitable models given by

$$\displaystyle{ \begin{array}{rcl} w\prime& =&\epsilon g(w,v,\epsilon ) \\ v\prime& =&f(w,v,\epsilon,I) = f_{1}(w,v,\epsilon ) + I\end{array} }$$

(3.31)

where $I \in [I_{0},I_{1}] \subset \mathbb{R}$ is an external (constant) drive of the excitable system, and the following assumptions hold (for many two-dimensional neuronal models):

Assumption 1.

The critical manifold S of system(3.31)is cubic shaped, i.e.

$$\displaystyle{S = S_{a}^{-}\cup {F}^{-}\cup S_{ r} \cup {F}^{+} \cup S_{ a}^{+}\,,}$$

with attracting outer branches $S_{a}^{\pm }$ , repelling middle branch S _r , and folds F ^± .

Assumption 2.

The (unforced) system(3.31)with I = 0 has one, two or three equilibria. In the corresponding reduced problem, one equilibrium is located on the lower attracting branch S _a ⁻ and it is stable. Each of the other two equilibria, if they exist, are located on the middle branch S _r .

Example 3.3.

The Morris-Lecar (ML) model [46] was originally developed to study the electrical activity of barnacle muscle fiber. Later it was popularised as a model for neural excitability; see e.g. Izhikevich [31] where a large collection of minimal conductance based 2D ML-type models is introduced. We use the ML-type model from Rinzel and Ermentrout [52] in the following form (as in Prescott et al [48]):

$$\displaystyle{ \begin{array}{rcl} w\prime& =&\phi [w_{\infty }(V ) - w]/\tau _{w}(V ) \\ CV \prime& =& - I_{ion}(w,V ) + I_{stim}\,,\end{array} }$$

(3.32)

with functions

$$\displaystyle{ \begin{array}{rcl} I_{ion}(w,V )& =& - (g_{f}m_{\infty }(V )(V - E_{f}) + g_{s}w(V - E_{s}) + g_{l}(V - E_{l})) \\ m_{\infty }(V )& =&[1 +\tanh ((V - V _{1})/V _{2})]/2 \\ w_{\infty }(V )& =&[1 +\tanh ((V - V _{3})/V _{4})]/2 \\ \tau _{w}(V )& =&1/\cosh ((V - V _{3})/(2V _{4}))\,. \end{array} }$$

(3.33)

V models the voltage membrane potential and $I_{ion}(V ) = I_{fast} + I_{slow} + I_{leak}$ represents the ionic currents of the model which consist of a fast non-inactivating current $I_{fast} = g_{f}m_{\infty }(V )(V - E_{f})$, a delayed rectifier type current $I_{slow} = g_{s}w(V - E_{s})$, and a leak current $I_{leak} = g_{l}(V - V _{l})$. The parameter I _stim represents the injected current step. The activation variable w of the I _slow current provides the slow voltage-dependent negative feedback required for excitability. Its dynamics are described by the sigmoidal activation function w _∞ (V ) and the bell-shaped voltage dependent time-scale τ _w (V )∕ϕ. The activation of the fast I _fast current is assumed instantaneous and, hence, its activation variable is set to m = m _∞ (V ).

A representative parameter set of this ML model is given by $g_{f} = 20\,\mathrm{mS}/{\mathrm{cm}}^{2}$, $g_{s} = 20\,\mathrm{mS}/{\mathrm{cm}}^{2}$, $g_{l} = 2\,\mathrm{mS}/{\mathrm{cm}}^{2}$ (maximal conductances of ion channels), E _f  = 50 mV, $E_{s} = -100\,\mathrm{mV}$, $E_{l} = -70\,\mathrm{mV}$ (Nernst potentials), capacitance $C = 2\,\upmu \mathrm{F}/{\mathrm{cm}}^{2}$, time scale factor $\phi = 0.1\,{\mathrm{ms}}^{-1}$ and auxiliary voltage parameters $V _{1} = -1.2\,\mathrm{mV}$, V ₂ = 18 mV, V ₃ = 0 mV, V ₄ = 10 mV.

To identify a slow-fast timescale structure explicitly in (3.32) we have to non-dimensionalise the model. This is done by introducing dimensionless variables $v = V/k_{v}$ and $t_{1} = t/k_{t}$ with typical reference scales for voltage k _v  = 100 mV and time $k_{t} = C/g_{max} = 0.1\,\mathrm{ms}$ where g _max  = 20 mS is a reference conductance scale. This leads to the dimensionless ML model,

$$\displaystyle{ \begin{array}{rcl} w\prime& =&\epsilon [w_{\infty }(v) - w]/\tau _{w}(v) =\epsilon g(w,v) \\ v\prime& =& -\bar{ I}_{ion}(w,v) +\bar{ I}_{stim} = f(w,v,\bar{I}_{stim}) = f_{1}(w,v) +\bar{ I}_{stim}\,,\end{array} }$$

(3.34)

with functions

$$\displaystyle{ \begin{array}{rcl} \bar{I}_{ion}(w,v)& =& - (\bar{g}_{f}m_{\infty }(v)(v -\bar{ E}_{f}) +\bar{ g}_{s}w(v -\bar{ E}_{s}) +\bar{ g}_{l}(v -\bar{ E}_{l})) \\ m_{\infty }(v)& =&[1 +\tanh ((k_{v}v - V _{1})/V _{2})]/2 \\ w_{\infty }(v)& =&[1 +\tanh ((k_{v}v - V _{3})/V _{4})]/2 \\ \tau _{w}(v)& =&1/\cosh ((k_{v}v - V _{3})/(2V _{4}))\,. \end{array} }$$

(3.35)

where $\bar{g}_{x} = g_{x}/g_{max}$, $\bar{E}_{x} = E_{x}/k_{v}$ (x = f, s, l), $\bar{I}_{stim} = I_{stim}/(k_{v}g_{max})$ and

$$\displaystyle{\epsilon:= (C/g_{max})\phi = 0.01}$$

is the singular perturbation parameter that measures the time-scale separation between the fast v dynamics and the slow w dynamics. This timescale separation can be enhanced by decreasing the capacitance C, slowing the w-dynamics via ϕ or increasing the maximum conductance of the ion channels. Hence, system (3.34) can be viewed as a singularly perturbed system.

Using the parameter values from above, it can be shown that the critical manifold is cubic shaped (Assumption 1) and that it has three equilibria for I = 0, one on the lower attracting branch and the other two are on the repelling middle branch (Assumption 2). By changing the system parameters, this model can be transformed into all three excitable neuron types; see [48] for more details.

Example 3.4.

We introduce a dimensionless hybrid of the Morris-Lecar and the FitzHugh-Nagumo (ML-FHN) model that combines important features of both:

$$\displaystyle{ \begin{array}{rcl} w\prime& =&\epsilon g(w,v) =\epsilon (w_{\infty }(v) - w) \\ v\prime& =&f(w,v,I) = v(v - a)(b - v) - w + I = F(v) - w + I\,,\end{array} }$$

(3.36)

with

$$\displaystyle{w_{\infty }(v) = [1 +\tanh ((v - v_{3})/v_{4})]/2}$$

with dimensionless parameters b > 0 > a, v ₃, v ₄ > 0, I is the primary bifurcation parameter and $\epsilon \ll 1$ as the singular perturbation parameter. Again, this singularly perturbed system has a cubic-shaped critical manifold (Assumption 1). Furthermore, the sigmoidal shaped activation function w _∞ (v) allows us to explore more easily the cases of different numbers of equilibria as described by Assumption 2. We focus on this ML-FHN model (3.36) to explore the notion of excitability. We fix the parameter $a = -0.5$, b = 1, and vary $(I,v_{3},v_{4})$.

3.1.1 The Geometry of Excitability

A classical physiology definition of excitability is that a large enough brief stimulus (“supra-threshold” pulse) triggers an action potential (large regenerative excursion). This implies the existence of a “threshold” that the stimulus must pass to evoke an action potential with a fairly constant amplitude. On the other hand, a graded response with intermediate amplitudes was already observed in the Hodgkin-Huxley model of the squid giant axon [29] as well as the FHN model [19, 20] which contradicts the traditional view that the action potential is an all-or-none event with a fixed amplitude. We will focus on a geometrical definition of excitability to avoid this ambiguity.

Fig. 3.4

Bifurcation diagrams for type I–III neurons of the ML-FHN model (3.36) together with f − I curves: (Type I) v ₃ = 0. 3, v ₄ = 0. 1; we observe a SNIC bifurcation for $I = I_{bif} = 0.079$ where the frequency approaches zero; (Type II) $v_{3} = -0.1$, v ₄ = 0. 1; we observe a singular HB bifurcation for $I = I_{bif} = 0.109$; note the small frequency band for the relaxation oscillation branch; (Type III) $v_{3} = -0.3$, v ₄ = 0. 1; there are no bifurcation for $I = [-0.4,0.4]$

As mentioned in the introduction, Hodgkin [29] identified three distinct types (classes) of excitability by applying a current step protocol to neurons:

• Type I neurons : depending on the strength of the injected current, action potentials can be generated with arbitrary low frequency; see Fig. 3.4.

• Type II neurons : Action potentials are generated in a certain frequency band that is relatively insensitive to changes in the strength of the injected current; see Fig. 3.4.

• Type III neurons : A single action potential is generated in response to a pulse of injected current. Repetitive spiking is not possible or can be only generated for extremely strong injected current.

Type I and type II neurons are able to fire trains of action potentials (tonic firing) if depolarized sufficiently strong which distinguishes them from type III neurons. This distinction points to a bifurcation in type I and type II neurons where the cell changes from an excitable to an oscillatory state. The main bifurcation parameter is given by I, the magnitude of the current step protocol. This leads to the following classical definition of excitability via bifurcation analysis under the variation of the applied current I [52]:

• Type I : The stable equilibrium (resting state) disappears via a saddle-node on invariant circle (SNIC) bifurcation ; see Fig. 3.4.

• Type II : The stable equilibrium (resting state) loses stability via an Andronov-Hopf bifurcation ; see Fig. 3.4.

• Type III : The equilibrium (resting state) remains stable for $I \in [I_{0},I_{1}]$; see Fig. 3.4.

Fig. 3.5

Two parameter bifurcation diagram $(v_{3},v_{4})$ of the ML-FHN model (3.36) with boundaries of type I, type II and type III neurons: the three dots indicate the parameter values used in Fig. 3.4

In the ML-FHN model (3.36) we are able to identify all three types of neurons by varying the parameters $(v_{3},v_{4})$ which change the position (v ₃) and maximum slope (v ₄) of the sigmoidal function w _∞ (v). Figure 3.5 shows the different regions in the parameter-space $(v_{3},v_{4})$ that correspond to the different excitability classes. The boundaries were found numerically using the software package AUTO [13]. The boundary between type II and type III is a continuation of the Andronov-Hopf bifurcation at a fixed I = I ₁. Hence, its position depends on the definition of the interval $I \in [I_{0},I_{1}]$ where the type III neuron must stay excitable. The boundary between type I and type II is a continuation of a cusp-bifurcation where the two folds coalesce. This boundary is not exact but defines a small strip where the transition happens. Note that fixing v ₄ (slope) and varying v ₃ (position) provides us with a simple way to change the model from type I to type II and to type III. Figure 3.4 was obtained in that way. Throughout the rest of the chapter, we will fix v ₄ = 0. 1 and use v ₃ as our second bifurcation parameter.

Fig. 3.6

ML-FHN model (3.36), singular limit bifurcations and their singular limit orbits: (type I) saddle-node homoclinic (SNIC) for v ₃ = 0. 3 and $I = I_{bif} = I_{bif}(v_{3}) \approx 0.079$; (type II) canard cycles for $v_{3} = -0.1$ and $I = I_{bif} = I_{bif}(v_{3}) \approx 0.109$

Fig. 3.7

ML-FHN model (3.36): nullclines under variation of I which leads to the (singular limit) definition of I _thr and I _bif for type I–III: (type I) I = I _bif at a saddle node bifurcation; (type II) I = I _bif at singular HB bifurcation; (type III) no bifurcation; (type I–III) I = I _thr when the w-coordinate of the equilibrium on $S_{a}^{-}$ for I = 0 equals the w-coordinate of the lower fold F ⁻ for I = I _thr . In the type I case, $I_{bif} = I_{thr}$. The bifurcation values I _bif respectively threshold values I _thr are not the same for the different types

Since the ML-FHN model (3.36) is a singularly perturbed system, we are able to provide the corresponding definition of excitability based on geometric singular perturbation theory:

• Type I : The stable equilibrium on the lower attracting branch S _a ⁻ disappears via a singular Bogdanov-Takens bifurcation at the lower fold F ⁻; see Fig. 3.6.

• Type II : The stable equilibrium on the lower attracting branch S _a ⁻ bifurcates via a singular Andronov-Hopf bifurcation at the lower fold F ⁻; see Fig. 3.6.

• Type III : The stable equilibrium on the lower attracting branch S _a ⁻ remains stable for $I \in [I_{0},I_{1}]$.

To identify the different types of excitability one has to look at the nullclines of the ML-FHN model (3.36). As can be seen in Fig. 3.7, for I = I _bif a type I neuron has a saddle-node bifurcation of equilibria at the lower fold F ⁻. This allows for the construction of a singular homoclinic orbit as follows (see Fig. 3.6): we start at the saddle-node equilibrium at the lower fold F ⁻ and concatenate a fast fiber of the layer problem that connects to the upper stable branch S _a ⁺. Then we follow the reduced (slow) flow towards the upper fold F ⁺ where we concatenate a fast fiber at F ⁺ that connects back towards the lower attracting branch S _a ⁻. Finally, we follow the reduced (slow) flow on S _a ⁻ towards the lower fold F ⁻ and hence end up at the saddle-node equilibrium. This homoclinic orbit is the singular limit representation of the SNIC shown in Fig. 3.4. The unfolding of this singular limit object is quite intricate [9], is closely related to a local slow-fast Bogdanov-Takens bifurcation [7] at the lower fold F ⁻ and goes beyond the aim of this chapter.

In the case of a type II neuron, the stable equilibrium on the lower branch S _a ⁻ crosses the lower fold F ⁻ at $I = I_{bif} = I_{bif}(v_{3})$ (note, it is a different value than for the type I case) and moves onto the unstable middle branch S _r ; see Fig. 3.7 (note, a precise definition of I = I _thr will be given in Sect. 3.3.2). This is the same mechanism as shown for the FHN model in Fig. 3.2. Hence, one can construct singular canard cycles that are formed through concatenations of slow canard segments and fast fibers as shown in Fig. 3.6. Note that these singular canard cycles have O(1) amplitude and have a frequency O(1) on the order of the slow time scale. These singular canard cycles will unfold to actual canard cycles as we turn on the singular perturbation parameter. The unfolding of these canard cycles, the canard explosion, happens within an exponentially small parameter interval of the bifurcation parameter near I = I _C . This canard explosion is preceded by a singular supercritical Andronov-Hopf bifurcation at I = I _H that creates small stable $O(\sqrt{\epsilon })$ amplitude limit cycles with nonzero intermediate frequencies of order $O(\sqrt{\epsilon })$ [39] and succeeded by relaxation oscillations with frequencies of order O(1); see Fig. 3.4. Hence the singular nature of the Andronov-Hopf bifurcation is encoded in both, amplitude and frequency. Note that the classic definition of type II excitability refers to the slow frequency band of the relaxation oscillations which does not vary much.

Fig. 3.8

ML-FHN model (3.36) with current step protocols for type I–III and time traces for different step currents I: (type I) for $I < I_{bif} = I_{thr}$ no spiking while for I > I _bif there is periodic (tonic) spiking; (type II) for I < I _thr no spiking, for $I_{thr} < I < I_{bif}$ a transient spike while for I > I _bif there is periodic (tonic) spiking; (type III) for I < I _thr no spiking while for I _thr  < I there is a transient spike

In the case of type III neurons, there is no bifurcation (see Fig. 3.4) and, hence, a type III neuron is excitable for all $I \in [I_{0},I_{1}]$, i.e. a type III neuron does not spike repetitively. On the other hand, as one observes in Fig. 3.8, the type III neuron is indeed excitable—it is able to elicit a single spike for a sufficiently strong injected current step I > I _thr .

3.1.2 Transient Responses

Let us consider possible transient responses of type I and type II neurons for I < I _bif , the minimum injected current step I _bif required for periodic tonic spiking. Type II neurons are also able to elicit a single spike for a sufficiently strong injected current step $I_{thr} < I < I_{bif}$; see Fig. 3.8. On the other hand, type I neurons are not able to elicit a single spike below the minimum injected current step I _bif required for periodic tonic spiking; see Fig. 3.8. Obviously, this transient behavior for type II neurons cannot be explained by the bifurcation structure identified in Fig. 3.7 since this transient behavior is found for $I_{thr} < I < I_{bif}$. It points to the ability of type II and III neurons to elicit single transient spikes under a current step protocol, while type I neurons are not able to produce this transient behaviour.

Fig. 3.9

Explanation of transient spiking property of type III neuron shown in Fig. 3.8: open circle indicates resting state for I = 0 while filled circle indicates the resting state for I > 0; the firing threshold manifold (dashed curve) for I > 0 is the extension of the middle repelling branch S _r, ε in backward time; (left panel) no spike since initial rest state is to the right of the firing threshold manifold; (right panel) transient spike since initial rest state is to the left of the firing threshold manifold

Figure 3.9 provides an explanation for the firing threshold I = I _thr in the case of a type III neuron. The rest state, I = 0 case in Fig. 3.9, on the lower attracting branch (the resting membrane potential of a neuron) is given by the intersection of the two nullclines, the critical manifold S and the sigmoidal w = w _∞ (v). When a current step I is injected, the critical manifold S shifts to the right. The old rest state is suddenly off S and it will follow the fast dynamics to find a stable attractor. If it follows a fast fiber of the lower stable branch S _a, ε ⁻ then the cell is not able to fire (right panel), but if it follows a fast fiber of the upper stable branch S _a, ε ⁺ then the cell will fire an action potential before it returns to the lower S _a, ε ⁻ and the new resting state (left panel). The firing threshold manifold [11, 18, 42, 48] is shown as a dashed curve. It is the extension of the unstable middle branch S _r, ε in backward time. In the singular limit, this firing threshold manifold is given by the concatenation of the branch S _r and the layer fiber attached to the lower fold F ⁻. By looking at Fig. 3.7 and the position of the equilibrium state for I = 0 relative to the nullclines for I > 0 it becomes now apparent why type II and type III neurons can fire transient spikes while type I neurons cannot.

This also points to a well known phenomenon in neuronal dynamics known as post-inhibitory rebound (PIR) [4, 21], where excitable neurons are able to fire an action potential when they are released after having received an inhibitory current input for a sufficient amount of time. Again, only type II and III neurons are able to create a post-inhibitory rebound while type I neurons cannot. Simply note that Fig. 3.8 could also be interpreted as a PIR current step protocol where cells have been held sufficiently long at I = 0 before they are released back to the original state I > 0.

It seems that the transient firing behavior observed for type II and type III neurons is a function of the external current amplitude only. This is actually a misconception because it also depends crucially on the dynamics of the external input. In a current step protocol, we are dealing with an instantaneous (fast) change in the external input, i.e. a fast input modulation. In the following, we will show that these transient behaviors can be explained in a more general context by applying a dynamic, nonautonomous approach to the problem under study.

3.2 Slow-Fast Excitable Systems with Dynamic Protocols

We focus on the ML-FHN model (3.36) with an external drive I(t):

$$\displaystyle{ \begin{array}{rcl} w\prime& =&\epsilon g(w,v) =\epsilon (w_{\infty }(v) - w) \\ v\prime& =&f(w,v,t) = F(v) - w + I(t)\,,\end{array} }$$

(3.37)

where we assume that I(t) is a sufficiently smooth function. This excludes the case of the current step protocol used in the previous section. We replace this protocol by a mollified version such as given by a smooth ramp or by a smooth pulse which resemble qualitatively certain classes of neuronal synaptic or network inputs.

System (3.37) is a singularly perturbed nonautonomous system. Is it possible to apply geometric singular perturbation theory to the nonautonomous case as well? In the following, we briefly highlight connections between geometric singular perturbation theory and nonautonomous attractor theory (see also Chap. 1 of this book).

3.2.1 Nonautonomous Systems and Canard Theory

Given a nonautonomous singularly perturbed system

$$\displaystyle{ \begin{array}{rcl} w\prime& =&\epsilon g(w,v,\epsilon,t) \\ v\prime& =&f(w,v,\epsilon,t) \end{array} }$$

(3.38)

where $w = (w_{1},\ldots,w_{k-1}) \in {\mathbb{R}}^{k-1}$ and $v = (v_{1},\ldots,v_{m}) \in {\mathbb{R}}^{m}$ are slow and fast phase space variables, $t \in \mathbb{R}$ is the fast time scale and the prime denotes the time derivative d∕dt. It is well known that such a nonautonomous system can be viewed as an extended autonomous system by increasing the phase space dimension by one, i.e.

$$\displaystyle{ \begin{array}{rcl} w\prime& =&\epsilon g(w,v,\epsilon,s) \\ v\prime& =&f(w,v,\epsilon,s) \\ s\prime& =&1\end{array} }$$

(3.39)

where $s \in \mathbb{R}$ is an additional (fast) dummy phase-space variable. Note, this system has no critical manifold S. Hence, the previously introduced geometric singular perturbation theory is only of limited use here. To be more precise, the fast dynamics of the (v, s)-variables are dominant throughout the phase space. Thus we can interpret this system as a regularly perturbed nonautonomous problem [36, 37, 50].

This apparent shortfall with respect to geometric singular perturbation theory diminishes immediately if we assume that the nonautonomous nature of the problem evolves slowly, i.e. g(v, w, ε, τ = ε t) and f(v, w, ε, τ = ε t) where $\epsilon \ll 1$ indicates the scale separation between the fast time scale t and the slow time scale τ which leads to

$$\displaystyle{ \begin{array}{rcl} s\prime& =&\epsilon \\ w\prime& =&\epsilon g(w,v,\epsilon,s) \\ v\prime& =&f(w,v,\epsilon,s)\,. \end{array} }$$

(3.40)

This system represents a special case of a singularly perturbed system (3.1) where $(w,s) \in {\mathbb{R}}^{k}$ are slow variables and $v \in {\mathbb{R}}^{m}$ are fast variables. The critical manifold is given by f = 0 and we can apply the theory given in Sect. 3.2. In particular, folded critical manifolds provide singularly perturbed systems with the opportunity to switch from the slow time scale to the fast time scale or from one attracting sheet of a critical manifold to another. As we have seen before, most models of excitability have cubic shaped critical manifolds (i.e. they have two folds) and, hence, have the ability to switch between different states (e.g. silent and active).

Furthermore, while system (3.40) possesses, in general, no equilibria, it may possess folded singularities. As described in Sect. 3.2.4, canards of folded saddle and folded node type have the potential to act as “effective separatrices” between different local attractor states in a dynamically driven multiple scales system. A dynamic drive itself (e.g., in the case of a periodic signal that regularly rises and falls) has the potential to create folded singularities and to form and change these effective separatrices. Hence, the specific nature of the dynamic drive determines which local attractor states can be reached through global mechanisms. This point of view has profound consequences in the analysis of excitable systems as we will show next. In particular, we will identify canards of folded saddle type as firing threshold manifolds.

3.2.2 Slow External Drive Protocols

We analyse a 2D singularly perturbed system with slow external drive I(ε t) given by

$$\displaystyle{ \begin{array}{rcl} w\prime& =&\epsilon g(w,v) =\epsilon (w_{\infty }(v) - w) \\ v\prime& =&f(w,v,t) = F(v) - w + I(\epsilon t)\,, \end{array} }$$

(3.41)

where the autonomous part of this model, i.e. system (3.41) with I(ε t) ≡ 0, fulfills Assumption 1 and 2. Obviously, the ML-FHN model (3.37) with slow external drive I(ε t) fulfills this requirement. We recast the 2D nonautonomous singularly perturbed problem as a 3D autonomous singularly perturbed problem,

$$\displaystyle{ \begin{array}{rcl} s\prime& =&\epsilon \\ w\prime& =&\epsilon g(w,v) =\epsilon (w_{\infty }(v) - w) \\ v\prime& =&f(w,v,s) = F(v) - w + I(s)\,,\end{array} }$$

(3.42)

where $(s,w) \in {\mathbb{R}}^{2}$ are the slow variables and $v \in \mathbb{R}$ is the fast variable.

Assumption 3.

The external slow drive I(s) is a C ^∞ function which is constant outside a finite interval $[{s}^{-},{s}^{+}]$ , i.e. I(s) = I ₀ for s < s ⁻ and I(s) = I ₁ for s > s ⁺ . I(s) is bounded, i.e. $I_{min} \leq I(s) \leq I_{max}\,,\forall s \in \mathbb{R}\,,$ such that type I and II neurons are in an excitable state for the maximal constant drive $I = I_{max} < I_{bif}$ .

Remark 3.14.

By Assumption 3, the function I′(s) = I _s is compactly supported. This is not necessary for the following analysis but makes it more convenient. We could relax the smoothness assumption on I(s). The constant states could also be relaxed to asymptotic states.

Example 3.5 (Ramp).

This is a mollified version of the current step protocol and is given by

$$\displaystyle{ I(s) = \frac{I_{1}} {2} \left (1 +\tanh \left (\frac{2(s - s_{0})} {s_{1}} \right )\right )\,,\quad \forall s \in [{s}^{-},{s}^{+}]\,, }$$

(3.43)

$I(s) = 0 = I_{min}$ for s < s ⁻ and $I(s) = I_{1} = I_{max}$ for s > s ⁺ for a sufficiently large choice of $[{s}^{-},{s}^{+}]$ centered around s ₀. The ramp has a maximal slope of $I_{1}/s_{1}$ when $I(s_{0}) = I_{1}/2$.

Example 3.6 (Pulse).

We model a symmetric pulse given by

$$\displaystyle{ I(s) = \frac{I_{1}} {\cosh \left (\frac{2(s-s_{0})} {s_{1}} \right )}\,,\quad \forall s \in [{s}^{-},{s}^{+}]\,, }$$

(3.44)

$I(s) = 0 = I_{min}$ for s < s ⁻ and for s > s ⁺ for a sufficiently large choice of $[{s}^{-},{s}^{+}]$ centered around s ₀ with $I(s_{0}) = I_{1} = I_{max}$. The pulse has its maximal slope of $I_{1}/s_{1}$ when $I(s_{0} + \frac{s_{1}} {4} \ln (3 - 2\sqrt{2})) = I_{1}/\sqrt{2}$.

Fig. 3.10

Type II neuron ($v_{3} = -0.1$) for $I_{th} < I_{1} = 0.09 < I_{bif}$: (a) ramp protocol (3.43) with s ₁ = 0. 5 (dark grey, no spike) and s ₁ = 0. 4 (bright grey, transient spike); note that the difference in the two ramp protocols is barely visible; (b) pulse protocol (3.44) with s ₁ = 2. 3 (dark grey, no spike) and s ₁ = 2. 2 (bright grey, transient spike). Note that the difference in the two ramp protocols is barely visible

Figure 3.10 shows ramp and pulse protocol examples. Note that the maximal drive I ₁ is the same in both cases, only the maximal slope of the ramp respectively the pulse varies (slightly). In both cases, a single spike is elicited if the slope of rising exceeds a certain threshold value. This clearly indicates that this type II neuron is a slope detector (for I < I _bif ). The same can be observed for type III neurons. In the following, we will use geometric singular perturbation theory to explain this phenomenon in detail.

3.2.3 Geometric Singular Perturbation Analysis

The critical manifold S of system (3.42) is given as a graph

$$\displaystyle{ w = W(s,v) = F(v) + I(s)\,. }$$

(3.45)

By Assumption 1, this manifold is cubic shaped, i.e. S has two folds F ^± for v = v ^± where $F_{v}({v}^{\pm }) = 0$ and $F_{vv}({v}^{\pm })\neq 0$ for all $s \in \mathbb{R}$. Note that $F_{v} = dF/dv$, $F_{vv} = {d}^{2}F/d{v}^{2}$. The geometry of the critical manifold S together with the stability properties of the three branches of S, outer branches $S_{a}^{\pm }$ are stable and middle branch S _r is unstable, imply that $F_{vv}({v}^{+}) < 0$ while $F_{vv}({v}^{-}) > 0$. Figure 3.11 shows the critical manifold in the case of a ramp respectively pulse protocol.

Fig. 3.11

Critical manifold (3.45) for (a) ramp and (b) pulse protocol; note that the ramp and pulse profiles are visible in the geometry of the critical manifold

Assumptions 2 and 3 are concerned with properties of the reduced problem of system (3.42). Since the critical manifold S is a graph w = W(s, v), we are able to project the reduced problem onto a single coordinate chart $(s,v) \in {\mathbb{R}}^{2}$ (compare with Sect. 3.2.2.1):

$$\displaystyle{ \begin{array}{rcl} \dot{s}& =&1 \\ - F_{v}\,\dot{v}& =&F(v) - w_{\infty }(v) + I(s) + I_{s}\,, \end{array} }$$

(3.46)

where $I_{s} = dI/ds$. This system is singular along the folds F ^± where F _v vanishes. We rescale time by $d\tau = -F_{v}\,d\tau _{1}$ in system (3.46) to obtain the desingularized system

$$\displaystyle{ \begin{array}{rcl} \dot{s}& =& - F_{v} \\ \dot{v}& =&F(v) - w_{\infty }(v) + I(s) + I_{s}\,,\end{array} }$$

(3.47)

where the overdot denotes now d∕dτ ₁. From the time rescaling it follows that the direction of the flow in (3.47) has to be reversed on the middle branch S _r where F _v  > 0 to obtain the corresponding reduced flow (3.46). Otherwise, the reduced flow (3.46) and the desingularized flow (3.47) are equivalent.

By Assumption 3, the drive I(s) is constant for $s \in (-\infty,{s}^{-}) \cup ({s}^{+},\infty )$. From Assumption 2 it follows that

$$\displaystyle{\dot{v} = F(v)-w_{\infty }(v)+I(s)+I_{s} = F(v)-w_{\infty }(v)+\bar{I} < 0\,,\forall s \in (-\infty,{s}^{-})\cup ({s}^{+},\infty )\,,}$$

where $\bar{I} = I_{0}$ or $\bar{I} = I_{1}$. This shows that the reduced flow cannot reach the lower fold F ⁻ from $S_{a}^{-}$ for a constant drive $\bar{I}$ confirming $I < I_{bif}$ for type I and type II neurons. For an action potential to occur we need necessarily that $\dot{v} > 0$ somewhere along the lower fold F ⁻ within the dynamic range of I(s) where I _s  > 0 (on the rising phase of I(s)). This implies that $\dot{v}$ must vanish in system (3.47) along the lower fold F ⁻, i.e.

$$\displaystyle{ \tilde{I}(s):= F({v}^{-}) - w_{ \infty }({v}^{-}) + I(s) + I_{ s} = 0\,, }$$

(3.48)

which is Definition 3.7 of a folded singularity. The type of these folded singularities is obtained by calculating the Jacobian of system (3.47),

$$\displaystyle{ J = \left (\begin{array}{cc} 0 & - F_{vv} \\ I_{s} + I_{ss}\,&F_{v} - w_{\infty,v} \end{array} \right )\,. }$$

(3.49)

Note that w _∞, v  > 0. Hence, the trace of the Jacobian evaluated along F ⁻ is

$$\displaystyle{\mathrm{tr} (J) = -w_{\infty,v} < 0\,.}$$

The determinant of the Jacobian evaluated along F ⁻ is given by

$$\displaystyle{\det (J) = F_{vv}(I_{s} + I_{ss})\,.}$$

Recall, we have F _vv  > 0 along F ⁻. The function $\tilde{I}(s)$ defined in (3.48) is constant and negative for $s \in (-\infty,{s}^{-}) \cap ({s}^{+},\infty )$. This implies, in general, an even number of folded singularities (if they exist). The derivative $\tilde{I}_{s}$ must be positive at the first (odd) folded singularity while negative at the second (even) singularity. Hence, det(J) > 0 for an odd folded singularity and det(J) < 0 for an even folded singularity. This implies that an odd folded singularity is either of folded node or folded focus type while an even folded singularity is of folded saddle type. From the structure of the Jacobian (3.49) it follows that the eigenvectors corresponding to negative eigenvalues have a positive slope while eigenvectors corresponding to positive eigenvalues have a negative slope.

Fig. 3.12

Reduced flow on the critical manifold S near the lower fold F ⁻ corresponding to Fig. 3.10a, ramp protocol: there are two folded singularities, a folded saddle (FS) and a folded focus (FF), ξ denotes the folded saddle canard that crosses from the lower stable branch S _a ⁻ via the FS singularity onto the repelling middle branch S _r . The canard ξ forms the firing threshold manifold. Note, the other canard of the FS singularity (the faux canard) crosses from S _r to S _a ⁻. The segment on S _a ⁻ forms a boundary that prevents trajectories to the right of ξ to spike

Fig. 3.13

Reduced flow shown in Fig. 3.12 projected onto coordinate chart (s, v) corresponding to Fig. 3.10a, ramp protocol: there are two folded singularities, a folded saddle (FS) and a folded focus (FF), ξ denotes the folded saddle canard that crosses from the lower stable branch S _a ⁻ via the FS singularity onto the repelling middle branch S _r . The canard ξ forms the firing threshold manifold. Note, the other canard of the FS singularity (the faux canard) crosses from S _r to S _a ⁻. The segment on S _a ⁻ forms a boundary that prevents trajectories to the right of ξ to spike

Fig. 3.14

Reduced flow projected onto coordinate chart (s, v) corresponding to Fig. 3.10b, pulse protocol: ξ denotes the folded saddle canard that forms the firing threshold manifold; see Fig. 3.13 caption for details

Figures 3.12 and 3.13 show an example of system (3.42) for a type II neuron with ramp protocol (3.43), where F(v) is given by the ML-FHN model (3.36). Figure 3.12 is a three-dimensional representation of the critical manifold S near the lower fold F ⁻ and Fig. 3.13 is the corresponding reduced flow on S projected onto the coordinate chart (s, v). The initial state on the stable branch S _a of the critical manifold is $({s}^{-},v_{rest}^{-})$ where $v = v_{rest}^{-}$ (the horizontal trajectory for s ≤ s ⁻) corresponds to the resting membrane potential of the neuron for s ≤ s ⁻, i.e. for I = 0. On the lower fold F ⁻ (dashed horizontal line), we observe two folded singularities, a folded focus (FF) respectively a folded saddle (FS). Note, $\dot{v} > 0$ along the segment of F ⁻ bounded by the two folded singularities. To reach this segment of the lower fold F ⁻ and, hence, to be able to elicit a spike, the initial state $({s}^{-},v_{rest}^{-})$ must be in the ‘domain of attraction’ of this segment (shown as a shaded region). This domain is bounded by the folded saddle canard ξ and a segment of the lower fold F ⁻. Thus the folded saddle canard ξ forms the firing threshold manifold on S _a ⁻.

As can be also seen in Fig. 3.13, the position of the canard ξ changes as the (maximal) slope of the drive I(s) changes. Clearly, folded singularities and their canards encode the complete temporal information of the drive I(s), i.e. amplitude, slope, curvature, etc. Figure 3.13a predicts no spike while Fig. 3.13b predicts a spike. These correspond to the two cases shown in Figs. 3.10a and 3.12 for the ramp protocol.

Similarly, Fig. 3.14a predicts no spike while Fig. 3.14b predicts a spike. These correspond to the two cases shown in Fig. 3.10b for the pulse protocol. Therefore, we can view this type II excitable neuron shown in Fig. 3.10 as a slope detector .

It is remarkable that dynamic, nonautonomous information such as the evolution profile of the external drive I(s) is encoded in the location of an invariant manifold of a singular perturbation problem, the canard. Here, in particular, we observe that only changing the slope is sufficient to elicit a spike. In general, our analysis provides a slow input modulation condition for transient phenomena based on canard theory.

3.2.4 Firing Threshold Amplitude I _thr

The previous analysis showed that the existence of a folded saddle singularity is a necessary but not a sufficient condition for a neuron model to be able to fire an action potential. At the heart of the issue lies the relative position of the folded saddle canard ξ that forms the firing threshold manifold in these models to the initial condition. Numerically, we found that any ramp with a maximal drive $I_{1} < I_{thr}$ is not able to elicit a spike independent of the slope of the ramp. Although a folded saddle singularity might exist, the domain of attraction for firing a spike bounded by the folded saddle canard ξ never encloses the initial condition given by the resting membrane potential.

Even if we formally take the limit s ₁ → 0 (at s = s ₀) which transforms the smooth ramp into a discontinuous step protocol, we are not able to elicit a spike. By looking at Fig. 3.7, it becomes immediately clear why the model neuron cannot spike. The shift of the critical manifold is not sufficient to pass the lower fold as discussed at the end of Sect. 3.3.1.1. Although the canard ξ represents the firing threshold manifold for slow dynamic changes, it can be continued towards the fast time-scale limit and it will converge to the firing threshold shown in Fig. 3.9 (dashed curve). Hence I = I _thr represents the fast time-scale limit of the minimum current amplitude needed to elicit a spike. The closer the amplitude I > I _thr to this limit I _thr the steeper the slope of the profile has to be. The same holds for type III neurons. This relates the concepts of fast and slow input modulations.

3.2.5 Bifurcation of Canards

Fig. 3.15

Bifurcation diagram of folded singularities under variation of the slope s ₁ for type II neuron with ramp protocol shown in Fig. 3.13: I ₁ = 0. 09 is fixed. For s ₁ ≈ 0. 83 we observe a folded saddle-node (FSN) type I bifurcation where two folded singularities annihilate each other. The vertical line at s ₁ ≈ 0. 47 indicates the firing slope threshold, i.e for sufficiently steep slope s ₁ < 0. 47, the type II neuron will transiently spike; compare with Fig. 3.10a

The existence of folded singularities and their associated canards is necessary for the transient spiking phenomenon observed. They are slope detectors . Figure 3.15 shows a folded singularity bifurcation diagram for a type II neuron under the variation of the slope s ₁ of the ramp (the amplitude is fixed). Folded singularities bifurcate at a saddle-node bifurcation of a folded saddle with a folded node. (Subsequently, the branch of folded nodes becomes a branch of folded foci.) This bifurcation is known as a folded saddle-node (FSN) of type I [40, 57]. Here, the type refers to the bifurcation, not to the type of neuron. This points to the importance of this bifurcation for the excitability of neurons.

In contrast, a FSN type II bifurcation [40, 57] indicates a transcritical bifurcation of a folded and an ordinary singularity bifurcation. This type of bifurcation usually happens in type II neurons close to I = I _bif . It corresponds to the unfolding of a singular Hopf bifurcation in singularly perturbed systems with two or more slow variables. The interested reader is referred to [10] and references therein.

4 Conclusion

There is a growing synergy between neurophysiology and dynamical systems. The abstraction and generalization of the mathematical approach can lead to the identification of, and deep insights into, common mathematical structures of rhythmicity and excitability across contexts. The demand for an adequate high-level description of cell function raises a number of challenges at the forefront of present-day research in the field of dynamical systems. We face fundamental challenges in trying to understand the relationships between intrinsic dynamics, stimuli, coupling, and patterns of synchrony in network models. The ability of neuronal networks to create spatio-temporal patterns, spontaneously or driven, and the ways in which neuromodulators reshape or totally change these patterns is of eminent interest for understanding neuronal dynamics.

The application of concepts and techniques from dynamical systems theory to neuronal dynamics continues to mature, especially to stationary rhythms and steady state attractors. Meanwhile, there is increasing awareness that transient dynamics play an important physiological role. Excitability of neurons [18, 29, 52] and networks are prime examples of transient dynamics, especially as responses to brief or non-stationary time-varying inputs. Recent developments in canard theory [26, 63, 64] have provided a new direction for understanding these transient dynamics that are modelled as nonautonomous multiple time-scale systems. It is well known that a nonautonomous system can be viewed as an extended autonomous system by increasing the phase space dimension by one. The key observation is that folded singularities are still well defined, while equilibria of the unforced system will not persist in the extended system. Thus canards have the potential to significantly shape the nature of solutions in nonautonomous multiple time-scales systems. We would like to stress this important point of view.

The take-home message lies in the realisation that folded singularities and associated canards create local transient “attractor” states in multiple scales problems. This is due to the fact that trajectories in the domain of attraction of folded singularities will reach and pass these folded singularities in finite slow time; folded singularities are not equilibrium states. In the context of neuronal excitability and as shown in [64], we identify canards of folded saddle type as firing threshold manifolds. We have demonstrated the role of such structures in comparing the dynamics of spike generation for neuron models in the different behavioral regimes of type I, II and III excitability. For type II and III we have revealed and characterized stimulus features that lead to spike generation for transient stimuli, most notably that a stimulus must rise fast enough for excitation.

Dynamic forcing has the potential to create folded singularities and to form these effective separatrices or to change the global return mechanism. Hence, the specific nature of the dynamic forcing determines which local attractor states can be reached through global mechanisms. This point of view has profound consequences in the analysis of excitable physiological systems such as in auditory brain stem neurons [42], modeling propofol anesthesia [41, 44] and cell calcium dynamics [26]. From a mathematical point of view, the time is “ripe” for forging (more) connections between nonautonomous attractor theory [36, 37] and geometric singular perturbation theory [17, 32].