General Patterns of Opposition Squares and 2n-gons

Abstract

In the first part of this paper we formulate the General Pattern of Squares of Opposition (GPSO), which comes in two forms. The first form is based on trichotomies whereas the second form is based on unilateral entailments. We then apply the two forms of GPSO to construct some new squares of opposition (SOs) not known to traditional logicians. In the second part of this paper we discuss the hexagons of opposition (6Os) as an alternative representation of trichotomies. We then generalize GPSO to the General Pattern of 2n-gons of Opposition (GP2nO), which also comes in two forms. The first form is based on n-chotomies whereas the second form is based on co-antecedent unilateral entailments. We finally introduce the notion of perfection associated with 2n-gons of opposition (2nOs) and point out that the fundamental difference between a SO and a 6O is that the former is imperfect while the latter is perfect. We also discuss how imperfect 2nOs can be perfected at different fine-grainedness.

1 Introduction

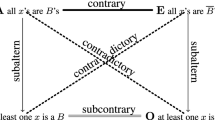
The square of opposition (SO) has been an important entity studied in traditional logic since the ancient times. Yet, for centuries logicians seemed to know only one type of SO, i.e. the Boethian SO composed of the universal/particular affirmative/negative propositions arranged in the four corners named A, E, I and O. These four propositions are linked up by four types of binary opposition relations whose definitions are given in Table 1.¹

Table 1 Opposition relations

In modern times, many scholars tried to unravel the underlying principles of opposition inferences with a view to achieving a new interpretation of SO. Such kind of studies includes Brown’s (1984) classification of 4 main types and 34 subtypes of SOs [4], Jaspers’ representation of SO in terms of two-dimensional Cartesian coordinate [6], Seuren’s formulation of the improved square notation based on his Valuation Space Model [9]. In this paper, we will generalize the traditional Boethian SO to a general pattern of SOs. After doing so, we can then go further by generalizing the notion of “squares of opposition” to “2n-gons of opposition”.

But before embarking, we have to clarify two points. First, in modern times some scholars (such as [5, 8, 11]) adopt a new definition of SOs based on the notions of negation and duality, rather than the traditional opposition relations as defined in Table 1. This paper will stick to the traditional definition of SOs and will not consider the new definition. Moreover, one should note that the general patterns discussed in this paper are derived from traditional SOs and are not generally applicable to the modern SOs (which should be more accurately called “squares of duality”).²

Second, this paper adopts a graph-theoretic rather than geometrical view on the figures representing the logical relations. Instead of constructing all sorts of higher-dimensional geometrical figures as was done by the n-Opposition theorists such as [7] and [10], we will represent the logical relations by 2-dimensional labeled multidigraphs, with the vertices representing the propositions and the arcs representing the opposition relations. The unilateral subalternate relations will be represented by single arcs with arrow heads, whereas the bilateral contrary, subcontrary and contradictory relations will be represented by arcs without arrow heads which are understood to be double arcs going in opposite directions. Under this graph-theoretic view, the angles and lengths of the arcs have no significance.

2 General Pattern of Squares of Opposition

2.1 Some Preliminary Observations

We start from some preliminary observations of the Boethian SO. Consider the subalternate relation between the A (i.e. “All S are P”) and I (i.e. “Some S are P”) statements first. One crucial point is that if we rewrite the I statement as the disjunction “All S are P ∨ Part of the S are P”,³ then the subalternate relation automatically obtains as it is only a special case of the unilateral entailment⁴ p ₁⇒ _u (p ₁∨p ₂) in propositional logic. The same can be said of the subalternate relation between the E (i.e. “All S are not P”, or equivalently “No S are P”) and O (i.e. “Some S are not P”, or equivalently “Not all S are P”) statements if we rewrite the O statement as the disjunction “No S are P ∨ Part of the S are P”. Moreover, we notice that the three statements “All S are P”, “Part of the S are P” and “No S are P” constitute a trichotomy, i.e. these three statements are pairwise mutually exclusive and collectively exhaustive. Thus, we may say that the SO is derived from a trichotomy.

Second, we observe that by virtue of the two contradictory relations (i.e. O≡¬A, E≡¬I), the two subalternate relations (i.e. A⇒ _u I and E⇒ _u O) are in fact contraposition of each other. Thus, we may also say that the SO is derived from a unilateral entailment (i.e. subalternate relation) and its contraposition.

2.2 Two Forms of the General Pattern of Squares of Opposition

We can generalize the above two observations to the General Pattern of Squares of Opposition (GPSO), which comes in two forms. The first form, henceforth GPSO1, is generalized from the first observation.

GPSO1

Given 3 non-trivial⁵ propositions (or propositional functions) p, q and r that constitute a trichotomy, we can construct a SO as shown in Fig. 1.

Fig. 1

GPSO1

In what follows we will show that the SO in Fig. 1 satisfies the definitions of the opposition relations. As mentioned above, the two subalternate relations are just special cases of p ₁⇒ _u (p ₁∨p ₂). The two contradictory relations follow from the fact that p, q and r constitute a trichotomy. The contrariety between p and r follows from the fact that any two members of a trichotomy are mutually exclusive but not collectively exhaustive. The subcontrariety between (p∨q) and (r∨q) follows from the fact that (p∨q)∨(r∨q)≡(p∨q∨r) and (p∨q)∧(r∨q)≡q. Thus, (p∨q) and (r∨q) are collectively exhaustive but not mutually exclusive.

The second form, henceforth GPSO2, is generalized from the second observation.

GPSO2

Given 2 non-trivial propositions (or propositional functions) s and t such that (a) $s \not\equiv t$; (b) they constitute a unilateral entailment: s⇒ _u t, we can construct a SO as shown in Fig. 2.

Fig. 2

GPSO2

In what follows we will show that the SO in Fig. 2 also satisfies the definitions of the opposition relations. First, by definition of this SO, the two subalternate and contradictory relations are obviously satisfied. Next we consider the contrary relation. This can be proved by showing that two propositions p ₁ and p ₂ are contrary to each other if and only if p ₁⇒ _u ¬p ₂. This unilateral entailment is equivalent to $(p_{1} \Rightarrow{\neg} p_{2}) \wedge({\neg} p_{2} \not\Rightarrow p_{1})$. This can be rewritten as $(p_{1} \wedge p_{2} \equiv F) \wedge(p_{1} \vee p_{2} \not\equiv T)$,⁶ which is equivalent to saying that p ₁ and p ₂ are mutually exclusive but not collectively exhaustive, and thus satisfy the contrary relation. Now since we have s⇒ _u t, it thus follows that s and ¬t are contrary to each other.

Finally we consider the subcontrary relation. This can be proved by showing that two propositions p ₁ and p ₂ are subcontrary to each other if and only if ¬p ₁ and ¬p ₂ are contrary to each other. Now the fact that ¬p ₁ and ¬p ₂ are contrary to each other can be expressed as $({\neg} p_{1} \wedge{\neg} p_{2} \equiv F) \wedge ({\neg} p_{1} \vee{\neg} p_{2} \not\equiv T)$, which is equivalent to $(p_{1} \vee p_{2} \equiv T) \wedge(p_{1} \wedge p_{2} \not\equiv F)$. This shows that p ₁ and p ₂ are collectively exhaustive but not mutually exclusive, and thus satisfy the subcontrary relation. As we have previously shown that s and ¬t are contrary to each other, it thus follows that ¬s and t are subcontrary to each other.

2.3 Relations Between GPSO1 and GPSO2

Although GPSO1 and GPSO2 are based on a trichotomy and a unilateral entailment, respectively, the two forms are in fact two sides of the same coin. Given one form, we can always transform it into the other form, which we will show below.

First, suppose we are given a SO constructed from GPSO1, we immediately get a unilateral entailment, i.e. p⇒ _u (p∨q) such that $p \not\equiv(p \vee q)$. With this unilateral entailment, we can then construct another SO by invoking GPSO2. Please note that if either of p, q, r is trivial, then either p or (p∨q) is trivial, or p≡(p∨q).

On the other hand, suppose we are given an SO constructed from GPSO2, then s, ¬t and (¬s∧t) constitute a trichotomy. To show that these three propositions are pairwise mutually exclusive, we first observe that s∧¬t≡F by the contrary relation between s and ¬t. Moreover, it is also obvious that s∧(¬s∧t)≡¬t∧(¬s∧t)≡F. To show that the three propositions are collectively exhaustive, it suffices to show that s∨¬t∨(¬s∧t)≡T, which is obvious after we expand the left-hand side into (s∨¬t∨¬s)∧(s∨¬t∨t). The above fact can be illustrated by Fig. 3 in which s and t are depicted as sets and the unilateral entailment is depicted as proper set inclusion. From Fig. 3 we can see that if s is a proper subset of t, then s, ¬t and (¬s∧t) constitute a partition of the universe.

Fig. 3

Correspondence between a unilateral entailment and a trichotomy

The above discussion shows that a unilateral entailment is closely related to a trichotomy. With this trichotomy, we can then construct another SO by invoking GPSO1. Please note that if either s or t is trivial, or s≡t, then either of s, ¬t, (¬s∧t) is trivial.

2.4 Applications of GPSO1

By applying the two forms of GPSO, a great number of SOs not known to traditional logicians can be easily constructed. We first see some examples of the application of GPSO1. Let 50<n<100, where n is a real number. Then the three intervals [0,100−n), [100−n,n] and (n,100] constitute a tripartition of the interval [0,100]. In other words, “Less than (100−n) % of S are P”, “Between (100−n) % and n % of S are P” and “More than n % of S are P” constitute a trichotomy. With this trichotomy, we can construct the SO shown in Fig. 4.

Fig. 4

SO of proportional quantifiers

Please note that in constructing the SO in Fig. 4, we have also made use of the following equivalences: “Less than (100−n) % of S are P” ≡ “More than n % of S are not P”; “At most n % of S are P” ≡ “At least (100−n) % of S are not P”.

The application of GPSO is not confined to quantified sentences, but may be extended to other types of sentences or even plain predicates. Suppose our domain of discourse consists of members of the pre-1789 French Estates General, which were divided into three estates: clergymen, noblemen and commoners, which constituted a trichotomy. If we now call “clergymen ∨ noblemen” the “privileged class” and “commoners ∨ noblemen” the “secular class”, then we may construct the SO shown in Fig. 5.

Fig. 5

SO of pre-1789 French Estates General

Although the SO in Fig. 5 is composed of plain predicates rather than propositions, these plain predicates may be seen as short forms of propositional function with a variable x. For example, “clergymen” in the SO may be seen as short form of the propositional function “x was a clergyman”.

2.5 Applications of GPSO2

According to GPSO2, a SO may be constructed from a unilateral entailment together with its contraposition. This is in fact the underlying principle of the “semiotic squares”. Given a pair of contrary concepts, such as “happy” and “unhappy”, we immediately obtain the unilateral entailment “happy ⇒ _u not unhappy”.⁷ With this unilateral entailment, we can then construct the semiotic square shown in Fig. 6.

Fig. 6

Semiotic square

Unilateral entailments may also occur between sentences with more than one quantifier, such as “Every boy loves every girl ⇒ _u Some boy loves some girl”. One interesting subtype of this kind of entailments consists of unilateral entailments between the active and passive forms of a sentence with more than one quantifier. This is the subject area of “scope dominance” studied by [2] and [1].⁸ These scholars have discovered a number of valid unilateral entailments involving sentences with more than one quantifier. Here is one such example:

$$ \mbox{Most boys love no girl} \Rightarrow_u \mbox{No girl is loved by most boys} $$

(2.1)

With this unilateral entailment, we can then construct the SO shown in Fig. 7.

Fig. 7

SO of scope dominance

We can thus see that by combining GPSO2 with the research findings on scope dominance, we can construct a great number of SOs composed of sentences with more than one quantifier.

3 General Pattern of 2n-gons of Opposition

3.1 Hexagons of Opposition

According to GPSO1, a SO can be derived from any trichotomy composed of 3 non-trivial propositions p, q and r. However, GPSO1 shows an asymmetry between these 3 propositions: while each of p and r appears as an independent proposition in the two upper corners (i.e. A and E), q only appears as parts of two disjunctions in the two lower corners (i.e. I and O).

To achieve symmetry, we need to add to the SO two new vertices denoted as Y and U corresponding to the propositions q and p∨r, respectively, thus expanding the SO to a hexagon of opposition (6O) proposed by [3] as shown in Fig. 8.

Fig. 8

Hexagon of opposition

Please note that this figure contains the Boethian SO AEIO as a subpart. For this reason, only those arcs not being part of AEIO are labeled. This figure also contains the AYE triangle of contrariety, IOU triangle of subcontrariety as well as two more SOs: AYUO and YEIU, as its subparts.

For ease of comparison with other 2n-gons below, the components of the above 6O can be rearranged into the form shown in Fig. 9 which is, graph-theoretically speaking, isomorphic with the original form (in Fig. 9, SA=subalternate, CD=contradictory, C=contrary, SC=subcontrary).

Fig. 9

6O constructed from a trichotomy

To avoid messing up the figure, some arcs in Fig. 9 have been left out, e.g. the SA arc leading from p to p∨q. One should view Fig. 9 on the understanding that there is a C arc between any two upper-row vertices, a SC arc between any two lower-row vertices and a SA arc leading from any upper-row vertex to any lower-row vertex not directly below it.

The above discussion shows that a trichotomy is best represented by a 6O. But as shown in Subsect. 2.3, trichotomies and unilateral entailments are closely related to each other. How can we construct a 6O from a unilateral entailment? If we review Fig. 3, then we can see that apart from the unilateral entailment s⇒ _u t, there is in fact another less obvious one with s as antecedent, i.e. s⇒ _u (s∨¬t). By properly arranging the 3 propositions s, t, (s∨¬t) and their contradictories ¬s, ¬t, (¬s∧t), we can then construct a 6O as shown in Fig. 10.

Fig. 10

6O constructed from a unilateral entailment

3.2 Two Forms of the General Pattern of 2n-gons of Opposition

The natural association between a trichotomy (or a unilateral entailment) and a 6O may be generalized to an association between a n-chotomy (or n−2 unilateral entailments) and a 2n-gon of opposition (2nO), resulting in the General Pattern of 2n-gons of Opposition (GP2nO), which also comes in two forms, denoted GP2nO1 and GP2nO2 below.

GP2nO1

Given n (n≥3) non-trivial propositions (or propositional functions) p ₁,p ₂,…,p _n that constitute a n-chotomy (i.e. p ₁,p ₂,…,p _n are collectively exhaustive and pairwise mutually exclusive), we can construct a 2nO as shown in Fig. 11 (many arcs have been left out from this figure).⁹

Fig. 11

GP2nO1

It is easy to see that the 2nO in Fig. 11 satisfies the definitions of the opposition relations. For example, any two lower-row propositions are subcontrary to each other because they contain some common disjuncts (hence not mutually exclusive), and they collectively contain all the n propositions as disjuncts (hence collectively exhaustive).

GP2nO2

Given n−1 (n≥3) non-trivial propositions (or propositional functions) s,t ₁,…,t _n−2 such that (a) any two of t ₁,…,t _n−2 satisfy the subcontrary relation; (b) $s \not\equiv\nobreak (t_{1} \wedge\cdots\wedge t_{n - 2})$; (c) they constitute (n−2) co-antecedent unilateral entailments (i.e. unilateral entailments with the same antecedent): s⇒ _u t ₁,… , s⇒ _u t _n−2, then we have an additional unilateral entailment: s⇒ _u (s∨¬t ₁∨⋯∨¬t _n−2) and we can construct a 2nO as shown in Fig. 12.

Fig. 12

GP2nO2

Next we show that the 2nO in Fig. 12 also satisfies the definitions of the opposition relations. The contradictory relations are obviously satisfied. So we consider the subalternate relations. The subalternate relations between s and t ₁, …, s and t _n−2, as well as the subalternate relations between ¬t ₁ and ¬s, …, ¬t _n−2 and ¬s are guaranteed by condition (c) above and its contraposition. We will now show that ¬t _i ⇒ _u t _j (1≤i,j≤n−2,i≠j). By condition (a) above, any t _i and t _j satisfy the subcontrary relation, which can be expressed as $(t_{i} \vee t_{j} \equiv T) \wedge(t_{i} \wedge t_{j} \not\equiv F)$. This is equivalent to (¬t _i ⇒t _j )∧(t _j ⇏¬t _i ), which can be rewritten as ¬t _i ⇒ _u t _j . The remaining subalternate relations in Fig. 12 are just special cases of unilateral entailments in propositional logic. For example, (¬s∧t ₁∧⋯∧¬t _n−2)⇒ _u t ₁ is just a special case of (p ₁∧p ₂)⇒ _u p ₁.

Next we consider the contrary relations. Since it has been shown that for any two distinct upper-row propositions p ₁ and p ₂, we have p ₁⇒ _u ¬p ₂, thus p ₁ and p ₂ are contrary to each other. Finally, since each lower-row proposition is the contradictory of the upper-row proposition directly above it, the subcontrariety between any two lower-row propositions follows from the contrariety between any two upper-row propositions.

3.3 Relations Between GP2nO1 and GP2nO2

Just like GPSO, the two forms of GP2nO are also interdefinable. If we are given a 2nO constructed from GP2nO1, then this 2nO contains n−1 propositions: p ₁, (p ₁∨p ₃∨⋯∨p _n ),…,(p ₁∨⋯∨p _n−2∨p _n ) that satisfy the three conditions of GP2nO2: (a) the subcontrariety between any two of (p ₁∨p ₃∨⋯∨p _n ),…,(p ₁∨⋯∨p _n−2∨p _n ) is guaranteed by the subcontrariety between any two lower-row propositions in this 2nO; (b) $p_{1} \not\equiv(p_{1} \vee p_{3} \vee\cdots \vee p_{n}) \wedge\cdots\wedge(p_{1} \vee\cdots\vee p_{n - 2} \vee p_{n})$ because the right-hand side is equivalent to (p ₁∨p _n ); (c) these propositions constitute (n−2) co-antecedent unilateral entailments: p ₁⇒ _u (p ₁∨p ₃∨⋯∨p _n ),…,p ₁⇒ _u (p ₁∨⋯∨p _n−2∨p _n ).

This 2nO also contains an additional unilateral entailment: p ₁⇒ _u (p ₁∨p ₂∨⋯∨p _n−1) whose antecedent is p ₁ and whose consequent has the correct form as stipulated in GP2nO2, because (p ₁∨p ₂∨⋯∨p _n−1)≡p ₁∨¬(p ₁∨p ₃∨⋯∨p _n )∨⋯∨¬(p ₁∨⋯∨p _n−2∨p _n ). Moreover, the arrangement of the 2n propositions of this 2nO also satisfies GP2nO2. Please also note that if either of p ₁,…,p _n is trivial, then either of the n−1 propositions given above is trivial, or p ₁≡(p ₁∨p ₃∨⋯∨p _n )∧⋯∧(p ₁∨⋯∨p _n−2∨p _n ). For example, if p ₂≡F, then (p ₁∨p ₃∨⋯∨p _n )≡T.

Conversely, if we are given a 2nO constructed from GP2nO2, then this 2nO contains n propositions s, ¬t ₁,…,¬t _n−2, (¬s∧t ₁∧⋯∧t _n−2) that constitute a n-chotomy. That these n propositions are pairwise mutually exclusive is guaranteed by the contrary relations among these propositions. To show that these propositions are collectively exhaustive, it suffices to show that s∨¬t ₁∨⋯∨¬t _n−2∨(¬s∧t ₁∧⋯∧t _n−2)≡T, which is obvious after we expand the left-hand side into (s∨¬t ₁∨⋯∨¬t _n−2∨¬s)∧(s∨¬t ₁∨⋯∨¬t _n−2∨t ₁)∧⋯∧(s∨¬t ₁∨⋯∨¬t _n−2∨t _n−2). The above fact can be illustrated by Fig. 13 for the case n=2, which shows that the two co-antecedent unilateral entailments s⇒ _u t ₁ and s⇒ _u t ₂ give rise to the additional unilateral entailment: s⇒ _u (s∨¬t ₁∨¬t ₂) and a 4-chotomy consisting of s, ¬t ₁, ¬t ₂ and (¬s∧t ₁∧t ₂).

Fig. 13

Correspondence between 2 co-antecedent unilateral entailments and a 4-chotomy

Moreover, the arrangement of the 2n propositions of this 2nO also satisfies GP2nO1. Please also note that if either of s, t ₁,…,t _n−2 is trivial, or s≡(t ₁∧⋯∧t _n−2), then either of s, ¬t ₁,…,¬t _n−2, (¬s∧t ₁∧⋯∧t _n−2) is trivial.

4 Perfection

Figures 11 and 12 show that every 2nO contains C(n,m) 2mOs as its proper subparts,¹⁰ for any m such that m<n and m≥2.¹¹ To distinguish these 2mOs from the 2nO, we need to introduce the notion of perfection.

We say that a 2nO is perfect if the disjunction of all its upper-row propositions ≡ the disjunction of all its lower-row propositions, otherwise it is imperfect. Given the pairwise subcontrariety of the lower-row propositions of any 2nO, this condition is equivalent to the fact that the disjunction of all its upper-row propositions ≡T.

According to this definition, any 2nO that satisfies GP2nO1 or GP2nO2 is perfect, whereas a 2mO (m<n) which is a proper subpart of a perfect 2nO is imperfect. Thus, the 6O proposed by modern scholars as depicted in Fig. 9 above is perfect whereas the traditional SO (i.e. 4O) is imperfect. Moreover, the fundamental difference between the 6O and SO in terms of symmetry with respect to the three propositions in a trichotomy can now be more formally captured by the notion of perfection, i.e. the symmetric 6O is perfect and the asymmetric SO is imperfect.

Given an imperfect 2mO, we can always make it perfect. But the outcome of the perfection process is not unique because an imperfect 2mO can be perfected at different fine-grainedness by combining or splitting propositions.

Let’s use an example to illustrate this point. Figure 14 shows an imperfect 4O because $(p_{1} \vee p_{2}) \not\equiv(p_{1} \vee p_{2} \vee p_{3} \vee p_{4})$.

Fig. 14

An imperfect 4O

The most straightforward way to perfect this 4O is to expand it into an 8O by adding two upper-row propositions: p ₃ and p ₄ (and corresponding lower-row propositions). But this is not the unique way. Another way is to expand this 4O into a 6O by adding just one upper-row proposition: (p ₃∨p ₄) (and the corresponding lower-row proposition). This is tantamount to combining the two propositions p ₃ and p ₄ into one, hence transforming the original 4-chotomy to a trichotomy (comprising the three propositions p ₁, p ₂ and (p ₃∨p ₄)). Still another way is to expand this 4O into a 10O by rewriting p ₄ as p _4a ∨p _4b and adding three upper-row propositions: p ₃, p _4a and p _4b (and corresponding lower-row propositions). This is tantamount to splitting the proposition p ₄ into two non-trivial propositions p _4a and p _4b such that p ₄≡p _4a ∨p _4b , hence transforming the original 4-chotomy to a 5-chotomy (comprising the five propositions p ₁, p ₂, p ₃, p _4a and p _4b ).

5 Conclusion

In this paper we have shown how the Boethian SO is related to trichotomies or unilateral entailments and then formulated the two forms of GPSO, which enables us to construct a great number of new SOs not known to traditional logicians. We have also discussed 6O as an alternative representation of a trichotomies. Intuitively, a 6O differs from a SO in that the former is symmetric while the latter is asymmetric with respect to the three propositions in a trichotomy. This difference can be more formally captured by the notion of perfection in that a 6O is a perfect representation of trichotomies, whereas a SO, being a proper subpart of a 6O, is imperfect. By further generalizing trichotomies and unilateral entailments to n-chotomies and co-antecedent unilateral entailments, respectively, we come up with the notion of 2n-gons and the two forms of GP2nO. We finally discuss the distinction between perfect and imperfect 2nOs. Thus, GPSO and GP2nO have very different nature, in that any SOs constructed from the two forms of GPSO are imperfect whereas any 2nOs (n≥3) constructed from the two forms of GP2nO are perfect.