On the Usage of Analytically Computed Adjoint Gradients in a Direct Optimization for Time-Optimal Control Problems

Abstract

This paper discusses time-optimal control problems and describes a workflow for the use of analytically computed adjoint gradients considering a discrete control parameterization. The adjoint gradients are used here to support a direct optimization method, such as Sequential Quadratic Programming (SQP), by providing analytically computed gradients and avoiding the elaborate numerical differentiation. In addition, the adjoint variables can be used to evaluate the necessary first-order optimality conditions regarding the Hamiltonian function and gives an opportunity to discuss the sensitivity of a solution with respect to the refinement of the discretization of the control. To further emphasize the advantages of adjoint gradients, there is also a discussion of the structure of analytical gradients computed by a direct differentiation method, and the difference in the dimensions compared to the adjoint approach is addressed. An example of trajectory planning for a robot shows application scenarios for the adjoint variables in a cubic spline parameterized control.

1 Introduction

Optimal control theory is based on the calculus of variations and deals with finding optimal trajectories for nonlinear dynamical systems, e.g. spacecrafts or multibody systems like robots. The works by Kelley [4] and Bryson and Ho [1] have to be mentioned as groundbreaking in the field of optimal control theory and serve as basis for extensive subsequent research, also in the field of time-optimal control.

As a special class of time-optimal control problems considering final constraints, one can cite the control of a robot arm designed in such a way that the operation time for a rest-to-rest maneuver becomes minimal. Following an indirect optimization approach, such problems can be transformed into a two-point boundary value problem, which can usually be solved by shooting or full collocation methods. Alternatively, a direct optimization approach can be pursued, in which the boundary value problem is posed as a nonlinear programming problem method, see e.g. [12] for the time-optimal trajectory planning considering the continuity required to respect technological limits of real robots.

An alternative to the mentioned methods is offered by indirect gradient methods, which are considered to be particularly robust with respect to initial controls. The work by Bryson and Ho [1] shows how the gradient can be computed straightforward using adjoint variables. With this gradient information optimal control problems can be solved iteratively by the use of nonlinear optimization routines, as described in the sense of optimal control or parameter identification in multibody systems e.g. in  [8]. The work by Eichmeir et al. [2] extends the theory for time-optimal control problems to dynamic systems under final constraints. Such problems arise e.g. in space vehicle dynamics during minimum time moon ascending/descending maneuvers or in robotics in the case that the time for a rest-to-rest maneuver should become a minimum. Such problems can be considered as two-point boundary value problems, with the major drawback of requiring an initial guess close to the optimal solution. Otherwise, the optimal control problem could be solved via the adjoint method which is an efficient way to compute the direction of the steepest descent of a cost functional. However, when using such indirect methods to solve optimal control problems, a major drawback appears in the computation of the Hamiltonian and the required derivatives: they may be complex and furthermore need to be recomputed often during the simulation. Moreover, depending on the variables or parameters to be identified in the optimal control strategy, it is difficult to assign a physical meaning to the adjoint variables.

This paper focuses on solving time-optimal control problems with a classical direct optimization method and then evaluating the respective optimality conditions based on an indirect optimization approach. The adjoint variables can be investigated to efficiently compute the gradients of the cost functional and the constraints. Moreover, the adjoint variables can be investigated to exploit the optimality conditions regarding the Hamiltonian function. To demonstrate the use of analytically computed adjoint gradients, the time-optimal trajectory planning of a Selective Compliance Assembly Robot Arm (SCARA) is solved by an SQP method and the optimality conditions regarding the Hamiltonian function are evaluated by the adjoints. The application shows the easy access to the adjoint gradients and discusses the latter mentioned role of the adjoint variables in the optimality conditions.

2 Use of Adjoint Variables in Direct Optimization Approaches

The aim of this paper is to determine a control $\textbf{u}(t) = \textbf{u}^*$ and a final time $t_f = t_f^*$ of a dynamical system

$$\begin{aligned} \dot{\textbf{x}}(t) = \textbf{f}(\textbf{x}(t),\textbf{u}(t)) \quad \text {with} \quad \textbf{x}(0) = \textbf{x}_0, \end{aligned}$$

(1)

such that the scalar performance measure

$$\begin{aligned} J(\textbf{x}(t),\textbf{u}(t),t_f) = \int _{t_0}^{t_f} \Big [1 + P(\textbf{x}(t),\textbf{u}(t))\Big ] \,\textrm{d}t \end{aligned}$$

(2)

becomes a minimum with respect to a final constraint

$$\begin{aligned} \boldsymbol{\phi }(\textbf{x}(t_f), t_f) = \textbf{0} \in \mathbb {R}^q. \end{aligned}$$

(3)

Inequality constraints on the state $\textbf{x} \in \mathbb {R}^n$ and the control $\textbf{u} \in \mathbb {R}^m$ are considered by the scalar penalty function P. To be specific, violations of inequality constraints within the time interval $t\in [t_0,\,t_f]$ are taken into account as an additional term in the cost functional in Eq. (2). The above optimal control problem can generally be solved by a direct or indirect optimization approach. In this paper, the original infinite dimensional optimization problem is transformed into a finite dimensional one by parameterizing the control with a finite set of optimization variables $\textbf{z} \in \mathbb {R}^z$ including the final time and the control parameterization. Thus, the resulting nonlinear programming (NLP) problem can be solved with classical direct optimization approaches such as the SQP method [9].

How to Interpret the Results from a Direct Optimization Algorithm An optimal point $\textbf{z}=\textbf{z}^*$ fulfills the well-known Karush-Kuhn-Tucker (KKT) conditions [3, 5], but these conditions do not provide any information about the quality of the control parameterization with respect to the infinite dimensional optimization problem. The basic idea to interpret an optimal point $\textbf{z}^*$ is to relate the direct optimization approach to Pontryagin’s minimum principle [11]. The optimality conditions based on an indirect optimization approach [2] can be used for this idea. Figure 1 illustrates a rough flowchart for the interpretation of results obtained by a direct optimization approach. This approach requires the Hamiltonian of the system to evaluate Pontryagin’s minimum principle. The Hamiltonian for time-optimal control problems related to the cost functional in Eq. (2) can be formulated as

$$\begin{aligned} \mathcal {H}(\textbf{x}(t), \textbf{u}(t), \boldsymbol{\lambda }(t)):= 1 + P(\textbf{x}(t),\textbf{u}(t)) + \boldsymbol{\lambda }(t)^\textsf{T} \textbf{f}(\textbf{x}(t),\textbf{u}(t)), \end{aligned}$$

(4)

in which the multiplier $\boldsymbol{\lambda }(t)=\textbf{p}(t) + \textbf{R}(t)\boldsymbol{\nu }$ is computed by a linear combination of the adjoint variables $\textbf{p}\in \mathbb {R}^{n}$ and $\textbf{R}\in \mathbb {R}^{n\times q}$. The vector $\boldsymbol{\nu }\in \mathbb {R}^{q}$ is a multiplier to combine both adjoint variables. A deep insight into the combination of both adjoint variables is presented in [2]. The Hamiltonian in Eq. (4) is used in Sect. 4 to interpret the results of a time-optimal control problem obtained by a direct optimization approach as depicted in Fig. 1.

Fig. 1.

Flowchart to interpret the results from a direct optimization algorithm with Pontryagin’s minimum principle

3 Computation of First-Order Derivatives

Classical gradient-based optimization algorithms rely on the derivatives of the cost functional and the constraints with respect to the optimization variables $\textbf{z}$. The computation of these gradients takes a key role in such optimization algorithms and the convergence of the optimization depends on the accuracy of the gradients. In addition to accuracy, efficient computation of gradients is especially important for large numbers of optimization variables. Thus, the computational effort to solve the optimization problem depends significantly on the efficient computation of gradients. Figure 2 summarizes the most common approaches for the computation of first-order gradients. The finite differences method is the easiest approach to code, but suffers in terms of computational effort especially for a large number of optimization variables. In case of using (forward or backward) finite differences, the state equations have to be solved $(1 + z)$ times in order to evaluate the numerical gradients with respect to z optimization variables. Thus, the number of forward simulations grows linearly with the number of optimization variables. In contrast to this numerical approach, the direct differentiation and the adjoint method are referred as analytical approaches to compute gradients. Both approaches lead to exact gradient information and using them in an optimization scheme leads to an increase in efficiency. The characteristics of the analytical approaches are discussed in the following sections.

Fig. 2.

Overview of approaches to compute first-order derivatives

3.1 Direct Differentiation Approach for Discrete Control Parameterization

The direct differentiation approach is based on the sensitivity of the state equations and is briefly discussed in this section. In this paper, the control is described by $\textbf{u}(t) = \textbf{C}\,\bar{\textbf{u}}$, in which the vector $\bar{\textbf{u}}^\textsf{T}=\left( \hat{\textbf{u}}_{1}^\textsf{T},\,\dots ,\,\hat{\textbf{u}}_{m}^\textsf{T}\right) \in \mathbb {R}^{m \cdot k}$ collects k grid nodes of the m equidistant time-discretized controls and the matrix $\textbf{C}(t)\in \mathbb {R}^{m \times m \cdot k}$ maps the grid nodes to a time dependent function. The interpolation matrix $\textbf{C}$ has to be determined once a priori and depends on the chosen interpolation order [6].

By using this control parameterization, the gradient of the cost functional is directly obtained by differentiating it with respect to the grid nodes as

$$\begin{aligned} \nabla _{\bar{\textbf{u}}} \, J^\textsf{T} =& \int _{t_0}^{t_f} \Big [ \frac{\partial P}{\partial \textbf{x}} \frac{\partial \textbf{x}}{\partial \bar{\textbf{u}}} + \frac{\partial P}{\partial \textbf{u}} \frac{\partial \textbf{u}}{\partial \bar{\textbf{u}}} \Big ] \,\textrm{d}t \end{aligned}$$

(5)

$$\begin{aligned} =&\int _{t_0}^{t_f} \Big [ P_{\textbf{x}} \textbf{x}_{\bar{\textbf{u}}} + P_{\textbf{u}} \textbf{C} \Big ] \,\textrm{d}t, \end{aligned}$$

(6)

in which the partial derivative of the parameterized control with respect to the grid nodes

$$\begin{aligned} \frac{\partial \textbf{u}}{\partial \bar{\textbf{u}}} = \textbf{C} \end{aligned}$$

(7)

has been utilized. Partial derivatives of an arbitrary function f with respect to x are denoted with subscripts, i.e. $f_x$. Similar to the gradient of the cost functional, the gradient of the final constraints in Eq. (3) can be calculated by direct differentiation as

$$\begin{aligned} \nabla _{\bar{\textbf{u}}} \, \boldsymbol{\phi }^\textsf{T} = \boldsymbol{\phi }_{\textbf{x}} \textbf{x}_{\bar{\textbf{u}}}. \end{aligned}$$

(8)

The resulting gradients in Eq. (6) and Eq. (8) involve the system sensitivity $\textbf{x}_{\bar{\textbf{u}}} \in \mathbb {R}^{n \times m \cdot k}$ which is obtained by differentiating the state equations with respect to the grid nodes as

$$\begin{aligned} \dot{\textbf{x}}_{\bar{\textbf{u}}} =\,& \textbf{f}_{\textbf{x}} \textbf{x}_{\bar{\textbf{u}}} + \textbf{f}_{\textbf{u}} \textbf{u}_{\bar{\textbf{u}}} \end{aligned}$$

(9)

$$\begin{aligned} =\,& \textbf{f}_{\textbf{x}} \textbf{x}_{\bar{\textbf{u}}} + \textbf{f}_{\textbf{u}} \textbf{C}. \end{aligned}$$

(10)

Initial conditions of the system sensitivity are defined as

$$\begin{aligned} \textbf{x}_{\bar{\textbf{u}}}(0) = \textbf{0}, \end{aligned}$$

(11)

since the initial conditions of the state equations do not depend on the grid nodes, i.e. $\textbf{x}(0) = \textbf{x}_0$. The system Jacobian $\textbf{f}_{\textbf{x}} \in \mathbb {R}^{n \times n}$ and $\textbf{f}_{\textbf{u}} \in \mathbb {R}^{n \times m}$ have to be calculated a priori, e.g., by analytical differentiation, in order to solve the matrix differential system in Eq. (10). Remark that the differential system depends on the number of grid nodes. Thus, the computational effort increases with the number of grid nodes.

3.2 Adjoint Gradient Approach for Discrete Control Parameterization

A large number of grid nodes leads to a large solution space and, therefore, the gradient computation leads to a high computational effort resulting from finite differences or direct differentiation. An efficient alternative to compute gradients analytically is the adjoint variable method which is based on the calculus of variations. Following the basic idea presented in the seventies by Bryson and Ho [1], an adjoint gradient approach for discrete control parameterizations is utilized. Lichtenecker et al. [6] derived the adjoint gradients for time-optimal control problems defined in Eqs. (1)–(3) for spline control parameterizations in the following form:

$$\begin{aligned} \nabla _{\bar{\textbf{u}}} \, J^\textsf{T} &= \int _{t_0}^{t_f} \left( \textbf{p}^\textsf{T} \textbf{f}_{\textbf{u}} + P_\textbf{u} \right) \textbf{C}\, \textrm{d}t, \end{aligned}$$

(12)

$$\begin{aligned} \nabla _{\bar{\textbf{u}}} \, \boldsymbol{\phi }^\textsf{T} &=\int _{t_0}^{t_f} \textbf{R}^\textsf{T} \textbf{f}_{\textbf{u}} \textbf{C}\, \textrm{d}t, \end{aligned}$$

(13)

in which the adjoint variables fulfill the (adjoint) system of differential equations

$$\begin{aligned} \dot{\textbf{p}} &= -P^\textsf{T}_\textbf{x} - \textbf{f}_{\textbf{x}}^\textsf{T} \textbf{p} &\text {with}& \quad &\textbf{p}(t_f) &= \textbf{0}, \end{aligned}$$

(14)

$$\begin{aligned} \dot{\textbf{R}} &= -\textbf{f}^\textsf{T}_\textbf{x}\textbf{R} &\text {with}& \quad &\textbf{R}(t_f) &= \boldsymbol{\phi }_{\textbf{x}}^\textsf{T}(\textbf{x}(t_f),t_f). \end{aligned}$$

(15)

Due to the final conditions, they have to be solved backward in time to compute the adjoint gradients. Moreover, it has to be emphasized that the size of the adjoint system does not grow with the number of grid nodes which is not the case for direct differentiation, see Sect. 3.3. The adjoint gradients in Eqs. (12) and (13) prove to be preferable regarding computational effort and accuracy in gradient based optimization strategies. For further details on adjoint gradients, the reader is referred to [2, 6].

How to Compute the Adjoint Gradients

The adjoint gradients in Eqs. (12) and (13) can be used for direct and indirect optimization algorithms. Both approaches are iterative methods and, therefore, the gradients have to be recomputed in each iteration. In this paper, we use a direct optimization method in order to compute the optimal control. Similar as shown in [10], Fig. 3 illustrates the application of adjoint gradients provided to a direct optimization method and is summarized with the following steps:

• 1. Select a direct optimization method which is able to use user-defined gradients, e.g. a classical SQP method or an Interior Point (IP) method.

• 2. The optimization algorithm proposes values $\textbf{z}_i$ for the optimization variables associated to the current i-th iteration. Starting from this view, the gradients have to be computed for the $(i+1)$-th iteration.

• 3. Solve the state equations related to the actual optimization variables and initial conditions using an ODE solver.

• 4. The cost functional and the final constraints can be evaluated.

• 5. Compute the adjoint variables $\textbf{p}$ and $\textbf{R}$ backward in time using Eqs. (14) and (15).

• 6. Finally, the adjoint gradients of the cost functional and the final constraints are computed by a time integration and provided to the optimization algorithm for the next iteration.

• 7. Steps (2) through (6) are repeated until the KKT conditions are fulfilled with respect to the optimal solution $\textbf{z}^*$.

Fig. 3.

Procedure for the use of adjoint gradients in direct optimization approaches

3.3 Discussion on Duality of Gradients

McNamara et al. [7] pointed out that the adjoint approach can be interpreted as a special case of linear duality and that the core of this method is based on a substitution of variables. This can be seen by considering the first term of the gradients of the cost functional in Eqs. (6) and (13), i.e.,

Both terms require the solution of a linear differential system, but it has to be emphasized that the size of the systems is different. The size of the system sensitivity depends on the number of states n, the number of controls m and on the number of grid nodes k, while the size of the adjoint system depends only on n. To compute the gradients, one can solve either the primal system (a) with dimension $(n \times m \cdot k)$ or the dual system (b) with dimension $(n \times 1)$. Thus, the adjoint approach is an efficient technique to incorporate especially a large number of grid nodes. A graphical interpretation of the dimensions occurring in the gradients of the cost functional is shown in Fig. 4, with a special focus on increasing the number of grid nodes.

Fig. 4.

Graphical interpretation of the dimensions occurring in the gradient of the cost functional with respect to the direct differentiation approach in Eq. (6) and the adjoint approach in Eq. (13)

4 Numerical Example

4.1 Task Description and Optimization Problem

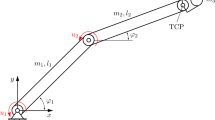
The analytically derived adjoint gradients in [6] are used for a direct optimization method in a time-optimal control problem of a SCARA with two rigid bodies. The goal is to manipulate the tool center point (TCP) of the robot depicted in Fig. 5 from an initial state to a final state in minimal operation time $t_f^*$ with a discrete control parameterization. To meet industrial requirements, the control is forced to be $\mathcal {C}^2$ continuous. Hence, the matrix $\textbf{C}$ is chosen such that the interpolation of each discretized control subinterval is performed by a cubic spline function. The state equations are obtained by introducing the state variables

$$\begin{aligned} \textbf{x}= (\varphi _1,\, \varphi _2,\, \omega _1,\, \omega _2)^\textsf{T}, \end{aligned}$$

(16)

in which $\dot{\varphi }_i = \omega _i$. The model parameters for the simulation are set as follows: $m_1=m_3={1}\,\textrm{kg}$, $m_2 = {0.5}\,\textrm{kg}$, $l_i={1}\,\textrm{m}$ and $J_i=m_il_i^2/12$, in which $i\in \{1,2\}$. The mass $m_3$ is considered as a point mass attached to the TCP.

The cost functional of the optimization problem is given in Eq. (2), in which the penalty term $P(\textbf{u}) = 10 ( P_1(u_1) + P_2(u_2))$ is used with

$$\begin{aligned} P_i(u_i):= \left\{ \begin{array}{ll} 0 &{} \quad \text {for} ~ |u_i |< u_{i,\textrm{max}}, \\ \frac{1}{2}(|u_i |- u_{i,\textrm{max}})^2 &{} \quad \text {otherwise.} \end{array} \right. \end{aligned}$$

(17)

Fig. 5.

SCARA with two rigid bodies in a general configuration

The final constraints of the system are defined as

$$\begin{aligned} \boldsymbol{\phi }(\varphi _1,\varphi _2, \omega _1,\omega _2):= \left. \begin{pmatrix} l_1 \cos (\varphi _1)+l_2\cos (\varphi _2) - x_f \\ l_1 \sin (\varphi _1)+l_2\sin (\varphi _2) - y_f \\ \omega _1 \\ \omega _2 \end{pmatrix}\right| _{t=t_f}, \end{aligned}$$

(18)

in which $x_f={1}\,\textrm{m}$ and $y_f={1}\,\textrm{m}$ denote the desired final configuration of the TCP. Physical bounds of the controls are given by $u_{1,\textrm{max}} = {4}\,\textrm{Nm}$ and $u_{2,\textrm{max}} = {2}\,\textrm{Nm}$.

The NLP contains the optimization variables $\textbf{z}^\textsf{T} = (t_f,\bar{\textbf{u}}^\textsf{T})$ and is solved with an SQP method. As an initial guess, the assumption for the final time is $t_f={2}\,\textrm{s}$ and the grid nodes are set to $\bar{\textbf{u}}=\textbf{0}$. Initial conditions of the state variables are set to $\textbf{x}_0= (-\pi /4,\,0,\,0,\,0 )^\textsf{T}$. In order to analyze the sensitivity of the solution to the refinement of the discretization of the control, both controls are equidistantly discretized in the time interval $t \in [0,t_f]$ with a set of grid nodes with various number $k\in \{5,10,20,30,40,50\}$.

4.2 Results

Figure 6 shows the optimal control history $\textbf{u}_k^*$ and the resulting trajectory of the TCP with respect to the defined number of grid nodes k. One can observe that the control becomes a bang-bang type control by increasing the number of grid nodes. It can also be seen that the TCP trajectory with $k=5$ grid nodes is noticeably different compared to controls in which the number of grid nodes is higher. This is due to the fact that in this case the optimal control cannot be represent a bang-bang structure. Theoretically, an infinite number of grid nodes will lead to the shortest possible final time. The final times for the six independent optimizations are $(k=5,t_f^*={1.9439}\,\textrm{s})$, $(10,{1.8633}\,\textrm{s})$, $(20,{1.8391}\,\textrm{s})$, $(30,{1.8325}\,\textrm{s})$, $(40,{1.8303}\,\textrm{s})$ and $(50,{1.8294}\,\textrm{s})$.

Fig. 6.

Optimal control history and TCP trajectory for various number of grid nodes

The optimal control with $k=50$ grid nodes and the corresponding switching functions, as defined in [2] for bang-bang controls, are shown in Fig. 7. The zero values of the control agree well with those of the switching functions $h_i$ and the Hamiltonian of the system is sufficiently small. Thus, the termination criteria shown in Fig. 1 is satisfied and a bang-bang control can be approximated with a sufficient number of grid nodes.

Fig. 7.

Initial controls, optimal controls and switching functions considering a cubic spline parameterization of the control

5 Conclusions

This paper presents a procedure for using adjoint variables in a direct optimization approach. The adjoint variables are examined in the context of two scenarios: The adjoint variables are used to compute the gradients during the optimization. In addition, the adjoint variables are used to evaluate Pontryagin’s minimum principle in order to discuss the optimization results obtained by an SQP method. A time-optimal control problem of a SCARA shows the versatile application of adjoint variables. Moreover, the computational effort for the computation of gradients can be reduced by considering adjoint gradients, especially when the number of grid nodes is large or the mechanical system is difficult to solve forward in time.