Abstract
It is well known that already the length of encrypted messages may reveal sensitive information about encrypted data. Fingerprinting attacks enable an adversary to determine web pages visited by a user and even the language and phrases spoken in voice-over-IP conversations.
Prior research has established the general perspective that a length-hiding padding which is long enough to improve security significantly incurs an unfeasibly large bandwidth overhead. We argue that this perspective is a consequence of the choice of the security models considered in prior works, which are based on classical indistinguishability of two messages, and that this does not reflect the attacker model of typical fingerprinting attacks well.
Therefore we propose a new perspective on length-hiding encryption, which aims to capture security against fingerprinting attacks more accurately. This makes it possible to concretely quantify the security provided by length-hiding padding against fingerprinting attacks, depending on the real message distribution of an application. We find that for many real-world applications (such as webservers with static content, DNS requests, Google search terms, or Wikipedia page visits) and their specific message distributions, even length-hiding padding with relatively small bandwidth overhead of only 2–5% can already significantly improve security against fingerprinting attacks. This gives rise to a new perspective on length-hiding encryption, which helps understanding how and under what conditions length-hiding encryption can be used to improve security.
Supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme, grant agreement 802823. We thank Hans-Jörg Bauer and Michael Simon, ZIM of University of Wuppertal, for their assistance with determining a real-world DNS host name distribution and the anonymous reviewers of CT-RSA 2022 for helpful comments.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
“Secure encryption” is today a very well-understood concept. However, standard cryptographic security definitions for encryption schemes (symmetric and asymmetric alike) consider a security experiment where an adversary chooses two plaintext messages \(m_{0}\) and \(m_{1}\), receives back an encryption of a randomly chosen message \(m^{*} \in \{m_{0}, m_{1}\}\), and then has to determine which of the two messages was encrypted. A common, crucial restriction of such security definitions is that the two messages must have equal length. Otherwise it may be trivial to determine the encrypted message based on the length of the given ciphertext, such that security in this sense is impossible to achieve.
There are other standard security notions, such as “real-or-random” definitions, where an adversary has to distinguish between an encryption of a chosen message m and a random string of equal length or simulation-based semantic security, which requires the existence of an efficient simulator that produces the same output as the adversary given only the length of a ciphertext (e.g., [1, 2, 18, 19]). All these definitions have in common that they do not provide security against attacks that are based on the length of messages.
Due to their simplicity and generality, these definitions have been extremely useful for building a general theory of secure encryption. However, assuming that only messages of equal length are encrypted is a necessary theoretical idealization and unrealistic from a practical perspective. In most real-world applications already the length of messages may reveal sensitive information.
The real-world relevance of hiding message lengths. Well-known examples of attacks leveraging message lengths consider a passive adversary that merely observes the encrypted network traffic and can identify web pages visited by a user [10, 16, 21, 23, 30], or the language and even phrases spoken in an encrypted voice-over-IP conversation [32, 33], all this without breaking the expected security of the underlying encryption scheme. Even revealing the length of user passwords makes it possible to identify individual users in TLS-encrypted sessions and provides an advantage in password guessing attacks [13], in particular when passwords are re-used across different services. Hence, it is a desirable goal to hide the length of transmitted messages in practice.
Impossibility of hiding message lengths in cryptographic theory. Tezcan and Vaudenay [29] considered the asymptotic setting commonly used in theoretical cryptography and showed essentially that efficiently hiding the length of messages is impossible for arbitrary message distributions. Concretely, an exponential-sized padding is necessary, if the adversary in a standard security experiment is allowed to choose arbitrary messages of different lengths, and one aims at achieving a negligible distinguishing advantage. This suggests that in theory it is impossible to hide plaintext length efficiently, which supports the common belief that a considerable bandwidth overhead incurred by length-hiding padding is inevitable.
Dependence of encrypted messages and length-hiding padding. In order to overcome this impossibility, Paterson, Ristenpart, and Shrimpton introduce the notion of length-hiding encryption (LHE) [24]. Essentially, LHE augments the encryption algorithm with an additional length-hiding parameter \(\ell \), which is specified by an application calling the encryption algorithm. The length-hiding parameter determines the amount of length-hiding padding used for a particular message. Secure LHE in the sense of [24] essentially guarantees security for plaintexts of different lengths, provided that the length-hiding parameter ensures that the corresponding ciphertexts have equal size. However, [24] does not yet explain how \(\ell \) can be chosen in order to obtain any security guarantees for realistic message distributions.
Furthermore, this work considers a classical “two-message indistinguishability” security model, where an adversary outputs two challenge messages \(m_{0}\) and \(m_{1}\) whose length difference must be bounded by some \(\varDelta \), i.e., it holds that \(0 \le \big | |m_{0}| - |m_{1}| \big | \le \varDelta \). Here, \(\varDelta \) depends on \(\ell \). Note that this requires the messages in the security experiment to be chosen depending on the length-hiding parameter used by the underlying encryption scheme.
We argue that in order to determine suitable length-hiding padding to protect against fingerprinting attacks on a given application layer protocol, such as HTTP, DNS, etc., we do not want to make the distribution of application-layer messages dependent on the used padding scheme, but rather the other way around. That is, we want to determine a suitable length-hiding parameter for the given message distribution of the application. Therefore we propose a security definition which does not mandate any a priori length difference \(\varDelta \) of messages, but rather quantifies the security of a certain padding length for a given message distribution (or an approximation thereof).
Quantifying the security of length-hiding encryption. There is currently no methodology that makes it possible to concretely assess and quantify the security of a given length-hiding padding scheme against fingerprinting attacks. In order to understand under which circumstances length-hiding schemes can reduce the effectivity of fingerprinting attacks without very large performance penalty, we have to analyze which concrete security guarantees can be obtained by length-hiding schemes with reasonable (i.e., non-exponential-sized) length-hiding parameters.
We know that suitable choice of a padding length must depend on the message distribution of an application (more precisely, on the distribution of the lengths of encrypted messages), as otherwise security is known to be not achievable [29]. In order to determine a suitable padding length for a given application in practice, it is therefore necessary to determine the message distribution of the given application. This can be achieved, for instance, by implementing a server-side monitoring algorithm that records (an approximation of) the distribution. This algorithm could run in set intervals and update the length-hiding parameter on the fly, if the distribution changes over time (e.g., due to changed web site contents or access patterns).
Our Contributions. We develop a methodology that makes it possible to concretely quantify the effect of LHE on the security of a given application. To this end, we introduce a new cryptographic security model, which aims to preserve the simplicity and generality of classical models, while capturing security against fingerprinting attacks in order to reflect such security requirements of applications. Based on this definition, we describe a methodology to concretely quantify the effect of LHE for a given application.
In a next step, we demonstrate the feasibility of our approach by applying it to different types of fingerprinting attacks. Each of these scenarios cover multiple application-based aspects such as which block mode (e.g., CBC, CTR) is used for encryption, or whether compression for transmitted data is enabled. Note that due to attacks such as CRIME [6], compression in TLS is usually disabled in practice; Qualys SSL Labs finds the percentage of websites using compression among the Alexa’s lists of most popular websites in the world to be 0.1% in November 2021Footnote 1 We further remark that we intentionally compare length-padding-after-compression to no-length-padding-no-compression. This allows us to emphasize that in some cases enabling compression might increase security. Since the security impact of such aspects are often very subtle, we provide a more detailed explanation in the full version of this work [8]. We summarize our results as follows:
-
Simple webpage fingerprinting. As a first example, we consider a website consisting of many static HTML pages, a user that visits one page, and an adversary that tries to determine the visited page based on the size of encrypted data. Since we want to base our analysis on a publicly-available web site with static contents, we used the IACR Cryptology ePrint archive at https://eprint.iacr.org/2020/.Footnote 2
We find that switching from counter mode to block mode encryption already decreases the advantage of the adversary from 0.74 to 0.14 (where an advantage of 1 means that the adversary can uniquely determine a web page, while 0 means that the size of the transmitted data reveals no information about the visited page). This makes fingerprinting much less effective, without noticeable bandwidth overhead.
Reducing the advantage to 0 costs about \(95\%\) bandwidth overhead without compression, however, by additionally using compression and advantage to 0 can even be achieved without any overhead, by slightly reducing the amount of data transmitted by \(0.3\%\). Hence, from a website fingerprinting perspective, it seems to make sense to enable LHE, possibly in combination with compression, on this server.
-
Web page fingerprinting with patterns. In order to analyze more complex fingerprinting attacks, we again consider the IACR Cryptology ePrint Archive and an adversary that tries to determine the visited page based on the size of encrypted data. This time, we consider a user that first visits the web page of a random paper from the year 2020, and then downloads the corresponding paper (a pdf file). Note that this yields a much more distinguishable pattern, in particular due to the highly varying size of pdf documents, and the fact that pdf files are not as easily compressible as text-based web pages.
We find that the advantage in counter mode is 1, that is, all papers are uniquely identifiable, such that the encryption provides no security at all against such attacks. This can be reduced to 0.12 by applying length-hiding padding with a bandwidth overhead of only about \(2.4\%\). Hence, LHE can significantly improve security against fingerprinting at negligible overhead, which refutes the common belief that a significant overhead is necessary in order to achieve a considerable security improvement.
-
Google search term fingerprinting. Here we consider the scenario that one user is searching some term in a search engine. A passive adversary observes the encrypted traffic and tries to determine which search term the user is searching for. We used 503 most popular search terms from the daily search trends published by Google at https://trends.google.com/trends/ in a time period of one month in Spring 2021.
We find that without LHE an adversary achieves very high advantage of almost 1. LHE with only 2% bandwidth overhead can reduce this very significantly to only 0.07. In combination with compression, the advantage can be reduced to 0.006, while reducing the amount of transmitted data by 50%.
-
Simple Wikipedia fingerprinting. All the three application examples above consider a uniform message distribution, which does not necessarily capture the message distribution in the real-world applications. Obtaining real-world message distributions, e.g. by capturing Internet traffic, is difficult (for practical reasons, as well as due to privacy concerns). However, the Wikimedia Foundation publishes statistics of the Wikipedia website since May 2015, which provides us with the real distribution of visited webpages of the Wikipedia website. To better demonstrate the feasibility of our approach with respect to real-world message distributions, we carry out a webpage fingerprinting analysis for the Wikipedia webpages in simple English language, based on the real webpage visit distribution of May 2021.
We find that without LHE an adversary achieves very high trivial advantage (0.875). LHE with only 2% bandwidth overhead can reduce this to 0.13. In combination with compression, the advantage can be reduced to 0.0058, while reducing the amount of transmitted data by 50%.
-
DNS fingerprinting. Here we consider the Domain Name System (DNS) protocol and DNS request/response pairs. This setting is particularly interesting because there is an increasing trend to encrypt DNS protocol messages to hide the requested domain names. However, it turns out that the length of DNS requests/response pairs exhibit a very distinctive pattern, which make it easy to determine the requested domain name from the ciphertext length. We consider two different settings:
-
1.
A user that issues a DNS request for a randomly chosen host name from 1,000 most popular hosts according to the Majestic Million list.
-
2.
In collaboration with the IT department of a medium-sized university (with 23k students and 3.5k staff members), we collected the host names of DNS requests performed by staff and students within a 24 h time interval in July 2021. The data collection was carried out under supervision of the university data privacy officer and in accordance with applicable data protection laws. In particular, only the hostnames and their frequency were collected, but not the requesting IP addresses or any other personal data. This provides us with a real-world message distribution that makes it possible to determine the security and appropriate padding sizes for this particular DNS service.
In both cases, the adversary that tries to determine the requested host name based on the size of request and response.
In the Majestic Million case, we find that the advantage of an adversary can be reduced from 0.644 (in counter mode without compression) down to 0.01 with a bandwidth overhead of about 79% without compression, or 57% with. For the university DNS case, the advantage of an adversary can be reduced from 0.551 (in counter mode without compression) to below 0.01 with a bandwidth overhead of about 54% without compression.
-
1.
In summary, we find that LHE can, contrary to the common belief, improve security against fingerprinting attacks very significantly, often with minor bandwidth overhead. This also confirms the recent tendency to switch from block-mode to counter-mode encryption indeed makes fingerprinting attacks much more effective.
We support our theoretical model and calculations with a proof-of-concept implementation in form of an Apache module. Our implementation consists of two parts. One part is a server-side monitoring algorithm that records (an approximation of) the message distribution and computes a suitable length-hiding parameter. The other part applies the length-hiding parameter as input to the encryption procedure of server responses. We used this proof-of-concept implementation to validate the results of our theoretical analysis.
Application of our results. Some standards and implementations of cryptographic protocols already provide means to conceal the length of plaintexts, in order to prevent fingerprinting attacks or reduce their effectivity. One such example is the TLS 1.3 standard [25], which directly supports the use of length-hiding padding and functions as basis of our implementation.
Another example of an Internet standard that supports length-hiding padding is DNS. RFC 8467 [22] describes block-length padding, which recommends to pad all DNS requests to a multiple of 128 bytes and all DNS responses to a multiple of 468 bytes (as originally proposed in [9]). We remark that these numbers are derived from an empirical analysis conducted specifically for DNS, and that we do not yet have a clear methodology to quantify to which degree they improve security concretely.
Related Works. The work of Boldyreva et al. [3] focuses on hiding message boundaries in a ciphertext stream with fragmented message transmission. This work is similar in spirit to ours in the sense that it tries to find a balance between the conflicting aims of keeping the generality and simplicity of traditional security definitions on the one hand, and developing an approach that can be used to provide meaningful provable security analyses of practical schemes on the other hand.
A very recent work on length-hiding encryption is due to Degabriele [5], which will appear at ACM CCS 2021. We compare our approach with the one in [5] in the full version [8] of our work.
Fingerprinting attacks have been intensively studied in the context of web page fingerprinting, deanonymization of Tor private channels, and other applications such as LTE/4G. Early approaches were based on the length of encrypted messages, as well as their direction and the frequency of messages [15, 16, 21]. More recent approaches use additional features advanced analysis techniques based on machine learning [14, 20, 28]. Also active attacks have been considered [20, 27]. Countermeasures to fingerprinting attacks were proposed [31, 34], but could be broken with refined analysis methods [7, 28]. Cai et al. [4] give a systematic analysis of attacks and defenses to understand what features convey the most information.
We note that many works on the feasibility of fingerprinting attacks make use of side-channels beyond message lengths and we discuss this in the full version of our work [8].
Outline of this Paper. In Sect. 2 we describe a new perspective on LHE, which is more suitable for our approach, and conveniently yields schemes that follow the standard syntax of symmetric encryption schemes. Furthermore, we establish a definitional framework to analyze and quantify the concrete effect of LHE. Section 3 contains the results of an empirical analysis of different real-world message distributions. In Sect. 4 we present our implementation of LHE and compare its performance with our empirical results.
2 A New Perspective on Length-Hiding Encryption
Now we can describe our new perspective on length-hiding encryption (LHE), which makes it possible to concretely quantify the effect of length-hiding padding on security. We first introduce a new syntactical notion of LHE in Sect. 2.1 and a corresponding security experiment in Sect. 2.2. Based on these foundations, we can then define the trivial success probability and the trivial advantage to concretely quantify the security of an encryption scheme with respect to different length-hiding parameters.
In the full version of our work [8], we also discuss k-anonymity as an alternative approach and explain why we consider it as not suitable for our purposes.
2.1 A New Syntactical Definition
We first recap the formal definition of symmetric-key encryption.
Definition 1
(Symmetric-key encryption). A symmetric-key encryption scheme \(\mathsf {SE}\) consists of two algorithms \(\mathsf {E}\) and \(\mathsf {D}\). The (possibly) randomized encryption algorithm \(\mathsf {E}\) takes input a secret key \(\mathsf {sk}\) and a plaintext \(m\in \{0,1\} ^*\), and outputs a ciphertext \(\mathsf {ct}\). The deterministic decryption algorithm \(\mathsf {D}\) takes input a secret key \(\mathsf {sk}\) and a ciphertext \(\mathsf {ct}\) then outputs a plaintext m or a symbol \(\bot \). The correctness of \(\mathsf {SE}\) requires that \(\mathsf {D} _\mathsf {sk} (\mathsf {E} _\mathsf {sk} (m))=m\) for all \(\mathsf {sk} \in \{0,1\} ^k\) and \(m\in \{0,1\} ^*\).
Note that, in the above definition, the ciphertext length is implicitly defined by the encryption algorithm and cannot be altered or controlled outside the algorithm. Paterson et al. introduced the concept of length-hiding encryption in [24], which makes it possible to control the ciphertext length outside the encryption algorithm. In this paper we will work with a slightly different perspective, which we consider as more practical.
Recall that in [24] the length-hiding parameter \(\ell \) is the total ciphertext length and it is an explicit input to the encryption algorithm. The parameter can be controlled by the adversary in the security experiment, the only restriction is that it must be at least as large as the largest of the two messages submitted by the adversary in the indistinguishability security experiment. We believe this does not capture real-world attacks based on ciphertext lengths very well, because it considers only the indistinguishability of two messages that are encrypted with respect to the same ciphertext length \(\ell \).
To protect against such attacks, we find it more practical to view the length hiding parameter as a fixed system parameter and to make the ciphertexts length dependent on both \(\ell \) and the size of encrypted messages. More precisely, the global parameter \(\ell \) (of a symmetric-key encryption scheme) defines a fixed function which maps plaintext length to certain ciphertext length.
Now, for any symmetric-key encryption scheme \(\mathsf {SE}\), we formalize a new symmetric-key encryption scheme \(\mathsf {SE} ^{(\ell )}\) as the scheme \(\mathsf {SE}\) instantiated with length hiding parameter \(\ell \) as follows.
Definition 2
(Symmetric-key encryption with length-hiding parameter \(\ell \)). Let \(\mathsf {SE} = (\mathsf {E},\mathsf {D})\) be a symmetric encryption scheme. Let \(\mathsf {pad} (m,\ell )\) be a function that pads a plaintext m such that
That is, \(\mathsf {pad} \) applies length-hiding padding to the plaintext m such that the length of \(\mathsf {pad} (m,\ell )\) is an integer multiple of \(\ell \). Let \(\mathsf {pad} ^{-1}\) be the function that removes the padding, that is, \(\mathsf {pad} ^{-1}(\mathsf {pad} (m,\ell )) = m\) for all m and \(\mathsf {pad} ^{-1}(\bot ) = \bot \). We call \(\ell \) the length-hiding parameter and define the length-hiding encryption scheme \(\mathsf {SE} ^{(\ell )} = (\mathsf {E} ^{(\ell )},\mathsf {D} ^{(\ell )})\) as
Note that in particular we have \(\mathsf {SE} ^{(1)} = \mathsf {SE} \).
Padding a message to a multiple of some parameter \(\ell \) is a generalization of the block-length padding scheme proposed in [9] and recommended for encrypted DNS requests in RFC 8467 [22].
Note that this scheme allows to capture “perfect” length-hiding padding, where the length-hiding parameter \(\ell \) is at least as large as the largest possible message in an application, such that all ciphertexts have identical length and no information is leaked through the length. However, if \(\ell \) is smaller, then we will get weaker security guarantees. We will show that this is very useful to achieve a trade-off between improved resilience to attacks based on message length and bandwidth overhead of the length-hiding padding. Furthermore, we will analyze the concrete impact of different length-hiding parameters on the security and bandwidth requirements of an application.
Security notions for symmetric-key encryption schemes. Since \(\mathsf {SE} ^{(\ell )}\) follows the standard syntax of encryption schemes for all \(\ell \in \mathbb {N} \), standard security definitions (without considering length leakage) for symmetric-key encryption apply to it. There are many different ways to define security for symmetric-key encryption schemes. In this paper we will consider two flavors of standard IND-CCA security, the IND-M-CCA security and the IND-C-CCA security. Both provide protection for message privacy but none of them provides protection against length leakage. However, they serve as an important tool in our approach to capture the effectiveness of length-hiding encryption.
IND-M-CCA security. The first notion is the indistinguishability of encryptions of chosen messages from encryptions of random strings. It is equivalent to the classical “left-or-right” definition where an adversary outputs two messages \(m_{0}\) and \(m_{1}\), receives back an encryption of message \(m_{b}\) for a random  , and has to determine b.
, and has to determine b.
Definition 3
(IND-M-CCA security). A symmetric-key encryption scheme \(\mathsf {SE} = (\mathsf {E}, \mathsf {D})\) is \(\mathsf {IND}\text {-}\mathsf {M}\text {-}\mathsf {CCA}\) secure if for any PPT adversary \(\mathcal {A}\), the advantage
is negligible, where game \(\mathsf {IND}\text {-}\mathsf {M}\text {-}\mathsf {CCA} ^{\mathsf {SE}}\) is defined in Fig. 1.
IND-C-CCA security. The second notion we consider is indistinguishability of ciphertexts from random strings (the “IND” notion in [18]), which is commonly used in recent works, such as [11, 12]. This security considers the “ciphertext pseudorandomness” of the symmetric-key encryption scheme.
Definition 4
(IND-C-CCA security). A symmetric-key encryption scheme \(\mathsf {SE} = (\mathsf {E}, \mathsf {D})\) is \(\mathsf {IND}\text {-}\mathsf {C}\text {-}\mathsf {CCA}\) secure if for any PPT adversary \(\mathcal {A}\), the advantage
is negligible, where game \(\mathsf {IND}\text {-}\mathsf {C}\text {-}\mathsf {CCA} ^{\mathsf {SE}}\) is defined in Fig. 1.
Since the length-hiding parameter \(\ell \) is a global system parameter and known to the adversary (the adversary does not have to break the scheme or make any encryption or decryption queries to know this parameter), we point out that the length-hiding property is orthogonal to the exact oracle query ability of the adversary. Our choice to consider security against chosen-ciphertext attacks should merely serve as a concrete example. For instance, CPA security is easily obtained by removing the decryption oracle, passive eavesdropping by additionally removing the encryption oracle. It is also possible to consider advanced security notions, such as misuse-resistant encryption [26], where the adversary is able to specify the nonce used by an encryption algorithm. Furthermore, it can be considered in both the symmetric-key and the public-key setting. We chose security against chosen-ciphertext attacks in order to demonstrate that the approach works also with this rather strong standard security definition.
2.2 New Security Model
Our objective is to define a model that is independent of a particular application, but capable of capturing complex application settings where multiple messages of varying lengths are encrypted using multiple keys and the adversary wants to deduce information about these messages from the ciphertexts. Therefore we parametrize our security model as follows:
-
Message distribution. Note that the information an adversary can deduce from the size of observed ciphertexts depends inherently on the message distribution of a given application, and possibly other application-specific properties, such as observable patterns of messages, for instance. Since we want to preserve as much of the simplicity and generality of classical security models as possible, our new security definition is parametrized by a message distribution \(\mathsf {M}\) of a given application.
For instance, in the web page fingerprinting setting, the distribution \(\mathsf {M}\) would assign probabilities to different web pages on a server. If a client performs a search with an Internet search engine, then
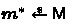 would correspond to the messages exchanged between a client and the search engine. Note that, in this case, the message distribution \(\mathsf {M} \) is defined by the client and the server may not know this distribution \(\mathsf {M} \) beforehand. However, we consider strong adversaries that know \(\mathsf {M} \) so that it obtains some a prior knowledge about this search term.
would correspond to the messages exchanged between a client and the search engine. Note that, in this case, the message distribution \(\mathsf {M} \) is defined by the client and the server may not know this distribution \(\mathsf {M} \) beforehand. However, we consider strong adversaries that know \(\mathsf {M} \) so that it obtains some a prior knowledge about this search term. -
Specification of data to-be-protected. We introduce a function \(\mathcal {P} \) which specifies the information that an adversary wants to learn about the encrypted data. For instance, if a client performs a search with an Internet search engine and the adversary wants to learn the search term, then the data exchanged between client and search engine would be
 , and the goal of the adversary would be to determine the search term \(\mathcal {P} (\boldsymbol{m}^*)\).
, and the goal of the adversary would be to determine the search term \(\mathcal {P} (\boldsymbol{m}^*)\). -
Multiple symmetric keys. We want to be able to consider complex fingerprinting attacks on applications transmitting encrypted data. For instance, in the context of Internet search engines a client might first connect to a search engine and to perform a search, then connect to a DNS server to make a DNS request for the first search result, and then connect to the server hosting the corresponding web site. We will consider a setting where all three connections are encrypted, such that this involves three different encrypted sessions with three different, independent symmetric keys.Footnote 3 In order to reflect this accurately, we need to define a security model which involves d symmetric keys.
-
Adversarial model. Finally, we need to specify the capabilities that we grant the attacker. We will consider chosen-ciphertext attacks (CCA), as already discussed in Sect. 2.1.
In Sect. 3, we will show how to define \(\mathsf {M} \), \(\mathcal {P} \), and d for a particular given applications to obtain concrete security statements for this application. In most practical cases, \(\mathcal {P}\) will be efficiently computable, but we do not have to demand this.
Security Experiment. Motivated by this discussion, we define the \((\mathsf {SE},\mathsf {M},\mathcal {P},d)\text {-}\mathsf {CCA}\) security experiment based on the game described in Fig. 2. In this game, we consider an encryption scheme \(\mathsf {SE}\) with \(d\ge 1\) independent secret keys and a message distribution \(\mathsf {M}\) that outputs \(t \ge 1\) messages where \(t=t_1+\ldots +t_d\) for some \(t_1,\ldots ,t_d\in \mathbb {N}\). We model \(\mathsf {M}\) as a probabilistic algorithm defining a message distribution over \(\left( \{0,1\} ^*\right) ^t\). In the sequel it will be convenient to view the output of \(\mathsf {M}\) as a tuple of tuples of messages  . Here \((m_{ij})_{j\in [t_i]}\) is the tuple of messages encrypted under the i-th symmetric key \(\mathsf {sk} _i\). The function \(\mathcal {P} \) maps \(\mathcal {P}: \left( \{0,1\} ^*\right) ^t \rightarrow \{0,1\} ^{*}\).
. Here \((m_{ij})_{j\in [t_i]}\) is the tuple of messages encrypted under the i-th symmetric key \(\mathsf {sk} _i\). The function \(\mathcal {P} \) maps \(\mathcal {P}: \left( \{0,1\} ^*\right) ^t \rightarrow \{0,1\} ^{*}\).
Definition 5
For any adversary \(\mathcal {A}\), define the success probability of \(\mathcal {A}\) in game \((\mathsf {SE},\mathsf {M},\mathcal {P},d)\text {-}\mathsf {CCA}\) as the probability that \(\mathcal {A}\) is able to determine \(\mathcal {P} (\boldsymbol{m}^*)\). Formally:
Our security model is restricted in the sense that 1) it only considers the single-challenge setting and 2) the message distribution is fixed and not adaptively chosen by the adversary. Our security notion could be generalized to capture both aspects; however, this seems not to provide any non-trivial additional insight to the impact of length-hiding encryption and therefore we chose not to do this.
Non-triviality of \(\mathsf {M} \) and \(\mathcal {P} \). In the sequel we will only consider \(\mathsf {M} \) and \(\mathcal {P} \) such that there exist \(\boldsymbol{m}\) and \(\boldsymbol{m'}\) such that  ,
,  , and \(\mathcal {P} (\boldsymbol{m}) \ne \mathcal {P} (\boldsymbol{m'})\). This is necessary for technical reasons, but also sufficient because we would otherwise not get a meaningful notion of security (because otherwise it would be trivial to predict \(\mathcal {P} \) with respect to \(\mathsf {M}\) with success probability 1, even without seeing any ciphertexts).
, and \(\mathcal {P} (\boldsymbol{m}) \ne \mathcal {P} (\boldsymbol{m'})\). This is necessary for technical reasons, but also sufficient because we would otherwise not get a meaningful notion of security (because otherwise it would be trivial to predict \(\mathcal {P} \) with respect to \(\mathsf {M}\) with success probability 1, even without seeing any ciphertexts).
Our security definition implies non-adaptive IND-M-CCA security where messages are chosen non-adaptively. We discuss this in the full version of our work [8].
2.3 Trivial Success Probability and Advantage
Trivial success probability. We introduce the trivial success probability of an adversary, which captures the success probability that an adversary trivially obtains from the length of ciphertexts, without “breaking” the underlying encryption scheme \(\mathsf {SE} \). Note that this depends on the degree to which \(\mathsf {SE} \) hides the size of plaintexts, the message distribution \(\mathsf {M}\), and the function \(\mathcal {P}\).
Definition 6
The trivial success probability with respect to \((\mathsf {SE},\mathsf {M},\mathcal {P})\) is defined as the largest possible probability of guessing \(\mathcal {P} (\boldsymbol{m}^*)\), given \(\mathsf {M} \), \(\mathcal {P}\), and the size of the ciphertexts \((|\mathsf {ct} ^*_{ij}|)_{i\in [d],j\in [t_i]} \), but not the ciphertexts themselves. More formally,
where  ,
,  and
and  for \(i \in [d], j\in [t_i]\) and where the maximum is taken over all algorithms \(\mathcal S\).
for \(i \in [d], j\in [t_i]\) and where the maximum is taken over all algorithms \(\mathcal S\).
The following property is necessary to avoid contrived and unnatural examples of encryption schemes, where the length of ciphertexts depends not only on the size of the message, but also on the secret key. To our best knowledge, this property is met by any concrete symmetric encryption schemes, except for contrived counterexamples.
Definition 7
We say an encryption scheme \(\mathsf {SE} =(\mathsf {E},\mathsf {D})\) has secret key oblivious ciphertext length distribution if for any \(m\in \{0,1\}^*\), any \(\mathsf {sk},\mathsf {sk} '\in \{0,1\}^k\), \(|\mathsf {E} _{\mathsf {sk}}(m)|\) distributes identically to \(|\mathsf {E} _{\mathsf {sk} '}(m)|\).
If we would restrict to settings with deterministic padding length, then we could instead require \(|\mathsf {E} _{\mathsf {sk}}(m)|=|\mathsf {E} _{\mathsf {sk} '}(m)|\). However, we will also consider randomized padding, so that it is necessary to require identical distribution of ciphertext lengths.
Relation between trivial and real success probability. We will now prove that \(\mathcal {A}\) ’s real success probability \(\mathsf {RealSucc}(\mathsf {SE},\mathsf {M},\mathcal {P},d,\mathcal {A})\) cannot exceed the trivial success probability \(\mathsf {TrivSucc}({\mathsf {SE},\mathsf {M},\mathcal {P}})\) significantly, provided that \(\mathsf {SE} \) is IND-C-CCA secure in the sense of Definition 4 and satisfies Definition 7. This establishes that in order to minimize \(\mathsf {RealSucc}(\mathsf {SE},\mathsf {M},\mathcal {P},d,\mathcal {A})\) it suffices to minimize \(\mathsf {TrivSucc}({\mathsf {SE},\mathsf {M},\mathcal {P}})\).
Theorem 8
For any encryption scheme \(\mathsf {SE}\) that has secret key oblivious ciphertext length distribution in the sense of Definition 7, any message distribution \(\mathsf {M}\), any property \(\mathcal {P}\) and any adversary \(\mathcal {A}\), we can construct an adversary \(\mathcal {B}\) such that
The running time of \(\mathcal {B}\) is \(T(\mathcal {B})\approx T(\mathcal {A})+T(\mathsf {M})+T(\mathcal {P})+(t+q_e)\cdot T(\mathsf {E})+q_d\cdot T(\mathsf {D})\), where \(T(\mathsf {M})\) is the time to sample messages from distribution \(\mathsf {M}\), \(T(\mathcal {P})\) is the time to evaluate \(\mathcal {P}\), \(T(\mathsf {E})\) is the time to execute the encryption algorithm once, \(T(\mathsf {D})\) is the time to execute the decryption algorithm once, \(q_e\) is the number of \(\textsc {Enc}\) queries made by \(\mathcal {A}\) and \(q_d\) is the number of Dec queries made by \(\mathcal {A}\).
Due to space limitations, we defer the proof to the full version of our work [8].
Theorem 8 provides an upper bound of the adversary’s success probability in our practical “real world” security model and this bound is a sum of the CCA advantage with the trivial success probability. So if the encryption scheme itself is secure in the standard sense (i.e., the IND-C-CCA advantage of any adversary is negligible, which is provided by the IND-C-CCA security of the scheme) then the sum is close to the trivial advantage. In this way, we can focus on reducing the trivial success probability by choosing a proper length-hiding encryption scheme to reduce the information that is leaked through ciphertext length.
In the following, we show a methodology of evaluating the “effectiveness” of length-hiding encryption in reducing the trivial success probability. Intuitively speaking, we first define the “most likely probability” to capture prior information leaked by the distribution \(\mathsf {M} \) known to the adversary. And this probability provides a lower bound for the trivial success probability. For any concrete encryption scheme, we compare its trivial success probability with this lower bound to evaluate its “effectiveness” in hiding the length information. And we further quantify it by providing a new definition of trivial advantage.
Trivial advantage. Based on the trivial success probability, we define the trivial advantage with respect to encryption scheme \(\mathsf {SE} \), message distribution \(\mathsf {M} \), and property \(\mathcal {P} \) as follows.
Definition 9
For message distribution \(\mathsf {M} \) and property \(\mathcal {P} \), let
denote the probability of the most likely output of \(\mathcal {P} \) on input \(\boldsymbol{m}^*\), where  . The trivial advantage with respect to \((\mathsf {SE},\mathsf {M},\mathcal {P})\) is defined as difference between the trivial success probability and \(\mathsf {PrMostLikely}(\mathsf {M}, \mathcal {P})\), scaled to an number that ranges from 0 to 1 for any \(\mathsf {M} \) and \(\mathcal {P} \):
. The trivial advantage with respect to \((\mathsf {SE},\mathsf {M},\mathcal {P})\) is defined as difference between the trivial success probability and \(\mathsf {PrMostLikely}(\mathsf {M}, \mathcal {P})\), scaled to an number that ranges from 0 to 1 for any \(\mathsf {M} \) and \(\mathcal {P} \):
Recall that we consider \(\mathsf {M} \) and \(\mathcal {P} \) such that there exist \(\boldsymbol{m}\) and \(\boldsymbol{m'}\) such that \(\Pr [\boldsymbol{m}^*=\boldsymbol{m}] >0\), \(\Pr [\boldsymbol{m}^* = \boldsymbol{m'}] >0\), and \(\mathcal {P} (\boldsymbol{m}) \ne \mathcal {P} (\boldsymbol{m'})\), as otherwise it is trivial to predict \(\mathcal {P} \) with respect to \(\mathsf {M}\) with success probability 1. Therefore we have \(\mathsf {PrMostLikely}(\mathsf {M}, \mathcal {P}) < 1\).
3 Analysis of Real-World Message Distributions
In this section, we will consider different types of attacks, where an adversary observes encrypted communication and wants to determine the plaintext based on the communication pattern. As a concrete example we consider counter mode encryption (with AES-GCM, for instance) where the adversary is able to determine the size of the encrypted message precisely, as well as block mode encryption (using AES-CBC as an example) where the adversary is able to determine the size of the encrypted message up to the minimal message padding required for this mode. We apply our methodology to concretely calculate the trivial advantage for the considered message distribution \(\mathsf {M} \) and function \(\mathcal {P} \) that we define for each application. Then we compare the results to the same schemes, but using length-hiding encryption with different length-hiding parameters. This makes it possible to quantify the security gained by length-hiding encryption and compression precisely. Most interestingly, we will show that relatively small length-hiding parameters are able to significantly reduce the effectivity of fingerprinting attacks.
In all the subsequent parts of this work, we will use different units for the length-hiding parameter for counter mode and block mode encryption. The reason for this is that counter mode ciphers (like AES-GCM) usually encrypt messages byte-wise, therefore the size of ciphertexts and the length-hiding parameter \(\ell \) are measured in bytes. Block ciphers (like AES-CBC) encrypts messages block-wise, so we will measure the size of ciphertexts and \(\ell \) in blocks, where one block corresponds to the block size of the underlying block cipher (16 bytes in case of AES).
Due to space limitations, we only include two examples in the body, which we deemed most simple (i.e., simple website fingerprinting and simple Wikipedia fingerprinting). However, we also consider more complex examples (i.e., webpage fingerprinting with patterns, Google search term fingerprinting, and DNS fingerprinting) in the full version of this work [8].
3.1 Simple Website Fingerprinting
Adversarial model. We consider an adversary performing a website fingerprinting attack against the IACR ePrint archiveFootnote 4 at https://eprint.iacr.org/2020/, based on the size of encrypted data. The ePrint page for the year 2020 links to 1620 different subpages, one for each archived research papers. We chose the year 2020 because it is the most recent year where the number of archived research papers was fixed at the time this paper is written, which makes the analysis more easily reproducible. Each subpage contains the title, list of authors, abstract, and some other metadata for one archived research paper.
Let \(\mathcal {M} := \{m_{1}, \ldots , m_{1620}\}\) be the set of the 1620 different web pages. We assume that a user Alice picks one out of these 1620 subpages uniformly at random and then visits the corresponding page. Hence, the message distribution \(\mathsf {M} _{\mathsf {e}}\) that we consider here is the uniform distribution over \(\mathcal {M}\). The adversary tries to guess the subpage visited by Alice. Hence, the adversary outputs an index \(i \in \{1, \ldots , 1620\}\), such that we define function \(\mathcal {P} \) as \(\mathcal {P}: \mathcal {M} \rightarrow [1, 1620]\) for \(\qquad m_{i} \mapsto i\).
Considered encryption schemes. The IACR ePrint server uses TLS 1.2 and allows the client and the server to negotiate one out of two different symmetric ciphers for the encryption of payload data:
-
Counter mode. The first option is AES-GCM, which is essentially a stream cipher and we refer it as \(\mathsf {SE} ^{(\ell )}_{\mathrm {CTR}}\). Note that in this case the attacker learns the size of the underlying plaintext exactly (in case of TLS the attacker merely has to subtract a known constant from the ciphertext size), provided that no length-hiding padding is used (\(\ell =1\)).
-
Block mode. The second option is AES-CBC and we refer it as \(\mathsf {SE} ^{(\ell )}_{\mathrm {BLK}}\). Due to the padding required by CBC-mode encryption, the attacker learns only that the plaintext lies within a certain (small) range even if no length-hiding padding is used (\(\ell =1\)). Since the block size of AES is 16 bytes, AES-CBC uses a padding of length between 1 and 16 bytes, this holds also for AES-CBC in TLS 1.2.
We decided to use these two algorithms as the basis of our analysis, since they cover both a stream cipher and a block mode cipher, and are very widely used in practice. We consider a length-hiding padding with length-hiding parameter \(\ell \in \mathbb {N} \). Ciphertexts are padded to a multiple of \(\ell \) bytes for \(\mathsf {SE} ^{(\ell )}_{\mathrm {CTR}}\), and \(\ell \) blocks for \(\mathsf {SE} ^{(\ell )}_{\mathrm {BLK}}\). Thus, if \(\ell =1\), then no additional length-hiding padding is used.
We also consider enabled compression where the full plaintext message is compressed using the gzip algorithm, which implements DEFLATE compression (a combination of the LZ77 algorithm and Huffman coding). This is the algorithm standardized for use in TLS versions up to 1.2 [17], and therefore seems to be a reasonable choice for an analysis of real-world algorithms.
In order to indicate whether compression is used, we will refer to the encryption algorithm as \(\mathsf {SE} ^{(\ell )}_{\mathrm {M},\mathrm {C}}\) where \(\mathrm {M}\in \{\mathrm {CTR},\mathrm {BLK}\}\) represents its mode and \(\mathrm {C}\in \{\text {True},\text {False}\}\) represents whether compression is applied before encryption.
Empirical Data Generation. We implemented a simple script that downloaded all subpages of https://eprint.iacr.org/2020/ and determined the size of the page in both uncompressed and compressed form. These sizes are stored in a database and enable us to compute the sizeFootnote 5 of counter- and block-mode ciphertexts that encrypt the pages in compressed or uncompressed form, with and without length-hiding encryption, and with respect to different length-hiding parameters.
Calculating the trivial advantage \(\mathsf {TrivAdv}(\mathsf {SE} ^{(\ell )}_{\mathrm {M},\mathrm {C}},\mathsf {M} _{\mathsf {e}})\). We determined the number |U| of uniquely identifiable web pages, the size \(|S_\mathsf {max} |\) of the largest set of pages of identical size, the number \(|\mathcal {S}|\) of different possible ciphertext lengths, and the trivial advantage \(\mathsf {TrivAdv}(\mathsf {SE} ^{(\ell )}_{\mathrm {M},\mathrm {C}},\mathsf {M} _{\mathsf {e}})\) for both counter mode and block mode encryption, with and without compression, and with respect to different length-hiding parameters, and with respect to the uniform distribution \(\mathsf {M} _{\mathsf {e}}\) over the ePrint 2020 webpages.
Recall that the trivial success probability is defined as
where the probability is over the random choice  and \(\mathsf {ct} ^{*}\) is the encryption of \(m^{*}\). Since \(\mathsf {M} _{\mathsf {e}}\) is the uniform distribution, the trivial success probability for a given ciphertext length \(\lambda \) is equal to the number of messages \(m^{*} \in \mathcal {M}\) that encrypt to a ciphertext of the given length \(\lambda = |\mathsf {ct} ^{*}|\). Hence, defining \(\mathcal {M}_{\lambda } := \{m \in \mathcal {M} : |\mathsf {E} _\mathsf {sk} (m)| = \lambda \}\) as the set of messages that encrypt to a ciphertext of size \(\lambda \), we have
and \(\mathsf {ct} ^{*}\) is the encryption of \(m^{*}\). Since \(\mathsf {M} _{\mathsf {e}}\) is the uniform distribution, the trivial success probability for a given ciphertext length \(\lambda \) is equal to the number of messages \(m^{*} \in \mathcal {M}\) that encrypt to a ciphertext of the given length \(\lambda = |\mathsf {ct} ^{*}|\). Hence, defining \(\mathcal {M}_{\lambda } := \{m \in \mathcal {M} : |\mathsf {E} _\mathsf {sk} (m)| = \lambda \}\) as the set of messages that encrypt to a ciphertext of size \(\lambda \), we have
Hence, the trivial advantage is \(\mathsf {TrivAdv}(\mathsf {SE} ^{(\ell )}_{\mathrm {M},\mathrm {C}},\mathsf {M} _{\mathsf {e}}, \mathcal {P}) \)
We consider length-hiding block mode ciphertexts with \(\ell \in \{1, 5, 10, 25 \}\) and counter mode ciphertexts with \(\ell \in \{1, 80, 160, 400 \}\). Table 1 summarizes the results of this analysis.
Achieving a Trivial Advantage of 0. Note that according to Table 1 an increasing length-hiding parameter \(\ell \) reduces the trivial advantage significantly, but not to 0. This may be sufficient to make traffic analysis attacks significantly less effective, but for some applications a trivial advantage of 0 may be desirable.
Rows 9, 10, 19 and 20 of Table 1 give the minimal length-hiding parameter \(\ell \) that is necessary to reduce the trivial advantage to 0.
Conclusions. For the message distribution considered in this section, we come to the following conclusions:
-
A block mode of operation improves the indistinguishability of the considered web pages, compared to a counter mode when \(\ell = 1\). In combination with length-hiding encryption and compression, the adversary’s trivial advantage can be reduced from 0.7400 (in counter mode without compression) down to 0.0037 (in block mode with compression and length-hiding parameter \(\ell = 25\)), together with a reduction in traffic by \(45.278\%\).
-
In most cases compression reduces the trivial advantage of the adversary by a factor of about 2 or better. The only exception is counter mode without length-hiding padding, where the reduction is still by a significant factor of about 1.5.
-
Compression significantly reduces the number |U| of uniquely identifiable web pages in all cases by a factor of 2 or better, and increases the size \(|S_\mathsf {max} |\) of the largest set of pages of identical size.
-
To analyze the impact of different length-hiding parameters and compression on communication complexity, we also measured the total amount of data transferred from the server to the client when each of the 1620 web pages is accessed exactly once. Note that compression not only reduces the adversary’s advantage by a factor around 2, but also reduces the communication complexity by a factor around 2.
-
Without compression, even for a relatively large LHE parameter \(\ell \), such as \(400 = 25 \cdot 16\) for counter mode or 25 for block mode encryption, the added communication complexity is relatively small, in particular when compared to the corresponding reduction in the adversary’s trivial advantage.
-
Achieving a trivial advantage of 0 costs a traffic overhead \(159\%\) without compression and even reduces traffic with compression.
We also consider a more powerful fingerprinting attack on the IACR ePrint archive website based on user patterns and another fingerprinting attack on the Google search engine. Due to space limitations, these two sections can be found in the full version of our work [8].
3.2 Simple Wikipedia Fingerprinting
Adversarial model. We consider webpage fingerprinting attack on the Wikipedia website. In this model, a user visits the Wikipedia website. A passive adversary observes the encrypted traffic and tries to determine the visited page.
Considered algorithms. Same as in Sect. 3.1.
Empirical data generation. The Wikimedia Foundation publishes pageview statistics of the Wikipedia website since May 2015. The pageview statistics contain the number of requests for each webpage in Wikipedia, which provides us with a real world message distribution of Wikipedia pages. We used the pageview data of May 2021 from https://dumps.wikimedia.org/other/pageviews/readme.html. We considered the data for 164270 webpages written in simple English and used a script issuing an HTTP HEAD-request for every webpage to determine the size, in uncompressed and in compressed form. These values are stored in a database and used to compute the size of counter- and block-mode ciphertexts for these schemes that encrypt the web page in either compressed or uncompressed form, with or without length-hiding encryption, and with respect to different length-hiding parameters. We note that the Simple Wikipedia project has a total number of 260478 webpages, as of May 2021, but not all webpages were accessed at least once during this period. Therefore we consider only the subset of webpages that were accessed in the considered time period (thus, the message distribution implicitly assigns a probability of zero to other pages).
Let \(\mathcal {M} := \{m_{1}, \ldots , m_{164270}\}\) be the set of different Simple Wikipedia webpages accessed in May 2021. We assume that the user picks one out of the 164270 webpages according to the distribution (denoted by \(\mathsf {M} _{\mathsf {Wiki}}\)) based on the pageview statistics and then gets the corresponding encrypted webpage. The adversary tries to guess the webpage. Hence, the adversary outputs an index \(i \in \{1, \ldots , 164270\}\), such that we define function \(\mathcal {P} \) as \(\mathcal {P}: \mathcal {M} \rightarrow [1, 164270]\), for \( m_{i} \mapsto i\).
Calculating the trivial advantage. Table 2 summarizes the results of the analysis. We calculate \(\mathsf {TrivAdv}(\mathsf {SE} ^{(\ell )}_{\mathrm {M},\mathrm {C}},\mathsf {M} _{\mathsf {Wiki}})\) for \(\mathrm {M}\in \{\mathrm {CTR},\mathrm {BLK}\}\), \(\mathrm {C}\in \{\text {True},\text {False}\}\) and different length-hiding parameter \(\ell \).
Conclusions. Table 2 allows us to make the following observations:
-
The adversary achieves very high trivial advantage (0.875) when \(\ell =1\). This indicates that the adversary could successfully identify the webpage with high probability only from the ciphertext length.
-
Compression reduces the overhead incurred by length-hiding encryption, and also reduces the trivial advantage.
-
A length-hiding parameter of 40K in the CTR mode (resp. 2.5K in the BLK mode) reduces the trivial advantage to 0.01 and increases the total data by about 23% without compression, but reduces about 50% total data with compression.
We believe that the example of Wikipedia webpage fingerprinting illustrates very well that length-hiding encryption with proper length-hiding parameter together with compression provides us with both security and bandwidth reduction for real-world message distributions.
Beyond the above analyses, we have conducted two more analyses on DNS fingerprinting (one using random host names from the Majestic Million list, the other using real-world DNS data collected in cooperation with a medium-sized university), which can be found in the full version of our work [8].
4 Implementation and Analysis
We have implemented our new approach as an Apache module, based on the most recent versions of an Apache HTTP server (Apache/2.4.38) and the OpenSSL library (version 1.1.1d) for Debian 10. The implementation is currently experimental, we plan to make a more stable version publicly available.
The implementation consists of two components. The first component monitors the server’s requests and responses. It stores the block-length and number of occurrences of requests to static URLs and the corresponding responses in a database. This database then provides an approximation of the server’s message distribution, which will be used by the second component to determine an appropriate length-hiding parameter \(\ell \). Furthermore, this component applies length-hiding padding to plaintext messages. Since OpenSSL currently does not support length-hiding padding beyond the last fragment of a plaintext, even though this is possible according to the TLS 1.3 standard, our experimental implementation currently simulates padding beyond frame bounds by appending NULL-bytes to the plaintext.Footnote 6
The second component of our implementation computes the length-hiding parameter \(\ell \), based on the request-response database and a given upper bound on the desired trivial advantage. It computes the smallest \(\ell \) that satisfies this trivial advantage for the message distribution defined by the database. Currently, the computation proceeds iteratively, that is, at first it tests whether the parameter \(\ell = 1\) satisfies the trivial advantage bound. If it does not, \(\ell \) is incremented and the process repeated until an optimal value \(\ell \) is found. Since the trivial advantage does not necessarily decrease monotonously for a given message distributionsFootnote 7, this approach yields the smallest possible value \(\ell \). The resulting parameter \(\ell \) is then used to define the size of length-hiding padding in the first component. Note that the second component can run in the background at predefined times (e.g., once per hour or once per day).
4.1 Validation of Pencil-and-Paper Analysis
To validate the theoretical pencil-and-paper analysis from Sect. 3 we configured the webserver as a proxy for the IACR ePrint server (resp. Google search engine). Then we requested each of the webpages (resp. search terms) once, to establish the same message distribution that was considered in Sect. 3. We used our implementation to record the message distribution, determine the LHE parameter \(\ell \), and then again accessed every web page once. We considered both AES-GCM and AES-CBC cipher suites. In all cases, we were able to accurately reproduce our results.
So far we have considered only the case without compression, for the following reason. The plaintext data is accessible from within an Apache module by accessing an appropriate “data bucket” of the Apache processing filter chain. This enabled us to circumvent the fact that OpenSSL currently does not support length-hiding padding beyond the last fragment of a plaintext, by padding the plaintext directly with NULL bytes. However, in order to apply the same approach to compressed plaintext data, we would need access to a bucket that contains the plaintext after compression, but before encryption. This seems not possible from an Apache module, and therefore we could not yet validate the pencil-and-paper analysis of compress-then-encrypt.
In future work we aim to perform further experiments, on a public web server with real-world message distributions and with compression. To this end, we have to extend OpenSSL to allow for length-hiding padding beyond the TLS fragment boundary, by appending further TLS fragments, if necessary. Such low-level modifications to OpenSSL and experiments on a public web server in production require significant additional care. Therefore we view this as out of scope of the present paper and leave this for future work.
5 Conclusions
Fingerprinting attacks are a very powerful technique to extract information from an encrypted channel, which are known to be very difficult to defend against. We have introduced a methodology that makes it possible to concretely quantify the security gained by length-hiding encryption. Our goal is to go beyond the assumption that the length of a ciphertext does reveal sensitive information, which is typically made implicitly in theoretical security models. In this sense, understanding security in presence of messages of different lengths contributes to our understanding of “secure encryption” in general.
We find that a surprisingly small amount of padding that incurs only a minor bandwidth overhead of a few percent can already reduce the advantage of an adversary very significantly. Even only the use of block mode encryption schemes, whose padding provides some very simple form of length-hiding encryption, may already reduce the concrete advantage of fingerprinting attacks very significantly. We also observe that the general recommendation to disable compression before encryption in all applications seems overgeneralized. While useful and necessary in some applications (when active attacks are feasible), in some other cases (e.g., “big brother” attacks) it may be harmful to security. It is therefore necessary to consider the security requirements of the application at hand with a more detailed analysis.
Notes
- 1.
- 2.
We also considered basing this analysis on other web sites, such as Wikipedia and a user that accesses a certain Wikipedia page. However, the IACR ePrint server also enables us to easily consider a natural extension to more complex access pattern, see below.
- 3.
In practice the TLS protocol would be used for these three connections, where different keys are used for sending and receiving data, but we view these keys as a single symmetric key.
- 4.
We use this server since URLs from the IACR ePrint archive are particularly easy to parse and analyse.
- 5.
To make our calculation more realistic, we consider the ciphertext is split across TLS fragments with a maximum payload of \(2^{14}\) bytes per fragment, whereby each fragment needs an additional 22 bytes reserved for the fragment header. The length for all the TLS headers is also considered and summed to the ciphertext length.
- 6.
As we will discuss below, we aim to extend OpenSSL to allow for length-hiding padding beyond the TLS fragment boundary, by appending further TLS fragments, if necessary.
- 7.
For example, if we have only two messages with length 12 and 17, a block length of 10 would perfectly hide everything, while a block length of 15 would not.
References
Bellare, M., Desai, A., Jokipii, E., Rogaway, P.: A concrete security treatment of symmetric encryption. In: 38th FOCS, pp. 394–403. IEEE Computer Society Press (1997)
Bellare, M., Namprempre, C.: Authenticated encryption: relations among notions and analysis of the generic composition paradigm. J. Cryptol. 21(4), 469–491 (2008)
Boldyreva, A., Degabriele, J.P., Paterson, K.G., Stam, M.: Security of symmetric encryption in the presence of ciphertext fragmentation. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 682–699. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_40
Cai, X., Nithyanand, R., Wang, T., Johnson, R., Goldberg, I.: A systematic approach to developing and evaluating website fingerprinting defenses. In: ACM CCS 2014, pp. 227–238. ACM Press (2014)
Degabriele, J.P.: Hiding the lengths of encrypted messages via Gaussian padding. In: ACM CCS 2021 (2021, to appear). Preliminary copy directly obtained from the author
Duong, T., Rizzo, J.: The CRIME attack (2012). http://www.ekoparty.org/archive/2012/CRIME_ekoparty2012.pdf
Dyer, K.P., Coull, S.E., Ristenpart, T., Shrimpton, T.: Peek-a-boo, i still see you: why efficient traffic analysis countermeasures fail. In: 2012 IEEE Symposium on Security and Privacy, pp. 332–346. IEEE Computer Society Press (2012)
Gellert, K., Jager, T., Lyu, L., Neuschulten, T.: On fingerprinting attacks and length-hiding encryption. Cryptology ePrint Archive, Report 2021/1027 (2021). https://eprint.iacr.org/2021/1027
Gillmor, D.K.: Empirical DNS padding policy (2017). https://dns.cmrg.net/ndss2017-dprive-empirical-DNS-traffic-size.pdf
Gong, X., Borisov, N., Kiyavash, N., Schear, N.: Website detection using remote traffic analysis. In: Fischer-Hübner, S., Wright, M. (eds.) PETS 2012. LNCS, vol. 7384, pp. 58–78. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31680-7_4
Gueron, S., Lindell, Y.: GCM-SIV: full nonce misuse-resistant authenticated encryption at under one cycle per byte. In: ACM CCS 2015, pp. 109–119. ACM Press (2015)
Gueron, S., Lindell, Y.: Simpleenc and simpleencsmall - an authenticated encryption mode for the lightweight setting. Cryptology ePrint Archive, Report 2019/712 (2019). https://eprint.iacr.org/2019/712
Harsha, B., Morton, R., Blocki, J., Springer, J., Dark, M.: Bicycle attacks considered harmful: Quantifying the damage of widespread password length leakage (2020)
Hayes, J., Danezis, G.: k-fingerprinting: a robust scalable website fingerprinting technique. In: USENIX Security 2016, pp. 1187–1203. USENIX Association (2016)
Herrmann, D., Wendolsky, R., Federrath, H.: Website fingerprinting: attacking popular privacy enhancing technologies with the multinomial Naïve-Bayes classifier. In: CCSW, pp. 31–42. ACM (2009)
Hintz, A.: Fingerprinting websites using traffic analysis. In: Dingledine, R., Syverson, P. (eds.) PET 2002. LNCS, vol. 2482, pp. 171–178. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36467-6_13
Hollenbeck, S.: Transport Layer Security Protocol Compression Methods. RFC 3749 (2004). https://doi.org/10.17487/RFC3749, https://rfc-editor.org/rfc/rfc3749.txt
Jager, T., Stam, M., Stanley-Oakes, R., Warinschi, B.: Multi-key authenticated encryption with corruptions: reductions are lossy. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 409–441. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_14
Katz, J., Yung, M.: Characterization of security notions for probabilistic private-key encryption. J. Cryptol. 19(1), 67–95 (2006)
Kohls, K., Rupprecht, D., Holz, T., Pöpper, C.: Lost traffic encryption: fingerprinting LTE/4G traffic on layer two. In: WiSec, pp. 249–260. ACM (2019)
Liberatore, M., Levine, B.N.: Inferring the source of encrypted HTTP connections. In: ACM CCS 2006, pp. 255–263. ACM Press (2006)
Mayrhofer, A.: Padding policies for extension mechanisms for DNS (EDNS(0)). RFC 8467 (2018). https://doi.org/10.17487/RFC8467, https://rfc-editor.org/rfc/rfc8467.txt
Miller, B., Huang, L., Joseph, A.D., Tygar, J.D.: I know why you went to the clinic: risks and realization of HTTPS traffic analysis. In: De Cristofaro, E., Murdoch, S.J. (eds.) PETS 2014. LNCS, vol. 8555, pp. 143–163. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08506-7_8
Paterson, K.G., Ristenpart, T., Shrimpton, T.: Tag size does matter: attacks and proofs for the TLS record protocol. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 372–389. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_20
Rescorla, E.: The Transport Layer Security (TLS) protocol Version 1.3. RFC 8446 (2018). https://doi.org/10.17487/RFC8446, https://rfc-editor.org/rfc/rfc8446.txt
Rogaway, P., Shrimpton, T.: A provable-security treatment of the key-wrap problem. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 373–390. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_23
Shusterman, A., et al.: Robust website fingerprinting through the cache occupancy channel. In: USENIX Security 2019, pp. 639–656. USENIX Association (2019)
Sirinam, P., Imani, M., Juárez, M., Wright, M.: Deep fingerprinting: undermining website fingerprinting defenses with deep learning. In: ACM CCS 2018, pp. 1928–1943. ACM Press (2018)
Tezcan, C., Vaudenay, S.: On hiding a plaintext length by Preencryption. In: Lopez, J., Tsudik, G. (eds.) ACNS 2011. LNCS, vol. 6715, pp. 345–358. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21554-4_20
Wang, T., Goldberg, I.: On realistically attacking tor with website fingerprinting. PoPETs 2016(4), 21–36 (2016)
Wang, T., Goldberg, I.: Walkie-talkie: an efficient defense against passive website fingerprinting attacks. In: USENIX Security 2017, pp. 1375–1390. USENIX Association (2017)
Wright, C.V., Ballard, L., Coull, S.E., Monrose, F., Masson, G.M.: Spot me if you can: Uncovering spoken phrases in encrypted VoIP conversations. In: 2008 IEEE Symposium on Security and Privacy. pp. 35–49. IEEE Computer Society Press, 2008
Wright, C.V., Ballard, L., Monrose, F., Masson, G.M.: Language identification of encrypted VoIP traffic: Alejandra y roberto or alice and bob? In: USENIX Security 2007. USENIX Association, 2007
Wright, C.V., Coull, S.E., Monrose, F.: Traffic morphing: An efficient defense against statistical traffic analysis. In: NDSS 2009. The Internet Society, 2009
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Gellert, K., Jager, T., Lyu, L., Neuschulten, T. (2022). On Fingerprinting Attacks and Length-Hiding Encryption. In: Galbraith, S.D. (eds) Topics in Cryptology – CT-RSA 2022. CT-RSA 2022. Lecture Notes in Computer Science(), vol 13161. Springer, Cham. https://doi.org/10.1007/978-3-030-95312-6_15
Download citation
DOI: https://doi.org/10.1007/978-3-030-95312-6_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-95311-9
Online ISBN: 978-3-030-95312-6
eBook Packages: Computer ScienceComputer Science (R0)






 . The gray background codes only applies to game
. The gray background codes only applies to game 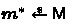 would correspond to the messages exchanged between a client and the search engine. Note that, in this case, the message distribution
would correspond to the messages exchanged between a client and the search engine. Note that, in this case, the message distribution  , and the goal of the adversary would be to determine the search term
, and the goal of the adversary would be to determine the search term 