Abstract
Time-lock puzzles are a mechanism for sending messages “to the future”, by allowing a sender to quickly generate a puzzle with an underlying message that remains hidden until a receiver spends a moderately large amount of time solving it. We introduce and construct a variant of a time-lock puzzle which is non-malleable, which roughly guarantees that it is impossible to “maul” a puzzle into one for a related message without solving it.
Using non-malleable time-lock puzzles, we achieve the following applications:
-
The first fair non-interactive multi-party protocols for coin flipping and auctions in the plain model without setup.
-
Practically efficient fair multi-party protocols for coin flipping and auctions proven secure in the (auxiliary-input) random oracle model.
As a key step towards proving the security of our protocols, we introduce the notion of functional non-malleability, which protects against tampering attacks that affect a specific function of the related messages. To support an unbounded number of participants in our protocols, our time-lock puzzles satisfy functional non-malleability in the fully concurrent setting. We additionally show that standard (non-functional) non-malleability is impossible to achieve in the concurrent setting (even in the random oracle model).
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Time-lock puzzles (TLPs), introduced by Rivest, Shamir, and Wagner [45], are a cryptographic mechanism for committing to a message, where a sender can (quickly) generate a puzzle with a solution that remains hidden until the receiver spends a moderately large amount of time solving it (even in the presence of parallel processors). Rivest et al. [45] gave a very efficient construction of TLPs where security relies on the repeated squaring assumption. This assumption postulates, roughly, that it is impossible to significantly speed up repeated modular exponentiations in a group of unknown order, even when using many parallel processors. This construction and assumption have proven extremely useful in various (and sometimes unexpected) applications [9, 15, 19, 33, 36, 44, 50], some of which have already been implemented and deployed in existing systems.
Non-malleability. In a Man-In-the-Middle (MIM) attack, an eavesdropper tries to actively maul intermediate messages to compromise the integrity of the underlying values. To address such attacks, Dolev, Dwork and Naor [18] introduced the general concept of non-malleability in the context of cryptographic commitments. Roughly speaking, non-malleable commitments are an extension of plain cryptographic commitments (that guarantee binding and hiding) with the additional property that no adversary can maul a commitment for a given value into a commitment to a “related” value. As this is a fundamental concept with many applications, there has been a tremendous amount of research on this topic [1, 11, 12, 22,23,24, 27, 29,30,31,32,33, 35, 39,40,41, 43, 49].
Non-malleable TLPs and Applications. To date, non-malleability has not been considered in the context of TLPs (or other timed primitives).Footnote 1 Indeed, the construction of TLPs of [45] is malleable.Footnote 2 This fact actually has negative consequences in various settings where TLPs could be useful. For instance, consider a scenario where n parties perform an auction by posting bids on a public bulletin board. To implement this fairly, a natural approach is to use a commit-and-reveal style protocol, where each party commits to its bid on the board, and once all bids are posted each party publishes its opening. Clearly, one has to use non-malleable commitments to guarantee that bids are independent (otherwise, a malicious party can potentially bid for the maximal other bid plus 1). However, non-malleability is not enough since there is a fairness issue: a malicious party may refuse to open after seeing all other bids and so other parties will never know what the unopened bid was.
Using non-malleable TLPs to “commit” to the bids solves this problem. Indeed, the puzzle of a party who refuses to reveal its bid can be recovered after some moderately large amount of time by all honest parties. This style of protocol can also be used for fair multi-party collective coin flipping where n parties wish to agree on a common unbiased coin. There, each party encodes a random bit via a TLP and all parties will eventually agree on the parity of those bits.Footnote 3 This gives a highly desirable collective coin flipping protocol with an important property that we refer to as optimistic efficiency: when all parties are honest and publish their “openings” immediately after seeing all puzzles, the protocol terminates and all parties agree on an unbiased bit. As we will see, no other known protocol for this (highly important) task has this property. Even ignoring optimistic efficiency, such a protocol yields a fully non-interactive coin flipping protocol where each participant solves all published puzzles.
1.1 Our Results
To present our results, we start with a high level definition of a non-malleable TLP. Recall that for some secret s and difficulty t, a time-lock puzzle enables sampling a puzzle z which can be solved in time t to recover s, but guarantees that s remains hidden to any adversary running in time less than t.
For non-malleability, we require that any man-in-the-middle (MIM) attacker \(\mathcal {A}\) that receives a puzzle z “on the left" cannot output a different puzzle \(\widetilde{z} \) “on the right" to a related value. Formally, we consider the (inefficient) distribution \(\mathsf {mim} _\mathcal{{A}}(t,s)\) that samples a puzzle z to s, gets \(\widetilde{z} \leftarrow \mathcal{{A}}(z)\), and outputs the value \(\widetilde{s} \) computed by solving \(\widetilde{z} \). However, if \(z = \widetilde{z} \), then \(\widetilde{s} = \bot \) (since simply forwarding the commitment does not count as a valid mauling attack). Then, non-malleability requires that for any solution s and MIM attacker with depth much less than t (so it cannot break hiding), the distribution for a value s given by \(\mathsf {mim} _\mathcal{{A}}(t,s)\) is indistinguishable from the distribution \(\mathsf {mim} _\mathcal{{A}}(t,0)\) for an unrelated value, 0. We emphasize that indistinguishability should hold even against arbitrary polynomial time or even unbounded distinguishers that, in particular, can solve the TLP. We also consider the natural extension to the bounded concurrent setting [42], where the MIM attacker \(\mathcal {A}\) receives \(n_{\mathsf {left}}\) concurrent puzzles on the left and attempts to generate \(n_\mathsf {right}\) puzzles on the right to related values. In this setting, the distinguisher receives the solutions to all \(n_{\mathsf {right}}\) puzzles. We refer to this as \((n_{\mathsf {left}},n_{\mathsf {right}})\)-concurrency.
We next give our main results. First, we present our results on non-malleable time-lock puzzles, and we discuss the various notions of non-malleability that we consider in this setting. Next, we show how to additionally satisfy a strong public verifiability property using a specific time-lock puzzle based on repeated squaring. Finally, we discuss the applications of our constructions for fair multi-party protocols.
Non-malleable Time-Lock Puzzles. We give two different constructions of non-malleable TLPs. We emphasize that, as explained above, this primitive is not only natural on its own right, but also has important applications to the design of secure protocols for various basic tasks. Our first construction is practically efficient, relies on the existence of any given TLP [6, 45], and is proven secure in the (auxiliary-input) random oracle model [47].
Theorem 1.1
(Informal; See Theorem 4.2 and Corollary 4.3). For every  , assuming that there is a TLP (supporting 1-bit messages) that is secure for attackers of size
, assuming that there is a TLP (supporting 1-bit messages) that is secure for attackers of size  , there exists an \((n_{\mathsf {left}},n_{\mathsf {right}})\)-concurrent non-malleable TLP supporting messages of length L. The scheme is proven secure in the auxiliary-input random oracle model.
, there exists an \((n_{\mathsf {left}},n_{\mathsf {right}})\)-concurrent non-malleable TLP supporting messages of length L. The scheme is proven secure in the auxiliary-input random oracle model.
In terms of security, our reduction is depth preserving: if the given TLP is secure against attackers of depth  , where \(\alpha (\cdot )\) is a fixed polynomial independent of T denoting the advantage of an attacker, then the resulting non-malleable TLP is secure against attackers of depth
, where \(\alpha (\cdot )\) is a fixed polynomial independent of T denoting the advantage of an attacker, then the resulting non-malleable TLP is secure against attackers of depth  for a related fixed polynomial \(\alpha '(\cdot )\). In particular, the dependence on T in hardness is preserved. Additionally, note that if
for a related fixed polynomial \(\alpha '(\cdot )\). In particular, the dependence on T in hardness is preserved. Additionally, note that if  , then the underlying TLP only needs to be polynomially secure.
, then the underlying TLP only needs to be polynomially secure.
Instantiating the TLP with the construction of [45], our scheme is extremely efficient: encoding a message requires a single invocation of a random oracle and few (modular) exponentiations. Additionally, our construction is very simple to describe: to generate a puzzle for a solution s with randomness r, we sample a puzzle for (s, r) using randomness which itself depends (via the random oracle) on s and r.Footnote 4 Nevertheless, the proof of security turns out to be somewhat tricky and non-trivial; see Sect. 2 for details.
We prove that our scheme is non-malleable against all polynomial-size attackers that cannot solve the puzzles (and this is inherent as the latter ones can easily maul any puzzle). We even allow the attacker’s description to depend arbitrarily on the random oracle. We formalize this notion by showing that our TLP is non-malleable in the auxiliary-input random oracle model, a model that was introduced by Unruh [47] (see also [14]) in order to capture preprocessing attacks, where a non-uniform attacker obtains an advice string that depends arbitrarily on the random oracle. Thus, in a sense, our construction does not require any form of attacker-independent setup.
Our second construction is proven secure in the plain model (without any form of setup) and is based on the non-malleable code for bounded polynomial depth tampering functions due to [15]. This construction relies on a variety of assumptions (including keyless hash functions and non-interactive witness indistinguishable proofs) and is less practically efficient. While the main technical ideas for the construction and proof are given in [15], the threat model they consider is weaker than what we require for non-malleable TLPs; for example, they only consider plain (non-concurrent) non-malleability and do not require security against re-randomization attacks (mauling a code word for m into a different code word for m). We show how to extend their construction to our setting, and prove the following theorem.
Theorem 1.2
(Informal). Assume a time-lock puzzle, a keyless multi-collision resistant hash function, a non-interactive witness indistinguishable proof for \(\mathsf {NP}\), and injective one-way functions, all sub-exponentially secure. Then, there exists a bounded concurrent non-malleable time-lock puzzle secure against polynomial size adversaries.
We emphasize that both of our constructions only achieve bounded concurrency, where the number of instances the attacker participates in is a priori bounded (and the scheme may depend on this bound). We show that the stronger notion of full concurrency, which does not place such limitations and is achievable in all other standard settings of non-malleability, is actually impossible to achieve for TLPs. Therefore, our result is best possible in this sense.
Theorem 1.3
(Informal). There is no fully concurrent non-malleable TLP (even in the random oracle model).
In a nutshell, the impossibility from Theorem 1.3 is proven by the following generic MIM attack. Given a puzzle z, if the number of “sessions” the attacker can participate in is at least as large as |z|, they can essentially generate |z| puzzles encoding the bits of z. Since the distinguisher of the MIM game (which is now given those bits) can run in arbitrary polynomial time, it can simply solve the original puzzle and recover the original solution in full. We emphasize that this attack only requires a polynomial-time distinguisher. This attack is circumvented in the bounded concurrency setting (Theorem 1.1) by setting the length of the puzzle to be longer than the concurrency bound. Specifically, to support n concurrent puzzles on the right, we can set the message length to \(L \cdot n\), which is what results in exponential security loss \(2^{L \cdot n}\) as discussed above.
Functional Non-malleability. We note that the attack on fully concurrent non-malleable time-lock puzzles crucially relies on the fact that the distinguisher in the MIM game can solve the underlying puzzles. However, it is easy to see that if the distinguisher is restricted to bounded depth, this attack fails. One could define a weaker notion of non-malleability where the MIM distinguisher is depth-bounded, but this results in a weaker security guarantee. In particular, we show in the full version of the paper that there exists a natural TLP construction that satisfies this (weaker) definition yet has a valid mauling attack.Footnote 5
In light of this observation, we introduce a new definition of non-malleability that generalizes the standard definition considered in Theorem 1.1. We call the notion functional non-malleability and, as the name suggests, the security notion is parameterized by a class of functions \(\mathcal F\). Denote by L the bit-length of the messages we want to support and by n the number of sessions that the MIM attacker participates in on the right. We think of \(f\in \mathcal F\) as some bounded depth function of the form \(f:(\{0,1\}^L)^n\rightarrow \{0,1\}^m\), which is the target function of the input messages that the MIM adversary is trying to bias. Specifically, the distinguisher of the MIM game now receives the output of the function f when applied to the values underlying the puzzles given by the MIM adversary. When \(\mathcal F\) includes all identity functions (which are bounded depth and have output length \(m = n \cdot L\)), functional non-malleability implies the standard definition of concurrent non-malleability (as the distinguisher just gets all the messages from the n mauled puzzles).
Naturally, it makes sense to ask what guarantees can we get if we a priori restrict f, say in its output length, without limiting the number of sessions n. This turns out to particularly useful when the application at hand only requires non-malleability against a specific form of tampering functions (this indeed will be the case for us below). Concretely, let \(\mathcal {F} _{m}\) be the class of all functions whose output length is at most m bits and which can be computed in depth polynomial in the security parameter  and in \(\log (n \cdot L)\) (using the notation given above). Then, we have the following result.
and in \(\log (n \cdot L)\) (using the notation given above). Then, we have the following result.
Theorem 1.4
(Informal; See Theorem 4.2). Assuming that there exists a TLP, then for every  there exists a fully concurrent functional non-malleable TLP for the class of functions \(\mathcal F_{m}\). The scheme is proven secure in the auxiliary-input random oracle model assuming the given TLP is secure for all attackers of size at most
there exists a fully concurrent functional non-malleable TLP for the class of functions \(\mathcal F_{m}\). The scheme is proven secure in the auxiliary-input random oracle model assuming the given TLP is secure for all attackers of size at most  .
.
The above construction is depth preserving in the same way as the construction from Theorem 1.1. Further, note that as long as  , we only require standard polynomial hardness from the given TLP. We remark that Theorem 1.4 will turn out to be instrumental for our applications we discuss below. We also believe that the abstraction of functional non-malleability is important on its own right and view it as an independent contribution. We also show how to achieve fully concurrent functional non-malleability for our plain model construction.
, we only require standard polynomial hardness from the given TLP. We remark that Theorem 1.4 will turn out to be instrumental for our applications we discuss below. We also believe that the abstraction of functional non-malleability is important on its own right and view it as an independent contribution. We also show how to achieve fully concurrent functional non-malleability for our plain model construction.
Publicly Verifiable Time-Lock Puzzles. In addition to non-malleability, we construct TLPs that also have a public verifiability property: after a party solves the puzzle, they can publish the underlying solution together with a proof which can be later used by anyone to quickly verify the correctness of the solution. We emphasize that this must hold even if the solver determines that the puzzle has no valid solution. We believe this primitive is of independent interest.
We build our non-malleable, publicly verifiable TLP assuming a very weak form of (partially) trusted setup. The setup of our TLP consists of a set of many public parameters where we only assume that at least one of them was generated honestly. We call this model the All-But-One-string (ABO-string) model.Footnote 6 We design this to fit into our multi-party protocol application (see Theorem 1.7 below) in such a way where the parties themselves will generate this setup in the puzzle generation phase. Indeed, as we discuss below, publicly verifiable TLPs in the ABO-string model will imply coin flipping without setup.
Theorem 1.5
(Informal). Assuming the repeated squaring assumption, there exists a publicly verifiable non-malleable TLP in the ABO-string model. The construction is proven secure in the auxiliary-input random oracle model.
Our construction is depth preserving and has security which depends on the message length. In particular, the security of the resulting TLP is the same as in the constructions in Theorem 1.1 and Theorem 1.4, depending on the type of non-malleability desired for the resulting TLP.
To construct our publicly verifiable TLP, we use a strong trapdoor VDF which is why our construction is not generic from any time-lock puzzle. Somewhat surprisingly, we need to leverage specific properties of the trapdoor VDF of Pietrzak’s [44] using the group of signed quadratic residues \(\mathrm {QR}_{N}^{+} \) where N is a product of safe primes.Footnote 7 For an overview of our construction, see Sect. 2.2.
Fair Multi-Party Auctions and Coin Flipping. As we mentioned above, an appealing application of non-malleable TLPs is for tasks such as fair multi-party auctions or coin flipping. Our protocols (for both tasks) are extremely efficient and consist of just two phases: first each party “commits” to their bid/randomness using some puzzle, and then after all puzzles are made public, each party publishes its solution. If some party refuses to open their puzzle, a force-opening phase is performed. Alternatively, we can instantiate our protocols in the fully non-interactive setting where all parties solve every other puzzle.
In what follows, we focus on the task of fair multi-party coin flipping, which is a core building block in recent proof-of-stake blockchain designs; see below. The application to auctions follows in a similar manner. It is convenient to consider our protocol in a setting where there is a public bulletin board. Any party can publish a puzzle to the bulletin board during the commit phase and then publish its solution after some pre-specified amount of time has elapsed.
Relying only our concurrent, functional non-malleable (not necessarily publicly verifiable) TLP constructions, all of our protocols (both non-interactive and two-phase) satisfy fairness, informally defined as follows:
-
Fairness: No malicious adversary (controlling all but one party) can bias the output of the protocol, even by aborting early. Namely, as long as there is at least one honest participating party, the output will be a (nearly) uniformly random value.
Our two-phase “commit-and-reveal” style protocols have the additional efficiency guarantee:
-
Optimistic Efficiency: If all participating parties are honest, then the protocol terminates within two message rounds (without the need to wait the pre-specified amount of time for the second phase), and all parties can efficiently verify the output of the protocol.
Using our construction of a publicly verifiable non-malleable TLP, we satisfy the following public verifiability property:
-
Public Verifiability: In the case that any participating party is dishonest and does not publish their solution, any party can break the puzzle in a moderate amount of time and provide a publicly verifiable proof of the solution. We even require that an honest party can prove that a published puzzle has no valid solution.
We focus on two main results from the above discussion, although we get a variety of different protocols depending on what TLP we start with and how we instantiate the protocol. First, we construct fully non-interactive protocols in the plain model without any setup.
Theorem 1.6
(Informal; see Theorem 5.3). Assume a time-lock puzzle, a keyless multi-collision resistant hash function, a non-interactive witness indistinguishable proof for \(\mathsf {NP}\), and injective one-way functions, all sub-exponentially secure. Then, there exist fully non-interactive, fair multi-party coin flipping and auction protocols. The protocols support an unbounded number of participants and require no setup.
Next, we achieve efficient, publicly verifiable two-phase protocols in the auxiliary input random oracle model.
Theorem 1.7
(Informal; See Theorem 5.1). Assuming the repeated squaring assumption, there exist two-phase fair multi-party coin flipping and auction protocols that satisfy optimistic efficiency and public verifiability. The protocols support an unbounded number of participants and require no trusted setup. Security is proven in the auxiliary-input random oracle.
The differences between the protocols achieved in these two theorems is that the first is non-interactive and has no setup, while the second is two rounds and is in the random oracle model, yet leverages this to achieve public verifiability and better concrete efficiency. We emphasize that both of the protocols support polynomial-length outputs, relying on sub-exponential security of the underlying time-lock puzzle.
We also emphasize that our protocols support an a priori unbounded number of participants. This may seems strange in light of our impossibility from Theorem 1.3. We bypass this lower bound (as mentioned above) by observing that for most natural applications (including coin flipping and auctions), the notion of functional non-malleability from Theorem 1.4 suffices. The key insight is that we only need indistinguishability with respect to specific depth-bounded functions with a priori bounded output lengths (e.g., parity for coin flipping, or taking the maximum for auctions). Since the output length in both cases is known, we can actually support full concurrency which translates into having an unbounded number of participants.
For auctions, we note that our protocols are the first multi-party protocols under any assumption that satisfy fairness against malicious adversaries and requires no adversary-independent setup—using the timed commitments of [9] works only in the two-party setting and additionally relies on trusted setup, and using the homomorphic time-lock puzzles of [36] does not satisfy fairness in the presence of malicious adversaries. For coin flipping, our two-round protocol is the first multi-party protocol that is fair against malicious adversaries while satisfying optimistic efficiency. Next, we provide a more in depth comparison of our non-interactive coin flipping protocol with existing solutions.
Simulation-Based Fairness. As mentioned above, we show that our protocols are fair in the sense that no malicious adversary can bias the output of the protocol. This suffices for applications which only use the output of the protocol. To capture applications that additionally depend on the protocol transcript, we show that our protocol satisfies simulation security with full fairness in the programmable random oracle model. This guarantees that the protocol execution in the presence of a malicious adversary (even one aborting early) can be simulated to a uniformly random output in an ideal model where every honest party receives the output (regardless of whether any malicious party aborts early).
Non-interactive Coin Flipping. We emphasize that our non-interactive coin flipping protocol of Theorem 1.6 is the first such protocol without any form of setup in the plain model. Specifically, we mean that there is no common random string or any assumed common function. Still, our practically efficient protocol of Theorem 1.7 as a non-interactive protocol still enjoys some benefits over existing schemes.
In the non-interactive setting, Boneh et al. [7] proposed a VDF-based protocol. Specifically, each party publishes a random string \(r_i\) and then the agreed upon coin is defined by running a VDF on the seed \(H(r_1\Vert \ldots \Vert r_n)\), where H is a random oracle. As the VDF must be evaluated to obtain the output, this type of protocol does not satisfy optimistic efficiency. Nevertheless, the VDF-based protocol has the advantage that only a single slow computation needs to be computed, whereas our non-interactive protocol requires n such computations for n participants (which can be done in parallel). Malavolta and Thyagarajan [36] address this inefficiency in the context of time-lock puzzles (which do allow for the option of optimistic efficiency) by constructing homomorphic time-lock puzzles, where many separate puzzles can be combined into a single puzzle to be solved. However, their TLP scheme is malleable and so cannot be directly used to obtain a fair protocol against malicious adversaries.Footnote 8 In the two-phase setting, however, our publicly verifiable protocol has the property that only a single honest party needs to solve each puzzle, and this computation can easily be delegated to an external server.
The VDF-based scheme of [7] can be based on repeated squaring in a group of unknown order based on the publicly verifiable proofs of [44, 50]. In this setting, the protocols can either be instantiated using RSA groups that require attacker-independent trusted setup, or based on class groups that rely only on a common random string. As we do in this work, the common random string can be implemented in the ABO-string model using a random oracle (which the attacker may depend on arbitrarily). Therefore, when restricting our attention to protocols without attacker-independent setup, the previous VDF-based protocols are based on less standard assumptions on class groups, whereas we give a protocol that can be instantiated from more standard assumptions on RSA groups with better concrete efficiency.
Privacy. Let us remark that the protocols that we described guarantee fairness but not privacy. The latter, however, can be obtained in specific applications by composing our protocols with existing privacy-preserving tools such as Anonize [26].
1.2 Related Work
Timed Commitments. Boneh and Naor [9] introduced timed commitments, which can be viewed as a publicly verifiable and interactive TLP. They additionally require that the puzzle (which is an interactive commitment) convinces the receiver that if they brute-force the solution, they will succeed. Because of this additional property, their commitment scheme is interactive and relies on a less standard assumption called the generalized Blum-Blum-Shub assumption. Their scheme is additionally malleable.
Fair Coin Flipping in Blockchains. Generating unbiased bits is one of the largest bottlenecks in modern proof-of-stake crypto-currency designs [5, 16, 17]. Recall that in a proof-of-stake blockchains, the idea is, very roughly speaking, to enforce “one vote per unit of stake”. This is usually implemented by choosing random small committees at every epoch and letting that committee decide on the next block. The main question is how to obtain “pure” randomness so that the chosen committee is really “random”.
One option is to use the hash of an old-enough block as the randomness. Unfortunately, it is known that the hash of a block is not completely unbiased: an attacker can essentially fully control about logarithmically many of its bits. In existing systems, this is mitigated by “blowing up” parameters to compensate for the (small yet meaningful) advantage the attacker has, making those systems much less efficient. Using a mechanism that generates unbiased bits, we could make proof-of-stake crypto-currencies much more efficient.
1.3 Concurrent Work
Several related papers [3, 4, 28] have been developed concurrently and independently to this work.Footnote 9 The works of Baum et al. [3, 4] formalize and construct various (publicly verifiable) time-based primitives, including TLPs, under the Universal Composability (UC) framework [10]. Katz et al. [28] (among other results, less related to ours) introduce and construct non-malleable non-interactive timed commitments. While the notions that are introduced and studied are related, the results are all incomparable as each paper has a somewhat different motivation which leads to different definitions and results.
Comparison with [28]. Let us start by comparing definitions. Katz et al. consider a CCA-style definition adapted to the depth-bounded setting. In the classical setting of unbounded polynomial-time attackers, CCA security definitions are usually stronger than “only” non-malleability, but this is not generally true in the depth-bounded setting.
In more detail, they consider a depth-bounded version of CCA security, where the attacker (who is also the distinguisher) is bounded to run in time less than the hardness of the timed primitive. We, on the other hand, allow the distinguisher of the MIM game to be unbounded (while only the attacker is bounded). We believe this is an important distinction and we provide more insights into the differences between the bounded and unbounded distinguisher settings in the full version. Specifically, we show that non-malleability with a depth-bounded distinguisher is (essentially) equivalent to our definition of functional non-malleability with output length 1. We also give a construction separating the definitions of non-malleability with an unbounded vs. depth-bounded distinguisher, showing that non-malleability in the bounded distinguisher setting gives a strictly weaker security guarantee.
Regarding the primitives constructed, recall that timed commitments [9] (ignoring non-malleability for now) allow one to commit to a message m in such a way that the commitment hides m up to some time T, yet the verifier can be sure that it can be force opened to some value after roughly T time. In contrast, plain TLPs are not necessarily guaranteed to contain valid messages. In this context, our notion of publicly-verifiable TLPs is in between these two notions: we treat puzzles without a solution as invalid (say encoding \(\bot \)) but we additionally provide a way to publicly verify that this is the case after it has been solved. Nevertheless, we note that the construction of Katz et al. does not imply a TLP since their commitment procedure takes T time (while TLP generation should take time essentially independent of T).
Additionally, their constructions achieve non-malleability through the use of NIZKs following the Naor-Yung [37] paradigm for CCA-secure encryption. Known (even interactive) zero-knowledge proofs for correctness of time-lock puzzles are quite expensive (see, e.g., Boneh-Naor [9] which requires parallel repetition). Using generic NIZKs (even in the random oracle model) would be even worse.
Regarding assumptions, their construction is proven secure in the algebraic group model [20] and relies on trusted setup, while ours is proven secure in the (auxiliary-input) random oracle model and hence requires no trusted setup independent of the adversary. Both constructions rely on repeated squaring as the source of depth-hardness, and theirs additionally makes use of NIZKs (which require setup).
Comparison with [3, 4]. Baum et al. consider a UC-style definition, which is generally stronger than non-malleability. In this setting, the environment takes the place of the distinguisher in the MIM game. Their definition is closer to ours as the environment may run for an arbitrary polynomial number of rounds and thus does not restrict the depth of the distinguisher. In terms of modeling, the construction of a UC-secure TLP in [4] relies on a programmable random oracle, whereas our construction relies on a non-programmable (auxiliary-input) random oracle. In fact, they prove that their notion of UC security cannot be achieved in the non-programmable random oracle model.
In a follow-up work [3], they show that their time-lock puzzle construction satisfies a notion of public verifiability. However, they achieve public verifiability only for honestly generated puzzles, that is, one can prove that a puzzle has a solution s, but cannot prove that a puzzle has no solution. In our terminology, we refer to this as one-sided public verifiability In contrast, our construction achieves full verifiability. This property is crucial for our efficient coin flipping protocol since it allows only one honest party to (attempt to) solve any invalid puzzle. With only one-sided public verifiability, every participant would need to solve all invalid puzzles, and the output of the coin-flip can only be efficiently verified (in time less than T) in the case that all puzzles are honestly generated.
1.4 Paper Organization
In Sect. 2, we give an overview of our techniques. Next, we give preliminaries in Sect. 3. In Sect. 4, we give our construction of functional non-malleable time-lock puzzles in the random oracle model. In Sect. 5, we give our construction of fair multi-party coin flipping. In Appendix A we discuss the various notions of non-malleability for TLPs introduced in this and related works. Additional results are provided in the full version, including our non-malleable TLP construction in the plain model, an impossibility result for unbounded concurrency, our publicly verifiable TLP construction, our simulation-secure coin flipping protocol, and a separation between unbounded and depth-bounded non-malleability.
2 Technical Overview
In Sect. 2.1, we give an overview of our non-malleable time-lock puzzle construction (in the random oracle model) and its proof of security. Then in Sect. 2.2, we overview our construction of publicly verifiable (and non-malleable) time-lock puzzles from repeated squaring. Finally in Sect. 2.3, we discuss how our non-malleable time-lock puzzle constructions can be used for fair multi-party coin flipping with various desirable properties.
We start by recalling the definition of TLPs, as necessary to give an overview of our techniques. A TLP consists of two algorithms \((\mathsf {Gen}, \mathsf {Sol})\). \(\mathsf {Gen} \) is a probabilistic procedure that takes as input an embedded solution s and a time parameter t, and outputs a puzzle z. \(\mathsf {Sol} \) is a deterministic procedure that on input a puzzle z for time bound t, outputs a solution in depth (or parallel time) roughly t. We note that TLPs can be thought of as a fine-grained analogue to commitments where “hardness” of the puzzle means that the puzzles are hiding against distinguishers of depth less than t. On the other hand, hiding can be broken in depth t (using \(\mathsf {Sol} \)). Additionally, we require that \(\mathsf {Sol} \) always finds the correct underlying solution s for a puzzle z. This corresponds to perfect binding in the language of commitments.
2.1 Non-malleability for Time-Lock Puzzles
In this section, we overview our non-malleable time-lock puzzle construction in the random oracle model (for the plain model construction, we refer the reader to the overview in [15], as the main ideas are the same). Our construction relies on any time-lock puzzle \(\mathsf {TLP} \) and a common random oracle \(\mathcal {O} \). We now describe our non-malleable TLP, which we denote \(\mathsf {nmTLP} \). In order to generate a puzzle for a solution s that can be broken in time t, \(\mathsf {nmTLP}.\mathsf {Gen} \) uses randomness r and feeds \(s\Vert r\) into the random oracle to get a string \(r_\mathsf {tlp} \). It then uses \(\mathsf {TLP}.\mathsf {Gen} \) to create a puzzle with difficulty t for \(s\Vert r\) using randomness \(r_\mathsf {tlp} \). That is,

Note that in order to solve the puzzle output by \(\mathsf {nmTLP}.\mathsf {Gen} \), it suffices to just solve the puzzle generated using \(\mathsf {TLP}.\mathsf {Gen} \), which takes time t. In other words, \(\mathsf {nmTLP}.\mathsf {Sol} (t,z)\) simply computes \(s \Vert r = \mathsf {TLP}.\mathsf {Sol} (t,z)\) and outputs s. In fact, the solver can even check to make sure that the solutions s is valid by checking that \(s = \mathsf {TLP}.\mathsf {Gen} (t, s;r)\).
We note that our construction is conceptually similar to the Fujisaki-Okamoto (FO) transformation [21] for transforming CPA-secure encryption to CCA-secure encryption using a random oracle. However, as we will see below, our proof is substantially different. In particular, the FO transformation achieves unbounded CCA security, which we show is impossible in our setting!
Hardness. To show the hardness of \(\mathsf {nmTLP}\) relative to a random oracle, we rely on the hardness of \(\mathsf {TLP}\) in the plain model, against attackers of depth much less than t. At a high level, we show that breaking the hardness of \(\mathsf {nmTLP}\) requires either guessing the randomness r used to generate the randomness \(r_{\mathsf {tlp}} = \mathcal {O} (s || r)\) for the underlying puzzle, or directly breaking the hardness of \(\mathsf {TLP}\), both of which are infeasible for bounded attackers. To formalize this, we consider any depth-bounded distinguisher \(\mathcal {D} ^{\mathcal {O}}\), who receives as input a \(\mathsf {nmTLP} \) puzzle \(z \) corresponding to solution \(s_{0}\) or \(s_{1}\) and distinguishes the two cases with non-negligible probability. By construction, \(z \) actually corresponds to a \(\mathsf {TLP}\) puzzle for \(s_{0} || r_{0}\) or \(s_{1} || r_{1}\), so we would like to use \(\mathcal {D} \) to construct a distinguisher against the hardness of \(\mathsf {TLP}\).
We first note that if \(\mathcal {D} \) never makes a query to \(\mathcal {O} \) containing the randomness \(r_{b}\) underlying \(z \), then we can simulate \(\mathcal {O} \) by lazily sampling it in the plain model, and hence use \(\mathcal {D} \) as a distinguisher for the hardness of \(\mathsf {TLP}\). If \(\mathcal {D} \) does make a query containing \(r_{b}\), then with overwhelming probability it must have received a puzzle corresponding to \(s_{b} || r_{b}\) (since in this case, \(r_{1-b}\) is independent of \(\mathcal {D} \) and its input \(z \)). Moreover, all of its queries up until that point have uniformly random answers independent of \(z \), so we can simulate them as well, up until receiving this query. Therefore, in both cases, we can carry out this attack in the plain model and rely on the hardness of \(\mathsf {TLP}\).
Non-malleability. To show non-malleability of \(\mathsf {nmTLP}\), we want to argue that any depth-bounded man-in-the-middle (MIM) attacker \(\mathcal{{A}}\) cannot maul a puzzle z for s (received on the left) to a puzzle \(\widetilde{z} \) (output on the right) for a related value \(\widetilde{s} \not = s\). At a high level, whenever \(\mathcal{{A}}\) changes the underlying value s to \(\widetilde{s} \), then the output of the random oracle on \(\widetilde{s} \) is now uniformly random and independent of z. Indeed, we show that for any fixed puzzle \(\widetilde{z} \) and a value \(\widetilde{s} \), a randomly generated puzzle for \(\widetilde{s} \) will not be equal to \(\widetilde{z} \) with high probability (otherwise we show how to break the hardness of \(\mathsf {TLP} \)). So, intuitively, the only way to generate a valid puzzle \(\widetilde{z} \) for \(\widetilde{s} \) is to “know” the underlying value \(\widetilde{s} \), but hardness intuitively implies that no depth-bounded adversary can “know” s.
We formalize this intuition by a hybrid argument to show that the MIM distribution \(\widetilde{s} \leftarrow \mathsf {mim} _\mathcal{{A}}(t,s)\) is indistinguishable from \(\mathsf {mim} _\mathcal{{A}}(t,0)\). At a high level, we first replace the inefficient distribution \(\mathsf {mim} _\mathcal{{A}}(t,s)\) by a low-depth circuit \(\mathcal {B} \). At this point, we want to use the hiding property to indistinguishably swap the puzzle to 0, so the hybrid is now unrelated to s. We describe the key ideas for these hybrids below.
For the first hybrid, the key insight is that we can compute \(\mathsf {mim} _\mathcal{{A}}(t,s)\) in low depth using an algorithm \(\mathcal {B} \) by simply looking at the oracle queries made by \(\mathcal{{A}}\). In this sense, we are relying on the extractability property of random oracles to say that \(\mathcal {A}\) must know any valid value \(\widetilde{s} \) it generates a puzzle for. Specifically, let \(\widetilde{z} \) be the output of \(\mathcal {A}\). For every query \((s_i \Vert r_i)\) that \(\mathcal {A}\) makes to \(\mathcal {O} \), \(\mathcal {B} \) outputs \(s_i\) if \(\widetilde{z} = \mathsf {nmTLP} (t,s_i \Vert r_i; \mathcal {O} (s_i \Vert r_i))\). If there are no such queries, \(\mathcal {B} \) outputs \(\bot \). \(\mathcal {B} \) requires depth comparable to the depth of \(\mathcal {A}\) since all of these checks can be done in parallel. Furthermore, the output of \(\mathcal {B} \) is indistinguishable from the true output given the above observation that \(\mathcal{{A}}\) cannot output a valid puzzle for a value it doesn’t query.
For the next hybrid, we would like to indistinguishably replace the underlying puzzle for s with a puzzle for 0, which would suffice to show non-malleability. Because \(\mathcal {B} \) is low-depth, it seems that we should be able to use the hiding property of \(\mathsf {nmTLP} \) to say that the output of \(\mathcal {B} \) does not depend on the underlying value s. Specifically, we want to conclude that if the output of \(\mathcal {B} \) (who outputs many bits) is statistically far when the underlying value is s versus 0, then there exists a distinguisher (who outputs a single bit) that can distinguish puzzles for s and 0. Towards this claim, we show how to “flatten" any (possibly unbounded) distinguisher \(\mathcal {D} \) who distinguishes between the output of \(\mathcal {B} \) in the case where the underlying value is s versus 0. Specifically, we encode the truth table of \(\mathcal {D} \) as a low-depth distinguishing circuit of size roughly  to make this reduction go through. As a result, we need to rely on a sub-exponentially security of the underlying TLP when
to make this reduction go through. As a result, we need to rely on a sub-exponentially security of the underlying TLP when  . Namely, the underlying TLP cannot be broken by sub-exponential sized circuits with depth much less than t. However, when
. Namely, the underlying TLP cannot be broken by sub-exponential sized circuits with depth much less than t. However, when  , we only need to rely on polynomial security of the underlying TLP.
, we only need to rely on polynomial security of the underlying TLP.
Impossibility of Fully Concurrent Non-malleability. Ideally, we would like to achieve fully concurrent non-malleability, meaning that any MIM attacker that receives any polynomial n number of puzzles on the left cannot maul them to n puzzles for related values. However, we show that this is impossible to achieve.
Consider an arbitrary TLP for a polynomial time bound t. We construct a MIM attacker \(\mathcal {A}\) that receives only a single puzzle z on the left with solution s where the length of z is L. Then, \(\mathcal {A}\) can split z into L bits and output a puzzle on the right for each bit of the puzzle z. Then, the values underlying the puzzles output by \(\mathcal {A}\) when viewed together yield z, which is related to the value s! More formally, there exists a polynomial time distinguisher that solves the puzzle z in polynomial time t and can distinguish \(\mathcal {A}\)’s output in the case when it receives a puzzle for s or an unrelated value, say 0.
This implies that for any n which is greater than the size of a puzzle, the TLP cannot be non-malleable against MIM attackers who output at most n puzzles on the right. At a high level, the impossibility follows from the fact that hardness does not hold against arbitrary polynomial-time distinguishers (which usually is the case for hiding of standard commitments).
Despite this impossibility, we show that we actually can achieve concurrent non-malleability against a specific class of distinguishers in the non-malleability game. We refer to this notion as concurrent functional non-malleability.
Achieving Concurrent Functional Non-malleability. In many applications, we only need a form of non-malleability to hold with respect to certain classes of functions. For example, in our application to coin flipping, we only need that a puzzle z with solution s cannot be mauled to a set of puzzles \(\widetilde{z_1},\ldots ,\widetilde{z_n} \) with underlying values \(\widetilde{s_1}, \ldots , \widetilde{s_n} \) such that \(\bigoplus _{i \in [n]} \widetilde{s_i} \) “depends on” s. With this in mind, we define a concurrent functional non-malleability with respect to a class of functions \(\mathcal {F} \). We say that a TLP satisfies functional non-malleability for a class \(\mathcal {F} \) if the output of \(f(\mathsf {mim} _\mathcal{{A}}(t,s))\) is indistinguishable from \(f(\mathsf {mim} _\mathcal{{A}}(t,0))\) for any \(f \in \mathcal {F} \), which also naturally generalizes to the concurrent setting. We note that functional non-malleability for a class \(\mathcal {F} \) actually implies standard non-malleability whenever the class \(\mathcal {F} \) contains the identity function, so functional non-malleability generalizes the standard notion of non-malleability.
Going back to the proof of standard (non-concurrent) non-malleability for our construction \(\mathsf {nmTLP} \), we observe that the security we need for the underlying time-lock puzzle we use depends on \(2^{|s|}\) where |s| is the size of the puzzle solutions. Specifically, given any distinguisher in the non-malleability that had input of size |s|, we were able to construct a distinguisher for hardness of size \(2^{|s|}\). In fact, this exact same proof works in the context of concurrent functional non-malleability for functions f that have low depth and bounded output length m. We require f to be low depth so the reduction constitutes a valid attack against hardness, and then we only require security proportional to \(2^m\)!
We briefly discuss how our \(\mathsf {nmTLP} \) construction works for concurrent functional non-malleability for the class \(\mathcal {F} _m\) of function with low depth and output length m. Specifically, for every m, we define a scheme \(\mathsf {nmTLP} _m\) assuming that \(\mathsf {TLP} \) is secure against attackers of size roughly \(2^m\). Because \(\mathsf {TLP} \) requires security against \(2^m\) size attackers, our construction \(\mathsf {nmTLP} _m\) also only achieves security against \(2^m\) size attackers. As such, our \(\mathsf {nmTLP}.\mathsf {Gen} \) algorithm needs to use at least  bits of randomness (otherwise an attacker could cycle through all choices of randomness to break security). Recall that \(\mathsf {nmTLP} _m.\mathsf {Gen} \) with randomness r outputs a puzzle using \(\mathsf {TLP}.\mathsf {Gen} \) with solution \(s \Vert r\). As a result, if we want to support solutions of size |s| in \(\mathsf {nmTLP} _m\), we need our underlying TLP to support solutions of size
bits of randomness (otherwise an attacker could cycle through all choices of randomness to break security). Recall that \(\mathsf {nmTLP} _m.\mathsf {Gen} \) with randomness r outputs a puzzle using \(\mathsf {TLP}.\mathsf {Gen} \) with solution \(s \Vert r\). As a result, if we want to support solutions of size |s| in \(\mathsf {nmTLP} _m\), we need our underlying TLP to support solutions of size  . By correctness, this implies that our schemes outputs puzzles of size roughly
. By correctness, this implies that our schemes outputs puzzles of size roughly  .
.
Bounded Concurrent Non-malleability. Our construction of time-lock puzzles for concurrent functional non-malleability can also be seen as a construction for bounded concurrent (plain) non-malleability. Specifically, consider the case where the MIM attacker outputs at most n puzzles on the right. We can think of this as functional non-malleability where the low depth function is simply identity on \(n \cdot |s|\) bits. From the above discussion, this implies a protocol assuming a TLP with security against size \(2^{n \cdot |s|}\) attackers, with puzzles of size roughly  .
.
Security in the Auxiliary-Input Random Oracle Model. Finally, we note that the most of our constructions and formal proofs are in the auxiliary-input random oracle model (AI-ROM) introduced by Unruh [47]. In this model, the non-uniform attacker is allowed to depend arbitrarily on the random oracle, so there is no attacker-independent non-uniform advice. At a high level, we use the result from [47] to conclude that the view of any bounded-size MIM attacker \(\mathcal {A}\) with oracle access to \(\mathcal {O} \) (where \(\mathcal {A}\) may depend arbitrarily on \(\mathcal {O} \)) is indistinguishable the view of \(\mathcal {A}\) with access to a “lazily sampled” oracle \(\mathcal {P} \) that is fixed at a set of points F (which depend on \(\mathcal {A}\)). Formally, in the non-malleability analysis, we switch to an intermediate hybrid where the MIM attacker has access to a partially fixed, lazily sampled oracle \(\mathcal {P} \). Then, because the MIM attacker \(\mathcal {A}\) must maul honestly generated puzzles that have high entropy, we show that it is necessary for \(\mathcal {A}\) to query the oracle \(\mathcal {P} \) outside the fixed set of points F. From this, we carefully show that a similar analysis follows as discussed above for the ROM.
2.2 Publicly Verifiable Time-Lock Puzzles
We observe that the non-malleable time-lock puzzle construction \(\mathsf {nmTLP} \) we described above has a very natural—yet incomplete—public verifiability property. Solving a puzzle yields both the solution s and the randomness r use to generate that puzzle. As such, anyone who solves a valid puzzle can send the opening r to another party, and convince them that s is the unique valid solution to the puzzle. However, we emphasize that this only works for valid puzzles and solutions.
Consider the following problematic scenario for our \(\mathsf {nmTLP}\) construction. Suppose a party “commits” to a value via a puzzle z and refuses to open the commitment. As we said before, if z is a valid puzzle, any party can solve the puzzle, get the solution s and an opening r that proves that s is the unique solution. What if the puzzle corresponds to no solution? We refer to this scenario by saying that the puzzle corresponds to the solution \(\bot \). In this case (by definition), there is no solution s and opening r for any such that \(z = \mathsf {Gen} (t,s;r)\). Anyone who solve the invalid puzzle—which requires a lot of computational power—will be able to conclude that the puzzle is malformed, but they will not be able to convince anyone else that this is the case. Ideally, we would have a time-lock puzzle where \(\mathsf {Sol} \) additionally outputs a publicly verifiable proof \(\pi \) that the solution it computes is correct, even if the solution may be \(\bot \)! We refer to such a time-lock puzzle as a publicly verifiable time-lock puzzle. We next discuss the definition and our construction of publicly verifiable time-lock puzzles.
Defining Public Verifiability. More formally, a publicly verifiable time-lock puzzle consists of algorithms  . As with normal time-lock puzzles, \(\mathsf {Gen} (t,s)\) outputs a puzzle z. The algorithm \(\mathsf {Sol} (t,z)\) outputs the solution s as well as a proof \(\pi \) that it computed s correctly. Finally
. As with normal time-lock puzzles, \(\mathsf {Gen} (t,s)\) outputs a puzzle z. The algorithm \(\mathsf {Sol} (t,z)\) outputs the solution s as well as a proof \(\pi \) that it computed s correctly. Finally  checks that s is indeed the correct solution for the puzzle z (corresponding to \(\mathsf {Sol} (t,z)\)), using the proof \(\pi \). In addition to \((\mathsf {Gen}, \mathsf {Sol})\) being a valid time-lock puzzle, we require that \(\mathsf {Sol} \) and
checks that s is indeed the correct solution for the puzzle z (corresponding to \(\mathsf {Sol} (t,z)\)), using the proof \(\pi \). In addition to \((\mathsf {Gen}, \mathsf {Sol})\) being a valid time-lock puzzle, we require that \(\mathsf {Sol} \) and  constitute a sound non-interactive argument. In fact, we require a very strong notion of soundness. We need it to be the case that even for maliciously chosen puzzles that have no solution, the time-lock puzzle is still sound—even against the adversary that generated the malformed puzzle. In other words, we require that no attacker can compute a puzzle z, a value \(s'\), and a proof \(\pi '\) such that
constitute a sound non-interactive argument. In fact, we require a very strong notion of soundness. We need it to be the case that even for maliciously chosen puzzles that have no solution, the time-lock puzzle is still sound—even against the adversary that generated the malformed puzzle. In other words, we require that no attacker can compute a puzzle z, a value \(s'\), and a proof \(\pi '\) such that  accepts yet \(s'\) is not the value s computed by \(\mathsf {Sol} (t,z)\), which may be \(\bot \).
accepts yet \(s'\) is not the value s computed by \(\mathsf {Sol} (t,z)\), which may be \(\bot \).
Ideally, we would want a publicly verifiable time-lock puzzle that requires no setup. We instead consider a weak form of setup which we refer to as the All-But-One-string (ABO-string) model. In this model, \(\mathsf {Sol} \) and  additionally take as input a string
additionally take as input a string  , and we require that soundness holds as long as one of the values of \(\mathsf {crs} _i\) is sampled uniformly (without necessarily knowing which one); this is why we refer to it as the all-but-one string model. We note that in multi-party protocols, the ABO-string model is realistic as each participant \(i \in [n]\) can post a value for \(\mathsf {crs} _i\). Then, we require soundness to hold as long as one participant is honest, which is a reasonable assumption in this multi-party setting.
, and we require that soundness holds as long as one of the values of \(\mathsf {crs} _i\) is sampled uniformly (without necessarily knowing which one); this is why we refer to it as the all-but-one string model. We note that in multi-party protocols, the ABO-string model is realistic as each participant \(i \in [n]\) can post a value for \(\mathsf {crs} _i\). Then, we require soundness to hold as long as one participant is honest, which is a reasonable assumption in this multi-party setting.
Constructing Publicly Verifiable Time-Lock Puzzles. Our construction of a publicly verifiable time-lock puzzle follows the blueprint of Rivest, Shamir, and Wagner [45] for constructing time-lock puzzles from repeated squaring. Namely, we use the output of a sequential function (repeated squaring in a suitable group) essentially as one-time pad to mask the value underlying the time-lock puzzle. As in [45], we require that the sequential function has a trapdoor so that puzzles can be generated efficiently. Unlike [45], we additionally require that the sequential function is publicly verifiable to enable publicly verifiability for the time-lock puzzle. Finally, we apply the non-malleability transformation described above to achieve full public verifiability. In what follows, we describe each of these steps in more detail.
For the underlying sequential function, we use what we call a strong trapdoor verifiable delay function (VDF). A VDF (introduced by Boneh et al. [7]) is a publicly verifiable sequential function that can be computed in time t but not much faster, even with lots of parallelism. A trapdoor VDF (formalized by Wesolowski [50]) additionally has a trapdoor for quick evaluation. We require a trapdoor VDF in the ABO-string model that satisfies additional properties required by our application. While the properties we define—and achieve—are heavily tailored towards our application, we believe some of the techniques may be of independent interest. More specifically, a strong trapdoor VDF comes with a  algorithm to generate inputs for an evaluation algorithm
algorithm to generate inputs for an evaluation algorithm  . We emphasize that, even in the ABO-string model,
. We emphasize that, even in the ABO-string model,  is independent of any form of setup. Previous definitions of VDFs require the proof to be sound with probability over an honestly sampled input. In contrast, we require that the proof is sound for any maliciously chosen input that is in the support of the
is independent of any form of setup. Previous definitions of VDFs require the proof to be sound with probability over an honestly sampled input. In contrast, we require that the proof is sound for any maliciously chosen input that is in the support of the
 algorithm. We note that this property is satisfied by a variant of Pietrzak’s VDF [44] based on repeated squaring. At a high level, this is because Pietrzak’s VDF is sound (at least in the random oracle model) for any group of unknown order where no adversary can find a group of low order (see e.g.[8] for further discussion), so by using any RSA group with no low order elements (as in [44]), the proof is sound even if the group is maliciously chosen (yet still a valid RSA group), which gives the strong property we need. We note that the proof of soundness for our strong trapdoor VDF in the ABO-string and auxiliary-input random oracle model follows by a similar argument to that of [44] in the (plain) random oracle model after applying Unruh’s result [47].
algorithm. We note that this property is satisfied by a variant of Pietrzak’s VDF [44] based on repeated squaring. At a high level, this is because Pietrzak’s VDF is sound (at least in the random oracle model) for any group of unknown order where no adversary can find a group of low order (see e.g.[8] for further discussion), so by using any RSA group with no low order elements (as in [44]), the proof is sound even if the group is maliciously chosen (yet still a valid RSA group), which gives the strong property we need. We note that the proof of soundness for our strong trapdoor VDF in the ABO-string and auxiliary-input random oracle model follows by a similar argument to that of [44] in the (plain) random oracle model after applying Unruh’s result [47].
Next, we construct what we refer to as a one-sided publicly verifiable time-lock puzzle in the ABO-string model by using the strong trapdoor VDF in the RSW-style construction described above. By one-sided, we mean that completeness and soundness hold only for puzzles in the support of \(\mathsf {Gen} \) (again, we emphasize that this is in contrast to a randomly sampled puzzle). Then, our full construction applies our non-malleability transformation to a one-sided publicly verifiable time-lock puzzle. We already argued that the non-malleability transformation provides a form of public verifiability for puzzles z in the support of \(\mathsf {Gen} \). Namely, anyone can prove to another party that a valid puzzle z has a solution s, but the proof may not be sound when trying to prove that a puzzle has no solution. However, we next show that if the underlying puzzle satisfies one-sided public verifiability, then the resulting (non-malleable) publicly verifiable TLP is sound for any  (possibly not in the support of \(\mathsf {Gen} \)).
(possibly not in the support of \(\mathsf {Gen} \)).
Proof of Full Public Verifiability. Let  be the TLP resulting from applying our non-malleability transformation to a one-sided PV TLP
be the TLP resulting from applying our non-malleability transformation to a one-sided PV TLP  . Consider any puzzle
. Consider any puzzle  . If z is in the support of \(\mathsf {Gen} \), we want to ensure that no one can prove that \(s' = \bot \) is a valid solution. At the same time, if z is not in the support of \(\mathsf {Gen} \), we want to ensure that no one can prove that \(s' \not = \bot \) is a valid solution.
. If z is in the support of \(\mathsf {Gen} \), we want to ensure that no one can prove that \(s' = \bot \) is a valid solution. At the same time, if z is not in the support of \(\mathsf {Gen} \), we want to ensure that no one can prove that \(s' \not = \bot \) is a valid solution.
When we run \(\mathsf {Sol} (t,z)\), we first run \(\mathsf {Sol} _\mathsf {tlp} (t,z)\) and get a solution \(s_\mathsf {tlp} = \hat{s}\Vert \hat{r}\) with a proof \(\pi _\mathsf {tlp} \). If \(\hat{r}\) is a valid opening for the proposed solution \(\hat{s}\), then \(\mathsf {Sol} \) can simply output the solution \(s = \hat{s}\) and the proof \(\pi = \hat{r}\). If \(\hat{r}\) is not a valid opening for \(\hat{s}\), \(\mathsf {Sol} \) must output \(\bot \) and a proof \(\pi \) that this is the case. We set \(\pi = (s_\mathsf {tlp}, \pi _\mathsf {tlp})\), which intuitively gives anyone else a way to “shortcut” the computation of \(\mathsf {Sol} _\mathsf {tlp} \).
Now suppose that an adversary tries to falsely convince you that a puzzle z with no solution has a solution \(s' \not = \bot \) using a proof \(\pi ' = r'\). To do so, it must be the case that \(r'\) is a valid opening for \(s'\) with respect to \(\mathsf {Gen} \). But if that were the case, then z would have a solution, in contradiction.
On the other hand, suppose that an adversary tries to falsely convince you that a puzzle z with solution s has no solution, i.e. \(s' = \bot \), using a proof \(\pi ' = (s_\mathsf {tlp} ', \pi _\mathsf {tlp} ')\). Since z has a solution, it means that z is in the support of \(\mathsf {Gen} _\mathsf {tlp} \). By one-sided public verifiability, this means that \(\pi _\mathsf {tlp} '\) is a valid proof that \(s_\mathsf {tlp} ' = \hat{s} \Vert \hat{r}\) is the correct solution to z with respect to \(\mathsf {Gen} _\mathsf {tlp} \). So if \(\hat{r}\) is not a valid opening for \(\hat{s}\) with respect to \(\mathsf {Gen} \), we know the adversary must be lying. In other words, the only way the adversary can cheat is by cheating in the underlying one-sided PV TLP on a puzzle z in the support of \(\mathsf {Gen} _\mathsf {tlp} \).
Discussion of Our Non-malleable PV TLP. We note that the publicly verifiable time-lock puzzle we described above can be made to satisfy the same non-malleability guarantees as we discuss in Sect. 2.1 (as we construct it using the same transformation but with a specific underlying time-lock puzzle). Thus, assuming the repeated squaring assumption, we get a publicly verifiable time-lock puzzle that satisfies concurrent function non-malleability for any class of low depth functions \(\mathcal {F} _m\) with output length m. Our construction is in the ABO-string model, and we prove security in the auxiliary-input random oracle model (which is needed for soundness of the strong trapdoor VDF in the ABO-string model in addition to the non-malleability transformation). This model is reasonable for our practical applications to multi-party protocols, as we will see below. Due to the fact that this is a non-black box construction, we note that it does not apply to our non-malleable TLP construction in the plain model.
We also note that our explicit repeated squaring assumption states that repeated squaring in RSA groups for n-bit integers cannot be sped up even by adversaries of size roughly \(2^m\). The repeated squaring assumption is closely related to the assumption on factoring (which has recently been formalized in different generic models by the works of [28, 46]). The current best known algorithms for factoring run in time at least \(2^{n^{1/3}}\). In the case where  , for example, we only require that polynomial-size attackers cannot speed up repeated squaring, which is a relatively mild assumption. In the case where m is larger, say
, for example, we only require that polynomial-size attackers cannot speed up repeated squaring, which is a relatively mild assumption. In the case where m is larger, say  , then we need to choose n to be at least
, then we need to choose n to be at least  (based on known algorithms for factoring). This gives an example of the various trade-offs we get for the security and efficiency of our construction depending on the class of low depth functions \(\mathcal {F} _m\) that we want non-malleability for.
(based on known algorithms for factoring). This gives an example of the various trade-offs we get for the security and efficiency of our construction depending on the class of low depth functions \(\mathcal {F} _m\) that we want non-malleability for.
2.3 Fair Multi-party Protocols
We will focus on coin flipping for concreteness, and note that for auctions the ideas are similar. We give a protocol in auxiliary-input random oracle model, and one in the plain model, depending on which non-malleable TLP construction we use to instantiate it (which result in different guarantees). Here, we describe our random oracle protocol, which captures the main ideas and various properties we can achieve.
At a high level, the coin flipping protocol is very simple. Each party chooses a random bit and publishes a time-lock puzzle that encodes the chosen bit. After all puzzles are published, each party opens their puzzle by revealing the bit that they used as well as the randomness used to generate the puzzle. Any puzzle that is not opened can be “solved” after a moderately large amount of time t. Once all puzzles have been opened, the agreed upon bit (i.e., the output of the protocol) is the XOR of all revealed bits. The above protocol template is appealing because it naturally satisfies optimistic efficiency: if all parties are honest and open their puzzles, the protocol terminates immediately. When using time-lock puzzles which are both non-malleable (as discussed in Sect. 2.1) and publicly verifiable (as discussed in Sect. 2.2), we achieve the following highly desirable properties:
-
Fairness: No malicious party can bias the output of the protocol. This crucially relies on non-malleability for the underlying time-lock puzzle. For a protocol with n participants, we need the time-lock puzzle to satisfy n-concurrent non-malleability. This guarantees that as long as one party is honest, the output of the protocol will be (at least statistically close to) a uniformly random bit.
-
Unbounded participants: Anyone can participate in the protocol. This property might come as a surprise since we show fully concurrent non-malleability is impossible to achieve. However, we emphasize that our time-lock puzzle achieves fully concurrent functional non-malleability for the XOR function. This allows us to deal with any a priori unbounded number of participants, which is important in many decentralized and distributed settings.
-
Public verifiability: Only one party needs to solve each unopened puzzle, and can provide a publicly verifiable proof that it solved it correctly. This follows immediately by the public verifiability property we achieve for the underlying time-lock puzzle. Without this property, any unopened puzzles may need to be solved by every party that want to know the output of the protocol, which is prohibitively expensive. However, public verifiability instead opens up the application to any party, not even involved in the protocol. Furthermore, this work can even be delegated to an external server since trust is guaranteed by the attached proof.
We note that our non-malleable and publicly verifiable time-lock puzzle is defined in the All-But-One-string (ABO-string) model, which is required for public verifiability. To implement this model, we have each participant i publish a fresh random string  in addition to its puzzle \(z_i\). Then, whenever some party tries to solve (or verify) a puzzle, it puts all of the random strings together as a multi-common random string \(\mathsf {mcrs} = (\mathsf {crs} _1,\ldots , \mathsf {crs} _n)\) from all n participants, and uses this for the publicly verifiable proof. As long as a single party is honest and publishes a random string \(\mathsf {crs} _i\) independent of all other participants, then the publicly verifiable proof system will be sound.
in addition to its puzzle \(z_i\). Then, whenever some party tries to solve (or verify) a puzzle, it puts all of the random strings together as a multi-common random string \(\mathsf {mcrs} = (\mathsf {crs} _1,\ldots , \mathsf {crs} _n)\) from all n participants, and uses this for the publicly verifiable proof. As long as a single party is honest and publishes a random string \(\mathsf {crs} _i\) independent of all other participants, then the publicly verifiable proof system will be sound.
Simulation-Based Fairness. Finally, we discuss how fairness in the above protocol can be strengthened to a simulation-style definition. Consider running our protocol to get a value s, where s is the XOR of bits underlying the adversary’s and honest players’ time-lock puzzles. In our simulation-secure protocol, we will set the output to \(\mathcal {O} (s)\) where \(\mathcal {O} \) is a programmable random oracle. This enables a simulator running in polynomial time to solve the adversary’s puzzles and program \(\mathcal {O} (s)\) to the desired output value. It then suffices to show that the adversary \(\mathcal {A}\) does not detect this change in the oracle, meaning that \(\mathcal {A}\) does not query s before publishing its time-lock puzzles. We observe that if \(\mathcal {A}\) does indeed query s, it implies an adversary against the game-based fairness of our protocol, that runs \(\mathcal {A}\) to get s and outputs a TLP to s along with \(\mathcal {A}\)’s puzzles, thus biasing the output to \(s \oplus s=0\). We note that this shows that game-based fairness for a standard commit-and-reveal style protocol (with TLPs instead of commitments) can be generically transformed into a simulation-secure protocol by feeding the output into a programmable random oracle.
3 Preliminaries
We first define time-lock puzzles without any additional properties.
Definition 3.1
Let \(B :\mathbb {N} \rightarrow \mathbb {N} \). A B-hard time-lock puzzle (TLP) is a tuple \((\mathsf {Gen}, \mathsf {Sol})\) with the following syntax:
-
 : A PPT algorithm that on input a security parameter
: A PPT algorithm that on input a security parameter  , a difficulty parameter \(t \in \mathbb {N} \), and a solution
, a difficulty parameter \(t \in \mathbb {N} \), and a solution  , outputs a puzzle
, outputs a puzzle  .
. -
 : A deterministic algorithm that on input a security parameter
: A deterministic algorithm that on input a security parameter  , a difficulty parameter \(t \in \mathbb {N} \), and a puzzle
, a difficulty parameter \(t \in \mathbb {N} \), and a puzzle  , outputs a solution
, outputs a solution  .
.
We require \((\mathsf {Gen},\mathsf {Sol})\) to satisfy the following properties.
-
Correctness: For every
 , solution
, solution  , and
, and  , it holds that
, it holds that  .
. -
Efficiency: There exist a polynomial p such that for all
 ,
,  is computable in time
is computable in time  .
. -
B-Hardness: There exists a positive polynomial function \(\alpha \) such that for all functions T and non-uniform distinguishers
 satisfying
satisfying  ,
,  , and
, and  for all
for all  , there exists a negligible function
, there exists a negligible function  such that for all
such that for all  , and
, and  ,
, 
where the probabilities are over the randomness of \(\mathsf {Gen} \) and
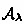 .
.
When  , we say that the TLP is polynomially-hard.
, we say that the TLP is polynomially-hard.
In the above definition, we assume for simplicity that the solutions s are  -bits long. We can naturally generalize this to consider the case where solutions have some specified length
-bits long. We can naturally generalize this to consider the case where solutions have some specified length  . We emphasize that the notion of B-hardness above suffices to capture both polynomial security and sub-exponential security, as it captures hardness against adversaries of size
. We emphasize that the notion of B-hardness above suffices to capture both polynomial security and sub-exponential security, as it captures hardness against adversaries of size  , up to polynomial factors.
, up to polynomial factors.
Non-malleable Time-Lock Puzzles. To formalize non-malleability in the context of time-lock puzzles, we introduce a Man-In-the-Middle (MIM) adversary. Because time-lock puzzles are designed to be broken in some depth t, we restrict our MIM adversary to have at most depth  for a function \(\alpha \) denoting the advantage of the adversary. Furthermore, we allow for concurrent MIM adversaries that possibly interact with many senders and receivers at the same time.
for a function \(\alpha \) denoting the advantage of the adversary. Furthermore, we allow for concurrent MIM adversaries that possibly interact with many senders and receivers at the same time.
Definition 3.2
(MIM Adversaries). Let \(n_L, n_R, B_{\mathsf {nm}},\alpha ,T :\mathbb {N} \rightarrow \mathbb {N} \). An \((n_L , n_R , B_{\mathsf {nm}},\alpha ,T)\)-Man-In-the-Middle (MIM) adversary is a non-uniform algorithm  satisfying
satisfying  and
and  for all
for all  that receives
that receives  puzzles on the left and outputs
puzzles on the left and outputs  puzzles on the right.
puzzles on the right.
We next define the MIM distribution, which corresponds to the values underlying the puzzles output by the MIM adversary. To capture adversaries that simply forward one of the puzzles on the left to a receiver on the right, we set the value for any forwarded puzzle to be \(\bot \).
Definition 3.3
(MIM Distribution]).Let \(n_L, n_R, B_{\mathsf {nm}},\alpha ,T :\mathbb {N} \rightarrow \mathbb {N} \). Let  be an \((n_L,n_R,B_{\mathsf {nm}},\alpha ,T)\)-MIM adversary. For any
be an \((n_L,n_R,B_{\mathsf {nm}},\alpha ,T)\)-MIM adversary. For any  and
and  , we define the distribution
, we define the distribution

as follows.  receives puzzles
receives puzzles  for all
for all  and outputs puzzles
and outputs puzzles  . Then for each
. Then for each  , we define
, we define

Intuitively, a time-lock puzzle is non-malleable if the MIM distribution of a bounded depth attacker does not depend on the solutions underlying the puzzles it receives on the left. We formalize this definition below.
Definition 3.4
(Concurrent Non-malleable). Let \(n_L, n_R, B_{\mathsf {nm}} :\mathbb {N} \rightarrow \mathbb {N} \). A time-lock puzzle is \((n_{L},n_{R})\)-concurrent non-malleable against adversaries of size \(B_{\mathsf {nm}}\) if there exists a positive polynomial \(\alpha \) such that for every function T with  for all
for all  , and every \((n_{L},n_{R},B_{\mathsf {nm}},\alpha ,T)\)-MIM adversary
, and every \((n_{L},n_{R},B_{\mathsf {nm}},\alpha ,T)\)-MIM adversary  , the following holds.
, the following holds.
For any distinguisher \(\mathcal {D} \), there exists a negligible function  such that for all
such that for all  and
and  ,
,

When  , we say the TLP is \((n_{L},n_{R})\)-concurrent non-malleable. When this only holds against non-uniform PPT distinguishers \(\mathcal {D} \), we say that the time-lock puzzle is computationally \((n_{L},n_{R})\)-concurrent non-malleable.
, we say the TLP is \((n_{L},n_{R})\)-concurrent non-malleable. When this only holds against non-uniform PPT distinguishers \(\mathcal {D} \), we say that the time-lock puzzle is computationally \((n_{L},n_{R})\)-concurrent non-malleable.
Relation to Non-malleable Commitments. When defining non-malleability for TLPs, a natural attempt is to view TLPs as commitments, and give a definition analogous to non-malleable commitments. This is usually formalized as either non-malleability with respect to commitment, or non-malleability with respect to extraction. The former notion requires that no man-in-the-middle adversary can maul a commitment z to s into a commitment \(\widetilde{z} \) whose unique underlying value is related to s, whereas the latter notion requires that \(\mathcal {E} (\widetilde{z})\) is unrelated to s, where \(\mathcal {E} \) is a given extractor. When \(\mathcal {E} \) has the guarantee that it outputs the committed value on valid commitments and \(\bot \) on invalid ones, these notions are equivalent. However, when considering extractors that may output arbitrary values when given invalid commitments, these notions are incomparable in general. In the context of time-lock puzzles, we observe that \(\mathsf {Sol} \) is the natural extractor for \(\mathsf {Gen} \), and moreover that non-malleability should capture adversaries that maul a puzzle into one that solves to a related value. Therefore, our definition above is analogous to non-malleability with respect to extraction, where \(\mathsf {Sol} \) is the extractor.
Next, we consider standard variants for the definition of non-malleable above.
Definition 3.5
We say the a TLP satisfies the following non-malleability properties when Definition 3.4 holds against \((n_L, n_R, B_{\mathsf {nm}}, \alpha , T)\)-MIM adversaries for the following settings of \(n_L\) and \(n_R\):
-
fully concurrent non-malleable if the definition holds against any
 ,
, -
one-many non-malleable if the definition holds for any
 and \(n_{L} = 1\),
and \(n_{L} = 1\), -
n-concurrent non-malleable if the definition holds for \(n_{L} = n_{R} = n\),
-
one-n non-malleable for
 and \(n_R = n\),
and \(n_R = n\), -
and simply non-malleable (not concurrent) for
 .
.
4 Non-malleable Time-Lock Puzzles
We start by defining the notion of functional non-malleability for time-lock puzzles. Then, we give the transformation from any time-lock puzzle to one that satisfies concurrent functional non-malleability for depth bounded functions, in the auxiliary input random oracle model, and discuss how this result implies a time-lock puzzle satisfying bounded concurrent (standard) non-malleability.
Functional Non-malleability. In the following definition, we focus on the case of unbounded concurrency, but note that can be defined for restricted cases as in Definition 3.5.
Definition 4.1
(Concurrent Functional Non-malleable). Let \(B_{\mathsf {nm}}, L : \mathbb {N} \rightarrow \mathbb {N} \), and \((\mathsf {Gen},\mathsf {Sol})\) be a time-lock puzzle for messages of length  . Let \(\mathcal {F} \) be a class of functions of the form
. Let \(\mathcal {F} \) be a class of functions of the form  . We say that \((\mathsf {Gen}, \mathsf {Sol})\) is concurrent functional non-malleable for \(\mathcal {F} \) against \(B_{\mathsf {nm}}\)-size adversaries if for any function \(f \in \mathcal {F} \) and polynomial n, there exists a polynomial \(\alpha \) such that for every function T with
. We say that \((\mathsf {Gen}, \mathsf {Sol})\) is concurrent functional non-malleable for \(\mathcal {F} \) against \(B_{\mathsf {nm}}\)-size adversaries if for any function \(f \in \mathcal {F} \) and polynomial n, there exists a polynomial \(\alpha \) such that for every function T with  for all \(\lambda \in \mathbb {N} \), every \((n,n,B_{\mathsf {nm}},\alpha ,T)\)-MIM adversary
for all \(\lambda \in \mathbb {N} \), every \((n,n,B_{\mathsf {nm}},\alpha ,T)\)-MIM adversary  , the following holds.
, the following holds.
For any distinguisher \(\mathcal {D} \), there exists a negligible function  such that for all \(\lambda \in \mathbb {N} \) and
such that for all \(\lambda \in \mathbb {N} \) and  ,
,

When \(B_{\mathsf {nm}}(\lambda ) = 1\), we say the TLP is concurrent functional non-malleable for \(\mathcal {F} \). When the above only holds against non-uniform PPT distinguishers \(\mathcal {D} \), we say the TLP is computationally functional non-malleable for \(\mathcal {F} \).
We note that functional non-malleability for a class \(\mathcal {F} \) that contains the identity function \(\mathsf {id} \) implies standard non-malleability as \(\mathcal {D} (\mathsf {id} (\vec {\widetilde{s}})) = \mathcal {D} (\vec {\widetilde{s}})\).
4.1 Non-malleable Time-Lock Puzzle Construction
In this section, we give our construction of a fully concurrent functional non-malleable time-lock puzzle for functions with bounded depth and output length. We rely on the following building blocks and parameters.
-
A function m denoting the output length for our function non-malleability. We require
 . Throughout this section, where \(\lambda \) is clear from context, we let \(m = m(\lambda )\).
. Throughout this section, where \(\lambda \) is clear from context, we let \(m = m(\lambda )\). -
A \(B_{\mathsf {tlp}}\)-hard time-lock puzzle \(\mathsf {TLP} = (\mathsf {Gen} _{\mathsf {tlp}},\mathsf {Sol} _{\mathsf {tlp}})\) for \(B_{\mathsf {tlp}}(\lambda ) = 2^{3m}\). We let
 be the bits of randomness needed for \(\mathsf {TLP} \) on security parameter \(\lambda \), for solutions of length \(2m+2\lambda \).
be the bits of randomness needed for \(\mathsf {TLP} \) on security parameter \(\lambda \), for solutions of length \(2m+2\lambda \). -
A class of functions \(\mathcal {F} _{m}\) of the form
 . We assume that there exists a polynomial d such that for every polynomial n, every function \(f \in \mathcal {F} _{m}\) can be computed in depth \(d(\lambda ,\log n(\lambda ))\) and polynomial size on inputs of length at most \(\lambda \cdot n(\lambda )\).
. We assume that there exists a polynomial d such that for every polynomial n, every function \(f \in \mathcal {F} _{m}\) can be computed in depth \(d(\lambda ,\log n(\lambda ))\) and polynomial size on inputs of length at most \(\lambda \cdot n(\lambda )\). -
A random oracle
 , where \(\mathcal {O} \) on input
, where \(\mathcal {O} \) on input  outputs a random value
outputs a random value  .
.
Our construction  in the random oracle model:
in the random oracle model:
-
 :
: -
1.
Get \(r' = \mathcal {O} (s,r)\).
-
2.
Output
 .
.
-
1.
-
 :
: -
1.
Compute
 and parse \(s ' = s || r\).
and parse \(s ' = s || r\). -
2.
If
 , output \(s \).
, output \(s \). -
3.
If not, output \(\bot \).
-
1.
Theorem 4.2
(Fully Concurrent Functional Non-Malleable TLPs). Let  , \(B_{\mathsf {hard}} (\lambda ) = 2^{m(\lambda )}\), and \(B_{\mathsf {tlp}} (\lambda ) = 2^{3m(\lambda )}\). Assuming \(\mathsf {TLP} \) is a \(B_{\mathsf {tlp}} \)-hard time-lock puzzle, then \(\mathsf {nmTLP} _{m}\) is a \(B_{\mathsf {hard}} \)-hard fully concurrent functional non-malleable time-lock puzzle in the AI-ROM for the class of functions \(\mathcal {F} _{m}\).
, \(B_{\mathsf {hard}} (\lambda ) = 2^{m(\lambda )}\), and \(B_{\mathsf {tlp}} (\lambda ) = 2^{3m(\lambda )}\). Assuming \(\mathsf {TLP} \) is a \(B_{\mathsf {tlp}} \)-hard time-lock puzzle, then \(\mathsf {nmTLP} _{m}\) is a \(B_{\mathsf {hard}} \)-hard fully concurrent functional non-malleable time-lock puzzle in the AI-ROM for the class of functions \(\mathcal {F} _{m}\).
We observe the following corollaries to the above theorem:
-
If \(m(\lambda ) \in O(\log (\lambda ))\) then we can simply assume a polynomially-hard TLP.
-
For any
 , our theorem follows by assuming a sub-exponentially secure TLP. Specifically, it suffices that there exists a constant \(\gamma \in (0,1)\) such that \(B_{\mathsf {tlp}} (\lambda ) = 2^{\lambda ^{\gamma }}\), and we can instantiate this with
, our theorem follows by assuming a sub-exponentially secure TLP. Specifically, it suffices that there exists a constant \(\gamma \in (0,1)\) such that \(B_{\mathsf {tlp}} (\lambda ) = 2^{\lambda ^{\gamma }}\), and we can instantiate this with  bits of randomness.
bits of randomness.
We also observe that the above theorem can be used to get n-bounded concurrency for any polynomial n, simply by setting the output length m of the functions in \(\mathcal {F} _{m}\) to \(\lambda \cdot n(\lambda )\). Specifically, let \(f_{\mathsf {id}}\) be the identity function with input and output length \(\lambda \cdot n(\lambda )\). Since \(f_{\mathsf {id}} \in \mathcal {F} _{\lambda \cdot n(\lambda )}\), a fully concurrent functional non-malleable TLP for \(\mathcal {F} _{\lambda \cdot n(\lambda )}\) implies an n-concurrent non-malleable TLP, which gives the following corollary.
Corollary 4.3
(n-Concurrent Non-Malleable TLPs). Let  , \(B_{\mathsf {hard}} (\lambda ) = 2^{\lambda \cdot n(\lambda )}\), and \(B_{\mathsf {tlp}} (\lambda ) = 2^{3\lambda \cdot n(\lambda )}\). Assuming \(\mathsf {TLP} \) is a \(B_{\mathsf {tlp}} \)-hard time-lock puzzle, then \(\mathsf {nmTLP} _{\lambda \cdot n(\lambda )}\) is a \(B_{\mathsf {hard}} \)-hard n-concurrent non-malleable time-lock puzzle in the AI-ROM.
, \(B_{\mathsf {hard}} (\lambda ) = 2^{\lambda \cdot n(\lambda )}\), and \(B_{\mathsf {tlp}} (\lambda ) = 2^{3\lambda \cdot n(\lambda )}\). Assuming \(\mathsf {TLP} \) is a \(B_{\mathsf {tlp}} \)-hard time-lock puzzle, then \(\mathsf {nmTLP} _{\lambda \cdot n(\lambda )}\) is a \(B_{\mathsf {hard}} \)-hard n-concurrent non-malleable time-lock puzzle in the AI-ROM.
The proof of Theorem 4.2 is deferred to the full version.
5 Applications to Multi-party Coin Flipping and Auctions
In this section, we discuss our fair multi-party protocols. We focus on the case of multi-party coin flipping and address auctions in Remark 1 below. We note that this section focuses on game-based fairness, and the extension to simulation security is given in the full version.
Our multi-party coin flipping protocol is based generically on any time-lock puzzle. Fairness follows when the time-lock puzzle satisfies concurrent functional non-malleability for the XOR function \(f_\oplus \). Specifically, in order to produce L bits of randomness, we need concurrent functional non-malleability for the function  that on input \((r_1,\ldots , r_n)\) outputs \(\bigoplus _{r_i \not = \bot } r_i\). Our protocol satisfies various additional properties, depending on the time-lock puzzle:
that on input \((r_1,\ldots , r_n)\) outputs \(\bigoplus _{r_i \not = \bot } r_i\). Our protocol satisfies various additional properties, depending on the time-lock puzzle:
-
Given a publicly verifiable time-lock puzzle, the resulting protocol is publicly verifiable. In this setting, our protocol can either be made interactive, or non-interactive.
-
If the time-lock puzzle is not publicly verifiable, the resulting protocol is non-interactive, and does not achieve public verifiability.
In what follows, we present our results in the public verifiability setting, and discuss differences with the non-publicly verifiable setting when relevant.
We describe our protocol in a public bulletin board model, where any party may “publish” a message that all other parties will see within some fixed time. Our protocol consists four phases: a commit phase, open phase, force open phase, and output phase. The commit and open phases consist of a single synchronous round of communication where all participating parties publish a message on the bulletin board. The force open phase can be computed by any party, and only needs to be computed by a single (honest) party if the underlying time-lock puzzle is publicly verifiable. Once all puzzles have been opened (or force opened), any party can run the output phase to get the output of the protocol. In the non-interactive version of the protocol, the open phase is omitted and every party runs the force open phase themselves, and uses the resulting values to compute the output of the protocol locally. When we refer to an honest participant, we mean a party that runs the protocol as specified, independent of all other participants.
For any \(L :\mathbb {N} \rightarrow \mathbb {N} \), let  be a publicly verifiable time-lock puzzle (in the ABO string model) with message length \(L(\lambda )\) that satisfies concurrent functional non-malleability for the function \(f_\oplus \) (which has output length \(L(\lambda )\)). We additionally let \(\alpha (\lambda )\) be the advantage of any attacker guaranteed by the functional non-malleability of the time-lock puzzle. The protocol takes as common input a security parameter \(\lambda \) and a polynomial time bound \(t = T(\lambda )\) that satisfies the following requirements. First, we require that the commit phase takes time less than \(T(\lambda ) / \alpha (\lambda )\) such that functional non-malleability (and hence hardness) are preserved during the protocol. At the same time, the commit phase needs to be long enough so that all participants can generate and publish their puzzles.
be a publicly verifiable time-lock puzzle (in the ABO string model) with message length \(L(\lambda )\) that satisfies concurrent functional non-malleability for the function \(f_\oplus \) (which has output length \(L(\lambda )\)). We additionally let \(\alpha (\lambda )\) be the advantage of any attacker guaranteed by the functional non-malleability of the time-lock puzzle. The protocol takes as common input a security parameter \(\lambda \) and a polynomial time bound \(t = T(\lambda )\) that satisfies the following requirements. First, we require that the commit phase takes time less than \(T(\lambda ) / \alpha (\lambda )\) such that functional non-malleability (and hence hardness) are preserved during the protocol. At the same time, the commit phase needs to be long enough so that all participants can generate and publish their puzzles.
-
Commit phase: Each participant i samples
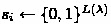 and
and  , computes
, computes 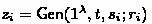 , and publishes \(z_i\) and \(\mathsf {crs} _i\). Let \(\mathsf {mcrs} = (\mathsf {crs} _1,\ldots , \mathsf {crs} _n)\). Any puzzle that is a copy of a previously posted puzzle is ignored.
, and publishes \(z_i\) and \(\mathsf {crs} _i\). Let \(\mathsf {mcrs} = (\mathsf {crs} _1,\ldots , \mathsf {crs} _n)\). Any puzzle that is a copy of a previously posted puzzle is ignored. -
Open phase: Each participant i that published in the commit phase publishes the solution \(s_i\) and with an opening \(r_i\).
-
Force open phase: For each puzzle \(z_j\), if either (a) there is no published solution \(s_j\) and opening \(r_j\) or (b) if
 , compute and publish
, compute and publish  (where \(s_j\) might be \(\bot \)).
(where \(s_j\) might be \(\bot \)). -
Output phase: If for every puzzle \(z_j\) and solution \(s_j\), either (a) there is a published opening \(r_j\) such that
 or (b) a published proof \(\pi _j\) such that
or (b) a published proof \(\pi _j\) such that  , then output \(s = \bigoplus _{s_j \not = \bot } s_j\).
, then output \(s = \bigoplus _{s_j \not = \bot } s_j\).
We note that the protocol above does not assume an a priori bound on the number of participants. Furthermore, there is no external setup needed by the protocol. All participants, however, do publish a random string  that can be used to implement the ABO-string model for
that can be used to implement the ABO-string model for  .
.
Theorem 5.1
Let  . Assume the existence of a publicly verifiable time-lock puzzle for \(L(\lambda )\) bit messages in the ABO-string model that satisfies concurrent function non-malleability for \(f_\oplus \) with \(L(\lambda )\) bit output. Then, there exists a multi-party coin flipping protocol that outputs \(L(\lambda )\) bits and satisfies optimistic efficiency, fairness, and public verifiability. The protocol supports an unbounded number of participants and requires no adversary-independent trusted setup.
. Assume the existence of a publicly verifiable time-lock puzzle for \(L(\lambda )\) bit messages in the ABO-string model that satisfies concurrent function non-malleability for \(f_\oplus \) with \(L(\lambda )\) bit output. Then, there exists a multi-party coin flipping protocol that outputs \(L(\lambda )\) bits and satisfies optimistic efficiency, fairness, and public verifiability. The protocol supports an unbounded number of participants and requires no adversary-independent trusted setup.
We obtain the following result by using our publicly verifiable non-malleable TLP construction (given in the full version) with the above theorem.
Corollary 5.2
Let \(B,L :\mathbb {N} \rightarrow \mathbb {N} \) where \(B(\lambda ) = 2^{3L(\lambda )}\). Assuming the B-repeated squaring assumption for \(\mathsf {RSWGen}\), there exists a multi-party coin flipping protocol that outputs \(L(\lambda )\) bits and satisfies optimistic efficiency, fairness, and public verifiability. The protocol supports an unbounded number of participants and requires no adversary-independent trusted setup. Security is proven in the auxiliary-input random oracle model.
Finally, we note that if we instead start with our non-malleable time-lock puzzle in the plain model (which is not publicly verifiable) the non-interactive variant of our protocol gives non-interactive coin flipping in the plain model. In particular, we obtain the following theorem based on our plain model construction (given in the full version).
Theorem 5.3
Let \(L :\mathbb {N} \rightarrow \mathbb {N} \) and \(S(\lambda ) = 2^{\lambda +L(\lambda )}\). Assume a time-lock puzzle, a keyless multi-collision resistant hash function, a non-interactive witness indistinguishable proof for \(\mathsf {NP}\), and injective one-way functions, all sub-exponentially secure, where in particular the time-lock puzzle is secure against polynomial-depth adversaries of size S. Then, there exist fully non-interactive fair multi-party coin flipping protocol that outputs \(L(\lambda )\) bits, where fairness holds against non-uniform polynomial time distinguishers. The protocol supports an unbounded number of participants and requires no setup.
We note that if we only consider protocols that output \(L(\lambda ) \in O(\log \lambda )\) bits, then fairness against polynomial time distinguishers implies statistical fairness. This is because if there is an unbounded distinguisher for \(O(\log \lambda )\) bits, we can construct a polynomial time distinguisher that simply hard codes the truth table of the unbounded distinguisher.
We remark how we can adapt our protocol to deal with auctions.
Remark 1 (Multi-Party Auctions)
For our application to auctions, we consider a standard second-price, sealed-bid auction, in which the auctioned item is assigned to the highest bidder who pays the second highest bid for the item. We assume some form of authenticated channels so we can know the bidders’ identities in order to distribute the auctioned items. We leave these as external implementation details for the protocol. The main protocol proceeds as follows.
In the commit phase, each participant computes a time-lock puzzle to their bid. The open and force open phases are identical to the case of coin flipping. Then in the output phase, we need to determine the identity of the highest bidder and the value of the second highest bid.
The function that computes the output consists of finding the top two values in a set. This can be computed in low depth (doing a tree of comparisons in parallel) and has output length \(\log n + \log M\) where n is the number of participants and M is a bound on the largest valid bid. Thus, using our publicly verifiable time-lock puzzle that satisfies concurrent functional non-malleability for this function, the resulting protocol is secure assuming  security for the repeated squaring assumption. Assuming n and M are polynomially bounded, we only need polynomial security assumptions.
security for the repeated squaring assumption. Assuming n and M are polynomially bounded, we only need polynomial security assumptions.
The proof of Theorem 5.1 is deferred to the full version.
Notes
- 1.
- 2.
The puzzle of [45] for a message s and difficulty T is a tuple \((g,N,T, s\oplus g^{2^T}\bmod N)\), where N is an RSA group modulus and g is a random element from \(\mathbb Z_N\). The puzzle is trivially malleable since the message is one-time padded.
- 3.
In the context of coin flipping, if a malicious party aborts prematurely, this can bias the output [13] causing the fairness issue mentioned above. Boneh and Naor [9] used timed primitives and interaction to circumvent the issue in the two-party case, but we care about the multi-party case and prefer to avoid interaction as much as possible.
- 4.
We note that our construction is conceptually similar to the Fujisaki-Okamoto (FO) transformation [21] used to generically transform any CPA-secure public-key encryption scheme into a CCA-secure one using a random oracle. However, since our setting and required guarantees are different, the actual proof turns out to be much more delicate and challenging.
- 5.
As we discuss in the Sect. 1.3, concurrent works allow the distinguisher to be bounded depth.
- 6.
Our ABO-string model is a variant of the multi-string model of Groth and Ostrovsky [25], where it is assumed that a majority of the public parameters are honestly generated.
- 7.
For this, we assume that sampling uniformly random safe primes can be done efficiently; this is a pretty common assumption, see [48] for more details.
- 8.
It is possible to make this protocol maliciously secure using concurrent non-malleable zero-knowledge proofs [2, 32, 34, 38], proving that each party acted honestly, but this (1) makes the construction significantly less efficient, and (2) requires either trusted setup and additional hardness assumptions, or additional rounds of interaction.
- 9.
References
Barak, B.: Constant-round coin-tossing with a man in the middle or realizing the shared random string model. In: 43rd Symposium on Foundations of Computer Science FOCS, pp. 345–355 (2002)
Barak, B., Prabhakaran, M., Sahai, A.: Concurrent non-malleable zero knowledge. In: 47th Annual IEEE Symposium on Foundations of Computer Science (FOCS), pp. 345–354 (2006)
Baum, C., David, B., Dowsley, R., Nielsen, J.B., Oechsner, S.: Craft: composable randomness and almost fairness from time. Cryptology ePrint Archive, Report 2020/784 (2020). https://eprint.iacr.org/2020/784
Baum, C., David, B., Dowsley, R., Nielsen, J.B., Oechsner, S.: TARDIS: a foundation of time-lock puzzles in UC. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021. LNCS, vol. 12698, pp. 429–459. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77883-5_15
Bentov, I., Pass, R., Shi, E.: Snow white: provably secure proofs of stake. IACR Cryptol. ePrint Arch. 2016, 919 (2016)
Bitansky, N., Goldwasser, S., Jain, A., Paneth, O., Vaikuntanathan, V., Waters, B.: Time-lock puzzles from randomized encodings. In: ITCS (2016)
Boneh, D., Bonneau, J., Bünz, B., Fisch, B.: Verifiable delay functions. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10991, pp. 757–788. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96884-1_25
Boneh, D., Bünz, B., Fisch, B.: A survey of two verifiable delay functions. IACR Cryptol. ePrint Arch. 2018, 712 (2018)
Boneh, D., Naor, M.: Timed commitments. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 236–254. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44598-6_15
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: FOCS, pp. 136–145. IEEE Computer Society (2001)
Ciampi, M., Ostrovsky, R., Siniscalchi, L., Visconti, I.: Concurrent non-malleable commitments (and more) in 3 rounds. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 270–299. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_10
Ciampi, M., Ostrovsky, R., Siniscalchi, L., Visconti, I.: Four-round concurrent non-malleable commitments from one-way functions. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 127–157. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_5
Cleve, R.: Limits on the security of coin flips when half the processors are faulty (extended abstract). In: Proceedings of the 18th Annual ACM Symposium on Theory of Computing, STOC, pp. 364–369 (1986)
Coretti, S., Dodis, Y., Guo, S., Steinberger, J.: Random oracles and non-uniformity. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 227–258. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_9
Dachman-Soled, D., Komargodski, I., Pass, R.: Non-malleable codes for bounded parallel-time tampering. In: Malkin, T., Peikert, C. (eds.) CRYPTO 2021. LNCS, vol. 12827, pp. 535–565. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-84252-9_18
Daian, P., Pass, R., Shi, E.: Snow White: robustly reconfigurable consensus and applications to provably secure proof of stake. In: Goldberg, I., Moore, T. (eds.) FC 2019. LNCS, vol. 11598, pp. 23–41. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-32101-7_2
David, B., Gaži, P., Kiayias, A., Russell, A.: Ouroboros praos: an adaptively-secure, semi-synchronous proof-of-stake blockchain. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 66–98. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_3
Dolev, D., Dwork, C., Naor, M.: Non-malleable cryptography (extended abstract). In: Proceedings of the 23rd Annual ACM Symposium on Theory of Computing, STOC, pp. 542–552 (1991)
Ephraim, N., Freitag, C., Komargodski, I., Pass, R.: Continuous verifiable delay functions. IACR Cryptol. ePrint Arch. 2019, 619 (2019)
Fuchsbauer, G., Kiltz, E., Loss, J.: The algebraic group model and its applications. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 33–62. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_2
Fujisaki, E., Okamoto, T.: Secure integration of asymmetric and symmetric encryption schemes. J. Cryptol. 26(1), 80–101 (2013)
Goyal, V.: Constant round non-malleable protocols using one way functions. In: Fortnow, L., Vadhan, S.P. (eds.) Proceedings of the 43rd ACM Symposium on Theory of Computing, STOC, pp. 695–704 (2011)
Goyal, V., Lee, C., Ostrovsky, R., Visconti, I.: Constructing non-malleable commitments: a black-box approach. In: 53rd Annual IEEE Symposium on Foundations of Computer Science, FOCS, pp. 51–60 (2012)
Goyal, V., Pandey, O., Richelson, S.: Textbook non-malleable commitments. In: Proceedings of the 48th Annual ACM SIGACT Symposium on Theory of Computing, STOC, pp. 1128–1141 (2016)
Groth, J., Ostrovsky, R.: Cryptography in the multi-string model. J. Cryptol. 27(3), 506–543 (2014)
Hohenberger, S., Myers, S., Pass, R., Shelat, A.: An overview of ANONIZE: a large-scale anonymous survey system. IEEE Secur. Priv. 13(2), 22–29 (2015)
Kalai, Y.T., Khurana, D.: Non-interactive non-malleability from quantum supremacy. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 552–582. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_18
Katz, J., Loss, J., Xu, J.: On the security of time-lock puzzles and timed commitments. In: Pass, R., Pietrzak, K. (eds.) TCC 2020. LNCS, vol. 12552, pp. 390–413. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64381-2_14
Khurana, D.: Round optimal concurrent non-malleability from polynomial hardness. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10678, pp. 139–171. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_5
Khurana, D., Sahai, A.: How to achieve non-malleability in one or two rounds. In: 58th IEEE Annual Symposium on Foundations of Computer Science, FOCS, pp. 564–575 (2017)
Lin, H., Pass, R.: Non-malleability amplification. In: Proceedings of the 41st Annual ACM Symposium on Theory of Computing, STOC, pp. 189–198 (2009)
Lin, H., Pass, R.: Constant-round non-malleable commitments from any one-way function. In: Proceedings of the 43rd ACM Symposium on Theory of Computing, STOC, pp. 705–714 (2011)
Lin, H., Pass, R., Soni, P.: Two-round and non-interactive concurrent non-malleable commitments from time-lock puzzles. In: 58th IEEE Annual Symposium on Foundations of Computer Science, FOCS, pp. 576–587. IEEE Computer Society (2017)
Lin, H., Pass, R., Tseng, W.-L.D., Venkitasubramaniam, M.: Concurrent non-malleable zero knowledge proofs. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 429–446. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_23
Lin, H., Pass, R., Venkitasubramaniam, M.: Concurrent non-malleable commitments from any one-way function. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 571–588. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_31
Malavolta, G., Thyagarajan, S.A.K.: Homomorphic time-lock puzzles and applications. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11692, pp. 620–649. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26948-7_22
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen ciphertext attacks. In: STOC, pp. 427–437. ACM (1990)
Ostrovsky, R., Pandey, O., Visconti, I.: Efficiency preserving transformations for concurrent non-malleable zero knowledge. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 535–552. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_32
Pandey, O., Pass, R., Vaikuntanathan, V.: Adaptive one-way functions and applications. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 57–74. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_4
Pass, R., Rosen, A.: Concurrent non-malleable commitments. In: 46th Annual IEEE Symposium on Foundations of Computer Science (FOCS), pp. 563–572 (2005)
Pass, R., Rosen, A.: New and improved constructions of non-malleable cryptographic protocols. In: Proceedings of the 37th Annual ACM Symposium on Theory of Computing, STOC, pp. 533–542 (2005)
Pass, R., Rosen, A.: Concurrent nonmalleable commitments. SIAM J. Comput. 37(6), 1891–1925 (2008)
Pass, R., Wee, H.: Constant-round non-malleable commitments from sub-exponential one-way functions. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 638–655. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_32
Pietrzak, K.: Simple verifiable delay functions. In: 10th Innovations in Theoretical Computer Science Conference, ITCS, pp. 60:1–60:15 (2019)
Rivest, R.L., Shamir, A., Wagner, D.A.: Time-lock puzzles and timed-release crypto,: technical report. Massachusetts Institute of Technology, Cambridge, MA, USA (1996)
Rotem, L., Segev, G.: Generically speeding-up repeated squaring is equivalent to factoring: sharp thresholds for all generic-ring delay functions. In: Micciancio, D., Ristenpart, T. (eds.) CRYPTO 2020. LNCS, vol. 12172, pp. 481–509. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-56877-1_17
Unruh, D.: Random oracles and auxiliary input. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 205–223. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_12
Von Zur Gathen, J., Shparlinski, I.E.: Generating safe primes. J. Math. Cryptol. 7(4), 333–365 (2013)
Wee, H.: Black-box, round-efficient secure computation via non-malleability amplification. In: FOCS (2010)
Wesolowski, B.: Efficient verifiable delay functions. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11478, pp. 379–407. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_13
Acknowledgements
This work was supported in part by NSF Award SATC-1704788, NSF Award RI-1703846, NSF Award DGE-1650441, AFOSR Award FA9550-18-1-0267, DARPA Award HR00110C0086, and a JP Morgan Faculty Award. Ilan Komargodski is supported in part by an Alon Young Faculty Fellowship and by an ISF grant (No. 1774/20). This research is based upon work supported in part by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), via 2019-19-020700006. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies, either expressed or implied, of ODNI, IARPA, or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for governmental purposes notwithstanding any copyright annotation therein.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Discussion of Non-malleable Definitions
A Discussion of Non-malleable Definitions
We briefly discuss the different notions of non-malleability studied in this work. Specifically, we compare standard non-malleability (Definition 3.4), non- malleability against depth-bounded distinguishers, and functional non-malleability (Definition 4.1). In Sect. 1.3, we also discuss the definitions considered in the concurrent works of [3, 4, 28].
Common to all of our definitions, there is a depth-bounded man-in-the-middle (MIM) attacker, which we call \(\mathcal {A}\), that on input a puzzle z with solution s tries to output a different puzzle \(\tilde{z}\) to a related value \(\tilde{s}\). Here, \(\mathcal {A}\) is depth-bounded relative to the difficulty of the puzzle, so it should not be able to solve the puzzle. The definitions vary in what it means for \(\tilde{s}\) to be “related” to s. For our standard notion of non-malleability, we require that no unbounded distinguisher \(\mathcal {D} \) on input \(\tilde{s}\) can tell if it came from the experiment starting with s or the all-zero string. In the definition of non-malleability against depth-bounded distinguishers, \(\mathcal {D} \) is restricted to be depth-bounded in the same way as \(\mathcal {A}\). In the case of functional non-malleability, the (unbounded) distinguisher \(\mathcal {D} \) receives instead as input \(f(\tilde{s})\) where f is a low-depth function. We parameterize functional non-malleability by an output length m. When \(m = |s|\), this captures plain non-malleability by considering f to be the identity function. When \(m = 1\), this captures depth-bounded distinguisher non-malleability as f essentially plays the role of the depth-bounded distinguisher \(\mathcal {D} \). In Theorem 4.2, we show how to construct a time-lock puzzle satisfying functional non-malleability for any output length m assuming a time-lock puzzle that is  secure.
secure.
When considering concurrent non-malleability, the MIM attacker \(\mathcal {A}\) receives possibly multiple puzzles \(z_1,\ldots , z_{n_L}\) that have solutions \(s_1,\ldots , s_{n_L}\) as input and tries to output multiple puzzles \(\tilde{z}_1, \ldots , \tilde{z}_{n_R}\) (different from its inputs) corresponding to \(\tilde{s}_1, \ldots , \tilde{s}_{n_R}\). In the most general form, we can consider some distinguisher \(\mathcal {D} \) that receives as input \(f(\tilde{s}_1,\ldots , \tilde{s}_{n_R})\) and tries to tell if it came from the experiment starting with \(s_1,\ldots , s_{n_L}\) or with \(n_{L}\) all-zero strings. We show in the full version that if the MIM attacker can encode a time-lock puzzle into the value \(f(\tilde{s}_1,\ldots , \tilde{s}_{n_R})\) (where f may be the identity), then the construction cannot be secure against an unbounded distinguisher. In particular, if the function’s output length m is greater than the output length of the time-lock puzzle, the scheme may not be secure. On the other hand, our construction of Theorem 4.2 works for functional non-malleability even in the fully concurrent setting, as the output length of f is bounded. So, as long as the output length of the function f is sufficiently small, we can support unbounded concurrency.
Finally, our separation in the full version gives a construction that satisfies plain (non-concurrent) non-malleability against depth-bounded distinguishers yet does not satisfy non-malleability against unbounded distinguishers. We remark that in the setting where the message length for the puzzle is 1 bit, these notions are equivalent by simply considering the depth-bounded distinguisher that outputs the bit it gets as input. Moreover, it can be shown that they are equivalent as long as the message length is in \(O(\log \lambda )\). Therefore, this separation necessarily relies on the fact that the message length for the puzzle is in \(\omega (\log \lambda )\).
We summarize the various relationships between the definitions in Fig. 1.
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Freitag, C., Komargodski, I., Pass, R., Sirkin, N. (2021). Non-malleable Time-Lock Puzzles and Applications. In: Nissim, K., Waters, B. (eds) Theory of Cryptography. TCC 2021. Lecture Notes in Computer Science(), vol 13044. Springer, Cham. https://doi.org/10.1007/978-3-030-90456-2_15
Download citation
DOI: https://doi.org/10.1007/978-3-030-90456-2_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-90455-5
Online ISBN: 978-3-030-90456-2
eBook Packages: Computer ScienceComputer Science (R0)





 : A PPT algorithm that on input a security parameter
: A PPT algorithm that on input a security parameter  , a difficulty parameter
, a difficulty parameter  , outputs a puzzle
, outputs a puzzle  .
. : A deterministic algorithm that on input a security parameter
: A deterministic algorithm that on input a security parameter  , a difficulty parameter
, a difficulty parameter  , outputs a solution
, outputs a solution  .
. , solution
, solution  , and
, and  , it holds that
, it holds that  .
. ,
,  is computable in time
is computable in time  .
. satisfying
satisfying  ,
,  , and
, and  for all
for all  , there exists a negligible function
, there exists a negligible function  such that for all
such that for all  , and
, and  ,
, 
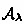 .
. ,
, and
and  and
and  .
. . Throughout this section, where
. Throughout this section, where  be the bits of randomness needed for
be the bits of randomness needed for  . We assume that there exists a polynomial d such that for every polynomial n, every function
. We assume that there exists a polynomial d such that for every polynomial n, every function  , where
, where  outputs a random value
outputs a random value  .
. :
:  .
. :
:  and parse
and parse  , output
, output  , our theorem follows by assuming a sub-exponentially secure TLP. Specifically, it suffices that there exists a constant
, our theorem follows by assuming a sub-exponentially secure TLP. Specifically, it suffices that there exists a constant  bits of randomness.
bits of randomness.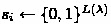 and
and  , computes
, computes 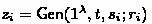 , and publishes
, and publishes  , compute and publish
, compute and publish  (where
(where  or (b) a published proof
or (b) a published proof  , then output
, then output 
