Separable Reversible Data Hiding Based on Integer Mapping and Multi-MSB Prediction for Encrypted 3D Mesh Models

Abstract

Extensive research has been conducted on image-based reversible data hiding in encrypted domain (RDH-ED) methods, but these methods cannot be directly applied to other cover medium, such as text, audio, video, and 3D mesh. With the widespread use of 3D mesh on the Internet, the use of 3D mesh as cover medium for RDH has gradually become a research topic. The main challenge of studying RDH based on 3D mesh is that the data structure of 3D mesh is complex and the geometric structure is irregular. In this paper, we propose a separable RDH-ED method based on integer mapping and multiple most significant bit (Multi-MSB) prediction. Firstly, all vertices of 3D mesh are divided into “embedded” set and “reference” set, and floating-point vertex values are mapped to integers. Then, sender calculates prediction error of the “embedded” set. Data hider embeds additional data by replacing the Multi-MSB of the encrypted vertex coordinates of the “embedded” set without prediction error. According to different permissions, legal recipients can obtain the original mesh, the additional data or both of them by using the proposed separable method. Experimental results prove that the proposed method outperforms state-of-the-art methods.

1 Introduction

Reversible data hiding (RDH) methods [1,2,3,4,5,6] can recover cover medium losslessly after extracting embedded data, and are widely used in military, medical, remote sensing, law enforcement and other sensitive fields. The classic RDH methods are mainly based on lossless compression [1, 2], difference expansion [3, 4] and histogram shifting [5, 6]. With the rapid development of cloud computing, the demand for privacy protection is growing. In order to store or share files safely, the original content is converted to unreadable ciphertext using encryption, and then additional data is embedded directly in the ciphertext. In some scenarios, it is vital to restore the original content losslessly after decrypting and extracting the additional data. This privacy protection scenario triggers RDH-ED to manage ciphertext data. RDH-ED methods can be mainly classified into two categories: vacating room after encryption (VRAE) [7,8,9] and reserving room before encryption (RRBE) [10, 11].

Zhang et al. [7] proposed a VRAE method for the first time. The encrypted image was divided into several non-overlapping blocks, and additional data was embedded by flipping the least significant bit (LSB) of the encrypted data. With the emergence of new application requirements in different scenarios, Zhang et al. [8] proposed a separable RDH-ED method for the first time. In this method, the least significant bit (LSB) of the encrypted image was losslessly compressed by a specific matrix multiplication, and the separability of data extraction and image restoration was realized. Compared with VRAE method, RRBE method has better performance in the accuracy of data extraction and image restoration. Ma et al. [10] first proposed RRBE method, which achieved data extraction error-free and lossless image restoration, and truly achieved reversibility. This method released a part of the original image by shifting the histogram, and embedded data by replacing the LSB of the encrypted pixel. Then, Puteaux et al. [11] predicted the MSB of the pixel, and embedded additional data through bit replacement according to the position indicator map.

Image-based RDH methods have been extensively studied, but these methods cannot be directly applied to other cover medium, such as text, audio, video and 3D mesh. Due to the wide application and huge inherent capacity of 3D mesh, 3D mesh was considered as a potential covering medium for RDH. At present, the research was still in its infancy, and many scientific and technological problems need to be solved. According to the literature, the existing RDH methods based on 3D model were mainly divided into four domains: spatial domain [12,13,14], transform domain [15], compressed domain [16] and encrypted domain [17,18,19].

The method in [17] was the first work on reversible data hiding in encrypted 3D mesh. Jiang et al. [17] flipped the LSBs of each vertex to embed one bit of data. The recipient used a smoothness estimation function for data extraction and mesh recovery. In order to improve the embedding capacity, Moshin et al. [18] proposed a two-layer embedding scheme based on homomorphic encryption. The sender of the first-tier used the histogram shifting to embed the additional data, and the second-tier cloud manager used the self-blind property of homomorphic encryption to embed the additional data into the marked encrypted mesh. However, due to the large ciphertext expansion and high computational complexity of Paillier cipher system, this method [18] was not efficient in practical application. Recently, Tsai et al. [19] used spatial coding technology with embedding threshold to embed additional data, and the embedding capacity has been improved. Due to the bit error rate in data extraction, the application of this method has certain limitations. In order to make full use of the model local correlation, we embedded additional data on the x-axis, y-axis, and z-axis of the vertices, replacing the n MSB bits of each coordinate axis with n bits of additional data. Compared with [17,18,19], the proposed method vacated more room for additional data embedding.

In this paper, we propose a separable RDH method for encrypted 3D mesh based on integer mapping and Multi-MSB prediction. The main contributions of this paper are as follows: (1) Multi-MSB embedding strategy is adopted to obtain higher embedding capacity. (2) By making full use of the correlation of adjacent vertices in natural mesh, the recipient can recover the Multi-MSB of the “embedded” vertex by Ring-prediction, so as to achieve lossless recovery mesh. (3) The proposed method can ensure the data extraction is error-free and separable, which is of great significance to privacy protection.

In this paper, Sect. 2 introduces the proposed method. Section 3 presents the analysis of experimental results. Section 4 concludes this paper and describes the future work.

2 Proposed Method

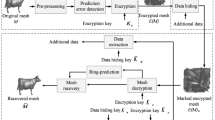
Figure 1 shows the framework of the proposed method. Firstly, the sender divides the original 3D mesh into “embedded” set and “reference” set. The sender analyzes the vertex information with prediction errors in the “embedded” set and records it as auxiliary information. The data hider uses the Multi-MSB bit replacement strategy to embed additional data into the encrypted 3D mesh E(M) , and can obtain the marked encrypted mesh E(M)w. According to different permissions, legal recipients can obtain the original mesh, the additional data or both of them by using the proposed separable method.

Fig. 1.

Framework of the proposed method.

2.1 Pre-processing

According to the suggestion of [20], sender can perform lossy compression in different application scenarios. According to the different precision m, the corresponding integer value is between $-10^{{m}}$ and $10^{{m}}$, where ${{m}}\in$[1, 33]. Normalizing floating point coordinates v$_{i,j}$ to integer coordinates $\bar{v}$ $_{i,j}$ as

$$\begin{aligned} {\bar{v}_{i,j}}=\lfloor {v_{i,j}}\times 10^{{m}}\rfloor , \end{aligned}$$

(1)

where i is the ith vertex, ${j}\in \{{x,y,z}\}$, v$_{i,j}$ is the original set of floating point vertices and $\bar{v}_{i,j}$ is the set of integer vertices.

Recipient can convert the processed integer coordinates back to floating point coordinates by Eq. (2).

$$\begin{aligned} {\hat{v}_{i,j}}={\bar{v}_{i,j}} / 10^{{m}}, \end{aligned}$$

(2)

the value of m corresponds to the bit-length l of integer coordinates as

$$\begin{aligned} {l} = \left\{ \begin{array}{ll} 8,\qquad \quad &{}{1\le {{m}} \le 2}\\ 16,\qquad \quad &{} {3\le {{m}} \le 4}\\ 32,\qquad \quad &{} {5\le {{m}} \le 9}\\ 64,\qquad \quad &{} {10\le {{m}} \le 33}. \end{array} \right. \end{aligned}$$

(3)

2.2 Prediction Error Detection

The “embedded” set ${s}_{e}$ is used to embed additional data, and the “reference” set ${s}_{n}$ is used to recover the mesh without modifying the vertices during the whole process. We traverse all the vertices contained in the face data in ascending order, and assume that ${F} = ({f}_1, {f}_2\ldots {f}_{M}$) represents the face data sequence, where f$_{i}$=(v$_{i,x}$, v$_{i,y}$, v$_{i,z}$), M is the number of face data. Assuming that f$_{n}$=(v$_{n,x}$, v$_{n,y}$, v$_{n,z}$) is the next face sequence to be traversed, and both ${s}_{e}$ and ${s}_{n}$ are initially 0. If there is no vertex in f$_{n}$ in ${s}_{e}$ or ${s}_{n}$, we choose the first vertex in f$_{n}$ to add f$_{n,x}$ to ${s}_{e}$, and add f$_{n,y}$ and f$_{n,z}$ to ${s}_{n}$. Figure 2 shows the close view of the Cow mesh and its vertex connections. The blue vertices in Fig. 2 are the “embedded” set vertices, the vertices marked in yellow are the “reference” vertices, and the red vertices are the vertices to be traversed.

Fig. 2.

The close view of Cow mesh and its vertex connection relationship. (Color figure online)

An example shows that when the m is 6, the process of selecting the maximum embedding length L without prediction error is as follows: we predict each bit of the prediction coordinates in the order of reference coordinates from MSB to LSB until a certain bit has prediction error. As shown in Fig. 3, the x coordinates of an “embedded” vertex numbered 1 has the MSB 0. The sender counts the number of 0 and 1 occurrences of the MSB of the “reference” vertex coordinates numbered 2, 3, 4, 5, 7, 8. If the number of 0s is greater than or equal to the number of 1s, the MSB of the “embedded” vertex coordinates numbered 1 is predicted to be 0. Then, the prediction of 2-MSB and 3-MSB are counted until the maximum embedding length k1 is found. According to Fig. 3, it can be found that the prediction error occurred in the bit prediction when embedding length is t1=17. Therefore, it can be concluded that the maximum embedding length t1 is 16 of x coordinates when the m is 6 on the Cow mesh. The maximum embedding length of vertex coordinate x is calculated as t1. Similarly, we calculate the maximum embedding length of vertex coordinate y, z axises as t2 and t3. At this time, the maximum embedding length of this vertex is min$\{{{t1}}, {{t2}}, {{t3}}\}$. In the data embedding stage, the final maximum embedding length L of the embedded vertex is the minimum embedding length of all “embedded” vertex coordinates. After the prediction error detection of the x-axis, y-axis and z-axis coordinates of the vertex coordinates, if n $\ge$ 1, we call vertex numbered 1 as the “embedded” vertex without prediction error in ${s}_{e}$. Otherwise, the vertex index information records as auxiliary information.

Fig. 3.

An example of prediction error detection for vertex 1 of Cow mesh.

2.3 Encryption

The sender uses Eq. (4) to convert the pre-processed vertex integer coordinates into binary.

$$\begin{aligned} {{b}_{i,j,u}}=\lfloor {\bar{v}_{i,j}}/ 2^{{u}}\rfloor \quad {mod}\quad 2,\qquad {{u}}=0, 1\ldots {{l}}-1, \end{aligned}$$

(4)

where $\lfloor .\rfloor$ is a floor function and ${l}\le {{i}}\le {{N}}$ and ${{j}}\in \{{{x,y,z}}\}$, the l of the coordinate can be obtained by Eq. (3).

The sender encrypts the bit stream of the original 3D mesh ${b}_{i,j,u}$ by stream cipher function generated pesudo-random bits ${c}_{i,j,u}$, and obtains the encrypted coordinate binary stream ${e}_{i,j,u}$.

$$\begin{aligned} {{e}_{i,j,u}}={{b}_{i,j,u}} \oplus {{c}_{i,j,u}}, \end{aligned}$$

(5)

where $\oplus$ stands for exclusive OR.

The encrypted mesh can be obtained by Eq. (6)

$$\begin{aligned} {{E}_{i,j}}=\sum _{u=0}^{l-1}{{e}_{i,j,u}} \times 10^{{m}}, \end{aligned}$$

(6)

where ${E}_{i,j}$ are the integral values of coordinates.

2.4 Data Hiding

The data hider first calculates ${s}_{e}$ and ${s}_{n}$, and embeds the data into the n-MSB of the vertices in ${s}_{e}$ without prediction error. The n-MSB of x, y, and z coordinates is replaced by n bits respectively. Finally, each vertex in ${s}_{e}$ uses Eq. (7) to embed 3n bits.

$$\begin{aligned} {{v_{i,j}}^{\prime \prime }}={s_{1}}\times 2^{{l}-1}+{s_{2}}\times 2^{{l}-2}+\ldots +{s_{n}}\times 2^{{l}-{n}}+{{v_{i,j}}^{\prime }}mod 2^{{l}-(n+1)}, \end{aligned}$$

(7)

where s$_{k}$ is additional data and ${l}\le {{k}} \le {n}$, n is embedding length and $1\le {{n}} \le {L}$, ${{v_{i,j}}^{\prime }}\in {{s}_{e}}$ is the vertex after pre-processing and encryption, ${v_{i,j}}^{\prime \prime }$ is the vertex of marked encrypted mesh.

2.5 Data Extraction and Mesh Recovery

Extraction with only Data Hiding Key. The n-MSB is extracted from the vertex coordinates of the ${s}_{e}$, and then the data hiding key Kw can be used to obtain the plaintext additional data.

$$\begin{aligned} {s_{k}} ={{v_{i,j}}^{\prime \prime }}/2^{l-k}, \qquad {1\le {k} \le n} \end{aligned}$$

(8)

where ${{v_{i,j}}^{\prime \prime }}\in {{s}_{e}}$ is vertex of the marked encrypted mesh.

Mesh Recovery with only Encryption Key. The recipient can recover the E(M)w to get the M with Encryption Key Ke. After mesh decryption and Ring-prediction, the M can be obtained.

The pseudorandom bits ${c}_{i,j,u}$ are generated by the encryption key Ke, and is used to perform XOR function with ${e}_{i,j,u}^{\prime \prime }$ to decrypt the E(M)w.

$$\begin{aligned} {{b}_{i,j,u}^{\prime \prime }}= {{e}_{i,j,u}^{\prime \prime }}\oplus {{c}_{i,j,u}}, \end{aligned}$$

(9)

where ${e}_{i,j,u}^{\prime \prime }$ is the binary stream of the marked encrypted mesh, ${b}_{i,j,u}^{\prime \prime }$ is the binary stream of the decrypted mesh with additional data and ${u}=0, 1\ldots {l}-1$.

After decrypting the E(M)w, since the ${s}_{n}$ has not been modified in the whole process, the coordinate value after decryption is the original coordinate value. In order to recover the coordinate values in the ${s}_{e}$, after decryption of the E(M)w, the recipient can predict the n-MSB of the embedded vertices by embedding the n-MSB of adjacent vertices around the vertices, which is called Ring-prediction.

Extraction and Mesh Recovery with both Keys. In this case, the recipient can extract the additional data and recover the original 3D mesh perfectly. Note that data extraction step needs to be performed before mesh restoration.

3 Experimental Results and Discussion

In this section, we analyze the embedding capacity and reversibility of the proposed method, and compare the performance with state-of-the-art methods [17,18,19]. The experimental environment is MATLAB R2018b. Four standard original meshes, Beetle, Mushroom, Mannequin, and Elephant are used to demonstrate the experimental performance. Two data sets used for performance evaluation are: The Princeton Shape Retrieval and Analysis Group¹ and The Stanford 3D Scanning Repository². In Sect. 3.1, we analyze the key indicator embedding capacity of the proposed method. In Sect. 3.2, Hausdorff distance and signal-to-noise ratio (SNR) are used to evaluate the geometric and visual quality of the proposed method, that is to evaluate reversibility. In Sect. 3.3, the performance comparison of the proposed method and the state-of-the-art methods is given. The additional data is a randomly generated 0/1 sequence.

3.1 Embedding Capacity

The embedding rate (ER) is defined as the ratio of the number of embedding bits to the number of vertices in the mesh model, that is, the number of bits per vertex (bpv). This section mainly discusses the impact on embedding rate under different m and embedding length n. Figure 4 show that when m takes a fixed value, with the increase of n, the embedding rate first increases and reaches the maximum embedding rate, and then shows a decreasing trend. Taking the Beetle as an example, when m = 2 and n = 5, the embedding rate is 3.70 bpv. When m = 3 and n = 8, the embedding rate is 7.74 bpv. When m = 5 and n = 17, the maximum embedding rate is 16.51 bpv. When m = 6 and n = 14, the embedding rate is 13.64 bpv, and the embedding rate shows a downward trend. Similarly, when m = 5 and n = 15, the maximum embedding rate of the Mushroom is 16.72 bpv. When m = 5 and n = 15, the maximum embedding rate of the Mannequin is 13.66 bpv. When m = 5 and n = 18, the maximum embedding rate of Elephant is 18.12 bpv.

Fig. 4.

The trend of embedding rate under different m and n on four test meshes.

3.2 Geometric and Visual Quality

For differences that cannot be distinguished by the naked eye, Hausdorff distance and SNR can be used to measure the geometric distortion. Hausdorff distance is defined as follows:

$$\begin{aligned} H(A,B)=max({h}(A,B),{h}(B,A)), \end{aligned}$$

(10)

$$\begin{aligned} {h}(A,B)=max({a}\in A)min({b}\in B) \parallel {a}-{b}\parallel , \end{aligned}$$

(11)

$$\begin{aligned} {h}(B,A)=max({b}\in B)min({a}\in A) \parallel {b}-{a}\parallel , \end{aligned}$$

(12)

where $\parallel .\parallel$ is the distance between point a of set A and point b of set B (such as L2), a and b are the number of elements in the set.

The signal-to-noise ratio (SNR) is defined as follows: SNR=

$$\begin{aligned} 10 \times \lg \frac{ \sum _{i=1}^{N} [(v_{i,x}-\overline{v}_x)^2+(v_{i,y}-\overline{v}_y)^2+(v_{i,z}-\overline{v}_z)^2]}{ \sum _{i=1}^{N} [(g_{i,x}-\overline{v}_x)^2+(g_{i,y}-\overline{v}_y)^2 +(g_{i,z}-\overline{v}_z)^2 ] }, \end{aligned}$$

(13)

where $\bar{v}_x$,$\bar{v}_y$,$\bar{v}_z$ are the averages of the mesh coordinates,$v_{i,x}$ ,$v_{i,y}$ ,$v_{i,z}$ are the original coordinates, g$_{i,x}$, g$_{i,y}$, g$_{i,z}$ are the modified mesh coordinates, N is the number of vertices.

Fig. 5.

The Hausdorff distance and SNR on different m under maximum embedding rate on four test meshes. (a) Hausdorff distance, (b) SNR.

Fig. 6.

Illustrative examples showing the appearance of the mesh of different stages when m = 5. From left to right is the original mesh, encrypted mesh, marked encrypted mesh and recovered mesh.

Figure 5(a) shows that with the increase of m, the recipient gets a higher quality recovered mesh. As shown in Fig. 5(b), as m increases, SNR gradually increases and tends to $\infty$, which indicates that the recovered meshes becomes higher. Thus, the proposed method achieves reversibility by adjusting m. Figure 6 shows the visual effects of each stage when m = 5, including the original mesh, the encrypted mesh, the marked encrypted mesh, and the recovered mesh. Figure 6 shows that in terms of visual quality, there is no visually perceptible difference between the original mesh and the recovered mesh obtained by the proposed method, that is, the method proposed does not introduce perceptible distortion.

3.3 Performance Comparison

In this section, we compared the embedding rate of our method with methods [17,18,19]. Jiang et al. [17] embeds 1bit into each vertex by flipping the three LSBs of the vertex in the data hiding stage. Since the embedding rate is limited by the mesh connectivity, the embedding rate is lower than 0.5bpv. Mohsin’s method [18] after two layers of embedding, the embedding rate reaches 6 bpv. Tsai et al. [19] uses spatial coding technology with embedding threshold to embed additional data into the vertices, and the embedding rate is about 7.68 bpv. The proposed method replaces the nMSB bits of the vertices in the “embedded” set with the n bits of the additional data, so each vertex is embedded with 3n bits. The proposed method makes full use of the local correlation of the model, and the embedding rate is improved. Figure 7(a) shows that the embedding rate of the proposed method on Beetle is 16.51 bpv, while the embedding rate of Jiang et al., Mohsin and Tsai et al. are 0.35 bpv, 6.00 bpv and 7.68 bpv, respectively.

In order to verify the effectiveness of the experiment, we tested the performance of embedding rate on the Princeton Shape Retrieval and Analysis Group data set. It can be seen from Fig. 7(b) that the average embedding rate of the proposed method is 14.25 bpv, while the average embedding rate of Jiang et al., Mohsin et al. and Tsai et al. method is 0.36 bpv, 6.00 bpv and 7.68 bpv, respectively. In summary, the experimental results show that the embedding rate of the proposed method is higher than that of the state-of-the-art methods [17,18,19].

Fig. 7.

Comparison of the proposed method and the state-of-the-art methods on embedding rate. (a) Maximum embedding rate on four test meshes. (b) Average embedding rate on Princeton Shape Retrieval and Analysis Group data set.

3.4 Feature Comparison

Table 1 shows the feature comparison of the proposed method and the state-of-the-art methods [17,18,19]. Jiang et al. [17] method and Mohsin et al. [18] method must decrypt the mesh when extracting additional data, both of which are inseparable methods. The proposed method realizes that data extraction and mesh recovery are separable. The average bit error rate of the data extracted by the method of Jiang et al. is 4.22$\%$. In the method of Tsai et al. [19], the data extraction error is relatively large. The proposed method can extract data completely without error. In addition, by combining the value of m and Ring-prediction, the proposed method achieves error-free in mesh recovery stage. E$_d$ represents error-free in data extraction. E$_r$ represents error-free in mesh recovery.

Table 1. Feature comparison of the proposed method and the state-of-the-art methods.

3.5 Performance Analysis on Dense Meshes

The experimental results in Table 2 show that the experiments on dense meshes show the applicability and effectiveness of the method. Taking Dragon as an example, we can find that the maximum embedding rate is 17.3890 bpv, while the Hausdorff distance is 0.0086 (${10}^{{-3}}$), the SNR is 101.1375. The data shows that this method also achieves a higher embedding rate on dense meshes. The recipient obtains a higher-quality recovered mesh through the Ring-prediction.

Table 2. Performance analysis on dense meshes

4 Conclusions

In this paper, a separable RDH method for encrypted 3D mesh based on integer mapping and Multi-MSB prediction is proposed. The proposed method achieves a balance between capacity and distortion. To get large embedding capacity while ensuring data extraction and mesh recovery separable and error-free, Multi-MSB embedding strategy is used. To obtain high-quality recovered mesh, Ring-prediction is adopted. The results prove that the proposed method improves the embedding capacity compared with the state-of-the-art methods. A major limitation is that the embedding capacity is still limited by mesh connectivity. How to design a more effective algorithm to improve the embedding capacity could be the future work.