Keywords

1 Introduction

Graphs are common data structure that interpret the interrelationship of objects, and real-world data is increasingly represented as graph data. The purpose of graph analysis is to extract a large amount of hidden information from data, thus deriving many important tasks. The purpose of semi-supervised node classification task is to use a small number of labeled nodes to predict the labels of a large number of unlabeled nodes.

In recent years, graph neural networks have shown remarkable results in node representation learning, and GCN [9] being one of the most popular models. Existing GCNs models often follow the message-passing manner to obtain the embedding of all nodes by aggregating the node features within the node neighborhood. However, recent studies have provided some new insights into the mechanisms of GCNs. Li et al. [5] prove that the convolution operation of GCNs is actually a kind of Laplacian smoothing, and explores the multi-layer structure. Wu et al. [6] show that graph structure as low-pass-type filter on node features. Zheng et al. [12] utilize the Louvain-variant algorithm and jump connection to obtain different granularity of node features and graph structure information for adequate feature propagation.

Most of the current GCNs rely on the structural information of graph, which can seriously affect the model performance when the structure of graph is not optimal. The reason may be that most of the current GCNs rely on the structural information of the graph to classify. In this work, we retain graph structure information and feature similarity, consider the influence of the mixed information of the two on the results, and introduce the attention mechanism for classification.

2 Related Work

The first representative work of applying deep learning models to graph structure data is network embedding, which learns fixed-length representations for each node by constraining the proximity of nodes, such as DeepWalk [1], Node2Vec [2]. After that, the research defines graph convolution in the spectral space based on convolution theorem. ChebNet [3] parameterize the convolution kernel in the spectral approach, which avoids the characteristic decomposition of the Laplace matrix and greatly reduces the complexity. Kipf [9] simplifie the ChebNet parameters and proposes a first-order graph convolution neural network. SGC [4] put the first-order graph convolution neural introduces the first-order approximation of Chebyshev polynomials, which further simplifies the mechanism. With the increasing importance of attention mechanism, it has a considerable impact in various fields. GAT [7] leverage the attention mechanism to learn the relative weights between two connected nodes. GNNA [14] improve the embeddedness of users and projects by introducing attention mechanisms and high-level connectivity.

Some experiments show that the graph neural network is inefficient when the graph structure is noisy and incomplete. kNN-GCN [8] take the k-nearest neighbor graph created from the node features as input. DEMO-Net [13] formulate the feature aggregation into a multi-task learning problem according to nodes’ degree values. AM-GCN [10] use consistency constraints and disparity constraints to obtain information and improves the ability to fuse network topology and node features. SimP-GCN [11] make use of self-supervised methods for node classification and explore the different effects of GCNs on assortative and disassortative graphs. Hence, it motivates us to develop a new approach that combines graph structure and feature similarity on the node classification task.

3 The Proposed Model

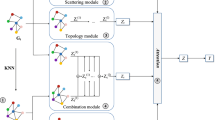
The key point is that Mif-GCN license node features to propagate in both structure space and feature space, because we consider that the classification rules of datasets depend on graph structure or feature similarity. We propose a mixed graph convolution module to adaptively balance the mixed information from initial graph and feature graph, which may contain hidden information. This module is designed to explore depth-related information.

3.1 Multi-Channel Convolution Module

Feature Graph Construction.

We first calculate the cosine similarity between the features of each node pair and construct the similarity matrix \({\mathbf{S}} \in {\mathbb{R}}^{n \times n}\). Then, we select predetermined number of nodes to establish the connection relationship, in order to obtain a k-nearest neighbor (kNN) graph \(G_{f} = \left( {{\mathbf{A}}_{f} ,{\mathbf{X}}} \right)\).

The cosine similarity can be calculated from the cosine of the angle between two vectors:

$$ {\mathbf{S}}_{jk} = \frac{{{\mathbf{x}}_{j} \cdot {\mathbf{x}}_{k} }}{{\left| {{\mathbf{x}}_{j} } \right|\,\left| {{\mathbf{x}}_{k} } \right|}} $$
(1)

Where \({\mathbf{X}}_{j}\) and \({\mathbf{X}}_{k}\) are the feature vectors of nodes j and k Fig. 1.

Fig. 1.
figure 1

The framework of the proposed Mif-GCN model.

Full size image

Initial Graph Convolution Module and Feature Graph Convolution Module.

In this module, node features are propagated in structure space and feature space separately so that we can distinguish correlations. Both modules use the typical GCN to get the node representation.

Then with the initial graph \(G_{i} = \left( {{\mathbf{A}}_{i} ,{\mathbf{X}}} \right)\), the \(l{\text{ - th}}\) layer output \({\mathbf{Z}}_{i}^{\left( l \right)}\) can be represented as:

$$ {\mathbf{Z}}_{i}^{\left( l \right)} {\mathbf{ = }}ReLU\left( {{\tilde{\mathbf{D}}}_{i}^{{ - \frac{1}{2}}} {\tilde{\mathbf{A}}}_{i} {\tilde{\mathbf{D}}}_{i}^{{ - \frac{1}{2}}} {\mathbf{Z}}_{i}^{{\left( {l - 1} \right)}} {\mathbf{W}}_{i}^{\left( l \right)} } \right) $$
(2)

Where \({\mathbf{W}}_{i}^{\left( l \right)}\) is the weight matrix of the \(l{\text{ - th}}\) layer, \({\tilde{\mathbf{A}}}_{i}\) is the adjacency matrix of the initial graph of the added self-loop and \({\tilde{\mathbf{D}}}_{i}\) is the diagonal matrix of \({\tilde{\mathbf{A}}}_{i}\). We have \({\tilde{\mathbf{A}}}_{i} {\mathbf{ = A}}_{i} {\mathbf{ + I}}\),\({\mathbf{A}}_{i}\) is the adjacency matrix of the initial graph, \({\mathbf{I}}\) is the identity matrix. \(ReLU\) is the ReLU activation function and \({\mathbf{Z}}_{i}^{\left( 0 \right)} {\mathbf{ = X}}\).

Then with the feature graph \(G_{f} = \left( {{\mathbf{A}}_{f} ,{\mathbf{X}}} \right)\), the \(l{\text{ - th}}\) layer output \({\mathbf{Z}}_{f}^{\left( l \right)}\) can be represented as:

$$ {\mathbf{Z}}_{f}^{\left( l \right)} {\mathbf{ = }}ReLU\left( {{\tilde{\mathbf{D}}}_{f}^{{ - \frac{1}{2}}} {\tilde{\mathbf{A}}}_{f} {\tilde{\mathbf{D}}}_{f}^{{ - \frac{1}{2}}} {\mathbf{Z}}_{f}^{{\left( {l - 1} \right)}} {\mathbf{W}}_{f}^{\left( l \right)} } \right) $$
(3)

Where \({\mathbf{A}}_{f}\) is the adjacency matrix of the feature graph, \({\mathbf{Z}}_{f}^{\left( 0 \right)} {\mathbf{ = X}}\), other parameters are the same as Eq. (2).

Mixed Graph Convolution Module.

This module can mix information from the initial and feature graphs. We define a goal vector to balance the degree of contribution from the two graphs. Then, this module gets the node embedding.

Then with the initial graph and the feature graph, the \(l{\text{ - th}}\) layer output of the mixed propagation matrix \({\mathbf{P}}^{\left( l \right)}\) can be represented as:

$$ {\mathbf{P}}^{\left( l \right)} = {\mathbf{g}}^{\left( l \right)} *{\tilde{\mathbf{D}}}_{i}^{{ - \frac{1}{2}}} {\tilde{\mathbf{A}}}_{i} {\tilde{\mathbf{D}}}_{i}^{{ - \frac{1}{2}}} + \left( {1 - {\mathbf{g}}^{\left( l \right)} } \right)*{\tilde{\mathbf{D}}}_{f}^{{ - \frac{1}{2}}} {\tilde{\mathbf{A}}}_{f} {\tilde{\mathbf{D}}}_{f}^{{ - \frac{1}{2}}} $$
(4)

Where \({\mathbf{g}}^{\left( l \right)} \in {\mathbb{R}}^{n}\) is the goal vector that balances the information from the initial and feature graphs, \(^{\prime}*^{\prime}\) denotes the operation of multiplying the \(j{\text{ - th}}\) element of a vector with the \(j{\text{ - th}}\) row of a matrix. \({\mathbf{g}}^{\left( l \right)}\) can combine information from two graphs to different degrees.

Then the \(l{\text{ - th}}\) layer output of goal vector \({\mathbf{g}}^{\left( l \right)}\) can be represented as:

$$ {\mathbf{g}}^{\left( l \right)} {\mathbf{ = }}\sigma \left( {{\mathbf{\rm Z}}_{i}^{{\left( {l - 1} \right)}} {\mathbf{W}}_{g}^{\left( l \right)} {\mathbf{ + b}}_{g}^{\left( l \right)} } \right) $$
(5)

Where \({\mathbf{\rm Z}}_{i}^{{\left( {l - 1} \right)}} \in {\mathbb{R}}^{{n \times d^{{\left( {l - 1} \right)}} }}\) is the input hidden representation of the previous layer, and \({\mathbf{\rm Z}}_{i}^{\left( 0 \right)} {\mathbf{ = X}}\). \({\mathbf{W}}_{g}^{\left( l \right)} \in {\mathbb{R}}^{{d^{{\left( {l - 1} \right)}} \times 1}}\) and \({\mathbf{b}}_{g}^{\left( l \right)}\) are parameters in order to calculate \({\mathbf{g}}^{\left( l \right)}\). \(\sigma\) denotes the sigmoid activation function.

Then with the mixed propagation matrix \({\mathbf{P}}^{\left( l \right)}\), the \(l{\text{ - th}}\) layer output \({\mathbf{Z}}_{m}^{\left( l \right)}\) can be represented as:

$$ {\mathbf{Z}}_{m}^{\left( l \right)} = \sigma \left( {{\mathbf{P}}^{\left( l \right)} {\mathbf{Z}}_{m}^{{\left( {l - 1} \right)}} {\mathbf{W}}_{m}^{\left( l \right)} } \right) $$
(6)

Where \({\mathbf{P}}^{\left( l \right)}\) denotes the mixed propagation matrix and \({\mathbf{Z}}_{m}^{\left( 0 \right)} = {\text{X}}\),\({\mathbf{W}}_{m}^{\left( l \right)}\) is the parameter, here \(\sigma\) denotes the sigmoid activation function.

3.2 Attention Mechanism

We use the attention mechanism to combine to get the final node embedding. The ultimate goal is to explore the most relevant information in the three embeddings. \({\mathbf{Z}}_{I} ,{\mathbf{Z}}_{F} ,{\mathbf{Z}}_{M}\) contain the embedding of n nodes,\({{\varvec{\upalpha}}}_{i} ,{{\varvec{\upalpha}}}_{f} ,{{\varvec{\upalpha}}}_{m}\) represent the respective attention values.

For node \({\text{j}}\),\({\mathbf{z}}_{F}^{j} \in {\mathbb{R}}^{1 \times h}\) denotes the embedding of node \({\text{j}}\) in \({\mathbf{Z}}_{F}\). Then use a weight vector \(\overrightarrow {{\mathbf{a}}} \in {\mathbb{R}}^{{h^{\prime} \times 1}}\) to obtain the attention values \(\omega_{F}^{j}\):

$$ \omega_{F}^{j} = {\vec{\mathbf{a}}}^{T} \cdot tanh\left( {{\mathbf{W}} \cdot {\mathbf{z}}_{F}^{j} } \right) $$
(7)

Where \({\mathbf{W}} \in {\mathbb{R}}^{{h^{\prime} \times h}}\) are parameters. Similarly, we get the attention values \(\omega_{I}^{j}\) and \(\omega_{M}^{j}\) for node j in \({\mathbf{Z}}_{I}\) and \({\mathbf{Z}}_{M}\).

Then we use the \(softmax\) activation function to obtain \({{\varvec{\upalpha}}}_{F}^{j}\):

$$ {{\varvec{\upalpha}}}_{F}^{j} = softmax\left( {\omega_{F}^{j} } \right) = \frac{{exp(\omega_{F}^{j} )}}{{exp(\omega_{I}^{j} ) + exp(\omega_{F}^{j} ) + exp(\omega_{M}^{j} )}} $$
(8)

Where \({{\varvec{\upalpha}}}_{F}^{j}\) is the percentage of embedding. Similarly, we can get \({{\varvec{\upalpha}}}_{I}^{j}\) and \({{\varvec{\upalpha}}}_{M}^{j}\). For all n nodes, there are \({{\varvec{\upalpha}}}_{{\varvec{I}}} = diag\left( {{{\varvec{\upalpha}}}_{I}^{1} ,{{\varvec{\upalpha}}}_{I}^{2} , \cdot \cdot \cdot ,{{\varvec{\upalpha}}}_{I}^{n} } \right)\),\({{\varvec{\upalpha}}}_{{\varvec{F}}} = diag\left( {{{\varvec{\upalpha}}}_{F}^{1} ,{{\varvec{\upalpha}}}_{F}^{2} , \cdot \cdot \cdot ,{{\varvec{\upalpha}}}_{F}^{n} } \right)\) and \({{\varvec{\upalpha}}}_{{\varvec{M}}} = diag\left( {{{\varvec{\upalpha}}}_{M}^{1} ,{{\varvec{\upalpha}}}_{M}^{2} , \cdot \cdot \cdot ,{{\varvec{\upalpha}}}_{M}^{n} } \right)\).

Finally, we combine the three embeddings to obtain \({\mathbf{Z}}\):

$$ {\mathbf{Z}} = \left( {{{\varvec{\upalpha}}}_{{\varvec{I}}} \cdot {\mathbf{Z}}_{I} + {{\varvec{\upalpha}}}_{{\varvec{F}}} \cdot {\mathbf{Z}}_{F} + {{\varvec{\upalpha}}}_{{\varvec{M}}} \cdot {\mathbf{Z}}_{M} } \right) $$
(9)

3.3 Objective Function

Our model has shown good results without adding other loss functions. We use the cross-entropy error as our overall objective function.

Then with the final embedding \({\mathbf{Z}}\), We can get the class predictions for n nodes as \({\hat{\mathbf{Y}}}\):

$$ {\hat{\mathbf{Y}}} = softmax\left( {{\mathbf{W}} \cdot {\mathbf{Z}} + {\mathbf{b}}} \right) $$
(10)

Where \(softmax\) is a commonly used activation function for classification.

If the training set is \(L\), for each \(l \in L\), \({\mathbf{Y}}_{l}\) denotes the real label and \({\hat{\mathbf{Y}}}_{l}\) denotes the predicted label. Then, our classification loss can be expressed as:

$$ \mathcal{L}_{class} = - \sum\nolimits_{l \in L} {\sum\nolimits_{j = 1}^{C} {{\mathbf{Y}}_{lj} \ln {\hat{\mathbf{Y}}}_{lj}} } $$
(11)

4 Experiments

4.1 Experimental Settings

Datasets.

We selecte a representative dataset and four complex relational datasets for our experiments, which include paper citation networks (Citeseer and ACM) and social networks (UAI2010, BlogCatalog and Flickr). The statistics of these datasets are shown in Table 1.

Table 1. Dataset statistics.
Full size table

Parameters Setting.

To validate our experiments, we choose 20 nodes per class as the training set and 1000 nodes as the test set. We set hidden layer units \(nhid1 \in \left\{ {512,768} \right\}\) and \(nhid2 \in \left\{ {32,128,256} \right\}\). We set learning rate \(0.0002 \sim 0.0005\), dropout rate is 0.5, \({\text{weight decay}} \in \left\{ {5e - 3,5e - 4} \right\}\) and \(k \in \left\{ {2 \ldots 8} \right\}\). For other baseline methods, we refer to the default parameter settings in the authors’ implementation. For all experiments, we run 10 times and recorded the average results. And we use accuracy (ACC) and macro F1 score (F1) to evaluate the performance of the model.

4.2 Node Classification

In this subsection, we discuss the classification effects of each model on different datasets. The experimental results are shown in Table 2.

Table 2. Node classification accuracy (%). The best performance is highlighted in bold.
Full size table

In the paper citation networks, the existing methods have achieved relatively excellent results, which shows the consistency of our method. In the social relationship networks, our method, kNN-GCN and AM-GCN have all achieved good results. This phenomenon may be that they retain the feature similarity between nodes. Other models showed varying degrees of fluctuation and even failure. The reason may be that they depend on graph structure for classification. The importance of node similarity for GCN is further confirmed.

The experimental results show that our model Mif-GCN outperforms other comparison baselines. Our model removes the mixed graph convolution module as If-GCN. Comparing If-GCN and Mif-GCN, the results show the effectiveness of our model. We visualize the attention trend graph. Among the three types of social networks, the feature graph convolution module and the mixed graph convolution module are more valued. They make the classification results biased toward the favorable side.

5 Conclusion

We propose Mif-GCN, a framework that simultaneously preserves graph structure and features similarity. We consider classification rules on different datasets including simple and complex graphs, our method is more generally applicable to networks with complex node relationships.