Abstract
This paper presents an Event-B meta-modelisation of an Event-B project restricted to its context hierarchy which introduces the functional part of a development through sets, constants, axioms and theorems. We study the proposal of a new mechanism for Event-B. It consists in allowing to instantiate in a new context an already proved theorem in a given context. We investigate the validation of the instantiation mechanism in order to prove the validity of imported theorems. We also compare the proposal with similar mechanisms available within some existing theorem provers.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Event-B [1] is a formal method for the rigorous development of systems. One of its salient features is the Rodin tool [2] which offers an integrated environment for developing and proving. The aim of the EBRP (Enhancing Event-B and Rodin Plus) projectFootnote 1 is to enhance the framework offered by Rodin in order to better support reuse in Event-B developments thanks to the introduction of generic theories and data types. This enhancement follows the initial work of [4, 7]. As a first step of the project, a light extension of the Event-B language and tool has been proposed. In this paper, we investigate an Event-B meta-level description of this extension. An Event-B model consists in a functional model made of an acyclic graph of contexts and a dynamic model using the functional part which consists of successive event-based machine refinements. We focus here on the new reusability mechanism currently studied by the EBRP project for the functional model. It consists in reusing (importing) instances of theorems and axioms considered to be parameterized by the sets and constants declared in their context. The aim of this paper is to validate this importation mechanism: more precisely, we wish to establish the validity of an instance of an imported theorem. For this purpose, we propose a meta-level study of Event-B context structure extended with importation clauses. Figure 1 shows the meta modelisation of a standard Event-B context and its extension with importation/instanciation clauses.
The rest of the paper is structured as follows: Section 2 presents an Event-B meta-model of an Event-B project made of contexts. Section 3 extends this meta-model by the proposed importation mechanism. Section 4 presents similar mechanisms that can be found in other proof environments. Section 5 concludes this paper.
2 Event-B Contexts
In this section, we give a meta-level description of a project made of a hierarchy of contexts. Starting with a high level description of formulas (context cFormula), we introduce the subset of valid formulas (context cValidity) and describe the project structure as a set of contexts (context cProject). Semantics constraints are introduced through the contexts cStatic and cSemantics. The new importation feature is introduced in the cImport context with semantic constraints in cImportStatic and cImportSemantics. To summarize, the standard representation is structured as a set of contexts corresponding to the left hand side of Fig. 1 and the proposed extension in its right hand side. Moreover, we illustrate the architecture of these contexts through UML-like diagramsFootnote 2.
2.1 Formulas
Formulas (see Fig. 2) are modelled at an abstract level. Its free variables are either sets (acting as base types) or constants. A formula denotes either an expression or a predicate. Some expressions (left unspecified here) denote types. The text of a formula is not considered.
However, the relations ref_sets and ref_csts associate respectively the referenced sets and constants. Formulas are partitioned into Expression and Predicate. Note that we have not modeled the type of an expression and typing constraints. Note also that we could have declared the two relations ref_sets and ref_csts as functions to power sets of sets or constants. However, it would make more difficult to use the relational composition in order to navigate through the metamodel. These notions are declared through the following labelled (the ‘@’ tag) Event-B axiomsFootnote 3:

A Type is seen as a special expression which only refers to sets (not constants)Footnote 4.

An important operation on formulas is substitution (subst): a set can be replaced by a Type and a constant by an Expression. The main static property of a substitution: subst_ref is that unreferenced sets and constants can be removed from the substitution domain. This expressed through a domain restriction (\(\lhd \)). We use this property to show that an imported instance of a theorem remains a theoremFootnote 5 Footnote 6 Footnote 7.

2.2 Validity
We first introduce a sequent as a pair formed by a set of hypothesis predicates and a conclusion predicate. Valid sequents are introduced as a subset.

With respect to our concerns, we consider only two axioms about sequents: monotony and substitution of free identifiers which are sets and constants. The first one states that if the hypotheses of a valid sequent are enriched, the sequent remains valid.

2.3 Project
A project contains contexts denoted by the set Context linked by the extend relation extend. extend is declared irreflexive and transitive (Fig. 3).

Sets and constants are defined within contexts. A set or a context is defined onceFootnote 8. Note that a set or a constant can be present in unrelated contexts (through the extend relation).

In a context, assertions are stated. An assertion is characterized by a predicate. assertion defines the relation between contexts and assertions. Axioms and theorems define distinct assertions.

axiom and thm are respectively the restriction of assertion to axioms and theorems.

2.4 Static Correcness
The static correctness of a project is introduced in the context cStatic. First, sets and constants used by an assertion should be visible from the current context (Fig. 4).

Second, well-formedness conditions are introduced through the subset WFC of Theorem. Static correctness is defined by associating through the wd partial function a wellformedness condition to a formula. It is an assertion to be proven, i.e. a theorem.

Furthermore, a WFC is well formed by construction and thus does not appear in the domain of wd.

The well-definedness condition of a formula does not reference new sets or constants with respect to the initial formula.

2.5 Semantics
The soundness of a context is established through the proof of the validity of its theorems. The proof is abstracted by specifying axioms it uses. We introduce them through the depends relation (Fig. 5).

An assertion can only depend on assertions that are visible from the current context. We also state that an assertion depends on its well-definedness condition.

Moreover, the depends relation is supposed to be irreflexive and transitive.

A sequent is built from theorems. Its hypotheses are all the assertions on which the theorem depends. Its conclusion is the predicate associated to the theorem itself. The semantics of the theorem annotation is thus defined by stating that this sequent is valid.

3 Instantiation of Assertions
This section presents a metamodelisation and the validation of an instanciation mechanism proposed by the EBRP project. It is structured as a set of contexts as shown by the right hand side of Fig. 1.
3.1 Informal Presentation
Let us consider a simple generic example with an axiom used to prove a theorem:

Within a tool developed by the EBRP project, the proposed syntax to achieve the instanciation of th1 in context instance1 is given as a comment. It contains three fields: the context to be imported, instanciation parameters and the name of the target assertion. The instanciated formula can then be automatically generated.
Theorem th1 can be proved in context gen using axiom atm1. th is a (considered correct) instance of th1. However, while it is expected that importing a theorem should give a theorem, actually th is not a theorem. For the assertion “imported theorems are valid" to be valid, a sufficient condition can be that all previous axioms should be imported before as theorems (to be proved), and with the same instance parameters. This is illustrated by the context instance2 (see Fig. 6).

So imported axioms appearing before imported theorems should become proof obligations (thus marked as theorems). Imported theorems should not be proved again and thus appear as axioms.
Here, the theorem PO cannot be proved. It follows that unsoundness of the context instance2 is clearly pointed out, which is the expected behavior. To sum up, instance1 should be rejected because an axiom preceding th1 has not be imported as theorem; instance2 is accepted by the static type checker but cannot be validated by the user. instance3 is an example satisfying the static rules and for which the proof obligation for atm1 instance can be discharged.

3.2 Importation of External Assertions
Importation points are added to standard Event-B assertions inside contexts. An importation point is a reference to an assertion of a remote context. Three kind of importations are distinguished: imported axioms, imported theorems and obligations (Fig. 7).

Obligations should be proved by the importing context and are thus declared as a subset of Theorem. An ImportedTheorem is valid by construction. An ImportedAxiom is an instance of an axiom that remains axiomatic in the importing context.
Note that imported theorems should not be proved again. Either their correctness are guaranteed by a meta-level argument (Transformation verification approach), or a proof can be automatically generated and checked (translation validation approach).

Last, a substitution of remote sets and constants is associated to each importation point. Sets are substituted by type expressions and thus only refer to sets. Constants are substituted by any expression of compatible type and may refer to sets or constantsFootnote 9.

Referred sets and constants should be visible by the importing context. All remotely accessed sets and constants should be substituted.

Note that the model could be refined to introduce typing conditions and constrain expressions to be used by substitutions.
3.3 Static Verification of Importations
In order to guarantee the validity of imported theorems, we link the dependency relation and importation clauses: all dependent assertions on which the imported assertion depends should also be imported. The importing clause should depend on these imports. Derived imports should use compatible substitutions, i.e. common sets or constants should be substituted by the same expressions.

3.4 Correctness of Theorem Instantiation
We first define the semantics of an imported assertion as the assertion obtained by applying the substitution declared in the importation clause to the imported assertion:

The correctness theorem states that the sequent formed by assertions on which the import depends and imported statement is valid. The imported statement can be itself an instance of another distant statement. We thus suppose that the union of the dependency and importation graphs is acyclic. The base case of the result is then given by the following theorem:

Given a context ctx and an importation point imp,
-
let th=importedAssertion(imp) and suppose it is a theorem. By axiom THM_V of cSemantics (Sect. 2.5) the following sequent is valid:
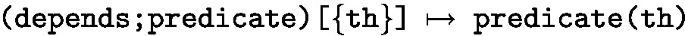
-
Using the set and constant substitutions (S, C) declared in importation point imp, we have predicate(imp) = subst(S,C,predicate(th)) through axiom importPredicate of Sect. 3.4.
-
Using axiom subst_V of Sect. 2.2, we can instanciate the sequent to get a new valid sequent \(Sq_2\):
 .
. -
Thanks to axiom import_depends of Sect. 3.3, antecedents of the imported theorem have been imported before with compatible substitutions, i.e. imp depends on these importation points.
-
Thanks to axiom subst_ref of Sect. 2.1, applying substitutions (S, C) gives the same result.
-
Thus, thanks to the monotonicity of validity (axiom Valid_mono of Sect. 2.2), the sequent concluding on th and containing its dependencies contains enough hypotheses to be valid.
4 Related Concepts
In this section, we review modularity constructs that can be found in various theorem provers. We reuse the same example to illustrate their features and compare them with respect to some key features.
4.1 Section Mechanism in Coq
Variables or hypotheses can be declared in a Coq [10] section and used freely in the rest of the section.

When the section is closed, variables or hypotheses used by definitions or theorems are made parameters. Here th1 is now seen as a function parameterized by a type T, a proof of axm1 property, and a proof that T is inhabited. An instance of th1 can be obtained through a partial call of th1 with a type and a proof, leading to th definition.

Note that it is not necessary to introduce the lemma unit_eq before instantiating the theorem th1: a proof obligation could be generated through the use of Program Definition.
4.2 Module Mechanism in Coq
The theorem th1 is now proved inside a parameterized module (or functor). Its parameter is typed by the module type tGen declaring T and axm1.

In order to use the contents of Gen, it must be instanciated by passing a module compliant with tGen. We introduce the module U defining a one-element type and proving the required property. Then Gen can be instanciated, which leads to the module instance I.

4.3 Locales in Isabelle/HOL
Locales [3] introduce a module system in the theorem prover Isabelle [11]. In the following, the locale gen is parameterized by the variable T typed as a set over the polymorphic type ’a and states the assumption atm1 over the variables of the set T. Thanks to this assumption, the theorem th1 is then proved.

The constant S is then defined as the singleton \(\{1\}\). The latter set is used to give an intepretation to the locale gen. Then, this intepretation requires to discharge the assumptions of the locale considered as proof obligations. After unfolding the definition of S and thanks to the powerful tactic auto these obligations is automatic.

4.4 Clones of Why3
In why3 [5], a theory can declare abstract types and axioms which are used to prove theorems:

The theory can be instanciated by given values to abstract types. Then axioms automatically become proof obligations. Proof attempts are then performed by the tool, and the contents of the instantiated theory become available to check remaining declarations of the Instance theory. The mechanism is less heavy but similar to Coq modules.

4.5 Modules of TLA\(^+\)
In TLA\(^+\) [8], modules can state assumptions and use them for proofs.

In order to instantiate a module, one has to provide the constants (and the variables) that are used in this module. It is also possible to inherit the theorems of this instantiated module. However, each such theorem has an additional hypothesis consisting of the assumptions of the instantiated module. Otherwise stated, the reuse of a theorem is possible once the assumptions of its module have been discharged.

4.6 Summary
In this section, we summarize some features offered by the module systems of the different proof environments. We have considered three criteria:
-
The instantiation syntax: is it possible to extract a single theorem from a module? How formal parameters are given? Do they take implicit values (effective parameter with the same name as the formal parameter)?
-
Interaction with provers: is it possible to prove obligations before instantiating the module, during module instantiation, or does the parameter property become a hypothesis of the extracted theorem?
-
Extensibility of generic modules: is it possible to extend the generic theory by adding new parameters or new theorems?
Coq Sections | Coq Modules | Isabelle | Why3 | TLA | Rodin | |
|---|---|---|---|---|---|---|
Theorem import |
|
| ||||
Named parameters |
|
| ||||
Implicit parameters |
|
| ||||
Type param. synthesis |
|
|
|
|
|
|
Anticipated proof |
|
|
|
|
| |
Proof obligation |
|
|
|
| ||
Axioms as assumptions |
|
| ||||
Extensibility |
|
|
|
|
|
As said in the introduction, the current integration of these features is investigated as a light extension of the Rodin tool. Ticks in the Rodin column indicate in-development features. Extensibility is by nature present through Rodin context extension. The other features presented in the table have no impact on the meta-level analysis and will be reflected by the choices done in the final IDE of the tool under construction.
5 Conclusion
In this paper, we have tried to put forward the meta level description of an extension currently studied within the EBRP project. The aim of this meta-modelisation is to validate the expected properties of theorem instantiation. It has been done using current Event-B contexts. This axiomatic formalization could be considered as the formal specification of a static semantic checker of (extended) Event-B models. Also, an interesting evolution of this work could be to take into account the enhancements that are currently being implemented within the EBRP project, as well as some features already available within the plugin theory [7] (inductive types, definition by cases, ...). It would be an interesting validation of these enhancements. A more ambitious aim would be to standardize the syntax and semantics of Event-B [6] through Event-B. It would need to take into account machines, refinements, types, ....
Notes
- 1.
The project EBRP is supported by the French research agency: ANR.
- 2.
We could have used the UML-B plugin [9].
- 3.
\(A\leftrightarrow B\) denotes the set of relations from A to B: \(A\leftrightarrow B \triangleq \mathcal{P}(A\times B)\).
- 4.
\(\lhd \) denotes domain restriction: \(s\lhd r \triangleq r \cap (s\times \mathbf {ran}(r))\).
- 5.
\(x\mapsto y\) denotes the ordered pair (x, y).
- 6.
\(s\nrightarrow t\) denotes a partial function.
- 7.
r[s] denotes the relational image by r of the set s: \(r[s] \triangleq \mathbf {ran}(s\lhd r)\).
- 8.
\(r_1;r_2\) denotes relation composition, usually denoted \(r_2 \circ r_1\). It is used to navigate in the metamodel along a chain of links.
- 9.
\(r\otimes s \triangleq \{x \mapsto (y \mapsto z) ~\mid ~ x\mapsto y \in r \wedge x\mapsto z \in s\}\).
References
Abrial, J.-R.: Modeling in Event-B: System and Software Engineering. Cambridge University Press, New York (2010)
Abrial, J.-R., Butler, M., Hallerstede, S., Hoang, T.S., Mehta, F., Voisin, L.: Rodin: an open toolset for modelling and reasoning in Event-B. Int. J. Softw. Tools Technol. Transf. 12(6), 447–466 (2010)
Ballarin, C.: Locales: a module system for mathematical theories. J. Autom. Reason. 52(2), 123–153 (2014)
Butler, M., Maamria, I.: Practical theory extension in Event-B. In: Liu, Z., Woodcock, J., Zhu, H. (eds.) Theories of Programming and Formal Methods. LNCS, vol. 8051, pp. 67–81. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39698-4_5
Filliâtre, J.-C., Paskevich, A.: Why3—where programs meet provers. In: Felleisen, M., Gardner, P. (eds.) ESOP 2013. LNCS, vol. 7792, pp. 125–128. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37036-6_8
Hallerstede, S.: On the purpose of Event-B proof obligations. Formal Aspects Comput. 23(1), 133–150 (2011)
Hoang, T.S., Voisin, L., Salehi, A., Butler, M.J, Wilkinson, T., Beauger, N.: Theory Plug-in for Rodin 3.x. CoRR, abs/1701.08625 (2017)
Lamport, L.: Specifying Systems: The TLA+ Language and Tools for Hardware and Software Engineers. Addison-Wesley, Boston (2002)
Snook, C., Butler, M.: UML-B: a plug-in for the Event-B tool set. In: Börger, E., Butler, M., Bowen, J.P., Boca, P. (eds.) ABZ 2008. LNCS, vol. 5238, p. 344. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-87603-8_32
The Coq Development Team. The Coq Proof Assistant, January 2021
Wenzel, M., Paulson, L.C., Nipkow, T.: The Isabelle framework. In: Mohamed, O.A., Muñoz, C., Tahar, S. (eds.) TPHOLs 2008. LNCS, vol. 5170, pp. 33–38. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-71067-7_7
Acknowledgement
We thank the anonymous reviewers for their helpful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Bodeveix, JP., Filali, M. (2021). Event-B Formalization of Event-B Contexts. In: Raschke, A., Méry, D. (eds) Rigorous State-Based Methods. ABZ 2021. Lecture Notes in Computer Science(), vol 12709. Springer, Cham. https://doi.org/10.1007/978-3-030-77543-8_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-77543-8_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-77542-1
Online ISBN: 978-3-030-77543-8
eBook Packages: Computer ScienceComputer Science (R0)












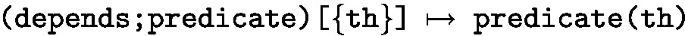
 .
.


























