Abstract
This paper studies the operations of public announcement of statements and public utterance of questions in the context of substructutral inquisitive epistemic logic. It was shown elsewhere that the logical laws governing the modalities of knowing and entertaining from standard inquisitive epistemic logic generalize smoothly to substructural logics. In this paper we show that the situation is different with the reduction axioms that in the standard setting govern the modality of public announcement/utterance. The standard reduction axioms depend on some features of classical logic that are not preserved in substructural logics. Using an additional auxiliary modality, we show how to overcome this obstacle and formulate an alternative set of reduction axioms for the public announcement/utterance modality that can be used even in the context of our general non-classical setting.
The work on this paper was supported by grant no. 18-19162Y of the Czech Science Foundation.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Public announcement logic (\(\mathsf {PAL}\), see, e.g. [9]), as a particular form of dynamic epistemic logic, aims at capturing the logical structure of public communication and reasoning about agents, and their changing believes and knowledge. In other words, it is concerned with reasoning involving information about the dynamics of information accessible to other agents. Inquisitive dynamic epistemic logic (\(\mathsf {IDEL}\), see [3, 4]) enriches \(\mathsf {PAL}\) with the realm of questions. Agents are equipped not only with information states but also with issues and not only statements but also questions may be publicly announced/uttered.
The standard dynamic epistemic logic, as well as its inquisitive extension, are based on classical logic. The aim of this paper is to present a general semantic framework that can serve as a basis for non-classical inquisitive dynamic epistemic logics. It incorporates public announcement logic based on substructural logic but at the same time applies to a language involving questions.
Our approach relies significantly on the static framework for substructural inquisitive epistemic logics developed in [5]. The main contribution of this paper is an extension of this particular framework with an extra layer that allows one to capture the dynamics of publicly announcing statements and raising issues. The resulting semantics can be seen as a generalization of the semantics of \(\mathsf {IDEL}\). However, we will see that the reduction axioms for the public announcement/utterance modality used in [4] to syntactically characterize \(\mathsf {IDEL}\) are not valid in our more general setting. Our solution to this problem is that we add to the language an auxiliary modality for which simple and elegant reduction axioms can be formulated, and we will reduce the public announcement/utterance modality to this additional modality.
2 The Object Language
The object language we will work with involves atomic formulas and the following logical symbols: (a) standard logical symbols used in propositional substructural logics, namely the constant for contradiction (\(\bot \)), the constant for logical truth (\(\mathsf {t}\)), negation (\(\lnot \)), implication (\(\rightarrow \)), extensional conjunction (\(\wedge \)), intensional conjunction (\(\otimes \)), declarative disjunction (\(\vee \)); (b) a binary connective  that is called inquisitive disjunction and that allows one to form disjunctive and polar (yes/no) questions so that
that is called inquisitive disjunction and that allows one to form disjunctive and polar (yes/no) questions so that  amounts to the disjunctive question whether p or q, and
amounts to the disjunctive question whether p or q, and  to the polar question whether p (see, e.g., [2]); (c) two epistemic modalities, \(I_a\) and \(E_a\) (where a represents an agent); (d) a dynamic public utterance modality \([\varphi ]\);Footnote 1 (e) an auxiliary dynamic modality \(\{\varphi \}\). We will also use equivalence as a defined symbol: \(\varphi \leftrightarrow \psi =_{def} (\varphi \rightarrow \psi ) \wedge (\psi \rightarrow \varphi )\). The resulting language will be called \(\mathcal {L}_{SIDEL}\) (the language of Substructural Inquisitive Dynamic Epistemic Logic). It can be defined in the following compact way:
to the polar question whether p (see, e.g., [2]); (c) two epistemic modalities, \(I_a\) and \(E_a\) (where a represents an agent); (d) a dynamic public utterance modality \([\varphi ]\);Footnote 1 (e) an auxiliary dynamic modality \(\{\varphi \}\). We will also use equivalence as a defined symbol: \(\varphi \leftrightarrow \psi =_{def} (\varphi \rightarrow \psi ) \wedge (\psi \rightarrow \varphi )\). The resulting language will be called \(\mathcal {L}_{SIDEL}\) (the language of Substructural Inquisitive Dynamic Epistemic Logic). It can be defined in the following compact way:

The modality \(I_a\) is interpreted as meaning: according to a’s information. This modality can be applied to statements as well as to questions. In particular, we have the following basic cases:Footnote 2

The modality \(E_a\) is called an entertaining modality. When applied to statements this modality is assumed to behave just like \(I_a\) but its behavior differs when it is applied to questions. This modality does not have a direct counterpart in natural language but its meaning can be illustrated as follows. Assume, for example, that an agent would like to have the information whether there are two or three apples on a table. We also say that this is the agent’s issue. This presupposes that the agent already has the information that at least one of these numbers is correct and she wants to know which one it is. In that case we say that the agent entertains the question whether there are two or three apples on the table but also, for example, that she entertains the question whether there is an even or odd number of apples on the table because every information that resolves the former issue (two or three?), resolves also the latter one (even or odd?).
In the standard framework of inquisitive epistemic logic the entertaining modality serves mainly as a mean to define a more common wondering modality in this way: \(W_a \varphi =_{df} E_a \varphi \wedge \lnot I_a \varphi \). In our example, the agent for instance also entertains the question whether there are less or more than five apples on the table because every information that resolves her issue (two or three?) trivially resolves also this question (less or more than five?). However, the agent does not wonder whether there are less or more than five apples on the table because this question is already resolved by her information that there are either two or three apples on the table.

For a statement \(\alpha \) the formula \([\varphi ] \alpha \) means: after a public utterance of \(\varphi \), \(\alpha \) would be established. For example, assume that the agent a has the information that if there are not two apples on the table then there are three apples there, which is formalized as \(I_a(\lnot p \rightarrow q)\). Then it holds that after a public utterance that there are not two apples on the table, the agent will have the information that there are three apples there, which is formalized as \([\lnot p] I_a q\). However, if \([\varphi ]\) is applied to a question (e.g. a question of the form  ) the result is typically again a question. For instance,
) the result is typically again a question. For instance,  amounts to: after a public utterance of \(\varphi \), would \(\alpha \) or \(\beta \) be established? More concretely, in the example above,
amounts to: after a public utterance of \(\varphi \), would \(\alpha \) or \(\beta \) be established? More concretely, in the example above,  would encode the following question: after a public utterance that there are not two apples on the table, would the agent a have the information that there are three apples on the table?
would encode the following question: after a public utterance that there are not two apples on the table, would the agent a have the information that there are three apples on the table?
The modality \(\{\varphi \}\) is auxiliary. It will help us to characterize syntactically the logic of \([\varphi ]\). There is a subtle difference between \([\varphi ]\) and \(\{\varphi \}\) which will be clear after the semantics of these operators is introduced in Sect. 4.
3 Substructural Inquisitive Epistemic Logic
In this section, we will focus on the static fragment of \(\mathcal {L}_{SIDEL}\) basically recapitulating the framework of [5]. The proofs of the results presented in this section are also worked out in [5]. The new contribution of this paper, which concerns the treatment of the dynamic modality \([\varphi ]\) with the help of the modality \(\{\varphi \}\), will be presented in the next section. The language \(\mathcal {L}_{SIDEL}\) without the two dynamic modalities will be denoted as \(\mathcal {L}_{SIEL}\).
Our semantics of \(\mathcal {L}_{SIEL}\) is based on the idea of information states as points with respect to which formulas are evaluated. In standard semantic frameworks of epistemic logic, as well as in the standard inquisitive semantics, an information state is modeled as a set of possible worlds. Information states thus form a complete atomic Boolean algebra (the algebra of all sets of possible worlds). In our more general setting, more general algebraic structures will be employed and information states will be regarded as primitive entities characterized by their role within such structures.
In the semantics of standard inquisitive epistemic logic there is a crucial interplay between the layer of possible worlds and the layer of information states. In our generalization we need to have an analogue of these two layers. However, since we intend to base the framework on non-classical logics we will need to employ on the “lower layer” a notion that is more general than the notion of a possible world. Inspired by situation semantics [1], the generalized possible worlds will be called situations.
If we look just at the Boolean algebra of information states in the standard framework, possible worlds correspond to the atoms in the algebra, i.e. to the singleton states. From the lattice-theoretic point of view, a characteristic feature of singletons is that they are completely join-irreducible elements in the algebra of information state. This will be also the definitory feature of situations, the analogues of worlds in our general setting.
Moreover, in the standard setting, where information states are represented by sets of possible worlds, every information state can be viewed as union (i.e. set-theoretic join) of a set of singletons (i.e. completely join-irreducible states). We will need to preserve also this feature. So, in our framework, we will require that every information state can be expressed as the join of a set of situations (completely join-irreducible elements).
We will also need a formal notion of an issue. An issue will be represented by a set of information states that can be intuitively viewed as those states that resolve the issue. Like in the standard inquisitive semantics, we will require that such a set must be downward closed and nonempty. The former condition is motivated by interpreting \(s \sqsubseteq t\) (where \(\sqsubseteq \) is the lattice ordering) as saying that s is informationally stronger than t.Footnote 3 The latter condition is motivated by interpreting the bottom element of the lattice as the absolutely inconsistent state in which everything holds. A more detailed explanation of how particular features of the framework are motivated is contained in [5]. Let us summarize the definition of situations and issues.
Definition 1
Let \(L=\langle S, \sqsubseteq \rangle \) be a complete lattice (of information states), where \(\bigsqcup X\) denotes the join of X w.r.t. \(\sqsubseteq \). An element \(s \in S\) is called a situation in L iff it is completely join-irreducible, i.e. \(s= \bigsqcup X\) only if \(s=t\), for some \(t \in X\). For any \(s \in S\), the set of situations below s, i.e. the set \(\{i \in S~|~\)i\( \text { is a situation such that }i \sqsubseteq s \}\) will be denoted as Sit(s). An issue in L is any nonempty downward closed subset of S.
We will denote situations by the letters \(i, j, \ldots \) and arbitrary states by \(s, t, \ldots \)
The models of our semantics also involve a compatibility relation C among states, a binary operation \(\cdot \) representing fusion of two states, the logical state 1, and, for each agent, an inquisitive state map assigning to each situation an issue interpreted as the issue of the agent in the situation. A valuation will be a function that assigns to every atomic formula an information state.
Definition 2
An abstract epistemic information model (AEI-model, for short) is a structure \(\mathcal {M} = \langle S, \sqsubseteq , C, \cdot , 1, \{\varSigma _{a}\}_{a \in \mathcal {A}}, V \rangle \) such that (a) \(\langle S, \sqsubseteq \rangle \) is a complete lattice; (b) every state from S is identical to the join of a set of situations, that is, for any \(s \in S\), \(s=\bigsqcup Sit(s)\); (c) 1 is a left-identity with respect to fusion, i.e. \(1 \cdot s = s\); (d) \(\sqcap \) and \(\cdot \) distribute over arbitrary joins from both directions; (e) C is symmetric; (f) \(sC(\bigsqcup X)\) iff there is \(t \in X\) such that sCt; (g) for each agent \(a \in \mathcal {A}\), \(\varSigma _a\) is a function assigning issues to situations and satisfying: if i, j are situations such that \(i \sqsubseteq j\) then \(\varSigma _a (i) \subseteq \varSigma _a (j)\); (h) \(V(p) \in S\).
In accordance with the standard framework of inquisitive epistemic logic we will denote the information state of the agent a in the situation i (in a given AEI-model \(\mathcal {M}\)) as \(\sigma _a(i)\) and we define:
Note that each AEI-model is based on a complete lattice and so it is bounded and has the least element (the meet of all states). We will denote this special state as 0. This state will represent an absolutely inconsistent state that supports every piece of information (see Theorem 1(a)).
It might be useful to see in which sense AEI-models generalize structures that naturally arise from the standard Kripke models for epistemic logic. An epistemic Kripke model is a structure \(\langle W, \{R_a\}_{a \in \mathcal {A}}, V \rangle \), where W is a nonempty set (of possible worlds); for each agent \(a \in \mathcal {A}\), \(R_a\) is a binary (accessibility) relation on W such that \(R_a(w)\) represents the information state of the agent a in the world w, i.e. the set of those worlds that are compatible with a’s information in w; and V is a valuation function such that \(V(p) \subseteq W\). We will not assume any special properties of the accessibility relations such as “factivity” (\(w \in R_a(w)\)).
Every Kripke model \(\mathcal {K}=\langle W, \{R_a\}_{a \in \mathcal {A}}, V \rangle \) determines a particular AEI-model \(\mathcal {M}_\mathcal {K} = \langle S, \sqsubseteq , C, \cdot , 1, \{\varSigma _a\}_{a \in \mathcal {A}}, V \rangle \), where \(S=\mathcal {P}(W)\) (i.e. the power set of W); \(\sqsubseteq \) is identical with \(\subseteq \) (so that situations are singletons); sCt iff \(s \cap t \ne \emptyset \); \(s \cdot t = s \cap t\); \(1=W\); and \(s \in \varSigma _a (\{w\})\) iff \(s \subseteq R_a (w)\). V is a valuation in \(\mathcal {K}\) as well as in \(\mathcal {M}_\mathcal {K}\). It can be easily verified that every structure \(\mathcal {M}_\mathcal {K}\) that arises in this way from a Kripke model \(\mathcal {K}\) satisfies all the conditions required in Definition 2 and thus is an example of an AEI-model.
Formulas of the language \(\mathcal {L}_{SIDEL}\) are evaluated with respect to states of AEI-models. The support conditions fixing the semantic behaviour of the logical symbols from \(\mathcal {L}_{SIEL}\) are defined as follows (the support conditions for the dynamic modalities from \(\mathcal {L}_{SIDEL}\) will be defined in the next section):
-
\(\mathcal {M}, s \Vdash p\) iff \(s \sqsubseteq V(p)\),
-
\(\mathcal {M}, s \Vdash \bot \) iff \(s = 0\),
-
\(\mathcal {M}, s \Vdash \mathsf {t}\) iff \(s \sqsubseteq 1\),
-
\(\mathcal {M}, s \Vdash \lnot \varphi \) iff for any \(t \in S\), if tCs then \(\mathcal {M}, t \nVdash \varphi \),
-
\(\mathcal {M}, s \Vdash \varphi \rightarrow \psi \) iff for any \(t \in S\), if \(\mathcal {M}, t \Vdash \varphi \), then \(\mathcal {M}, s \cdot t \Vdash \psi \),
-
\(\mathcal {M}, s \Vdash \varphi \wedge \psi \) iff \(\mathcal {M}, s \Vdash \varphi \) and \(\mathcal {M}, s \Vdash \psi \),
-
\(\mathcal {M}, s \Vdash \varphi \otimes \psi \) iff for some \(t, u \in S\), \(s \sqsubseteq t \cdot u\), \(\mathcal {M}, t \Vdash \varphi \) and \(\mathcal {M}, u \Vdash \psi \),
-
\(\mathcal {M}, s \Vdash \varphi \vee \psi \) iff for some \(t, u \in S\), \(s \sqsubseteq t \sqcup u\), \(\mathcal {M}, t \Vdash \varphi \) and \(\mathcal {M}, u \Vdash \psi \),
-
 iff \(\mathcal {M}, s \Vdash \varphi \) or \(\mathcal {M}, s \Vdash \psi \),
iff \(\mathcal {M}, s \Vdash \varphi \) or \(\mathcal {M}, s \Vdash \psi \), -
\(\mathcal {M}, s \Vdash I_a \varphi \) iff for any \(i \in Sit(s)\), \(\mathcal {M}, \sigma _a(i) \Vdash \varphi \),
-
\(\mathcal {M}, s \Vdash E_a \varphi \) iff for any \(i \in Sit(s)\) and for any \(t \in \varSigma _a(i)\), \(\mathcal {M}, t \Vdash \varphi \).
We say that \(\varphi \) is valid in \(\mathcal {M}\) if \(\varphi \) is supported by the state 1 in \(\mathcal {M}\). The set of states that support \(\varphi \) in \(\mathcal {M}\) will be denoted as \(|| \varphi ||_{\mathcal {M}}\) (where the subscript \(\mathcal {M}\) will be usually omitted) and it will be called the proposition expressed by \(\varphi \) in \(\mathcal {M}\). The logic of all AEI-models for the language \(\mathcal {L}_{SIEL}\) will be called \(\mathsf {SIEL}\) (Substructural Inquisitive Epistemic Logic). We say that \(\varphi \) is \(\mathsf {SIEL}\)-valid if it is valid in every AEI-model. We say that two formulas are \(\mathsf {SIEL}\)-equivalent if in all AEI-models they are supported by the same states.
In the particular cases of AEI-models generated by Kripke models the above support conditions are intimately related to standard truth conditions. Let us consider only the logical symbols \(\lnot , \rightarrow , \wedge , \vee , I_a\) with their standard truth conditions:
-
\(\mathcal {K}, w \vDash p\) iff \(w \in V(p)\),
-
\(\mathcal {K}, w \vDash \lnot \alpha \) iff \(\mathcal {K}, w \nvDash \alpha \),
-
\(\mathcal {K}, w \vDash \alpha \wedge \beta \) iff \(\mathcal {K}, w \vDash \alpha \) and \(\mathcal {K}, w \vDash \beta \),
-
\(\mathcal {K}, w \vDash \alpha \vee \beta \) iff \(\mathcal {K}, w \vDash \alpha \) or \(\mathcal {K}, w \vDash \beta \),
-
\(\mathcal {K}, w \vDash \alpha \rightarrow \beta \) iff \(\mathcal {K}, w \nvDash \alpha \) or \(\mathcal {K}, w \vDash \beta \),
-
\(\mathcal {K}, w \vDash I_a \alpha \) iff for all \(v \in R_a(w)\), \(\mathcal {K}, v \vDash \alpha \).
Then the support conditions above correspond to truth conditions in the following sense. For any Kripke model \(\mathcal {K}\), any \(s \subseteq W\), and any formula \(\alpha \) in the simplified language for which the truth conditions were just introduced, it holds that
Let us continue with the description of the most important general features of our semantics. Note that an implication \(\varphi \rightarrow \psi \) is valid in a model \(\mathcal {M}\) iff for any state s in \(\mathcal {M}\), if \(\mathcal {M}, s \Vdash \varphi \) then \(\mathcal {M}, s \Vdash \psi \). It is also useful to observe that at situations, the support conditions for the modalities \(I_a\) and \(E_a\) may be significantly simplified. Assume that i is a situation of a given AEI-model \(\mathcal {M}\). Then it holds:
-
(a)
\(\mathcal {M}, i \Vdash I_a \varphi \) iff \(\mathcal {M}, \sigma _a(i) \Vdash \varphi \),
-
(b)
\(\mathcal {M}, i \Vdash E_a \varphi \) iff for any \(t \in \varSigma _a(i)\), \(\mathcal {M}, t \Vdash \varphi \).
Let us define the set of declarative \(\mathcal {L}_{SIEL}\)-formulas as the smallest set containing all atomic formulas, \(\bot \), \(\mathsf {t}\), containing all \(\mathcal {L}_{SIEL}\)-formulas of the form \(I_a \varphi \), \(E_a \varphi \) and closed under the connectives \(\lnot , \rightarrow , \wedge , \otimes , \vee \). Declarative formulas represent statements (note that even if \(\varphi \) represents a question, \(I_a \varphi \) and \(E_a \varphi \) are always statements). The following theorem expresses the most crucial features of the support relation.
Theorem 1
In every AEI-model: (a) every \(\mathcal {L}_{SIEL}\)-formula is supported by the state 0; (b) the support of \(\mathcal {L}_{SIEL}\)-formulas is downward persistent, i.e., if a \(\mathcal {L}_{SIEL}\)-formula is supported by a state s and \(t \sqsubseteq s\) then it is also supported by the state t; (c) the support of declarative \(\mathcal {L}_{SIEL}\)-formulas is closed under arbitrary joins, i.e., if a declarative \(\mathcal {L}_{SIEL}\)-formula is supported by each state \(s \in X\), then it is also supported by the state \(\bigsqcup X\).
It follows from (a) and (b) of Theorem 1 that every \(\mathcal {L}_{SIEL}\)-formula expresses an issue. For any \(\mathcal {L}_{SIEL}\)-formula \(\varphi \) we define the informational content of \(\varphi \), denoted as \(info(\varphi )\), as follows:
If \(\varphi \) represents a question, \(info(\varphi )\) captures the information presupposed by the question. (For example, the question whether p or q presupposes the information that p or q.) Now, the meaning of Theorem 1(c) can be interpreted as stating that declarative formulas express a special kind of issues, namely those issues that contain their own informational content (\(info(\varphi ) \in || \varphi ||\)). Let us call the issues that are already resolved by their own presuppositions, i.e. that contain their own join, declarative propositions. Declarative propositions are semantic counterparts of statements.
Now, we can present a syntactic characterization of \(\mathsf {SIEL}\)-validity. We say that an \(\mathcal {L}_{SIEL}\)-formula is \(\mathsf {SIEL}\)-provable if it is provable in the axiomatic system formulated in Table 1.Footnote 4 The system is a basic substructural logic that can be characterized as non-associative, distributive Full Lambek Logic with a paraconsistent negation and with only one implication (of course the second implication \(\leftarrow \) that is normally present in Full Lambek Logic could be easily added), and extended with inquisitive disjunction and the epistemic modalities \(I_a\), \(E_a\).Footnote 5
Theorem 2
For every \(\mathcal {L}_{SIEL}\)-formula \(\varphi \), \(\varphi \) is \(\mathsf {SIEL}\)-valid if and only if \(\varphi \) is \(\mathsf {SIEL}\)-provable.
The following two results express crucial features of \(\mathsf {SIEL}\)-validity. The first one is a disjunctive normal form theorem.
Theorem 3
For every \(\mathcal {L}_{SIEL}\)-formula \(\varphi \) there is a finite set of declarative \(\mathcal {L}_{SIEL}\)-formulas \(\mathcal {R}(\varphi )= \{ \alpha _1, \ldots , \alpha _n \}\) s.t. \(\varphi \) is \(\mathsf {SIEL}\)-equivalent to  .
.
Note that it follows from Theorem 3 that if an \(\mathcal {L}_{SIEL}\)-formula expresses a declarative proposition it must be \(\mathsf {SIEL}\)-equivalent to a declarative \(\mathcal {L}_{SIEL}\)-formula. Another crucial feature of \(\mathsf {SIEL}\)-validity is the disjunction property of the inquisitive disjunction.
Theorem 4
The logic \(\mathsf {SIEL}\) has the inquisitive disjunction property, that is,  is \(\mathsf {SIEL}\)-valid only if \(\varphi \) or \(\psi \) is \(\mathsf {SIEL}\)-valid.
is \(\mathsf {SIEL}\)-valid only if \(\varphi \) or \(\psi \) is \(\mathsf {SIEL}\)-valid.
Theorem 3 shows that every question in the language corresponds to a disjunctive question. The set \(\mathcal {R}(\varphi )\) can be seen as an exhaustive set of direct answers. Theorems 3 and 4 together imply that a question is \(\mathsf {SIEL}\)-valid iff a direct answer to the question is \(\mathsf {SIEL}\)-valid, i.e., iff the question can be resolved by logical means.
4 The Dynamics
The main goal of this paper is to extend the framework presented in the previous section with the semantics of the dynamic modality \([\varphi ]\). Our treatment of the dynamic modality is motivated by the framework developed in [4]. As in [4], we will attempt to characterize the logical behaviour of this modality by reduction axioms. However, in the substructural setting, we will face some obstacles that are not present in the classical setting of [4]. To overcome these obstacles we will employ the auxiliary modality \(\{\varphi \}\).
Take an arbitrary AEI-model \(\mathcal {M} = \langle S, \sqsubseteq , C, \cdot , 1, \{\varSigma _{a}\}_{a \in \mathcal {A}}, V \rangle \). Given two nonempty sets of states X and Y in \(\mathcal {M}\), one can define their fusion in the following way:
The result of this operation is always an issue. Assume that the support conditions for a \(\mathcal {L}_{SIDEL}\)-formula \(\varphi \) are already defined so that the set \(|| \varphi ||\) of states supporting the formula in \(\mathcal {M}\) is determined. We now assume that \(\varphi \) might be publicly uttered. Such a public utterance updates the issues of the agents. The updated model is defined as follows:
where for any situation i we have:
Later on, we will use the following proposition.
Proposition 1
Let \(\mathcal {M}\) be an AEI-model, i one of its situations, and \(\varphi \) any \(\mathcal {L}_{SIDEL}\)-formula. Then \(\bigsqcup \varSigma _a^{\varphi }(i) = \sigma _a(i) \cdot info(\varphi )\).
Proof
The following equations hold:
-
\(\sigma _a(i) \cdot info(\varphi ) = \bigsqcup \varSigma _a (i) \cdot \bigsqcup || \varphi || =\)
-
\(= \bigsqcup \{ \bigsqcup \varSigma _a (i) \cdot t~|~t \in || \varphi || \}=\)
-
\(=\bigsqcup \{ \bigsqcup \{ s \cdot t~|~s \in \varSigma _a (i) \}~|~t \in || \varphi || \}=\)
-
\(=\bigsqcup \{ s \cdot t~|~s \in \varSigma _a (i), t \in || \varphi || \}=\)
-
\(=\bigsqcup \{u \in S~|~\text {for some }s \in \varSigma _a(i), t \in || \varphi ||, u \sqsubseteq s \cdot t \}=\)
-
\(=\bigsqcup (\varSigma _a(i) \circ || \varphi ||) = \bigsqcup \varSigma _a^{\varphi }(i)\).
A public utterance of \(\varphi \) modifies the point of evaluation as well as the issues of the agents so that the semantic clause for \([\varphi ]\) can be specified as follows:
This clause generalizes the semantics of the standard public announcement operator. To see this, take again any epistemic Kripke model \(\mathcal {K}=\langle W, \{R_a\}_{a \in \mathcal {A}}, V \rangle \). Consider again the simplified language based on \(\lnot , \rightarrow , \wedge , \vee , I_a\), now also extended with the public announcement operator \([\alpha ]\). An update of \(\mathcal {K}\) by a formula \(\alpha \) of this language can be defined as \(\mathcal {K}^\alpha =\langle W, \{R^\alpha _a\}_{a \in \mathcal {A}}, V \rangle \), where
In this equation, \(info(\alpha )\) is just the set of all worlds in which \(\alpha \) is true in \(\mathcal {K}\). Given the correspondence between truth and support this is completely in accordance with the notation introduce above, for the set of all worlds in which \(\alpha \) is true in \(\mathcal {K}\) is identical to union of all states in \(\mathcal {M}_{\mathcal {K}}\) that support \(\alpha \), i.e. to \(\bigsqcup || \alpha ||\), which is exactly how we defined \(info(\alpha )\).
The update of a Kripke model is usually defined so that also the set of worlds W and the valuation Vare updated. But this is not an essential aspect of the semantics. One can easily obtain an equivalent semantics without updating these two components. Now consider the standard truth condition for public announcement:
Now the corresponding support condition in \(\mathcal {M}_{\mathcal {K}}\) is
Under this condition support by a state is still equivalent to truth in all the worlds of the state. Since fusion \(\cdot \) and intersection coincide in \(\mathcal {M}_{\mathcal {K}}\), this condition corresponds to our general condition for support of public utterance introduced above. This reasoning shows that our general semantics of public utterance can be viewed as a generalization of the standard semantics of public announcement.
The formula \(\{\varphi \} \psi \) behaves like \([\varphi ] \psi \) with the difference that the point of evaluation is not updated, only the issues of the agents are. The support condition for this modality is:
The logic of all AEI-models for the language \(\mathcal {L}_{SIDEL}\) will be called \(\mathsf {SIDEL}\) (Substructural Inquisitive Dynamic Epistemic Logic). We say that \(\varphi \) is \(\mathsf {SIDEL}\)-valid if it is valid in every AEI-model. Our main goal is to provide an axiomatic characterization of \(\mathsf {SIDEL}\)-validity. But first, it will be useful to formulate the following observation concerning AEI-models.
Proposition 2
For states s, t, u, v of any AEI-model it holds:
-
(a)
\(0 \cdot s = s \cdot 0 = 0\),
-
(b)
if \(s \sqsubseteq t\) and \(u \sqsubseteq v\) then \(s \cdot u \sqsubseteq t \cdot v\).
Proof
(a) It holds that \(0=\bigsqcup \emptyset \). So, \(0 \cdot s = (\bigsqcup \emptyset ) \cdot s = \bigsqcup \{ x \cdot s~|~x \in \emptyset \}= \bigsqcup \emptyset = 0\). The case of \(s \cdot 0\) is analogous.
(b) Assume \(s \sqsubseteq t\) and \(u \sqsubseteq v\). Then \((s \cdot u) \sqcup (t \cdot v) \sqsubseteq (s \cdot u) \sqcup (t \cdot u) \sqcup (s \cdot v) \sqcup (t \cdot v)=(s \sqcup t) \cdot (u \sqcup v) = t \cdot v\).
Let us define the set of declarative \(\mathcal {L}_{SIDEL}\)-formulas as the smallest set containing all atomic formulas, the constants \(\bot \), t, containing all \(\mathcal {L}_{SIDEL}\)-formulas of the forms \(I_a \varphi \), \(E_a \varphi \), closed under the connectives \(\lnot , \rightarrow , \wedge , \otimes , \vee \), and closed under the application of any \([\varphi ]\) and any \(\{ \varphi \}\), that is, if \(\varphi \) is any \(\mathcal {L}_{SIDEL}\)-formula and \(\alpha \) a declarative \(\mathcal {L}_{SIDEL}\)-formula then \([\varphi ] \alpha \) and \(\{ \varphi \} \alpha \) are declarative \(\mathcal {L}_{SIDEL}\)-formulas. From now on, we will use the letters \(\varphi , \psi , \chi , \vartheta \) as variables for arbitrary \(\mathcal {L}_{SIDEL}\)-formulas, and \(\alpha , \beta \) as variables for declarative \(\mathcal {L}_{SIDEL}\)-formulas. Now we can extend Theorem 1 to the language \(\mathcal {L}_{SIDEL}\).
Theorem 5
In every AEI-model: (a) every \(\mathcal {L}_{SIDEL}\)-formula is supported by the state 0; (b) the support of \(\mathcal {L}_{SIDEL}\)-formulas is downward persistent, i.e., if a \(\mathcal {L}_{SIDEL}\)-formula is supported by a state s and \(t \sqsubseteq s\) then it is also supported by the state t; (c) the support of declarative \(\mathcal {L}_{SIDEL}\)-formulas is closed under arbitrary joins, i.e., if a declarative \(\mathcal {L}_{SIDEL}\)-formula is supported by each state \(s \in X\), then it is supported also by the state \(\bigsqcup X\).
Proof
The theorem can be proved by induction. The inductive steps for the logical symbols from \(\mathcal {L}_{SIEL}\) are as in the proof of Theorem 1. We need to go through the inductive steps concerning the dynamic modalities. The inductive steps for \(\{\varphi \}\) are straightforward. We will consider only the steps for \([\varphi ]\). Take an AEI-model \(\mathcal {M}\) and assume that the claims (a)-(c) generally hold for some arbitrary \(\mathcal {L}_{SIDEL}\)-formulas \(\varphi , \psi \), and some declarative \(\mathcal {L}_{SIDEL}\)-formula \(\alpha \).
(a) We assume that \(\mathcal {M}^{\varphi }, 0 \Vdash \psi \). So, due to Proposition 2(a), we have also \(\mathcal {M}^{\varphi }, 0 \cdot info(\varphi ) \Vdash \psi \), i.e. \(\mathcal {M}, 0 \Vdash [\varphi ] \psi \).
(b) Assume that \(\mathcal {M}, s \Vdash [\varphi ] \psi \) and \(t \sqsubseteq s\). The former assumption amounts to \(\mathcal {M}^{\varphi }, s \cdot info(\varphi ) \Vdash \psi \). The inductive assumption and monotonicity of fusion (Proposition 2(b)) imply \(\mathcal {M}^{\varphi }, t \cdot info(\varphi ) \vDash \psi \), and hence \(\mathcal {M}, t \Vdash [\varphi ] \psi \).
(c) Assume \(\mathcal {M}, s \Vdash [\varphi ] \alpha \), for every \(s \in X\). That is, \(\mathcal {M}^{\varphi }, s \cdot info(\varphi ) \vDash \alpha \), for every \(s \in X\), and thus it follows from the inductive assumption for \(\alpha \) that \(\mathcal {M}^{\varphi }, \bigsqcup _{s \in X} (s \cdot info(\varphi )) \vDash \alpha \). Due to distributivity of fusion over arbitrary joins, \(\mathcal {M}^{\varphi }, (\bigsqcup X) \cdot info(\varphi ) \vDash \alpha \), and hence \(\mathcal {M}, \bigsqcup X \vDash [\varphi ] \alpha \).
We will often use the following proposition that shows that the support condition for implication can be significantly simplified if the consequent of the implication is declarative.
Proposition 3
For any state s of any AEI-model \(\mathcal {M}\), any \(\mathcal {L}_{SIDEL}\)-formula \(\varphi \), and any declarative \(\mathcal {L}_{SIDEL}\)-formula \(\alpha \):
Proof
First, assume \(\mathcal {M}, s \Vdash \varphi \rightarrow \alpha \). That means that \(\mathcal {M}, s \cdot t \Vdash \alpha \), for every \(t \in || \varphi ||\). Since \(\alpha \) is declarative, it follows from Theorem 5(c) that \(\mathcal {M}, s \cdot info(\varphi ) \Vdash \alpha \).
Second, assume \(\mathcal {M}, s \cdot info(\varphi ) \Vdash \alpha \). Take any t such that \(\mathcal {M}, t \Vdash \varphi \). Then (by Proposition 2(b)) \(s \cdot t \sqsubseteq s \cdot info(\varphi )\), and so (by Theorem 5(b)) \(\mathcal {M}, s \cdot t \Vdash \alpha \). It follows that \(\mathcal {M}, s \Vdash \varphi \rightarrow \alpha \).
In analogy to the standard public announcement logic \(\mathsf {PAL}\) we would like to characterize the modality \([\varphi ]\) by reduction axioms. However, here we have to face the problem that the standard reduction axioms rely on some features of classical logic that are not preserved in our substructural setting. In particular the standard reduction axioms for implication (\([\varphi ] (\psi \rightarrow \chi ) \leftrightarrow ([\varphi ] \psi \rightarrow [\varphi ] \chi )\)) and negation (\([\varphi ] \lnot \psi \leftrightarrow (\varphi \rightarrow \lnot [\varphi ] \psi )\)), are not \(\mathsf {SIDEL}\)-valid.
For example, as in \(\mathsf {PAL}\), \([p](q \rightarrow r)\) is \(\mathsf {SIDEL}\)-equivalent to \(p \rightarrow (q \rightarrow r)\), and \([p]q \rightarrow [p]r\) to \((p \rightarrow q) \rightarrow (p \rightarrow r)\). However, in contrast to classical logic on which \(\mathsf {PAL}\) is based, \(p \rightarrow (q \rightarrow r)\) is not \(\mathsf {SIDEL}\)-equivalent to \((p \rightarrow q) \rightarrow (p \rightarrow r)\), so the equivalence of \([p](q \rightarrow r)\) and \([p]q \rightarrow [p]r\) fails.
To show how the equivalence between \(p \rightarrow (q \rightarrow r)\) and \((p \rightarrow q) \rightarrow (p \rightarrow r)\) fails in our semantics consider the following artificial example of an AEI-model \(\mathcal {M} = \langle S, \sqsubseteq , C, \cdot , 1, \{\varSigma _{a}\}_{a \in \mathcal {A}}, V \rangle \), where \(S=\mathcal {P}(\omega )\), i.e. states are sets of natural numbers; \(\sqsubseteq \) is the subset relation; C is empty; fusion is defined as follows: \(s \cdot t= \{ m + n~|~m \in s, n \in t \}\); \(1= \{ 0 \}\); for any \(a \in \mathcal {A}\) and any situation i, \(\varSigma _{a}(i)=\{ \emptyset \}\); and V is a valuation such that \(V(p)=V(q)=\{1\}\), and \(V(r)=\{ 2 \}\). Then it can be shown that \(\mathcal {M}\) is indeed an AEI-model. It holds that the state \(\{ 0 \}\) supports \(p \rightarrow (q \rightarrow r)\). To show this we can use Proposition 3: \(\mathcal {M}, \{ 0 \} \Vdash p \rightarrow (q \rightarrow r)\) iff \(\mathcal {M}, (\{ 0 \} \cdot info(p)) \cdot info(q) \Vdash r\), iff \(\mathcal {M}, (\{ 0 \} \cdot \{ 1 \}) \cdot \{ 1 \}\Vdash r\) iff \(\mathcal {M}, \{ 2 \}\Vdash r\) which holds. Moreover, \(\{ 0 \}\) supports \(p \rightarrow q\): \(\mathcal {M}, \{ 0 \} \Vdash p \rightarrow q\) iff \(\mathcal {M}, \{ 1 \} \Vdash q\), which also holds. But \(\{ 0 \}\) does not support \(p \rightarrow r\): \(\mathcal {M}, \{ 0 \} \Vdash p \rightarrow r\) iff \(\mathcal {M}, \{ 1 \} \Vdash r\), which does not hold.
To show that \([\varphi ] \lnot \psi \leftrightarrow (\varphi \rightarrow \lnot [\varphi ] \psi )\) fails, we can consider the following simple instance: \([p] \lnot q \leftrightarrow (p \rightarrow \lnot [p] q)\). As in \(\mathsf {PAL}\), \([p] \lnot q\) is \(\mathsf {SIDEL}\)-equivalent to \(p \rightarrow \lnot q\) and \(p \rightarrow \lnot [p] q\) to \(p \rightarrow \lnot (p \rightarrow q)\). Of course, \(p \rightarrow \lnot q\) and \(p \rightarrow \lnot (p \rightarrow q)\) are equivalent in classical logic but they are not \(\mathsf {SIDEL}\)-equivalent. To show a concrete counterexample, consider the AEI-model \(\mathcal {M}\) introduced in the previous paragraph and modify the definition of the compatibility relation C: we now define sCt iff \(0 \in s\) and \(1 \in t\), or \(1 \in s\) and \(0 \in t\). Let us denote this modified structure as \(\mathcal {N}\). It can be observed that \(\mathcal {N}\) is indeed an AEI-model. Moreover, it can be shown that \(\mathcal {N}, \{ 0 \} \Vdash p \rightarrow \lnot q\) but \(\mathcal {N}, \{ 0 \} \nVdash p \rightarrow \lnot (p \rightarrow q)\).
To overcome the failure of standard reduction axioms, we will exploit the auxiliary modality \(\{ \varphi \}\). We will use axioms allowing to reduce \([ \varphi ]\) to \(\{ \varphi \}\) and further axioms allowing to eliminate \(\{ \varphi \}\). Moreover, we will need rules that will guarantee that provably equivalent formulas are universally replaceable. The whole system of the extra axioms and rules is formulated in Table 2.
We say that an \(\mathcal {L}_{SIDEL}\)-formula is \(\mathsf {SIDEL}\)-provable if it is provable in the axiomatic system consisting of axioms and rules from Tables 1 and 2. We say that \(\varphi \) and \(\psi \) are \(\mathsf {SIDEL}\)-provably equivalent if \(\varphi \leftrightarrow \psi \) is \(\mathsf {SIDEL}\)-provable. We will need to show that \(\mathsf {SIDEL}\)-provably equivalent formulas are replaceable. Note that an alternative formulation of the axiomatic system would be obtained by replacing the rules DR1-DR4 with a rule allowing directly the replacement of equivalents. Nevertheless, with the rules DR1-DR4 we can show that this rule is admissible in the system.
Theorem 6
Assume that \(\varphi , \psi \) are \(\mathsf {SIDEL}\)-provably equivalent \(\mathcal {L}_{SIDEL}\)-formulas. Assume that \(\vartheta \) is a \(\mathcal {L}_{SIDEL}\)-formula containing \(\varphi \) as a subformula and \(\vartheta [\psi /\varphi ]\) is the result of replacing an occurrence of \(\varphi \) in \(\vartheta \) with \(\psi \). Then \(\vartheta \) and \(\vartheta [\psi /\varphi ]\) are \(\mathsf {SIDEL}\)-provably equivalent.
Proof
It is necessary to show that every operator in the language preserves provable equivalences. For example, in the case of \(\rightarrow \) that means that if \(\varphi \leftrightarrow \psi \) is \(\mathsf {SIDEL}\)-provable then, for any \(\mathcal {L}_{SIDEL}\)-formula \(\chi \), the formulas \((\varphi \rightarrow \chi ) \leftrightarrow (\psi \rightarrow \chi )\) and \((\chi \rightarrow \varphi ) \leftrightarrow (\chi \rightarrow \psi )\) are \(\mathsf {SIDEL}\)-provable. All operators of the language \(\mathcal {L}_{SIEL}\) have this property due to the axioms and rules from Table 1. For the dynamic operators this property says that if \(\varphi \leftrightarrow \psi \) is \(\mathsf {SIDEL}\)-provable then, for any \(\mathcal {L}_{SIDEL}\)-formula \(\chi \), \([ \chi ] \varphi \leftrightarrow [ \chi ] \psi \), \([\psi ] \chi \leftrightarrow [\varphi ] \chi \), \(\{ \chi \} \varphi \leftrightarrow \{ \chi \} \psi \), and \(\{ \psi \} \chi \leftrightarrow \{ \varphi \} \chi \) are \(\mathsf {SIDEL}\)-provable. This is guaranteed by the rules DR1-DR4.
We will also need the disjunctive normal form theorem for \(\mathsf {SIDEL}\)-provability.
Theorem 7
For each \(\mathcal {L}_{SIDEL}\)-formula \(\varphi \) there is a finite set of declarative \(\mathcal {L}_{SIDEL}\)-formulas \(\mathcal {R}(\varphi )= \{ \alpha _1, \ldots , \alpha _n \}\) such that \(\varphi \) is \(\mathsf {SIDEL}\)-provably equivalent to  .
.
Proof
This can be proved, like Theorem 3, by induction on the complexity of \(\varphi \). We have to add to the proof of Theorem 3 just the inductive steps for \([\varphi ]\) and \(\{ \varphi \}\). But these steps can be obtained using the axioms RA1 and RA11.
Now we can show that the axioms from Table 2 allow us to eliminate the dynamic modalities.
Theorem 8
For any \(\mathcal {L}_{SIDEL}\)-formula \(\varphi \) there is an \(\mathcal {L}_{SIEL}\)-formula \(\varphi ^{*}\) such that \(\varphi \) and \(\varphi ^{*}\) are \(\mathsf {SIDEL}\)-provably equivalent.
Proof
We will proceed in two steps. In the first step, we will find for any \(\mathcal {L}_{SIDEL}\)-formula \(\varphi \) an \(\mathsf {SIDEL}\)-provably equivalent \(\mathcal {L}_{SIDEL}\)-formula \(\varphi ^{\circ }\) that does not contain any occurrence of the dynamic modality \([ \psi ]\) (for any \(\psi \)). In the second step, we will transform \(\varphi ^{\circ }\) into the \(\mathsf {SIDEL}\)-provably equivalent \(\mathcal {L}_{SIEL}\)-formula \(\varphi ^{*}\) by eliminating all occurrences of the modality \(\{ \psi \}\).
Take any subformula of \(\varphi \) that is of the form \([\psi ] \chi \). According to Theorem 7 there are \(\mathcal {L}_{SIEL}\)-formulas \(\alpha _1, \ldots , \alpha _n\) such that \(\chi \) is \(\mathsf {SIDEL}\)-provably equivalent to  . Hence, \([\psi ] \chi \) must be \(\mathsf {SIDEL}\)-provably equivalent to the following:
. Hence, \([\psi ] \chi \) must be \(\mathsf {SIDEL}\)-provably equivalent to the following:
-
 (Theorem 7),
(Theorem 7), -
 (RA1),
(RA1), -
 (RA2).
(RA2).
In this way we can, step by step, eliminate all occurrences of the modality \([\psi ]\) from \(\varphi \) obtaining the formula \(\varphi ^{\circ }\).
In the formula \(\varphi ^{\circ }\) we can recursively eliminate, using the axioms RA3-RA13, all occurrences of the modality \(\{ \psi \}\). By this elimination we obtain the \(\mathcal {L}_{SIEL}\)-formula \(\varphi ^{*}\). The only case that needs to be discussed is the case \(\{ \varphi \} I_a \psi \) with non-declarative \(\psi \). Assume that \(\psi \) is \(\mathsf {SIDEL}\)-provably equivalent to  , and thus \(\{ \varphi \} I_a \psi \) is \(\mathsf {SIDEL}\)-provably equivalent to
, and thus \(\{ \varphi \} I_a \psi \) is \(\mathsf {SIDEL}\)-provably equivalent to  . The last formula is \(\mathsf {SIDEL}\)-provably equivalent (due to the axiom ID from Table 1 and RA10 from Table 2) to \(\{ \varphi \} I_a \beta _1 \vee \ldots \vee \{ \varphi \} I_a \beta _m\). Now we can apply RA13.
. The last formula is \(\mathsf {SIDEL}\)-provably equivalent (due to the axiom ID from Table 1 and RA10 from Table 2) to \(\{ \varphi \} I_a \beta _1 \vee \ldots \vee \{ \varphi \} I_a \beta _m\). Now we can apply RA13.
Let us illustrate the elimination with a simple example. Consider the formula  . In this case the dynamic modality can be eliminated in the following steps:
. In this case the dynamic modality can be eliminated in the following steps:
-
1.
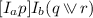
-
2.
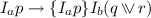 (RA2, Table 2)
(RA2, Table 2) -
3.
\(I_a p \rightarrow \{ I_a p \} (I_b q \vee I_b r)\) (ID, Table 1)
-
4.
\(I_a p \rightarrow (\{ I_a p \} I_b q \vee \{ I_a p \} I_b r)\) (RA10, Table 2)
-
5.
\(I_a p \rightarrow (I_b (I_a p \rightarrow \{ I_a p \} q) \vee I_b (I_a p \rightarrow \{ I_a p \} r))\) (RA13, Table 2)
-
6.
\(I_a p \rightarrow (I_b (I_a p \rightarrow q) \vee I_b (I_a p \rightarrow r))\) (RA3, Table 2)
The step 2 corresponds to \(\varphi ^{\circ }\) in the proof of Theorem 8 and the formula in the step 6 corresponds to \(\varphi ^{*}\) that is already in the language \(\mathcal {L}_{SIEL}\).
The following theorem shows that the system is sound with respect to our semantics.
Theorem 9
All instances of axioms RA1-RA13 are \(\mathsf {SIDEL}\)-valid. The rules DR1-DR4 preserve \(\mathsf {SIDEL}\)-validity.
Proof
We will discuss only some of the cases.
RA1:  iff
iff  iff \(\mathcal {M}^{\varphi }, s \cdot info(\varphi ) \Vdash \psi \) or \(\mathcal {M}^{\varphi }, s \cdot info(\varphi ) \Vdash \chi \) iff \(\mathcal {M}, s \Vdash [ \varphi ] \psi \) or \(\mathcal {M}, s \Vdash [ \varphi ] \chi \) iff
iff \(\mathcal {M}^{\varphi }, s \cdot info(\varphi ) \Vdash \psi \) or \(\mathcal {M}^{\varphi }, s \cdot info(\varphi ) \Vdash \chi \) iff \(\mathcal {M}, s \Vdash [ \varphi ] \psi \) or \(\mathcal {M}, s \Vdash [ \varphi ] \chi \) iff  .
.
RA2: \(\mathcal {M}, s \Vdash [\varphi ] \alpha \) iff \(\mathcal {M}^{\varphi }, s \cdot info(\varphi ) \Vdash \alpha \) iff \(\mathcal {M}, s \cdot info(\varphi ) \Vdash \{\varphi \} \alpha \) iff \(\mathcal {M}, s \Vdash \varphi \rightarrow \{\varphi \} \alpha \).
RA3: \(\mathcal {M}, s \Vdash \{ \varphi \} p\) iff \(\mathcal {M}^{\varphi }, s \Vdash p\) iff \(\mathcal {M}, s \Vdash p\).
RA6: \(\mathcal {M}, s \Vdash \{ \varphi \} \lnot \psi \) iff \(\mathcal {M}^{\varphi }, s \Vdash \lnot \psi \) iff for any t, if sCt then \(\mathcal {M}^{\varphi }, t \nVdash \psi \) iff for any t, if sCt then \(\mathcal {M}, t \nVdash \{ \varphi \} \psi \) iff \(\mathcal {M}, s \Vdash \lnot \{ \varphi \} \psi \).
RA7: \(\mathcal {M}, s \Vdash \{ \varphi \} (\psi \rightarrow \chi )\) iff \(\mathcal {M}^{\varphi }, s \Vdash \psi \rightarrow \chi \) iff for any t, if \(\mathcal {M}^{\varphi }, t \Vdash \psi \) then \(\mathcal {M}^{\varphi }, s \cdot t \Vdash \chi \) iff for any t, if \(\mathcal {M}, t \Vdash \{ \varphi \} \psi \) then \(\mathcal {M}, s \cdot t \Vdash \{ \varphi \} \chi \) iff \(\mathcal {M}, s \Vdash \{ \varphi \} \psi \rightarrow \{ \varphi \} \chi \).
RA12: \(\mathcal {M}, s \Vdash \{ \varphi \} E_a \psi \) iff \(\mathcal {M}^{\varphi }, s \Vdash E_a \psi \) iff for any \(i \in Sit(s)\), for any \(t \in \varSigma _a (i) \circ || \varphi ||\), \(\mathcal {M}^{\varphi }, t \Vdash \psi \) iff for any \(i \in Sit(s)\), for any \(t \in \varSigma _a (i) \circ || \varphi ||\), \(\mathcal {M}, t \Vdash \{ \varphi \} \psi \) iff for any \(i \in Sit(s)\), for any \(u \in \varSigma _a (i)\) and for any v, if \(\mathcal {M}, v \Vdash \varphi \) then \(\mathcal {M}, u \cdot v \Vdash \{ \varphi \} \psi \) iff for any \(i \in Sit(s)\), for any \(u \in \varSigma _a (i)\), \(\mathcal {M}, u \Vdash \varphi \rightarrow \{ \varphi \} \psi \) iff \(\mathcal {M}, s \Vdash E_a (\varphi \rightarrow \{ \varphi \} \psi )\).
RA13: \(\mathcal {M}, s \Vdash \{ \varphi \} I_a \alpha \) iff \(\mathcal {M}^{\varphi }, s \Vdash I_a \alpha \) iff for any \(i \in Sit(s)\), \(\mathcal {M}^{\varphi }, \bigsqcup \varSigma _a^{\varphi } (i) \Vdash \alpha \) iff for any \(i \in Sit(s)\), \(\mathcal {M}, \bigsqcup \varSigma _a^{\varphi }(i) \Vdash \{ \varphi \} \alpha \) iff (using Proposition 1) for any \(i \in Sit(s)\), \(\mathcal {M}, \sigma _a(i) \cdot info(\varphi ) \Vdash \{ \varphi \} \alpha \) iff for any \(i \in Sit(s)\), \(\mathcal {M}, \sigma _a(i) \Vdash \varphi \rightarrow \{ \varphi \} \alpha \) iff \(\mathcal {M}, s \Vdash I_a (\varphi \rightarrow \{ \varphi \} \alpha )\).
We have explained above that epistemic Kripke models determine particular AEI-models. Theorem 9 shows that the axioms and rules presented in Table 2 are sound with respect all AEI-models, and thus also with respect to those AEI-models that are determined by the Kripke models of the standard public announcement logic \(\mathsf {PAL}\). This means that if we take any formula \(\alpha \) of the language of \(\mathsf {PAL}\) (it can be a formula using only the operators \(\lnot , \rightarrow , \wedge , \vee , I_a, [\beta ]\)) then \(\alpha \) is equivalent to \(\alpha ^*\) also in \(\mathsf {PAL}\). In other words, the procedure of eliminating the public utterance modality that we introduced in this paper and that is based on the axioms RA1-RA13 can be used also in the context of \(\mathsf {PAL}\), though it differs from the standardly used procedure based on the standard reduction axioms.
The following theorem provides a sound and complete syntactic characterization of \(\mathsf {SIDEL}\)-validity through \(\mathsf {SIDEL}\)-provability.
Theorem 10
For every \(\mathcal {L}_{SIDEL}\)-formula \(\varphi \), \(\varphi \) is \(\mathsf {SIDEL}\)-valid if and only if \(\varphi \) is \(\mathsf {SIDEL}\)-provable.
Proof
Soundness, i.e. the right-to-left direction, is given by soundness of the \(\mathsf {SIEL}\)-axioms and rules, and by Theorem 9. Completeness, i.e. the left-to-right direction, can be proved as follows: Assume that \(\varphi \) is \(\mathsf {SIDEL}\)-valid. Due to Theorem 8, \(\varphi \) is \(\mathsf {SIDEL}\)-provably equivalent to the \(\mathcal {L}_{SIEL}\)-formula \(\varphi ^{*}\). Due to soundness of the system, \(\varphi ^{*}\) must be also \(\mathsf {SIDEL}\)-valid. Since \(\mathsf {SIDEL}\) is a conservative extension of \(\mathsf {SIEL}\), \(\varphi ^{*}\) is \(\mathsf {SIEL}\)-valid and hence \(\mathsf {SIEL}\)-provable. It follows that \(\varphi ^{*}\), and thus also \(\varphi \), is \(\mathsf {SIDEL}\)-provable.
Our next application of the previous results shows that the logic \(\mathsf {SIDEL}\) has the inquisitive disjunction property.
Theorem 11
The logic \(\mathsf {SIDEL}\) has the inquisitive disjunction property, that is,  is \(\mathsf {SIDEL}\)-valid only if \(\varphi \) or \(\psi \) is \(\mathsf {SIDEL}\)-valid.
is \(\mathsf {SIDEL}\)-valid only if \(\varphi \) or \(\psi \) is \(\mathsf {SIDEL}\)-valid.
Proof
Assume  is \(\mathsf {SIDEL}\)-valid. Then also
is \(\mathsf {SIDEL}\)-valid. Then also  is \(\mathsf {SIDEL}\)-valid, and thus \(\mathsf {SIEL}\)-valid. Since \(\mathsf {SIEL}\) has the inquisitive disjunction property, \(\varphi ^{*}\) or \(\psi ^{*}\) is \(\mathsf {SIEL}\)-valid. It follows that \(\varphi \) or \(\psi \) is \(\mathsf {SIDEL}\)-valid.
is \(\mathsf {SIDEL}\)-valid, and thus \(\mathsf {SIEL}\)-valid. Since \(\mathsf {SIEL}\) has the inquisitive disjunction property, \(\varphi ^{*}\) or \(\psi ^{*}\) is \(\mathsf {SIEL}\)-valid. It follows that \(\varphi \) or \(\psi \) is \(\mathsf {SIDEL}\)-valid.
5 Conclusion
To sum up, we have developed a logic \(\mathsf {SIDEL}\) of public announcement of statements and public utterance of questions based on a basic substructural logic. We focused on one particular minimal logic but the framework is quite flexible and can be adapted easily to other substructural logics. It was shown in [6, 7] how to obtain semantics for inquisitive versions of relevant logics, fuzzy logics and other substructural logics within the framework of information models. These logics could be further enriched with the epistemic modalities \(I_a, E_a\) and the dynamic modalities \([\varphi ], \{ \varphi \}\) using the same reduction axioms and the semantic approach elaborated in this paper.
The semantics of \(\mathsf {SIDEL}\) can be viewed as a generalization of the semantics of the inquisitive dynamic epistemic logic \(\mathsf {IDEL}\) developed in [4]. This observation implies that our reduction axioms are valid even in the context \(\mathsf {IDEL}\) and hence also in the context of \(\mathsf {PAL}\) since \(\mathsf {IDEL}\) just extends \(\mathsf {PAL}\) with the inquisitive dimension. In other words, the method of elimination of the dynamic modalities that we employed could be used also in \(\mathsf {IDEL}\) and \(\mathsf {PAL}\) in the sense that for any formula \(\varphi \) from the language of \(\mathsf {IDEL}\) (or \(\mathsf {PAL}\)), the corresponding formula \(\varphi ^{*}\), obtained by our reduction axioms from \(\varphi \), is equivalent to \(\varphi \) not only in \(\mathsf {SIDEL}\) but also in \(\mathsf {IDEL}\) (or \(\mathsf {PAL}\)).
On the other hand, as we showed above, in the context of \(\mathsf {SIDEL}\) we cannot use the reduction axioms that are normally used for \(\mathsf {IDEL}\) (or \(\mathsf {PAL}\)). To be more concrete, \(\mathsf {IDEL}\) uses the reduction axioms from Table 3. From these axioms only !Atom, !\(\bot \), !\(\wedge \), ! , and !\(I_a\) are \(\mathsf {SIDEL}\)-valid. However, the axioms !\(\rightarrow \) and !\(E_a\) are invalid in \(\mathsf {SIDEL}\).
, and !\(I_a\) are \(\mathsf {SIDEL}\)-valid. However, the axioms !\(\rightarrow \) and !\(E_a\) are invalid in \(\mathsf {SIDEL}\).
In future work we would like to explore whether our framework could be also seen as a generalization of Dynamic Logic of Questions developed in [8].
Notes
- 1.
It is common to interpret the modality \([\varphi ]\) as public announcement of \(\varphi \). However, we will follow [4] in using the term “public utterance” instead of “public announcement”. The reason is that \(\varphi \) may represent a question, e.g. the question whether p or q, and it seems that there is an intuitive difference between announcing whether p or q and uttering whether p or q. The former indicates that an answer to the question is uttered, while the latter means only that the question itself is uttered, which corresponds better to what the modality \([\varphi ]\) is supposed to model.
- 2.
In the standard inquisitive epistemic logic, the letter K, instead of I, is used for this modality since it is interpreted as knowing that/whether. However, in our more general framework, we will not assume the specific features of knowledge, as for example factivity (the agent can know only what is true) so the letter I seems to be more appropriate.
- 3.
In the standard setting \(s \sqsubseteq t\) reduces to \(s \subseteq t\). In that case, the set of worlds s is informationally stronger than t since it excludes more possibilities.
- 4.
In [5], the logic generated by this system is called \(\mathsf {InqSE}\).
- 5.
It is discussed in detail in [5] why the distributivity axiom D1 is needed.
References
Barwise, J., Perry, J.: Situations and Attitudes. MIT Press, Cambridge (2019)
Ciardelli, I., Groenendijk, J., Roelofsen, F.: Inquisitive Semantics. Oxford University Press, Oxford (2019)
Ciardelli, I., Roelofsen, F.: Inquisitive dynamic epistemic logic. Synthese 192(6), 1643–1687 (2015). https://doi.org/10.1007/s11229-014-0404-7
Ciardelli, I.: The dynamic logic of stating and asking: a study of inquisitive dynamic modalities. In: Baltag, A., Seligman, J., Yamada, T. (eds.) LORI 2017. LNCS, vol. 10455, pp. 240–255. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-55665-8_17
Punčochář, V., Sedlár, I.: Epistemic extensions of substructural inquisitive logics (Submitted manuscript)
Punčochář, V.: Substructural inquisitive logics. Rev. Symb. Logic 12(2), 296–330 (2019)
Punčochář, V.: A relevant logic of questions. J. Philos. Logic 49(5), 905–939 (2020). https://doi.org/10.1007/s10992-019-09541-9
van Benthem, J., Minicǎ, Ş.: Toward a dynamic logic of questions. J. Philos. Logic 41(4), 633–669 (2012)
van Ditmarsch, H., van der Hoek, W., Kooi, B.: Dynamic Epistemic Logic. Springer, Dordrecht (2007). https://doi.org/10.1007/978-1-4020-5839-4
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Punčochář, V. (2020). Inquisitive Dynamic Epistemic Logic in a Non-classical Setting. In: Martins, M.A., Sedlár, I. (eds) Dynamic Logic. New Trends and Applications. DaLi 2020. Lecture Notes in Computer Science(), vol 12569. Springer, Cham. https://doi.org/10.1007/978-3-030-65840-3_13
Download citation
DOI: https://doi.org/10.1007/978-3-030-65840-3_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-65839-7
Online ISBN: 978-3-030-65840-3
eBook Packages: Computer ScienceComputer Science (R0)





 iff
iff  (Theorem
(Theorem  (RA1),
(RA1), (RA2).
(RA2).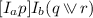
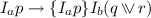 (RA2, Table
(RA2, Table