Abstract
Model learning (a.k.a. active automata learning) is a highly effective technique for obtaining black-box finite state models of software components. We show how one can boost the performance of model learning techniques for register automata by extracting the constraints on input and output parameters from a run, and making this grey-box information available to the learner. More specifically, we provide new implementations of the tree oracle and equivalence oracle from the RALib tool, which use the derived constraints. We extract the constraints from runs of Python programs using an existing tainting library for Python, and compare our grey-box version of RALib with the existing black-box version on several benchmarks, including some data structures from Python’s standard library. Our proof-of-principle implementation results in almost two orders of magnitude improvement in terms of numbers of inputs sent to the software system. Our approach, which can be generalized to richer model classes, also enables RALib to learn models that are out of reach of black-box techniques, such as combination locks.
B. Garhewal—Supported by NWO TOP project 612.001.852 “Grey-box learning of Interfaces for Refactoring Legacy Software (GIRLS)”.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Model learning, also known as active automata learning, is a black-box technique for constructing state machine models of software and hardware components from information obtained through testing (i.e., providing inputs and observing the resulting outputs). Model learning has been successfully used in numerous applications, for instance for generating conformance test suites of software components [13], finding mistakes in implementations of security-critical protocols [8,9,10], learning interfaces of classes in software libraries [14], and checking that a legacy component and a refactored implementation have the same behaviour [19]. We refer to [17, 20] for surveys and further references.
In many applications it is crucial for models to describe control flow, i.e., states of a component, data flow, i.e., constraints on data parameters that are passed when the component interacts with its environment, as well as the mutual influence between control flow and data flow. Such models often take the form of extended finite state machines (EFSMs). Recently, various techniques have been employed to extend automata learning to a specific class of EFSMs called register automata, which combine control flow with guards and assignments to data variables [1, 2, 6].
While these works demonstrate that it is theoretically possible to infer such richer models, the presented approaches do not scale well and are not yet satisfactorily developed for richer classes of models (c.f. [16]): Existing techniques either rely on manually constructed mappers that abstract the data aspects of input and output symbols into a finite alphabet, or otherwise infer guards and assignments from black-box observations of test outputs. The latter can be costly, especially for models where control flow depends on test on data parameters in input: in this case, learning an exact guard that separates two control flow branches may require a large number of queries.
One promising strategy for addressing the challenge of identifying data-flow constraints is to augment learning algorithms with white-box information extraction methods, which are able to obtain information about the System Under Test (SUT) at lower cost than black-box techniques. Several researchers have explored this idea. Giannakopoulou et al. [11] develop an active learning algorithm that infers safe interfaces of software components with guarded actions. In their model, the teacher is implemented using concolic execution for the identification of guards. Cho et al. [7] present MACE an approach for concolic exploration of protocol behaviour. The approach uses active automata learning for discovering so-called deep states in the protocol behaviour. From these states, concolic execution is employed in order to discover vulnerabilities. Similarly, Botinčan and Babć [4] present a learning algorithm for inferring models of stream transducers that integrates active automata learning with symbolic execution and counterexample-guided abstraction refinement. They show how the models can be used to verify properties of input sanitizers in Web applications. Finally, Howar et al. [15] extend the work of [11] and integrate knowledge obtained through static code analysis about the potential effects of component method invocations on a component’s state to improve the performance during symbolic queries. So far, however, white-box techniques have never been integrated with learning algorithms for register automata.
In this article, we present the first active learning algorithm for a general class of register automata that uses white-box techniques. More specifically, we show how dynamic taint analysis can be used to efficiently extract constraints on input and output parameters from a test, and how these constraints can be used to improve the performance of the \( SL ^{*}\) algorithm of Cassel et al. [6]. The \( SL ^{*}\) algorithm generalizes the classical \( L ^*\) algorithm of Angluin [3] and has been used successfully to learn register automaton models, for instance of Linux and Windows implementations of TCP [9]. We have implemented the presented method on top of RALib [5], a library that provides an implementation of the \( SL ^{*}\) algorithm.
The integration of the two techniques (dynamic taint analysis and learning of register automata models) can be explained most easily with reference to the architecture of RALib, shown in Fig. 1, which is a variation of the Minimally Adequate Teacher (MAT) framework of [3]: In the MAT framework, learning is viewed as a game in which a learner has to infer the behaviour of an unknown register automaton \(\mathcal {M}\) by asking queries to a teacher. We postulate \(\mathcal {M}\) models the behaviour of a System Under Test (SUT). In the learning phase, the learner (that is, \( SL ^{*}\)) is allowed to ask questions to the teacher in the form of tree queries (TQs) and the teacher responds with symbolic decision trees (SDTs). In order to construct these SDTs, the teacher uses a tree oracle, which queries the SUT with membership queries (MQs) and receives a yes/no reply to each. Typically, the tree oracle asks multiple MQs to answer a single tree query in order to infer causal impact and flow of data values. Based on the answers on a number of tree queries, the learner constructs a hypothesis in the form of a register automaton \(\mathcal {H}\). The learner submits \(\mathcal {H}\) as an equivalence query (EQ) to the teacher, asking whether \(\mathcal {H}\) is equivalent to the SUT model \(\mathcal {M}\). The teacher uses an equivalence oracle to answer equivalence queries. Typically, the equivalence oracle asks multiple MQs to answer a single equivalence query. If, for all membership queries, the output produced by the SUT is consistent with hypothesis \(\mathcal {H}\), the answer to the equivalence query is ‘Yes’ (indicating learning is complete). Otherwise, the answer ‘No’ is provided, together with a counterexample (CE) that indicates a difference between \(\mathcal {H}\) and \(\mathcal {M}\). Based on this CE, learning continues. In this extended MAT framework, we have constructed new implementations of the tree oracle and equivalence oracle that leverage the constraints on input and output parameters that are imposed by a program run: dynamic tainting is used to extract the constraints on parameters that are encountered during a run of a program. Our implementation learns models of Python programs, using an existing tainting library for Python [12]. Effectively, the combination of the \( SL ^{*}\) with our new tree and equivalence oracles constitutes a grey-box learning algorithm, since we only give the learner partial information about the internal structure of the SUT.
We compare our grey-box tree and equivalence oracles with the existing black-box versions of these oracles on several benchmarks, including Python’s queue and set modules. Our proof-of-concept implementationFootnote 1 results in almost two orders of magnitude improvement in terms of numbers of inputs sent to the software system. Our approach, which generalises to richer model classes, also enables RALib to learn models that are completely out of reach for black-box techniques, such as combination locks. The full version of this article (with proofs for correctness) is available onlineFootnote 2.
Outline: Section 2 contains preliminaries; Section 3 discusses tainting in our Python SUTs; Section 4 contains the algorithms we use to answer TQs using tainting and the definition for the tainted equivalence oracle needed to learn combination lock automata; Section 5 contains the experimental evaluation of our technique; and Sect. 6 concludes.
2 Preliminary Definitions and Constructions
This section contains the definitions and constructions necessary to understand active automata learning for models with dataflow. We first define the concept of a structure, followed by guards, data languages, register automata, and finally symbolic decision trees.
Definition 1
(Structure). A structure \( \mathcal {S}= \langle {} R, \mathcal {D},\mathcal {R} \rangle \) is a triple where R is a set of relation symbols, each equipped with an arity, \(\mathcal {D}\) is an infinite domain of data values, and \(\mathcal {R}\) contains a distinguished n-ary relation \(r^{\mathcal {R}} \subseteq \mathcal {D}^n\) for each n-ary relation symbol \(r \in R\).
In the remainder of this article, we fix a structure \( \mathcal {S}= \langle {} R, \mathcal {D},\mathcal {R} \rangle \), where R contains a binary relation symbol \(=\) and unary relation symbols \(=c\), for each c contained in a finite set C of constant symbols, \(\mathcal {D}\) equals the set \(\mathbb {N}\) of natural numbers, \(=^{\mathcal {R}}\) is interpreted as the equality predicate on \(\mathbb {N}\), and to each symbol \(c \in C\) a natural number \(n_c\) is associated such that \((=c)^{\mathcal {R}} = \{ n_c \}\).
Guards are a restricted type of Boolean formulas that may contain relation symbols from R.
Definition 2
(Guards). We postulate a countably infinite set \(\mathcal {V}= \{ v_1, v_2,\ldots \}\) of variables. In addition, there is a variable \(p \not \in \mathcal {V}\) that will play a special role as formal parameter of input symbols; we write \(\mathcal {V}^+ = \mathcal {V}\cup \{ p \}\). A guard is a conjunction of relation symbols and negated relation symbols over variables. Formally, the set of guards is inductively defined as follows:
-
If \(r\in R\) is an n-ary relation symbol and \(x_1 ,\ldots , x_n\) are variables from \(\mathcal {V}^+\), then \(r(x_1,\ldots ,x_n)\) and \(\lnot r(x_1,\ldots ,x_n)\) are guards.
-
If \(g_1\) and \(g_2\) are guards then \(g_1 \wedge g_2\) is a guard.
Let \(X \subset \mathcal {V}^+\). We say that g is a guard over X if all variables that occur in g are contained in X. A variable renaming is a function \(\sigma :X \rightarrow \mathcal {V}^+\). If g is a guard over X then \(g[\sigma ]\) is the guard obtained by replacing each variable x in g by \(\sigma (x)\).
Next, we define the notion of a data language. For this, we fix a finite set of actions \(\varSigma \). A data symbol \(\alpha (d)\) is a pair consisting of an action \(\alpha \in \varSigma \) and a data value \(d \in \mathcal {D}\). While relations may have arbitrary arity, we will assume that all actions have an arity of one to ease notation and simplify the text. A data word is a finite sequence of data symbols, and a data language is a set of data words. We denote concatenation of data words w and \(w'\) by \(w \cdot w'\), where \(w\) is the prefix and \(w'\) is the suffix. \( Acts (w)\) denotes the sequence of actions \(\alpha _1 \alpha _2 \ldots \alpha _n\) in \(w\), and \( Vals (w)\) denotes the sequence of data values \(d_1 d_2 \ldots d_n\) in \(w\). We refer to a sequence of actions in \(\varSigma ^{*}\) as a symbolic suffix. If w is a symbolic suffix then we write \(\llbracket {} w \rrbracket \) for the set of data words u with \( Acts (u) = w\).
Data languages may be represented by register automaton, defined below.
Definition 3
(Register Automaton). A Register Automaton (RA) is a tuple \(\mathscr {M}= (L, l_0, \mathcal {X}, \varGamma , \lambda )\) where
-
\(L\) is a finite set of locations, with \(l_0\) as the initial location;
-
\(\mathcal {X}\) maps each location \(l \in L\) to a finite set of registers \(\mathcal {X}(l)\);
-
\(\varGamma \) is a finite set of transitions, each of the form \(\langle {} l, \alpha (p), g, \pi , l' \rangle \), where
-
\(l, l'\) are source and target locations respectively,
-
\(\alpha (p)\) is a parametrised action,
-
\(g\) is a guard over \(\mathcal {X}(l) \cup \left\{ p\right\} \), and
-
\(\pi \) is an assignment mapping from \(\mathcal {X}(l')\) to \(\mathcal {X}(l) \cup \left\{ p\right\} \); and
-
-
\(\lambda \) maps each location in \(L\) to either accepting \((+)\) or rejecting \((-)\).
We require that \(\mathscr {M}\) is deterministic in the sense that for each location \(l \in L\) and input symbol \(\alpha \in \varSigma \), the conjunction of the guards of any pair of distinct \(\alpha \)-transitions with source l is not satisfiable. \(\mathscr {M}\) is completely specified if for all \(\alpha \)-transitions out of a location, the disjunction of the guards of the \(\alpha \)-transitions is a tautology. \(\mathscr {M}\) is said to be simple if there are no registers in the initial location, i.e., \(\mathcal {X}(l_{0}) = \varnothing \). In this text, all RAs are assumed to be completely specified and simple, unless explicitly stated otherwise. Locations \(l \in L\) with \(\lambda (l) = +\) are called accepting, and locations with \(\lambda (l) = -\) rejecting.
Example 1
(FIFO-buffer). The register automaton displayed in Fig. 2 models a FIFO-buffer with capacity 2. It has three accepting locations \(l_0\), \(l_1\) and \(l_2\) (denoted by a double circle), and one rejecting “sink” location \(l_3\) (denoted by a single circle). Function \(\mathcal {X}\) assigns the empty set of registers to locations \(l_0\) and \(l_3\), singleton set \(\left\{ x\right\} \) to location \(l_1\), and set \(\left\{ x, y\right\} \) to \(l_2\).
2.1 Semantics of a RA
We now formalise the semantics of an RA. A valuation of a set of variables X is a function \(\nu : X \rightarrow \mathcal {D}\) that assigns data values to variables in X. If \(\nu \) is a valuation of X and g is a guard over X then  is defined inductively by:
is defined inductively by:
-
 iff \((\nu (x_1),\ldots ,\nu (x_n)) \in r^{\mathcal {R}}\)
iff \((\nu (x_1),\ldots ,\nu (x_n)) \in r^{\mathcal {R}}\) -
 iff \((\nu (x_1),\ldots ,\nu (x_n)) \not \in r^{\mathcal {R}}\)
iff \((\nu (x_1),\ldots ,\nu (x_n)) \not \in r^{\mathcal {R}}\) -
 iff
iff 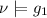 and
and 
A state of a RA \( \mathscr {M}= (L, l_0, \mathcal {X}, \varGamma , \lambda )\) is a pair \(\langle {} l,\nu \rangle \), where \(l \in L\) is a location and \(\nu : \mathcal {X}(l) \xrightarrow []{} \mathcal {D}\) is a valuation of the set of registers at location \(l\). A run of \(\mathscr {M}\) over data word \(w = \alpha _1(d_1) \ldots \alpha _n(d_n)\) is a sequence
where
-
for each \(0 \le i \le n\), \(\langle {} l_i, \nu _i \rangle \) is a state (with \(l_0\) the initial location),
-
for each \(0 < i \le n\), \(\langle {} l_{i-1}, \alpha _i(p), g_i, \pi _i, l_i \rangle \in \varGamma \) such that \( \iota _i \vDash g_i \) and \(\nu _i = \iota _i \circ \pi _i \), where \(\iota _i = \nu _{i-1} \cup \{ [p \mapsto d_{i}] \}\) extends \(\nu _{i-1}\) by mapping p to \(d_i\).
A run is accepting if \(\lambda (l_n) = + \), else rejecting. The language of \(\mathscr {M}\), notation \(L(\mathscr {M})\), is the set of words w such that \(\mathscr {M}\) has an accepting run over w. Word w is accepted (rejected) under valuation \(\nu _0\) if \(\mathscr {M}\) has an accepting (rejecting) run that starts in state \(\langle l_0, \nu _o \rangle \).
Example 2
Consider the FIFO-buffer example from Fig. 2. This RA has a run

and thus the trace is \(\mathsf{Push}(7) ~ \mathsf{Push}(7)~ \mathsf{Pop}(7) ~ \mathsf{Push}(5) ~ \mathsf{Pop}(7) ~ \mathsf{Pop}(5)\). \(\lrcorner \)
2.2 Symbolic Decision Tree
The \( SL ^*\) algorithm uses tree queries in place of membership queries. The arguments of a tree query are a prefix data word u and a symbolic suffix w, i.e., a data word with uninstantiated data parameters. The response to a tree query is a so called symbolic decision tree (SDT), which has the form of tree-shaped register automaton that accepts/rejects suffixes obtained by instantiating data parameters in one of the symbolic suffixes. Let us illustrate this on the FIFO-buffer example from Fig. 2 for the prefix \(\mathsf{Push}(5)~ \mathsf{Push}(7)\) and the symbolic suffix \(\mathsf{Pop}~ \mathsf{Pop}\). The acceptance/rejection of suffixes obtained by instantiating data parameters after \(\mathsf{Push}(5) ~ \mathsf{Push}(7)\) can be represented by the SDT in Fig. 3. In the initial location, values 5 and 7 from the prefix are stored in registers \(x_1\) and \(x_2\), respectively. Thus, SDTs will generally not be simple RAs. Moreover, since the leaves of an SDT have no outgoing transitions, they are also not completely specified. We use the convention that register \(x_i\) stores the \(i^{ th }\) data value. Thus, initially, register \(x_1\) contains value 5 and register \(x_2\) contains value 7. The initial transitions in the SDT contain an update \(x_3 := p\), and the final transitions an update \(x_4 :=p\). For readability, these updates are not displayed in the diagram. The SDT accepts suffixes of form \(\mathsf{Pop}(d_1) ~ \mathsf{Pop}(d_2)\) iff \(d_1\) equals the value stored in register \(x_1\), and \(d_2\) equals the data value stored in register \(x_2\). For a more detailed discussion of SDTs we refer to [6].
3 Tainting
We postulate that the behaviour of the SUT (in our case: a Python program) can be modeled by a register automaton \(\mathscr {M}\). In a black-box setting, observations on the SUT will then correspond to words from the data language of \(\mathscr {M}\). In this section, we will describe the additional observations that a learner can make in a grey-box setting, where the constraints on the data parameters that are imposed within a run become visible. In this setting, observations of the learner will correspond to what we call tainted words of \(\mathscr {M}\). Tainting semantics is an extension of the standard semantics in which each input value is “tainted” with a unique marker from \(\mathcal {V}\). In a data word \(w = \alpha _1(d_1) \alpha _2(d_2) \ldots \alpha _n(d_n)\), the first data value \(d_1\) is tainted with marker \(v_1\), the second data value \(d_2\) with \(v_2\), etc. While the same data value may occur repeatedly in a data word, all the markers are different.
3.1 Semantics of Tainting
A tainted state of a RA \( \mathscr {M}= (L, l_0, \mathcal {X}, \varGamma , \lambda )\) is a triple \(\langle {} l,\nu , \zeta \rangle \), where \(l \in L\) is a location, \(\nu : \mathcal {X}(l) \rightarrow \mathcal {D}\) is a valuation, and \(\zeta : \mathcal {X}(l) \rightarrow \mathcal {V}\) is a function that assigns a marker to each register of l. A tainted run of \(\mathscr {M}\) over data word \(w = \alpha _1(d_1) \ldots \alpha _n(d_n)\) is a sequence
where
-
\(\langle {} l_0, \nu _0 \rangle \xrightarrow {\alpha _1(d_1), g_1, \pi _1} \!\langle {} l_1, \nu _1 \rangle \ldots \!\langle {} l_{n-1}, \nu _{n-1} \rangle \xrightarrow {\alpha _n(d_n), g_n, \pi _n} \!\langle {} l_n, \nu _n \rangle \) is a run of \(\mathscr {M}\),
-
for each \(0 \le i \le n\), \(\langle {} l_i, \nu _i, \zeta _i \rangle \) is a tainted state,
-
for each \(0 < i \le n\), \(\zeta _i = \kappa _i \circ \pi _i\), where \(\kappa _i = \zeta _{i-1} \cup \{ (p,v_i) \}\).
The tainted word of \(\tau \) is the sequence \(w = \alpha _1 (d_1) G_1 \alpha _2 (d_2) G_2 \cdots \alpha _n (d_n) G_n\), where \(G_i = g_i[\kappa _i]\), for \(0 < i \le n\). We define \( constraints _{\mathscr {M}}(\tau ) = [G_1,\ldots , G_n]\).
Let \(w = \alpha _1(d_1) \ldots \alpha _n(d_n)\) be a data word. Since register automata are deterministic, there is a unique tainted run \(\tau \) over w. We define \( constraints _{\mathscr {M}}(w) = constraints _{\mathscr {M}}(\tau )\), that is, the constraints associated to a data word are the constraints of the unique tainted run that corresponds to it. In the untainted setting a membership query for data word w leads to a response “yes” if \(w \in L(\mathscr {M})\), and a response “no” otherwise, but in a tainted setting the predicates \( constraints _{\mathscr {M}}(w)\) are also included in the response, and provide additional information that the learner may use.
Example 3
Consider the FIFO-buffer example from Fig. 2. This RA has a tainted run
(For readability, guards \(g_i\) and assignments \(\pi _i\) have been left out.) The constraints in the corresponding tainted trace can be computed as follows:

and thus the tainted word is:
and the corresponding list of constraints is \( [ \top , \top , v_3 = v_1, \top , v_5 = v_2, v_6 = v_4]\). \(\lrcorner \)
Various techniques can be used to observe tainted traces, for instance symbolic and concolic execution. In this work, we have used a library called “taintedstr” to achieve tainting in Python and make tainted traces available to the learner.
3.2 Tainting in Python
Tainting in Python is achieved by using a library called “taintedstr”Footnote 3, which implements a “tstr” (tainted string) class. We do not discuss the entire implementation in detail, but only introduce the portions relevant to our work. The “tstr” class works by operator overloading: each operator is overloaded to record its own invocation. The tstr class overloads the implementation of the “__eq__” (equality) method in Python’s str class, amongst others. In this text, we only consider the equality method. A tstr object \(x\) can be considered as a triple \(\langle {} o, t, cs \rangle \), where \(o\) is the (base) string object, \(t\) is the taint value associated with string \(o\), and \( cs \) is a set of comparisons made by \(x\) with other objects, where each comparison \(c \in cs \) is a triple \(\langle {} f, a, b \rangle \) with \(f\) the name of the binary method invoked on \(x\), \(a\) a copy of \(x\), and \(b\) the argument supplied to \(f\).
Each a method \(f\) in the tstr class is an overloaded implementation of the relevant (base) method \(f\) as follows:

We present a short example of how such an overloaded method would work below:
Example 4
(tstr tainting). Consider two tstr objects: \(x_1 = \langle {} \text {``1''} , 1, \emptyset \rangle \) and \(x_2 = \langle {} \text {``1''}, 2, \emptyset \rangle \). Calling \(x_1 == x_2 \) returns True as \(x_{1}.o = x_{2}.o\). As a side-effect of f, the set of comparisons \(x_{1}.cs\) is updated with the triple \(c = \langle {} \text {``}\_\_\text {eq}\_\_\text {''}, x_1, x_2 \rangle \). We may then confirm that \(x_1\) is compared to \(x_2\) by checking the taint values of the variables in comparison \(c\): \(x_1.t = 1\) and \(x_2.t = 2\).
Note, our approach to tainting limits the recorded information to operations performed on a tstr object. Consider the following snippet, where \(x_1, x_2, x_3\) are tstr objects with \(1,2,3\) as taint values respectively:

If the base values of \(x_1\) and \(x_2\) are equal, the Python interpreter will “short-circuit” the if-statement and the second condition, \(x_2 \ne x_3\), will not be evaluated. Thus, we only obtain one comparison: \(x_{1} = x_{2}\). On the other hand, if the base values of \(x_1\) and \(x_2\) are not equal, the interpreter will not short-circuit, and both comparisons will be recorded as \( \left\{ x_2 = x_3, x_1 \ne x_2\right\} \). However, the external negation operation will not be recorded by any of the tstr objects: the negation was not performed on the tstr objects. \(\lrcorner \)
4 Learning Register Automata Using Tainting
Given an SUT and a tree query, we generate an SDT in the following steps: (i) construct a characteristic predicate of the tree query (Algorithm 1) using membership and guard queries, (ii) transform the characteristic predicate into an SDT (Algorithm 2), and (iii) minimise the obtained SDT (Algorithm 3).
4.1 Tainted Tree Oracle
Construction of Characteristic Predicate. For \(u = \alpha (d_1) \cdots \alpha _k(d_k)\) a data word, \(\nu _u\) denotes the valuation of \(\left\{ x_1,\ldots ,x_k\right\} \) with \(\nu _u(x_i) = d_i\), for \(1 \le i \le k\). Suppose u is a prefix and \(w= \alpha _{k+1} \cdots \alpha _{k+n}\) is a symbolic suffix. Then H is a characteristic predicate for u and w in \(\mathscr {M}\) if, for each valuation \(\nu \) of \(\left\{ x_1,\ldots , x_{k+n}\right\} \) that extends \(\nu _u\),

that is, H characterizes the data words \(u'\) with \( Acts (u') = w\) such that \(u \cdot u'\) is accepted by \(\mathscr {M}\). In the case of the FIFO-buffer example from Fig. 2, a characteristic predicate for prefix \(\mathsf{Push}(5)~ \mathsf{Push}(7)\) and symbolic suffix \(\mathsf{Pop}~ \mathsf{Pop}\) is \(x_3 = x_1 \wedge x_4 = x_2\). A characteristic predicate for the empty prefix and symbolic suffix \(\mathsf{Pop}\) is \(\perp \), since this trace will inevitably lead to the sink location \(l_3\) and there are no accepting words.
Algorithm 1 shows how a characteristic predicate may be computed by systematically exploring all the (finitely many) paths of \(\mathscr {M}\) with prefix u and suffix w using tainted membership queries. During the execution of Algorithm 1, predicate G describes the part of the parameter space that still needs to be explored, whereas H is the characteristic predicate for the part of the parameter space that has been covered. We use the notation \(H \equiv T\) to indicate syntactic equivalence, and \(H = T\) to indicate logical equivalence. Note, if there exists no parameter space to be explored (i.e., w is empty) and \(u \in L(\mathscr {M})\), the algorithm returns \(H \equiv \perp \vee \top \) (as the empty conjunction equals \(\top \)).

Example 5
(Algorithm 1). Consider the FIFO-buffer example and the tree query with prefix \(\mathsf{Push}(5)~ \mathsf{Push}(7)\) and symbolic suffix \(\mathsf{Pop}~ \mathsf{Pop}\). After the prefix location \(l_2\) is reached. From there, three paths are possible with actions \(\mathsf{Pop}~ \mathsf{Pop}\): \(l_2 l_3 l_3\), \(l_2 l_1 l_3\) and \(l_2 l_1 l_0\). We consider an example run of Algorithm 1.
Initially, \(G_0 \equiv \top \) and \(H_0 \equiv \perp \). Let \(\nu _1 = [ x_1 \mapsto 5, x_2 \mapsto 7, x_3 \mapsto 1, x_4 \mapsto 1]\). Then \(\nu _1\) extends \(\nu _u\) and  . The resulting tainted run corresponds to path \(l_2 l_3 l_3\) and so the tainted query gives path constraint \(I_1 \equiv x_3 \ne x_1 \wedge \top \). Since the tainted run is rejecting, \(H_1 \equiv \perp \) and \(G_1 \equiv \top \wedge \lnot I_1\).
. The resulting tainted run corresponds to path \(l_2 l_3 l_3\) and so the tainted query gives path constraint \(I_1 \equiv x_3 \ne x_1 \wedge \top \). Since the tainted run is rejecting, \(H_1 \equiv \perp \) and \(G_1 \equiv \top \wedge \lnot I_1\).
In the next iteration, we set \(\nu _2 = [ x_1 \mapsto 5, x_2 \mapsto 7, x_3 \mapsto 5, x_4 \mapsto 1]\). Then \(\nu _2\) extends \(\nu _u\) and  . The resulting tainted run corresponds to path \(l_2 l_1 l_3\) and so the tainted query gives path constraint \(I_2 \equiv x_3 = x_1 \wedge x_4 \ne x_2\). Since the tainted run is rejecting, \(H_2 \equiv \perp \) and \(G_2 \equiv \top \wedge \lnot I_1 \wedge \lnot I_2\).
. The resulting tainted run corresponds to path \(l_2 l_1 l_3\) and so the tainted query gives path constraint \(I_2 \equiv x_3 = x_1 \wedge x_4 \ne x_2\). Since the tainted run is rejecting, \(H_2 \equiv \perp \) and \(G_2 \equiv \top \wedge \lnot I_1 \wedge \lnot I_2\).
In the final iteration, we set \(\nu _3 = [ x_1 \mapsto 5, x_2 \mapsto 7, x_3 \mapsto 5, x_4 \mapsto 7]\). Then \(\nu _3\) extends \(\nu _u\) and  . The resulting tainted run corresponds to path \(l_2 l_1 l_0\) and the tainted query gives path constraint \(I_3 \equiv x_3 = x_1 \wedge x_4 = x_2\). Now the tainted run is accepting, so \(H_3 \equiv \perp \vee I_3\) and \(G_3 = \top \wedge \lnot I_1 \wedge \lnot I_2 \wedge \lnot I_3\). As \(G_3\) is unsatisfiable, the algorithm terminates and returns characteristic predicate \(H_3\).
. The resulting tainted run corresponds to path \(l_2 l_1 l_0\) and the tainted query gives path constraint \(I_3 \equiv x_3 = x_1 \wedge x_4 = x_2\). Now the tainted run is accepting, so \(H_3 \equiv \perp \vee I_3\) and \(G_3 = \top \wedge \lnot I_1 \wedge \lnot I_2 \wedge \lnot I_3\). As \(G_3\) is unsatisfiable, the algorithm terminates and returns characteristic predicate \(H_3\).
Construction of a Non-minimal SDT. For each tree query with prefix u and symbolic suffix w, the corresponding characteristic predicate H is sufficient to construct an SDT using Algorithm 2.

We construct the SDT recursively while processing each action in the symbolic suffix \(w= \alpha _{k+1} \cdots \alpha _{k+m}\) in order. The valuation \(\nu \) is unnecessary, as there are no guards defined over the prefix parameters. During the execution of Algorithm 2, for a suffix action \(\alpha (x_{n}) \), the potential set \(I_t \) contains the set of parameters to which \(x_{n}\) is compared to in H. Each element in \(I_{t}\) can be either a formal parameter in the tree query or a constant. For each parameter \(x_{i} \in I_{t}\) we construct an equality sub-tree where \(x_{n} = x_{i}\). We also construct a disequality sub-tree where \(x_{n}\) is not equal to any of the parameters in \(I_{t}\). The base case (i.e., \(w = \epsilon \)) return an accepting or rejecting leaf node according to the characteristic predicate at the base case: if \(H \iff \bot \) then rejecting, else accepting. Example 6 provides a short explanation of Algorithm 2.
Example 6
(Algorithm 2). Consider a characteristic predicate \(H \equiv I_{1} \vee I_{2} \vee I_{3} \vee I_{4}\), where \(I_{1} \equiv x_{2} \ne x_{1} \wedge x_{3} \ne x_{1}\), \(I_{2} \equiv x_{2} = x_{1} \wedge x_{3} \ne x_{1}\), \(I_{3} \equiv x_2 \ne x_{1} \wedge x_3 = x_{1}\), \(I_{4} \equiv x_2 = x_{1} \wedge x_3 = x_{1}\). We discuss only the construction of the sub-tree rooted at node \(s_{21}\) for the SDT visualised in Fig. 4a; the construction of the remainder is similar.
Initially, \(x_{n} = x_{k+1} = x_{2}\). Potential set \(I_{t}\) for \(x_{2}\) is \(\left\{ x_{1}\right\} \) as H contains the literals \(x_{2} = x_{1}\) and \(x_{2} \ne x_{1}\). Consider the construction of the equality guard \(g := x_{2} = x_{1}\). The new characteristic predicate is \(H' \equiv (I_{2} \wedge g) \vee (I_{4} \wedge g)\), as \(I_{1}\) and \(I_{3}\) are unsatisfiable when conjugated with g.
For the next call, with \(n=3\), the current variable is \(x_{3}\), with predicate \(H = H'\) (from the parent instance). We obtain the potential set for \(x_{3}\) as \(\left\{ x_{1}\right\} \). The equality guard is \(g' := x_{3} = x_{1}\) with the new characteristic predicate \(H'' \equiv I_{4} \wedge g \wedge g'\), i.e., \(H'' \iff x_{2} = x_{1} \wedge x_{3} = x_{1}\) (note, \(I_{2} \wedge g \wedge g'\) is unsatisfiable). In the next call, we have \(n = 4\), thus we compute a leaf. As \(H''\) is not \(\bot \), we return an accepting leaf t. The disequality guard is \(g'' := x_{3} \ne x_{1}\) with characteristic predicate \(H''' \iff x_{2} = x_{1} \wedge x_{3} = x_{1} \wedge x_{3} \ne x_{1} \iff \bot \). In the next call, we have \(n=4\), and we return a non-accepting leaf \(t'\). The two trees t and \(t'\) are added as sub-trees with their respective guards \(g'\) and \(g''\) to a new tree rooted at node \(s_{21}\) (see Fig. 4a). \(\lrcorner \)
SDT Minimisation. Example 6 showed a characteristic predicate H containing redundant comparisons, resulting in the non-minimal SDT in Fig. 4a. We use Algorithm 3 to minimise the SDT in Fig. 4a to the SDT in Fig. 4b.

We present an example of the application of Algorithm 3, shown for the SDT of Fig. 4a. Figure 4a visualises a non-minimal SDT \(\mathcal {T}\), where \(s_{20}\) and \(s_{21}\) (in red) are essentially “duplicates” of each other: the sub-tree for node \(s_{20}\) is isomorphic to the sub-tree for node \(s_{21}\) under the relabelling “\(x_2 = x_1\)”. We indicate this relabelling using the notation \(\mathcal {T}[s_{20}]\langle {} x_1, x_2 \rangle \) and the isomorphism relation under the relabelling as \(\mathcal {T}[s_{20}]\langle {} x_1, x_2 \rangle \simeq \mathcal {T}[s_{21}]\). Algorithm 3 accepts the non-minimal SDT of Fig. 4a and produces the equivalent minimal SDT in Fig. 4b. Nodes \(s_{20}\) and \(s_{21}\) are merged into one node, \(s_2\), marked in green. We can observe that both SDTs still encode the same decision tree. With Algorithm 3, we have completed our tainted tree oracle, and can now proceed to the tainted equivalence oracle.
4.2 Tainted Equivalence Oracle
The tainted equivalence oracle (TEO), similar to its non-tainted counterpart, accepts a hypothesis \(\mathcal {H}\) and verifies whether \(\mathcal {H}\) is equivalent to register automaton \(\mathcal {M}\) that models the SUT. If \(\mathcal {H}\) and \(\mathcal {M}\) are equivalent, the oracle replies “yes”, otherwise it returns “no” together with a CE. The RandomWalk Equivalence Oracle in RALib constructs random traces in order to find a CE.
Definition 4
(Tainted Equivalence Oracle). For a given hypothesis \(\mathcal {H}\), maximum word length n, and an SUT \(\mathcal {S}\), a tainted equivalence oracle is a function \(\mathcal {O}_{\mathcal {E}}(\mathcal {H}, n, \mathcal {S})\) for all tainted traces w of \(\mathcal {S}\) where \(| w | \le n\), \( \mathcal {O}_{\mathcal {E}} (\mathcal {H}, n, \mathcal {S}) \) returns w if \( w \in \mathcal {L}(\mathcal {H}) \iff w \in \mathcal {L}(\mathcal {S}) \) is false, and ‘Yes’ otherwise.
The TEO is similar to the construction of the characteristic predicate to find a CE: we randomly generate a symbolic suffix of specified length n (with an empty prefix), and construct a predicate H for the query. For each trace w satisfying a guard in H, we confirm whether \(w \in \mathcal {L}(\mathcal {H}) \iff w \in \mathcal {L}(\mathcal {M})\). If false, w is a CE. If no w is false, then we randomly generate another symbolic suffix. In practise, we bound the number of symbolic suffixes to generate. Example 7 presents a scenario of a combination lock automaton that can be learned (relatively easily) using a TEO but cannot be handled by normal oracles.
Example 7
(Combination Lock RA). A combination lock is a type of RA which requires a sequence of specific inputs to ‘unlock’. Figure 5 presents an RA \(\mathcal {C}\) with a ‘4-digit’ combination lock that can be unlocked by the sequence \( w = \alpha (c_0)\alpha (c_1)\alpha (c_2)\alpha (c_3)\), where \(\left\{ c_0, c_1, c_2, c_3\right\} \) are constants. Consider a case where a hypothesis \(\mathcal {H}\) is being checked for equivalence against the RA \(\mathcal {C}\) with \(w \not \in \mathcal {L}(\mathcal {H})\). While it would be difficult for a normal equivalence oracle to generate the word \(w\) randomly; the tainted equivalence oracle will record at every location the comparison of input data value \(p\) with some constant \(c_i\) and explore all corresponding guards at the location, eventually constructing the word \(w\).
For the combination lock automaton, we may note that as the ‘depth’ of the lock increases, the possibility of randomly finding a CE decreases. \(\lrcorner \)
5 Experimental Evaluation
We have used stubbed versions of the Python FIFO-Queue and Set modulesFootnote 4 for learning the FIFO and Set models, while the Combination Lock automata were constructed manually. Source code for all other models was obtained by translating existing benchmarks from [18] (see also automata.cs.ru.nl) to Python code. We also utilise a ‘reset’ operation: A ‘reset’ operation brings an SUT back to its initial state, and is counted as an ‘input’ for our purposes. Furthermore, each experiment was repeated 30 times with different random seeds. Each experiment was bounded according to the following constraints: learning phase: \(10^9\) inputs and \(5 \times 10^7\) resets; testing phase: \(10^9\) inputs and \(5 \times 10^4\) resets; length of the longest word during testing: 50; and a ten-minute timeout for the learner to respond.
Figure 6 gives an overview of our experimental results. We use the notation ‘TTO’ to represent ‘Tainted Tree Oracle’ (with similar labels for the other oracles). In the figure, we can see that as the size of the container increases, the difference between the fully tainted version (TTO+TEO, in blue) and the completely untainted version (NTO+NEO, in red) increases. In the case where only a tainted tree oracle is used (TTO+NEO, in green), we see that it is following the fully tainted version closely (for the FIFO models) and is slightly better in the case of the SET models.
Benchmark plots: Number of symbols used with tainted oracles (blue and green) are generally lower than with normal oracles (red and orange). Note that the y-axis is log-scaled. Additionally, normal oracles are unable to learn the Combination Lock and Repetition automata and are hence not plotted. (Color figure online)
The addition of the TEO gives a conclusive advantage for the Combination Lock and Repetition benchmarks. The addition of the TTO by itself results in significantly fewer number of symbols, even without the tainted equivalence oracle (TTO v/s NTO, compare the green and red lines). With the exception of the Combination Lock and Repetition benchmarks, the TTO+TEO combination does not provide vastly better results in comparison to the TTO+NEO results, however, it is still (slightly) better. We note that—as expected—the NEO does not manage to provide CEs for the Repetition and Combination Lock automata. The TEO is therefore much more useful for finding CEs in SUTs which utilise constants.
6 Conclusions and Future Work
In this article, we have presented an integration of dynamic taint analysis, a white-box technique for tracing data flow, and register automata learning, a black-box technique for inferring behavioral models of components. The combination of the two methods improves upon the state-of-the-art in terms of the class of systems for which models can be generated and in terms of performance: Tainting makes it possible to infer data-flow constraints even in instances with a high intrinsic complexity (e.g., in the case of so-called combination locks). Our implementation outperforms pure black-box learning by two orders of magnitude with a growing impact in the presence of multiple data parameters and registers. Both improvements are important steps towards the applicability of model learning in practice as they will help scaling to industrial use cases.
At the same time our evaluation shows the need for further improvements: Currently, the \( SL ^*\) algorithm uses symbolic decision trees and tree queries globally, a well-understood weakness of learning algorithms that are based on observation tables. It also uses individual tree oracles each type of operation and relies on syntactic equivalence of decision trees. A more advanced learning algorithm for extended finite state machines will be able to consume fewer tree queries, leverage semantic equivalence of decision trees. Deeper integration with white-box techniques could enable the analysis of many (and more involved) operations on data values.
Notes
- 1.
Available at https://bitbucket.org/toonlenaerts/taintralib/src/basic.
- 2.
- 3.
See [12] and https://github.com/vrthra/taintedstr.
- 4.
From Python’s queue module and standard library, respectively.
References
Aarts, F., Heidarian, F., Kuppens, H., Olsen, P., Vaandrager, F.: Automata learning through counterexample guided abstraction refinement. In: Giannakopoulou, D., Méry, D. (eds.) FM 2012. LNCS, vol. 7436, pp. 10–27. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32759-9_4
Aarts, F., Jonsson, B., Uijen, J., Vaandrager, F.: Generating models of infinite-state communication protocols using regular inference with abstraction. Formal Meth. Syst. Des. 46(1), 1–41 (2015). https://doi.org/10.1007/s10703-014-0216-x
Angluin, D.: Learning regular sets from queries and counterexamples. Inf. Comput. 75(2), 87–106 (1987)
Botinčan, M., Babić, D.: Sigma*: symbolic learning of input-output specifications. In: POPL 2013, pp. 443–456. ACM, New York (2013)
Cassel, S., Howar, F., Jonsson, B., Steffen, B.: Learning extended finite state machines. In: Giannakopoulou, D., Salaün, G. (eds.) SEFM 2014. LNCS, vol. 8702, pp. 250–264. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10431-7_18
Cassel, S., Howar, F., Jonsson, B., Steffen, B.: Active learning for extended finite state machines. Formal Aspects Comput. 28(2), 233–263 (2016). https://doi.org/10.1007/s00165-016-0355-5
Cho, C.Y., Babić, D., Poosankam, P., Chen, K.Z., Wu, E.X., Song, D.: MACE: model-inference-assisted concolic exploration for protocol and vulnerability discovery. In: SEC 2011, p. 10. USENIX, Berkeley, USA (2011)
Fiterău-Broştean, P., Janssen, R., Vaandrager, F.: Combining model learning and model checking to analyze TCP implementations. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9780, pp. 454–471. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41540-6_25
Fiterău-Broştean, P., Howar, F.: Learning-based testing the sliding window behavior of TCP implementations. In: Petrucci, L., Seceleanu, C., Cavalcanti, A. (eds.) FMICS/AVoCS - 2017. LNCS, vol. 10471, pp. 185–200. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-67113-0_12
Fiterău-Broştean, P., Lenaerts, T., Poll, E., de Ruiter, J., Vaandrager, F., Verleg, P.: Model learning and model checking of SSH implementations. In: SPIN 2017, pp. 142–151. ACM, New York (2017)
Giannakopoulou, D., Rakamarić, Z., Raman, V.: Symbolic learning of component interfaces. In: Miné, A., Schmidt, D. (eds.) SAS 2012. LNCS, vol. 7460, pp. 248–264. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33125-1_18
Gopinath, R., Mathis, B., Höschele, M., Kampmann, A., Zeller, A.: Sample-free learning of input grammars for comprehensive software fuzzing. CoRR abs/1810.08289 (2018)
Hagerer, A., Margaria, T., Niese, O., Steffen, B., Brune, G., Ide, H.D.: Efficient regression testing of CTI-systems: testing a complex call-center solution. Ann. Rev. Commun. IEC 55, 1033–1040 (2001)
Howar, F., Isberner, M., Steffen, B., Bauer, O., Jonsson, B.: Inferring semantic interfaces of data structures. In: Margaria, T., Steffen, B. (eds.) ISoLA 2012. LNCS, vol. 7609, pp. 554–571. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34026-0_41
Howar, F., Giannakopoulou, D., Rakamarić, Z.: Hybrid learning: interface generation through static, dynamic, and symbolic analysis. In: ISSTA 2013, pp. 268–279. ACM, New York (2013)
Howar, F., Jonsson, B., Vaandrager, F.: Combining black-box and white-box techniques for learning register automata. In: Steffen, B., Woeginger, G. (eds.) Computing and Software Science. LNCS, vol. 10000, pp. 563–588. Springer, Cham (2019). https://doi.org/10.1007/978-3-319-91908-9_26
Howar, F., Steffen, B.: Active automata learning in practice. In: Bennaceur, A., Hähnle, R., Meinke, K. (eds.) Machine Learning for Dynamic Software Analysis: Potentials and Limits. LNCS, vol. 11026, pp. 123–148. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96562-8_5
Neider, D., Smetsers, R., Vaandrager, F., Kuppens, H.: Benchmarks for automata learning and conformance testing. In: Margaria, T., Graf, S., Larsen, K.G. (eds.) Models, Mindsets, Meta: The What, the How, and the Why Not?. LNCS, vol. 11200, pp. 390–416. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-22348-9_23
Schuts, M., Hooman, J., Vaandrager, F.: Refactoring of legacy software using model learning and equivalence checking: an industrial experience report. In: Ábrahám, E., Huisman, M. (eds.) IFM 2016. LNCS, vol. 9681, pp. 311–325. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-33693-0_20
Vaandrager, F.: Model learning. Commun. ACM 60(2), 86–95 (2017)
Acknowledgement
We are grateful to Andreas Zeller for explaining the use of tainting for dynamic tracking of constraints, and to Rahul Gopinath for helping us with his library for tainting Python programs. We also thank the anonymous reviewers for their suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Garhewal, B., Vaandrager, F., Howar, F., Schrijvers, T., Lenaerts, T., Smits, R. (2020). Grey-Box Learning of Register Automata. In: Dongol, B., Troubitsyna, E. (eds) Integrated Formal Methods. IFM 2020. Lecture Notes in Computer Science(), vol 12546. Springer, Cham. https://doi.org/10.1007/978-3-030-63461-2_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-63461-2_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-63460-5
Online ISBN: 978-3-030-63461-2
eBook Packages: Computer ScienceComputer Science (R0)







 iff
iff  iff
iff  iff
iff 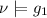 and
and 



