Time Correlation Exponents in Last Passage Percolation

Abstract

For directed last passage percolation on $\mathbb {Z}^2$ with exponential passage times on the vertices, let T _n denote the last passage time from (0, 0) to (n, n). We consider asymptotic two point correlation functions of the sequence T _n. In particular we consider Corr(T _n, T _r) for r ≤ n where r, n →∞ with r ≪ n or n − r ≪ n. Establishing a conjecture from Ferrari and Spohn (SIGMA 12:074, 2016), we show that in the former case $\mathrm {Corr}(T_{n}, T_{r})=\varTheta ((\frac {r}{n})^{1/3})$ whereas in the latter case $1-{\mathrm {Corr}}(T_{n}, T_{r})=\varTheta ((\frac {n-r}{n})^{2/3})$. The argument revolves around finer understanding of polymer geometry and is expected to go through for a larger class of integrable models of last passage percolation. As a by-product of the proof, we also get quantitative estimates for locally Brownian nature of pre-limits of Airy₂ process coming from exponential LPP, a result of independent interest.

In memory of Vladas Sidoravicius

1 Introduction and Statement of Results

We consider directed last passage percolation on $\mathbb {Z}^2$ with i.i.d. exponential weights on the vertices. We have a random field

$$\displaystyle \begin{aligned}\omega=\{\omega_{v}: v\in \mathbb{Z}^2\}\end{aligned}$$

where ω _v are i.i.d. standard Exponential variables. For any two points u and v with u ≼ v in the usual partial order, we shall denote by T _u,v the last passage time from u to v; i.e., the maximum weight among all weights of all directed paths from u to v (the weight of a path is the sum of the field along the path). By Γ _u,v, we shall denote the almost surely unique path that attains the maximum- this will be called a polymer or a geodesic. This is one of the canonical examples of an integrable model in the so-called KPZ universality class [7, 18], and has been extensively studied also due to its connection to Totally Asymmetric Simple Exclusion process on $\mathbb {Z}$. For notational convenience let us denote (r, r) for any $r\in \mathbb {Z}$ by r and T _0,n by T _n and similarly Γ _0,n by Γ _n. It is well known [18] that n ^−1∕3(T _n − 4n) has a distributional limit (a scalar multiple of the GUE Tracy–Widom distribution), and further it has uniform (in n) exponential tail estimates [1, 24]. Although the scaled and centered field obtained from {T _0,(x,y)}_x+y=2n using the KPZ scaling factors of n ^2∕3 in space and n ^1∕3 in polymer weight has been intensively studied and the scaling limit as n →∞ identified to be the Airy₂ process (minus a parabola), much less is known about the evolution of the random field in time i.e., across various values of n. However very recently there has been some attempts to understand the latter, see [2, 20,21,22,23, 25, 26] for some recent progress.

In this paper, we study two point functions describing the ‘aging’ properties of the above evolution. More precisely we investigate the correlation structure of the tight sequence of random variables n ^−1∕3(T _n − 4n) across n. In particular, let us define for $r\le n\in \mathbb {N}$

$$\displaystyle \begin{aligned}\rho(n,r)=: \mbox{Corr} (T_{n}, T_{r} ).\end{aligned}$$

We are interested in the dependence of ρ(n, r) on n and r as they become large. Observe that the FKG inequality implies that ρ(n, r) ≥ 0. Heuristically, one would expect that ρ(n, r) is close to 1 and 0 for |n − r|≪ n and r ≪ n respectively.

Our main result in this paper establishes the exponents governing the rate of correlation decay and thus identifies up to constants the asymptotics of ρ in these regimes establishing a prediction from [16]. Namely we show

$$\displaystyle \begin{aligned} \rho(n,r)=\varTheta((\frac{r}{n})^{1/3}) \mbox{ if } 1\ll r\ll n \mbox{ and } \rho(n,r)=1-\varTheta ((\frac{n-r}{n})^{2/3}) \mbox{ if } 1\ll n-r \ll n. \end{aligned}$$

It turns out that the upper bound in the former case is similar to the lower bound in the latter case, and the lower bound in the former case is similar to to the upper bound in the latter case. We club these statements in the following two theorems.

Theorem 1

There exists $r_0\in \mathbb {N}$ and positive absolute constants δ ₁ , C ₁ , C ₂ such that the following hold.

• (i) For r ₀ < r < δ ₁ n and for all n sufficiently large we have

  $$\displaystyle \begin{aligned}\rho (n,r)\leq C_1 \left( \frac{r}{n} \right)^{1/3}.\end{aligned} $$

• (ii) For r ₀ < n − r < δ ₁ n and for all n sufficiently large we have

  $$\displaystyle \begin{aligned}1-\rho (n,r)\leq C_2 \left( \frac{n-r}{n} \right)^{2/3}.\end{aligned}$$

Theorem 2

There exists $r_0\in \mathbb {N}$ and positive absolute constants δ ₁ , C ₃ , C ₄ such that the following hold.

• (i) For r ₀ < r < δ ₁ n and for all n sufficiently large we have

  $$\displaystyle \begin{aligned}\rho (n,r)\geq C_3 \left( \frac{r}{n} \right)^{1/3}.\end{aligned} $$

• (ii) For r ₀ < n − r < δ ₁ n and for all n sufficiently large we have

  $$\displaystyle \begin{aligned}1-\rho (n,r)\geq C_4 \left( \frac{n-r}{n} \right)^{2/3}.\end{aligned}$$

1.1 Note on the History of This Problem and This Paper

These exponents were conjectured in [16] using partly rigorous analysis, and as far as we are aware was first rigorously obtained in an unpublished work of Corwin and Hammond [10] in the context of Airy line ensemble using the Brownian Gibbs property of the same established in [11]. A related work studying time correlation for KPZ equation has since appeared [12]. Days before posting the first version of this paper on arXiv in July 2018, we came across [15] which considers the same problem. Working with rescaled last passage percolation [15] analyzes the limiting quantity r(τ) :=lim_n→∞Corr(T _n, T _τn). They establish the existence of the limit and consider the τ → 0 and τ → 1 asymptotics establishing the same exponents as in Theorems 1 and 2. The approach in [15] uses comparison with stationary LPP using exit points [9] together with using weak convergence to Airy process leading to natural variational formulas. In the limiting regime they get a sharper estimate obtaining an explicit expression of the first order term, providing rigorous proofs of some of the conjectures in [16]. In contrast, our approach hinges on using the moderate deviation estimates for point-to-point last passage time to understand local fluctuations in polymer geometry following the approach taken in [3, 6] leading to results for finite n, also allowing us to analyze situations r ≪ n or n − r ≪ n, which can’t be read off from weak convergence. Our work is completely independent of [15].

The ideas in this paper has since been further developed in a joint work with Lingfu Zhang [5] to treat the case of flat initial data (i.e., line-to-point last passage percolation) in the τ → 0 limit, and the remaining conjectured exponent from [16] has been established there. As it turns out, the upper bound in the case of flat initial data requires rather different arguments, but the lower bound in [5] further develops the same line of arguments as in the original version of this paper, and improves upon some of the estimates proved there. As such, in this version, we have decided to omit some of the details of the proof of Theorem 2, and we refer to the relevant steps in [5] instead. We expect this class of ideas and estimates to be crucial in further enhancing our understanding of temporal correlations in the KPZ universality class with more general initial conditions.

1.2 Local Fluctuations of the Weight Profile

In the process of proving Theorems 1 and 2 we prove a certain auxiliary result of independent interest. Namely, we establish a local regularity property of the pre-limiting profile of Airy₂ process obtained from the exponential LPP model. We need to introduce some notations before making the formal statement. For $n\in \mathbb {N}, s\in \mathbb {Z}$ with |s| < n we define

$$\displaystyle \begin{aligned}L_{n,s}:= T_{\mathbf{0},(n+s,n-s)}.\end{aligned}$$

It is known [7] that

$$\displaystyle \begin{aligned}\mathcal{L}_n(x):=2^{-4/3}n^{-1/3}(L_{n,x(2n)^{2/3}}-4n)\end{aligned}$$

converges in the sense of finite dimensional distributions to the $\mathcal {A}_2(x)-x^{2}$ where $\mathcal {A}_2(\cdot )$ denotes the stationary Airy₂ process (tightness, and hence weak convergence is also known, see e.g. [14]). It is known that the latter locally looks like Brownian motion [17, 27] and hence one would expect that $\mathcal {L}_n(x)-\mathcal {L}_n(0)$ will have a fluctuation of order x ^1∕2 for small x. We prove a quantitative version of the same at all shorter scales.

Theorem 3

There exist constants s ₀ > 0, z ₀ > 0 and C, c > 0 such that the following holds for all s > s ₀ , z > z ₀ and for all n > Cs ^3∕2:

$$\displaystyle \begin{aligned}\mathbb{P}\left (\sup_{s': |s'|<s} L_{n,s'}-L_{n,0} \geq zs^{1/2}\right) \leq e^{-cz^{4/9}}.\end{aligned}$$

Such an estimate was first obtained in [17] for Brownian last passage percolation using the Brownian Gibbs resampling property of the pre-limiting line ensemble in that model (a more refined version appears in a very recent work [8]). Observe that one would expect the Gaussian exponent z ² in the upper bound of the probability in the statement of the theorem and that is what is obtained in [17]. We, on the other hand, use a cruder argument to obtain only a stretched exponential decay. However, we have not tried to optimize the exponent 4∕9 which is not even sharp for our arguments.

1.3 Key Ideas and Organization of the Paper

Before jumping in to proofs, we present the key reasons driving the exponents and the main ingredients of the proofs of Theorems 1 and 2. Since the reasons governing the behaviour of ρ(n, r) when r ≪ n and ρ(n, r) when n − r ≪ n are almost symmetric, in this section we will mostly discuss the former case for the sake of brevity. The key realization driving the argument is that Γ _n should overlap significantly with Γ _r up to the region {x + y ≤ 2r}. Then at a very high level one can speculate that Cov(T _r, T _n) should be of the order of the variance of the amount of overlap, which because of the previous sentence should be of the same order as Var(T _r) = O(r ^2∕3) (using the well known sharp estimates of the variance). All of this points to a correlation of the order of $(\frac {r}{n})^{1/3}$.

We now mention a few key ingredients used to make the above heuristic rigorous. The upper bound is relatively straightforward. For convenience, as we shall do throughout the paper, let us denote T _r by X and let T _n = Z + W where Z is the weight of the first part of the polymer Γ _n i.e. the part from 0 to the line x + y = 2r and W is the weight of the path from x + y = 2r to n. See Fig. 1. Let v = (r + s, r − s) be the vertex at which Γ _n intersects the line x + y = 2r. It is well known since the work of Johansson [19] that if r is say n∕2 then |s| = O(r ^2∕3). However the polymer is in some sense self similar and hence one expects that the above result should also hold even when at scales r ≪ n. Indeed a quantitative version of such a result was established in [6]. This tells us that |X − Z| = O(r ^1∕3) by standard results about polymer fluctuations at scale r ^2∕3 around the point r. Moreover relying on this we also prove the local Brownian-like square root fluctuations of the distance profile T _w,n as w varies over vertices of the form (r + s, r − s) when |s| = O(r ^2∕3) showing that |W − Y | = O((r ^2∕3)^1∕2) = O(r ^1∕3) where Y  is T _r,n (hence is independent of X). Given the above information, the upper bound, i.e., Theorem 1 is a simple consequence of Cauchy–Schwarz inequality.

Fig. 1

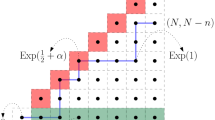
The figure illustrates the polymers of interest, Γ _r with weight X, Γ _r,n, with weight Y, Γ _n comprised of Γ _0,v and Γ _v,n with weights Z and W respectively where v is the point of intersection of Γ _n with the line x + y = 2r. The second figure illustrates our strategy to create barriers (deep blue) around a narrow strip (light blue) to ensure that Γ _r and Γ _0,v stay localized inside the latter and hence overlaps significantly creating a situation where the covariance between X and Z + W is approximated by the variance of the former

However, the lower bound is significantly more delicate since one has to rule out cancellations to show that indeed the heuristic mentioned at the beginning of the section is correct. At a very high level the strategy is to condition on a large part of the noise space in a way which allows us to control cancellations and prove the desired lower bound on ρ(n, r). To do this the first thing to come to our aid is the FKG inequality. If with positive probability β (independent of r, n) the conditioned environment is such that $\rho (n,r)\ge \varTheta (\frac {r}{n})^{1/3},$ then since ρ(n, r) ≥ 0 pointwise on the conditioned environment (using the FKG inequality), averaging over the latter yields the lower bound $\rho (n,r)\ge \beta \varTheta (\frac {r}{n})^{1/3}$. Our strategy of choosing the part of the environment to condition on consists of ensuring that, with positive probability, the polymer Γ _r is localized i.e., it is confined to a thin cylinder R _θ of size r × θr ^2∕3 for some small θ and ensuring Γ _n essentially agrees with Γ _r up to the line x + y = 2r. This is obtained by creating a bad region (barrier) around the thin cylinder making it suboptimal for the polymer to venture out of R _θ. This then implies that under such a conditioning, up to certain correction terms Cov(T _r, T _n) is equal to Var(T _r). At this point we prove a sharp estimate on variance of polymer weights constrained to lie in R _θ showing that it scales like θ ^−1∕2 r ^2∕3 as θ goes to 0. Thus for θ small enough, the variance term is large enough and dominates all the correction terms yielding the sought lower bound of Θ(r ^2∕3) on the covariance and hence Theorem 2.

We now briefly describe how to use the exact same strategy to bound ρ(r, n) in the regime n − r ≪ n. We will discuss the more delicate Theorem 2. Note that in this case we are aiming to prove a lower bound on 1 − ρ(n, r) and hence an upper bound on ρ(n, r). Thus the natural strategy to adopt would be to show that even after conditioning on T _r, T _n is not completely determined and there is still some fluctuation left. In fact, as expected, our arguments will show that the latter is of the same order as the fluctuation of T _r,n i.e., Var(T _n|T _r) = Θ((n − r)^2∕3) on a positive measure part of the space. Thus we get

$$\displaystyle \begin{aligned}\varTheta((n-r)^{2/3})\le \inf_{\lambda}\mathrm{Var}(T_n-\lambda T_r)= (1-\mbox{Corr}^2(T_r,T_n))\mathrm{{Var}}(T_n).\end{aligned}$$

This, along with the fact that Var(T _n) = Θ(n ^2∕3), completes the proof.

It is worth emphasizing that while we do crucially make use of the integrability of the exponential LPP model, it is done only in a rather limited nature via the input of weak convergence to Tracy–Widom distribution [18] and the moderate deviation estimates coming from [1, 24]. Therefore we expect our methods to be applicable to a large class of integrable LPP models where such estimates are known. In particular, we do not use any information about the limiting Airy process. As already mentioned, our approach hinges on the fine understanding of the local polymer geometry, following the sequence of recent works [3, 4, 6]. By virtue of being geometric, our proof is also robust, and as already mentioned, similar ideas have already been used in [5] to treat the case of flat initial condition, which does not yet seem accessible by any other method. We extensively draw from some of the estimates derived in those previous works, while introducing some new elements to advance the understanding of polymer geometry. Crucial ingredients include moderate deviations estimates to establish concentration for passage times across parallelograms. This idea originated in [3] and the particular estimates required for the time correlation problems are gathered in [5, Section 4]; we shall be extensively quoting from that source.

1.4 Organization of the Paper

The rest of the paper is organized as follows. We first prove Theorem 3 in Sect. 2. Then we use Theorem 3 to prove Theorem 1 in Sect. 3. Proof of Theorem 2 is done in Sect. 4.

2 Local Fluctuations of Weight Profile: Proof of Theorem 3

As alluded to before, in the case s = Θ(n ^2∕3), one can read off a qualitative version of this result from the limiting Airy process which ceases to provide any relevant information when s ≪ n ^2∕3. Although it is known that Brownian motion arises as a week limit at some shorter scale [27], we need some finer estimates for finite n. Such a result was indeed achieved in [17] in the special case of Brownian LPP crucially relying on the Brownian Gibbs property of the pre-limiting line ensemble. We shall take a more robust, geometric approach which hinges on establishing that the profile $\{L_{n,s'}-L_{n,0}: |s'|<s\}$ is with high probability determined by the vertex weights in the region

$$\displaystyle \begin{aligned}\{(x,y): 2n-C_{*}s^{3/2} \leq (x+y)\leq 2n\}\end{aligned}$$

for some large constant C _∗. To this end we have the following proposition.

Proposition 1

In the set-up of Theorem 3, consider $\varGamma =\varGamma _{\mathbf {0}, (n+s',n-s')}$ . Let t ≥ 1 and let v = (v ₁(s′, t, s), v ₂(s′, t, s)) denote the point at with Γ intersects the anti-diagonal x + y = 2n − 2t ^∗ s ^3∕2 . There exists s ₀ > 0, y ₀ > 0 and c, C > 0 such that the following holds for all s > s ₀ , t ≥ 1, y > y ₀ and for all n > Cr ^3∕2:

$$\displaystyle \begin{aligned}\mathbb{P}\left (\sup_{|s'|<s} |v_1(s',t,s)-(n-t^{*}s^{3/2})|\geq y t^{2/3}s \right) \leq e^{-cy^2}\end{aligned} $$

where $t^{*}=\min \{t, \frac {n}{s^{3/2}}\}$.

See Fig. 2 for an illustration of the setting in Proposition 1 and the associated event.

Fig. 2

The figure illustrates the setting of Proposition 1 where the geodesic from 0 to any point in an interval $\mathbb {L}$ of length 2s centered at n on the line x + y = 2n is unlikely to intersect the line x + y = 2(n − ts ^3∕2) outside the line segment $\mathbb {L}_{t,s,y}$ of length 2yt ^2∕3 s centered at (n − ts ^3∕2, n − ts ^3∕2). Thus it is unlikely that the black path would be a geodesic

Proof

Clearly, the case t ^∗≠ t is trivial by the directed-ness of the geodesic. For the other case, observe first that by polymer ordering, it suffices to prove the result for s′ = ±r. This case can be read off from the proof of Theorem 3 in [6] (see also Remark 1.3 there about the non-optimality of the exponent).

As in Fig. 2, let $\mathbb {L}$ denote the line segment joining (n + s, n − s) and (n − s, n + s) and $\mathbb {L}_{t,s,y}$ denote the line segment joining (n − t ^∗ s ^3∕2 − yt ^2∕3 s, n − t ^∗ s ^3∕2 + yt ^2∕3 s) and (n − t ^∗ s ^3∕2 + yt ^2∕3 s, n − t ^∗ s ^3∕2 − yt ^2∕3 s) . Clearly on the large probability event (for large y) implied by Proposition 1, the profile:

$$\displaystyle \begin{aligned}\{L_{n,s'}-L_{n,0}: |s'|<s\}\end{aligned} $$

can be upper bounded by using the passage times T _u,v where $u\in \mathbb {L}_{t,s,y}$ and $v\in \mathbb {L}$. The next proposition states a concentration result for these passage times around their expectations.

Proposition 2

Let $\delta \in (0,\frac {1}{3})$ be fixed. Set $\mathbb {L}':=\mathbb {L}_{t,s,t^{\delta }}$ . Then there exists s ₀, y ₀ > 0 and c > 0 such that for all s > s ₀, y > y ₀ and t ≥ 1 we have

$$\displaystyle \begin{aligned}\mathbb{P}\left( {\sup_{u\in \mathbb{L}', v\in \mathbb{L}} |T_{u,v}-\mathbb{E} T_{u,v}| \geq y{t^{1/3+\delta/2}}s^{1/2}} \right) \leq e^{-cy}.\end{aligned}$$

The same bound holds for u = 0 if t ≠ t ^∗.

Proof

This follows from [5, Theorem 4.2] by observing that the slope between any two pair of points in $\mathbb {L}$ and $\mathbb {L}'$ remain between 1∕2 and 2 (here we use the fact that $\delta < \frac {1}{3}$, and s is sufficiently large).

We can now complete the proof of Theorem 3. The basic strategy is the following. To bound $L_{n,s'}-L_{n,0}$ we back up a little bit and look at where the geodesic $\varGamma _{\mathbf {0}, (n+s',n-s')}$ intersects the line $\mathbb {L}'$ from Proposition 2 for an appropriate choice of the parameters. Calling that u _∗ the proof proceeds by bounding $|T_{u_*,v}-T_{u_*, \mathbf {n}}|$ and using the simple observation that $L_{n,0}\geq T_{\mathbf {0}, u_*}+ T_{u_*, \mathbf {n}}$.

Proof of Theorem 3

Let z > 0 sufficiently large be fixed. Let t = z ^4∕3 and let $\mathcal {A}$ denote the event that

$$\displaystyle \begin{aligned}\left \{\sup_{s': |s'|<s} |v_1(s',t, s)-(n-t^*s^{3/2})|\geq z^{10/9}s\right\}\end{aligned}$$

Use Proposition 1 with the above value of t and y = z ^2∕9 to conclude that $\mathbb {P}(\mathcal {A})\leq e^{-cz^{4/9}}$ (as z is sufficiently large). We shall now consider two cases separately: (i) t = t ^∗ and (ii) t ≠ t ^∗.

In case (i), let $\mathbb {L}'$ be defined as in Proposition 2 with δ = 1∕6 (any arbitrary choice for δ ∈ (0, 1∕3) would work, but would give a different tail exponent) and the choice of t as before. Let $\mathcal {B}$ denote the event that

$$\displaystyle \begin{aligned}\left\{ {\sup_{u\in \mathbb{L}', v, v'\in \mathbb{L}} |T_{u,v}-T_{u,v'}| \geq zs^{1/2}} \right\}.\end{aligned}$$

Observe now that, for u = (u ₁, u ₂) and v = (v ₁, v ₂) as above, we have, by Basu et al. [5, Theorem 4.1], that

$$\displaystyle \begin{aligned}|\mathbb{E} T_{u,v}-(\sqrt{v_1-u_1}+ \sqrt{v_2-u_2})^2|\leq Ct^{1/3}s^{1/2}\end{aligned}$$

for some C > 0. By a Taylor expansion, it follows that, for u, v, v′ as above we have for some C′

$$\displaystyle \begin{aligned}\sup_{u\in \mathbb{L}', v, v'\in \mathbb{L}}|\mathbb{E} T_{u,v}-\mathbb{E} T_{u,v'}|\leq C't^{1/3}s^{1/2} \leq \frac{z}{2}s^{1/2}\end{aligned}$$

where the final inequality follows from our choice of t and z sufficiently large. Using Proposition 2 with the choices above, y = z ^4∕9, we get from the above that for z sufficiently large, we have $\mathbb {P}(\mathcal {B})\leq e^{-cz^{4/9}}$. It remains to prove that on $\mathcal {A}^{c} \cap \mathcal {B}^c$ we have

$$\displaystyle \begin{aligned}\left\{\sup_{s': |s'|<s} L_{n,s'}-L_{n,0} \leq zs^{1/2}\right\}.\end{aligned}$$

To see this, let s _∗ with |s _∗|≤ s be such that

$$\displaystyle \begin{aligned}L_{n, s_*}=\sup_{s': |s'|<s} L_{n,s'}.\end{aligned} $$

Let v := (n + s _∗, n − s _∗). On $\mathcal {A}^c$, the geodesic $\varGamma _{\mathbf {0}, (n+s_*,n-s_*)}$ intersects the line segment $\mathbb {L}'$, let u _∗ be the intersection point. On $\mathcal {B}^c$ we have $|T_{u_*,v}-T_{u_*, \mathbf {n}}|\leq zs^{1/2}$. The claim is established by observing that $L_{n,0}\geq T_{\mathbf {0}, u_*}+ T_{u_*, \mathbf {n}}$.¹

In case (ii), we proceed as before but now notice that u _∗ = 0. The same argument now can be repeated with $\mathcal {B}'$ defined as

$$\displaystyle \begin{aligned}\left\{ {\sup_{v, v'\in \mathbb{L}} |T_{\mathbf{0},v}-T_{\mathbf{0},v'}| \geq zs^{1/2}} \right\}.\end{aligned} $$

Observe now that since t ≠ t ^∗, we must have n ≤ ts ^3∕2. Using [5, Theorem 4.1] as before it follows that for some C > 0

$$\displaystyle \begin{aligned}\sup_{v, v'\in \mathbb{L}} |\mathbb{E} T_{\mathbf{0},v}-\mathbb{E} T_{\mathbf{0},v'}|\leq Cn^{1/3}\leq Ct^{1/3}s^{1/2}\leq \frac{z}{2}s^{1/2}\end{aligned} $$

where the last inequality follows as before by taking z sufficiently large and our choice of t. Using the above and Proposition 2 as before we show that $\mathbb {P}(\mathcal {B}')\leq e^{-cz^{4/9}}$. The rest of the proof is identical with the previous case.

3 Proof of Upper Bounds

In this section we shall prove Theorem 1 using Theorem 3 and Proposition 1. As we shall see, the proofs of parts (i) and (ii) rely on much of the same ingredients. Before proceeding further let us introduce some notation that will be used throughout this section.

Before diving in to the proofs we adopt the convention of ignoring the values of the vertices {ω _(x,y) : x + y = 2r}. This would enable us to write cleaner equations of the form T _n = T _0,v + T _v,n where v is the unique vertex Γ _n ∩{x + y = 2r}. However since by definition, the random v can be one of 2r possible vertices, whose maximum value is no more than $\log r$ with an exponential tail, it does not create any change in the computations throughout the paper since all the objects that we deal with, have fluctuations of the order of r ^1∕3. We shall adopt this convention throughout the remainder of this paper, and not comment further on this topic. It will be easy to verify the minor details in each case, and we leave that to the reader.

For any path γ, we shall denote by ℓ(γ), the weight of the path. Let Γ := Γ _n denote the polymer from 0 to n. Let v = (v ₁, v ₂) denote the point at which Γ intersects the line {x + y = 2r}. Recall from Sect. 1 that T _r := T _0,r. Let us define (see Fig. 1)

$$\displaystyle \begin{aligned} X&:=T_{r},\,\,\, Y:=T_{\mathbf{r},\mathbf{n}}, \\ Z&:=\ell(\varGamma_{\mathbf{0},v}) \text{ and } W:=\ell(\varGamma_{v,\mathbf{n}}). \end{aligned} $$

(1)

Thus by definition T _n = Z + W.² Finally we shall denote by X ^∗ the weight of the polymer, denoted by Γ ^∗, from 0 to the line {x + y = 2r}.

We shall need some preparatory results. First we want to show that (Z − X)₊ is tight at scale r ^1∕3. Observing that X ^∗≥ Z, this is a consequence of [5, Theorem 4.1] that r ^−1∕3(X ^∗− X) has stretched exponential tails: for all y large enough and for all r large enough

$$\displaystyle \begin{aligned} \mathbb{P}(X^*-X\ge yr^{1/3})\leq e^{-cy^{1/3}}. \end{aligned} $$

(2)

The next lemma shall show that W − Y  is also typically of order r ^1∕3. Notice that if r ≪ n, now we can no-longer replace W by the weight of the line-to-point polymer from the line {x + y = 2r} to n. This is where we shall need the full power of Proposition 1 and Theorem 3.

Lemma 1

There exists positive constants r ₀, y ₀ and C, c > 0 such that for all r > r ₀ and y > y ₀ and n > Cr we have

$$\displaystyle \begin{aligned}\mathbb{P}(W-Y>yr^{1/3})\leq e^{-cy^{1/3}}.\end{aligned}$$

Proof

For z > 0, let $\mathcal {A}_{z}$ denote the event |v ₁ − r|≥ zr ^2∕3 and $\mathcal {B}_{z}$ denote the event that

$$\displaystyle \begin{aligned}\sup_{|s|\leq zr^{2/3}} T_{(r+s,r-s),\mathbf{n}} -T_{\mathbf{r},\mathbf{n}} \geq yr^{1/3}.\end{aligned}$$

Clearly for every z > 0,

$$\displaystyle \begin{aligned}\mathbb{P}(W-Y>yr^{1/3})\leq \mathbb{P}(\mathcal{A}_z)+\mathbb{P}(\mathcal{B}_{z}).\end{aligned}$$

The lemma follows by taking z = y ^1∕6 and using Proposition 1 and Theorem 3 to bound $\mathbb {P}(\mathcal {A}_z)$ and $\mathbb {P}(\mathcal {B}_{z})$ respectively. Note that in the last application, Theorem 3 is applied for the inverted ensemble i.e., replace n by 0, 0 by n and r by n −r .

We can now prove the following proposition which immediately implies Theorem 1, (i) as Var T _n = Θ(n ^2∕3), and Var T _r = Θ(r ^2∕3).

Proposition 3

There exists absolute constants r ₀, δ ₁ and C such that we have for all r ₀ < r < δ ₁ n and n sufficiently large

$$\displaystyle \begin{aligned}\mathrm{{Cov}} (T_{n}, T_{r}) \leq Cr^{2/3}.\end{aligned}$$

Proof

We need to upper bound

$$\displaystyle \begin{aligned}\mathrm{{Cov}} (X, Z+W)= \mathrm{{Cov}}(X,Z)+ \mathrm{{Cov}}(X,W).\end{aligned}$$

we bound the two terms separately. Clearly, by Cauchy–Schwarz inequality and the observation Var X = Θ(r ^2∕3), to prove Cov(X, Z) ≤ Cr ^2∕3, it suffices to show that Var Z = O(r ^2∕3). Now notice that, $\mathrm {{Var}}(Z) \leq 2(\mathrm {{Var}} X + \mathbb {E} (X-Z)^2)$. Observing Y − W ≤ Z − X ≤ X ^∗− X, and using (2) and Lemma 1 it follows that $\mathbb {E} (X-Z)^2= O(r^{2/3})$ which in turn implies Cov(X, Z) ≤ Cr ^2∕3 for some absolute constant C.

For the second term in the above decomposition observe that

$$\displaystyle \begin{aligned}\mathrm{{Cov}}(X,W)=\mathrm{{Cov}}(X,W-Y)\end{aligned}$$

because X and Y  are independent. Using Cauchy–Schwarz inequality again, it suffices to show that $\mathbb {E} (Y-W)^2=O(r^{2/3})$. Observing as before that W − Y ≥ X − Z ≥ X − X ^∗, this follows from (2) and Lemma 1. This completes the proof of the proposition.

To prove Theorem 1, (ii) we shall need the following easy observation.

Observation 1

For any two random variables U and V  we have

$$\displaystyle \begin{aligned}{\mathrm {Var}}(U-V)\geq (1-\mathrm{{Corr}}^2(U,V)){\mathrm {Var}}(U).\end{aligned}$$

The observation follows from noticing that

$$\displaystyle \begin{aligned} (1-\mbox{Corr}^2(U,V))\mathrm{{Var}}(U)=\inf_{\lambda\in \mathbb{R}} \mathrm{Var}(U-\lambda V)\le \mathrm{ {Var}}(U-V). \end{aligned} $$

Using Observation 1, the following Proposition immediately implies Theorem 1, (ii).

Proposition 4

There exists $r_0\in \mathbb {N}$ and positive absolute constants δ ₁ , C, for all r such that δ ₁ n > (n − r) > r ₀ , and all n sufficiently large we have

$$\displaystyle \begin{aligned}\mathrm{{Var}}~(T_{n}-T_{r})\leq C(n-r)^{2/3}.\end{aligned}$$

Proof

Recalling X, Y, Z, W as defined at the beginning of this section, we need to upper bound Var(Z + W − X). Expanding we get that,

$$\displaystyle \begin{aligned}\mathrm{{Var}} (Z+W-X)= \mathrm{{Var}}(Z-X) +\mathrm{{Var}}(W)+ 2\mathrm{{Cov}} (Z-X,W).\end{aligned}$$

We shall show each of the terms above is O((n − r)^2∕3) separately. In fact, by Cauchy–Schwarz inequality it suffices to only show that bound for the first two terms. Notice that the picture is same as before except the roles of r and (n − r) has been reversed. Using the proof of Lemma 1 we can now show that

$$\displaystyle \begin{aligned}\mathbb{P}(Z-X \geq y (n-r)^{1/3})\leq e^{-cy^{1/4}}\end{aligned}$$

and using (2) again it follows that

$$\displaystyle \begin{aligned}\mathbb{P}(W-Y \geq y (n-r)^{1/3})\leq e^{-cy^{1/4}}\end{aligned}$$

for all y sufficiently large. As in the proof of Proposition 3, this is then used to argue that Var(Z − X) = O((n − r)^2∕3), and $\mathbb {E}[W-Y]^2= O((n-r)^{2/3})$, which together with the observation that Var Y = O((n − r)^2∕3) completes the proof of the proposition.

4 Proof of Lower Bounds

We now move towards proving Theorem 2. As in the proof of Theorem 1, parts (i) and (ii) of Theorem 2 have rather similar proofs as well (after exchanging the roles of r and n − r). In this section we describe in detail the line of argument leading to the proof of Theorem 2, (i). We shall first complete the proof modulo the key result Proposition 6. We shall give a sketch of how the same strategy is used to prove Theorem 2, (ii). The final subsection will be dedicated to the proof of Proposition 6.

For the readers’ benefit, we recall briefly the strategy outlined in Sect. 1.3. By the FKG inequality, it should suffice to obtain a lower bound on the conditional correlation on an event with probability bounded uniformly below. By the trivial observation Cov(X, X + Y ) = Θ(r ^2∕3), a very natural way to construct such an event is to ask that v is very close to r which will imply X ≈ Z and Y ≈ W (using Theorem 3). However one needs to be careful so that there will be enough fluctuation left in the conditional environment. To this end, it turns out one can construct such an event measurable with respect to the configuration outside a thin strip of width Θ(r ^2∕3) around the straightline joining 0 to r.

For θ > 0, let $R_{\theta }\subseteq \mathbb {Z}^2$ be defined as follows:

$$\displaystyle \begin{aligned}R_{\theta}:=\{(x,y)\in \mathbb{Z}^2: 0\leq x+y\leq 2r~\text{and}~|x-y|\leq \theta r^{2/3}\}.\end{aligned}$$

Let denote a weight configuration outside R _θ. Let $\mathcal {F}_{\theta }$ denote the σ-algebra generated by the set of all such configurations Ω _θ. Observe that events measurable with respect to $\mathcal {F}_{\theta }$ can be written as subsets of Ω _θ, and we shall often adopt this interpretation without explicitly mentioning it. The major step in the proof is the following proposition.

Proposition 5

There exist absolute positive constants β, δ ₁, θ, C > 0 sufficiently small such that for δ ₁ n > r > r ₀ and n sufficiently large there exists an event $\mathcal {E}$ measurable with respect to $\mathcal {F}_{\theta }$ with $\mathbb {P}(\mathcal {E})\geq \beta$ and the following property: for all weight configuration $\omega \in \mathcal {E}$ we have

$$\displaystyle \begin{aligned}\mathrm{{Cov}} (T_{n}, T_{r}\mid \omega) > Cr^{2/3}.\end{aligned}$$

The proof of Theorem 2, (i) using Proposition 5 is straightforward.

Proof of Theorem 2, (i)

Observe that for each fixed weight configuration ω ⊂ Ω _θ on the vertices outside R _θ, both T _n and T _r are increasing in the weight configuration on R _θ. Observe also that $\mathbb {E}[T_{n}\mid \mathcal {F}_{\theta }]$ and $\mathbb {E}[T_{r}\mid \mathcal {F}_{\theta }]$ are both again increasing in the configuration ω. Applying the FKG inequality twice (in the third and fifth lines of the following computation) together with Proposition 5 (in the third line of the following computation while dealing with the integral over $\mathcal {E}$) then implies

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathbb{E} T_{n} T_{r} & =&\displaystyle \mathbb{E} \left( \mathbb{E} [T_{n} T_{r} \mid \mathcal{F}_{\theta}]\right)\\ & =&\displaystyle \int_{\mathcal{E}} \mathbb{E} [T_{n} T_{r} \mid \mathcal{F}_{\theta}] d\omega + \int_{\mathcal{E} ^c} \mathbb{E} [T_{n} T_{r} \mid \mathcal{F}_{\theta}] d\omega\\ & \geq &\displaystyle \int_{\mathcal{E}} \mathbb{E} [T_{n}\mid \mathcal{F}_{\theta}] \mathbb{E}[T_{r} \mid \mathcal{F}_{\theta}] d\omega + C\beta r^{2/3} + \int_{\mathcal{E} ^c} \mathbb{E} [T_{n}\mid \mathcal{F}_{\theta}] \mathbb{E}[T_{r} \mid \mathcal{F}_{\theta}] d\omega \\ & {=} &\displaystyle \mathbb{E}\left( \mathbb{E} [T_{n}\mid \mathcal{F}_{\theta}] \mathbb{E}[T_{r} \mid \mathcal{F}_{\theta}]\right)+C\beta r^{2/3}\\ & \geq &\displaystyle \mathbb{E}[T_n]\mathbb{E}[T_{r}]+C\beta r^{2/3}; \end{array} \end{aligned} $$

which is what we set out to prove.

4.1 Constructing a Suitable Environment

The key step in the proof of Proposition 5, is the construction of $\mathcal {E}$, towards which we now move. For easy reference we recall the notations already introduced in Sect. 3, that we will use again.

$$\displaystyle \begin{aligned} X&:=T_{r},\,\,\, Y:=T_{\mathbf{r},\mathbf{n}}, Z:=\ell(\varGamma_{\mathbf{0},v}) \text{ and } W:=\ell(\varGamma_{v,\mathbf{n}}).\\ X^*&:=\max \{\ell(\varGamma_{\mathbf{0},w}): w\in \mathbb{L}_{r}\}, \end{aligned} $$

where $\mathbb {L}_{r}$ denote the line {x + y = 2r}. We shall also denote by X _∗ (resp. X _θ) the weight of the best path from 0 to r that does not exit R _2θ (resp. R _θ). Finally for ϕ > θ, $\mathbb {L}_{r,\phi }$ shall denote the line segment joining (r − ϕr ^2∕3, r + ϕr ^2∕3) and (r + ϕr ^2∕3, r − ϕr ^2∕3). We shall denote by X _ϕ the weight of the best path from 0 to $\mathbb {L}_{r,\phi }$, and by Y _ϕ the weight of the best path from $\mathbb {L}_{r,\phi }$ to n.

The event $\mathcal {E}$ will depend on a number of parameters ϕ ₀, ϕ, L, c ₀ (and naturally θ), the choices of which shall be specified later.

The event will consist of two major parts.

• 1. Regular fluctuation of the profile $\{T_{w,\mathbf {n}}:w\in \mathbb {L}_{r,\phi }\}$ : Let $\mathcal {E}_1$ denote the event that

  $$\displaystyle \begin{aligned} &\left\{ \sup_{w\in \mathbb{L}_{r,\phi_0}} T_{w,\mathbf{n}}- T_{\mathbf{r}, \mathbf{n}} \leq \phi_0^{1/2}\log ^9 (\theta^{-1}) r^{1/3}\right\} \cap\\ &\left\{ \sup_{w\in \mathbb{L}_{r,\phi}\setminus \mathbb{L}_{r,\phi_0}} T_{w,\mathbf{n}}- \sqrt{|w_1-w_2|}\log^{9}(\theta^{-1}) \leq T_{\mathbf{r}, \mathbf{n}} \right\}, \end{aligned} $$

  where w = (w ₁, w ₂). Our choice of parameters (see below) would ensure ϕ ₀ ≪ ϕ. Observe that $\mathcal {E}_1$ only depends on the weight configuration above the line $\mathbb {L}_{r}$.

• 2. Barrier around R _θ: Let U ₁ (resp. U ₂) denote a r × (ϕ − θ)r ^2∕3 rectangle whose one set of parallel sides are aligned with the lines x + y = 0 and x + y = 2r respectively and whose left (resp. left right) side coincides with the right (resp. left) side of R _θ.³ For any point $u=(u_1,u_2)\in \mathbb {Z}^2$, let d(u) := u ₁ + u ₂. Also, for any region U, and points u, v ∈ U, let us denote, by $T_{u,v}^{U}$ to be the weight of the best path from u to v that does not exit U. Let $\mathcal {E}_2$ denote the following event measurable with respect to the configuration in U ₁:

  $$\displaystyle \begin{aligned}T^{U_1}_{u,u'}-\mathbb{E} T_{u,u'} \leq -Lr^{1/3} ~\forall u,u' \in U_1 ~\text{with}~ |d(u)-d(u')|\geq \frac{r}{L}.\end{aligned}$$

  Let $\mathcal {E}_{3}$ denote the same event with U ₁ replaced by U ₂. We set $\mathcal {E}_4:=\mathcal {E}_2\cap \mathcal {E}_3$.

4.1.1 Choice of Parameters

We need to fix our choice of parameters appearing in the definitions of the above events before proceeding to proving probability bounds for the same. Throughout the sequel c ₀ is a small enough universal constant, we shall choose θ to be an arbitrarily small constant; and L ≫ ϕ ≫ ϕ ₀. We need to choose ϕ ₀ poly-logarithmic in θ ⁻¹, ϕ a large inverse power of θ, and L a much larger inverse power of θ depending on ϕ. For concreteness we shall fix $\phi _0=\log ^{10}(\frac {1}{\theta }), \phi =(\frac {1}{\theta })^{30}$ and L = ϕ ³⁰. Given all of these we shall take r sufficiently large, and r∕n sufficiently small. Throughout the remainder of this paper we shall work with this fixed choice of parameters.

4.2 Construction of $\mathcal {E}$

We are now ready to define the event $\mathcal {E}$. First we define certain nice events conditioned on $\mathcal {E}_4$ towards the proof of Proposition 5.

• 1. Let $\mathcal {E}_5$ denote the set of all $\omega =\omega _{\theta }\in \mathcal {E}_1 \cap \mathcal {E}_4$ such that

  $$\displaystyle \begin{aligned}\mathbb{E}[(X^*-X_*)^2\mid \omega] \leq 10r^{2/3},\end{aligned}$$

• 2. Let $\mathcal {E}_6$ denote the set of all $\omega =\omega _{\theta }\in \mathcal {E}_4\cap \mathcal {E}_1$ such that

  $$\displaystyle \begin{aligned}\mathbb{E}[(Z+W-Y-X_*)^2 \mid \omega] \leq 40 \phi_0^2 r^{2/3}.\end{aligned}$$

• 3. Let $\mathcal {E}_7$ denote the set of all $\omega \in \mathcal {E}_4\cap \mathcal {E}_1$ such that

  $$\displaystyle \begin{aligned}\mathrm{{Var}}~(X_*\mid \omega) \geq c_0\theta^{-1/2} r^{2/3}\end{aligned}$$

  where c ₀ is a sufficiently small constant to be chosen appropriately later (independent of θ) and θ will be chosen sufficiently small.

We shall set

$$\displaystyle \begin{aligned} \mathcal{E}:= \mathcal{E}_5 \cap \mathcal{E}_6\cap \mathcal{E}_{7}. \end{aligned} $$

(3)

4.3 Proof of Proposition 5

It remains to prove Proposition 5 using the $\mathcal {E}$ defined above. First we need to state the desired lower bound for $\mathbb {P}(\mathcal {E})$.

Proposition 6

There exists β > 0 depending on all parameters such that $\mathbb {P}(\mathcal {E})>\beta$.

Deferring the proof of this proposition to Sect. 4.4, we first finish the proof of Proposition 5.

Proof of Proposition 5

Let $\mathcal {E}$ be as defined above. By Proposition 6 we know that $\mathbb {P}(\mathcal {E})$ is bounded below as required. Fix $\omega =\omega _{\theta }\in \mathcal {E}$. Observe that Y  is a deterministic function of ω. Using linearity of covariance and Cauchy–Schwarz inequality, we have for each $\omega \in \mathcal {E},$

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathrm{{Cov}} (X, Z+W \mid \omega) & =&\displaystyle \mathrm{{Cov}} (X, Z+W-Y \mid \omega)\\ & =&\displaystyle \mathrm{{Cov}}(X_*, Z+W-Y\mid \omega)\\ & &\displaystyle + \mathrm{{Cov}}(X-X_*, Z+W-Y \mid \omega)\\ & =&\displaystyle \mathrm{{Var}} (X_*\mid \omega)\\ & &\displaystyle + \mathrm{{Cov}}(X_*, Z+W-Y-X_* \mid \omega)\\ & +&\displaystyle \mathrm{{Cov}}(X-X_*,X_*\mid \omega)\\ & &\displaystyle + \mathrm{{Cov}} (X-X_*,Z+W-Y-X_*\mid \omega)\\ & \geq &\displaystyle \mathrm{{Var}} (X_*\mid \omega)-\sqrt{\mathrm{{Var}}(X^*)}\\ & &\displaystyle \times\left(\sqrt{\mathrm{{Var}}(X-X_*\mid \omega)}+\sqrt{\mathrm{{Var}}(Z+W-Y-X_*\mid \omega)}\right)\\ & &\displaystyle - \sqrt{\mathrm{{Var}}(X-X_*\mid \omega)}\sqrt{\mathrm{{Var}}(Z+W-Y-X_*\mid \omega)}. \end{array} \end{aligned} $$

By definition of $\mathcal {E}_5$, and the observation that X ^∗≥ X ≥ X _∗ we get that for each $\omega \in \mathcal {E}$, Var(X − X _∗∣ω) ≤ 10r ^2∕3. By definition of $\mathcal {E}_6$, $\mathrm {{Var}}(Z+W-Y-X_*\mid \omega )=O(\phi _0^{2} r^{2/3}).$ The proof is completed by the definition of $\mathcal {E}_7$, observing that by our choices of parameters θ ^−1∕4 ≫ ϕ ₀ (whch ensures that the first term dominates in the above expression).

We now illustrate how the proof of Theorem 2, (ii) can be completed along the same lines. We shall only provide a sketch.

Proof of Theorem 2, (ii)

First observe that in the notation of the above proof, using Cauchy–Schwarz inequality, and the fact that Y  is a deterministic function of ω, we have, as above, that for all $\omega \in \mathcal {E}$,

$$\displaystyle \begin{aligned}\mathrm{Var}(Z+W\mid \omega) \geq \mathrm{Var}(X_*\mid \omega)-2\sqrt{\mathrm{ Var}(Z+W-Y-X_*\mid \omega)}\sqrt{\mathrm{Var}(X_*\mid \omega)}.\end{aligned}$$

By definition of $\mathcal {E}_6$ and $\mathcal {E}_7$, we get that for θ sufficiently small and for all $\omega \in \mathcal {E}$, we have Var(Z + W∣ω) ≥ c(θ)r ^2∕3 for some c(θ) > 0. Now we make the same definitions as before, but interchange the roles of r and (n − r). Let the event corresponding to $\mathcal {E}$ be now denoted $\widetilde {\mathcal {E}}$. The analogue of Proposition 6 and the above observation now implies that for 1 ≪ n − r ≪ n there exists a positive probability set $\widetilde {\mathcal {E}}$ such that for each $\omega \in \widetilde {\mathcal {E}}$, Var(T _n∣ω) ≥ c(n − r)^2∕3 (and T _r is a deterministic function of $\omega \in \widetilde {\mathcal {E}}$). This implies for some constant c′ > 0 we have

$$\displaystyle \begin{aligned}c'(n-r)^{2/3} \le \inf_{\lambda}\mathrm{Var}(T_n-\lambda T_r)= (1-\mbox{Corr}^2(T_r,T_n))\mathrm{{Var}}(T_n);\end{aligned}$$

which completes the proof.

The remainder of the paper is devoted to the proof of Proposition 6.

4.4 Proof of Proposition 6

The proof has two parts. First we consider the event $\mathcal {E}_1\cap \mathcal {E}_4$ and show that it has probability bounded below. Then we show that conditional on $\mathcal {E}_1\cap \mathcal {E}_4$ each of the events $\mathcal {E}_5$, $\mathcal {E}_6$ and $\mathcal {E}_7$ has probability close to one. Since $\mathcal {E}_1$ and $\mathcal {E}_4$ are independent it suffices to lower bound their probabilities separately.

Lemma 2

There exists positive constants r ₀ , δ ₁ such that for all δ ₁ n > r > r ₀ , we have

$$\displaystyle \begin{aligned}\mathbb{P}(\mathcal{E}_1)\geq 1-e^{-c\log ^{4} (\theta^{-1})}.\end{aligned}$$

Proof

Recall the two events whose intersection $\mathcal {E}_1$ consists of. That the first of those has probability at least $1-e^{-c\log ^{4} (\theta ^{-1})}$ is an immediate consequence of Theorem 3. The probability lower bound for the second event also follows by writing the line segment $\mathbb {L}_{r,\phi }$ as an increasing union over $\mathbb {L}_{r,i}$ for i = 1, 2…, ϕ, applying Theorem 3 for each and taking a union bound.

The next lemma, quoted from [5] without proof, shows that $\mathcal {E}_4$ occurs with positive probability.

Lemma 3 ([5, Lemma 6.5])

There exists 𝜖 = 𝜖(ϕ, L) > 0 such that $\mathbb {P}(\mathcal {E}_4)>\epsilon$.

Let us now move towards bounding the conditional probabilities of $\mathcal {E}_5,\mathcal {E}_6$ and $\mathcal {E}_7$ given $\mathcal {E}_1\cap \mathcal {E}_4$. Notice that $\mathcal {E}_5$ is independent of $\mathcal {E}_1$ and hence for those it suffices to consider conditional probability given $\mathcal {E}_4$ only. We need the following result from [5].

Lemma 4 ([5, Lemma 6.6])

There exists positive constants r ₀ , δ ₁ such that for all δ ₁ n > r > r ₀ , and θ sufficiently small, we have

$$\displaystyle \begin{aligned}\mathbb{E}[(X^*-X_*)^2 \mid \mathcal{E}_4] \leq r^{2/3}.\end{aligned}$$

Lemma 5

There exists positive constants r ₀ , δ ₁ such that for all δ ₁ n > r > r ₀ , we have

$$\displaystyle \begin{aligned}\mathbb{E}[(Z+W-Y-X_*)^2 \mid \mathcal{E}_1 \cap \mathcal{E}_4] \leq 4\phi_0^2 r^{2/3}.\end{aligned}$$

We shall come back to the proof of Lemma 5 at the end of this subsection.

Lemma 6

There exists positive constants r ₀ , δ ₁ and c ₀ such that for all δ ₁ n > r > r ₀ , we have

$$\displaystyle \begin{aligned}\mathbb{P}[\mathrm{{Var}} [X_* \mid \omega_{\theta}]\geq c_0\theta^{-1/2} r^{2/3} \mid \mathcal{E}_1\cap \mathcal{E}_4]\geq 0.9.\end{aligned}$$

Essentially the same statement is proved in [5, (43)] and we shall omit the proof. See the proofs of [5, Lemma 6.9, Lemma 6.10].

We can now complete the proof of Proposition 6.

Proof of Proposition 6

Observe that by Markov inequality (and the fact that $\mathcal {E}_1$ is independent of $\mathcal {E}_4$ and $\mathcal {E}_5$) we have $\mathbb {P}(\mathcal {E}_5\mid \mathcal {E}_1 \cap \mathcal {E}_4)\geq 0.9$ and $\mathbb {P}(\mathcal {E}_6\mid \mathcal {E}_1\cap \mathcal {E}_4)\geq 0.9$ and $\mathbb {P}(\mathcal {E}_7\mid \mathcal {E}_1\cap \mathcal {E}_4)\geq 0.9$ using Lemmas 4, 5, and 6 respectively. Combined, these give $\mathbb {P}(\mathcal {E} \mid \mathcal {E}_1\cap \mathcal {E}_4)\geq 0.7$. Observe further that by Lemmas 2 and 3 and the fact that $\mathcal {E}_1$ and $\mathcal {E}_4$ are independent implies that for θ sufficiently small we have $\mathbb {P}(\mathcal {E}_1\cap \mathcal {E}_4)\geq \epsilon /2$. The proof of the proposition is completed by choosing β = 𝜖∕4.

It remains to prove Lemma 5. It is in spirit similar (in fact somewhat easier) to the proof of [5, Lemma 6.7] but several ingredients are different.

Proof of Lemma 5

Let A denote the event that the point v where the geodesic Γ _n from 0 to n intersects $\mathbb {L}_r$ lies in $\mathbb {L}_{r,\phi _0}$. We write

$$\displaystyle \begin{aligned} &\mathbb{E}[(Z+W-Y-X_*)^2 \mid \mathcal{E}_1\cap \mathcal{E}_4]\\ &\quad =\mathbb{E}[(Z+W-Y-X_*)^2 1_A \mid \mathcal{E}_1\cap \mathcal{E}_4]+\mathbb{E}[(Z+W-Y-X_*)^2 1_{A^c}\mid \mathcal{E}_1 \cap \mathcal{E}_4]\\ &\quad \le \mathbb{E}[(Z+W-Y-X_*)^2 1_A \mid \mathcal{E}_1\cap \mathcal{E}_4]+\mathbb{E}[(Z+W-Y-X_{\theta})^2 1_{A^c}\mid \mathcal{E}_1\cap \mathcal{E}_4] \end{aligned} $$

where the inequality is a consequence of 0 ≤ Z + W − Y − X _∗≤ Z + W − Y − X _θ.

To bound the first term, we notice that, on A, $|Z-Y|\leq \sup _{w \in \mathbb {L}_{r,\phi _0}}|T_{w,\mathbf {{n}}}-Y|$, and consequently

$$\displaystyle \begin{aligned} &\mathbb{E}[(Z+W-Y-X_*)^2 1_A \mid\mathcal{E}_1\cap \mathcal{E}_4] \\ &\quad \le O\left(\mathbb{E}\left[\sup_{w \in \mathbb{L}_{r,\phi_0}}|T_{w,\mathbf{{n}}}-Y|{}^2\mid \mathcal{E}_1\right]+\mathbb{E}[(X^*-X_*)^2\mid \mathcal{E}_4]\right)\\ &\quad =O(\phi_0 r^{2/3}) \end{aligned} $$

where in the first inequality we use the fact that $\sup _{w \in \mathbb {L}_{r,\phi _0}}|T_{w,\mathbf {{n}}}-Y|{ }^2$ is independent of $\mathcal {E}_4$ and the last inequality is a consequence of Theorem 3, Lemmas 2 and 4.

Now for the second term, using Cauchy–Schwarz inequality we get

$$\displaystyle \begin{aligned}\mathbb{E}[(Z+W-Y-X_{\theta})^2 1_{A^c}\mid \mathcal{E}_1\cap \mathcal{E}_4]\leq \mathbb{P}[A^c\mid \mathcal{E}_1\cap \mathcal{E}_4]^{1/2} \mathbb{E}[(Z+W-Y-X_{\theta})^4\mid \mathcal{E}_1\cap \mathcal{E}_4]^{1/2}.\end{aligned}$$

Now we claim that $\mathbb {P}(A\mid \mathcal {E}_1\cap \mathcal {E}_4)\ge 1-e^{-\log ^2(\theta )}$. This is proved in Lemma 7 below. Also notice that since $\mathcal {E}_1$ and $\mathcal {E}_4$ are independent, Lemma 2 implies that for θ sufficiently small we have $\mathbb {E}[(Z+W-Y-X_{\theta })^4\mid \mathcal {E}_1\cap \mathcal {E}_4]\leq 2\mathbb {E}[(Z+W-Y-X_{\theta })^4\mid \mathcal {E}_4]$. Further observe that the event $\mathcal {E}_4$ is decreasing in the configuration R _θ, and the FKG inequality implies that conditioning on $\mathcal {E}_4$ makes the configuration outside R _θ stochastically smaller. Since (Z + W − Y − X _θ) is positive and increasing in the configuration outside R _θ, we thus have

$$\displaystyle \begin{aligned}\mathbb{E}[(Z+W-Y-X_{\theta})^4\mid \mathcal{E}_4]\le \mathbb{E}[(Z+W-Y-X_{\theta})^4].\end{aligned}$$

Finally, as Z ≤ X ^∗ and Z + W − Y − X _θ ≥ 0

$$\displaystyle \begin{aligned}E[(Z+W-Y-X_\theta)^4] &\le \mathbb{E}[(X^*+W-Y-X_\theta)^4]\\ &\le O(\mathbb{E}[(X^*-X_{\theta})^4]+\mathbb{E}[(W-Y)^4])\\ &=O(\theta^{-4}r^{4/3}). \end{aligned} $$

For the last equality we use [5, Proposition 4.5] to show $\mathbb {E}[(X_{\theta }-4r)^{4}]=O(\theta ^{-4}r^{4/3})$, use [5, Theorem 4.1] to get $\mathbb {E}[(X^*-4r)^{4}]=O(r^{4/3})$ and deduce $\mathbb {E}[(W-Y)^4]=O(r^{4/3})$ from Lemma 1 as in the proof of Proposition 3. By taking θ sufficiently small, this concludes the proof of the proposition modulo Lemma 7 below.

Lemma 7

In the set up of the proof of Proposition 6 , we have $\mathbb {P}(A\mid \mathcal {E}_1\cap \mathcal {E}_4)\geq 1-e^{-\log ^2(\theta )}$ for all θ sufficiently small.

For this proof we make numerous uses of the estimate in [5, Theorem 4.2] which states that for an r × r ^2∕3 rectangle (or parallelogram) R and for pairs of u, w ∈ R such that the slope joining u, w is bounded away from 0 and infinity we have $\inf _{u,w} r^{-1/3}(T_{u,w}-\mathbb {E} T_{u,w})$ and $\sup _{u,w}r^{-1/3}(T_{u,w}-\mathbb {E} T_{u,w})$ both have stretched exponential tails.

Proof

We shall construct a number of large probability events which together will imply A. Let $\mathcal {A}_{\mathrm {loc},\phi }$ denote the event that for some $w\in \mathbb {L}_{r}\setminus \mathbb {L}_{r, \phi ^{1/2}}$ we have

$$\displaystyle \begin{aligned}T_{\mathbf{0},w}+T_{w,\mathbf{n}}\geq X_{\theta}+T_{\mathbf{r},\mathbf{n}}.\end{aligned}$$

Let $\mathcal {A}_{\theta ,1}$ denote the event that for all $v'=(v^{\prime }_1,v^{\prime }_2)\in R_{\theta }$ with 2r − 2θ ^3∕2 r ≤ d(v′) ≤ 2r − θ ^3∕2 r, we have

$$\displaystyle \begin{aligned}T_{v^{\prime},\mathbf{r}}^{R_{\theta}}\geq 2(2r-d(v'))-\theta^{1/2}r^{1/3} \log^{5} (\frac{1}{\theta}).\end{aligned}$$

Let $\mathcal {A}_{\theta ,2}$ denote the event that for all v′ as above and for all $w\in \mathbb {L}_{r,\phi ^{1/2}}\setminus \mathbb {L}_{r,\phi _0}$ we have

$$\displaystyle \begin{aligned}T_{v^{\prime},w}-\mathbb{E} T_{v',w} \leq \theta^{1/2}r^{1/3} \log^{10} (\frac{1}{\theta}).\end{aligned}$$

Finally, let $\widetilde {\mathcal {E}}$ denote the event that for any $w'\in \mathbb {L}_{r,\phi ^{1/2}}\setminus \mathbb {L}_{r,\phi _0}$ and the geodesic Γ′ from 0 to w′ there exists v′∈ R _θ ∩ Γ′ with 2r − 2θ ^3∕2 r ≤ d(v′) ≤ 2r − θ ^3∕2 r such that from 0 to v′, Γ′ is entirely contained in R _2θ.

We first claim that $\mathcal {E}_1\cap \widetilde {\mathcal {E}} \cap \mathcal {A}_{\theta ,1}\cap \mathcal {A}_{\theta ,2} \cap (\mathcal {A}_{\mathrm {loc},\phi })^c \subseteq A$. Indeed, observe first that $(\mathcal {A}_{\mathrm {loc},\phi })^c$ implies that $v:=\varGamma \cap \mathbb {L}_r\in \mathbb {L}_{r,\phi ^{1/2}}$. Then notice that for any $w'=(w^{\prime }_1,w^{\prime }_2)\in \mathbb {L}_{r,\phi ^{1/2}}\setminus \mathbb {L}_{r,\phi _0}$, $\widetilde {\mathcal {E}}$ implies that

$$\displaystyle \begin{aligned}T_{\mathbf{0},w^{\prime}}-X_*\leq \sup_{v^{\prime}} [T_{v^{\prime},w^{\prime}}-T_{v^{\prime},\mathbf{r}}^{R_{\theta}}]\end{aligned}$$

where the supremum is taken over all v′∈ R _θ such that 2r − 2θ ^3∕2 r ≤ d(v ^′) ≤ 2r − θ ^3∕2 r.

Recall, for w′ as above, the lower bound on $Y-T_{w',\mathbf {n}}$ given by the definition of $\mathcal {E}_1$. Using this together with the fact that $\mathbb {E} T_{v^{\prime },w^{\prime }}\leq 2(2r-d(v'))- \frac {|w^{\prime }_1-w^{\prime }_2|{ }^2}{50\theta ^{3/2}r}$ (this is a consequence of the moderate deviation estimate [5, Theorem 4.1]) and the definitions of $\mathcal {A}_{\theta ,1}$ and $\mathcal {A}_{\theta , 2}$, it follows that on $\mathcal {E}_1\cap \mathcal {A}_{\theta ,1}\cap \mathcal {A}_{\theta ,2}$ we have

$$\displaystyle \begin{aligned}\sup_{v^{\prime}} [T_{v,w^{\prime}}-T_{v^{\prime},\mathbf{r}}^{R_{\theta}}] \leq Y-T_{w',\mathbf{n}}\end{aligned}$$

where the supremum over v′ is as before. It therefore follows that on $\mathcal {E}_1\cap \mathcal {E}' \cap \mathcal {A}_{\theta ,1}\cap \mathcal {A}_{\theta ,2}$ we have

$$\displaystyle \begin{aligned}T_{\mathbf{0},w^{\prime}}-X_*\leq Y-T_{w^{\prime},\mathbf{n}}\end{aligned}$$

for each $w'\in {\mathbb {L}_{r,\phi ^{1/2}}\setminus \mathbb {L}_{r,\phi _0}}$. This completes the proof of the claim.

Now the barrier event $\mathcal {E}_4$ is designed in such a way that a path from 0 to w′ as above is penalised more heavily than a path constrained to stay within R _θ (as $L\gg \phi \gg \frac {1}{\theta }$). Formalising this, [5, Lemma 6.12] implies (the event $\widetilde {\mathcal {E}}$ defined there is slightly different, where the starting point of the geodesic is also allowed to vary around 0 but the same proof works) $\mathbb {P}((\widetilde {\mathcal {E}})^{c}\mid \mathcal {E}_4)\leq e^{-\log ^3 (1/\theta )}$. It follows from [5, Theorem 4.2] that $\mathbb {P}(\mathcal {A}_{\theta , 1})^c\leq e^{-\log ^{5/2}(1/\theta )}$ for all θ small. Next, notice that by dividing $\mathbb {L}_{r,\phi ^{1/2}}\setminus \mathbb {L}_{r,\phi _0}$ into intervals of length θr ^2∕3, applying [5, Theorem 4.2] and taking a union bound and using the FKG inequality it follows that $\mathbb {P}((\mathcal {A}_{\theta , 2})^c\mid \mathcal {E}_4)\leq e^{-\log ^3(1/\theta )}$. It remains to upper bound $\mathbb {P}(\mathcal {A}_{\mathrm {loc},\phi }\mid \mathcal {E}_4)$.

To this end, set $S_j:=\mathbb {L}_{r,j+1}\setminus \mathbb {L}_{r,j}$. Our objective is to show that with high probability, $Y+X_{\theta }\geq \sup _{w\in S_j} T_{\mathbf {0}, w}+\sup _{w\in S_j} T_{w, \mathbf {{n}}}$. Let $\mathcal {C}_{j}$ denote the event that $\sup _{w\in S_j} T_{\mathbf {0}, w} -X_{\theta } \geq \inf _{w\in S_j} Y-T_{w, \mathbf {{n}}}$. Clearly, for j > ϕ ^1∕2, we can upper bound $\mathbb {P}(\mathcal {C}_{j})$ by

$$\displaystyle \begin{aligned} &\mathbb{P}(\sup_{w\in S_j} T_{\mathbf{0}, w}-4r \geq -0.001 j^{2}r^{1/3})\\ &\quad +\mathbb{P}(X_{\theta}\leq 4r-0.001j^{2}r^{1/3})+\mathbb{P}(\inf_{w\in S_j} Y-T_{w, \mathbf{{n}}}\leq -0.002j^{2}r^{1/3}). \end{aligned} $$

Using [5, Theorem 4.2] for j < 0.9r ^1∕3 and [5, (13)] together with a union bound for j ≥ 0.9r ^1∕3, we can show that the first probability is upper bounded by $e^{-cj^{3/2}}$ (and the same is true conditionally on $\mathcal {E}_4$ by the FKG inequality). By Basu et al. [5, Theorem 4.2] and a simple concentration inequality for sums of θ ^−3∕2 many independent subexponential variables at scale θ ^1∕2 r ^1∕3 (see the proof of [5, Proposition 4.5]) we get that the second probability is upper bounded by $e^{-cj^2 \theta }$, whereas the third probability, by Theorem 3, is upper bounded by $e^{-cj^{2/3}}$. Notice also that the second and third events above are independent of $\mathcal {E}_4$. Summing over all j > ϕ ^1∕2 and using that ϕ is a large power of θ ⁻¹ gives the result gives that $\mathbb {P}(\mathcal {A}_{\mathrm {loc}}^{\phi }\mid \mathcal {E}_4)\leq e^{-\log ^3(1/\theta )}$.

Combining all these together and using $\mathcal {E}_1$ is independent of $\mathcal {E}_4$ together with Lemma 3 gives us $\mathbb {P}(A\mid \mathcal {E}_1\cap \mathcal {E}_4)\geq 1-e^{-\log ^2(\theta )}$ for all θ sufficiently small, as desired.

4.5 A Note on the Variance of Constrained Last Passage Time

Before concluding we also comment that the proof of Lemma 6 (see the proof of [5, Lemma 6.9]) can be used to obtain the sharp order of variance of the weight of the best path constrained to stay within a thin cylinder. In particular one can show that for θ ≤ 1 and r sufficiently large, Var X _θ = Θ(θ ^−1∕2 r ^2∕3) answering a question raised in [13]. The lower bound in the above statement can be proved using a simpler version of the argument used in the proof of [5, Lemma 6.9]. Upper bound follows from a Poincaré inequality argument after revealing θ ^3∕2 r × θr ^2∕3 rectangles one by one and using [5, Theorem 4.2].