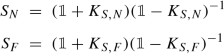Abstract
The core results of the Kreı̆n-Višik-Birman theory of self-adjoint extensions of semi-bounded symmetric operators are reproduced, both in their original and in a more modern formulation, with a comprehensive discussion that includes missing details, elucidative steps, and intermediate results of independent interest.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
This work has a two-fold purpose. On the one hand it aims at reproducing in their original form the key results of the so-called Kreı̆n-Višik-Birman theory of self-adjoint extensions of semi-bounded symmetric operators, providing an expanded discussion, including missing details and supplementary formulas, of the original works, that up to a large extent are written in a rather compact style and are available in Russian only. On the other hand, the goal is to give evidence of how the original results can be equivalently re-written into what is now the more modern formulation of the theory, as it can be found in the (relatively limited) literature in English language on the subject, formulation which is derived by alternatives means, typically boundary triplets techniques.
The whole field is nowadays undoubtedly classical, and in fact to some extent even superseded by more modern mathematical techniques. Let us then give evidence in this Introduction of the context and of the degree of novelty of this work.
Self-adjointness and self-adjoint extension theory constitute a well-established branch of functional analysis and operator theory, with deep-rooted motivations and applications, among others, in the boundary value problems for partial differential equations and in the mathematical methods for quantum mechanics and quantum field theory. At the highest level of generality, it is von Neumann’s celebrated theory of self-adjoint extensions that provides, very elegantly, the complete solution to the problem of finding self-adjoint operators that extend a given densely defined symmetric operator S on a given Hilbert space \(\mathscr {H}\). As well known, the whole family of such extensions is naturally indexed by all the unitary maps U between the subspaces \(\ker (S^*-z)\) and \(\ker (S^*-\overline {z})\) of \(\mathscr {H}\) for a fixed \(z\in \mathbb {C}\setminus \mathbb {R}\), the condition that such subspaces be isomorphic being necessary and sufficient for the problem to have a solution; each extension S U is determined by an explicit constructive recipe, given U and the above subspaces.
A relevant special case is when S is semi-bounded—one customarily assumes it to be bounded below, and so shall we henceforth—which is in fact a typical situation in the quest for stable quantum mechanical Hamiltonians. In this case \(\ker (S^*-z)\) and \(\ker (S^*-\overline {z})\) are necessarily isomorphic, which guarantees the existence of self-adjoint extensions. Among them, a canonical form construction (independent of von Neumann’s theory) shows that there exists a distinguished one, the Friedrichs extension S F, whose bottom coincides with the one of S, which is characterised by being the only self-adjoint extension whose domain is entirely contained in the form domain of S, and which has the property to be the largest among all self-adjoint extensions of S, in the sense of the operator ordering “\(\geqslant \)” for self-adjoint operators.
The first systematic extension theory for semi-bounded operators is due to Kreı̆n. Kreı̆n’s theory shows that all self-adjoint extensions of S, whose bottom is above a prescribed reference level \(m\in \mathbb {R}\), are naturally ordered, in the sense of “\(\geqslant \)”, between the Friedrichs extension from above (the “rigid” (жёсткое) extension, in Kreı̆n’s terminology), and a unique lowest extension S N from below, whose bottom is not less than the chosen m, the so-called Kreı̆n-von Neumann extension (the “soft” (мягкое) extension). In short: \(S_F\geqslant \widetilde {S}\geqslant S_N\) for any such extension \(\widetilde {S}\). (Let us refer to appendix A for a more detailed summary of von Neumann’s and Kreı̆n’s extension theory, or to modern overviews such as [56, Chapter X] and [60, Chapter 13].)
By the Kreı̆n-Višik-Birman (KVB) theory (where the order here reflects the chronological appearance of the seminal works of Kreı̆n [34], Višik [66], and Birman [8]), one means a development of Kreı̆n’s original theory, in the form of an explicit and extremely convenient classification of all self-adjoint extensions of a given semi-bounded and densely defined symmetric operator S, both in the operator sense and in the quadratic form sense.
As the distinction “Kreı̆n vs KVB” may appear a somewhat artificial retrospective, let us emphasize the following. In Kreı̆n’s original work [34] each extension of S is proved to be bijectively associated with a self-adjoint extension, with unit norm, of the Kreı̆n transform  of S. This way, a difficult self-adjoint extension problem (extension of S) is shown to be equivalent to an easier one (extension of the Kreı̆n transform of S), yet no general parametrisation of the extensions of S is given. The full KVB theory provides in addition a parametrisation of the extensions, labelling each of them in the form S
B where B runs over all self-adjoint operators acting on Hilbert subspaces of
of S. This way, a difficult self-adjoint extension problem (extension of S) is shown to be equivalent to an easier one (extension of the Kreı̆n transform of S), yet no general parametrisation of the extensions of S is given. The full KVB theory provides in addition a parametrisation of the extensions, labelling each of them in the form S
B where B runs over all self-adjoint operators acting on Hilbert subspaces of  , for some large enough \(\lambda \geqslant 0\).
, for some large enough \(\lambda \geqslant 0\).
The KVB theory has a number of features that make it in many respects more informative as compared to von Neumann’s. First and most importantly, the KVB parametrisation B ↔ S B identifies special subclasses of extensions of S, such as those whose bottom is above a prescribed level, in terms of a corresponding subclass of parameters B. In particular, both the Friedrichs extension S F and the Kreı̆n-von Neumann extension S N of S relative to a given reference lower bound can be selected a priori, meaning that the special parameter B that identifies S F or S N is explicitly known. In contrast, the parametrisation U ↔ S U based on unitaries U provided by von Neumann’s theory does not identify a priori the particular U that gives S F or S N. An amount of further relevant information concerning each extension, including invertibility, semi-boundedness, and special features of its negative spectrum (finiteness, multiplicity, accumulation points) turn out to be controlled by the analogous properties of the extension parameter. Furthermore, the KVB extension theory has a natural and explicit re-formulation in terms of quadratic forms, an obviously missing feature in von Neumann’s theory. On this last point, it is worth emphasizing that whereas the KVB classification of the extensions as operators is completely general, the classification in terms of the corresponding quadratic forms only applies to the family of semi-bounded self-adjoint extensions of S, while unbounded below extensions (if any) escape this part of the theory.Footnote 1
For several historical and scientific reasons (a fact that itself would indeed deserve a separate study) the mathematical literature in English language on the KVB theory is considerably more limited as compared to von Neumann’s theory. Over the decades the tendency has been in general to re-derive and discuss the main results through routes and with notation and “mathematical flavour” that differ from the original formulation.
At the price of an unavoidable oversimplification, we can say that while in the applications to quantum mechanics von Neumann’s theory has achieved a dominant role, and is nowadays a textbooks standard, on a more abstract mathematical level the original results of Kreı̆n, Višik, and Birman, and their applications to boundary value problems for elliptic PDE, have eventually found a natural evolution and generalisation within the modern theory of boundary triplets. Thus, in modern terms the deficiency space  is referred to as a boundary value space, this space is then equipped with a boundary triplet structure, and the extensions of S are parametrised by linear relations on the boundary space, with a distinguished position for the Friedrichs and the Kreı̆n-von Neumann extensions that are intrinsically encoded in the choice of the boundary triplet.
is referred to as a boundary value space, this space is then equipped with a boundary triplet structure, and the extensions of S are parametrised by linear relations on the boundary space, with a distinguished position for the Friedrichs and the Kreı̆n-von Neumann extensions that are intrinsically encoded in the choice of the boundary triplet.
However, this work is neither meant nor going to move from the point of view of the boundary triplet theory, which is surely a beautiful and prolific scheme within which one can indeed retrieve the old results of Kreı̆n, Višik, and Birman—in fact, the latter approach is already available in the literature: for example a recent, concise, and relatively complete survey of the re-derivation of Kreı̆n, Višik, and Birman from the boundary triplet theory may be found in [60, Chapters 13 and 14], and in the references therein.
Our perspective, instead, is primarily motivated by the use of the KVB theory in the rigorous construction of quantum Hamiltonians of particle systems with contact interactions and, more generally, in the extension theory of quantum Hamiltonians of few-body and many-body systems where the interaction is singular enough so as to make perturbative techniques inapplicable, and hence to give rise to a multiplicity of self-adjoint realisations to qualify and classify. This is a realm where customarily the largest part of the mathematics is worked out by means of the ‘dominant’ extension theory a la von Neumann, or by the theory of quadratic forms on Hilbert space, and to a lesser extent by means of tools from non-standard analysis or boundary triplets. However, results from Kreı̆n and Birman have been known since long to bring in this context complementary or also new information: one paradigmatic instance is the study of particle Hamiltonians of contact interaction carried on by trailblazers such as Berezin, Faddeev, and above all Minlos and his school [45, 50, 51]—an ample historical survey of which is in [41, Section 2], further references being provided here at the end of Sect. 4. In the above-mentioned contexts, as we shall elaborate further later, comprehensive references in the literature are, and have been over the decades, quite limited in number and scope (as discussed in Sect. 4), due also to the circumstance that most of the original sources were available in Russian only.
The last considerations constitute our motivations for the present note, the object of which is therefore: first, to provide an exhaustive recapitulation of the KVB theory and of its ‘elementary’ derivation in the original operator-theoretic framework, thus with no reference to more modern superstructures such as boundary triplets; second, to reproduce, neatly and directly from the original formulation, the ‘modern’ version of the main results of the theory, that is, the version appearing essentially in all the (western) literature after Kreı̆n, Višik, and Birman, and derived therein through more involved and more general schemes.
To this aim, in Sect. 2 we devote a careful effort to replicate the original results of the KVB theory, in order to make it accessible in its full rigour (and in English language) with respect to its initial version, that is, by filling certain gaps of the original proofs, supplementing the material with non-ambiguous notation and elucidative steps, producing and highlighting intermediate results that have their own independent interest. In a way, and this is our first novelty, the outcome is a complete and self-consistent “reading guide” for the original results and for the route to demonstrate them, together with a clean presentation of all the main statements that are mostly referred to in the applications, significantly Theorem 1 (together with the special cases (5) and (7)), Theorems 2, 3, and 4, and Proposition 2.
Mirroring such analysis, in Sect. 3 we reproduce an alternative, equivalent version of the main results of the KVB theory. These statements are actually those by which (part of) the KVB theory has been presented, re-derived, discussed, and applied in the subsequent literature in English language. Typically this was done by means of modern boundary-triplet-based extension techniques, whereas the novelty here is to derive such results directly from the original ones, with the minimum amount of operator theory (the key is the inversion mechanism of our Proposition 3). Thus, Sect. 3 has the two-fold feature of proving the equivalence between “modern” and “original” formulations and of providing another reference scheme of all main results, significantly Theorems 5, 6, and 7, Proposition 4, Theorem 8, and Proposition 5.
In Sect. 4 we place the KVB theory into a concise historical perspective of motivations, further developments, and applications.
In Sect. 5 we complete the main core of the theory with results that characterise relevant properties of the extensions, such as invertibility, semi-boundedness, and other special features of the negative discrete spectrum, in terms of the corresponding properties of the extension parameter.
In Sect. 6 we discuss, within the KVB formalism, the structure of resolvents of self-adjoint extensions, in the form of Kreı̆n-like resolvent formulas. The results emerging from Sects. 5 and 6 corroborates the picture that the KVB extension parametrisation is in many fundamental aspects more informative than von Neumann’s parametrisation.
Last, in Sect. 7 we show how the general formulas of the KVB theory apply to simple examples in which the extension problem by means of von Neumann’s theory is already well known, so as to make the comparison between the two approaches evident.
For reference and comparison purposes, in the final Appendix we organised an exhaustive summary of von Neumann’s and of Kreı̆n’s self-adjoint extension theories, with special emphasis on the two “distinguished” extensions, the Friedrichs and the Kreı̆n-von Neumann one.
Notation
Essentially all the notation adopted here is standard, let us only emphasize the following. Concerning the various sums of spaces that will occur, we shall denote by \(\dotplus \) the direct sum of vector spaces, by ⊕ the direct orthogonal sum of closed Hilbert subspaces of the same underlying Hilbert space \(\mathscr {H}\) (the space where the initial symmetric and densely defined operator is taken), and by \(\boxplus \) the direct sum of subspaces of \(\mathscr {H}\) that are orthogonal to each other but are not a priori all closed. For any given symmetric operator S with domain \(\mathscr {D}(S)\), we shall denote by m(S) the “bottom” of S, i.e., its greatest lower bound
S being semi-bounded means therefore m(S) > −∞. Let us also adopt the customary convention to distinguish the operator domain and the form domain of any given densely defined and symmetric operator S by means of the notation \(\mathscr {D}(S)\) vs \(\mathscr {D}[S]\). To avoid ambiguities, V
⊥ will always denote the orthogonal complement of a subspace V of \(\mathscr {H}\) with respect to \(\mathscr {H}\) itself: when interested in the orthogonal complement of V within a closed subspace K of \(\mathscr {H}\) we shall keep the extended notation V
⊥∩ K. Analogously, the closure \(\overline {V}\) of the considered subspaces will be always meant with respect to the norm-topology of the underlying Hilbert space \(\mathscr {H}\). As no particular ambiguity arises in our formulas when referring to the identity operator, we shall use the symbol  for it irrespectively of the subspace of \(\mathscr {H}\) it acts on. As for the spectral measure of a self-adjoint operator A we shall use the standard notation dE
(A) (see, e.g., [60, Chapters 4 and 5]). As customary, σ(T) and ρ(T) shall denote, respectively, the spectrum and the resolvent set of an operator T on Hilbert space.
for it irrespectively of the subspace of \(\mathscr {H}\) it acts on. As for the spectral measure of a self-adjoint operator A we shall use the standard notation dE
(A) (see, e.g., [60, Chapters 4 and 5]). As customary, σ(T) and ρ(T) shall denote, respectively, the spectrum and the resolvent set of an operator T on Hilbert space.
2 Fundamental Results in the KVB Theory: Original Version
In this Section we reproduce, through an expanded and more detailed discussion, the pillars of the KVB theory for self-adjoint extensions of bounded below symmetric operator, in the form they were established in the original works Kreı̆n [34], Višik [66], and Birman [8]. The main statements are Lemma 1, Theorem 1, Remark 1, Theorems 2, 3, and 4, and Proposition 2 below. The notation, when applicable, is kept on purpose the same as that of those works.
2.1 General Assumptions: Choice of a Reference Lower Bound
In the following we shall assume that S is a semi-bounded (below), not necessarily closed, densely defined symmetric operator acting on a Hilbert space \(\mathscr {H}\). Unlike the early developments of the theory (Kreı̆n’s theory), no restriction is imposed to the magnitude of the deficiency indices \(\dim \ker (S^*\pm \mathrm {i})\) of S: in particular, they can also be infinite.
It is not restrictive to assume further
for in the general case one applies the discussion that follows to the strictly positive operator  , λ > −m(S), and then re-express trivially the final results in terms of the original S.
, λ > −m(S), and then re-express trivially the final results in terms of the original S.
Associated to S are two canonical, distinguished self-adjoint extensions, the well-known Friedrichs extension S F and Kreı̆n-von Neumann extension S N. Whereas a complete summary of the construction and of the properties of such extensions is presented in appendix A.2, which we will be making reference to whenever in the following we shall need a particular attribute of S F or S N for the proofs, let us recall here their distinguishing features.
The extension S F is semi-bounded and with the same bottom m(S F) = m(S) of S. Its quadratic form is precisely the closure of the (closable) quadratic form associated with S. In fact, S F is the restriction of S ∗ to the domain \(\mathscr {D}[S]\cap \mathscr {D}(S^*)\). Among all self-adjoint extensions of S, S F is the only one whose operator domain is contained in \(\mathscr {D}[S]\), and moreover S F is larger than any other semi-bounded extension \(\widetilde {S}\) of S, in the sense of the ordering \(S_F\geqslant \widetilde {S}\) (which, in particular, means \(\mathscr {D}[S_F] \subset \mathscr {D}[\widetilde {S}]\)).
Thus, the choice m(S) > 0 implies that the Friedrichs extension S F of S is invertible with bounded inverse defined everywhere on \(\mathscr {H}\): this will allow \(S_F^{-1}\) to enter directly the discussion. In the general case in which S F is not necessarily invertible, the role of \(S_F^{-1}\) can be naturally replaced in many respects (but not all) by the inverse \(\widetilde {S}^{-1}\) of any a priori known self-adjoint extension \(\widetilde {S}\) of S, which thus takes the role of given “datum” of the theory. As an example see the role played by the Friedrichs extension in the proofs of Lemma 5 and Theorems 3, 4.
With the choice m(S) > 0, the level 0 becomes naturally the reference value with respect to which to express the other distinguished (canonically given) extension of S, the Kreı̆n-von Neumann extension S N. It is qualified among all other positive self-adjoint extensions \(\widetilde {S}\) of S by being the unique smallest, in the sense \(\widetilde {S}\geqslant S_N\).
We underline that unlike Kreı̆n’s original theory and many of the recent presentations of the KVB theory, the discussion here is not going to be restricted to the positive self-adjoint extensions of S. On the contrary, we shall present the full theory that includes also those extensions, if any, with finite negative bottom, or even unbounded below.
2.2 Adjoint of a Semi-Bounded Symmetric Operator: Regular and Singular Part
The first step of the theory is to describe the structure of the domain of the adjoint S ∗ of S. Recall that a characterisation of \(\mathscr {D}(S^*)\) is already given by von Neumann’s formula

which is valid, more generally, for any densely defined S. The KVB theory works with a “real” version of (3), with z = 0 and with the space
instead of the two deficiency spaces  and
and  . With a self-explanatory nomenclature, U shall henceforth be referred to as the deficiency space of S, with no restriction on \(\dim U\).
. With a self-explanatory nomenclature, U shall henceforth be referred to as the deficiency space of S, with no restriction on \(\dim U\).
The result consists of a decomposition of \(\mathscr {D}(S^*)\) first proved by Kreı̆n (see also Remark 21) and a further refinement, initially due to Višik, to which Birman gave later an alternative proof.
Lemma 1 (Kreı̆n Decomposition Formula for \(\mathscr {D}(S^*)\))
For a densely defined symmetric operator S with positive bottom,
Proof
\(\mathscr {D}(S^*)\supset \mathscr {D}(S_F)+\ker S^*\) because each summand is a subspace of \(\mathscr {D}(S^*)\). As for the opposite inclusion, one can always decompose an arbitrary \(g\in \mathscr {D}(S^*)\) as \(g=S_F^{-1}S^*g+(g-S_F^{-1}S^*g)\), where \(S_F^{-1}S^*g\in \mathscr {D}(S_F)\), and where \(g-S_F^{-1}S^*g\in \ker S^*\), because \(S^*(g-S_F^{-1}S^*g)=S^*g-S^*g=0\). Last, the sum in the r.h.s. of (5) is direct because any \(g\in \mathscr {D}(S_F)\cap \ker S^*\) is necessarily in \(\ker S_F\) (S F g = S ∗ g = 0), and from 0 < m(S) = m(S F) one has \(\ker S_F=\{0\}\). □
Theorem 1 (Višik-Birman Decomposition Formula for \(\mathscr {D}(S^*)\))
For a densely defined symmetric operator S with positive bottom,
Proof
Let \(U=\ker S^*\). As in the proof of Lemma 1, \(\mathscr {D}(S^*)\supset \mathscr {D}(\overline {S})\dotplus S_F^{-1} U\dotplus U\) is obvious and conversely any \(g\in \mathscr {D}(S^*)\) can be written as \(g=S_F^{-1}S^*g+u\) for some \(u\in U=\ker S^*\). In turn, owing to \(\mathscr {H}=\overline {\mathrm {ran} S}\oplus \ker S^*\), one writes \(S^*g=h_0+\widetilde {u}\), and hence \(S_F^{-1}S^*g=S_F^{-1} h_0+S_F^{-1}\widetilde {u}\), for some \(\widetilde {u}\in U\) and h 0 =limn→∞ Sφ n for some sequence (φ n)n in \(\mathscr {D}(S)\). From \(\varphi _n= S_F^{-1}S\varphi _n\to S_F^{-1}h_0\) and Sφ n → h 0 as n →∞, and from the closability of S, one deduces that \(f:=S_F^{-1}h_0\in \mathscr {D}(\overline {S})\). Therefore, \(g=f+S_F^{-1}\widetilde {u}+u\), which proves \(\mathscr {D}(S^*)\subset \mathscr {D}(\overline {S})+S_F^{-1} U+U\). Last, one concludes that the sum in (6) is direct as follows: if \(g=f+S_F^{-1}\widetilde {u}+u=0\), then \(0=S^*g=\overline {S}f+\widetilde {u}\), which forces \(\overline {S}f=\widetilde {u}=0\) because \(\overline {S}f\perp \widetilde {u}\); then also \(f=S_F^{-1}\overline {S}f=0\) and, from g = 0, also u = 0. □
Remark 1
The argument of the proof above can be repeated to conclude
and hence
Indeed, while it is obvious that the r.h.s. of (7) is contained in the l.h.s., conversely one takes a generic \(g\in \mathscr {D}(S_F)\) and decomposes \(S_Fg=h_0+\widetilde {u}\) with \(h_0\in \overline {\mathrm {ran} S}\) and \(\widetilde {u}\in U\) as above, whence, by the same argument, \(g=S_F^{-1}h_0+S_F^{-1}\widetilde {u}\) with \(S_F^{-1}h_0\in \mathscr {D}(\overline {S})\).
Remark 2
Precisely as in the remark above, one also concludes that
for any self-adjoint extension \(\widetilde {S}\) of S that is invertible everywhere on \(\mathscr {H}\).
Remark 3
Since S is closable and injective (m(S) > 0), then as well known
Thus, in the above proof one could claim immediately that \(h_0=\overline {S}f\) for some \(f\in \mathscr {D}(\overline {S})\), whence \(S_F^{-1}h_0=S_F^{-1}\overline {S}f=f\in \mathscr {D}(\overline {S})\).
Remark 4
In view of the applications in which S and S F are differential operators on an L 2-space and hence \(\mathscr {D}(S_F)\) indicates an amount of regularity of its elements, it is convenient to regard \(\mathscr {D}(S_F)=\mathscr {D}(\overline {S})\dotplus S_F^{-1} U\) in (6) as the “regular component” and, in contrast, \(U=\ker S^*\) as the “singular component” of the domain of S ∗.
Remark 5
In all the previous formulas the assumption m(S) > 0 only played a role to guarantee the existence of the everywhere defined and bounded operator \(S_F^{-1}\). It is straightforward to adapt the arguments above to prove the following: if S is a symmetric and densely defined operator on \(\mathscr {H}\) and \(\widetilde {S}\) is a self-adjoint extension of S, then for any \(z\in \rho (\widetilde {S})\) (the resolvent set of \(\widetilde {S}\))



2.3 Višik’s B Operator
To a generic self-adjoint extension of S one associates, canonically with respect to the decomposition (6), a self-adjoint operator B acting on a Hilbert subspace of \(\ker S^*\). This “Višik’s B operator” defined in (23) below (introduced first by Višik in [66]) turns out to be a convenient label to index the self-adjoint extensions of S: this is going to be done in formula (24) proved in the end of this Subsection.
Let \(\widetilde {S}\) be a self-adjoint extension of S. Correspondingly, let U 0 and U 1 be the two closed subspaces of \(U=\ker S^*\) (and hence of \(\mathscr {H}\)), and let \(\mathscr {H}_+\) be the closed subspace of \(\mathscr {H}\), uniquely associated to \(\widetilde {S}\) by means of the definitions
Thus,
Let \(P_+:\mathscr {H}\to \mathscr {H}\) be the orthogonal projection onto \(\mathscr {H}_+\).
The operator \(\widetilde {S}\) has the following properties.
Lemma 2
-
(i)
\(\overline {\mathrm {ran} S}\oplus U_1\;=\;\mathscr {H}_+\;=\;\overline {\mathrm {ran}\widetilde {S}}\) , i.e., \(\mathrm {ran}\widetilde {S}\) is dense in \(\mathscr {H}_+\)
-
(ii)
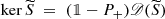
-
(iii)
\(\mathscr {D}(\widetilde {S})=(\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+)\boxplus \ker \widetilde {S}=P_+\mathscr {D}(\widetilde {S})\boxplus \ker \widetilde {S}\) and also \(\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+=P_+\mathscr {D}(\widetilde {S})\)
-
(iv)
\(\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+\) is dense in \(\mathscr {H}_+\)
-
(v)
\(\widetilde {S}\) maps \(\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+\) into \(\mathscr {H}_+\)
-
(vi)
\(\mathrm {ran}\widetilde {S}=\mathrm {ran} \overline {S}\,\boxplus \,\widetilde {U}_1\) where \(\widetilde {U}_1\) is a dense subspace of U 1 uniquely identified by \(\widetilde {S}\).
Proof
(i) follows by (15), because \(\overline {\mathrm {ran}\widetilde {S}}\) is the orthogonal complement to \(\ker \widetilde {S}\) in \(\mathscr {H}\) (owing to the self-adjointness of \(\widetilde {S}\)). In (ii) the “⊃” inclusion is obvious and conversely, if \(u_0\in \ker \widetilde {S}\subset \mathscr {D}(\widetilde {S})\), then  . To establish (iii), decompose a generic \(g\in \mathscr {D}(\widetilde {S})\) as g = f
+ + u
0 for some \(f_+\in \mathscr {H}_+\) and \(u_0\in U_0=\ker \widetilde {S}\) (using \(\mathscr {H}=\mathscr {H}_+\oplus \ker \widetilde {S}\)): since \(f_+=g-u_0\in \mathscr {D}(\widetilde {S})\), then \(f_+\in \mathscr {D}(\widetilde {S})\cap \mathscr {H}_+\) and therefore \(\mathscr {D}(\widetilde {S})\subset (\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+)\boxplus \ker \widetilde {S}\). The opposite inclusion is obvious, thus \(\mathscr {D}(\widetilde {S})=(\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+)\boxplus \ker \widetilde {S}\). It remains to prove that \(\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+=P_+\mathscr {D}(\widetilde {S})\): the inclusion \(\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+\subset P_+\mathscr {D}(\widetilde {S})\) is obvious, as for the converse, if \(h=P_+ g\in P_+\mathscr {D}(\widetilde {S})\) for some \(g\in \mathscr {D}(\widetilde {S})\), decompose g = f
+ + u
0 in view of \(\mathscr {D}(\widetilde {S})=(\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+)\boxplus \ker \widetilde {S}\), then \(h= P_+ g = f_+\in \mathscr {D}(\widetilde {S})\cap \mathscr {H}_+\), which completes the proof. To establish (iv), for fixed arbitrary \(h_+\in \mathscr {H}_+\) let \((f_n)_{n\in \mathbb {N}}\) be a sequence in \(\mathscr {D}(\widetilde {S})\) of approximants of h
+ (indeed \(\mathscr {D}(\widetilde {S})\) is dense in \(\mathscr {H}\)): then, as n →∞, f
n → h
+ implies P
+
f
n → h
+. (v) is an immediate consequence of (i), because \(\widetilde {S}\) maps \(\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+\) into \(\mathrm {ran} \widetilde {S}\). Last, let us prove (vi). Recall that \(\overline {\mathrm {ran} S}=\mathrm {ran}\overline {S}\), because S is closable and injective (m(S) > 0). Set \(\widetilde {U}_1:=\{u_g\in U_1\,|\,\widetilde {S}g=\overline {S}f_g+u_g\text{ for }g\in \mathscr {D}(\widetilde {S})\}\), where \(f_g\in \mathscr {D}(\overline {S})\) and u
g ∈ U
1 are uniquely determined by the given \(g\in \mathscr {D}(\widetilde {S})\) through (i) and the decomposition \(\overline {\mathrm {ran}\widetilde {S}}=\mathscr {H}_+=\mathrm {ran} \overline {S}\oplus U_1\). The inclusions \(\mathrm {ran}\widetilde {S}\subset \mathrm {ran} \overline {S}\boxplus \widetilde {U}_1\) and \(\mathrm {ran}\widetilde {S}\supset \mathrm {ran} \overline {S}\) are obvious, furthermore \(\mathrm {ran}\widetilde {S}\supset \widetilde {U}_1\) because each \(\widetilde {u}_1\in \widetilde {U}_1\) is by definition the difference of two elements in \(\mathrm {ran}\widetilde {S}\). Thus, \(\mathrm {ran}\widetilde {S}=\mathrm {ran} \overline {S}\boxplus \widetilde {U}_1\). It remains to prove the density of \(\widetilde {U}_1\) in U
1. Given an arbitrary \(u_1\in U_1\subset \mathscr {H}_+\) and a sequence \((\widetilde {S}g_n)_{n\in \mathbb {N}}\in \mathrm {ran}\widetilde {S}\) of approximants of u
1 (owing to the density of \(\mathrm {ran}\widetilde {S}\) in \(\mathscr {H}_+\)), decompose \(\widetilde {S}g_n=\overline {S}f_n+\widetilde {u}_n\), for some \(f_n\in \mathscr {D}(\overline {S})\) and \(\widetilde {u}_n\in \widetilde {U}_1\), in view of \(\mathrm {ran}\widetilde {S}=\mathrm {ran} \overline {S}\boxplus \widetilde {U}_1\): denoting by \(P_1:\mathscr {H}_+\to \mathscr {H}_+\) the orthogonal projection onto U
1, one has \(u_1=P_1u_1=P_1\lim _n(\overline {S}f_n+\widetilde {u}_n)=\lim _n\widetilde {u}_n\), which shows that \((\widetilde {u}_n)_{n\in \mathbb {N}}\) is a sequence in \(\widetilde {U}_1\) of approximants of u
1. □
. To establish (iii), decompose a generic \(g\in \mathscr {D}(\widetilde {S})\) as g = f
+ + u
0 for some \(f_+\in \mathscr {H}_+\) and \(u_0\in U_0=\ker \widetilde {S}\) (using \(\mathscr {H}=\mathscr {H}_+\oplus \ker \widetilde {S}\)): since \(f_+=g-u_0\in \mathscr {D}(\widetilde {S})\), then \(f_+\in \mathscr {D}(\widetilde {S})\cap \mathscr {H}_+\) and therefore \(\mathscr {D}(\widetilde {S})\subset (\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+)\boxplus \ker \widetilde {S}\). The opposite inclusion is obvious, thus \(\mathscr {D}(\widetilde {S})=(\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+)\boxplus \ker \widetilde {S}\). It remains to prove that \(\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+=P_+\mathscr {D}(\widetilde {S})\): the inclusion \(\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+\subset P_+\mathscr {D}(\widetilde {S})\) is obvious, as for the converse, if \(h=P_+ g\in P_+\mathscr {D}(\widetilde {S})\) for some \(g\in \mathscr {D}(\widetilde {S})\), decompose g = f
+ + u
0 in view of \(\mathscr {D}(\widetilde {S})=(\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+)\boxplus \ker \widetilde {S}\), then \(h= P_+ g = f_+\in \mathscr {D}(\widetilde {S})\cap \mathscr {H}_+\), which completes the proof. To establish (iv), for fixed arbitrary \(h_+\in \mathscr {H}_+\) let \((f_n)_{n\in \mathbb {N}}\) be a sequence in \(\mathscr {D}(\widetilde {S})\) of approximants of h
+ (indeed \(\mathscr {D}(\widetilde {S})\) is dense in \(\mathscr {H}\)): then, as n →∞, f
n → h
+ implies P
+
f
n → h
+. (v) is an immediate consequence of (i), because \(\widetilde {S}\) maps \(\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+\) into \(\mathrm {ran} \widetilde {S}\). Last, let us prove (vi). Recall that \(\overline {\mathrm {ran} S}=\mathrm {ran}\overline {S}\), because S is closable and injective (m(S) > 0). Set \(\widetilde {U}_1:=\{u_g\in U_1\,|\,\widetilde {S}g=\overline {S}f_g+u_g\text{ for }g\in \mathscr {D}(\widetilde {S})\}\), where \(f_g\in \mathscr {D}(\overline {S})\) and u
g ∈ U
1 are uniquely determined by the given \(g\in \mathscr {D}(\widetilde {S})\) through (i) and the decomposition \(\overline {\mathrm {ran}\widetilde {S}}=\mathscr {H}_+=\mathrm {ran} \overline {S}\oplus U_1\). The inclusions \(\mathrm {ran}\widetilde {S}\subset \mathrm {ran} \overline {S}\boxplus \widetilde {U}_1\) and \(\mathrm {ran}\widetilde {S}\supset \mathrm {ran} \overline {S}\) are obvious, furthermore \(\mathrm {ran}\widetilde {S}\supset \widetilde {U}_1\) because each \(\widetilde {u}_1\in \widetilde {U}_1\) is by definition the difference of two elements in \(\mathrm {ran}\widetilde {S}\). Thus, \(\mathrm {ran}\widetilde {S}=\mathrm {ran} \overline {S}\boxplus \widetilde {U}_1\). It remains to prove the density of \(\widetilde {U}_1\) in U
1. Given an arbitrary \(u_1\in U_1\subset \mathscr {H}_+\) and a sequence \((\widetilde {S}g_n)_{n\in \mathbb {N}}\in \mathrm {ran}\widetilde {S}\) of approximants of u
1 (owing to the density of \(\mathrm {ran}\widetilde {S}\) in \(\mathscr {H}_+\)), decompose \(\widetilde {S}g_n=\overline {S}f_n+\widetilde {u}_n\), for some \(f_n\in \mathscr {D}(\overline {S})\) and \(\widetilde {u}_n\in \widetilde {U}_1\), in view of \(\mathrm {ran}\widetilde {S}=\mathrm {ran} \overline {S}\boxplus \widetilde {U}_1\): denoting by \(P_1:\mathscr {H}_+\to \mathscr {H}_+\) the orthogonal projection onto U
1, one has \(u_1=P_1u_1=P_1\lim _n(\overline {S}f_n+\widetilde {u}_n)=\lim _n\widetilde {u}_n\), which shows that \((\widetilde {u}_n)_{n\in \mathbb {N}}\) is a sequence in \(\widetilde {U}_1\) of approximants of u
1. □
Since \(\widetilde {S}\) maps \(\mathscr {D}(\widetilde {S})\cap \mathscr {H}_+\) into \(\mathscr {H}_+\) and trivially U 0 into itself, and since P + maps \(\mathscr {D}(\widetilde {S})\) into itself (Lemma 2(iii)), then \(\mathscr {H}_+\) and U 0 are reducing subspaces for \(\widetilde {S}\) (see, e.g., [60, Prop. 1.15]). The non-trivial (i.e., non-zero) part of \(\widetilde {S}\) in this reduction is the operator
which is therefore a densely defined, injective, and self-adjoint operator on the Hilbert space \(\mathscr {H}_+\). Explicitly,
The inverse of \(\widetilde {S}_+\) (on \(\mathscr {H}_+\)) is the self-adjoint operator \(\widetilde {S}_+^{-1}\) with
and hence
((20) follows from \(\widetilde {S}_+^{-1} (\widetilde {S} P_+f)=P_+f\) in (18), letting now f run on \(\mathscr {D}(\overline {S})\) only: the r.h.s. gives \(P_+\mathscr {D}(\overline {S})\), in the l.h.s. one uses that \(\widetilde {S}P_+f=\widetilde {S}f=\overline {S}f\ \forall f\in \mathscr {D}(\overline {S})\) and hence \(\{\widetilde {S}P_+f\,|\,f\in \mathscr {D}(\overline {S})\}=\mathrm {ran} \overline {S}\).)
Furthermore, by setting

one defines a self-adjoint operator \(\mathscr {S}^{-1}\) on the whole \(\mathscr {H}\), with reducing subspaces \(\mathscr {H}_+=\overline {\mathrm {ran}\widetilde {S}}\) and \(U_0=\ker \widetilde {S}\).
Two further useful properties are the following.
Lemma 3
-
(i)
\(\mathscr {D}(\overline {S})+U_0\;=\;P_+\mathscr {D}(\overline {S})\,\boxplus \,U_0\)
-
(ii)
\(P_+\mathscr {D}(\widetilde {S})\;=\;P_+\mathscr {D}(\overline {S})+\mathscr {S}^{-1}\widetilde {U}_1\).
Proof
The inclusion \(\mathscr {D}(\overline {S})+U_0\subset P_+\mathscr {D}(\overline {S})\,\boxplus \,U_0\) in (i) follows from the fact that each summand in the l.h.s. belongs to the sum in the r.h.s., in particular,  . Conversely, given a generic \(h=P_+f\in P_+\mathscr {D}(\overline {S})\) for some \(f\in \mathscr {D}(\overline {S})\) and u
0 ∈ U
0, then \(h+u_0=f+u_0^{\prime }\) with
. Conversely, given a generic \(h=P_+f\in P_+\mathscr {D}(\overline {S})\) for some \(f\in \mathscr {D}(\overline {S})\) and u
0 ∈ U
0, then \(h+u_0=f+u_0^{\prime }\) with  , which proves the inclusion \(\mathscr {D}(\overline {S})+U_0\supset P_+\mathscr {D}(\overline {S})\,\boxplus \,U_0\). (ii) follows by applying \(\mathscr {S}^{-1}\) to the decomposition \(\mathrm {ran}\widetilde {S}=\mathrm {ran} \overline {S}\boxplus \widetilde {U}_1\) of Lemma 2(vi), for on the l.h.s. one gets \(\mathscr {S}^{-1}\mathrm {ran}\widetilde {S}=P_+\mathscr {D}(\widetilde {S})\), owing to (21), whereas on the r.h.s. one gets \(\mathscr {S}^{-1}\mathrm {ran} \overline {S}=P_+\mathscr {D}(\overline {S})\), owing to (20). □
, which proves the inclusion \(\mathscr {D}(\overline {S})+U_0\supset P_+\mathscr {D}(\overline {S})\,\boxplus \,U_0\). (ii) follows by applying \(\mathscr {S}^{-1}\) to the decomposition \(\mathrm {ran}\widetilde {S}=\mathrm {ran} \overline {S}\boxplus \widetilde {U}_1\) of Lemma 2(vi), for on the l.h.s. one gets \(\mathscr {S}^{-1}\mathrm {ran}\widetilde {S}=P_+\mathscr {D}(\widetilde {S})\), owing to (21), whereas on the r.h.s. one gets \(\mathscr {S}^{-1}\mathrm {ran} \overline {S}=P_+\mathscr {D}(\overline {S})\), owing to (20). □
Summarising so far, the given operator S and the given self-adjoint extension \(\widetilde {S}\) determine canonically (and, in fact, constructively) the closed subspace U 1 of \(\ker S^*\), the dense subspace \(\widetilde {U}_1\) in U 1, the closed subspace \(\mathscr {H}_+=\overline {\mathrm {ran}\widetilde {S}}=\mathrm {ran}\overline {S}\oplus U_1\) of \(\mathscr {H}\) (equivalently, the orthogonal projection P + onto \(\mathscr {H}_+\)), and the self-adjoint operator \(\mathscr {S}^{-1}\) on \(\mathscr {H}\), with the properties discussed above. In terms of these data, one defines

a self-adjoint operator on \(\mathscr {H}\) with the following properties.
Lemma 4
-
(i)
\(\mathscr {B}\) is self-adjoint on \(\mathscr {H}\) and it is bounded if and only if the inverse of \(\widetilde {S}\upharpoonright \big (\mathscr {D}(\widetilde {S})\cap \overline {\mathrm {ran}\widetilde {S}}\,\big )\) (i.e., \(\widetilde {S}_+^{-1}\) ) is bounded as an operator on \(\mathscr {H}_+\).
-
(ii)
With respect to the decomposition (15) \(\mathscr {H}=\mathrm {ran}\overline {S}\oplus U_1\oplus U_0\) , one has \(\mathscr {D}(\mathscr {B})=\mathrm {ran} \overline {S}\,\boxplus \,\widetilde {U}_1\,\boxplus \,U_0\), \(\mathscr {B}\,\mathrm {ran} \overline {S}=\{0\}\), \(\mathscr {B}\,\widetilde {U}_1\subset U_1\) , and \(\mathscr {B}\,U_0=\{0\}\).
Proof
(i) is obvious from the definition of \(\mathscr {B}\) and of \(\mathscr {S}^{-1}\): the former is bounded if and only if the latter is. As for (ii), \(\mathscr {D}(\mathscr {B})=\mathrm {ran}\widetilde {S}\,\boxplus \,\ker \widetilde {S}=\mathrm {ran} \overline {S}\,\boxplus \,\widetilde {U}_1\,\boxplus \,U_0\) follows from (22) and Lemma 2(vi). Moreover, \(\mathscr {B}\,U_0=\{0\}\) is obvious from (21) and (22). To see that \(\mathscr {B}\,\mathrm {ran} \overline {S}=\{0\}\) let \(f\in \mathscr {D}(\overline {S})\), then \(\mathscr {B} \overline {S}f=\mathscr {S}^{-1}\overline {S}f-P_+ S_F^{-1}\overline {S}f=\widetilde {S}_+^{-1}\overline {S}f-P_+f=P_+f-P_+f=0\), where we used (22) and \(\mathrm {ran} \overline {S}\subset \mathscr {H}_+\) in the first equality, (21) in the second equality, and (20) in the third equality. In view of the decomposition \(\mathscr {H}=\mathrm {ran}\overline {S}\oplus U_1\oplus U_0\), \(\mathscr {D}(\mathscr {B})=\mathrm {ran} \overline {S}\,\boxplus \,\widetilde {U}_1\,\boxplus \,U_0\), the self-adjointness of \(\mathscr {B}\) and the fact that \(\mathscr {B}\,\mathrm {ran} \overline {S}=\{0\}\) and \(\mathscr {B}\,U_0=\{0\}\) imply necessarily \(\mathscr {B}\,\widetilde {U}_1\subset U_1\). □
As a direct consequence of Lemma 4 above, the restriction of \(\mathscr {B}\) to \(\widetilde {U}_1\), i.e., the operator
is a self-adjoint operator on the Hilbert space U 1 (with dense domain \(\widetilde {U}_1\)), which itself is canonically determined by \(\widetilde {S}\). The interest towards this operator B is due the following fundamental property.
Proposition 1 (B-Decomposition Formula)
Proof
One has
This identity, together with
yields \(\mathscr {D}(\widetilde {S})=\mathscr {D}(\overline {S})+(S_F^{-1}+B)\widetilde {U}_1+U_0\), and this sum is direct because if \(\mathscr {D}(\widetilde S) \ni g = f + (S_F^{-1}+B)\tilde u_1 +u_0=f+S_F^{-1}\tilde u_1 + (B\tilde u_1 +u_0)\), then, according to (6) and (14), g = 0 implies f = 0, \(\tilde u_1=0\) and u 0 = 0. Thus, in order to prove (24) it only remains to prove (*). For the inclusion \(P_+(S_F^{-1}+B)\widetilde {U}_1+U_0\subset (S_F^{-1}+B)\widetilde {U}_1+U_0\) pick \(\psi :=P_+(S_F^{-1}+B)\widetilde {u}_1+u_0\) for generic \(\widetilde {u}_1\in \widetilde {U}_1\) and u 0 ∈ U 0. From (23), from the fact that \(\widetilde {u}_1=P_+\widetilde {u}_1\), and from \(P_+\mathscr {S}^{-1}\widetilde {u}_1=\mathscr {S}^{-1}\widetilde {u}_1\) (which follows from (21)), one has
as well as
where \(u_0^{\prime }:=S_F^{-1}\widetilde {u}_1-P_+S_F^{-1}\widetilde {u}_1\in \,\mathscr {H}\ominus \mathscr {H}_+=U_0\); therefore,
which proves that \(\psi \in (S_F^{-1}+B)\widetilde {U}_1+U_0\). The opposite inclusion to establish (*), that is, \(P_+(S_F^{-1}+B)\widetilde {U}_1+U_0\supset (S_F^{-1}+B)\widetilde {U}_1+U_0\), is proved repeating the same argument in reverse order. □
2.4 Classification of All Self-Adjoint Extensions: Operator Formulation
After characterising the structure (6) of \(\mathscr {D}(S^*)\) and providing the decomposition (24) of \(\mathscr {D}(\widetilde {S})\) for a generic self-adjoint extension \(\widetilde {S}\) in terms of its B-operator, the next fundamental result in the KVB theory is the fact that the B-decomposition actually classifies all self-adjoint extensions of S.
Theorem 2 (Višik-Birman Representation Theorem)
Let S be a densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) with positive bottom (m(S) > 0). There is a one-to-one correspondence between the family of the self-adjoint extensions of S on \(\mathscr {H}\) and the family of the self-adjoint operators on Hilbert subspaces of \(\ker S^*\) , that is, the collection of triples \((U_1,\widetilde {U}_1,B)\) , where U 1 is a closed subspace of \(\ker S^*\), \(\widetilde {U}_1\) is a dense subspace of U 1 , and B is a self-adjoint operator on the Hilbert space U 1 with domain \(\mathscr {D}(B)=\widetilde {U}_1\) . For each such triple, let U 0 be the closed subspace of \(\ker S^*\) defined by \(\ker S^*=U_0\oplus U_1\) . Then, in this correspondence S B ↔ B, each self-adjoint extension S B of S is given by
Proof
The fact that each self-adjoint extension of S is precisely of the form S B is the content of Proposition 1, where B is Višik’s B operator associated to the considered self-adjoint extension. Conversely, one has to prove that each operator on \(\mathscr {H}\) of the form S B above is a self-adjoint extension of S, and that the correspondence S B ↔ B is one-to-one.
Fixed \((U_1,\widetilde {U}_1,B)\) as in the statement, let us consider the corresponding S B. One sees from (25) that S B is densely defined (\(\mathscr {D}(S_B)\supset \mathscr {D}(S)\)) and it is an operator extension of S (\(S_B f=\overline {S}f\) for all \(f\in \mathscr {D}(\overline {S})\)). In fact, S B is a symmetric extension: for two generic elements of \(\mathscr {D}(S_B)\) one has
(where in the first step we used that \(\langle B\widetilde {u}_1^{\prime },\overline {S}f\rangle =\langle S^* B \widetilde {u}_1^{\prime },f\rangle =0\), \(\langle u_0^{\prime },\overline {S}f\rangle =\langle S^*u_0^{\prime },f\rangle =0\), \(\langle u_0^{\prime },\widetilde {u}_1\rangle =0\), in the second step we used the symmetry of \(\overline {S}\), the self-adjointness of \(S_F^{-1}\) and B, and the properties of the adjoint S ∗, and in the last step we used that \(\langle \overline {S}f^{\prime },B\widetilde {u}_1\rangle =\langle f^{\prime },S^*B\widetilde {u}_1\rangle =0\), \(\langle \overline {S}f^{\prime },u_0\rangle =\langle f^{\prime },S^*u_0\rangle =0\), \(\langle \widetilde {u}_1^{\prime },u_0\rangle =0\)). Therefore, S ⊂ S B ⊂ S B ∗⊂ S ∗ and in order to show that S B = S B ∗ it suffices to prove that \(\mathscr {D}(S_B)\supset \mathscr {D}({S_B}^{*})\).
Let us then pick \(h\in \mathscr {D}({S_B}^{*})\), generic. Since S B ∗⊂ S ∗, one has \(h=\varphi +S_F^{-1}\overline {v}+v\) by (6) for some \(\varphi \in \mathscr {D}(\overline {S})\) and \(v,\overline {v}\in U=\ker S^*\), and \({S_B}^{*}h=\overline {S}\varphi +\overline {v}\). Actually \(\overline {v}\in U_1\), because U = U 0 ⊕ U 1 and \(\langle \overline {v},u_0\rangle =\langle {S_B}^{*}h,u_0\rangle -\langle \overline {S}\varphi ,u_0\rangle =\langle h,S_Bu_0\rangle -\langle \varphi ,S^*u_0\rangle =\langle h-\varphi ,S^*u_0\rangle =0\ \forall u_0\in U_0\). Thus, representing v = v 0 + v 1, v 0 ∈ U 0, v 1 ∈ U 1, one writes
In order to recognise this vector to belong to \(\mathscr {D}(S_B)\), let us exploit the identity \(\langle h,S_B k\rangle =\langle S_B^*h,k\rangle \), valid \(\forall k\in \mathscr {D}(S_B)\), for the k’s of the special form \(k=f+(S_F^{-1}+B)\widetilde {u}_1\), \(f\in \mathscr {D}(\overline {S})\), \(\widetilde {u}_1\in \mathscr {D}(B)\). In this case
(indeed, \(S_B B\widetilde {u}_1=S^*B\widetilde {u}_1=0\), \(\varphi +S_F^{-1}\overline {v}\in \mathscr {D}(S_F)\), \(f+S_F^{-1}\widetilde {u}_1\in \mathscr {D}(S_F)\), \(\langle v_1+v_0,\overline {S}f\rangle =\langle S^*(v_1+v_0),f\rangle =0\), and \(\langle v_0,\widetilde {u}_1\rangle =0\)) and
(indeed, \(\langle \overline {S}\varphi ,B\widetilde {u}_1\rangle =\varphi ,S^*B\widetilde {u}_1\rangle =0\)). Equating these two expressions and using the self-adjointness of S F yields
which implies, owing to the self-adjointness of B, \(\overline {v}\in \mathscr {D}(B)\) and \(B\overline {v}=v_1\). Thus, the above decomposition for h reads now
for some \(\overline {v}\in \mathscr {D}(B)=\widetilde {U}_1\) and v 0 ∈ U 0, thus proving that \(h\in \mathscr {D}(S_B)\).
Last, one proves that the operator B in the decomposition (25) is unique and therefore the correspondence between self-adjoint extensions of S and operators of the form S B is one-to-one. Indeed, if
where \(\ker S^*=U_0\oplus U_1=U_0^{\prime }\oplus U_1^{\prime }\) and where B and B ′ are self-adjoint operators, respectively on the Hilbert spaces U 1 and \(U_1^{\prime }\), with domain, respectively, \(\widetilde {U}_1\) and \(\widetilde {U}_1^{\prime }\), then the action of S B on an arbitrary element \(g\in \mathscr {D}(S_B)\) gives, in terms of the decomposition \(g=f+(S_F^{-1}+B)\widetilde {u}_1+u_0=f^{\prime }+(S_F^{-1}+B^{\prime })\widetilde {u}^{\prime }_1+u^{\prime }_0\), \(S_Bg=\overline {S}f+\widetilde {u}_1=\overline {S}f^{\prime }+\widetilde {u}_1^{\prime }\); each sum belongs to the orthogonal sum \(\mathscr {H}=\overline {\mathrm {ran} S}\oplus \ker S^*\), whence \(\widetilde {u}_1=\widetilde {u}_1^{\prime }\) and, by injectivity of S, f = f ′ (whence also \(u_0=u^{\prime }_0\)); thus, \(\widetilde {u}_1=\widetilde {u}_1^{\prime }\) and, after taking the closure \(U_1=U_1^{\prime }\) and \(U_0=U_0^{\prime }\); this also implies \(B\widetilde {u}_1=B^{\prime }\widetilde {u}_1\), whence B = B ′. □
2.5 Characterisation of Semi-Bounded Extensions: Operator Version
A further relevant feature of the KVB theory is that the general classification (25) of Theorem 2 allows to identify special subclasses of self-adjoint extensions of S, significantly those that are bounded below, or in particular positive or also strictly positive, in terms of suitable subclasses of the corresponding B-operators in the representation (25).
In this respect, the convenient characterisation is expressed in terms of the inverse of B, more precisely of the self-adjoint operator \(B_\star ^{-1}\) on the Hilbert space
which is a Hilbert subspace of \(\ker S^*\) (recall the notation \(\ker S_B\equiv U_0\), \(\ker S^*\equiv U\), and observe that \(\overline {\mathrm {ran} B}\,\oplus \,\ker S_B\subset U_1\oplus U_0=U=\ker S^*\)), defined by

It is fair to refer to \(B_\star ^{-1}\) as “Birman’s operator”, for it is Birman who first determined and exploited its properties (Lemma 5 and Theorem 3 below).
For reference purposes, in (27) we intentionally kept Birman’s original notation [8]. A more precise definition of the operator \(B_\star ^{-1}\) is the following

where we used the decompositions \(U_1=\overline {\mathscr {D}(B)}=\overline {\mathrm {ran} B}\oplus \ker B\) and \(\widetilde {U}_1=\mathscr {D}(B)=(\mathscr {D}(B)\cap \overline {\mathrm {ran} B})\boxplus \ker B\). Thus, the action of \(B_\star ^{-1}\) on a generic element \(B\widetilde {u}_1\in \mathrm {ran} B\) is given, in view of the decomposition \(\widetilde {u}_1=z+z_0\) for some \(z\in \mathscr {D}(B)\cap \overline {\mathrm {ran} B}\) and \(z_0\in \ker B\), by \(B_\star ^{-1}B\widetilde {u}_1=z\).
Remark 6
One has
Indeed, according to (25), any \(g\in \mathscr {D}(S_B)\) decomposes for some \(f_0\in \mathscr {D}(\overline {S})\), \(\widetilde {u}_1\in \widetilde {U}_1=\mathscr {D}(B)\), \(u_0\in U_0=\ker S^*\cap \mathscr {D}(B)^\perp \) as \(g=f_0+(S_F^{-1}+B)\widetilde {u}_1+u_0=f+v\), where \(f:=f_0+S_F^{-1}\widetilde {u}_1\in \mathscr {D}(S_F)\) and (by (28)) \(v:=B\widetilde {u}_1+u_0\in \mathscr {D}(B_\star ^{-1})\). The sum in the r.h.s. of (29) is direct because if \(v\in \mathscr {D}(S_F)\cap \mathscr {D}(B_\star ^{-1})\), then \(v\in \ker S^*\) by definition (27) and hence \(\|v\|{ }^2=\langle S_F S_F^{-1}v,v\rangle =\langle S_F^{-1}v,S_Fv\rangle =\langle S_F^{-1}v,S^*v\rangle =0\). Observe, conversely, that inclusion is generically strict. Indeed, for a generic \(h\in \mathscr {D}(S_F)\dotplus \mathscr {D}(B_\star ^{-1})\) one writes, according to (7) and (28), \(h=(f_0+S_F^{-1}\widetilde {u}_1+B\widetilde {u}_1+u_0)+S_F^{-1}(u-\widetilde {u}_1)\) for some \(f_0\in \mathscr {D}(\overline {S})\), \(\widetilde {u}_1\in \mathscr {D}(B)\), \(u_0\in \ker S^*\cap \mathscr {D}(B)^\perp \), \(u\in \ker S^*\), and this is not enough to use (25) and deduce that \(h\in \mathscr {D}(S_B)\).
Lemma 5
-
(i)
If, with respect to the notation of (25) and (28), S B is a self-adjoint extension of a given densely defined symmetric operator S with positive bottom (m(S) > 0), then
$$\displaystyle \begin{aligned} \mathscr{D}(B_\star^{-1})\;\subset\;\mathscr{D}[S_B]\cap\ker S^*\,. \end{aligned} $$(30) -
(ii)
If in addition S B is bounded below , then
$$\displaystyle \begin{aligned} S_B[v_1,v_2]\;=\;\langle v_1,B_\star^{-1} v_2\rangle\qquad \quad \forall v_1,v_2\in\mathscr{D}(B_\star^{-1})\,. \end{aligned} $$(31)
Proof
The fact that \(\mathscr {D}(B_\star ^{-1})\subset \ker S^*\) is stated in the definition (27). To prove that \(\mathscr {D}(B_\star ^{-1})\subset \mathscr {D}[S_B]\), decompose an arbitrary \(v\in \mathscr {D}(B_\star ^{-1})\), according to (28), as \(v=B\widetilde {u}_1+u_0\) for some \(\widetilde {u}_1\in \mathscr {D}(B)\!\setminus \!\ker B\subset \widetilde {U}_1\) and \(u_0\in U_0=\ker S_B\). From \(v=\big ((S_F^{-1}+B)\widetilde {u}_1+u_0\big )-S_F^{-1}\widetilde {u}_1\) one can then regard v as the difference between an element in \(\mathscr {D}(S_B)\), according to (25), and an element in \(\mathscr {D}(S_F)\). Since \(\mathscr {D}(S_B)\subset \mathscr {D}[S_B]\) and \(\mathscr {D}(S_F)\subset \mathscr {D}[S_F]\subset \mathscr {D}[S_B]\) (the Friedrichs extension has the smallest form domain among all semi-bounded extensions, Theorem 15(vii)), then \(v\in \mathscr {D}[S_B]\), which proves \(\mathscr {D}(B_\star ^{-1})\subset \mathscr {D}[S_B]\) and completes the proof of (30). To prove (31), consider again an arbitrary \(v=B\widetilde {u}_1+u_0\) in \(\mathscr {D}(B_\star ^{-1})\) as above: for \(f:=S_F^{-1}\widetilde {u}_1\in \mathscr {D}(S_F)\) and \(g:=f+v=S_F^{-1}\widetilde {u}_1+B\widetilde {u}_1+u_0\in \mathscr {D}(S_B)\), one has \(S_B g=\widetilde {u}_1=S_F f\), \(B_\star ^{-1}v=\widetilde {u}_1\), and
All this is still valid irrespectively of the semi-boundedness of S B. On the other hand, if S B is bounded below, then a central result in Kreı̆n’s theory of self-adjoint extensions (see (127) quoted in appendix A.3) states that S B[f, v] = 0 for any \(f\in \mathscr {D}[S_F]\) and any \(v\in \mathscr {D}[S_B]\cap \ker S^*\) (which is what holds for f and v in the present case, owing to (i)), whence
Thus, by comparison, \(S_B[v,v]=\langle v,B_\star ^{-1}v\rangle \ \forall v\in \mathscr {D}(B_\star ^{-1})\). (31) then follows by polarisation. □
Theorem 3 (Characterisation of Semi-Bounded Extensions)
Let S be a densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) with positive bottom (m(S) > 0). If, with respect to the notation of (25) and (28), S B is a self-adjoint extension of S, and if α < m(S), then

As an immediate consequence, \(m(B_\star ^{-1})\geqslant m(S_B)\) for any semi-bounded S B . In particular, positivity or strict positivity of the bottom of S B is equivalent to the same property for \(B_\star ^{-1}\) , that is,
Moreover, if \(m(B_\star ^{-1})>-m(S)\) , then
Proof
Let us start with the proof of (32). Observe that the fact that S B is bounded below by α is equivalently expressed as \(S_B[g]\geqslant \alpha \|g\|{ }^2\ \forall g\in \mathscr {D}[S_B]\). For generic \(f\in \mathscr {D}(S_F)\) and \(v\in \mathscr {D}(B_\star ^{-1})\), one has that \(g:=f+v\in \mathscr {D}[S_B]\) and \(S_B[v]=\langle v,B_\star ^{-1}v\rangle \) (Lemma 5). On the other hand, since \(v\in \mathscr {D}[S_B]\cap \ker S^*\) (Lemma 5), then S B[f, v] = 0 (owing to (127)). Therefore, \(S_B[g]=S_B[f+v]=S_F[f]+S_B[v]=\langle f,S_Ff\rangle +\langle v,B_\star ^{-1} v\rangle \). Thus, the assumption that S B is bounded below by α reads, for all such g’s,
whence also, replacing f↦λf, v↦μv,
Since α < m(S), and hence 〈f, S F f〉− α∥f∥2 > 0, inequality (ii) holds true if and only if
for arbitrary \(f\in \mathscr {D}(S_F)\) and \(v\in \mathscr {D}(B_\star ^{-1})\), which is therefore a necessary condition for S B to be bounded below by α. Condition (iii) is in fact also sufficient. To see this, decompose an arbitrary \(g\in \mathscr {D}(S_B)\) as g = f + v for some \(f\in \mathscr {D}(S_F)\) and \(v\in \mathscr {D}(B_\star ^{-1})\) (which is always possible, as observed in Remark 6) and apply (iii) to this case: one then obtains (ii) owing to α < m(S), which in turns yields (i) when λ = μ = 1; from (i) one goes back to \(S_B[g]\geqslant \alpha \|g\|{ }^2\) following in reverse order the same steps discussed at the beginning. Thus, (iii) is equivalent to the fact that S B is bounded below by α. By re-writing (iii) as

and by the fact that the above inequality is valid for arbitrary \(f\in \mathscr {D}(S_F)\) and hence holds true also when the supremum over such f’s is taken, one finds

by means of a standard operator-theoretic argument applied to the bottom-positive operator  (Lemma 6). This completes the proof of (32).
(Lemma 6). This completes the proof of (32).
From (32) one deduces immediately both the first equivalence of (33), by taking α = 0, and the implication “\(m(S_B)>0\Rightarrow m(B_\star ^{-1})>0\)” in the second equivalence of (33), because \(m(B_\star ^{-1})\geqslant m(S_B)\). Conversely, if \(m(B_\star ^{-1})>0\), then it follows from (27)–(28) that \(B_\star ^{-1}\) has a bounded inverse, that \(U_0=\ker S_B=\{0\}\), and that \(B:\mathscr {D}(B)\equiv \widetilde {U}_1\subset U_1\to U_1\) is bounded; this, in turn, implies by Lemma 4(ii) and by (23) that the operator \(\mathscr {B}\) defined in (22) is bounded, which by Lemma 4(i) means that S B has a bounded inverse (densely defined) on the whole \(\mathscr {H}_+\) and therefore (\(\mathscr {H}=\mathscr {H}_+\oplus U_0\)) on the whole \(\mathscr {H}\). This fact excludes that m(S B) = 0, and since \(m(B_\star ^{-1})>0\Rightarrow m(S_B)\geqslant 0\) by the first of (33), one finally concludes m(S B) > 0, which completes the proof of (33).
Last, it only remains to prove \(m(S_B)\geqslant m(S)m(B_\star ^{-1})(m(S)+m(B_\star ^{-1}))^{-1}\) in (34) (assuming \(m(B_\star ^{-1})>-m(S)\)). In this case, for
one has α < m(S) = m(S F) and \(m(B_\star ^{-1})=\alpha \,m(S)(m(S)-\alpha )^{-1}\), whence \((m(S)-\alpha )^{-1}\geqslant (S_F-\alpha )^{-1}\) and

Owing to (32), the latter inequality is equivalent to \(m(S_B)\geqslant \alpha \), which completes the proof of (34). □
Lemma 6
If A is a self-adjoint operator on a Hilbert space \(\mathscr {H}\) with positive bottom (m(A) > 0), then
Proof
Setting g := A 1∕2 f one has
and since |〈g, A −1∕2 h〉| attains its maximum for g = A −1∕2 h∕∥A −1∕2 h∥, the conclusion then follows. □
2.6 Characterisation of Semi-Bounded Extensions: Form Version
The operator characterisation of the semi-bounded self-adjoint extensions of S provided by Theorem 3 has the virtue that it can be directly reformulated in terms of the quadratic form associated with an extension. The result is a very clean expression of \(\mathscr {D}[S_B]\) in terms of the intrinsic space \(\mathscr {D}[S_F]\) and the additional space \(\mathscr {D}[B_\star ^{-1}]\), where B (equivalently, \(B_\star ^{-1}\)) plays the role of the “parameter” of the extension also in the form sense. This is a plus as compared to von Neumann’s characterisation (Theorem 14), for the latter only classifies the self-adjoint extensions of S by indexing each operator extension S U in terms of a unitary U acting between defect subspaces, whereas the quadratic form associated with each S U has no explicit description in terms of U.
Theorem 4 (Characterisation of Semi-Bounded Extensions—form Version)
Let S be a densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) with positive bottom (m(S) > 0) and, with respect to the notation of (25) and (28), let S B be a semi-bounded (not necessarily positive) self-adjoint extension of S. Then
and
As a consequence,
and
Remark 7
Identity (35) is the form version of the inclusion (29) for operator domains, the latter holding for a generic (not necessarily semi-bounded) extension S B. Property (36) represents the actual improvement of the KVB theory, as compared to Kreı̆n’s original theory, as far as the quadratic forms of the extensions are concerned. Recall indeed that Kreı̆n’s original theory (see Sect. I and (126) in the Appendix) establishes, for a generic semi-bounded self-adjoint extension \(\widetilde {S}\) of a densely defined symmetric operator S with positive bottom, the property
What the KVB theory does in addition to (39), is therefore to characterise the space \(\mathscr {D}[\widetilde {S}]\cap \ker S^*\) in terms of the parameter B (equivalently, \(B_\star ^{-1}\)) of each semi-bounded extension.
Proof (Proof of Theorem 4)
Let us fix \(\alpha \in \mathbb {R}\) such that α < m(S B) and |α| > 1. To establish the inclusion \(\mathscr {D}[B_\star ^{-1}]\subset \mathscr {D}[S_B]\cap \ker S^*\) in (35) let us exploit the fact that \(\mathscr {D}[B_\star ^{-1}]\) is the completion of \(\mathscr {D}(B_\star ^{-1})\) in the norm associated with the scalar product
(indeed, owing to Theorem 3), \(m(B_\star ^{-1})\geqslant m(S_B)>\alpha \)), whereas \(\mathscr {D}[S_B]\) is complete in the norm associated with the scalar product
Owing to Lemma 5, \(\mathscr {D}(B_\star ^{-1})\subset \mathscr {D}[S_B]\) and
thus the \(\|\,\|{ }_{B_\star ^{-1}}\)-completion of \(\mathscr {D}(B_\star ^{-1})\) does not exceed \(\mathscr {D}[S_B]\). On the other hand,
and the r.h.s. above is obviously a norm with respect to which \(\ker S^*\) is closed: therefore the \(\|\,\|{ }_{B_\star ^{-1}}\)-completion of \(\mathscr {D}(B_\star ^{-1})\) does not exceed \(\ker S^*\) either. This proves \(\mathscr {D}[B_\star ^{-1}]\subset \mathscr {D}[S_B]\cap \ker S^*\). For the opposite inclusion, let us preliminarily observe that the assumption m(S B) > α implies
(where \(\|v\|{ }_{B_\star ^{-1}}=\|v\|{ }_{S_B}\ \forall v\in \mathscr {D}(B_\star ^{-1})\) was used), as seen already in the course of the proof of Theorem 3, when condition (iii) therein was established. Let us also remark that \(\mathscr {D}[S_F]\) is a \(\|\,\|{ }_{S_B}\)-closed subspace of \(\mathscr {D}[S_B]\) (which follows from \(\mathscr {D}[S_F]\subset \mathscr {D}[S_B]\), from \(S_B[f]=S_F[f]\ \forall f\in \mathscr {D}[S_F]\), and from \(m(S_F)\geqslant m(S_B)>\alpha \), see Theorem 15), and so is \(\mathscr {D}[B_\star ^{-1}]\) (as discussed previously in this proof). Let now \(u\in \mathscr {D}[S_B]\cap \ker S^*\), arbitrary, and let \((g_n)_{n\in \mathbb {N}}\) be a sequence in \(\mathscr {D}(S_B)\) of approximants of u in the \(\|\,\|{ }_{S_B}\)-norm. As remarked with (29), g n = f n + v n for some \(f_n\in \mathscr {D}(S_F)\) and \(v_n\in \mathscr {D}(B_\star ^{-1})\), which are both vectors in \(\mathscr {D}[S_B]\). From this and from (*) above one has
Since 1 − α −2 > 0, one deduces that both \((f_n)_{n\in \mathbb {N}}\) and \((v_n)_{n\in \mathbb {N}}\) are Cauchy sequences, respectively, in \(\mathscr {D}[S_F]\) and \(\mathscr {D}[B_\star ^{-1}]\), with respect to the topology of the \(\|\,\|{ }_{S_B}\)-norm, with limits, say, \(f_n\to f\in \mathscr {D}[S_F]\) and \(v_n\to v\in \mathscr {D}[B_\star ^{-1}]\) as n →∞. Taking n →∞ in g n = f n + v n thus yields u = f + v. Having proved above that \(\mathscr {D}[B_\star ^{-1}]\subset \ker S^*\), one therefore concludes \(f=u-v\in \ker S^*\), which together with \(f\in \mathscr {D}[S_F]\) implies f = 0 (indeed m(S F) = m(S) > 0 and hence \(\mathscr {D}[S_F]\cap \ker S^*=\{0\}\)). Then \(u=v\in \mathscr {D}[B_\star ^{-1}]\), which complete the proof of \(\mathscr {D}[B_\star ^{-1}]\supset \mathscr {D}[S_B]\cap \ker S^*\) and establishes finally (35). Coming now to the proof of (36), the identity \(\mathscr {D}[S_B]=\mathscr {D}[S_F]\dotplus \mathscr {D}[B_\star ^{-1}]\) is a direct consequence of (35) and of (39). Furthermore, owing to the fact that \(\mathscr {D}[B_\star ^{-1}]\) is closed in \(\mathscr {D}[S_B]\), identity (31) lifts to \(S_B[v_1,v_2]=B_\star ^{-1}[v_1,v_2]\ \forall v_1,v_2\in \mathscr {D}[B_\star ^{-1}]\), which allows do deduce also the second part of (36) from (39). □
2.7 Parametrisation of Distinguished Extensions: S F and S N
One recognises in formulas (25) and (36) the special parameter B (equivalently, \(B_\star ^{-1}\)) that selects, among all positive self-adjoint extensions S B, the Friedrichs extension S F or the Kreı̆n-von Neumann extension S N. (The characterisation and a survey of the main properties of S F and S N can be found, respectively, in Theorems 15–16 and in Theorems 17–18.) This is another plus with respect to von Neumann’s theory, where S F or S N are not identifiable a priori by a special choice of the unitary that labels each extension.
The result can be summarised as follows


the details of which are discussed in the following Proposition.
Proposition 2
Let S be a densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) with positive bottom (m(S) > 0) and let S B be a positive self-adjoint extension of S, parametrised by B (equivalently, by \(B_\star ^{-1}\) ) according to Theorems 2 and 4.
-
(i)
S B is the Friedrichs extension when \(\mathscr {D}[B_\star ^{-1}]=\{0\}\) , equivalently, when \(\mathscr {D}(B)=\ker S^*\) and \(Bu=0\ \forall u\in \ker S^*\).
-
(ii)
S B is the Kreı̆n-von Neumann extension when \(\mathscr {D}(B_\star ^{-1})=\mathscr {D}[B_\star ^{-1}]=\ker S^*\) and \(B_\star ^{-1}u=0\ \forall u\in \ker S^*\) ; equivalently, when \(\mathscr {D}(B)=\{0\}\).
Proof
Concerning part (i), \(\mathscr {D}[B_\star ^{-1}]=\{0\}\) follows from (36) when S B = S F. Hence also \(\mathscr {D}(B_\star ^{-1})=\{0\}\), which implies ranB = {0} (owing to (27)), that is, B is the zero operator on its domain. Comparing (7) and (25) one therefore has U 0 = {0}, \(\widetilde {U}_1=U_1=\ker S^*\), and hence \(\mathscr {D}(B)=\ker S^*\). As for part (ii), \(\mathscr {D}[B_\star ^{-1}]=\ker S^*\) follows by comparing (36), when S B = S N, with the property (119) of S N. This, together with \(S_N[u]=0\ \forall u\in \ker S^*\) (given by (118)) and with \(B_\star ^{-1}[u]=S_B[u]=S_N[u]\ \forall u\in \mathscr {D}[B_\star ^{-1}]\) (given by (36) when S B = S N), yields \(B_\star ^{-1}[u]=0\ \forall u\in \mathscr {D}[B_\star ^{-1}]\), that is, \(B_\star ^{-1}[u]\) is the zero operator on its domain and hence \(\mathscr {D}(B_\star ^{-1})=\mathscr {D}[B_\star ^{-1}]=\ker S^*\). In turn, (119) now gives \(\mathscr {D}(B_\star ^{-1})=\ker S^*=\ker S_N\), and therefore (27) (when S B = S F) yields ranB = {0}. Comparing (119) and (25) one therefore has \(U_0=\ker S^*\), \(\widetilde {U}_1=U_1=\{0\}\), and hence \(\mathscr {D}(B)=\{0\}\). □
Remark 8
The customary convention, adopted in (40)–(41), to label the Friedrichs extension formally with “\(B_\star ^{-1}=\infty \)” and the Kreı̆n-von Neumann extension formally with “B = ∞” (where it is understood that the considered operator has trivial domain {0}), is to make the labelling consistent with the ordering (37).
Remark 9
In the case in which \(S_F^{-1}\) is replaced by the inverse \(\widetilde S^{-1}\) of an invertible self-adjoint extension \(\widetilde S\) of S, there is no canonical choice any longer for the parameter B to select the Friedrichs extension S F. However, it remains true that “B = ∞” parametrises the Kreı̆n-von Neumann extension (S N) while \(B=\mathbb {O}\) parametrises \(\widetilde S\) instead of S F.
3 Equivalent Formulations of the KVB Theory
Theorems 2, 3, and 4, and Proposition 2 above are not in the form they have customarily appeared in the mathematical literature in English language that followed the original works [8, 34, 66], nor are their proofs. While we defer to the next Section a more detailed comparison with the more recent formulations, let us discuss in this Section a natural alternative parametrisation of the extensions which is equivalent to the original one provided by the original KVB theory.
In fact, this alternative arises naturally when the roles of the parameters B and \(B_\star ^{-1}\) are interchanged. Both B and \(B_\star ^{-1}\) are self-adjoint operators acting on Hilbert subspaces of \(\ker S^*\). Although these two parameters are not exactly the inverse of each other, the definition of \(B_\star ^{-1}\) resembles very much an operator inversion. Proposition 3 and Remarks 10 and 11 here below highlight the general properties of such an “inversion” mechanism. This will provide the ground to establish Theorems 5, 6, and 7 as an equivalent version, respectively, of Theorems 2, 3, and 4.
Proposition 3
Let \(\mathscr {K}\) be a Hilbert space and let \(\mathscr {S}(\mathscr {K})\) be the collection of the self-adjoint operators acting on Hilbert subspaces of \(\mathscr {K}\) . Given \(T\in \mathscr {S}(\mathscr {K})\) , let V be the closed subspace of \(\mathscr {K}\) which T acts on, with domain \(\mathscr {D}(T)\equiv \widetilde {V}\) dense in V , and let W := V ⊥ , i.e., \(\mathscr {K}=V\oplus W\) . Let ϕ(T) be the densely defined operator acting on the Hilbert subspace \(\overline {\mathrm {ran} T}\oplus W\) of \(\mathscr {K}\) defined by

Then:
-
(i)
\(\phi (T)\in \mathscr {S}(\mathscr {K})\),
-
(ii)
the map \(\phi :\mathscr {S}(\mathscr {K})\to \mathscr {S}(\mathscr {K})\) is a bijection on \(\mathscr {S}(\mathscr {K})\),
-
(iii)
ϕ 2 = ı, the identity map on \(\mathscr {S}(\mathscr {K})\) , that is, ϕ −1 = ϕ.
Remark 10
In shorts, ϕ provides a transformation of T that is similar to the inversion. More precisely, although T is in general not invertible, ϕ(T) inverts T on ranT, while it is the zero operator on the orthogonal complement in \(\mathscr {K}\) of the Hilbert subspace where T was acting on. In particular, if T is densely defined in \(\mathscr {K}\) itself and invertible, then ϕ(T) = T −1, that is, ϕ is precisely the inversion transformation.
Remark 11
By comparing (28) and (42) in the special case \(\mathscr {K}=\ker S^*\), T = B, V = U 1, and \(W=U_0=\ker S_B\), one concludes that \(B_\star ^{-1}=\phi (B)\), that is, the Birman operator \(B_\star ^{-1}\) is precisely the ϕ-inversion of the Višik operator B.
Proof (Proof of Proposition 3)
The self-adjointness of ϕ(T) on the Hilbert space \(\overline {\mathrm {ran} T}\oplus W\) is a standard and straightforward consequence of its definition. For the rest of the proof, it obviously suffices to show that ϕ(ϕ(T)) = T for any \(T\in \mathscr {S}(\mathscr {K})\). By definition the operator ϕ(T) acts on the Hilbert space \(V^{\prime }:=\overline {\mathrm {ran} T}\oplus W\) with domain \(\widetilde {V}^{\prime }:=\mathrm {ran} T\boxplus W\) dense in V ′. Setting W ′ := V ′ ⊥, in view of the decomposition \(\mathscr {K}=V^{\prime }\oplus W^{\prime }\) the operator ϕ(ϕ(T)) is therefore determined, by definition, as the operator that acts on the Hilbert subspace \(\overline {\mathrm {ran}\,\phi (T)}\oplus W^{\prime }\) of \(\mathscr {K}\) according to

Since \(V=\overline {\mathrm {ran} T}\oplus \ker T\), and hence \(\mathscr {K}=\overline {\mathrm {ran} T}\oplus \ker T\oplus W\), then \(W^{\prime }=\ker T\). Thus,

and \(\phi (\phi (T)) w^{\prime }=0=Tw^{\prime }\ \forall w^{\prime }\in W^{\prime }=\ker T\). It remains to show that ϕ(ϕ(T)) and T agree also on \(\mathscr {D}(T)\cap \overline {\mathrm {ran} T})\). In fact, if v is a vector in such a subspace, then v = ϕ(T)Tv and in view of ϕ(ϕ(T))ϕ(T)Tv = Tv one has ϕ(ϕ(T))v = Tv. This completes the proof that ϕ(ϕ(T))v = Tv for any \(v\in \mathscr {D}(T)\) and since the two operators have also the same domain, the conclusion is ϕ(ϕ(T)) = T. □
We are now in the condition of re-stating the main results of the KVB extension theory established in Sect. 2 in the equivalent form that follows.
Theorem 5 (Classification of Self-Adjoint Extensions—Operator Version)
Let S be a densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) with positive bottom (m(S) > 0). There is a one-to-one correspondence between the family of all self-adjoint extensions of S on \(\mathscr {H}\) and the family of the self-adjoint operators on Hilbert subspaces of \(\ker S^*\) . If T is any such operator, in the correspondence T ↔ S T each self-adjoint extension S T of S is given by
Theorem 6 (Characterisation of Semi-Bounded Extensions)
Let S be a densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) with positive bottom (m(S) > 0). If, with respect to the notation of (43), S T is a self-adjoint extension of S, and if α < m(S), then

As an immediate consequence, \(m(T)\geqslant m(S_T)\) for any semi-bounded S T . In particular, positivity or strict positivity of the bottom of S T is equivalent to the same property for T, that is,
Moreover, if m(T) > −m(S), then
Theorem 7 (Characterisation of Semi-Bounded Extensions—form Version)
Let S be a densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) with positive bottom (m(S) > 0) and, with respect to the notation of (43), let S T be a semi-bounded (not necessarily positive) self-adjoint extension of S. Then
and
As a consequence,
and
Proposition 4 (Parametrisation of S F and S N)
Let S be a densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) with positive bottom (m(S) > 0) and let S T be a positive self-adjoint extension of S, parametrised by T according to Theorems 5 and 7.
-
(i)
S T is the Friedrichs extension when \(\mathscr {D}[T]=\{0\}\) (“ T = ∞”).
-
(ii)
S T is the Kreı̆n-von Neumann extension when \(\mathscr {D}(T)=\mathscr {D}[T]=\ker S^*\) and \(Tu=0\ \forall u\in \ker S^*\) ( \(\,T=\mathbb {O}\) ).
Proof (Proof of Theorem 5)
Let S B be a generic self-adjoint extension of S, parametrised by B according to Theorem 2, formula (25). Correspondingly, let \(B_\star ^{-1}\) be the Birman’s operator introduced in (27)–(28). First of all, we claim that S B is precisely of the form S T in (43) above where \(T=B_\star ^{-1}\). To prove that, consider a generic element \(g=f+(S_F^{-1}+B)\widetilde {u}_1+u_0\) of \(\mathscr {D}(S_B)\), as given by the decomposition (25) for some \(f\in \mathscr {D}(\overline {S})\), \(\widetilde {u}_1\in \widetilde {U}_1=\mathscr {D}(B)\), and \(u_0\in U_0=\ker S^*\cap \mathscr {D}(B)^\perp =\ker S_B\). We write \(\widetilde {u}_1=z+w\) for some \(w\in \ker B\) and some \(z\in \mathscr {D}(B)\cap \overline {\mathrm {ran} B}\) that are uniquely identified by the decomposition \(U_1=\overline {\mathscr {D}(B)}=\overline {\mathrm {ran} B}\oplus \ker B\), \(\mathscr {D}(B)=(\mathscr {D}(B)\cap \overline {\mathrm {ran} B})\boxplus \ker B\). Owing to (28), \(v:=B\widetilde {u}_1+u_0=B z+u_0\in \mathscr {D}(B_\star ^{-1})\) and \(B_\star ^{-1} v=z\). Moreover, from
one deduces that \(\ker B=\ker S^*\cap \mathscr {D}(B_\star ^{-1})^\perp \). Therefore,
that is, g is an element of \(\mathscr {D}(S_T)\) defined in (43) above with \(T=B_\star ^{-1}\). It is straightforward to go through the same arguments and decompositions in reverse order to conclude that any vector of the form \(S_F^{-1}(B_\star ^{-1} v+w)+v\), where \( v\in \mathscr {D}(B_\star ^{-1})\) and \(w\in \ker S^*\cap \mathscr {D}(B_\star ^{-1})^\perp \), can be re-written as \((S_F^{-1}+B)\widetilde {u}_1+u_0\) for \(\widetilde {u}_1\in \widetilde {U}_1=\mathscr {D}(B)\), and u 0 ∈ U 0 determined by
which proves that any \(g\in \mathscr {D}(S_T)\) is also an element of \(\mathscr {D}(S_B)\). Thus, (25) and (43) define the same domain: \(\mathscr {D}(S_B)=\mathscr {D}(S_T)\) for \(T=B_\star ^{-1}\). Since S B and S T are the restrictions to such a common domain of the same operator S ∗, then S B = S T for \(T=B_\star ^{-1}\), and the initial claim is proved. As a consequence of this and of the one-to-one correspondence S B ↔ B of Theorem 2, the self-adjoint extensions of S are all of the form S T of (43) for some self-adjoint operator T on a Hilbert subspace of \(\ker S^*\). What remains to be proved is that when T runs in the family \(\mathscr {S}(\ker S^*)\) of the self-adjoint operators on Hilbert subspaces of \(\ker S^*\), the corresponding S T’s give the whole family of self-adjoint extensions of S. This follows at once by Proposition 3, since by (25) \(B_\star ^{-1}=\phi (B)\) and ϕ is a bijection in \(\mathscr {S}(\ker S^*)\). □
Proof (Proof of Theorems 6, 7, and Proposition 4)
All statements follow at once from their original versions, respectively Theorems 3, 4, and Proposition 2, and from the fact that the extension parameter T is precisely the parameter \(B_\star ^{-1}\) in Theorems 3, 4, and Proposition 2. □
Remark 12 (Equivalence of Theorems 2 and 5)
Our arguments in the proof of Theorem 5 actually show also that the original Višik-Birman representation Theorem 2 can be deduced from Theorem 5 and that therefore the two Theorems are equivalent. Indeed, assuming the representation (43) for a generic self-adjoint extension S T of S, our argument shows that the ϕ-inverse B := ϕ(T) of the parameter T allows to rewrite \(\mathscr {D}(S_T)\) in the form \(\mathscr {D}(S_B)\) of (25) and therefore all self-adjoint extensions of S have the form \(S_B=S^*\upharpoonright \mathscr {D}(S_B)\) for some \(B\in \mathscr {S}(\ker S^*)\); moreover, since by Proposition 3 ϕ is a bijection on \(\mathscr {S}(\ker S^*)\), one concludes that when B runs in \(\mathscr {S}(\ker S^*)\) the corresponding S B exhausts the whole family of self-adjoint extensions of S, thus obtaining Theorem 2.
Let us discuss in the last part of this Section yet another equivalent formulation of the general representation theorem for self-adjoint extensions.
Theorem 8 (Classification of Self-Adjoint Extensions—Operator Version)
Let S be a densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) with positive bottom (m(S) > 0). There is a one-to-one correspondence between the family of all self-adjoint extensions of S on \(\mathscr {H}\) and the family of the self-adjoint operators on Hilbert subspaces of \(\ker S^*\) . If T is any such operator, \(P_T:\mathscr {H}\to \mathscr {H}\) is the orthogonal projection onto \(\overline {\mathscr {D}(T)}\) , and \(P_*:\mathscr {D}(S^*)\to \mathscr {D}(S^*)\) is the (non-orthogonal, in general) projection onto \(\ker S^*\) with respect to Kreı̆n’s decomposition formula \(\mathscr {D}(S^*)=\mathscr {D}(S_F)\dotplus \ker S^*\) (Lemma 1), then in the correspondence T ↔ S T each self-adjoint extension S T of S is given by
Proposition 5
The parameter T in (51) is precisely the same as in (43), that is, the representation given in Theorem 8 is the same as the one given in Theorem 5 . In other words, the two theorems are equivalent . In particular, given a self-adjoint extension \(\widetilde {S}\) of S, its extension parameter T (i.e., the operator T for which \(\widetilde {S}=S_T\) ) is the operator acting on the Hilbert space \(\overline {P_*\mathscr {D}(\widetilde {S})}\) with domain \(\mathscr {D}(T)=P_*\mathscr {D}(\widetilde {S})\) and action \(TP_{*} g=P_T S_Tg\ \forall g\in \mathscr {D}(\widetilde {S})\).
Proof (Proof of Theorem 8 and Proposition 5)
All one needs to prove is the that the domain \(\mathscr {D}(S_T)\) given by (43) can be re-written in the form (51) with the same T. If \(g=f+S_F^{-1}(Tv+w)+v\) is a generic element of the space \(\mathscr {D}(S_T)\) defined by (43), then P ∗ g = v (by Kreı̆n’s decomposition formula), \(S^*g=\overline {S}f+Tv+w\), and P T S ∗ g = Tv. Thus, \(P_*g\in \mathscr {D}(T)\) and TP ∗ g = Tv = P T S ∗ g, which proves that g belongs to the domain defined in (51). For the converse, recall that for any \(g\in \mathscr {D}(S^*)\) the Višik-Birman decomposition formula (6) gives \(g=f+S_F^{-1}u+P_* g\) for some \(f\in \mathscr {D}(\overline {S})\) and \(u\in \ker S^*\). If now g belongs to the domain defined in (51), then \(v:=P_* g\in \mathscr {D}(T)\subset \ker S^*\) for some \(T\in \mathscr {S}(\ker S^*)\), and the decomposition \(\ker S^*=\overline {\mathscr {D}(T)}\oplus (\ker S^*\cap \mathscr {D}(T)^\perp )\) gives u = P T u + w for some \(w\in \ker S^*\cap \mathscr {D}(T)^\perp \): since \(P_T S^*g=P_T(\overline {S}f+u)=P_Tu\) and (51) prescribes also P T S ∗ g = Tv, then P T u = Tv and u = Tv + w: this proves that \(g=f+S_F^{-1}(Tv+w)+v\), which belongs to the domain \(\mathscr {D}(S_T)\) given by (43). Thus, (43) and (51) define (for the same T) the same space \(\mathscr {D}(S_T)\). □
4 Comparisons with the Subsequent Literature in English
Before proceeding on to the further aspects of the theory (Sects. 5 and 6), the discussion developed so far gives the opportunity of a short historical retrospective.
The KVB self-adjoint extension theory was developed (in Russian) in the course of a decade between the mid 1940s and the mid 1950s. This was not the result of a coherent programme.
Kreı̆n’s focus in [34] was the complete answer to the problem, risen up by von Neumann [67], of finding and characterising semi-bounded extensions of a given semi-bounded and densely defined symmetric operator S. von Neumann himself had provided one particular solution (the extension S N, in the present notation) and later Stone [64, Theorem 9.21] had proved, for the finite deficiency indices case, the existence of a self-adjoint extension \(\widetilde {S}\) with the much more interesting feature that \(m(\widetilde {S})=m(S)\), followed by Friedrichs [19] who had constructed his eponymous extension (S F, in the present notation). The framework for Višik’s work [66] was instead the study of the boundary conditions needed for certain resolvability properties of boundary value problems associated with an elliptic differential operator L, say, Lu = h with datum h and unknown u in a region \(\Omega \subset \mathbb {R}^d\). Two operators on L 2( Ω) are naturally associated to L, a “minimal” operator L 0 and a “maximal” L 1 (with L 0 ⊂ L 1), and one considers a suitable family of realisations \(\widetilde {S}\) of L between them (\(L_0\subset \widetilde {S}\subset L_1\)) that are determined by boundary conditions at ∂ Ω; the question is to find such conditions for any considered realisation \(\widetilde {S}\), each boundary condition being expressed in terms of boundary operators \(\mathscr {D}(\widetilde {S})\to \mathscr {D}'(\partial \Omega )\) and operators between functional spaces over ∂ Ω. Višik focused, among other cases, on the case where L 0 = S is densely defined and symmetric on L 2( Ω), L 1 = S ∗, and \(\widetilde {S}\) is a self-adjoint extension of S, and he provided the one-to-one representation \(\widetilde {S}\equiv S_B\leftrightarrow B\) of Theorem 2, where B is a suitable boundary operator. Concerning Birman, the motivation in [8] was to characterise further the correspondence S B ↔ B along a two-fold direction: to relate the semi-boundedness and other spectral properties of S B with the analogous properties of the parameter B (both in the operator and in the quadratic form sense), and to include also the case of infinite deficiency indices, which had not been covered by Kreı̆n.
Since the mid 1950s, as already commented, the self-adjoint extension theory based in the results of Kreı̆n, Višik, and Birman has found a rather limited space within the mathematical literature in English, presumably for a multiplicity of reasons that, language and geo-political barriers apart, are related with the distance between the fields which such results were applied to, boundary value problems for PDE on the one hand, and quantum-mechanical Hamiltonians on the other. This refers both to Kreı̆n’s characterisation of the semi-bounded extensions (that is, Theorem 20), which at least received a partial discussion in 1954s Riesz and Nagy’s treatise on Functional Analysis [57, §125], and to a much larger extent to the Višik-Birman representation Theorem 2 as well as its application to semi-bounded extensions, Theorems 3, and 4.
As oversimplified as the following statement may appear, the main comprehensive discussions of the KVB theory of self-adjoint extensions that were produced within the “western” mathematical literature are,
-
1.
from the perspective of boundary value problems for elliptic differential operators: Grubb’s 1968 theory on the “universal parametrisation of extensions” [28];
-
2.
from the perspective of general operator theory on Hilbert spaces (with the point of view of quantum-mechanical and Schrödinger operator applications): Faris’s 1975 lecture notes on self-adjoint operators [18] and, above all, Alonso’s and Simon’s 1980 “propaganda” article on the KVB theory [3].
Grubb’s work [28] (see also its modern survey in [30, Chapter 13]) lies within the general study of boundary conditions for elliptic partial differential operators and the associated boundary value problem, therefore a field that is closely related with Višik’s approach. As a tool, [28] develops an abstract extension theory for closed and densely defined operators on Hilbert space, with a specific treatment of the symmetric case and the corresponding self-adjoint extensions. This is done by means of Hilbert space and operator graph methods that resemble very much those used by Kreı̆n, Višik, and Birman some 20 years earlier, so that it is fair to regard [28, Chapter II] as an independent route to the general self-adjoint extension characterisation already provided by the KVB theory, together with a novel generalisation to a wider class of extensions. The form by which the work [28] classifies the self-adjoint extensions of a given densely defined (and closed) symmetric operator S with positive bottom is essentially that of Theorem 8 (see [28, Theorem II.2.1]), that here we have derived directly from (and actually proved to be equivalent to) Višik-Birman representation Theorem 2.Footnote 2 [28] reproduces also the bound on m(S T) in terms of m(T), expressed here by (46) of Theorem 6 (see [30, Theorem 13.17]), as well as Kreı̆n’s decomposition formula for quadratic forms, here expressed by (126) of Theorem 20(iii) (see [30, Theorem 13.19]). Grubb’s theory, however, does not cover the quadratic form side of the extension scheme, it only concerns the operator level.
Faris’s presentation in [18], on the other hand, is explicitly motivated by general mathematical problems for quantum mechanics (with no reference to Grubb’s previous work). It includes a concise derivation of formula (48) of Theorem 7, limited to the case of positive self-adjoint extensions of a given densely defined symmetric operator S with positive bottom (see [18, Theorem 15.3]), which is obtained independently in the same spirit as Birman’s work.
Along the same line, in fact independently from Grubb’s and Faris’s previous discussions, Alonso and Simon in [3] revisit a large part of the KVB theory (again, only for positive extensions of S, with m(S) > 0) with some originality of viewpoint that gives primary emphasis to the notion of quadratic form. First, they classify the positive extensions in terms of positive forms on \(\ker S^*\), thus reproducing both Kreı̆n’s extension theorem, with a statement that is essentially Theorem 20(ii), and Birman’s characterisation of the forms of positive extensions, essentially stating it as (48) and (49) in Theorem 7 (see [3, Section 2]). Then, by means of operator graph techniques, they derive the operator version of the corresponding classification, with the same statement as in Theorem here 5 (see [3, Section 3]).
It is worth remarking that all the above-mentioned works use the parametrisation of the operator domains of the extensions in terms of the operator T used in Sect. 3, instead of the original parameter B used by Višik and Birman for Theorem 2.
One further relevant contribution is the work of Ando and Nishio [5] that appears immediately after Grubb’s and is practically ignored by Faris’s and by Alonso’s and Simon’s. By means of an ad hoc analysis that in fact does not use the general tools and formulas of the KVB theory, [5] investigates the structure of the (quadratic form of the) Kreı̆n-von Neumann extension S N of a densely defined and positive symmetric operator S, and characterises it in the form of Theorem 18 in the Appendix. Ando and Nishio [5] also provides a necessary and sufficient condition for S to admit positive self-adjoint extensions (even when the \(\mathscr {D}(S)\) is not dense or closed), as reviewed in Theorem 19.
The positive self-adjoint extensions of a given positive and densely defined symmetric operator are also the object of a recent study by Arlinskiı̆ and Tsekanovskiı̆ [6], where several results of the KVB theory are reproduced in a somewhat alternative form.
As mentioned already, in more recent times the extension picture of Kreı̆n, Višik, and Birman, as well as that of Grubb’s approach (following an idea that can be traced back to Calkin [11]), has found at an abstract analytic and operator-theoretic level a natural generalisation in the form of the modern theory of boundary triplets (introduced by Kočubeı̆ [32] and Bruk [10]) and gamma fields and Weyl functions associated with boundary triplets (invented by Derkach and Malamud [15]). This is a vast subject with applications to abstract extension theory, to elliptic boundary value problems, and to the theory of local point interactions, with many fundamental contributions that can be traced in the works of Derkach and Malamud [15], Gorbachuk, Gorbachuk, and Kochubeı̆ [25, 27], Albeverio and Kurasov [1], Amrein and Pearson [4], Behrndt and Langer [7], Ryzhov [58, 59], Posilicano [54], Brown, Grubb, and Wood [9], Grubb [30], Kostenko and Malamud [33], Malamud [36, 37], Malamud and Neidhardt [38], Derkach, Hassi, Malamud and de Snoo [16], and in the references therein. For example, in [60, Chapter 14] one may find a detailed derivation of Theorems 5 and 7 (but only for positive extensions of S with m(S) > 0) by means of boundary triplet techniques. Remark 14 below collects further references to fundamental works of the modern theory of boundary triplets that reproduce results that one can obtain directly within the original KVB theory.
One of the purposes of the present work is to avoid using these modern instances and to discuss instead the emergence of the KVB theory, both in its original formulation and in what today is the ‘boundary-triplet-derived’ modern formulation, but using only the ‘elementary’ operator-theoretic setting. This makes the theory particularly suited to the application we are concerned most, that is, models of quantum mechanical Hamiltonians of particle systems with zero-range (or very singular) interaction. In this context, for the classification of all possible self-adjoint realisation of the ‘physically driven’ Hamiltonian, the characterisation provided by Theorems 5, 6, and 7, and Proposition 4, turns out to be the most applicable and fruitful, as may be found in many past and recent works on the subject [20,21,22,23, 39,40,41,42,43,44,45,46,47,48,49,50,51,52,53, 63].
5 Invertibility, Semi-Boundedness, and Negative Spectrum
In this Section we complete the discussion of the main results that can be proved within the KVB theory, focusing on the link between relevant features (such as invertibility, semi-boundedness, structure of the negative spectrum) of a self-adjoint extension of a given densely defined symmetric operator S with positive bottom, and the corresponding features of the extension parameter given by the theory. Such a close link allows one to appreciate even more the effectiveness of the KVB extension parameter, as compared to von Neumann’s parametrisation. We adopt here the notation T ↔ S T for the parametrisation of the extensions—see Sect. 3.
A first link between S T and T, which is straightforward although it is not explicitly present in Birman’s original work, is the following.
Theorem 9 (Invertibility)
Let S be a densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) with positive bottom (m(S) > 0) and let S T be a generic self-adjoint extension of S according to the parametrisation (43) of Theorem 5 . Then
-
(i)
S T is injective ⇔ T is injective,
-
(ii)
S T is surjective ⇔ T is surjective,
-
(iii)
S T is invertible on the whole \(\mathscr {H}\ \Leftrightarrow \ T\) is invertible on the whole \(\overline {\mathscr {D}(T)}\).
Proof
Assume that S T is injective and let \(v\in \mathscr {D}(T)\) be such that Tv = 0. Then v is an element in \(\mathscr {D}(S_T)\), because it is a vector of the form (43), \(g=f+S_F^{-1}(Tv+w)+v\), with f = w = 0. Since S T v = 0, by injectivity of S T one concludes that v = 0. Conversely, if T is injective and for some \(g=f+S_F^{-1}(Tv+w)+v\in \mathscr {D}(S_T)\) one has S T g = 0, then \(\overline {S}f+Tv+w=0\). Since \(\overline {S}f+Tv+w\in \mathrm {ran}\overline {S}\boxplus \mathrm {ran} T\boxplus (\ker S^*\cap \mathscr {D}(T)^\perp )\), one must have \(\overline {S}f=Tv=w=0\). Owing to the injectivity of \(\overline {S}\) and T, f = v = 0 and hence g = 0. This completes the proof of (i). As for (ii), in the notation of (43) one has that \(\mathrm {ran} \,S_T=\mathrm {ran}\overline {S}\boxplus \mathrm {ran} T\boxplus (\ker S^*\cap \mathscr {D}(T)^\perp )\) and in fact \(\mathrm {ran}\overline {S}=\overline {\mathrm {ran} S}\) (Remark 3). Thus, T is surjective \(\Leftrightarrow \ \mathrm {ran} T\boxplus (\ker S^*\cap \mathscr {D}(T)^\perp )=\overline {\mathrm {ran} T}\oplus (\ker S^*\cap \mathscr {D}(T)^\perp )=\ker S^*\ \Leftrightarrow \ \mathrm {ran} S_T=\overline {\mathrm {ran} S}\oplus \ker S^*=\mathscr {H}\ \Leftrightarrow \ S_T\) is surjective. (iii) is an obvious consequence of (i) and (ii). □
Remark 13
Noticeably, Višik-Birman’s original parametrisation S B ↔ B for the extensions does not allow to control invertibility, as opposed to the parametrisation S T ↔ T. Indeed, the identity \(\ker S_B=U_0\equiv \ker S^*\cap \mathscr {D}(B)^\perp \) (that follows immediately from (14) and (25)) shows that the injectivity of S B and the injectivity of B are unrelated, and the identity \(\mathrm {ran} S_B=\overline {\mathrm {ran} S}\oplus \mathscr {D}(B)\) shows that the surjectivity of S B and the surjectivity of B are unrelated too.
Semi-boundedness is another relevant feature of the self-adjoint extensions that can be controlled in terms of the KVB extension parameter. The sub-family of the semi-bounded self-adjoint extensions of S is the object of Theorem 3 (equivalently, of Theorem 6). Here below we supplement the information of that theorem with the answer to the question on whether the semi-boundedness of S T and of T are equivalent. This is another result that is not explicitly present in Birman’s discussion, although it follows from it. As a consequence, we derive within the KVB theory the fact that when S has a finite deficiency index all its self-adjoint extensions are bounded below.
Theorem 10 (Semi-Boundedness)
Let S be a densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) with positive bottom (m(S) > 0), \(P_K:\mathscr {H}\to \mathscr {H}\) be the orthogonal projection onto \(\ker S^*\) , and for each α < m(S) let

Let S T be a generic self-adjoint extension of S according to the parametrisation (43) of Theorem 5 . Assume that m(T) ∈ [−∞, 0), that is, T is either unbounded below or with finite negative bottom (otherwise it is already known by (45) in Theorem 6 that \(m(T)\geqslant 0\ \Leftrightarrow \ m(S_T)\geqslant 0\) ). Then the two conditions
-
(i)
S T is bounded below (on \(\mathscr {H}\) )
-
(ii)
T is bounded below (on \(\overline {\mathscr {D}(T)}\) )
are equivalent if and only if M(α) “diverges to −∞ uniformly as α →−∞”, meaning that ∀R > 0 ∃ α
R < 0 such that  for each \(\alpha \leqslant \alpha _R\).
for each \(\alpha \leqslant \alpha _R\).
Proof
Since (i) ⇒ (ii) is always true (owing to (44) in Theorem 6), what must be proven is the equivalence between the implication (ii) ⇒ (i) and the condition of uniform divergence to −∞ for M(α). Assume (ii) ⇒ (i), that is, assume that for arbitrary R > −m(T) the condition  implies
implies  for some α
R < 0 and hence also
for some α
R < 0 and hence also  (if the lower bound α
R was non-negative, then m(T) would be non-negative too, against the assumption). In turn, owing to (44) and (52),
(if the lower bound α
R was non-negative, then m(T) would be non-negative too, against the assumption). In turn, owing to (44) and (52),  is equivalent to \(T\geqslant M(\alpha )\ \forall \alpha \leqslant \alpha _R\). Then, for
is equivalent to \(T\geqslant M(\alpha )\ \forall \alpha \leqslant \alpha _R\). Then, for  to imply \(T\geqslant M(\alpha )\ \forall \alpha \leqslant \alpha _R\), necessarily
to imply \(T\geqslant M(\alpha )\ \forall \alpha \leqslant \alpha _R\), necessarily  . Conversely, assume now that for arbitrary R > 0 there exists α
R such that
. Conversely, assume now that for arbitrary R > 0 there exists α
R such that  : we want to deduce (ii) ⇒ (i). To this aim, assume that T is bounded below and apply the assumption for R = −m(T): for the corresponding α
R one has
: we want to deduce (ii) ⇒ (i). To this aim, assume that T is bounded below and apply the assumption for R = −m(T): for the corresponding α
R one has  , which by (44) implies
, which by (44) implies  . □
. □
Corollary 1 (Finite Deficiency Index)
If S is a semi-bounded and densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) with finite deficiency index, then
-
(i)
the semi-boundedness of S T is equivalent to the semi-boundedness of T;
-
(ii)
any self-adjoint extension of S is bounded below.
Proof
It is not restrictive to assume m(S) > 0 and hence \(\dim \ker S^*<\infty \). Part (ii) follows from (i) because T is now defined on a finite-dimensional Hilbert space and is therefore bounded. Part (i) follows from Theorem 10 once one shows that M(α) diverges uniformly to −∞. Irrespectively of whether \(\dim \ker S^*\) is finite or not,
Indeed, for any \(u\in \ker S^*\) one has \(u\notin \mathscr {D}[S_F]\) (see (119)), whence
where \(\mathrm {d} E^{(S_F)}\) denotes the spectral measure of S F; therefore, since \(\frac {\lambda \alpha }{\lambda -\alpha }\to -\lambda \) as α →−∞,

Under the additional assumption \(\dim \ker S^*<\infty \) let us now show that (53) implies a uniform divergence in the sense of Theorem 10. For arbitrarily fixed R > 0 decompose u = f R + v R with
Observe that \(f_R\in \mathscr {D}(S_F)\), because
while necessarily \(v_R\notin \mathscr {D}(S_F)\) because \(u\notin \mathscr {D}(S_F)\). One has
In the second integral in the r.h.s above λ > 2R, whence \(2R>\frac {2R\lambda }{2\lambda -2R}\): therefore, choosing α < −2R implies \(-\alpha >\frac {2R\lambda }{2\lambda -2R}\) and the latter condition is equivalent to \(\frac {\lambda \alpha }{\lambda -\alpha }<-R\), thus
Let us now exploit the assumption \(\dim \ker S^*=d\) for some \(d\in \mathbb {N}\) in order to estimate the first integral in the r.h.s of (a). Obviously there is \(d_R\in \mathbb {N}\), \(d_R\leqslant d\), such that
and let \(\{\varphi _{R,1},\dots ,\varphi _{R,d_R}\}\) be an orthonormal basis of this d R-dimensional subspace of \(\mathscr {D}(S_F)\). Decompose \(f_R=f_{R,1}+\cdots +f_{R,d_R}\) with f R,j := 〈φ R,j, f R〉φ R,j, j = 1, …, d R. Then
Where the \(\widetilde \varphi _{R,j}\in \ker S^{*}\) are inverse images under \(E^{(S_F)}([0,2R])\) of the orthonormal basis, so that the last line just uses the fact that \(E^{(S_F)}([0,2R])\) is a orthogonal projection. Owing to (53), each \(\langle \widetilde \varphi _{R,j},M(\alpha )\widetilde \varphi _{R,j}\rangle \) diverges to −∞ as α →−∞: there is only a finite number of them (and it does not exceed d), so there is a common threshold α R < 0 such that
Therefore
(α R only depends on R (and on d), not on f R). Plugging the bounds (b) and (d) into (a) yields
for \(\alpha <\min \{-2R,\alpha _R\}\). From the arbitrariness of \(u\in \ker S^*\) and of R > 0 one concludes that M(α) →−∞ uniformly as α →−∞. □
Corollary 2
If S is a semi-bounded and densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) , whose bottom is positive (m(S) > 0) and whose Friedrichs extension has compact inverse \(S_F^{-1}\) , then the semi-boundedness of S T is equivalent to the semi-boundedness of T.
Proof
Since \(S_F^{-1}\) is compact, the spectrum of S F only consists of a discrete set of eigenvalues, each of finite multiplicity, whence the bound (c) in the proof of Corollary 1 and the same conclusion as in Corollary 1(i). □
Remark 14
The question of Theorem 10 and its corollaries deal with is sometimes referred to as the “semi-boundedness problem”, that is, the problem of finding conditions under which the semi-boundedness of S T and of T are equivalent (in general or under special circumstances). The fact that the compactness of \(S_F^{-1}\) is a sufficient condition (that is, Corollary 2) was noted originally by Grubb [29] and by Gorbačuk and Mihaı̆lec [26] in the mid 1970s. More than a decade later the same property, and more generally the necessary and sufficient condition provided by Theorem 10, was proved with a boundary triplets language by Derkach and Malamud [15]. In fact, it is easy to recognise that the operator-valued function α↦M(α) defined in (52) is the Weyl function of a standard boundary triplet [60, Example 14.12]. In [15, Section 3] one can also find examples in which such a condition is violated. The conclusion of Corollary 1(ii) is easy to establish also with general Hilbert space and spectral arguments, with no reference to the KVB theory—see, e.g., [17, Lemma XIII.7.22] or [56, Theorem X.1, first corollary]).
Theorem 10 and (the proof of) Corollary 1 have a further noticeable consequence.
Corollary 3 (“Finite-Dimensional” Extensions are Always Semi-Bounded)
Given a semi-bounded and densely defined symmetric operator S on a Hilbert space \(\mathscr {H}\) , whose bottom is positive (m(S) > 0), all the self-adjoint extensions of S T of S for which the parameter T, in the parametrisation (43) of Theorem 5 , is a self-adjoint operator acting on a finite-dimensional subspace of \(\ker S^*\) are semi-bounded. For the occurrence of unbounded below self-adjoint extensions it is necessary (not sufficient) that \(\dim \overline {\mathscr {D}(T)}=\infty \).
Proof
T is bounded (and hence also semi-bounded) because the Hilbert space \(\overline {\mathscr {D}(T)}\) it acts on has finite dimension. Let \(P_T:\mathscr {H}\to \mathscr {H}\) be the orthogonal projection onto \(\overline {\mathscr {D}(T)}\) and set

One can repeat for \(\widetilde {M}(\alpha )\) the same arguments used in the proof of Corollary 1 to establish the uniform divergence of M(α) to −∞, thus obtaining the same property for \(\widetilde {M}(\alpha )\) on the finite-dimensional space \(\overline {\mathscr {D}(T)}\) (the assumption \(\dim \overline {\mathscr {D}(T)}=d<+\infty \) implies \(\dim E^{(S_F)}([0,2R])\overline {\mathscr {D}(T)}=d_R\leqslant d\), which is the analogue of formula (c) in the proof of Corollary 1, whence the same conclusion). Therefore ∃ α < 0, with |α| sufficiently large, such that

which implies m(S T) > α owing to (44). □
Remark 15
It is also worth remarking that unless S is essentially self-adjoint, in all other cases (i.e., whenever \(\dim \ker S^*\geqslant 1\)) there is no uniform lower bound to the bottoms of the semi-bounded self-adjoint extensions of S. This is an immediate consequence of the bound \(m(T)\geqslant m(S_T)\) given by (44) in Theorem 6, since it is enough to consider extension parameters  for arbitrary γ > 0.
for arbitrary γ > 0.
In the remaining part of this Section we turn to the negative spectrum of an extension S T. It turns out that relevant properties of the negative discrete spectrum of S T are controlled by the analogous properties for T. We cast in Theorem 11 and Corollary 4 below results that are found in Birman’s original work [8] (formulated therein with the original parametrisation S B ↔ B), apart from a number of ambiguities and redundancies that we have cleaned up.
For convenience let us define
Theorem 11 (Negative Spectrum)
Let S be a densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) with positive bottom (m(S) > 0) and let S T be a generic self-adjoint extension of S according to the parametrisation (43) of Theorem 5 . Then σ −(S T) consists of a bounded below set of finite-rank eigenvalues of S T whose only possible accumulation point is 0 if and only if σ −(T) has the same property. When this is the case, and \(\lambda _1\leqslant \lambda _2\leqslant \cdots <0\) and \(t_1\leqslant t_2\leqslant \cdots <0\) are the ordered sequences of negative eigenvalues (counted with multiplicity) of S T and of T respectively, then
-
ground state of \(S_T\ =\ \lambda _1\ \leqslant \ t_1\ =\) ground state of T,
-
\(\lambda _k\leqslant t_k\) for k = 1, 2, …
Corollary 4
For some \(N\in \mathbb {N}\) , σ −(S T) consists of N eigenvalues if and only if σ −(T) consists of N eigenvalues. (Here the eigenvalues are counted with multiplicity.)
Remark 16
We observe that no restriction is assumed on the dimension of \(\ker S^*\), that is, the deficiency index of S can be infinite as well. In fact, as long as \(\dim \ker S^*<+\infty \), Corollary 4 could be deduced directly by combining Theorems 19 and 20 of Kreı̆n’s original work [34] with the subsequent results of Višik and Birman that are stated here in Theorems 5 and 7.
A further consequence is the following.
Corollary 5
-
(i)
If S has finite deficiency index ( \(\dim \ker S^*<+\infty \) ), then all self-adjoint extensions of S have finite negative spectrum, with finite-dimensional eigenvalues.
-
(ii)
If, in the sense of the parametrisation (43) of Theorem 5 , S T is a self-adjoint extension of S where the parameter T acts on a finite-dimensional subspace of \(\ker S^*\) , then the negative spectrum σ −(S T) of S T is finite, with finite-dimensional eigenvalues.
In preparation for the proof of Theorem 11 and its corollaries, let us denote by \(\mathrm {d} E^{(S_T)}\) and by dE (T), respectively, the spectral measure of S T and of T on \(\mathbb {R}\). For generic \(v\in \mathscr {D}(T)\) one also has \(v\in \mathscr {D}[S_T]\) with 〈v, Tv〉 = S T[v], owing to (48) (see also (31)), whence
Let us also single out two useful facts (the first is straightforward).
Lemma 7
If V and W are closed subspaces of \(\mathscr {H}\) with \(\dim V<+\infty \) and \(\dim W>\dim V\) , then W ∩ V ⊥≠ {0}.
Lemma 8
If ε > 0 and, for some \(N\in \mathbb {N}\) , g 1, …, g N are linearly independent elements in \(\mathscr {D}(S_T)\cap E^{(S_T)}((-\infty ,-\varepsilon ])\mathscr {H}\) , then the corresponding v 1, …, v N given by the decomposition (43) \(g_k=f_k+S_F^{-1}(Tv_k+w_k)+v_k\) , k = 1, …, N, are linearly independent in \(\mathscr {D}(T)\).
Proof
If \(\sum _{k=1}^N c_k v_k=0\) for some \(c_1,\dots ,c_N\in \mathbb {C}\), then \(g:=\sum _{k=1}^N c_k g_k=\sum _{k=1}^N c_k (f_k+S_F^{-1}(Tv_k+w_k))\in \mathscr {D}(S_F)\), whence \(\langle g,S_T g\rangle =\langle g,S_F g\rangle \geqslant m(S)\|g\|{ }^2\geqslant 0\). On the other hand,
(where in the second identity we used that \(g\in \mathscr {D}(S_T)\cap E^{(S_T)}((-\infty ,-\varepsilon ])\mathscr {H}\)), therefore g = 0 and hence, by assumption, c 1 = ⋯ = c N = 0. □
Proof (Proof of Theorem 11)
Assume that σ −(S T) consists of a bounded below set of finite-rank eigenvalues of S T whose only possible accumulation point is 0. In particular, −∞ < m(S T) < 0 which, by (44)–(45), implies also \(m(S_T)\leqslant m(T)<0\). If, for contradiction, σ −(T) does not satisfy the same property of σ −(S T), then there exists ε > 0 such that \(\dim E^{(T)}([m(T),-\varepsilon ])\overline {\mathscr {D}(T)}=+\infty \), whereas by assumption \(\dim E^{(S_T)}([m(S_T),-\frac {1}{2}\varepsilon ])\mathscr {H}<+\infty \). By Lemma 7 \(\exists \,v\in E^{(T)}([m(T),-\varepsilon ])\overline {\mathscr {D}(T)}\), v ≠ 0, \(v\perp E^{(S_T)}([m(S_T),-\frac {1}{2}\varepsilon ])\mathscr {H}\). As a consequence of this and of (55),
which is a contradiction because v ≠ 0. For the converse, assume that σ −(T) consists of a bounded below set of finite-rank eigenvalues of T whose only possible accumulation point is 0. In particular, −∞ < m(T) < 0. If, for contradiction, σ −(S T) does not satisfy the same property of σ −(T), then \(\dim E^{(S_T)}((-\infty ,-\varepsilon ])\mathscr {H}=+\infty \) for some ε > 0. Therefore also
because \(E^{(S_T)}((-\infty ,-\varepsilon ])\mathscr {H}\cap \mathscr {D}(S_T)\) is dense in \(E^{(S_T)}((-\infty ,-\varepsilon ])\mathscr {H}\). Based on the decomposition (43) for generic \(g\in \mathscr {D}(S_T)\) (namely, \(g=f+S_F^{-1}(Tv+w)+v\)), set
In fact, owing to Lemma 8, any v ∈ V ε identifies uniquely the corresponding \(g\in E^{(S_T)}(-\infty ,-\varepsilon ])\mathscr {H}\cap \mathscr {D}(S_T)\). Furthermore, Lemma 8 and (*) yield \(\dim V_\varepsilon =+\infty \). On the other hand, let \(h\in \mathbb {R}\) with \(0<h<\min \{-m(T),\frac {\varepsilon m(S)}{2m(S)+\varepsilon }\}\): by assumption
Lemma 7 and (*)-(**) then imply the existence of a non-zero v ∈ V ε with \(v\perp E^{(T)}([m(T),-h])\overline {\mathscr {D}(T)}\). For such v one has
which can be re-written equivalently as
The last inequality implies
If g is the vector in \(E^{(S_T)}(-\infty ,-\varepsilon ])\mathscr {H}\cap \mathscr {D}(S_T)\) that corresponds to such v ∈ V ε, by repeating the very same reasoning as in the proof of Theorem 3 one sees that the latter condition is equivalent to \(\langle g,S_T g\rangle \geqslant -\frac {\varepsilon }{2}\|g\|{ }^2\). However, this last finding is not compatible with the fact that
whence the contradiction. This completes the proof of the equivalence of the considered condition for σ −(S T) and σ −(T). When such a condition holds and the eigenvalues are labelled as in the statement of the theorem, obviously \(\lambda _1=m(S_T)\leqslant m(T)=t_1\) (by (44)), while the fact that \(\lambda _k\leqslant t_k\) for k = 1, 2, … is a consequence of the min-max principle for the self-adjoint operators S T and T, owing to the fact (Theorem 7) that \(S_T\leqslant T\). □
Proof (Proof of Corollary 4)
Owing to Theorem 11,
is equivalent to
and when this is the case \(\lambda _1=m(S_T)\leqslant m(T)=t_1\). If M > N, then \(\exists \,v\in (E^{(T)}([m(T),-\varepsilon ])\overline {\mathscr {D}(T)})\cap (E^{(S_T)}([m(S_T),0))\mathscr {H})^\perp \), v ≠ 0, for some ε > 0 (in fact, ∀ε ∈ (0, |t M|)), as a consequence of Lemma 7. Moreover, \(v\in \mathscr {D}(T)\) because
whence also \(v\in \mathscr {D}[S_T]\) with S T[v] = 〈v, Tv〉, owing to (48). As a consequence of this and of (55),
a contradiction. If instead M < N, let us use the fact that for some ε > 0 (in fact ∀ε ∈ (0, |λ N|)) Lemma 8 applied to the space V ε introduced in the proof of Theorem 11 yields \(\dim V_\varepsilon \geqslant N\): then, owing to Lemma 7, \(\exists \,v\in V_\varepsilon \cap (E^{(T)}([m(T),0))\overline {\mathscr {D}(T)})^\perp \), v ≠ 0. In turn, as already observed in the proof of Theorem 11, this v identifies uniquely a non-zero element \(g\in E^{(S_T)}([m(S_T),-\varepsilon ])\mathscr {H}\subset \mathscr {D}(S_T) \) for which \(g-v\in \mathscr {D}(S_F)\). For such g and v, (48) yields \(\langle g,S_T g\rangle \geqslant \langle v,Tv\rangle \). With these findings,
another contradiction. Thus, the conclusion is necessarily M = N. □
Proof (Proof of Corollary 5)
In either case (i) and (ii) the extension parameter T is self-adjoint on a finite-dimensional space, therefore its spectrum only consists of a finite number of (finite-dimensional) eigenvalues. This is true in particular for the negative spectrum of T. Then the conclusion follows from Corollary 4. □
6 Resolvents of Self-Adjoint Extensions
We turn now to the discussion of the structure of the resolvent of self-adjoint extensions.
In fact, this is a context in which the theory of boundary triplets (the modern theory that has “incorporated” the original KVB results, see Sect. 4) has deepest results, including the appropriate abstract language to reproduce in full generality the celebrated Kreı̆n-Naimark resolvent formula—see, e.g., the comprehensive overview in [60, Chapter 14]. Here we content ourselves to discuss some direct applications of the KVB theory. We thus derive the formula of the inverse of an invertible extension in terms of its KVB extension parameter and of the “canonical” Friedrichs extension (Theorem 12), and from it we derive resolvent formulas (Corollary 6 and Theorem 13) originally established, in implicit form, by Kreı̆n [34, Theorem 20].
Theorem 12 (Resolvent Formula for Invertible Extensions)
Let S be a densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) with positive bottom (m(S) > 0). Let, in terms of the decomposition and parametrisation (43) of Theorem 5 , S T be a generic self-adjoint extension of S and \(P_T:\mathscr {H}\to \mathscr {H}\) be the orthogonal projection onto \(\overline {\mathscr {D}(T)}\) . If S T is invertible on the whole \(\mathscr {H}\) , then T is invertible on the whole \(\overline {\mathscr {D}(T)}\) and
Proof
The invertibility (with everywhere defined inverse) of T is guaranteed by Theorem 9(iii). Thus, (56) is an identity between bounded self-adjoint operators (their boundedness following by the inverse mapping theorem). For a generic \(h\in \mathscr {H}=\mathrm {ran}\, S_T\) one has h = S T g for some \(g=f+S_F^{-1}(Tv+w)+v=F+v\), where \(f\in \mathscr {D}(\overline {S})\), \(v\in \mathscr {D}(T)\), \(w=\ker S^*\cap \mathscr {D}(T)\) (Theorem 5), and hence \(F\in \mathscr {D}(S_F)\) (Remark 1). Then
On the other hand
and
whence the conclusion \(\langle h, S_T^{-1} h\rangle =\langle h, S_F^{-1} h\rangle +\langle h, P_T T^{-1} P_T h\rangle \). □
Remark 17
In terms of the equivalent parametrisation S B ↔ B of the self-adjoint extensions of S (Theorem 2), and denoting with \(P_B:\mathscr {H}\to \mathscr {H}\) the orthogonal projection onto \(\overline {\mathscr {D}(B)}\), Theorem 12 takes the following form: if S B is invertible on the whole \(\mathscr {H}\), then
(and B is not the zero operator on the whole \(\ker S^*\), unless S B = S F). Indeed, re-doing the proof above, for generic \(g\in \mathscr {D}(S_B)\) the parametrisation (25) yields \(g=f+(S_F^{-1}+B)\widetilde {u}_1+u_0\) for some \(f\in \mathscr {D}(\overline {S})\), \(\widetilde {u}_1\in \mathscr {D}(B)\), and \(u_0\in \ker S^*\cap \mathscr {D}(B)^\perp \), whence \(F:=f+S_F^{-1}\widetilde {u}_1\in \mathscr {D}(S_F)\), \(h:=S_Bg=S_F F=\overline {S}f+\widetilde {u}_1\), and \(\widetilde {u}_1=P_B S_B g\). Therefore,
Remark 18
With reference to the historical perspective of Sect. 4, Theorem 12 appears, in a formulation that is virtually the same as the present one, both in Grubb [28, Theorem 1.4] and, limited to S T’s with positive bottom, in Faris [18, Theorem 15.1].
Corollary 6
Let \(\widetilde {S}\) be a self-adjoint extension of S and let z < m(S) be such that  is invertible on the whole \(\mathscr {H}\) (for example a semi-bounded extension \(\widetilde {S}\) and a real number \(z<m(\widetilde {S})\)
). Let T(z) be the extension parameter, in the sense of the KVB parametrisation (43) of Theorem 5
, of the operator
is invertible on the whole \(\mathscr {H}\) (for example a semi-bounded extension \(\widetilde {S}\) and a real number \(z<m(\widetilde {S})\)
). Let T(z) be the extension parameter, in the sense of the KVB parametrisation (43) of Theorem 5
, of the operator  considered as a self-adjoint extension of the densely defined and bottom-positive symmetric operator
considered as a self-adjoint extension of the densely defined and bottom-positive symmetric operator  . Correspondingly, let P(z) be the orthogonal projection onto \(\overline {\mathscr {D}(T(z))}\)
. Then
. Correspondingly, let P(z) be the orthogonal projection onto \(\overline {\mathscr {D}(T(z))}\)
. Then

Proof
Since m(S(z)) = m(S) − z > 0, the assumptions of Theorem 12 are matched and (56) takes the form (58) owing to the fact that the Friedrichs extension of S(z) is precisely  (Theorem 15(vii)). □
(Theorem 15(vii)). □
Remark 19
Formula (58), in particular, shows that the resolvent difference  has non-zero matrix elements only on a suitable subspace of
has non-zero matrix elements only on a suitable subspace of  . (The dependence on z of the term P(z)T(z)−1
P(z) remains here somewhat implicit, although of course T(z) and P(z) are unambiguously and constructively well defined in terms of the given
. (The dependence on z of the term P(z)T(z)−1
P(z) remains here somewhat implicit, although of course T(z) and P(z) are unambiguously and constructively well defined in terms of the given  , as described in Proposition 5.)
, as described in Proposition 5.)
Let us now make (58) more explicit by reproducing a Kreı̆n-like resolvent formula (see, e.g., [2, Theorems A.2-A.3]).
Theorem 13 (Kreı̆n’s Resolvent Formula for Deficiency Index = 1)
Let S be a densely defined symmetric operator on a Hilbert space \(\mathscr {H}\) with positive bottom (m(S) > 0) and with deficiency index \(\dim \ker S^*=1\) . Let \(\widetilde {S}\) be a self-adjoint extension of S other than the Friedrichs extension S F . Let \(v\in \ker S^*\!\setminus \!\{0\}\) and for each \(z\in (-\infty ,m(S))\cap \rho (\widetilde {S})\) set

Then there exists an analytic function \(\beta :(-\infty ,m(S))\cap \rho (\widetilde {S})\to \mathbb {R}\) , with β(z) ≠ 0, such that

β(z), v(z), and (60) admit an analytic continuation to \(\rho (S_F)\cap \rho (\widetilde {S})\).
Proof
Because of the constance of the deficiency index,  . \(\widetilde {S}\) is semi-bounded (Corollary 1). Since \(z<m(\widetilde {S})\),
. \(\widetilde {S}\) is semi-bounded (Corollary 1). Since \(z<m(\widetilde {S})\),  is a bottom-positive self-adjoint extension of the densely defined and bottom-positive symmetric operator
is a bottom-positive self-adjoint extension of the densely defined and bottom-positive symmetric operator  . Its extension parameter T(z), in the sense of the KVB parametrisation, is the bottom-positive self-adjoint operator T(z) on the space
. Its extension parameter T(z), in the sense of the KVB parametrisation, is the bottom-positive self-adjoint operator T(z) on the space  which acts as the multiplication by a positive number t(z). (The positivity of the bottom of T(z) follows from
which acts as the multiplication by a positive number t(z). (The positivity of the bottom of T(z) follows from  , Theorem 10.) Clearly,
, Theorem 10.) Clearly,  . Moreover, v(z) ≠ 0 for each admissible z: this is obviously true if z = 0, and if it was not true for z ≠ 0, then
. Moreover, v(z) ≠ 0 for each admissible z: this is obviously true if z = 0, and if it was not true for z ≠ 0, then  , which would contradict
, which would contradict  (Remark 1, formula (8)). Thus, v(z) spans
(Remark 1, formula (8)). Thus, v(z) spans  and \(P_T:=\|v(z)\|{ }^{-2}|v(z)\rangle \langle v(z)|:\mathscr {H}\to \mathscr {H}\) is the orthogonal projection onto
and \(P_T:=\|v(z)\|{ }^{-2}|v(z)\rangle \langle v(z)|:\mathscr {H}\to \mathscr {H}\) is the orthogonal projection onto  . In this case, the resolvent formula (58) takes precisely the form (60) where β(z) := ∥v(z)∥−2
t(z)−1. Being a product of positive quantities, β(z) > 0. Moreover,
. In this case, the resolvent formula (58) takes precisely the form (60) where β(z) := ∥v(z)∥−2
t(z)−1. Being a product of positive quantities, β(z) > 0. Moreover,  and
and  are analytic operator-valued functions on the whole \(\rho (S_F)\cap \rho (\widetilde {S})\) (because of the analyticity of resolvents) and so is the vector-valued function z↦v(z) (because of the construction (59)). Therefore, taking the expectation of both sides of (60) on v(z) shows at once that z↦β(z) is analytic on \(\rho (S_F)\cap \rho (\widetilde {S})\), and real analytic on \((-\infty ,m(S))\cap \rho (\widetilde {S})\). □
are analytic operator-valued functions on the whole \(\rho (S_F)\cap \rho (\widetilde {S})\) (because of the analyticity of resolvents) and so is the vector-valued function z↦v(z) (because of the construction (59)). Therefore, taking the expectation of both sides of (60) on v(z) shows at once that z↦β(z) is analytic on \(\rho (S_F)\cap \rho (\widetilde {S})\), and real analytic on \((-\infty ,m(S))\cap \rho (\widetilde {S})\). □
7 Examples
7.1 “Free Quantum Particle” on Half-line
On the Hilbert space \(\mathscr {H}=L^2[0,+\infty )\) one considers the densely defined symmetric operator

S has bottom m(S) = 1. One has

thus all the extensions of S act as  on suitable restrictions of H
2(0, +∞). In particular,
on suitable restrictions of H
2(0, +∞). In particular,
and the Friedrichs extension of S has domain
that is, \(\mathscr {D}(S^*)\) with Dirichlet boundary condition at the origin.
Applying von Neumann’s theory one finds (see, e.g., [24, Chapter 6.2]) that the self-adjoint extensions of S constitute the family \(\{S_\nu \,|\,\nu \in (-\frac {\pi }{2},\frac {\pi }{2}]\}\), where each S
ν acts as  on the domain
on the domain
By inspection one sees that the Friedrichs extension of S is S π∕2.
In order to apply the KVB theory, one needs to identify \(\ker S^*\) and \(S_F^{-1}\). One easily finds
All self-adjoint extensions of S are therefore semi-bounded (Corollary 1). One also finds that the integral kernel of \(S_F^{-1}\) is
(see, e.g., [24, Chapter 6.2]). In fact, since \(S_F^{-1}\) only enters the formulas as acting on \(\ker S^*\), instead of (67) one can rather limit oneself to the problem
whose only solution in L 2[0, +∞) is \(\eta (x)=\frac {1}{2}\,x\,e^{-x}\). Thus, for fixed \(a\in \mathbb {C}\),
According to Theorem 5, the self-adjoint extensions of S are operators of the form S
T where T is a self-adjoint operator on subspaces of \(\ker S^*=\mathrm {Span}\{e^{-x}\}\), precisely the zero-dimensional subspace {0} or the whole Span{e
−x}. In the former case S
T = S
F (Proposition 4). In the latter, each such T acts as the multiplication T
β : e
−x↦βe
−x by a fixed \(\beta \in \mathbb {R}\), \(\mathscr {D}(T_\beta )=\mathrm {Span}\{e^{-x}\}=\ker S^*\), and \(\ker S^*\cap \mathscr {D}(T_\beta )^\perp =\{0\}\): by (43) and (68), the corresponding self-adjoint extension \(S_\beta \equiv S_{T_\beta }\) of S acts as  on the domain
on the domain
Observing that g(0) = a and \(g^{\prime }(0)=a(\frac {1}{2}\beta -1)\) for any \(g\in \mathscr {D}(S_\beta )\), (69) can be re-written as
Comparing (70) with (65) above, we see that S β is the extension S ν of von Neumann’s parametrisation with
which includes the Friedrichs extension (\(\nu =\frac {\pi }{2}\)) if one let β = +∞.
The same analysis can be equivalently performed in terms of the quadratic forms of the self-adjoint extensions of S, following Theorem 7 (which applies to this example since all extensions are semi-bounded). The reference form is the Friedrichs one, that is,
as one deduces from (64). Owing to (48), the form domain of any other extension is obtained by taking the direct sum of \(\mathscr {D}[S_T]=\mathscr {D}[S_F]\dotplus \mathscr {D}[T]\) where T ≡ T β = the multiplication by a real β on \(\mathscr {D}(T)=\mathrm {Span}\{e^{-x}\}=\mathscr {D}[T]\). Then (48) and (72) yield
Going backwards from this (closed and semi-bounded) form to the uniquely associated self-adjoint operator, a straightforward exercise would yield the domain \(\mathscr {D}(S_\beta )\) already determined by (70).
Concerning the bottom and the negative spectrum of a generic extension S β, one has m(T β) = β and σ(T β) = {β}, therefore Theorem 6 gives
and Corollary 4 implies that σ −(S β) consists of one single eigenvalue whenever β < 0. The explicit spectral analysis of S β gives σ −(S β) = ∅ if \(\beta \geqslant 2\) and σ −(S β) = {1 − (β∕2 − 1)2)} if β < 2 with normalised eigenfunction \(g_\beta (x)=\sqrt {2-\beta }\,e^{-(1-\beta /2)x}\), whence
We thus see that the bounds (74) are consistent with the “exact result” (75) (and that there are extensions other than the Friedrichs one whose bottom coincide with that of S).
As for the resolvents, for z > 0 one sees that  and by means of the formula ([24, Chapter 6.2])
and by means of the formula ([24, Chapter 6.2])

one finds

for z > 0 and z ≠ − (β∕2 − 1) if β < 2. This is precisely a Kreı̆n resolvent formula of the type (60). The corresponding integral kernel is

This expression can be continued analytically to complex z’s as stated in general in Theorem 13, see (83) below.
The shift by a unit constant introduced in the definition (61) of S guarantees that S has positive bottom. After having determined with (72)–(73) the quadratic forms of a generic self-adjoint extension of S, one can remove the shift and deduce that the self-adjoint extensions of the operator \(S^{\prime }=-\frac {\mathrm {d}^2}{\mathrm {d} x^2}\), \(\mathscr {D}(S^{\prime })=C^\infty _0(0,+\infty )\), constitute the family \(\{S^{\prime }_\beta \,|\,\beta \in (-\infty ,+\infty ]\}\) where for each \(\beta \in \mathbb {R}\) the element \(S^{\prime }_\beta \) is the extension with quadratic form
and hence with
whereas for β = ∞ one has the Friedrichs extensions
Similarly, one deduces from (78)

for z > 0 and z ≠ − (β∕2 − 1) if β < 2. This expression admits the analytic continuation

for \(k\in \mathbb {C}\) with \(\mathfrak {Im}k>0\) and k ≠ −i(β∕2 − 1) if β < 2, that is, the operator-valued map  is holomorphic.
is holomorphic.
7.2 “Free Quantum Particle” on an Interval
On the Hilbert space \(\mathscr {H}=L^2[0,1]\) one considers the densely defined symmetric operator
The positivity of the bottom of S can be seen by applying twice (to f, f ′ and to f ′, f ′′) Poincaré’s inequality
thus obtaining
One has
thus all the extensions of S act as \(-\frac {\mathrm {d}^2}{\mathrm {d} x^2}\) on suitable restrictions of H 2(0, 1). In particular,
and the Friedrichs extension of S has domain
that is, S F is the negative Laplacian with Dirichlet boundary conditions. Considering its spectrum, \(\sigma (S_F)=\{n^2\pi ^2\,|\,n\in \mathbb {N}\}\), one re-obtains (85) without using Poincaré’s inequality.
Applying von Neumann’s theory one finds (see, e.g., [24, Chapter 6.2]) that the self-adjoint extensions of S constitute the family {S U | U ∈ U(2)} where each S U acts as \(-\frac {\mathrm {d}^2}{\mathrm {d} x^2}\) on the domain
By inspection one sees that in this case the Friedrichs extension of S is the extension S
U indexed by  .
.
Let us apply now the KVB theory, identifying first of all \(\ker S^*\) and \(S_F^{-1}\). One has
All self-adjoint extensions of S are therefore semi-bounded (Corollary 1). As for \(S_F^{-1}\), all what we need here is its action on \(\ker S^*\) (the general inversion formula for the problem S F η = h with datum h can be found, for instance, in [24, Chapter 6.2]), therefore we consider the problem
for given \(a,b\in \mathbb {C}\), whose only solution is \(\eta (x)=(\frac {a}{2}+\frac {b}{6})x-\frac {a}{2}x^2-\frac {b}{6}x^3\). Thus,
Owing to (87), (90), and (91) above, the decomposition (7) reads
i.e., any \(F\in H^2(0,1)\cap H^1_{0}(0,1)\) determines uniquely \(f\in H^2_{0}(0,1)\) and \(a,b\in \mathbb {C}\) such that \(F(x)=f(x)+(\frac {a}{2}+\frac {b}{6})x-\frac {a}{2}x^2-\frac {b}{6}x^3\). Explicitly,
Analogously, the decomposition (5) reads
that is, any g ∈ H 2(0, 1) can be written as
for a unique \(F\in H^2(0,1)\cap H^1_{0}(0,1)\).
According to Theorem 5, the self-adjoint extensions of S are operators of the form S T where T is a self-adjoint operator on subspaces of \(\ker S^*=\mathrm {Span}\{\mathbf {1},x\}\), precisely
-
the zero-dimensional subspace {0}, in which case S T = S F (Proposition 4)
-
or the one-dimensional subspaces Span{1} or Span{a 1 + x}, \(a\in \mathbb {C}\), in which case T acts as the multiplication by a real number,
-
or the whole two-dimensional space \(\mathrm {Span}\{\mathbf {1},x\}\cong \mathbb {C}^2\), in which case T acts as the multiplication by a hermitian matrix.
For concreteness, let us work out in detail the case of the one-dimensional space Span{1} and of the self-adjoint operator T β on it, defined by T β 1 := β 1 for fixed \(\beta \in \mathbb {R}\). In this case \(\mathscr {D}(T_\beta )=\mathrm {Span}\{\mathbf {1}\}\) and \(\ker S^*\cap \mathscr {D}(T_\beta )^\perp =\mathrm {Span}\{2x-\mathbf {1}\}\): therefore, according to (43), the corresponding self-adjoint extension \(S_\beta \equiv S_{T_\beta }\) of S acts as \(-\frac {\mathrm {d}^2}{\mathrm {d} x^2}\) on the domain
By means of (91) (upon renaming the coefficients γ, δ), this is re-written as
which in turn, observing that g(0) = 2γ = g(1) and g ′(0) − g ′(1) = 2βγ for any \(g\in \mathscr {D}(S_\beta )\), can be further re-written as
The special case β = 0 corresponds to the self-adjoint extension with periodic boundary conditions: in the parametrisation (89) of von Neumann’s theory, this is the extension S U with U = ( 01 1 0 ). Concerning the bottom of the extensions of the form S β, clearly m(T β) = β, thus Theorem 6 gives
This is consistent with the explicit knowledge of σ(S β): for example \(\sigma (S_{\beta =0})=\{4\pi ^2 n^2\,|\,n\in \mathbb {Z}\}\), whence indeed m(S β=0) = 0. Moreover, since σ(T β) = {β} (simple eigenvalue), Corollary 4 implies that σ −(S β) consists of one single eigenvalue whenever β < 0.
All other cases of the above list can be discussed analogously: along the same line, (43) and (91) produce each time an expression like (92) for \(\mathscr {D}(S_T)\) that can be then cast in the form (93). For completeness, we give here the summary of all possible conditions of self-adjointness. The family of all self-adjoint extension of S is described by the following four families of boundary conditions:
where \(c\in \mathbb {C}\) and \(b_1,b_2\in \mathbb {R}\) are arbitrary parameters. For each boundary condition, the corresponding extension is the operator \(-\frac {\mathrm {d}^2}{\mathrm {d} x^2}\) acting on the H 2(0, 1)-functions that satisfy that one boundary condition. For instance, the extension S β determined by (93) correspond to the boundary condition of type (96) with c = 1 and b 1 = β. In term of the Višik-Birman extension parameter T, conditions of type (95) occur when \(\dim \mathscr {D}(T)=2\), conditions of type (96) or (97) occur when \(\dim \mathscr {D}(T)=1\), and condition (98) is precisely that occurring when \(\dim \mathscr {D}(T)=0\) (Dirichlet boundary conditions, Friedrichs extension). The well-known conditions (95)–(98) can be also found by means of boundary triplet techniques: see, e.g., [60, Example 14.10].
The same analysis can be equivalently performed in terms of the quadratic forms of the self-adjoint extensions of S, according to Theorem 7 (in the present case all extensions are semi-bounded). The reference form is the Friedrichs one, that is,
as one deduces from (88). The property m(S F) = π 2 reads
that is, Poincaré’s inequality. Owing to (48), the form domain of each extension is obtained by taking the direct sum of \(\mathscr {D}[S_T]=\mathscr {D}[S_F]\dotplus \mathscr {D}[T]\): in the present case \(\mathscr {D}[T]=\mathscr {D}(T)\), because of the finiteness of the deficiency index of S. For example, in the concrete case worked out above, that is, T ≡ T β = multiplication by a real β on \(\mathscr {D}(T)=\mathrm {Span}\{\mathbf {1}\}\), (48) and (99) yield
Then, going from this (closed and semi-bounded) form to the uniquely associated self-adjoint operator, a straightforward exercise would yield the domain \(\mathscr {D}(S_\beta )\) already determined by (93).
As for the Kreı̆n-von Neumann extension S N of S, this is the extension S T with \(T:\ker S^*\to \ker S^*\), \(Tv=0\ \forall v\in \ker S^*\) (Proposition 4), in which case (48) and (99) yield the quadratic form
The corresponding S N is either found by determining the self-adjoint operator associated to S N[⋅] or by applying directly (43) to the operator T under consideration:
(The latter boundary condition is of the form (95) with b 1 = b 2 = −c = 1.) S N has not to be confused with the self-adjoint extension with Neumann boundary conditions S N.bc, that is, the operator \(S_{N.bc}=\frac {\mathrm {d}^2}{\mathrm {d} x^2}\) with domain
and quadratic form
Although S N and S N.bc have the same form domain and the same (zero) bottom, S N is the smallest among all positive self-adjoint extensions of S (Theorem 17(i))—the inequality \(S_N[g]\leqslant S_{N.bc}[g]\) (which is strict whenever g(0) ≠ g(1)) can be also checked explicitly by comparing (102) with (105). In fact it is easy to compute explicitly (see, e.g., [3, Example 5.1])
where k j is the unique solution to \(\frac {1}{2}k=\tan {}(\frac {1}{2}k)\) in \((2\pi (j-1),2\pi (j-\frac {1}{2}))\) (moreover, \(k_j\to 2\pi (j-\frac {1}{2})\) as j → +∞), thus any even eigenvalue of S N is strictly smaller then the corresponding eigenvalue of S N.bc.
Notes
- 1.
If the subspaces
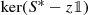 and
and 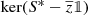 have the same finite dimension, it is easy to conclude that all self-adjoint extensions of S are bounded below, see, e.g., the Proposition on page 179 of [56]; if their common dimension is infinite instead, S may also admit self-adjoint extensions that are unbounded below. The occurrence of such unbounded below extensions may be presented as a mere “academic exercise” about operators on an infinite orthogonal sum of Hilbert spaces (see [56, Chapter 10], Problem 26) but in fact examples are known where they arise as quantum Hamiltonians of physical relevance—see, e.g., the possibility of unbounded below self-adjoint extensions for particle Hamiltonians with point interaction [14, 20, 21, 39,40,41, 51, 52].
have the same finite dimension, it is easy to conclude that all self-adjoint extensions of S are bounded below, see, e.g., the Proposition on page 179 of [56]; if their common dimension is infinite instead, S may also admit self-adjoint extensions that are unbounded below. The occurrence of such unbounded below extensions may be presented as a mere “academic exercise” about operators on an infinite orthogonal sum of Hilbert spaces (see [56, Chapter 10], Problem 26) but in fact examples are known where they arise as quantum Hamiltonians of physical relevance—see, e.g., the possibility of unbounded below self-adjoint extensions for particle Hamiltonians with point interaction [14, 20, 21, 39,40,41, 51, 52]. - 2.
The positivity of the bottom, m(S) > 0, is in fact only a special case of a more general assumption discussed in [28, Section II §2], that is, the assumption that \(\overline {S}\) has a bounded and everywhere defined inverse: in this general case \(S_F^{-1}\) is replaced by the inverse of another self-adjoint extension \(\widetilde {S}_0\) of S with bounded inverse—the existence of such \(\widetilde {S}_0\) is a result originally proved by Calkin [12].
- 3.
In fact, this is a result of Krasnosel’skii and Kreı̆n [35].
- 4.
By definition a closed and densely defined operator S on a Hilbert space \(\mathscr {H}\) is affiliated with a von Neumann algebra \(\mathfrak {M}\) on \(\mathscr {H}\) when for any unitary \(U\in \mathfrak {M}^{\prime }\) (the commutant of \(\mathfrak {M}\)) one has \(U\mathscr {D}(S)\subset \mathscr {D}(S)\) and USU ∗ = S on \(\mathscr {D}(S)\).
- 5.
The coincidence of the two deficiency indices of a semi-bounded and densely defined symmetric operator is a classical result (see, e.g., the first corollary to Theorem X.1 in [56]) which is a direct consequence of the above-mentioned Krasnosel’skii-Kreı̆n result [35] on the constance of the deficiency indices throughout each of the two complex half-planes. In fact, such an argument is more general and proves as well the coincidence of the deficiency indices of a symmetric and densely defined operator S such that \(\overline {S}\) has a real point in its resolvent set (see, e.g., the second corollary to Theorem X.1 in [56]). It is worth highlighting that the existence of a self-adjoint extension of a symmetric and densely defined S with a real point in the resolvent set of \(\overline {S}\) is an independent result, proved first by Calkin [12] and later re-proved by Kreı̆n [34].
References
Albeverio, S., Kurasov, P.: Singular perturbations of differential operators. In: London Mathematical Society Lecture Note Series, vol. 271. Cambridge University, Cambridge (2000). Solvable Schrödinger type operators
Albeverio, S., Gesztesy, F., Høegh-Krohn, R., Holden, H.: Solvable models in quantum mechanics. In: Texts and Monographs in Physics. Springer, New York (1988)
Alonso, A., Simon, B.: The Birman-Kreı̆n-Vishik theory of selfadjoint extensions of semibounded operators. J. Operator Theory 4, 251–270 (1980)
Amrein, W.O., Pearson, D.B.: Moperators: a generalisation of Weyl-Titchmarsh theory. J. Comput. Appl. Math. 171, 1–26 (2004)
Ando, T., Nishio, K.: Positive selfadjoint extensions of positive symmetric operators. Tôhoku Math. J. 22(2), 65–75 (1970)
Arlinskiı̆, Y., Tsekanovskiı̆, E.: The von Neumann problem for nonnegative symmetric operators. Integr. Equ. Oper. Theory 51, 319–356 (2005)
Behrndt, J., Langer, M.: Boundary value problems for elliptic partial differential operators on bounded domains. J. Funct. Anal. 243, 536–565 (2007)
Birman, M. v.: On the theory of self-adjoint extensions of positive definite operators. Mat. Sb. N.S. 38(80), 431–450 (1956)
Brown, B.M., Grubb, G., Wood, I.G.: M-functions for closed extensions of adjoint pairs of operators with applications to elliptic boundary problems. Math. Nachr. 282, 314–347 (2009)
Bruk, V.M.: On a class of boundary value problems with spectral parameter in the boundary condition. Math. USSR-Sbornik 29, 186 (1976)
Calkin, J.W.: Abstract symmetric boundary conditions, Trans. Am. Math. Soc. 45, 369–442 (1939)
Calkin, J.W.: Symmetric transformations in Hilbert space. Duke Math. J. 7, 504–508 (1940)
Coddington, E.A., de Snoo, H.S.V.: Positive selfadjoint extensions of positive symmetric subspaces. Math. Z. 159, 203–214 (1978)
Correggi, M., Dell’Antonio, G., Finco, D., Michelangeli, A., Teta, A.: Stability for a system of N fermions plus a different particle with zero-range interactions. Rev. Math. Phys. 24, 1250017, 32 (2012)
Derkach, V.A., Malamud, M.M.: Generalized resolvents and the boundary value problems for Hermitian operators with gaps. J. Funct. Anal. 95, 1–95 (1991)
Derkach, V., Hassi, S., Malamud, M., de Snoo, H.: Boundary triplets and Weyl functions. Recent developments. In: Operator Methods for Boundary Value Problems. London Mathematical of Society, Lecture Note Series, vol. 404. Cambridge University, Cambridge (2012), pp. 161–220
Dunford, N., Schwartz, J.T.: Linear operators. In: Part II: Spectral theory. Self Adjoint Operators in Hilbert Space, with the Assistance of William G. Bade and Robert G. Bartle. Interscience Publishers/Wiley, New York/London (1963)
Faris, W.G.: Self-adjoint operators. In: Lecture Notes in Mathematics, vol. 433. Springer, Berlin (1975)
Friedrichs, K.: Spektraltheorie halbbeschränkter Operatoren und Anwendung auf die Spektralzerlegung von Differentialoperatoren. Math. Ann. 109, 465–487 (1934)
Gallone, M., Michelangeli, A.: Discrete spectra for critical Dirac-Coulomb Hamiltonians. J. Math. Phys. 59, 062108, 19 (2018)
Gallone, M., Michelangeli, A.: Self-adjoint realisations of the Dirac-Coulomb Hamiltonian for heavy nuclei. Anal. Math. Phys. 9, 585–616 (2019)
Gallone, M., Michelangeli, A.: Hydrogenoid spectra with central perturbations. Rep. Math. Phys. 84, 215–243 (2019)
Gallone, M., Michelangeli, A., Pozzoli, E.: On geometric quantum confinement in Grushin-type manifolds. Z. Angew. Math. Phys. 70, Paper No. 158 (2019)
Gitman, D.M., Tyutin, I.V., Voronov, B.L.: Self-adjoint extensions in quantum mechanics. In: Progress in Mathematical Physics, vol. 62. Birkhäuser/Springer, New York (2012). General theory and applications to Schrödinger and Dirac equations with singular potentials
Gorbachuk, V.I., Gorbachuk, M.L.: Boundary value problems for operator differential equations. In: Mathematics and its Applications (Soviet Series). Kluwer Academic Publishers Group, Dordrecht (1991). Translated and revised from the 1984 Russian original
Gorbačuk, M.L., Mihaı̆lec, V.A.: Semibounded selfadjoint extensions of symmetric operators. Dokl. Akad. Nauk SSSR 226, 765–767 (1976)
Gorbachuk, V.I., Gorbachuk, M.L., Kochubeı̆, A.N.: The theory of extensions of symmetric operators, and boundary value problems for differential equations. Ukrain. Mat. Zh. 41, 1299–1313, 1436 (1989)
Grubb, G.: A characterization of the non-local boundary value problems associated with an elliptic operator. Ann. Scuola Norm. Sup. Pisa 22(3), 425–513 (1968)
Grubb, G.: Properties of normal boundary problems for elliptic even-order systems. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 1(1974), 1–61 (1975)
Grubb, G.: Distributions and operators. In: Graduate Texts in Mathematics, vol. 252. Springer, New York (2009)
Kadison, R.V.: Some notes on noncommutative analysis. In: Analysis at Urbana, Vol. II (Urbana, IL, 1986–1987). London Mathematical Society Lecture Note Series. Cambridge University, Cambridge (1989), pp. 243–257
Kočubeı̆, A.N.: Extensions of symmetric operators and of symmetric binary relations. Mat. Zametki 17, 41–48 (1975)
Kostenko, A.S., Malamud, M.M.: 1-D Schrödinger operators with local point interactions on a discrete set. J. Differ. Equ. 249, 253–304 (2010)
Kreı̆n, M.G.: The theory of self-adjoint extensions of semi-bounded Hermitian transformations and its applications. I. Rec. Math. [Mat. Sbornik] N.S. 20(62), 431–495 (1947)
Kreı̆n, M.G., Krasnosel′skiı̆, M.A.: Fundamental theorems on the extension of Hermitian operators and certain of their applications to the theory of orthogonal polynomials and the problem of moments. Uspehi Matem. Nauk (N. S.) 2, 60–106 (1947)
Malamud, M.M.: Certain classes of extension of a lacunary Hermitian operator. Ukr. Math. J. 44, 190–204 (1992)
Malamud, M.M.: Spectral theory of elliptic operators in exterior domains. Russ. J. Math. Phys. 17, 96–125 (2010)
Malamud, M.M., Neidhardt, H.: On the unitary equivalence of absolutely continuous parts of self-adjoint extensions. J. Funct. Anal. 260, 613–638 (2011)
Mel′nikov, A.M., Minlos, R.A.: On the pointlike interaction of three different particles. In: Many-particle Hamiltonians: spectra and scattering. Advantages of Soviet Mathematical. American Mathematical Society, Providence (1991), pp. 99–112
Mel′nikov, A.M., Minlos, R.A.: Point interaction of three different particles. Vestnik Moskov. Univ. Ser. I Mat. Mekh. 3, 3–6, 110 (1991)
Michelangeli, A., Ottolini, A.: On point interactions realised as Ter-Martirosyan-Skornyakov Hamiltonians. Rep. Math. Phys. 79, 215–260 (2017)
Michelangeli, A., Ottolini, A.: Multiplicity of self-adjoint realisations of the (2+1)-fermionic model of Ter-Martirosyan—Skornyakov type. Rep. Math. Phys. 81, 1–38 (2018)
Michelangeli, A., Pfeiffer, P.: Stability of the (2+2)-fermionic system with zero-range interaction. J. Phys. A. Math. Theoretical 49, 105301 (2016)
Michelangeli, A., Schmidbauer, C.: Binding properties of the (2+1)-fermion system with zero-range interspecies interaction. Phys. Rev. A 87, 053601 (2013)
Minlos, R.A.: On the point interaction of three particles. In: Applications of Selfadjoint Extensions in Quantum Physics (Dubna, 1987). Lecture Notes in Physics, vol. 324. Springer, Berlin (1989), pp. 138–145
Minlos, R.A.: On point-like interaction between n fermions and another particle. Mosc. Math. J. 11, 113–127, 182 (2011)
Minlos, R.A.: Remark on my paper On point-like interaction between n fermions and another particle. Mosc. Math. J. 11, 815–817, 822 (2011)
Minlos, R.A.: On point-like interaction between three particles: two fermions and another particle. ISRN Math. Phys. 2012, 230245 (2012)
Minlos, R.A.: On point-like interaction of three particles: two fermions and another particle. II. Mosc. Math. J. 14, 617–637, 642–643 (2014)
Minlos, R.A.: A system of three pointwise interacting quantum particles. Uspekhi Mat. Nauk 69, 145–172 (2014)
Minlos, R.A., Faddeev, L.D.: On the point interaction for a three-particle system in quantum mechanics. Soviet Phys. Dokl. 6, 1072–1074 (1962)
Minlos, R.A., Faddeev, L.D.: Comment on the problem of three particles with point interactions. Soviet Physics JETP 14, 1315–1316 (1962)
Minlos, R.A., Shermatov, M.K.: Point interaction of three particles. Vestnik Moskov. Univ. Ser. I Mat. Mekh., 44(6), 7–14, 97 (1989)
Posilicano, A.: A Kreı̆n-like formula for singular perturbations of self-adjoint operators and applications. J. Funct. Anal. 183, 109–147 (2001)
Prokaj, V., Sebestyén, Z.: On extremal positive operator extensions. Acta Sci. Math. (Szeged) 62, 485–491 (1996)
Reed, M., Simon, B.: Methods of Modern Mathematical Physics. II. Fourier Analysis, Self-Adjointness, Academic Press [Harcourt Brace Jovanovich], New York-London (1975)
Riesz, F., Sz.-Nagy, B.: Functional analysis. Frederick Ungar, New York (1955). Translated by Leo F. Boron
Ryzhov, V.: A general boundary value problem and its Weyl function. Opuscula Math. 27, 305–331 (2007)
Ryzhov, V.: Spectral Boundary Value Problems and their Linear Operators. arxiv.org/abs/0904.0276 (2009)
Schmüdgen, K.: Unbounded self-adjoint operators on Hilbert space. Graduate Texts in Mathematics, vol. 265. Springer, Dordrecht (2012)
Sebestyén, Z., Stochel, J.: Restrictions of positive selfadjoint operators. Acta Sci. Math. (Szeged) 55, 149–154 (1991)
Sebestyén, Z., Stochel, J.: Characterizations of positive selfadjoint extensions. Proc. Am. Math. Soc. 135, 1389–1397 (2007) (electronic)
Shermatov, M.K.: On the point interaction of two fermions and one particle of a different nature. Teoret. Mat. Fiz. 136, 257–270 (2003)
Stone, M.H.: Linear transformations in Hilbert space. American Mathematical Society Colloquium Publications, vol. 15. American Mathematical Society, Providence, 1932
Takesaki, M.: Tomita’s theory of modular Hilbert algebras and its applications. Lecture Notes in Mathematics, vol. 128. Springer, Berlin (1970)
Višik, M.I.: On general boundary problems for elliptic differential equations. Trudy Moskov. Mat. Obšč. 1, 187–246 (1952)
von Neumann, J.: Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren. Math. Ann. 102, 49–131 (1930)
Acknowledgements
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A. Appendix: Summary of von Neumann’s vs Kreı̆n’s Extension Theory
A. Appendix: Summary of von Neumann’s vs Kreı̆n’s Extension Theory
The material of this Appendix is completely classical and stems from the original works of von Neumann [67], Stone [64], Friedrichs [19], and Kreı̆n [34]. We give here a concise summary from a more modern perspective (see, e.g., [56, 60]) that includes also the Ando-Nishio characterisation of the Kreı̆n-von Neumann extension (first obtained in the work of Ando and Nishio [5] and later generalised by Coddington and de Snoo [13], and by Prokaj, Sebestyén, and Stochel [55, 61, 62]) as well as Kadison’s characterisation of the Friedrichs extension [31].
Roughly speaking, von Neumann’s theory can be regarded as the “complex version” and Kreı̆n’s theory as the “real version” of the same idea, that consists of checking whether a complex number w is real by seeing whether \(\frac {w-\mathrm {i}}{w+\mathrm {i}}\) is a phase (complex version), or alternatively checking whether w is real positive by seeing whether \(\frac {w-1}{w+1}\) lies in [−1, 1) (real version), based on the fact that \(w\mapsto \frac {w-\mathrm {i}}{w+\mathrm {i}}\) is a bijection of the real axis onto the complex unit circle without the point 1, and that \(w\mapsto \frac {w-1}{w+1}\) is a bijection of the non-negative half-line onto the interval [−1, 1).
1.1 A.1 von Neumann’s Theory
Fixed \(z\in \mathbb {C}\!\setminus \!\mathbb {R}\) and a Hilbert space \(\mathscr {H}\), the Cayley transform

is a bijective map of the set of densely defined symmetric operators on \(\mathscr {H}\) onto the set of all isometric (i.e., norm-preserving) operators V on \(\mathscr {H}\) for which  is dense in \(\mathscr {H}\). One has
is dense in \(\mathscr {H}\). One has

S is closed if and only if V S is, and if S ′ is another symmetric operator on \(\mathscr {H}\), then S ⊂ S ′ if and only if \(V_S\subset V_{S^{\prime }}\). The inverse map is the inverse Cayley transform

As a consequence, a densely defined symmetric operator S is self-adjoint if and only if its Cayley transform V
S is unitary: indeed, S = S
∗ if and only if  , which is equivalent to \(\mathscr {H}=\mathrm {ran}(V_S)=\mathscr {D}(V_S)\).
, which is equivalent to \(\mathscr {H}=\mathrm {ran}(V_S)=\mathscr {D}(V_S)\).
Thus, finding a self-adjoint extension of S, call it \(\widetilde {S}\), is equivalent to finding a unitary extension of V
S, which turns out to be \(V_{\widetilde {S}}\), and this is in turn equivalent to (taking the operator closure and) finding a unitary operator from \(\mathscr {D}(V_S)^\perp \) to (ranV
S)⊥, i.e., from  to
to  . This way the isometric V
S is extended to the unitary \(V_{\widetilde {S}}\) on the whole \(\mathscr {H}\) so that
. This way the isometric V
S is extended to the unitary \(V_{\widetilde {S}}\) on the whole \(\mathscr {H}\) so that

Obviously, this is possible if and only if  .
.
For a generic densely defined symmetric operator S each of the two dimensions above is actually constant in z throughout each of the two complex half-planes.Footnote 3 This justifies the unambiguous (z-independent) terminology of “deficiency indices” of S.
When the condition of equal deficiency indices is matched, then from (107) and from  one has
one has

and on a generic \(f+u-V_{\widetilde {S}}u\) in \(\mathscr {D}(\widetilde {S})\) (\(f\in \mathscr {D}(\overline {S})\),  ) the action of \(\widetilde {S}\), in view of (108), gives
) the action of \(\widetilde {S}\), in view of (108), gives

Because of (109), \(V_{\widetilde {S}}\) in the r.h.s. of (110) and of (111) has to be thought of as a unitary map  . Thus, summarising:
. Thus, summarising:
Theorem 14 (von Neumann’s Theorem on Self-Adjoint Extensions)
A densely defined symmetric operator S on a Hilbert space
\(\mathscr {H}\)
admits self-adjoint extensions if and only if S has equal deficiency indices. In this case there is a one-to-one correspondence between the self-adjoint extensions of S and the isomorphisms between
 and
and
 , where
\(z\in \mathbb {C}\!\setminus \!\mathbb {R}\)
is fixed and arbitrary. Each self-adjoint extension is of the form S
U
for some
, where
\(z\in \mathbb {C}\!\setminus \!\mathbb {R}\)
is fixed and arbitrary. Each self-adjoint extension is of the form S
U
for some
 , where
, where

For each S
U
, the unitary U is the restriction to  of the Cayley transform of S
U.
of the Cayley transform of S
U.
1.2 A.2 Friedrichs Extension and Kreı̆n-von Neumann Extension
If a given densely defined symmetric operator S on a Hilbert space \(\mathscr {H}\) is bounded below, then it surely admits self-adjoint extensions (see, e.g., [56], Corollary to Theorem X.1). In fact, in this case S has two distinguished extensions (possibly coinciding), the Friedrichs extension and Kreı̆n-von Neumann extension.
Theorem 15 (Friedrichs Extension)
Let S be a semi-bounded and densely defined symmetric operator on a Hilbert space \(\mathscr {H}\).
-
(i)
The form (f, g)↦〈f, Sg〉 with domain \(\mathscr {D}(S)\) is closable. Its closure is the form whose domain, denoted by \(\mathscr {D}[S]\) , is given by the completion of \(\mathscr {D}(S)\) with respect to the norm f↦〈f, Sf〉 + (1 − m(S))∥f∥2 , where m(S) is the bottom of S, and whose value S[f, g] on any two \(f,g\in \mathscr {D}[S]\) is given by S[f, g] =limn→∞〈f n, Sg n〉, where (f n)n and (g n)n are two sequences in \(\mathscr {D}(S)\) that converge, respectively, to f and g in the above norm.
-
(ii)
The form \((S[\cdot ],\mathscr {D}[S])\) is bounded below and closed. Therefore, the operator associated with \((S[\cdot ],\mathscr {D}[S])\) is self-adjoint. It is called the Friedrichs extension of S and denoted by S F . By definition
$$\displaystyle \begin{aligned} \mathscr{D}(S_F)\;&=\;\left\{f\in\mathscr{D}[S]\,\left| \begin{array}{c} \exists\,u_f\in\mathscr{H}\mathit{\text{ such that }} \\ S[f,g]=\langle u_f,g\rangle\;\:\forall g\in\mathscr{D}[S] \end{array}\!\right.\right\} \\ S_F f\;&:=\;u_f\,. \end{aligned} $$(113) -
(iii)
S F is a bounded below self-adjoint extension of S with the same greatest lower bound as S, i.e.,
$$\displaystyle \begin{aligned} m(S_F)\;=\;m(S)\,, \end{aligned} $$(114)and whose associated quadratic form coincides with the closure if the form (f, g)↦〈f, Sg〉 considered in (i)–(ii), i.e.,
$$\displaystyle \begin{aligned} \mathscr{D}[S_F]\;=\;\mathscr{D}[S]\,,\qquad S_F[f,g]\;=\;S[f,g]\,. \end{aligned} $$(115) -
(iv)
\(\mathscr {D}(S_F)=\mathscr {D}(S^*)\cap \mathscr {D}[S]\) and \(S_F=S^*\upharpoonright \mathscr {D}[S]\).
-
(v)
S F is the only self-adjoint extension of S whose operator domain is contained in \(\mathscr {D}[S]\).
-
(vi)
If \(\widetilde {S}\) is another bounded below self-adjoint extension of S, then \(S_F\geqslant \widetilde {S}\).
-
(vii)
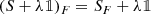 for \(\lambda \in \mathbb {R}\).
for \(\lambda \in \mathbb {R}\).
Theorem 16 (Friedrichs Extension—Kadison’s Construction [31])
Let S be a semi-bounded, closed, and densely defined symmetric operator on a Hilbert space \(\mathscr {H}\).
-
(i)
The inner product (f, g)↦〈f, Sg〉 + (1 − m(S))〈f, g〉 on \(\mathscr {D}(S)\) is positive definite. The corresponding completion \(\mathscr {D}^{\prime }\) is a subspace of \(\mathscr {H}\) (in fact, \(\mathscr {D}^{\prime }=\mathscr {D}[S]\) ) with \(\|g\|\leqslant \|g\|{ }_{\mathscr {D}^{\prime }}\).
-
(ii)
For each \(g\in \mathscr {H}\) , the functional f↦〈g, f〉 on \(\mathscr {D}(S)\) extends to a bounded linear functional on \((\mathscr {D}^{\prime },\|\,\|{ }_{\mathscr {D}^{\prime }}\!)\) with norm not exceeding ∥g∥, and consequently \(\exists \,!\,g^{\prime }\in \mathscr {D}(S^*)\cap \mathscr {D}^{\prime }\) such that
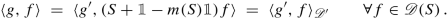
The map g↦g ′ is realised by a linear operator K (i.e., g ′ = Kg) such that \(K\in \mathscr {B}(\mathscr {H})\), \(\|K\|\leqslant 1\), \(K\geqslant \mathbb {O}\) , and K is injective.
-
(iii)
The operator
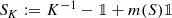 is a self-adjoint extension of S with m(S
K) = m(S) and \(\mathscr {D}(S_K)\subset \mathscr {D}^{\prime }\)
. It is the unique extension of S satisfying the last two properties.
is a self-adjoint extension of S with m(S
K) = m(S) and \(\mathscr {D}(S_K)\subset \mathscr {D}^{\prime }\)
. It is the unique extension of S satisfying the last two properties.
By comparison with Theorem 15 (v) one has that S K is precisely the Friedrichs extension of S: S K = S F.
Corollary 7
Under the assumptions of Theorem 16 , the Friedrichs extension S F (= S K ) of S is characterised by

The uniqueness of the Friedrichs extension (in the sense of Theorem 15(v) or Theorem 16(iii)) implies the additional noticeable property that follows. It is through this property that the Friedrichs extension plays a crucial, albeit somewhat hidden, role in the Tomita–Takesaki duality theory for von Neumann algebras and positive cones [65, §15].
Proposition 6 (The Friedrichs Extension Preserves the Affiliation with a von Neumann Algebra)
-
(i)
Let S be a closed, densely defined, and positive symmetric operator on a Hilbert space \(\mathscr {H}\) and let S F its Friedrichs extension. If U is a unitary operator on \(\mathscr {H}\) that commutes with S, in the sense that \(U\mathscr {D}(S)\subset \mathscr {D}(S)\) and USU ∗ = S on \(\mathscr {D}(S)\) , then U commutes with all the spectral projections of S F.
-
(ii)
More generally, if S is a closed, densely defined, and positive symmetric operator on a Hilbert space \(\mathscr {H}\) affiliated Footnote 4 with a von Neumann algebra \(\mathfrak {M}\) on \(\mathscr {H}\) , then its Friedrichs extension S F too is affiliated with \(\mathfrak {M}\).
The Friedrichs extension of S is a form construction, obtained canonically given the datum S. In contrast, the Kreı̆n-von Neumann extension of S is relative to a chosen reference lower bound to the bottom of S. Up to a trivial shift  for \(\lambda \geqslant 0\) sufficiently large, one can always assume S to be a positive and densely defined symmetric operator and the reference lower bound to be zero.
for \(\lambda \geqslant 0\) sufficiently large, one can always assume S to be a positive and densely defined symmetric operator and the reference lower bound to be zero.
Theorem 17 (Kreı̆n-von Neumann Extension)
Let S be a positive and densely defined symmetric operator on a Hilbert space \(\mathscr {H}\).
-
(i)
Among all positive self-adjoint extensions of S there exists a unique smallest extension S N in the sense of the operator ordering, that is, a unique extension with the property that \(\widetilde {S}\geqslant S_N\) for any positive self-adjoint extension \(\widetilde {S}\) of S. It is called the Kreı̆n-von Neumann extension.
-
(ii)
One has
$$\displaystyle \begin{aligned} \mathscr{D}(S_N)\;&=\;\mathscr{D}(\overline{S})\,+\,\ker S^* \\ S_N(f+u)\;&=\;\overline{S}f\qquad \forall f\in\mathscr{D}(\overline{S}),\;\forall u\in\ker S^* \end{aligned} $$(117)and (recall that \(\mathscr {D}[S]=\mathscr {D}[S_F]\) )
$$\displaystyle \begin{aligned} \mathscr{D}[S_N]\;&=\;\mathscr{D}[S_F]\,+\,\ker S^* \\ S_N[f+u,f^{\prime}+u^{\prime}]\;&=\;S_F[f,f^{\prime}]\qquad \forall f,f^{\prime}\in\mathscr{D}[S_F],\;\forall u,u^{\prime}\in\ker S^*. \end{aligned} $$(118)In particular, \(S_Nu=0\ \forall u\in \ker S^*\).
-
(iii)
If, in addition, S has positive bottom (m(S) > 0), then the sums in (117) and (118) are direct, that is,
$$\displaystyle \begin{aligned} \mathscr{D}(S_N)\;&=\;\mathscr{D}(\overline{S})\,\dotplus\,\ker S^* \\ \mathscr{D}[S_N]\;&=\;\mathscr{D}[S_F]\,\dotplus\,\ker S^*, \end{aligned} $$(119)and S N is the only positive self-adjoint extension of S satisfying the two properties \(\ker S^*\subset \mathscr {D}(S_N)\) and \(S_Nu=0\ \forall u\in \ker S^*\).
Theorem 18 (Kreı̆n-von Neumann Extension: Ando-Nishio Version)
Let S be a positive and densely defined symmetric operator on a Hilbert space \(\mathscr {H}\).
-
(i)
The linear space
$$\displaystyle \begin{aligned} \mathscr{E}(S)\;:=\;\left\{g\in\mathscr{H}\,\left| \begin{array}{c} \exists\,c_g\geqslant 0\mathit{\text{ such that }} \\ |\langle g,Sf\rangle|{}^2\;\leqslant\;c_g\,\langle f,Sf\rangle\;\:\forall f\in\mathscr{D}(S) \end{array}\right.\right\} \end{aligned} $$(120)contains \(\mathscr {D}(S)\) as well as the domain of any positive symmetric extension of S, in particular the domain of the Friedrichs extension S F. \(\mathscr {E}(S)\) is therefore dense in \(\mathscr {H}\).
-
(ii)
The Kreı̆n-von Neumann extension S N of S satisfies
$$\displaystyle \begin{aligned} \mathscr{D}[S_N]\;&=\;\mathscr{D}(S_N^{1/2})\;=\;\mathscr{E}(S) \\ S_N[g]\;&=\;\|S_N^{1/2}g\|{}^2\;=\;\nu(g) \end{aligned} $$(121)where ν(g) := the smallest number c g satisfying, for \(g\in \mathscr {E}(S)\) , the property \(|\langle g,Sf\rangle |{ }^2\leqslant c_g\,\langle f,Sf\rangle \ \forall f\in \mathscr {D}(S)\).
Remark 20
One has \(\nu (g)=\langle g,Sg\rangle \ \forall g\in \mathscr {D}(S)\) and \(\nu (g)=0\ \forall g\in \ker S^*\), consistently with (118) above.
Theorem 18 above has a counterpart when S is positive and symmetric with no a priori assumption on the density of \(\mathscr {D}(S)\) in \(\mathscr {H}\). In this case elementary counter-examples (see, e.g., [60, Example 13.2]) show that symmetry plus semi-boundedness of S is not enough to claim the existence of the Friedrichs extension or any other positive self-adjoint extension. On the other hand, there is a class of positive symmetric operators on \(\mathscr {H}\), with possibly neither dense nor closed domain, for which it is crucial for general theoretical purposes to have conditions that ensure the existence of positive self-adjoint extensions: this is the class of shifted Kreı̆n transforms of positive and densely defined symmetric operators on \(\mathscr {H}\), see Sect. I. Whence the relevance of the following result.
Theorem 19 (Ando-Nishio Bound and Existence Theorem)
Let S be a positive symmetric operator on a Hilbert space \(\mathscr {H}\) whose domain is not necessarily a dense or a closed subspace of \(\mathscr {H}\).
-
(i)
S admits a positive self-adjoint extension on \(\mathscr {H}\) if and only if the set \(\mathscr {E}(S)\) defined in (120) is dense in \(\mathscr {H}\).
-
(ii)
For given γ > 0, S has a bounded positive self-adjoint extension \(\widetilde {S}\) on \(\mathscr {H}\) such that \(\|\widetilde {S}\|\leqslant \gamma \) if and only if \(\|Sf\|{ }^2\leqslant \gamma \langle f,Sf\rangle \) for all \(f\in \mathscr {D}(S)\).
1.3 A.3 Kreı̆n’s Theory
Unlike von Neumann’s theory, Kreı̆n’s extension theory only deals with densely defined symmetric operators that are semi-bounded. In this case the existence of self-adjoint extension(s) is not an issue, as proved by Stone [64, Theorem 9.21] and Friedrichs [19]. In fact, in terms of the tools of von Neumann’s theory, semi-boundedness implies the coincidence of the two deficiency indices.Footnote 5
The Kreı̆n transform

is a bijective map of the set of all positive symmetric operators on a Hilbert space \(\mathscr {H}\) onto the set of all bounded symmetric operators K on \(\mathscr {H}\) for which \(\|K\|\leqslant 1\) and  , where for the operators of both sets the domain is possibly neither densely defined nor closed. In particular, if S is unbounded, then ∥K
S∥ = 1. The inverse map is the inverse Kreı̆n transform
, where for the operators of both sets the domain is possibly neither densely defined nor closed. In particular, if S is unbounded, then ∥K
S∥ = 1. The inverse map is the inverse Kreı̆n transform

In terms of the Kreı̆n transform, S is self-adjoint if and only if K S is self-adjoint. The Kreı̆n transform preserves the operator inclusion:
and on self-adjoint operators it preserves the operator ordering:
Theorem 20 (Kreı̆n’s Theorem on Self-Adjoint Extensions)
Let S be a densely defined and positive symmetric operator on a Hilbert space \(\mathscr {H}\) . Assume further that S is unbounded (otherwise the only self-adjoint extension of S is its operator closure \(\overline {S}\) ).
-
(i)
There is a one-to-one correspondence between the positive self-adjoint extensions of S and the self-adjoint extensions \(\widetilde {K}\) of the Kreı̆n transform K S that are bounded with \(\|\widetilde {K}\|= 1\) . For each such \(\widetilde {K}\) one necessarily has
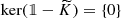 , which makes the inverse Kreı̆n transform of
\(\widetilde {K}\)
well defined. Any such
\(\widetilde {K}\)
identifies, via its inverse Kreı̆n transform, a positive self-adjoint extension
\(\widetilde {S}\)
of S (that is,
\(\widetilde {K}=K_{\widetilde {S}}\)
), and any positive self-adjoint extension of S is of this form.
, which makes the inverse Kreı̆n transform of
\(\widetilde {K}\)
well defined. Any such
\(\widetilde {K}\)
identifies, via its inverse Kreı̆n transform, a positive self-adjoint extension
\(\widetilde {S}\)
of S (that is,
\(\widetilde {K}=K_{\widetilde {S}}\)
), and any positive self-adjoint extension of S is of this form.
-
(ii)
The family of the self-adjoint extensions \(\widetilde {K}\) of K S with \(\|\widetilde {K}\|= 1\) admits two elements, K S,F and K S,N , such that a self-adjoint operator \(\widetilde {K}\) belongs to this family if and only if \(K_{S,N}\leqslant \widetilde {K}\leqslant K_{S,F}\) . The corresponding inverse Kreı̆n transforms of K S,F and K S,N are two positive self-adjoint extensions of S, respectively S F and S N , such that a self-adjoint operator \(\widetilde {S}\) is a positive self-adjoint extension of S if and only if \(S_N\leqslant \widetilde {S}\leqslant S_F\) . S F and S N are nothing but the Friedrichs and the Kreı̆n-von Neumann extensions of S (where the latter is defined with respect to the value zero as a reference lower bound), as given by Theorems 15 and 17.
-
(iii)
In the special case when S has positive bottom (m(S) > 0), for any semi-bounded self-adjoint extension \(\widetilde {S}\) of S one has
$$\displaystyle \begin{aligned} \mathscr{D}[\widetilde{S}]\;&=\;\mathscr{D}[S_F]\,+\,\mathscr{D}[\widetilde{S}]\cap\ker S^*\\ \widetilde{S}[f+u,f^{\prime}+u^{\prime}]\;&=\;S_F[f,f^{\prime}]\,+\,\widetilde{S}[u,u^{\prime}] \\ &\forall f,f^{\prime}\in\mathscr{D}[S_F],\;\forall u,u^{\prime}\in\mathscr{D}[\widetilde{S}]\cap\ker S^*. \end{aligned} $$(126)In particular,
$$\displaystyle \begin{aligned} \widetilde{S}[f,u]\;=\;0\qquad \forall f\in\mathscr{D}[S_F],\quad \forall u\in\mathscr{D}[\widetilde{S}]\cap\ker S^* \end{aligned} $$(127)and
$$\displaystyle \begin{aligned} \widetilde{S}\,\geqslant\,0\qquad \Leftrightarrow\qquad \widetilde{S}[u,u]\,\geqslant\,0\quad \forall u\in\mathscr{D}[\widetilde{S}]\cap\ker S^*. \end{aligned} $$(128)The sum in (126) is direct for any positive self-adjoint extension of S:
$$\displaystyle \begin{aligned} \mathscr{D}[\widetilde{S}]\;=\;\mathscr{D}[S_F]\,\dotplus\,\mathscr{D}[\widetilde{S}]\cap\ker S^*\qquad (m(S)>0,\;m(\widetilde{S})\geqslant 0)\,. \end{aligned} $$(129)
Remark 21
In part (iii) of Theorem 20 above one actually first establishes (127), which is an independent result, valid for any semi-bounded extension of a bottom-positive and densely defined symmetric operator S (see, e.g., [34, Lemma 8]). This automatically implies \(\widetilde {S}[f+u,f^{\prime }+u^{\prime }]=S_F[f,f^{\prime }]\,+\,\widetilde {S}[u,u^{\prime }]\) in (126). The decomposition \(\mathscr {D}[\widetilde {S}]=\mathscr {D}[S_F]+\mathscr {D}[\widetilde {S}]\cap \ker S^*\) in (126) requires an additional analysis, but in the special case of positive self-adjoint extensions it is a straightforward consequence of \(S_N\leqslant \widetilde {S}\leqslant S_F\) given by part (ii) and of the property (118) for the domain of S N. In the general case of semi-bounded extensions, the route to \(\mathscr {D}[\widetilde {S}]=\mathscr {D}[S_F]+\mathscr {D}[\widetilde {S}]\cap \ker S^*\) (see, e.g., [34, Lemma 7 and Theorem 15]), goes through (118) again and the structural property
for the domain of S ∗. For the relevance of the technique used to establish (130) we have included it, together with its proof, in the main part of this article (Sect. 2.2, Lemma 1).
Remark 22
Without the assumption m(S) > 0, the decomposition (126) for \(\mathscr {D}[\widetilde {S}]\) fails to be true for arbitrary semi-bounded extensions of S: the inclusion \(\mathscr {D}[\widetilde {S}]\supset \mathscr {D}[S_F]+\mathscr {D}[\widetilde {S}]\cap \ker S^*\) remains trivially valid, but can be proper.
Remark 23
The Kreı̆n transform reduces the (difficult) problem of describing all positive self-adjoint extensions of S to the (possibly easier) problem of finding all the self-adjoint extensions of K S with unit norm. The price, though, is that K S is not necessarily densely defined in \(\mathscr {H}\), which makes the search for the “minimal” extension K S,N and the “maximal” extension K S,F of K S on \(\mathscr {H}\) different from the “ordinary” extension theory of densely defined symmetric operators. A more explicit identification of K S,N and K S,F is due to Ando and Nishio [5] (and further developments) and proceeds as follows.
-
One considers the positive symmetric operators
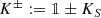 with common domain \(\mathscr {D}(K_S)\).
with common domain \(\mathscr {D}(K_S)\). -
Although \(\mathscr {D}(K_S)\) is not necessarily dense (which prevents one from introducing the Friedrichs extension), from the elementary inequality \(\|K^\pm x\|{ }^2\leqslant 2\langle x,K^\pm x\rangle \ \forall x\in \mathscr {D}(K^\pm )\) one sees that they satisfy a Ando-Nishio bound as in Theorem 19(ii).
-
Therefore, both K + and K − admit a bounded positive self-adjoint extension on \(\mathscr {H}\) with norm below 2, whence also (Theorem 17(ii)) the smallest positive self-adjoint extension \(K^{\pm }_N\), for which \(\|K^{\pm }_N\|\leqslant 2\) too.
-
One then checks that among all the self-adjoint extensions \(\widetilde {K}\) of K S on \(\mathscr {H}\) which are bounded with \(\|\widetilde {K}\|= 1\), the extension
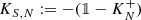 is the smallest and
is the smallest and 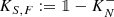 is the largest.
is the largest. -
The corresponding inverse Kreı̆n transforms
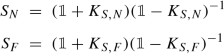 (131)
(131)are self-adjoint extensions of S (Theorem 20(i)) that, because of (125), are, respectively, the Kreı̆n-von Neumann and the Friedrichs extension of S.
Rights and permissions
Copyright information
© 2021 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Gallone, M., Michelangeli, A., Ottolini, A. (2021). Kreı̆n-Višik-Birman Self-Adjoint Extension Theory Revisited. In: Michelangeli, A. (eds) Mathematical Challenges of Zero-Range Physics. Springer INdAM Series, vol 42. Springer, Cham. https://doi.org/10.1007/978-3-030-60453-0_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-60453-0_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-60452-3
Online ISBN: 978-3-030-60453-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)




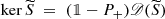
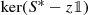 and
and 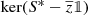 have the same finite dimension, it is easy to conclude that all self-adjoint extensions of S are bounded below, see, e.g., the Proposition on page 179 of [
have the same finite dimension, it is easy to conclude that all self-adjoint extensions of S are bounded below, see, e.g., the Proposition on page 179 of [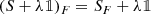 for
for 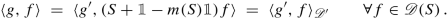
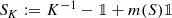 is a self-adjoint extension of S with m(S
K) = m(S) and
is a self-adjoint extension of S with m(S
K) = m(S) and 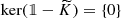 , which makes the inverse Kreı̆n transform of
, which makes the inverse Kreı̆n transform of
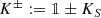 with common domain
with common domain 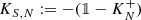 is the smallest and
is the smallest and 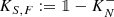 is the largest.
is the largest.