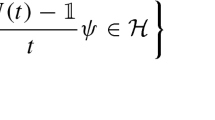Complex-self-adjointness

Abstract

We develop the concept of operators in Hilbert spaces which are similar to their adjoints via antiunitary operators, the latter being not necessarily involutive. We discuss extension theory, refined polar and singular-value decompositions, and antilinear eigenfunction expansions. The study is motivated by physical symmetries in quantum mechanics with non-self-adjoint operators.

1 Introduction

A fundamental postulate of quantum mechanics says that physical observables are represented by self-adjoint operators in Hilbert spaces. It does not mean that quantum theory is free of non-self-adjoint operators. For instance, physical symmetries are represented by unitary and antiunitary operators. There are also quantum open systems which are conveniently modelled by non-self-adjoint operators; more generally, the latter arise in many other areas of physics where the time evolution is not conservative. What is more, recent years have brought motivations for considering unconventional representations of observables by possibly non-self-adjoint operators which are however similar to self-adjoint operators (see [2] for a mathematical overview).

To cover these more general circumstances in the recent developments of quantum mechanics, the concept of linear operators H satisfying the complex-self-adjointness relation

$$\begin{aligned} H^* = C H C^{-1} \end{aligned}$$

(1)

with an antiunitary C was proposed in [3, 15, 16]. Here the physical meaning of C is typically a time-reversal symmetry or its composition with the parity and charge symmetries.

If C is involutive, i.e. $C^2=I$ (so that $C^{-1}=C$), then C is called conjugation and the operators satisfying (1) are sometimes called C-self-adjoint (see [11, Sect. I.4] and [6, Sect. III.5]). This class of operators represent a well studied area of functional analysis, notably due to the highly influential works of Garcia and Putinar [9, 10] (see also [18] and the excellent survey [8]).

However, it was pointed out in [15] that the involutive requirement about C is too restrictive once the spin is taken into account. Indeed, the time-reversal operator for fermionic systems modelled by the Pauli or Dirac operators is rather anti-involutive, i.e. $C^2=-I$. To cover these and other circumstances, the more general identity (1) was proposed in [15] (see also [16, Sect. 5.2.5.4]). Unfortunately, despite the prevailing physical motivations, there seem to be no systematic theory of the general complex-self-adjoint operators and the objective of this paper is precisely to initiate to fill in this gap.

The organisation of this paper is as follows. In Sect. 2, we introduce the concept of complex-symmetric and complex-self-adjoint operators and summarise their basic properties. The extension theory for symmetric and complex-symmetric operators is discussed in Sect. 3. We manage to go beyond the involutive approach of [6, Sect. III.5] in several directions, however, the question whether any C-symmetric operator admits a C-self-adjoint extension remains open (unless C is involutive). In Sect. 4, we extend the results of [10] about refined polar decompositions for C-self-adjoint operators to the present general setting. In Sects. 5 and  6, we try to extend the results of [10] about refined singular-value decompositions for compact C-self-adjoint operators and antilinear eigenfunction expansions for C-self-adjoint operators with compact resolvents, respectively. However, we manage to do so only under an extra hypothesis about the simplicity of the singular values. In Sect. 7 we present an operator in the spinorial Hilbert space $L^2(\mathbb {R};\mathbb {C}^2)$ which is complex-symmetric but for which there is no obvious involutive conjugation. Further illustrations, including examples in model spaces, are given in Sect. 8.

2 Definitions and basic properties

Let $\mathcal {H}$ be a complex separable Hilbert space; the norm and the inner product are denoted by $\Vert \cdot \Vert$ and $(\cdot ,\cdot )$, respectively, and our convention is that the latter is linear in the second component. A linear (respectively, antilinear) operator A in $\mathcal {H}$ is a function which sends every vector $\psi$ in a (linear) subspace $\textsf{D}(A) \subset \mathcal {H}$ called the domain of A to a vector $A\psi \in \mathcal {H}$ and satisfies the additivity condition $A(\phi + \psi ) = A\phi + A\psi$ for every $\phi , \psi \in \textsf{D}(A)$ together with the homogeneity (respectively, antihomogeneity) condition $A(\alpha \psi ) = \alpha A\psi$ (respectively, $A(\alpha \psi ) = \bar{\alpha }A\psi$ ) for every $\psi \in \textsf{D}(A)$ and $\alpha \in \mathbb {C}$. If $\textsf{D}(A) = \mathcal {H}$, the operator A is said to be defined on $\mathcal {H}$. We denote the range and kernel of A by $\textsf{R}(A)$ and $\textsf{N}(A)$, respectively.

An operator A on $\mathcal {H}$ is said to be isometric if it preserves the norm: $\Vert A\psi \Vert = \Vert \psi \Vert$ for every $\psi \in \mathcal {H}$. By the polarisation identity, it follows that $(A\phi ,A\psi ) = (\phi ,\psi )$ (respectively, $(A\phi ,A\psi ) = (\psi ,\phi )$) for every $\phi ,\psi \in \mathcal {H}$, provided that A is linear (respectively, antilinear). In either case, the adjoint of A coincides with the left inverse of A. More specifically, in distinction to some recent papers (see, e.g., [5, 14]), we use the same notation $A^*$ for the adjoint of any densely defined operator A: it satisfies $(\phi ,A\psi ) = (A^*\phi ,\psi )$ (respectively, $(\phi ,A\psi ) = \overline{(A^*\phi ,\psi )}$), for every $\psi \in \textsf{D}(A)$ and $\phi \in \textsf{D}(A^*)$, if A is linear (respectively, antilinear). Then the left-inverse property for the isometric operator A precisely means that $A^*A = I$, where I stands for the identity operator on $\mathcal {H}$. If, in addition, $\textsf{R}(A) = \mathcal {H}$, then A is called unitary or antiunitary depending on whether A is linear or antilinear, respectively. Then the adjoint of A coincides with the right inverse of A too, i.e. $AA^* = I$. In summary, A is bijective as an operator on $\mathcal {H}$ onto $\mathcal {H}$ and $A^{-1} = A^*$ if A is unitary or antiunitary. Any unitary or antiunitary operator A is bounded and boundedly invertible, in fact $\Vert A\Vert = 1 = \Vert A^{-1}\Vert$.

In the sequel, H stands for a generic linear operator in $\mathcal {H}$.

Definition 1

We say that H is complex-symmetric with respect to C (or briefly C-symmetric) if H is densely defined and there exists an antiunitary operator C in $\mathcal {H}$ such that the adjoint $H^*$ is an extension of $CHC^{-1}$, i.e. $CHC^{-1} \subset H^*$.

We say that H is complex-self-adjoint with respect to C (or briefly C-self-adjoint) if H is densely defined and there exists an antiunitary operator C in $\mathcal {H}$ such that $CHC^{-1} = H^*$.

We say that H is complex-symmetric (respectively, complex-self-adjoint) if there exists an antiunitary operator with respect to which it is complex-symmetric (respectively, complex-self-adjoint).

Remark 1

Since we allow for the concise notations “C-symmetric” and “C-self-adjoint”, it is important to emphasise that our definition generalises the usual concepts of just involutive antiunitary C (see [11, Sect. I.4] and [6, Sect. III.5] for the traditional references); in this special case, C is called conjugation. Occasionally, we shall use the same terminology in the present more general setting when C is not necessarily involutive.

At the same time, we warn the reader that the same notation is used in the theory of Krein spaces where C is a linear involution (see, e.g., [1]). Even more confusingly, in physics literature, the property of H being “C-symmetric” (with C unitary or antiunitary) occasionally means the commutation relation $[C,H]=0$ (which precisely means $CH = HC$). We refer to [16, Sect. 5.2.5] for an overview of these different notions.

The C-self-adjointness of H particularly requires that $C:\textsf{D}(H) \rightarrow \textsf{D}(H^*)$ is a bijection. Obviously, H is C-self-adjoint, if, and only if, $H^*$ is $C^{-1}$-self-adjoint.

If C is antiunitary, it is easily seen that

$$\begin{aligned} (\phi ,C\psi ) = (\psi ,C^{-1}\phi ) \end{aligned}$$

(2)

for every $\phi ,\psi \in \mathcal {H}$. Furthermore, for any densely defined linear operator H, it is easily shown that

$$\begin{aligned} (CHC^{-1})^* = CH^*C^{-1} \,. \end{aligned}$$

(3)

It follows that H is C-symmetric if, and only if, $H \subset C^{-1}H^*C = (C^{-1}HC)^*$ and this implies that H is closable, the closure being also C-symmetric. At the same time, by the closedness of the adjoint, any complex-self-adjoint operator is automatically closed.

Recall that the spectrum $\sigma (H)$ of any closed linear operator H in $\mathcal {H}$ is the set of those complex numbers $\lambda$ for which $H-\lambda I:\textsf{D}(H)\rightarrow \mathcal {H}$ is not bijective. The resolvent set is the complement $\rho (H):=\mathbb {C}\setminus \sigma (H)$. The point spectrum $\sigma _{\textrm{p}}(H)$ of H is the set of eigenvalues of H (i.e. the operator $H-\lambda I$ is not injective). For the surjectivity, one says that $\lambda \in \sigma (H)$ belongs to the continuous spectrum $\sigma _{\textrm{c}}(H)$ (respectively, residual spectrum $\sigma _{\textrm{r}}(H)$) of H if $\lambda \not \in \sigma _\textrm{p}(H)$ and the closure of the range $\textsf{R}(H-\lambda I)$ equals $\mathcal {H}$ (respectively, the closure is a proper subset of $\mathcal {H}$). If H is densely defined, then $\textsf{N}(H^*) = \textsf{R}(H)^\bot$, where $\bot$ denotes the orthogonal complement; consequently, one has the general characterisation

$$\begin{aligned} \sigma _{\textrm{r}}(H) = \left\{ \lambda \not \in \sigma _{\textrm{p}}(H): \ \bar{\lambda } \in \sigma _{\textrm{p}}(H^*)\right\} \,. \end{aligned}$$

(4)

It is well known that the residual spectrum of any self-adjoint operator is empty. It turns out that the same holds true for complex-self-adjoint operators. In the context of applications in quantum mechanics, this simple observation goes back to [3] and [15] in the involutive and the general case, respectively.

Proposition 1

Let H be a linear operator which is complex-self-adjoint. Then

$$\begin{aligned} \sigma _{\textrm{r}}(H) = \varnothing \,. \end{aligned}$$

Proof

Let H satisfy (1) with some antiunitary operator C. Then $\lambda$ is an eigenvalue of H (with eigenvector $\psi \in \textsf{D}(H)$) if, and only if, $\bar{\lambda }$ is an eigenvalue of $H^*$ (with eigenvector $C\psi \in \textsf{D}(H^*)$). So the absence of elements in the residual spectrum follows from the general formula (4). $\square$

3 Extension theory

The nullity (respectively, deficiency) of a linear operator H in $\mathcal {H}$ is $\textsf{nul}(H) := \dim \textsf{N}(H)$ (respectively, $\mathrm {\textsf{def}}(H) := \mathop {\textrm{codim}}\nolimits \textsf{R}(H)$). Recall that the codimension of a subspace $\mathcal {H}' \subset \mathcal {H}$ is defined as the dimension of the quotient space $\mathcal {H}/\mathcal {H}'$. If $\mathcal {H}'$ is closed, then $\mathop {\textrm{codim}}\nolimits \mathcal {H}' = \dim \mathcal {H}'^\bot$, where $\bot$ denotes the orthogonal complement.

If H is closed, it is well known (see, e.g., [6, Thm. III.2.3]) that $\mathrm {\textsf{def}}(H - \lambda I)$ is constant in each connected component of the exterior of the numerical range of H. In particular, if H is symmetric (i.e. H is densely defined and $H \subset H^*$), then the deficiency indices:

$$\begin{aligned} \textsf{m}_\pm (H) := \mathrm {\textsf{def}}(H - \lambda I) \,, \qquad \lambda \in \mathbb {C}_\mp := \{\lambda \in \mathbb {C}: \Im \lambda \lessgtr 0 \} \end{aligned}$$

are well defined and constant. By extension theory of symmetric operators (see, e.g., [6, Sect. III.4]), a symmetric operator H admits a self-adjoint extension if, and only if, $\textsf{m}_+(H) = \textsf{m}_-(H)$; H is self-adjoint if, and only if, $\textsf{m}_+(H) = 0 = \textsf{m}_-(H)$.

There are well-known examples of symmetric operators which do not admit any self-adjoint extension. It is interesting that these pathological situations can be excluded for operators admitting an antiunitary symmetry in the sense of the following definition.

Definition 2

We say that H is real with respect to C (or briefly C-real) if there exists an antiunitary operator C in $\mathcal {H}$ such that $CHC^{-1} = H$.

Remark 2

The definition is an extension of the terminology of [6, Thm. III.5.1] to not necessarily involutive operators C. In physical terms, the present general notion is equivalent to the commutation relation $[C,H]=0$ (cf. Remark 1).

The following theorem is an extension of [6, Thm. III.5.3], where the symmetry C was assumed to be involutive.

Theorem 1

Let H be a closed symmetric operator which is C-real. Then $\mathsf {\textsf{m}}_+(H) = \mathsf {\textsf{m}}_-(H)$. Consequently, H admits a self-adjoint extension.

Proof

Since H is C-real, it follows from (3) that also the adjoint $H^*$ is C-real. Note also that the range $\textsf{R}(H-\lambda I)$ is closed for $\lambda \in \mathbb {C}_\pm$. Consequently,

$$\begin{aligned} \begin{aligned} \mathcal {H}/ \textsf{R}(H + i I) \cong \textsf{R}(H + i I)^\bot&= \textsf{N}(H^* - i I) \\&= \textsf{N}((CHC^{-1})^*-iI) \\&= \textsf{N}(CH^*C^{-1}-iI) \\&= \textsf{N}(C(H^*+iI)C^{-1}) \\&= C \textsf{N}(H^*+iI) \,. \end{aligned} \end{aligned}$$

Since $\textsf{m}_\pm (H) = \dim \textsf{N}(H^* \mp i I)$ and C is a bijection, we have $\textsf{m}_+(H) = \textsf{m}_-(H)$. $\square$

We now turn to complex-symmetric operators. The following simple observation is an extension of [6, Lem. III.5.4], where the operator is assumed to be complex-symmetric/complex-self-adjoint with respect to (involutive) conjugations.

Lemma 1

Let H be a closed complex-symmetric operator. Then, for any $\lambda \in \mathbb {C}$,

(5)

so

If H is complex-self-adjoint, the inclusion and the inequality become equalities.

Proof

If H is C-symmetric, then $H \subset C^{-1} H^* C$, so for $f \in \textsf{D}(H)$

$$\begin{aligned} \begin{aligned} (H-\lambda I)f = 0&\Longleftrightarrow (C^{-1}H^*C-\lambda I)f = 0 \\&\Longleftrightarrow C^{-1}(H^*-\bar{\lambda }I)C f =0 \\&\Longleftrightarrow (H^*-\bar{\lambda }I)C f =0 \\&\Longleftrightarrow f \in C^{-1} \textsf{N}(H^*-\bar{\lambda }I) \,. \end{aligned} \end{aligned}$$

Thus, (5) holds. If H is C-self-adjoint, then $H = C^{-1} H^* C$, so $f \in \textsf{D}(H)$ if, and only if, $Cf \in \textsf{D}(H^*)$, therefore we have equality in (5). $\square$

Before we proceed further, let us recall (see, e.g., [6, Def. III.2.5]) that the field of regularity $\Pi (H)$ of H is defined as the set of complex points $\lambda$ for which there exist positive constants $k_\lambda$ such that $\Vert (H-\lambda I) \psi \Vert \ge k_\lambda \Vert \psi \Vert$ for all $\psi \in \textsf{D}(H)$. If H is closed, then $\Pi (H)$ coincides with the set of points $\lambda$ for which $\textsf{R}(H-\lambda I)$ is closed and $\textsf{nul}(H-\lambda I)=0$. In this case, $\lambda \mapsto \mathrm {\textsf{def}}(H-\lambda I)$ is constant in any connected component of $\Pi (H)$.

Now we are in a position to state the following generalisation of [6, Thm. III.5.5].

Theorem 2

A closed C-symmetric operator is C-self-adjoint if, and only if, $\mathsf {\textsf{def}}(H-\lambda I)=0$ for some, and hence all, $\lambda \in \Pi (H)$.

Proof

If H is complex-self-adjoint and $\lambda \in \Pi (H)$, then $\textsf{R}(H-\lambda I)$ is closed and Lemma 1 implies

$$\begin{aligned} \mathrm {\textsf{def}}(H-\lambda I) = \textsf{nul}(H^*-\bar{\lambda }I) = \textsf{nul}(H-\lambda I) =0 \,. \end{aligned}$$

Conversely, suppose that $\mathrm {\textsf{def}}(H-\lambda I)=0$ for some $\lambda \in \Pi (H)$. Then $\textsf{R}(H-\lambda I)=\mathcal {H}$ and

$$\begin{aligned} \textsf{R}(CHC^{-1}-\bar{\lambda }I) = \textsf{R}(C(H-\lambda I)C^{-1}) = \mathcal {H}\,. \end{aligned}$$

(6)

If $CHC^{-1} \not = H^*$, there exists a non-zero $\psi \in \textsf{D}(H^*) \setminus \textsf{D}(CHC^{-1})$. From (6),

$$\begin{aligned} (H^* - \bar{\lambda }I)\psi = (CHC^{-1}-\bar{\lambda }I) \phi \end{aligned}$$

for some $\phi \in \textsf{D}(CHC^{-1})$ and since $CHC^{-1} \subset H^*$ we have $(H^* - \bar{\lambda }I) (\psi -\phi ) = 0$. That is, $\psi -\phi \in \textsf{N}(H^* - \bar{\lambda }I)$. But $\textsf{N}(H^* - \bar{\lambda }I) = \textsf{R}(H - \lambda I)^\bot = \{0\}$ and consequently $\psi = \phi \in \textsf{D}(CHC^{-1})$, contradicting the hypothesis that $CHC^{-1} \not = H^*$. $\square$

Now, following [6, Sect. III.5.2], given a C-symmetric operator H, we define $A:=H$ and $B:=C^{-1} H C$. Then, for every $\psi \in \textsf{D}(A) = \textsf{D}(H)$ and $\phi \in \textsf{D}(B) = C^{-1}\textsf{D}(H)$, one has

$$\begin{aligned} (\phi ,A\psi ) = (\phi ,C^{-1}H^*C\psi ) = (H^*C\psi ,C\phi ) = (C\psi ,HC\phi ) = (B\phi ,\psi ) \,, \end{aligned}$$

where the second and last equalities employ (2). Hence, A and B are adjoint to each other. Also if $\lambda \in \Pi (A)$ and $\psi \in \textsf{D}(B)$,

$$\begin{aligned} \Vert (B-\bar{\lambda })\psi \Vert = \Vert C^{-1}(H-\lambda I)C\psi \Vert \ge k_\lambda \;\! \Vert C\psi \Vert = k_\lambda \;\! \Vert \psi \Vert \,, \end{aligned}$$

so that $\bar{\lambda }\in \Pi (B)$. Then the theory of extensions of closed operators (see [6, Sect. III.3]) yields the general formulae

$$\begin{aligned} \begin{aligned} \textsf{D}(B^*)&= \textsf{D}(A) \dot{+} \textsf{N}((A^*-\bar{\lambda }I)(B^*-\lambda I)) \,, \\ \textsf{D}(A^*)&= \textsf{D}(B) \dot{+} \textsf{N}((B^*-\lambda I)(A^*-\bar{\lambda }I)) \,. \end{aligned} \end{aligned}$$

Moreover, if $\mathrm {\textsf{def}}(A-\lambda I)$ and $\mathrm {\textsf{def}}(B-\bar{\lambda }I)$ are finite, then

$$\begin{aligned} \dim (\textsf{D}(B^*)/\textsf{D}(A)) = \dim (\textsf{D}(A^*)/\textsf{D}(B)) = \mathrm {\textsf{def}}(A-\lambda I) + \mathrm {\textsf{def}}(B-\bar{\lambda }I)\ \,. \end{aligned}$$

In our case, if $\lambda \in \Pi (H)$, then

$$\begin{aligned} \begin{aligned} \mathrm {\textsf{def}}(A-\lambda I)&= \textsf{nul}(H^*-\bar{\lambda }I) \\&= \textsf{nul}(C^{-1}(H^*-\bar{\lambda }I)C) \\&= \textsf{nul}(C^{-1}H^*C-\lambda I) \\&= \mathrm {\textsf{def}}((C^{-1}H^*C)^*-\bar{\lambda }I) \\&= \mathrm {\textsf{def}}(B-\bar{\lambda }I) \,. \end{aligned} \end{aligned}$$

We therefore obtain the following generalisation of [6, Thm. III.5.6].

Theorem 3

Let H be a closed C-symmetric operator with $\Pi (H) \not = \varnothing$. Then, for any $\lambda \in \Pi (H)$,

If $\mathsf {\textsf{def}}(H-\lambda I) < \infty$,

An immediate consequence of this theorem is the following generalisation of [6, Thm. III.5.7].

Corollary 1

If H is a closed complex-symmetric operator, then $\lambda \mapsto \mathsf {\textsf{def}}(H-\lambda I)$ is constant on $\Pi (H)$.

We leave as an open problem whether any C-symmetric operator has a C-self-adjoint extension. This is well known to hold if C is involutive (see [6, Thm. III.5.8]). However, the proof of [6, Thm. III.5.8] does not seem to extend to the general situation of the present paper.

4 Refined polar decomposition

Following [12, Sect. V.2.2], we first extend the notion of isometric operators introduced above. We say that a (linear or antilinear) operator A defined on $\mathcal {H}$ is partially isometric if there exists a closed subspace $\mathcal {M} \subset \mathcal {H}$ such that $\Vert A\psi \Vert =\Vert \psi \Vert$ for $\psi \in \mathcal {M}$ while $A\psi = 0$ for $\psi \in \mathcal {M}^\bot$. The closed subspaces $\mathcal {M}$ and $\mathcal {M}':=A\mathcal {M}$ are called the initial and final sets of A, respectively. Then we say that a partially isometric operator A is partially unitary or partially antiunitary depending on whether A is linear or antilinear, respectively.

It is well known (see, e.g., [12, Sect. VI.2.7]) that any densely defined, closed linear operator H in $\mathcal {H}$ admits a unique polar decomposition $H = U|H|$, where $|H|:=(H^*H)^{1/2}$ is non-negative and U is partially unitary with the initial set $\overline{\textsf{R}(|H|)}$ and the final set $\overline{\textsf{R}(H)}$. One has $\textsf{D}(|H|) = \textsf{D}(H)$ and $\textsf{N}(|H|) = \textsf{N}(H)$. At the same time, the polar decomposition of the adjoint reads $H^* = |H| U^*$.

The following refinement shows that if H is complex-self-adjoint, then U is also complex-self-adjoint (with respect to the same antiunitary operator C). Furthermore, U is a composition of another partially antiunitary operator commuting with H and the inverse of the original antiunitary operator. In the case of involutive antiunitary operators C, the result is due to [10, Thm. 2 & Thm. 9] and [10, Thm. 9]. If H is unbounded, however, it is assumed as an extra hypothesis in [10, Thm. 9] that zero is in the resolvent set of H. In our version of the theorem below, C does not need to be involutive and H can be unbounded without any further properties.

Theorem 4

Let H be a linear operator which is C-self-adjoint. Then

$$\begin{aligned} H = C^{-1}J|H| \,, \end{aligned}$$

(7)

where J is a partially antiunitary operator with the initial set and the final set , which commutes with |H|.

Before proving the theorem, let us argue that the result indeed implies that the partially unitary map from the polar decomposition of H is complex-self-adjoint.

Corollary 2

Let H be a linear operator which is C-self-adjoint. If $H = U |H|$ is its polar decomposition, then U is C-self-adjoint, too.

Proof

By Theorem 4, one has $U=C^{-1} J$. The complex-self-adjointness of H, identity (7) and the commutativity of |H| and J imply $H^* = CHC^{-1} = J|H|C^{-1} = |H|JC^{-1} = |H| U^*$. From this and the uniqueness of the polar decomposition of $H^*$, we deduce that $U^* = J C^{-1} = C U C^{-1}$, which is the desired claim. $\square$

The “hidden symmetry” J shares the same involutive properties as the “obvious symmetry” C.

Corollary 3

Assume the hypotheses and notations of Theorem 4. If C is involutive (respectively, anti-involutive), then the restriction of J on is involutive (respectively, anti-involutive).

Proof

As in the proof of the previous corollary, one has $U^* = JC^{-1}$ where $U:=C^{-1}J$. Consequently, for every $\psi \in \overline{\textsf{R}(|H|)}$, one has $J^2\psi = U^*CCU \psi = \pm U^*U \psi = \pm \psi$, where the plus (respectively, minus) sign holds if C is involutive (respectively, anti-involutive). $\square$

Now we proceed with the proof of Theorem 4.

Proof of Theorem 4

We extend the proof of [10, Thm. 2] to the case of C being not necessarily involutive. Write the polar decomposition $H = U|H|$ and note that the complex-self-adjointness of H implies

$$\begin{aligned} H = C^{-1} H^* C = C^{-1} |H| U^* C = C^{-1} (U^*U) |H| U^* C = \underbrace{(C^{-1} U^* C)}_{=:W} \underbrace{(C^{-1} U |H| U^* C)}_{=:A} \,. \end{aligned}$$

(8)

Here the last but one equality employs that $U^*U\psi = \psi$ for every $\psi \in \overline{\textsf{R}(|H|)}$, the initial set of U.

First, we observe that W is partially isometric. Indeed, using that $W^* = C^{-1}UC$, it is easily seen that $WW^*W = C^{-1} U^*UU^* C = W$, so the desired property holds due to the criterion [12, Prob. V.2.6]. Second, we claim that A is non-negative. Indeed, using (2), one has $(\psi ,A\psi ) = (U|H|U^*C\psi ,C\psi ) = (U^*C\psi ,|H|U^*C\psi )$ for every $\psi \in \textsf{D}(H)$, so the desired property follows by the non-negativity of |H|. Then the strategy of the proof is to show that the initial set of W coincides with the initial set of U. By the uniqueness of the polar decomposition of H, it will allow us to conclude that

$$\begin{aligned} W=U \qquad \text{ and } \qquad A=|H| \,. \end{aligned}$$

(9)

To show that the initial set of W coincides with the initial set of U, it is enough to prove that $\textsf{N}(W) = \textsf{N}(U) = \textsf{N}(H)$. Obviously, $\textsf{N}(W) = \textsf{N}(U^*C)$. At the same time, $\textsf{N}(A) = \textsf{N}(U |H| U^* C) = \textsf{N}(|H| U^* C) = \textsf{N}(U^* C) \,,$ where the last two equalities hold due to the facts that U and $U^*$ have $\overline{\textsf{R}(H)}$ as their initial and final sets, respectively, and the last equality also employs that |H| is self-adjoint. Hence, $\textsf{N}(W) = \textsf{N}(A)$. It remains to show that $\textsf{N}(A)=\textsf{N}(H)$. The inclusion $\textsf{N}(A) \subset \textsf{N}(H)$ is clear from (8). Conversely, if $\psi \in \textsf{N}(H)$, then (8) implies that $\psi \in \textsf{N}(A)$ or $A\psi \in \textsf{N}(W)$. But the latter is impossible unless $A\psi = 0$, because of the previously established fact $\textsf{N}(W) = \textsf{N}(A)$ and the self-adjointness of A. In summary, we have proved (9).

The first equality of (9) shows that U is C-self-adjoint. Moreover, defining $J:=CU$, one has $J=U^*C$. It follows that J is partially antiunitary with $\overline{\textsf{R}(|H|)}$ being both the initial and the final set. As a consequence of the second equality of (9) and the formula $J^{-1} = C^{-1}U$, one has $|H| = J^{-1}|H|J$. Hence, $J|H| = |H|J$, so J commutes with |H|. $\square$

5 Refined singular-value decomposition

We now turn to compact operators. Before stating and proving the refined singular-value decomposition, we establish an elementary result.

Lemma 2

Let $m \in \mathbb {N}^* := \mathbb {N}\setminus \{0\}$. Let $\mathcal {E}$ be an m-dimensional subspace of $\mathcal {H}$, let J be an antiunitary operator on $\mathcal {E}$ and assume that $\mathcal {E}$ is invariant under J. There exists an orthonormal basis $(\phi _1,\dots ,\phi _m)$ of $\mathcal {E}$ which is fixed by J, i.e. $J\phi _j=\phi _j$ for every $j \in \{1,\dots ,m\}$, provided one of the following conditions hold:

• (i) J is involutive;

• (ii) $m=1$.

Proof

The situation (i) is well known (see, e.g., [9, Lem. 1]), so we only prove (ii). Let $\psi \in \mathcal {E}$ be such that $\Vert \psi \Vert =1$. Since $\mathcal {E}=\mathop {\textrm{span}}\nolimits (\psi )$ in invariant under isometric J, there exists $\alpha \in \mathbb {R}$ such that $J\psi = e^{i\alpha }\psi$. Let us define $\phi := e^{i\beta }\psi$, where $\beta \in \mathbb {R}$ is to be chosen by requiring $J\phi =\phi$. An obvious solution is given by $\beta :=\alpha /2$. $\square$

Remark 3

The conclusion of Lemma 2 does not hold for a general non-involutive antiunitary J unless the extra hypothesis (ii) is assumed. Indeed, since $\mathcal {E}$ is invariant under the isometry J, it is easily seen that, if $(\psi _1,\dots ,\psi _m)$ is an orthonormal basis of $\mathcal {E}$, then $(J\psi _1,\dots ,J\psi _m)$ is one, too. Hence, there exist complex numbers $a_{jk}$ with $j,k \in \{1,\dots ,m\}$ such that $J\psi _k = \sum _{j=1}^m a_{jk}\psi _j$ and the matrix $A:=(a_{jk})$ is unitary. In fact, $a_{jk}=(\psi _j,J\psi _k)$. Let $B:=(b_{jk})$ be another unitary matrix and set $\phi _{k}:=\sum _{j=1}^m b_{jk}\psi _j$. Then the requirement $J\phi _j = \phi _j$ for every $j \in \{1,\dots ,m\}$ is equivalent to the matrix identity

$$\begin{aligned} B^* A \bar{B} = I \,, \end{aligned}$$

(10)

where I denotes the identity matrix in $\mathbb {C}^{m \times m}$. Using the unitarity of B, (10) is equivalent to $A \bar{B} = B$. Since $\bar{B}^T=B^*=B^{-1}=(\det B)^{-1} (\mathop {\textrm{cof}}\nolimits B)^T$, where $\mathop {\textrm{cof}}\nolimits B$ denotes the cofactor matrix of B, it follows that (10) is equivalent to

$$\begin{aligned} A \mathop {\textrm{cof}}\nolimits B = (\det B) B \,. \end{aligned}$$

(11)

If $m=2$, then (11) can be written as the homogeneous system

$$\begin{aligned} \begin{pmatrix} -\det B &{} -a_{12} &{} 0 &{} a_{11} \\ a_{12} &{} -\det B &{} -a_{11} &{} 0 \\ 0 &{} -a_{22} &{} -\det B &{} a_{21} \\ a_{22} &{} 0 &{} -a_{21} &{} -\det B \end{pmatrix} \begin{pmatrix} b_{11} \\ b_{12} \\ b_{21} \\ b_{22} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \end{pmatrix} \,. \end{aligned}$$

A necessary condition to guarantee the existence of a non-trivial solution is that the determinant of the square matrix equals zero:

$$\begin{aligned} (\det A)^2 + (\det B)^4 - (\det B)^2 \, (2 a_{11}a_{22}-a_{12}^2-a_{21}^2) = 0 \,. \end{aligned}$$

Using that (10) implies $(\det B)^2 = \det A$, the last condition reads

$$\begin{aligned} \det A \, (a_{12} - a_{21})^2 = 0 \,, \end{aligned}$$

whence $a_{12} = a_{21}$. Using the antiunitarity of J (cf. (2)), this symmetry requirement is equivalent to $(\psi _1,J\psi _2) = (\psi _1,J^{-1}\psi _2)$, which cannot be guaranteed in general unless $J^{-1}=J$.

Let H be a compact linear operator on $\mathcal {H}$. Recall that the eigenvalues of the self-adjoint operator |H| are called the singular values of H. They will be denoted by $\sigma _1, \sigma _2, \dots$, arranged so that $\sigma _1 \ge \sigma _2 \ge \dots \ge 0$, and repeated according to multiplicity. With the convention that $\sigma _j$ is defined to be zero for all sufficiently large j if H (and hence |H|) is of finite rank, we see that in all cases, $\mu _j \rightarrow 0$ as $j \rightarrow \infty$. It is well known that H and $H^*$ have the same singular values (cf. [6, Thm. II.5.7]).

In the case of involutive antiunitary operators, the following result is due to [10, Thm. 3].

Theorem 5

Let H be a compact linear operator on $\mathcal {H}$ which is C-self-adjoint. Assume that all the non-zero singular values $\sigma _j$ of H have multiplicity one or that C is involutive. There exist orthonormal eigenvectors $\phi _j$ of |H| corresponding to the non-zero eigenvalues $\sigma _j$ such that

$$\begin{aligned} H = \sum _{j=1}^\infty \sigma _j \, C^{-1}\phi _j \, (\phi _j,\cdot ) \qquad \text{ and } \qquad H^* = \sum _{j=1}^\infty \sigma _j \, \phi _j \, (C^{-1}\phi _j,\cdot ) \,. \end{aligned}$$

(12)

Proof

It is well known (see, e.g., [6, Thm. II.5.7]) that any compact linear operator H on $\mathcal {H}$ and its adjoint $H^*$ admit the decompositions

$$\begin{aligned} H = \sum _{j=1}^\infty \sigma _j \, \xi _j \, (\psi _j,\cdot ) \qquad \text{ and } \qquad H^* = \sum _{j=1}^\infty \sigma _j \, \psi _j \, (\xi _j,\cdot ) \,, \end{aligned}$$

(13)

where $\psi _j$ are orthonormal eigenvectors of |H| corresponding to the eigenvalues $\sigma _j$ and $\xi _j := \sigma _j^{-1} H\psi _j$ ($\sigma _j \not = 0$). The series in (13) are finite if H is of finite rank. Using Theorem 4, we get

$$\begin{aligned} \xi _j = C^{-1} J\psi _j \,. \end{aligned}$$

Moreover, since J commutes with |H|, it follows that $J\psi _j$ is an eigenvector of |H|, too.

Since H is compact, the mutually orthogonal eigenspaces $\mathcal {E}_n$ of |H| corresponding to the distinct non-zero eigenvalues $\mu _n$ are finite dimensional, say of dimension $m_n$. Relabelling the terms in the known decompositions (13), we may write

$$\begin{aligned} H = \sum _{n=1}^\infty \mu _n \sum _{k=1}^{m_n} C^{-1} J \psi _{n,k} \, (\psi _{n,k},\cdot ) \qquad \text{ and } \qquad H^* = \sum _{n=1}^\infty \mu _n \sum _{k=1}^{m_n} \psi _{n,k} \, (C^{-1} J\psi _{n,k},\cdot ) \,, \end{aligned}$$

where $(\psi _{n,1},\dots ,\psi _{n,m_n})$ is an orthonormal basis of $\mathcal {E}_n$. On each spectral subspace $\mathcal {E}_n$ of |H|, J restricts to an antiunitary operator and $J\mathcal {E}_n = \mathcal {E}_n$. By Lemma 2, there exists another orthonormal basis $(\phi _{n,1},\dots ,\phi _{n,m_n})$ of $\mathcal {E}_n$ which is fixed by J. Consequently,

$$\begin{aligned} H = \sum _{n=1}^\infty \mu _n \sum _{k=1}^{m_n} C^{-1} \phi _{n,k} \, (\phi _{n,k},\cdot ) \qquad \text{ and } \qquad H^* = \sum _{n=1}^\infty \mu _n \sum _{k=1}^{m_n} \phi _{n,k} \, (C^{-1}\phi _{n,k},\cdot ) \,. \end{aligned}$$

The desired representation (12) follows upon a suitable relabelling of terms. $\square$

Remark 4

If H is C-self-adjoint, then $H^*$ is $C^{-1}$-self-adjoint. Therefore one also has the alternative decomposition

$$\begin{aligned} H^* = \sum _{j=1}^\infty \sigma _j \, C \eta _j \, (\eta _j,\cdot ) \,, \end{aligned}$$

(14)

where $\eta _j$ are orthonormal eigenvectors of $|H^*|$ corresponding to the non-zero eigenvalues $\sigma _j$ (recall that H and $H^*$ have the same singular values). The second decomposition of (12) is consistent with (14). Indeed, from the formula $|H^*| = U |H| U^*$ (cf. [12, Eq. (VI.2.25)]), where U is the partially unitary operator from the polar decomposition of H, it is clear that $\phi _j$ is an eigenvector of |H| if, and only if, $\eta _j := U\phi _j$ is an eigenvector of $|H^*|$. However, in our case, $\eta _j = C^{-1} J \phi _j = C^{-1} \phi _j$, where the last equality holds because $\phi _j$ has been fixed by J in the proof of Theorem 5.

6 Antilinear eigenfunction expansions

There is no spectral-type theorem for complex-self-adjoint operators in general. In fact, there are well known examples of complex-self-adjoint operators with compact resolvent and empty spectrum (see, e.g., [17, Sect. VII.A]). Nevertheless, even for such pathological operators, there is always a canonically associated antilinear eigenvalue problem which has a complete set of mutually orthogonal eigenfunctions. This is the message of the following result, which is due to [10, Thm. 7] in the case of involutive antiunitary operators.

Theorem 6

Let H be a C-self-adjoint linear operator in an infinite-dimensional $\mathcal {H}$. Assume that H has a compact resolvent $R(z):=(H - z I)^{-1}$ for some complex number z. Furthermore, assume that all the singular values of R(z) have multiplicity one or that C is involutive. There exists an orthonormal basis $(\psi _j)_{j=1}^\infty$ of $\mathcal {H}$ consisting of solutions of the antilinear eigenvalue problem

$$\begin{aligned} (H - z I) \psi _j = \lambda _j C\psi _j \,, \end{aligned}$$

(15)

where $(\lambda _j)_{j=1}^\infty$ is an increasing sequence of positive numbers tending to $+\infty$.

Proof

First of all, notice that $\bar{z}$ belongs to the resolvent set of the adjoint $H^*$ and $R(z)^* = (H^*-\bar{z} I)^{-1}$ is a compact operator on $\mathcal {H}$, too. Indeed, since the residual spectrum of H is empty (cf. Proposition 1), $\bar{z} \not \in \sigma _\textrm{p}(H^*)$ and the operator $H^*-\bar{z} I$ is invertible. Since $H^*$ is also complex-self-adjoint, its residual spectrum is empty, too, so $\textsf{R}(H^*-\bar{z} I)$ is dense in $\mathcal {H}$. Since $\textsf{R}(H^*-\bar{z} I)$ is closed if, and only if, $\textsf{R}(H-z I)$ is closed (cf. [6, Thm. I.3.7]) and z belongs to the resolvent set of H, it follows that actually $\textsf{R}(H^*-\bar{z} I) = \mathcal {H}$. Hence, $R(z)^*$ is defined on $\mathcal {H}$. This fact enables us to conclude that R(z) is C-self-adjoint:

$$\begin{aligned} CR(z)C^{-1} = C (H-z I)^{-1} \underbrace{C^{-1} (H^*-\bar{z}I) C}_{H-z I} C^{-1} (H^*-\bar{z}I)^{-1} = R(z)^* \,. \end{aligned}$$

Now, by Theorem 5 applied to R(z), there exists an orthonormal basis $(\phi _j)_{j=1}^\infty$ of $\mathcal {H}$ (composed of eigenvectors of |R(z)|) such that

$$\begin{aligned} R(z) \phi _j = \sigma _j C^{-1} \phi _j, \end{aligned}$$

(16)

where $\sigma _j$ are the singular values of R(z). Recall that $(\sigma _j)_{j=1}^\infty$ is a decreasing sequence of positive numbers such that $\sigma _j \rightarrow 0$ as $j \rightarrow \infty$. Since each $C^{-1}\phi _j$ belongs to $\textsf{R}(R(z)) = \textsf{D}(H)$, we apply $H-z I$ to both sides of (16) and the desired result (15) follows with $\lambda _j := \sigma _j^{-1}$ and $\psi _j := C^{-1} \phi _j$. $\square$

Corollary 4

Under the hypotheses of Theorem 6,

$$\begin{aligned} \Vert R(z)\Vert = \frac{1}{\lambda _1} \,. \end{aligned}$$

This corollary is a useful tool for the study of pseudospectral properties of complex-self-adjoint operators. Recall that, given any positive number $\varepsilon$, the pseudospectrum $\sigma _\varepsilon (H)$ of a closed linear operator H is the union of its spectrum $\sigma (H)$ and all the complex numbers z such that $\Vert R(z)\Vert > \varepsilon ^{-1}$.

Corollary 5

Under the hypotheses of Theorem 6, if $\lambda _1 > \varepsilon$, then $z \in \sigma _\varepsilon (H)$.

7 Toy model: spinorial Hilbert space

In this section we introduce a one-parameric family of generically non-self-adjoint operators which are complex-self-adjoint with respect to an antiunitary operator, but the latter cannot be chosen, in any obvious way, to be involutive. Our motivation is the anti-involutive time-reversal operator for fermionic systems.

We begin with the self-adjoint one-dimensional Pauli operator in the Hilbert space $\mathcal {H}:= L^2(\mathbb {R};\mathbb {C}^2)$ defined by

$$\begin{aligned} H_0 := \begin{pmatrix} p^2 &{} 0 \\ 0 &{} p^2 \end{pmatrix} \,, \qquad \textsf{D}(H_0) := W^{2,2}(\mathbb {R};\mathbb {C}^2) \,, \end{aligned}$$

where $p\varphi :=-i\varphi '$ with $\textsf{D}(p):=W^{1,2}(\mathbb {R})$ is the (self-adjoint) momentum operator in $L^2(\mathbb {R})$. It is well known that $H_0$ is self-adjoint and $\sigma (H_0) = [0,+\infty )$. Physically, $H_0$ represents the quantum Hamiltonian of a non-relativistic spin $\frac{1}{2}$ particle on a line.

Obviously, $H_0$ is complex-self-adjoint with respect to a variety of antiunitary operators on $\mathcal {H}$, for instance,

$$\begin{aligned} K\psi := \bar{\psi } \,, \qquad C_1 := \sigma _1 K \,, \qquad C_2 := -i\sigma _2 K \,, \qquad C_3 := \sigma _3 K \,, \end{aligned}$$

where

$$\begin{aligned} \sigma _1 := \begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix} \,, \qquad \sigma _2 := \begin{pmatrix} 0 &{} -i \\ i &{} 0 \end{pmatrix} \,, \qquad \sigma _3 := \begin{pmatrix} 1 &{} 0 \\ 0 &{} -1 \end{pmatrix} \,, \end{aligned}$$

are the Pauli matrices. Here $K,C_1,C_3$ are involutive, while $C_2$ is anti-involutive. For the Schrödinger equation generated by the scalar Hamiltonian $p^2$ in $L^2(\mathbb {R})$, the time-reversal operator is represented by the complex conjugation K. For the Pauli equation, however, it is rather $C_2$ (or its multiple) which plays the role of the time-reversal operator (see, e.g., [19, Sect. 3]).

Now, let us consider the off-diagonal perturbation

$$\begin{aligned} V_\alpha := \begin{pmatrix} 0 &{} p \\ \alpha p &{} 0 \end{pmatrix} \,, \qquad \textsf{D}(V) := W^{1,2}(\mathbb {R};\mathbb {C}^2) \,, \end{aligned}$$

where $\alpha$ is a real parameter. For every $\alpha \in \mathbb {R}$, it is easy to see that $V_\alpha$ is relatively bounded with respect to $H_0$ with the relative bound less than one (actually, the bound can be chosen arbitrarily small). Consequently, $H_\alpha := H_0+V_\alpha$ with its natural domain $\textsf{D}(H_\alpha ) = \textsf{D}(H_0) \cap \textsf{D}(V_\alpha ) = W^{2,2}(\mathbb {R};\mathbb {C}^2)$ is closed. $H_\alpha$ is not self-adjoint unless $\alpha =1$. Indeed,

$$\begin{aligned} H_\alpha ^* = \begin{pmatrix} p^2 &{} \alpha p \\ p &{} p^2 \end{pmatrix} \,, \qquad \textsf{D}(H_\alpha ^*) = \textsf{D}(H_\alpha ) = W^{2,2}(\mathbb {R};\mathbb {C}^2) \,. \end{aligned}$$

It is straightforward to check that $H_\alpha$ is not $C_1$-self-adjoint, irrespectively of the value of $\alpha$. At the same time, $H_\alpha$ is not complex-self-adjoint with respect to K (respectively, $C_3$), unless $\alpha =-1$ (respectively, $\alpha =1$). However, $H_\alpha$ is $C_2$-self-adjoint, for every $\alpha \in \mathbb {R}$. What is more, there is no obvious conjugation with respect to which $H_\alpha$ is complex-self-adjoint, unless $\alpha = \pm 1$.

Proposition 2

Let $\alpha \in \mathbb {R}\setminus \{\pm 1\}$. There exists no antiunitary operator of multiplication by a constant matrix C satisfying $C^2=I$ and $H_\alpha ^* = C H_\alpha C^{-1}$.

Proof

By contradiction, let us assume that there exists an antiunitary operator of multiplication by a constant matrix C satisfying $C^2=I$ and $H_\alpha ^* = C H_\alpha C^{-1}$. Writing $C = AK$, where K is the complex conjugation, it follows that A is necessarily a unitary matrix of multiplication, say

$$\begin{aligned} A = \begin{pmatrix} a_{11} &{} a_{12} \\ a_{21} &{} a_{22} \end{pmatrix} \,, \qquad a_{11}, a_{12}, a_{21}, a_{22} \in \mathbb {C}\,. \end{aligned}$$

Hence, it is enough to show that the equations

$$\begin{aligned} H_\alpha ^* A = A KH_\alpha K \,, \qquad A\bar{A}^T = I \qquad \text{ and } \qquad A\bar{A} = I \end{aligned}$$

(17)

cannot be satisfied simultaneously. From the last two equations of (17), we particularly deduce that $a_{12}=a_{21}$. Then, using $\bar{p}=-p$, the first equation of (17) reads

$$\begin{aligned} \begin{pmatrix} a_{11} p^2+a_{12}\alpha p &{} a_{12} p^2+a_{22}\alpha p \\ a_{11} p+a_{12}p^2 &{} a_{12} p+a_{22} p^2 \\ \end{pmatrix} = \begin{pmatrix} a_{11} p^2-a_{12}\alpha p &{} -a_{11} p+a_{12} p^2 \\ a_{12} p^2 - a_{22} \alpha p &{} -a_{12} p + a_{22} p^2 \\ \end{pmatrix} \,. \end{aligned}$$

From the equations on the diagonal we deduce $a_{12} = 0$, while the off-diagonal equations yield $a_{22} \alpha = - a_{11}$ and $a_{11}=-\alpha a_{22}$. Taking the absolute value and using that $|a_{11}|=1=|a_{22}|$, it follows that $|\alpha |=1$. $\square$

We leave as an open problem whether $H_\alpha$ admits a more refined involutive antiunitary operator with respect to which it is complex-self-adjoint.

Using the Fourier transform, the spectrum of $H_\alpha$ can be computed explicitly:

$$\begin{aligned} \sigma (H_\alpha ) = {\left\{ \begin{array}{ll} \displaystyle \left[ -\frac{\alpha }{4},+\infty \right) &{} \text{ if } \quad \alpha \ge 0 \,, \\ \left\{ \lambda \in \mathbb {C}: \ \Re \lambda \ge 0 \ \wedge \ |\Im \lambda |^2 = |\alpha | \, \Re \lambda \right\} &{} \text{ if } \quad \alpha < 0 \,. \end{array}\right. } \end{aligned}$$

It is interesting that the spectrum is purely real for all non-negative $\alpha$ despite the fact that the operator $H_\alpha$ is self-adjoint only if $\alpha =1$. Since the reality of the spectrum is usually associated with some symmetries, let us mention that $H_\alpha$ is “$PC_2$-symmetric”, i.e. $[H_\alpha ,PC_2]=0$, with $P:=\sigma _1$. When $\alpha =0$, there is an abrupt transition to a parabolic curve which converges to the imaginary axis as $\alpha \rightarrow -\infty$.

Pseudospectral properties of $H_\alpha$ as well as perturbations by matrix-valued potentials should constitute an interesting area of a future research.

8 Further examples

The objective of this last section is to collect other examples of complex-self-adjoint operators with no obvious involutive conjugations, in a different Hilbert-space setting. We refer to [7] for more details on the present functional setup.

In what follows, $L^2(\mathbb {T}) =: L^2$ denotes the Lebesgue space of all complex-valued, square-integrable functions on the unit circle $\mathbb {T}$. The Hardy space $H^2(\mathbb {D}) =: H_+^2$ of the unit disk $\mathbb {D}$ is defined by

$$\begin{aligned} H^2(\mathbb {D}) := \{f \in L^2: \ \hat{f}(n) = 0 \ \text{ for } \ n<0 \} \,, \end{aligned}$$

where $\hat{f}(n)$ is the $n^\textrm{th}$ Fourier coefficient of $f \in L^2$. We also introduce

$$\begin{aligned} H_-^2 := \bar{z} \overline{H_+^2} = \{f \in L^2: \ \hat{f}(n) = 0 \ \text{ for } \ n \ge 0 \} \,. \end{aligned}$$

We have $L^2= H_+^2 \oplus H_-^2$. The orthogonal projections from $L^2$ to $H_\pm ^2$ will be denoted by $P^\pm$. By $L^\infty$ we denote the space of all complex-valued, essentially bounded functions on $\mathbb {T}$. By $H^\infty$ we denote the space of all functions analytic and bounded on $\mathbb {D}$, identified with a closed subspace of $L^\infty$.

Given an inner function (i.e. $\gamma \in H^\infty$ and $|\gamma |=1$ a.e. on $\mathbb {T}$), we associate to it the model space

$$\begin{aligned} K_\gamma := H^2 \ominus \gamma H^2 = \{f_+ \in H_+^2 : \ \bar{\gamma } f_+ = f_- \in H_-^2 \} \,. \end{aligned}$$

If $\gamma _1$ is another inner function such that $\gamma / \gamma _1 \in H^\infty$, we say that $\gamma _1$ divides $\gamma$ (we write $\gamma _1 \preceq \gamma$) and we can decompose

$$\begin{aligned} K_\gamma = K_{\gamma _1} \oplus \gamma _1 K_{\gamma /\gamma _1} \,. \end{aligned}$$

In each model space $K_\gamma$ we can define a natural involutive conjugation $C_\gamma$ given by

$$\begin{aligned} C_\gamma f := \gamma \bar{z} \bar{f} \end{aligned}$$

(18)

for every $f \in K_\gamma$.

8.1 Example 1

Let $\gamma ,\alpha ,\beta$ be inner functions, with $\gamma = \alpha \beta$. Then $K_\gamma$ admits two orthogonal decompositions,

$$\begin{aligned} K_\gamma = K_\alpha \oplus \alpha K_\beta \,, \qquad K_\gamma = K_\beta \oplus \beta K_\alpha \,. \end{aligned}$$

Consequently, every function $f \in K_\gamma$ admits two representations

$$\begin{aligned} f = f_{1,\alpha } + \alpha f_{2,\beta } \,, \qquad f = f_{1,\beta } + \beta f_{2,\alpha } \,, \end{aligned}$$

with $f_{1,\alpha }, f_{2,\alpha } \in K_\alpha$ and $f_{1,\beta }, f_{2,\beta } \in K_\beta$.

Let $\xi \in \mathbb {R}$ and define the antilinear operator $C_{\alpha ,\beta }$ on $K_\gamma$ by setting, for every $f \in K_\gamma$,

$$\begin{aligned} C_{\alpha ,\beta }(f) = C_{\alpha ,\beta }(f_{1,\alpha } + \alpha f_{2,\beta }) := e^{i\xi } C_\beta f_{2,\beta } + \beta C_\alpha f_{1,\alpha } \,, \end{aligned}$$

where $C_\beta (\varphi ) = \beta \bar{z} \bar{\varphi }$ for $\varphi \in K_\beta$ and $C_\alpha (\varphi ) = \alpha \bar{z} \bar{\varphi }$ for $\varphi \in K_\alpha$, according to (18).

Proposition 3

One has, for every $f \in K_\gamma$,

$$\begin{aligned} C_{\alpha ,\beta }^*(f) = C_{\alpha ,\beta }^*(f_{1,\beta } + \beta f_{2,\alpha }) = C_\alpha f_{2,\alpha } + e^{i\xi } \alpha C_\beta f_{1,\beta } \,. \end{aligned}$$

Proof

Let us abbreviate $C_{\alpha ,\beta } =: C$. For any $f,g \in K_\gamma$ with $f = f_{1,\alpha } + \alpha f_{2,\beta }$ and $g = g_{1,\beta } + \beta g_{2,\alpha }$, one has

$$\begin{aligned} (g,Cf) = \big (g_{1,\beta } + \beta g_{2,\alpha }, C(f_{1,\alpha } + \alpha f_{2,\beta })\big ) = \big (g_{1,\beta } + \beta g_{2,\alpha }, e^{i\xi } C_\beta f_{2,\beta } + \beta C_\alpha f_{1,\alpha } \big ) \,. \end{aligned}$$

Since $e^{i\xi } C_\beta f_{2,\beta } \in K_\beta \bot \beta H_+^2$ and $\beta C_\alpha f_{1,\alpha } \in \beta H_+^2 \bot K_\beta$, we get

$$\begin{aligned} \begin{aligned} (g,Cf)&= (g_{1,\beta },e^{i\xi } C_\beta f_{2,\beta }) + (\beta g_{2,\alpha },\beta C_\alpha f_{1,\alpha }) \\&= (e^{-i\xi } g_{1,\beta }, C_\beta f_{2,\beta }) + (g_{2,\alpha },C_\alpha f_{1,\alpha }) \\&= \big (f_{2,\beta },C_\beta (e^{-i\xi } g_{1,\beta })\big ) + (f_{1,\alpha },C_\alpha g_{2,\alpha }) \\&= (f_{2,\beta },e^{i\xi }C_\beta g_{1,\beta }) + (f_{1,\alpha },C_\alpha g_{2,\alpha }) \\&= (\alpha f_{2,\beta },\alpha e^{i\xi }C_\beta g_{1,\beta }) + (f_{1,\alpha },C_\alpha g_{2,\alpha }) \\&= (f_{1,\alpha } + \alpha f_{2,\beta }, C_\alpha g_{2,\alpha } + \alpha e^{i\xi }C_\beta g_{1,\beta }) \\&= (f,C^* g) \,, \end{aligned} \end{aligned}$$

as required by the adjoint of an antilinear operator. $\square$

Proposition 4

$C_{\alpha ,\beta }$ is antiunitary.

Proof

For every $f \in K_\gamma$, one has (again abbreviating $C_{\alpha ,\beta } =: C$)

$$\begin{aligned} \begin{aligned} C^* C f = C^* C (f_{1,\alpha } + \alpha f_{2,\beta })&= C^* (e^{i\xi } C_\beta f_{2,\beta } + \beta C_\alpha f_{1,\alpha }) \\&= C_\alpha (C_\alpha f_{1,\alpha }) + e^{i\xi } \alpha C_\beta (e^{i\xi } C_\beta f_{2,\beta } ) \\&= f_{1,\alpha } + \alpha f_{2,\beta } = f \,. \end{aligned} \end{aligned}$$

Analogously, one can show that $C C^* f = f$. $\square$

Remark 5

If $\alpha =\beta$, we have $C_{\alpha ,\alpha } (f_{1,\alpha } + \alpha f_{2,\alpha }) = e^{i\xi } f_{2,\alpha } + \alpha f_{1,\alpha }$ and

$$\begin{aligned} C_{\alpha ,\alpha }^2 (f_{1,\alpha } + \alpha f_{2,\alpha }) = e^{i\xi } f_{1,\alpha } + \alpha e^{-i\xi } f_{2,\alpha } \,. \end{aligned}$$

If $e^{i\xi } =1$, then $C_{\alpha ,\alpha }^2 = I$ and it turns out that $C_{\alpha ,\alpha }$ is the usual (involutive) conjugation $C_{\alpha ^2}$ on $K_{\alpha ^2}$, see (18). On the other hand, if $e^{i\xi } =-1$, then we have $C_{\alpha ,\alpha }^2 = -I$, with $C_{\alpha ,\alpha } f = -C_\alpha f_{2,\alpha } + \alpha C_\alpha f_{1,\alpha }$.

As an example of an operator on a model space $K_{\alpha ^2}$ which is $C_{\alpha ,\alpha }$-self-adjoint, but not $C_{\alpha ^2}$-self-adjoint, consider the case $e^{i\xi } =-1$, $\alpha := z^2$ and the operator H defined on $K_{z^4}$ (the space of polynomials of degree not greater than 3) by (with respect to the standard basis of $K_{z^4}$)

$$\begin{aligned} H := \begin{pmatrix} a_{11} &{} a_{12} &{} a_{13} &{} 0 \\ a_{21} &{} a_{22} &{} 0 &{} -a_{13} \\ a_{31} &{} 0 &{} a_{22} &{} a_{12} \\ 0 &{} - a_{31} &{} a_{21} &{} a_{11} \end{pmatrix} , \end{aligned}$$

where $a_{jk}$ with $j,k \in \{1,2,3\}$ are complex numbers. Then (abbreviating $C_{\alpha ,\alpha } =: C$)

$$\begin{aligned} CHC^{-1} = - CHC = H^* \,. \end{aligned}$$

8.2 Example 2

Let C be the antilinear operator defined on $L^2$ by

$$\begin{aligned} Cf := \frac{z-\bar{z}}{2} \ \overline{f(\bar{z})} + \frac{z+\bar{z}}{2} \ \overline{f(-\bar{z})} = z \ \frac{\overline{f(\bar{z})}+\overline{f(-\bar{z})}}{2} - \bar{z} \ \frac{\overline{f(\bar{z})}-\overline{f(-\bar{z})}}{2} \,. \end{aligned}$$

Proposition 5

$C^* = -C$.

Proof

For every $f,g \in L^2$, one has

$$\begin{aligned} (g,Cf) = \left( \frac{g(z)+g(-z)}{2} + \frac{g(z)-g(-z)}{2}, z \ \frac{\overline{f(\bar{z})}+\overline{f(-\bar{z})}}{2} - \bar{z} \ \frac{\overline{f(\bar{z})}-\overline{f(-\bar{z})}}{2} \right) . \end{aligned}$$

Noting that

$$\begin{aligned} \frac{g(z)+g(-z)}{2} \ { \bot } \ z \ \frac{\overline{f(\bar{z})}+\overline{f(-\bar{z})}}{2} \qquad \text{ and }\qquad \frac{g(z)-g(-z)}{2} \ {\bot } \ \bar{z} \ \frac{\overline{f(\bar{z})}-\overline{f(-\bar{z})}}{2} \,, \end{aligned}$$

we get

$$\begin{aligned} \begin{aligned} (g,Cf)&= \left( \frac{g(z)-g(-z)}{2} , z \ \frac{\overline{f(\bar{z})}+\overline{f(-\bar{z})}}{2} \right) \\ {}&\quad - \left( \frac{g(z)+g(-z)}{2} , \bar{z} \ \frac{\overline{f(\bar{z})}-\overline{f(-\bar{z})}}{2} \right) \\&= \left( \bar{z} \ \frac{g(z)-g(-z)}{2} , \frac{\overline{f(\bar{z})}+\overline{f(-\bar{z})}}{2} \right) \\ {}&\quad - \left( z \ \frac{g(z)+g(-z)}{2} , \frac{\overline{f(\bar{z})}-\overline{f(-\bar{z})}}{2} \right) \\&= \left( \frac{f(\bar{z})+f(-\bar{z})}{2} , z \ \frac{\overline{g(z)}-\overline{g(-z)}}{2} \right) \\ {}&\quad - \left( \frac{f(\bar{z})-f(-\bar{z})}{2} , \bar{z} \ \frac{\overline{g(z)}+\overline{g(-z)}}{2} \right) \\&= \left( \frac{f(z)+f(-z)}{2} , \bar{z} \ \frac{\overline{g(\bar{z})}-\overline{g(-\bar{z})}}{2} \right) \\ {}&\quad + \left( \frac{f(z)-f(-z)}{2} , -z \ \frac{\overline{g(\bar{z})}+\overline{g(-\bar{z})}}{2} \right) \\&= \left( f(z) , \bar{z} \ \frac{\overline{g(\bar{z})}-\overline{g(-\bar{z})}}{2} - z \ \frac{\overline{g(\bar{z})}+\overline{g(-\bar{z})}}{2} \right) = (f,-Cg) \,, \end{aligned} \end{aligned}$$

so the desired claim follows by the definition of the adjoint of an antilinear operator. $\square$

It is straightforward to verify the following claims.

Proposition 6

C is antiunitary and $C^2 = -I$.

It is perhaps less obvious that the Hardy space $H_+^2$ is left invariant by C.

Proposition 7

$C(H_+^2)=H_+^2$.

Proof

The claim follows from the observation that for $f \in H_+^2$ with $f(z) = a_0 + a_1 z + a_2 z^2 + a_3 z^3 + \dots$ we have that $Cf(z) = -\bar{a}_1 + \bar{a}_0 z - \bar{a}_3 z^2 + \bar{a}_2 z^3 + \dots$ $\square$

Remark 6

The usual conjugation in $H_+^2$ is given by (cf. [4, 13])

$$\begin{aligned} \tilde{C}f (z) := \overline{f(\bar{z})} \,, \end{aligned}$$

so that for $f(z) = a_0 + a_1 z + a_2 z^2 + \dots$ we have that $\tilde{C}f(z) = \bar{a}_0 + \bar{a}_1 z + \bar{a}_2 z^2 + \dots$

Corollary 6

$CP^\pm = P^\pm C$.

From Proposition 7, the restriction $C |_{H_+^2}$ is an anti-involutive conjugation on $H_+^2$, which we will also denote by C.

Proposition 8

If $\theta$ is an inner function such that

$$\begin{aligned} \theta (\bar{z}) = \theta (-\bar{z}) = \overline{\theta (z)} \end{aligned}$$

(19)

for all $z \in \mathbb {D}$, then $C(K_\theta ) = K_\theta$ and $\tilde{C}_\theta := C |_{K_\theta }$ defines an anti-involutive conjugation on $K_\theta$.

Proof

We have that $f_+ \in K_\theta$ if, and only if, $f_+ \in H_+^2$ and $\bar{\theta }f_+ = f_-$ where $f_- \in H_-^2$. Let $f_+$ be any element of $K_\theta$. Then

$$\begin{aligned} \begin{aligned} \overline{\theta (z)} f_+(z) = f_-(z)&\Longleftrightarrow \theta (\bar{z}) \overline{f_+(\bar{z})} = \overline{f_-(\bar{z})} \\&\Longleftrightarrow \overline{\theta (z)} \, \overline{f_+(\bar{z})} = \overline{f_-(\bar{z})} \\&\Longleftrightarrow \overline{\theta (-z)} \, \overline{f_+(-\bar{z})} = \overline{f_-(-\bar{z})} \\&\Longleftrightarrow \overline{\theta (z)} \, \overline{f_+(-\bar{z})} = \overline{f_-(-\bar{z})} \,. \end{aligned} \end{aligned}$$

Consequently,

$$\begin{aligned} \begin{aligned} \bar{\theta }\tilde{C}_\theta f(z)&= \overline{\theta (z)} \left( z \ \frac{\overline{f_+(\bar{z})}+\overline{f_+(-\bar{z})}}{2} - \bar{z} \ \frac{\overline{f_+(\bar{z})}-\overline{f_+(-\bar{z})}}{2} \right) \\&= z \ \frac{\overline{f_-(\bar{z})}+\overline{f_-(-\bar{z})}}{2} - \bar{z} \ \frac{\overline{f_-(\bar{z})}-\overline{f_-(-\bar{z})}}{2} \in H_-^2 \,. \end{aligned} \end{aligned}$$

Therefore $C(K_\theta ) \subset K_\theta$ and since $C^2 = -I$ we have also $K_\theta \subset C(K_\theta )$. $\square$

Remark 7

It follows that $C |_{K_\theta }$ is also an anti-involutive conjugation on $K_\theta$ if $\theta$ satisfies (19).

For example, if $\theta := z^4$ and $f_+(z) = a_0 + a_1 z + a_2 z^2 + a_3 z^3 \in K_{z^4}$, where $a_0,a_1,a_2,a_3$ are complex numbers, then $Cf_+(z) = -\bar{a}_1 + \bar{a}_0 z - \bar{a}_3 z^2 + \bar{a}_2 z^3 \in K_{z^4}$. (Comparing with the conjugation $C_{z^2,z^2}$ on $K_{z^4}$, defined in Sect. 8.1, we have $C_{z^2,z^2}f_+(z) = -\bar{a}_3 - \bar{a}_2 z + \bar{a}_1 z^2 + \bar{a}_0 z^3$.) An operator H defined on $K_{z^4}$ is C-self-adjoint if it is defined by a complex matrix of the form

$$\begin{aligned} H := \begin{pmatrix} a_{11} &{} 0 &{} a_{13} &{} a_{14} \\ 0 &{} a_{11} &{} a_{23} &{} a_{24} \\ a_{24} &{} -a_{14} &{} a_{33} &{} 0 \\ - a_{23} &{} a_{13} &{} 0 &{} a_{33} \end{pmatrix} . \end{aligned}$$

As an example of an operator on $H_+^2$ which is C-self-adjoint (denoting $C |_{H_+^2} =: C$), one can consider the following natural generalisation of Toeplitz operators (defined, for $\varphi \in L^\infty$, as $T_\varphi : H_+^2 \rightarrow H_+^2$, $T_\varphi f_+ := P^+ \varphi f_+$), with $\varphi _1, \varphi _2 \in L^\infty$:

$$\begin{aligned} T_{\varphi _1, \varphi _2} : H_+^2 \rightarrow H_+^2, \begin{aligned} T_{\varphi _1, \varphi _2} (f_+)&\!\!:= P^+ \left( \varphi _1(z) \ \frac{f_+(z)+f_+(-z)}{2} + \varphi _2(z) \ \frac{f_+(z)-f_+(-z)}{2} \right) \\&= P^+ \left( \frac{\varphi _1(z)+\varphi _2(z)}{2} \ f_+(z) + \frac{\varphi _1(z)-\varphi _2(z)}{2} \ f_+(-z) \right) . \end{aligned} \end{aligned}$$

We shall occasionally abbreviate $T_{\varphi _1, \varphi _2} =: T$.

Proposition 9

$T_{\varphi _1, \varphi _2} = 0$ if, and only if, $\varphi _1= \varphi _2 = 0$.

Proof

We have $T_{\varphi _1, \varphi _2} = 0$ if, and only if, $\textsf{N}(T_{\varphi _1, \varphi _2}) = H_+^2$, i.e., for any $f_+ \in H_+^2$

$$\begin{aligned} \varphi _1(z) \ \frac{f_+(z)+f_+(-z)}{2} + \varphi _2(z) \ \frac{f_+(z)-f_+(-z)}{2} \in H_-^2 \,. \end{aligned}$$

In particular, this must hold for any even function $f_+ \in H_+^2$. Taking $f_+ = 1$, this implies that $\varphi _1 \in H_-^2$; taking $f_+ = z^{2n}$ with $n \in \mathbb {N}$, we conclude that $\varphi _1 \in (\bar{z}^2)^n H_-^2$ for all $n \in \mathbb {N}$ and, therefore, $\varphi _1 = 0$. Analogously, taking $f_+$ to be any odd function in $H_+^2$, we conclude that $\varphi _2 = 0$. $\square$

Corollary 7

For $\varphi _1, \varphi _2, \tilde{\varphi }_1, \tilde{\varphi }_2 \in L^\infty$, we have

$$\begin{aligned} T_{\varphi _1, \varphi _2} = T_{\tilde{\varphi }_1, \tilde{\varphi }_2} \quad \Longleftrightarrow \quad (\varphi _1 = \tilde{\varphi }_1 \ \wedge \ \varphi _2 = \tilde{\varphi }_2) \,. \end{aligned}$$

Proposition 10

We have, for every $f_+ \in H_+^2$,

$$\begin{aligned} T_{\varphi _1, \varphi _2}^* (f_+) = P^+ \left( \frac{\overline{\varphi _1(z)}+\overline{\varphi _2(z)}}{2} \ f_+(z) + \frac{\overline{\varphi _1(-z)}-\overline{\varphi _2(-z)}}{2} \ f_+(-z) \right) . \end{aligned}$$

Proof

For any $f_+,g_+ \in H_+^2$, we have

$$\begin{aligned} \begin{aligned} (g_+,T f_+)&= \left( g_+(z), P^+ \left( \frac{\varphi _1(z)+\varphi _2(z)}{2} \ f_+(z) + \frac{\varphi _1(z)-\varphi _2(z)}{2} \ f_+(-z) \right) \right) \\&= \left( g_+(z), \frac{\varphi _1(z)+\varphi _2(z)}{2} \ f_+(z) \right) + \left( g_+(z), \frac{\varphi _1(z)-\varphi _2(z)}{2} \ f_+(-z) \right) \\&= \left( \frac{\overline{\varphi _1(z)}+\overline{\varphi _2(z)}}{2} \ g_+(z), f_+(z) \right) + \left( \frac{\overline{\varphi _1(z)}-\overline{\varphi _2(z)}}{2} \ g_+(z), f_+(-z) \right) \\&= \left( \frac{\overline{\varphi _1(z)}+\overline{\varphi _2(z)}}{2} \ g_+(z), f_+(z) \right) \\ {}&\quad + \left( \frac{\overline{\varphi _1(-z)}-\overline{\varphi _2(-z)}}{2} \ g_+(-z), f_+(z) \right) \\&= \left( P^+ \ \frac{\overline{\varphi _1(z)}+\overline{\varphi _2(z)}}{2} \ g_+(z), f_+(z) \right) \\ {}&\quad + \left( P^+ \ \frac{\overline{\varphi _1(-z)}-\overline{\varphi _2(-z)}}{2} \ g_+(-z), f_+(z) \right) \,, \end{aligned} \end{aligned}$$

which establishes the desired claim. $\square$

Proposition 11

We have $C T_{\varphi _1, \varphi _2} C^{-1} = T_{\varphi _1, \varphi _2}^*$ if, and only if,

$$\begin{aligned} -\bar{z} \varphi _1(z) + z \varphi _2(z) = z \varphi _1(\bar{z}) - \bar{z} \varphi _2(\bar{z}) \quad \text{ and }\quad \bar{z} \varphi _1(z) + z \varphi _2(z) = z \varphi _1(-\bar{z}) + \bar{z} \varphi _2(-\bar{z}) \,. \end{aligned}$$

(20)

Proof

On the one hand, we have

$$\begin{aligned} \begin{aligned} T C f_+&= P^+ \Bigg [ \frac{\varphi _1(z)+\varphi _2(z)}{2} \left( \frac{z-\bar{z}}{2} \, \overline{f_+(\bar{z})} + \frac{z+\bar{z}}{2} \, \overline{f_+(-\bar{z})} \right) \\&\quad \qquad +\frac{\varphi _1(z)-\varphi _2(z)}{2} \left( -\frac{z-\bar{z}}{2} \, \overline{f_+(-\bar{z})} - \frac{z+\bar{z}}{2} \, \overline{f_+(-\bar{z})} \right) \Bigg ] \\&= \frac{1}{2} \, P^+ \left[ (-\bar{z}\varphi _1(z) + z \varphi _2(z)) \, \overline{f_+(\bar{z})} + (\bar{z}\varphi _1(z) + z \varphi _2(z)) \, \overline{f_+(-\bar{z})} \right] . \end{aligned} \end{aligned}$$

On the other hand, we have

$$\begin{aligned} C T^* f_+= & {} C P^+ \left[ \frac{\overline{\varphi _1(z)}+\overline{\varphi _2(z)}}{2} f_+(z) + \frac{\overline{\varphi _1(-z)}-\overline{\varphi _2(-z)}}{2} f_+(-z) \right] \\= & {} P^+ C \left[ \frac{\overline{\varphi _1(z)}+\overline{\varphi _2(z)}}{2} f_+(z) + \frac{\overline{\varphi _1(-z)}-\overline{\varphi _2(-z)}}{2} f_+(-z) \right] \\= & {} P_+ \Bigg [ \frac{z-\bar{z}}{2} \left( \frac{\varphi _1(\bar{z})+\varphi _2(\bar{z})}{2} \ \overline{f_+(\bar{z})} + \frac{\varphi _1(-\bar{z})-\varphi _2(-\bar{z})}{2} \ \overline{f_+(-\bar{z})} \right) \\{} & {} +\frac{z+\bar{z}}{2} \left( \frac{\varphi _1(-\bar{z})+\varphi _2(-\bar{z})}{2} \ \overline{f_+(-\bar{z})} + \frac{\varphi _1(\bar{z})-\varphi _2(\bar{z})}{2} \ \overline{f_+(\bar{z})} \right) \Bigg ] \\= & {} \frac{1}{2} \, P^+ \left[ (z\varphi _1(\bar{z}) - \bar{z} \varphi _2(\bar{z})) \, \overline{f_+(\bar{z})} + (z\varphi _1(-\bar{z}) + \bar{z} \varphi _2(-\bar{z})) \, \overline{f_+(-\bar{z})} \right] . \end{aligned}$$

Consequently, taking Corollary 7 into account, we have $TC = CT^*$ if, and only if, (20) holds. $\square$

Remark 8

Condition (20) is particularly satisfied if

$$\begin{aligned} \varphi _1(\bar{z}) = \varphi _2(z) \qquad \text{ and } \qquad \frac{\varphi _1(z) -\varphi _1(-z)}{z} = - \frac{\varphi _1(\bar{z}) -\varphi _1(-\bar{z})}{\bar{z}} \,. \end{aligned}$$

8.3 Example 3

Let $D_j$, with $j \in \{1,2,3,4\}$, be antilinear operators on a Hilbert space $\mathcal {H}$ and consider the antilinear operator defined on $\mathcal {H}\oplus \mathcal {H}$ (which we identify with $\mathcal {H}^2$) by

$$\begin{aligned} C := \begin{pmatrix} D_1 &{} D_2 \\ D_3 &{} D_4 \end{pmatrix} . \end{aligned}$$

We have

$$\begin{aligned} C^* = \begin{pmatrix} D_1^* &{} D_3^* \\ D_2^* &{} D_4^* \end{pmatrix} . \end{aligned}$$

Consequently,

$$\begin{aligned} CC^* = I \qquad \Longleftrightarrow \qquad \left\{ \begin{aligned} D_1 D_1^* + D_2 D_2^* = I \,, \\ D_3 D_3^* + D_4 D_4^* = I \,, \\ D_1 D_3^* + D_2 D_4^* = 0 \,, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} C^* C = I \qquad \Longleftrightarrow \qquad \left\{ \begin{aligned} D_1^* D_1 + D_3^* D_3 = I \,, \\ D_2^* D_2 + D_4^* D_4 = I \,, \\ D_1^* D_2 + D_3^* D_4 = 0 \,. \end{aligned} \right. \end{aligned}$$

Involutive conjugations of this form for $\mathcal {H}:= H_+^2$ were studied in [5, 14]. Here we allow for a more abstract setting as well as for not necessarily involutive conjugations. In particular, C will be antinunitary and anti-involutive if, and only if,

$$\begin{aligned} \left\{ \begin{aligned} D_1&= -D_1^* \,, \\ D_4&= -D_4^* \,, \\ D_3&= -D_2^* \,, \end{aligned} \right. \qquad \text{ and } \qquad \left\{ \begin{aligned} D_2 D_2^* - D_1^2&= I \,, \\ D_2^* D_2 - D_4^2&= I \,, \\ D_1 D_2 + D_2 D_4&= 0 \,. \end{aligned} \right. \end{aligned}$$

For example, if D is antiunitary and anti-involutive, then

$$\begin{aligned} C_1 := \frac{1}{\sqrt{2}} \begin{pmatrix} -D &{} D \\ D &{} D \end{pmatrix} \end{aligned}$$

is also antiunitary and anti-involutive. Another example is given with $D_1 = 0 = D_4$, $D_2$ antiunitary and involutive, and $D_3 = -D_2^* = -D_2$; then

$$\begin{aligned} C_2 := \frac{1}{\sqrt{2}} \begin{pmatrix} 0 &{} D_2 \\ -D_2 &{} 0 \end{pmatrix} \end{aligned}$$

is an anti-involutive conjugation on $\mathcal {H}\oplus \mathcal {H}$.

Proposition 12

For any operator p on $\mathcal {H}$ such that $D_2 p D_2 = - p^*$, we have that

$$\begin{aligned} T_\alpha := \begin{pmatrix} p^2 &{} \alpha p \\ p &{} p^2 \end{pmatrix} , \qquad \alpha \in \mathbb {R}\,, \end{aligned}$$

is $C_2$-self-adjoint.

Proof

We have

$$\begin{aligned} \begin{aligned} C_2T_\alpha C_2^{-1}&= \begin{pmatrix} 0 &{} D_2 \\ -D_2 &{} 0 \end{pmatrix} \begin{pmatrix} p^2 &{} \alpha p \\ p &{} p^2 \end{pmatrix} \begin{pmatrix} 0 &{} -D_2 \\ D_2 &{} 0 \end{pmatrix} \\&= \begin{pmatrix} D_2 p^2 D_2 &{} -D_2 p D_2 \\ -\alpha D_2 p D_2 &{} D_2 p^2 D_2 \end{pmatrix} \\&= \begin{pmatrix} (p^*)^2 &{} p^* \\ \alpha p^* &{} (p^*)^2 \end{pmatrix} = T_\alpha ^* \,, \end{aligned} \end{aligned}$$

which establishes the desired result. $\square$

Remark 9

The example of Proposition 12 is of the type of the toy model considered in Sect. 7, except that in the former only bounded operators are considered.