Keywords

1 Introduction

Sequences of symbols or events are a fundamental type of data, found in many domains. For example, a sequence can model daily purchases made by a customer, a set of locations visited by a tourist, a text (a sequence of words), a time-ordered list of alarms generated by a computer system, and moves in a game such as chess. Several data mining tasks have been proposed to find patterns in sequences of events (symbols). While some tasks such as sequential pattern mining were proposed to find patterns common to multiple sequences  [11, 27] or across sequences  [29], other tasks have been studied to find patterns in a single long sequence of events. For example, this is the case of tasks such as periodic pattern mining (finding patterns appearing with regularity in a sequence)  [17] and peak pattern mining (finding patterns that have a high importance during a specific non-predefined time period)  [13]. But the task that is arguably the most popular of this type is frequent episode mining (FEM)  [15, 23], which consists of identifying all episodes (subsequences of events) that appear at least minsup times in a sequence of events. FEM can be applied to two types of input sequences, which are simple sequences (sequences where each event has a unique timestamp) and complex sequences (where simultaneous events are allowed). From this data, three types of episodes are mainly extracted, which are (1) parallel episodes (sets of events appearing simultaneously), (2) serial episodes (sets of events that are totally ordered by time), and (3) composite episodes (where parallel and serial episodes may be combined)  [23]. The first algorithms for FEM are WINEPI and MINEPI  [23]. WINEPI mines all parallel and serial episodes by performing a breadth-first search and using a sliding window. It counts the support (occurrence frequency) of an episode as the number of windows where the episode appears. However, this window-based frequency has the problem that an occurrence may be counted more than once  [16]. MINEPI adopts a breadth-first search approach but only look for minimal occurrences of episodes  [23]. To avoid the problem of the window-based frequency, two algorithms named MINEPI+ and EMMA  [15] adopt the head frequency measure  [16]. EMMA utilizes a depth-first search and a memory anchor technique. It was shown that EMMA outperforms MINEPI  [23] and MINEPI+  [15]. Episode mining is an active research area and many algorithms and extensions are developed every year such as to mine online episodes  [3] and high utility episodes  [21, 30].

Though episode mining has many applications  [15, 23], it is a difficult task because the search space can be very large. Although efficient algorithms were designed, a major limitation of traditional frequent episode mining algorithms is that setting the minsup parameter is difficult. If minsup is set too high, few episodes are found, and important episodes may not be discovered. But if minsup is set too low, an algorithm may become extremely slow, find too many episodes, and may even run out of memory or storage space. Because users typically have limited time and storage space to analyze episodes, they are generally interested in finding enough but not too many episodes. But selecting an appropriate minsup value to find just enough episodes is not easy as it depends on database characteristics that are initially unknown to the user. Hence, a user will typically apply an episode mining algorithm many times with various minsup values until just enough episodes are found, which is time-consuming.

To address this issue, this paper redefines the problem of frequent episode mining as that of top-k frequent episode mining, where the goal is to find the k most frequent episodes. The advantage of this definition is that the user can directly set k, the number of patterns to be found rather than setting the minsup parameter. To efficiently identify the top-k episodes in an event sequence, this paper presents an algorithm named TKE (Top-K Episode mining). It uses an internal minsup threshold that is initially set to 1. Then, TKE starts to search for episodes and gradually increases that threshold as frequent episodes are found. To increase that threshold as quickly as possible to reduce the search space, TKE applies a concept of dynamic search, which consists of exploring the most promising patterns first. Experiments were done on various types of sequences to evaluate TKE’s performance. Results have shown that TKE is efficient and is a valuable alternative to traditional episode mining algorithms.

The rest of this paper is organized as follows. Section 2 introduces the problem of frequent episode mining and presents the proposed problem definition. Section 3 describes the proposed algorithm. Then, Sect. 4 presents the experimental evaluation. Finally, Sect. 5 draws a conclusion and discuss research opportunities for extending this work.

2 Problem Definition

The traditional problem of frequent episode mining is defined as follows  [15, 23]. Let \(E = \{i_1,i_2,\ldots ,i_m\}\) be a finite set of events or symbols, also called items. An event set X is a subset of E, that is \(X \subseteq E\). A complex event sequence \(S = \langle (SE_{t_1}, t_1),\) \((SE_{t_2},t_2), \ldots ,\) \((SE_{t_n},t_n) \rangle \) is a time-ordered list of tuples of the form \((SE_{t_i}, t_i)\) where \(SE_{t_i} \subseteq E\) is the set of events appearing at timestamp \(t_i\), and \(t_i < t_j\) for any integers \(1 \le i < j \le n\). A set of events \(SE_{t_i}\) is called a simultaneous event set because they occurred at the same time. A complex event sequence where each event set contains a single event is called a simple event sequence. For the sake of brevity, in the following, timestamps having empty event sets are omitted when describing a complex event sequence.

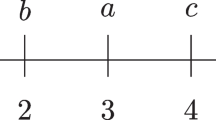
For instance, Fig. 1 (left) illustrates the complex event sequence \(S=\langle (\{a,c\}, \) \( t_1),\) \( (\{a\},t_2),\) \((\{a,b\},t_3),\) \((\{a\},t_6),\) \((\{a,b\},t_7),\) \((\{c\},t_8),\) \((\{b\},t_9),\) \((\{d\},t_{11}) \rangle \). That sequence indicates that a appeared with c at time \(t_1\), was followed by event a at \(t_2\), then a and b at \(t_3\), then a at \(t_6\), then a and b at \(t_7\), then c at \(t_8\), then b at \(t_9\), and finally d at \(t_{11}\). That sequence will be used as running example. This type of sequence can model various data such as alarm sequences  [23], cloud data  [2], network data  [18], stock data  [21], malicious attacks  [26], movements  [14], and customer transactions  [1, 3, 4, 7].

Fig. 1.
figure 1

A complex event sequence

Full size image

Frequent episode mining aims at discovering all subsequences of events called episodes [15, 23] that have a high support (many occurrences) in a sequence. Formally, an episode (also called composite episode) \(\alpha \) is a non-empty totally ordered set of simultaneous events of the form \(\langle X_1, X_2,\ldots , X_p\rangle \), where \(X_i \subseteq E\) and \(X_i\) appears before \(X_j\) for any integers \(1 \le i < j \le p\). An episode containing a single event set is called a parallel episode, while an episode where each event set contains a single event is called a serial episode. Thus, parallel episodes and serial episodes are special types of composite episodes.

There are different ways to calculate the support of an episode in a sequence. In this paper, we use the head frequency support, used by MINEPI+ and EMMA  [16], which was argued to be more useful than prior measures  [15]. The support is defined based on a concept of occurrence.

Definition 1 (Occurrence)

Let there be a complex event sequence \(S = \langle (SE_{t_1},\) \(t_1),\) \((SE_{t_2},t_2),\) \(\ldots ,\) \((SE_{t_n},t_n) \rangle \). An occurrence of the episode \(\alpha \) in S is a time interval \([t_s\), \(t_e]\) such that there exist integers \(t_s = z_1< z_2< \ldots < z_w = t_e\) such that \(X_1 \subseteq SE_{z_1}\), \(X_2 \subseteq SE_{z_2}\), ..., \(X_p \subseteq SE_{z_w}\). The timestamps \(t_s\) and \(t_e\) are called the start and end points of \([t_s\), \(t_e]\), respectively. The set of all occurrences of \(\alpha \) in a complex event sequence is denoted as \(occSet(\alpha )\).

For instance, the set of all occurrences of the composite episode \(\langle \{a\},\) \(\{a,b\}\} \rangle \) is \(occSet(\langle \{a\},\) \(\{a,b\}\} \rangle )\) = {\([t_1,t_3],\) \([t_1,t_7],\) \([t_2,t_3],\) \([t_2,t_7],\) \([t_6,t_7]\)}.

Definition 2 (Support)

The support of an episode \(\alpha \) is the number of distinct start points for its occurrences. It is denoted and defined as \(sup(\alpha ) = |\{t_s | [t_s, t_e] \in occSet(\alpha )\}|\)  [15].

For instance, if \(winlen=6\), the occurrences of the episode \(\alpha = \langle \{a\},\) \(\{a,b\} \rangle \) are \([t_1, t_3]\), \([t_2, t_3]\), \([t_3, t_7]\) and \([t_6, t_7]\). Because \(\alpha \) has four distinct start points (\(t_1, t_2, t_3,\) and \(t_6\)) and \(sup(\alpha ) = 4\). The problem of FEM is defined as follows.

Definition 3 (Frequent Episode mining)

Let there be a user-defined window length \(winlen>0\), a threshold \(minsup >0\) and a complex event sequence S. The problem of frequent episode mining consists of finding all frequent episodes, that is episodes having a support that is no less than minsup  [15].

For example, the frequent episodes found in the sequence of Fig. 1 for \(minsup =2\) and \(winlen=2\) are \(\langle \{a,b\} \rangle \), \(\langle \{a\}, \{b\} \rangle \), \(\langle \{a\}, \{a,b\} \rangle \), \(\langle \{a\}, \{a\} \rangle \), \(\langle \{a\}\rangle \), \(\langle \{b\}\rangle \), and \(\langle \{c\}\rangle \). Their support values are 2, 2, 2, 3, 5, 3, and 2 respectively.

To solve the problem of FEM, previous papers have relied on the downward closure property of the support, which states that the support of an episode is less than or equal to that of its prefix episodes  [15].

This paper redefines the problem of FEM as that of identifying the top-k frequent episodes, where minsup is replaced by a parameter k.

Definition 4 (Top-k Frequent Episode mining)

Let there be a user-defined window winlen, an integer \(k >0\) and a complex event sequence S. The problem of top-k frequent episode mining consists of finding a set T of k episodes such that their support is greater or equal to that of any other episodes not in T.

For example, the top-3 frequent subgraphs found in the complex event sequences of Fig. 1 are \(\langle \{a\}, \{a\} \rangle \), \(\langle \{a\}\rangle \), and \(\langle \{b\}\rangle \).

One should note that in the case where multiple episodes have the same support, the top-k frequent episode mining problem can have multiple solutions (different sets of episodes may form a set of top-k episodes). Moreover, for some datasets and winlen values, less than k episodes may be found.

The proposed problem is more difficult than traditional frequent episode mining since it is not known beforehand for which minsup value, the top-k episodes will be obtained. Hence, an algorithm may have to consider all episodes having a support greater than zero to identify the top-k episodes. Thus, the search space of top-k frequent episode mining is always equal or larger than that of traditional frequent episode mining with an optimal minsup value.

3 The TKE Algorithm

To efficiently solve the problem of top-k frequent episode mining, this paper proposes an algorithm named TKE (Top-k Episode Mining). It searches for frequent episodes while keeping a list of the current best episodes found until now. TKE relies on an internal minsup threshold initially set to 1, which is then gradually increased as more patterns are found. Increasing the internal threshold allows to reduce the search space. When the algorithm terminates the top-k episodes are found. TKE (Algorithm 1) has three input parameters: an input sequence, k and winlen. The output is a set of top-k frequent episodes. TKE consists of four phases, which are inspired by the EMMA algorithm  [15] but adapted for efficient top-k episode mining. EMMA was chosen as basis for TKE because it is one of the most efficient episode mining algorithms  [15].

Step 1. Finding the top-k events. TKE first sets \(minsup = 1\). Then, the algorithm scans the input sequence S once to count the support of each event. Then, the minsup threshold is set to that of the k-th most frequent event. Increasing the support at this step is an optimization called Single Episode Increase (SEI). Then, TKE removes all events having a support less than minsup from S, or ignore them from further processing. Then, TKE scans the database again to create a vertical structure called location list for each remaining (frequent) event. The set of frequent events is denoted as \(E'\). The location list structure is defined as follows.

Definition 5 (Location list)

Consider a sequence \(S = \langle (SE_{t_1}, t_1),\) \((SE_{t_2},t_2),\) \(\ldots ,\) \((SE_{t_n},t_n) \rangle \). Without loss of generality, assume that each event set is sorted according to a total order on events \(\prec \) (e.g. the lexicographical order \(a \prec b \prec c \prec d\)). Consider that an event e appears in an event set \(SE_{t_i}\) of S. It is then said that event e appears at the position \(\sum _{w = 1,\dots , i-1} |SE_{t_w}|\) \(+ |\{y | y \in SE_{t_i} \wedge y \prec e\}|\) of sequence S. Then, the location list of an event e is denoted as locList(e) and defined as the list of all its positions in S. The support of an event can be derived from its location list as \(sup(e) = |locList(e)|\).

For instance, consider the input sequence \(S=\langle (\{a,c\} ,t_1),\) \( (\{a\},t_2),\) \((\{a,b\},t_3),\) \((\{a\},t_6),\) \((\{a,b\},t_7),\) \((\{c\},t_8),\) \((\{b\},t_9),\) \((\{d\},t_{11}) \rangle \), that \(k = 3\) and \(winlen = 2\). After the first scan, it is found that the support of events a, b, c and d are 5, 3, 2 and 1, respectively. Then, minsup is set to the support of the k-th most frequent event, that is \(minsup = 2\). After removing infrequent events, the sequence S becomes \(S=\langle (\{a,c\} ,t_1),\) \( (\{a\},t_2),\) \((\{a,b\},t_3),\) \((\{a\},t_6),\) \((\{a,b\},t_7),\) \((\{c\},t_8),\) \((\{b\},t_9)\rangle \) Then, the location lists of a, b and c are built because their support is no less than 2. These lists are \(locList(a) = \{0, 2, 3, 5, 6\}\), \(locList(b) = \{4, 7, 9\}\) and \(locList(c) = \{1, 8\}\).

Step 2. Finding the top-k parallel episodes. The second step consists of finding the top-k parallel episodes by combining frequent events found in Step 1. This is implemented as follows. First, all the frequent events are inserted into a set PEpisodes. Then, TKE attempts to join each frequent episode \(ep \in PEpisodes\) with each frequent event \(e \in E' | e \not \in ep \wedge \forall f \in ep, f \prec e\) to generate a larger parallel episode \(newE = ep \cup \{e\}\), called a parallel extension of ep. The location list of newE is created, which is defined as \(locList(newE)= \{p | p \in locList(e) \wedge \exists q \in locList(ep) | t(p) = t(q) \}\), where t(p) denotes the timestamp corresponding to position p in S. Then, if the support of newE is no less than minsup according to its location list, then newE is inserted in PEpisodes, and then minsup is set to the support of the k-th most frequent episode in PEpisodes. Finally, all episodes in PEpisodes having a support less than minsup are removed. Then, PEpisodes contains the top-k frequent parallel episodes.

Consider the running example. The parallel extension of episode \(\langle \{a\}\rangle \) with event b is done to obtain the episode \(\langle \{a,b\}\rangle \) and its location list \(locList(\langle \{a,b\}\rangle )\) \(= \{4, 7\}\). Thus, \(sup(\langle \{a,b\}\rangle ) =\) \( |locList(\langle \{a,b\}\rangle )| = 2\). This process is performed to generate other parallel extensions such as \(\langle \{a,c\}\rangle \) and calculate their support values. After Step 2, the top-k parallel episodes are: \(\langle \{a\} \rangle \), \(\langle \{b\} \rangle \), \(\langle \{c\} \rangle \), and \(\langle \{a,b\}\rangle \), with support values of 5, 3, 2, 2, respectively, and \(minsup = 2\).

Step 3. Re-encoding the input sequence using parallel episodes. The next step is to re-encode the input sequence S using the top-k parallel episodes to obtain a re-encoded sequence \(S'\). This is done by replacing events in the input sequences by the top-k parallel episodes found in Step 2. For this purpose, a unique identifier is given to each top-k episode.

For instance, the IDs \(\#1\), \(\#2\), \(\#3\) and \(\#4\) are assigned to the top-k parallel episodes \(\langle \{a\} \rangle \), \(\langle \{b\} \rangle \), \(\langle \{c\} \rangle \), and \(\langle \{a,b\}\rangle \), respectively. Then, the input sequence is re-encoded as: \(S=\langle (\{\#1 \#3\} ,t_1),\) \((\{\#1\},t_2),\) \((\{\#1,\#2,\#4\},t_3),\) \((\{\#1\},t_6),\) \((\{\#1,\#2,\#4\},t_7),\) \((\{\#3\},t_8),\) \((\{\#2\},t_9)\rangle \).

Step 4. Finding the top-k composite episodes. Then, the TKE algorithm attempts to find the top-k composite episodes. First, the top-k parallel episodes are inserted into a set CEpisodes. Then, TKE attempts to join each frequent composite episodes \(ep \in CEpisodes\) with each frequent event \(e \in PEpisodes\) to generate a larger episode called a serial extension of ep by e. Formally, the serial extension of an episode ep \(= \langle SE_1,\) \(SE_2,\ldots ,\) \(SE_x \rangle \) with a parallel episode e yields the episode \(serialExtension(ep, e)=\) \(\langle SE_1,\) \(SE_2,\) \(\ldots , SE_x,\) \(e \rangle \). The bound list of newE is created, which is defined as follows:

Definition 6 (Bound list)

Consider a re-encoded sequence \(S' = \langle (SE_{t_1}, t_1),\) \((SE_{t_2},t_2),\) \(\ldots ,\) \((SE_{t_n},t_n) \rangle \), a composite episode ep and a parallel episode e. The bound list of e is denoted and defined as \(boundList(e)= \{[t,t]|e \in SE_t \in S'\}\). The bound list of the serial extension of the composite episode ep with e is defined as: \(boundList(serialExtension(ep,e))= \{[u,w]|\) \([u,v] \in boundList(ep)\) \(\wedge [w,w]\in boundList(e)\) \(\wedge w - u < winlen \) \(\wedge v < w \}\). The support of a composite episode ep can be derived from its bound list as \(sup(ep) = |\{t_s |[ts,te] \in boundList(ep)\}|\).

If the support of newE is no less than minsup according to its bound list, then newE is inserted in CEpisodes, and then minsup is set to the support of the k-th most frequent episode in CEpisodes. Finally, all episodes in CEpisodes having a support less than minsup are removed. At the end of this step, CEpisodes contains the top-k frequent composite episodes and the algorithm terminates.

For instance, the bound-list of \(S=\langle \{a\}, \{a\} \rangle \) is \(boundList(\langle \{a\},\) \(\{a\} \rangle ) = \) \(\{[t_1,t_2],\) \([t_2,t_3],\) \([t_6,t_7]\}\). Thus, \(sup(\langle \{a\}, \{a\} \rangle ) =\) \( |\{t_1, t_2, t_6\}| = 3\). Then, TKE considers other serial extensions and calculate their support values in the same way. After Step 4, \(minsup = 3\) and the top-k composite episodes are: \(\langle \{a\} \rangle \), \(\langle \{b\} \rangle \) and \(\langle \{a\},\{a\} \rangle \), with a support of 5, 4, and 3 respectively (the final result).

Completeness. It is easy to see that the TKE algorithm only eliminates episodes that are not top-k episodes since it starts from \(minsup = 1\) and gradually raises the minsup threshold when k episodes are found. Thus, TKE can be considered complete. However, it is interesting to notice that due to the definition of support, mining the top-k episodes may result in a set of episodes that is slightly different from that obtained by running EMMA with an optimal minimum support. The reason is that extending a frequent episode with an infrequent episode can result in a frequent episode. For example, if \(minsup = 3\) and \(winlen = 6\), \(sup(\langle \{a\}\rangle ) = 5\), and can be extended with \(\langle \{a,b\} \rangle \) having a support of 2 to generate the episode \(\langle \{a\}, \{a,b\} \rangle \) having a support of \(4 > 2\). Because EMMA has a fixed threshold, it eliminates \(\langle \{a,b\} \rangle \) early and ignore this extension, while TKE may consider this extension since it starts from \(minsup =1\) and may not increase minsup to a value greater than 2 before \(\langle \{a\}, \{a,b\} \rangle \) is generated. Hence, TKE can find episodes not found by EMMA.

Implementation Details. To have an efficient top-k algorithm, data structures are important. An operation that is performed many times is to update the current list of top-k events/episodes and retrieve the support of the k most frequent one. To optimize this step, the list of top-k events, PEpisodes and CEpisodes are implemented as priority queues (heaps).

Dynamic Search Optimization. It can also be observed that the search order is important. If TKE finds episodes having a high support early, the minsup threshold may be raised more quickly and a larger part of the search space may be pruned. To take advantage of this observation, an optimization called dynamic search is used. It consists of maintaining at any time a priority queue of episodes that can be extended to generate candidate episodes. Then, TKE is modified to always extend the episode from that queue that has the highest support before extending others. As it will be shown in the experiments, this optimization can greatly reduce TKE’s runtime.

figure a

4 Experimental Evaluation

Experiments have been done to evaluate the performance of the TKE algorithm. It has been implemented in Java and tested on a worsktation equipped with 32 GB of RAM and an Intel(R) Xeon(R) W-2123 processor. All memory measurements were done using the Java API. Three benchmark datasets have been used, named e-commerce, retail and kosarak. They are transaction databases having varied characteristics, which are commonly used for evaluating itemset  [13, 22] and episode  [3, 12, 30] mining algorithms. As in previous work, each item is considered as an event and each transaction as a simultaneous event set at a time point. e-commerce and retail are sparse customer transaction datasets, where each event set is a customer transaction and each event is a purchased item, while kosarak is a sequence of clicks on an Hungarian online portal website, which contains many long event sets. While e-commerce has real timestamps, retail and kosarak do not. Hence, for these datasets, the timestamp i was assigned to the i-th event set. The three datasets are described in Table 1 in terms of number of time points, number of distinct events, and average event set size.

Table 1. Dataset characteristics
Full size table

4.1 Influence of k and Optimizations on TKE’s Performance

A first experiment was done to (1) evaluate the influence of k on the runtime and memory usage of TKE, and to (2) evaluate the influence of optimizations on TKE’s performance. The winlen parameter was set to a fixed value of 10 on the three datasets, while the value of k was increased until a clear trend was observed, the runtime was too long or algorithms ran out of memory. Three versions of TKE were compared: (1) TKE (with all optimizations), (2) TKE without the SEI strategy and (3) TKE without dynamic search (using the depth-first search of EMMA). Results in terms of runtime and memory usage are reported in Fig. 2.

Fig. 2.
figure 2

Influence of k on runtime for different datasets.

Full size image

It is first observed that as k is increased, runtime and memory usage increase. This is reasonable because more episodes must be found, and thus more episodes must be considered as potential top-k episodes before minsup can be raised.

Second, it is observed that using the dynamic search greatly decreases runtime. For example, on the koarak dataset, when k = 800 , TKE with dynamic search can be twice faster than TKE with depth-first search, and on the retail dataset, when k = 10000, TKE with dynamic search is up to 7.5 times faster than TKE with depth-first search. These results are reasonable since the dynamic search explores episodes having the highest support first, and thus the internal minsup threshold may be raised more quickly than when using a depth-first search, which helps reducing the search space and thus the runtime. But on the e-commerce dataset, TKE with dynamic search is about as fast as TKE with depth-first search. The reason is that this dataset is relatively small and the time required for maintaining the candidate priority queue offset the benefits of using the dynamic search.

Third, it is observed that TKE with dynamic search generally consumes more memory than TKE without. This is because the former needs to maintain a priority queue to store potential frequent episodes and their bound lists. Note that on the e-commerce dataset, when \(k\ge 4000\), TKE without dynamic search runs out of memory. Hence, results are not shown in Fig. 2.

Fourth, it is found that the SEI strategy generally slightly reduces the runtime on these three datasets. This is because TKE raises the internal minsup threshold early using that strategy after the first scan of the input sequence, which helps to reduce the search space. Moreover, TKE with the SEI strategy consumes a little more memory than TKE without the SEI strategy since the former keeps a priority queue of size k to store the support of each frequent event during Step 1 of the algorithm.

4.2 Performance Comparison with EMMA Set with an Optimal minsup Threshold

A second experiment was done, to compare the performance of TKE with that of EMMA. Because TKE and EMMA are not designed for the same task (mining the top-k episodes and mining all the frequent episodes), it is difficult to compare them. Nonetheless, to provide a comparison of TKE and EMMA’s performance, we considered the scenario where the user would choose the optimal minsup value for EMMA to produce the same number of episodes as TKE. In this scenario, mining the top-k frequent episodes remains much more difficult than mining frequent episodes because for the former problem, the internal minsup threshold must be gradually increased from 1 during the search, while EMMA can directly use the optimal minsup threshold to reduce the search space. For this experiment, TKE without dynamic search was used. It was run with k values from 1 to 1000 and winlen = 10 on kosarak, while EMMA was run with minsup equal to the support of the least frequent episode found by TKE. It is to be noted that EMMA with this optimal minsup value can find less frequent episodes than TKE because EMMA can ignore some extensions with infrequent events, as mentioned in the previous section.

Results in terms of runtime, memory usage and number of patterns found by EMMA for an optimal minsup value are shown in Table 2. Results for e-commerce and retail are not shown but follow similar trends. It is observed that the runtime of TKE is more than that of EMMA, which is reasonable, given that top-k frequent episode mining is a more difficult than traditional frequent episode mining. In terms of memory, TKE requires more memory than EMMA, which is also reasonable since TKE needs to consider more potential patterns and to keep priority queues in memory to store potential top-k episodes and candidates.

It is important to notice that EMMA is run with an optimal minsup value. But in real life, the user doesn’t know the optimal minsup value in advance. To find a desired number of episodes, a user may need to try and adjust the minsup threshold several times. For example, if the user wants between 400 to 600 frequent episodes, minsup must be set between 0.3293 and 0.3055. That is to say, if the user doesn’t have any background knowledge about this dataset, there is only 0.3293 − 0.3055 = 2.38% chance of setting minsup accurately, which is a very narrow range of options. If the user sets the parameter slightly higher, EMMA will generate too few episodes. And if the user sets minsup slightly lower, EMMA may generate too many episodes and have a long runtime. For example, for minsup = 0.1, EMMA will generate more than 62 times the number of desired episodes and be almost 4 times slower than TKE. This clearly shows the advantages of using TKE when the user doesn’t have enough background knowledge about a dataset. Thus, to avoid using a trial-and-error approach to find a desired number of frequent episodes, this paper proposed the TKE algorithm, which directly let the user specify the number of episodes to be found.

Table 2. Comparison of TKE without dynamic search and EMMA with optimal minsup threshold on the kosarak dataset
Full size table

5 Conclusion

This paper has proposed to redefine the task of frequent episode mining as top-k frequent episode mining, and presented an efficient algorithm named TKE for this task. To apply the algorithm a user is only required to set k, the desired number of patterns. To increase its internal minsup threshold as quickly as possibleng the most promising patterns first. to reduce the search space, TKE applies a dynamic search, which consists of always explori A performance evaluation on real-life data has shown that TKE is efficient and is a valuable alternative to traditional episode mining algorithms. The source code of TKE as well as datasets can be downloaded from the SPMF data mining software http://www.philippe-fournier-viger.com/spmf/  [10]. For future work, extensions of TKE could be considered for variations such as mining episode using a hierarchy  [5], weighted closed episode mining  [19, 31], high-utility episode mining  [12, 21, 25] and episode mining in a stream  [20, 24]. Besides, we will consider designing algorithms for other pattern mining problems such as discovering significant trend sequences in dynamic attributed graphs  [6], frequent subgraphs  [8], high utility patterns  [28] and sequential patterns with cost/utility values  [9].