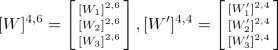Simulating Parallel Internal Column Contextual Array Grammars Using Two-Dimensional Parallel Restarting Automata with Multiple Windows

Abstract

The connection between picture languages and restarting automata has been established in Otto (2014). An interesting class of picture languages generated by parallel contextual array grammars was studied with application in image generation and analysis in Subramanian et al. (2008). In this paper, we introduce a variant of two dimensional restarting automata that accepts a subclass of parallel internal contextual array languages. We show that these automata can simulate parallel internal column contextual array grammars in reverse order.

1 Introduction

Syntactic approaches, on account of their structure-handling capability, have played an important role in the problem of description of picture patterns considered as connected digitized, finite arrays of symbols. Using the techniques of formal string language theory, various types of picture or array grammars have been introduced and investigated in [3, 9, 10, 24, 25]. Most of the array grammars are based on Chomskian string grammars. Some recent results on picture languages can be found in [2, 8, 18]. Another interesting class of string grammars, called the class of contextual grammars, was proposed by Marcus in [16]. A contextual grammar defines a string language by starting from a given finite set of strings and adjoining iteratively pairs of strings (called contexts) associated to sets of words (called selectors), to the strings already obtained. These contextual grammars [6, 23] are known to provide new approaches for a number of basic problems in formal language theory. Recently, extension of string contextual grammars to array structures has been attempted in [1, 7, 15, 23]. A new method of description of pictures of digitized rectangular arrays, through parallel contextual array grammars, was introduced [4, 26]. In this paper, we establish a relationship between two dimensional restarting automata and parallel internal column contextual array grammars.

The concept of restarting automaton was introduced in [14], in order to model the ‘analysis by reduction’, which is a technique used in linguistics to analyze sentences of natural languages. Analysis by reduction consists of step-wise simplifications (reductions) of a given (lexically disambiguated) extended sentence unless a correct simple sentence is obtained. A word is accepted until an error is found - the process continues until either the automaton accepts or an error is detected. Each simplification replaces a short part of the sentence by an even shorter one. The one dimensional restarting automaton contains a finite control unit, a head with a look-ahead window attached to a tape.

It has been shown in [12], that restarting automaton with delete (simply, DRA) can represent the analyzer for characterizing the class of contextual grammars with regular selector (CGR). Also [13] showed that restarting automata recognize a family of languages which can be generated by certain type of contextual grammars, called regular prefix contextual grammars with bounded infix (RPCGBI).

Here, we focus on two dimensional parallel restarting automata as we are dealing with rectangular picture languages and bring the concept of multiple windows in order to capture the parallel application of rules of parallel internal column contextual array grammars. A two dimensional parallel restarting automaton can delete adjoined sub-arrays in a cycle and followed by restart (DEL-RST). We exploit the DEL-RST operation to reverse the adjoining contexts that take place in a derivation of a parallel internal column contextual array grammar. We use two dimensional parallel restarting automaton with multiple windows to simulate parallel internal column contextual array grammars in reverse order.

The membership problem for a language asks whether, for a given grammar G and a string w, w belongs to the language generated by G or not.

The remainder of this paper is organized as follows. Section 2 describes the basic classes of contextual grammars in more detail which is followed by an example in Subsect. 2.1. Section 3 presents the new variant of two dimensional parallel restarting automata with multiple windows. In Sect. 4, we describe the connection between parallel internal column contextual array grammars and two dimensional parallel restarting automata with multiple windows, also an example is given in Subsect. 4.1 for better understanding. Subsection 4.2 presents some interesting properties of the proposed automata and in Subsect. 4.3 we discuss about the complexity of membership problem for parallel internal column contextual array languages, also we introduce some new definitions. Section 5 concludes the work and shows a future direction of work.

2 Preliminaries

Let V be a finite alphabet. We write $V^{*}$ for the set of all finite strings over V, which includes the empty string $\lambda$. An image or picture over V is a rectangular $m \times n$ array of elements of V or in short $[a_{ij}]_{m\times n}$. The set of all images over V is denoted by $V ^{**}$. A picture language or two dimensional language over V is a subset of $V ^{**}$. We define $V^{m,n}=\{A \in V^{**}\mid A$ has m rows and n columns}. If $a \in V$, then $[a^{m,n}]$ is the array over $\{a\}$ with m rows and n columns. In this paper, $\Lambda$ denotes any empty array. The notion of column concatenation is defined as follows: if A and B are two arrays where

If $L_{1}, L_{2}$ are two picture languages over an alphabet V, the column concatenation $L_1 \varPhi L_2$ of $L_1, L_2$ is defined by $L_1\varPhi L_2=\{A\varPhi B \mid A \in L_1, B \in L_2\}$. Column concatenation is only defined for pictures that have the same number of rows. Note that operation $\varPhi$ is associative. If X is an array, the set of all sub-arrays of X is denoted by sub(X). We now recall the notion of column array context [4, 26].

Definition 1

Let V be an alphabet. A column array context c over V is of the form

where $u_1, u_2$ are arrays of sizes $1\times p$, and $v_1, v_2$ are arrays of sizes $1\times q$, for some $p, q \ge 1$, and $\psi$ is a special symbol not in V.

The next definition deals with the parallel internal column contextual operation.

Definition 2

Let V be an alphabet, C a finite set of column array contexts over V, and $\varphi : V^{**}\rightarrow 2^C$ a mapping, called choice mapping. For an array , $j\le k, a_{ij} \in V$, we define $\hat{\varphi } : V^{**}\rightarrow 2^{V^{**}\psi V^{**}}$ such that $L\psi R \in \hat{\varphi } (A)$, where

and with $c_{i} \in C, (1\le i \le l-1)$ , not all need to be distinct. Given an array $X=[a_{ij}]$ of size $m\times n$, $a_{ij} \in V, X=X_1 \varPhi X_2 \varPhi X_3$ where

and $1\le p\le q \le n$, we write $X\Rightarrow _{in} Y$ if $Y=X_1\varPhi L\varPhi X_2 \varPhi R \varPhi X_3$ such that $L\psi R \in \hat{\varphi }(X_2)$. Here L and R are called left and right contexts respectively. We say that Y is obtained from X by parallel internal column contextual operation $(\Rightarrow )$.

Now we consider the notion of parallel internal column contextual array grammar [4, 26].

Definition 3

A parallel internal column contextual array grammar (PICCAG) is an ordered system $G=(V,\mathbf{A},C,\varphi )$, where V is an alphabet, $\mathbf{A}$ is a finite subset of $V^{**}$ called the axiom set, C is a finite set of column array contexts over V, $\varphi :V^{**}\rightarrow 2^{C}$ is the choice mapping which performs the parallel internal column contextual operation. When $\varphi$ is omitted we call G a parallel internal contextual array grammar without choice.

We already discussed the notion of $X\Rightarrow _{in} Y$ in the previous definition. Here we denote by $\Rightarrow ^*_{in}$ the reflexive transitive closure of $\Rightarrow _{in}$. The parallel internal column contextual array language (PICCAL) generated by G is defined as the set $L_{in}(G)=\{Y\in V^{**}\mid \exists X\in \mathbf{A}$ such that $X\Rightarrow ^*_{in} Y\}$.

2.1 Example

Let $G =(V,\mathbf{A},C,\varphi )$ be a parallel internal column contextual array grammar (PICCAG) where $V=\{a,b\}$, ,

, $\varphi$ is a choice mapping satisfying

Then,

, where $a^n=aa...a$ (n times) and , with m rows. A simple derivation of a member of $L_{in}(G)$ is as follows:

Now, if we consider a = white box and b = black box, we get a nice rectangular picture, see Fig. 1 and Fig. 2.

Fig. 1.

A rectangular picture of size $4\times 4$

Fig. 2.

A rectangular picture of size $4\times 6$

3 Two Dimensional Parallel Restarting Automata with Multiple Windows

It is interesting to find the connection between picture languages with deterministic two-dimensional three-way ordered restarting automata ($\text {det-2D-3W-ORWW}$) and deterministic two-dimensional extended two-way ordered restarting automata ($\text {det-2D-x2W-ORWW}$) in [19, 20].

In this section we present a variant of two dimensional restarting automaton called a two dimensional parallel restarting automaton with multiple windows ($\text {2D-PRA-W}_\mathrm{m}$) in order to simulate PICCAL in reverse order. Here we introduce multiple windows to deal with the parallel application of rules of parallel internal column contextual array grammars. This automaton works when PICCAG is given.

We describe the basic working nature of $\text {2D-PRA-W}_\mathrm{m}$. It contains finite control unit and multiple tapes and each tape is associated with individual head and they work in a parallel way. At several points, it cuts-off sub-arrays from each sub-window using DEL operation followed by restart (RST) operation, that is, DEL-RST. Here in each sub-window the same number of columns are deleted, this happens in exactly the same positions.

All the heads move together right along the individual tape until it takes any DEL-RST operation. RST implies that the restarting automaton places all the windows over the left border of the individual tape and it completes one cycle. After performing a DEL-RST operation, the restarting automaton is unable to remember any step of computation that was performed already.

Let W be an array of size $m \times n$, with $m \ge 2$. Assume

Now we present the concept of super window and sub-window.

where $[W]^{f+1,k}$ is called the super window (array) of size $((f+1)\times k)$ which contains sub-windows (arrays) $[W_i]^{2,k}$ of sizes $(2\times k)$ where $[W_i]^{2,k}=([\triangleleft ^{2,1}]\varPhi V^{2,k-1})\cup (V^{2,k})\cup (V^{2,k-1}\varPhi [\triangleright ^{2,1}]) \cup ([\triangleleft ^{2,1}]\varPhi V^{2, k-2}\varPhi [\triangleright ^{2,1}])$. Here f denotes the number of sub-windows. The second row of each ith sub-window $[W_i]^{2,k}$ overlaps with the first row of each $(i+1)$th sub-window $[W_{i+1}]^{2,k}$. Now we show the transition function $\delta$ of $\text {2D-PRA-W}_\mathrm{m}$ for set of sub-windows. Here $[\triangleleft ^{2,1}], [\triangleright ^{2,1}]$ denote one column and 2 rows of $\triangleleft , \triangleright$ marker respectively.

Suppose .

Now W can be viewed in the following way with the help of sub window and super window. The size of each sub window depends on the given grammar. Interestingly, size of super window depends on the number of sub window. (Discussed in detail in Theorem 1). We have shown below sub window $[W_1],[W_2],[W_3]$ and the super window [W] which contains $[W_1],[W_2],[W_3]$.

Let $G=PICCAG=(V,\mathbf{A},C,\varphi )$.

Definition 4

A two dimensional parallel restarting automaton with multiple window $(\text {2D-PRA-W}_\mathrm{m})$, is given through a 6-tuple, $M=(Q, V, \triangleleft , \triangleright , q_0,\delta )$ where

• Q is a finite set of states,

• V is the input alphabet,

• $\triangleleft , \triangleright$ are left border, right border markers respectively,

• $q_0\in Q$ is the initial state,

• $\delta : Q \times [W_i]^{2,k}\rightarrow 2^{((Q\times \{MVR, DEL-RST\})\cup \{Accept, Reject\})}$ is the transition function. This function describes four different types of transition steps:

  • MVR: $(q, MVR) \in \delta (q, ([W_i]^{2,k}, [W_{i+1}]^{2,k},...,[W_f]^{2,k}))$. Thus each sub-window of M sees the sub-array of size $2\times k$. Applying the transition function $\delta$, each sub-window of M moves through left to right using MVR until it takes DEL-RST or $\triangleright \notin [W_i]^{2,k}$.

  • DEL-RST: $(q_0, DEL-RST) \in \delta (q, ([W_i]^{2,k}, [W_{i+1}]^{2,k},...,[W_f]^{2,k}))$ : For possible contents of each sub-window, it deletes a subarray and causes M to move its sub-window to the left border marker $\triangleleft$ and re-enters into the initial state $q_0$.

  • ACCEPT: $Accept\in \delta (q,([W_i]^{2,k}, [W_{i+1}]^{2,k},...,[W_f]^{2,k}))$, it gets into an accepting state.

  • REJECT: $Reject\in \delta (q,([W_i]^{2,k}, [W_{i+1}]^{2,k},...,[W_f]^{2,k})) = \emptyset$ (i.e., when $\delta$ is undefined), then M will reject the input.

• Let $P \in V^{r,s}$ is accepted by $2D-PRA-W_{m}$ M, if there is a computation, which starts from the initial configuration $q_0[\triangleleft ^{r,1}]\varPhi P \varPhi [\triangleright ^{r,1}]$, and reaching the Accept state. By L(M), we denote the language consisting of all arrays accepted by M. In formal notation $L(M)=\{P \in V^{r,n}\mid q_0 [\triangleleft ^{r,1}]\varPhi P^{r,s} \varPhi [\triangleright ^{r,1}]\vdash ^{*}Accept \}$. Here $[\triangleleft ^{r,1}], [\triangleright ^{r,1}]$ denote one column and r rows of $\triangleleft , \triangleright$ marker respectively.

In general, the $\text {2D-PRA-W}_\mathrm{m}$ is nondeterministic, that is, there can be two or more instructions with the same left-hand side. If this is not the case, the automaton is deterministic.

Proposition 1

(Error preservation of $\text {2D-PRA-W}_\mathrm{m}$). If $[W]^{f+1,k}{\vdash _{M}^{*}} [W']^{f+1,k'}$ and $[W]^{f+1,k}\notin L(M)$ then $[W']^{f+1,k'}\notin L(M)$ where $[W]^{f+1,k}, [W']^{f+1,k'} \in V^{**}, k > k'$.

4 $\text {2D-PRA-W}_\mathrm{m}$ and PICCAG

Before we analyze the relationship between $\text {2D-PRA-W}_\mathrm{m}$ and PICCAG, which is the objective of this section, we first need to understand the relationship of DRA with string contextual grammars [12].

External contextual grammars were introduced by Marcus in 1969 [16]. Internal contextual grammars [22] produce strings starting from an axiom and in each step left context and right context are adjoined to the string based on certain string called selector present as a sub-string in the derived string. u, v are called left context and right context respectively. For more details on contextual grammars, we refer to [21].

• The selector in a contextual grammar can be of arbitrary type in nature, like regular, context-free etc, but the strings u, v are finite.

• Normal DRA works in the opposite way of contextual grammars in accepting strings [12]. In a normal DRA M, w is given as an input, it checks the items of the window with the contextual grammar G that any given rule has been used or not.

• If it finds that any rule has been used then the automaton deletes the left and right context u, v and takes the RST operation, otherwise takes MVR and checks whether any rule in G can be applied.

• In this way, the automaton simulates the derivation of contextual grammar in reverse order and if the input string can be reduced back to the axiom B¹, it implies that the string w can be generated using the given grammar G, thus $w\in L(G)$.

• Here the size of the tape of the automaton M is same as the size of the array w. Step by step, the automaton M only deletes subarrays of w, so the size of the tape becomes smaller and smaller.

In this paper, we adapt the working nature of DRA to solve membership problem for PICCAL. We show that the membership problem for PICCAL is solvable by the introduced $\text {2D-PRA-W}_\mathrm{m}$. The paradigm of this version of $\text {2D-PRA-W}_\mathrm{m}$ is closely related to PICCAG. A PICCAG works just in the opposite direction of $\text {2D-PRA-W}_\mathrm{m}$. The connection is established based on the following observation. For a PICCAG rule $\varphi [x_i]=L_i\psi R_i$, now if we present that in two-dimensional form-

where $\text {2D-PRA-W}_\mathrm{m}$ has to delete the left context $L_i$ and right context $R_i$, that is, $\varphi [x_i]=L_i\psi R_i$ is occurred as a subarray in the given input array. In that case, we informally say that a PICCAG rule is found in the window as a subarray.

Let M be $\text {2D-PRA-W}_\mathrm{m}$. A reduction system induced by M is $RS(M)=(V^{**}, \vdash _{M})$. For each PICCAG G, we define a reduction system induced by G as $RS(G)=(V^{**}, \Rightarrow ^{-1}_G)$ where $([W]^{f+1,k}\vdash ^{-1}_{M}[W']^{f+1,k'})$ iff $[W']^{f+1,k'}\Rightarrow _{G}[W]^{f+1,k}$.

With the above detail we will construct a $\text {2D-PRA-W}_\mathrm{m}$ in such a way that if $B \Rightarrow ^{*}_{G}P$ then $P\vdash ^{*}_{M}B$ for $P, B\in V^{**}, B \in \mathbf{A}$, thus $RS(G)=RS(M)$. Also $\mathcal{{L}}\text {2D-PRA-W}_\mathrm{m}$ denotes the class of languages accepted by $\text {2D-PRA-W}_\mathrm{m}$.

Theorem 1

For a PICCAG G, a $\text {2D-PRA-W}_\mathrm{m}$ automaton M can be constructed in such a way that $RS(G)=RS(M)$ and $L_{in}(G)=L(M)$.

Proof

Given a PICCAG $G=(V,\mathbf{A},C,\varphi )$ we have to construct a $\text {2D-PRA-W}_\mathrm{m}$ automaton $M=(Q, V, \triangleleft , \triangleright , q_0,\delta )$, that accepts $L_{in}(G)$ where

• $Q=\{q_0,q, Accept, Reject\}$

• V is the input alphabet

• $\triangleleft , \triangleright$ are left and right borders respectively and $\triangleleft , \triangleright \notin V$

• $q_0$ is the initial state.

• Here number of columns in each window of M will be $k = max(Rule_{max}, k_b+2)$ where $Rule_{max}$ is the maximum size given rule - $Rule_{max} = max\{|Rule_1|_c,$ $|Rule_2|_c,...,|Rule_n|_c\}$ where $|Rule_i|_c$ denotes the number of columns in the ith rule and $1 \le i \le n, n \ge 1$.

• Let $k_b$ be axiom size. 2 is added there for the left border $\triangleleft$ and the right border $\triangleright$. The reason for 2 is added with $k_b$ is to satisfy the accepting condition - ACCEPT - $Accept \in \delta (q, ([W_i]^{2,k}, [W_{i+1}]^{2,k},...,[W_f]^{2,k}))$ where $[W]^{f+1,k}=[\triangleleft ^{f+1,1}] \varPhi B \varPhi [\triangleright ^{f+1,1}]$ where $B \in \mathbf{A}$.

• If the rule is $Rule_i = (\varphi [x_i]=[L_i]\psi [R_i])$ where $x_i, L_i, R_i$ are arrays of size $2\times k, k\ge 1$, then we define $|Rule_i|_c=|x_i|_c+|L_i|_c+|R_i|_c$, $Rule_{max} = max\{|Rule_1|_c, |Rule_2|_c,...,|Rule_n|_c\}$

Lemma 1

If the input is $P^{m,n}$, then number of windows will be $m-1$.

Proof

Each window will take care of each rule in a parallel way. According to Definition 2, we know that if the input is P of size $m \times n$ then the number of parallel rules will be $m-1$, from this fact we can conclude this. (see example for better understanding)

• DEL-RST: The DEL-RST instruction of the $\text {2D-PRA-W}_\mathrm{m}$ for solving membership problem of PICCAL, works in the following manner:

  • Now M works in a parallel way on, $(q, ([W_i]^{2,k}, [W_{i+1}]^{2,k},...,[W_f]^{2,k}))$ where $i \ge 1$, and applies DEL-RST on each sub-window from state q to arrive at $((q_0,[W'_i]^{2,k'}), (q_0,[W'_{i+1}]^{2,k'}),...,(q_0,[W'_f]^{2,k'}))$ and eventually reaching $(q_0, ([W'_i]^{2,k'}, [W'_{i+1}]^{2,k'},...,[W'_f]^{2,k'}))$ where $[W']^{f+1,k'},[W'_i]^{2,k'}$ are scattered sub-array of $[W]^{f+1,k}, [W_i]^{2,k}$ respectively and $k>k'$, immediately followed by a RST instruction: RST $\in \delta (q, [W_i]^{2,k})$ for any possible contents $[W_i]^{2,k}$ of the window. If no PICCAG rule does belong to window as a subarray and $\triangleright$ does not belong to window ($\triangleright \notin [W_i]^{2,k}$) then the automaton takes MVR operation.

• ACCEPT: $Accept \in \delta (q, ([W_i]^{2,k}, [W_{i+1}]^{2,k},...,[W_f]^{2,k}))$ where $[W]^{f+1,k}=[\triangleleft ^{f+1,1}]\varPhi B \varPhi [\triangleright ^{f+1,1}]$ where $B \in \mathbf{A}$. Here $[\triangleleft ^{f+1,1}], [\triangleright ^{f+1,1}]$ denote one column of $\triangleleft , \triangleright$ marker respectively, here we deal with singleton axiom set.

• REJECT: $Reject \in \delta (q, ([W_i]^{2,k}, [W_{i+1}]^{2,k}..., [W_{f}]^{2,k})) = \emptyset$. That is when $\delta$ is undefined. In other words, when $2D-PRA-W_{m}$ is unable to take any of the DEL-RST or MVR operation, then the transition becomes undefined.

$\text {2D-PRA-W}_\mathrm{m}$ simulates the derivation of PICCAG in reverse order, in case of any PICCAG rule it deletes the left and right contexts using DEL-RST instruction which is defined already. For PICCAG, the derivation starts from the axiom to the generated array, the automaton starts the reduction from the generated array to the axiom. If $B\Rightarrow ^{*}_{G}P$ then $P\vdash ^{*}_{M}B$ where $P, B\in V^{**}, B\in \mathbf{A}$ is axiom, thus $RS(G)=RS(M)$.

Corollary 1

The membership problem for PICCAL can be solved by $\text {2D-PRA-W}_\mathrm{m}$.

Proof

We conclude this important result from Theorem 1.

4.1 Example

Consider the PICCAG G given in Example 2.1. Suppose is given as an input and we note that $P \in L_{in}(G)$. Now we can construct a $\text {2D-PRA-W}_\mathrm{m}$ automaton $M=(Q, V, \triangleleft , \triangleright , q_0,\delta )$, that accepts P where

• $Q=\{q_0,q, Accept, Reject\}$

• V is the input alphabet

• $\triangleleft , \triangleright$ are left and right borders respectively and $\triangleleft , \triangleright \notin V$

• $q_0$ is the initial state

• The number of columns in each window is $k=6$ and the number of windows is 3 respectively.

• In the first cycle, rule and $\triangleleft$ are not found in the window and so it takes MVR: $(q, MVR) \in \delta (q, ([W_1]^{2,6}, [W_{2}]^{2,6},[W_3]^{2,6}))$, where

• After taking the MVR operation the elements of windows get changed and M takes $DEL-RST$: $(q_0, ([W'_1]^{2,4},[W'_2]^{2,4}, [W'_3]^{2,4}))\in \delta (q, [W_1]^{2,6},[W_2]^{2,6},$ $[W_3]^{2,6}))$, where $[W'_i]^{2,4}$ is the scattered sub-array of $[W_i]^{2,6}, i \ge 1$ and

• In the next cycle, again M can take $DEL-RST : (q_0, ([W'_1]^{2,4},$$[W'_2]^{2,4}, [W'_3]^{2,4}))\in \delta (q_0, [W_1]^{2,6},[W_2]^{2,6}, [W_3]^{2,6}))$ where $[W'_i]^{2,4}$ is the scattered sub-array of $[W_i]^{2,6}, i \ge 1$ and

• In the next cycle, $Accept \in \delta (q_0, [W_1]^{2,6},[W_2]^{2,6},[W_3]^{2,6})$ where

In this way, every member of $L_{in}(G)$ is accepted by M. Now we consider the input and we note that $P' \notin L_{in}(G)$.

In the first cycle, rule and $\triangleleft$ are not found in the window, so it takes MVR: $(q, MVR) \in \delta (q, ([W_1]^{2,6}, [W_{2}]^{2,6},[W_3]^{2,6}))$, where

• Now M takes $DEL-RST$ : $(q_0, ([W'_1]^{2,4},[W'_2]^{2,4}, [W'_3]^{2,4}))\in \delta (q,([W_1]^{2,6},$$[W_2]^{2,6},$ $[W_3]^{2,6}))$, where $[W'_i]^{2,4}$ is the scattered sub-array of $[W_i]^{2,6}, i \ge 1$ and

  
  
  
  

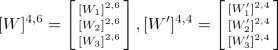
  In the next cycle, again M can take $DEL-RST : (q_0, ([W'_1]^{2,4},[W'_2]^{2,4},$$[W'_3]^{2,4}))\in \delta (q_0, ([W_1]^{2,6},[W_2]^{2,6}, [W_3]^{2,6}))$ where $[W'_i]^{2,4}$ is the scattered sub-array of $[W_i]^{2,6}, i \ge 1$ and

In the next cycle, it rejects because this time transition function is undefined. $Reject \in \delta (q_0, ([W_1]^{2,6},[W_2]^{2,6},[W_3]^{2,6}))$ where

4.2 Properties of $\text {2D-PRA-W}_\mathrm{m}$

In this section, we introduce some important properties of $\text {2D-PRA-W}_\mathrm{m}$.

Lemma 2

The language class $\mathcal{{L}}(\text {2D-PRA-W}_\mathrm{m})$ is closed under $180^\circ$ rotation.

Proof

Let $\text {2D-PRA-W}_\mathrm{m}$ be $M=(Q, V, \triangleleft , \triangleright , q_0,\delta )$, that accepts a language $L\subseteq V^{*,*}$ where $Q=\{q_0,q, Accept, Reject\}$, V is the input alphabet, $\triangleleft , \triangleright$ are left and right borders respectively and $\triangleleft , \triangleright \notin V$, $q_0$ is the initial state, $Accept\in \delta (q,([W_i]^{2,k}, [W_{i+1}]^{2,k},...,[W_f]^{2,k}))$, $Reject\in \delta (q,([W_i]^{2,k}, [W_{i+1}]^{2,k},...,[W_f]^{2,k}))$ $= \emptyset$ (i.e., when $\delta$ is undefined), then M will reject.

Now, from M we can construct $M_R$ (after $180^\circ$ rotation of M) where $M_R=(Q, V, \triangleleft , \triangleright , q_0,\delta )$, that accepts a language $L\subseteq V^{*,*}$ where $Q=\{q_0,q, Accept',$ $Reject\}$, V is the input alphabet, $\triangleleft , \triangleright$ are left and right borders respectively and $\triangleleft , \triangleright \notin V$, $q_0$ is the initial state, $Accept'\in \delta (q,({[W_i]{_R^{2,k}}}, {[W_{i+1}]{_R^{2,k}}},...,{[W_f]{_R^{2,k}}}))$ where ${[W_i]{_R^{2,k}}}$ is the ith sub-window after $180^\circ$ rotation of $[W_i]^{2,k}$ and $1 \le i \le f$, $Reject\in \delta (q,({[W_i]{_R^{2,k}}}, {[W_{i+1}]{_R^{2,k}}},...,{[W_f]{_R^{2,k}}})) = \emptyset$ (i.e., when $\delta$ is undefined), then M will reject the input.

Lemma 3

The language class $\mathcal{{L}}(\text {2D-PRA-W}_\mathrm{m})$ is closed under complement.

Proof

Let M be a $\text {2D-PRA-W}_\mathrm{m}$, that accepts a language $L\subseteq V^{*,*}$. Now, from M we can construct $M_c$ (complement of M) by interchanging undefined and accepting transitions.

Lemma 4

The language class $\mathcal{{L}}(\text {2D-PRA-W}_\mathrm{m})$ is closed under column concatenation.

Proof

Let $M_1$ be a $\text {2D-PRA-W}_\mathrm{m}$, on V, that accepts a language $L_1\subseteq V^{*,*}$ where $Accept\in \delta (q,([W_i]^{2,k}, [W_{i+1}]^{2,k},...,[W_f]^{2,k}))$. Consider $M_2$ be another $\text {2D-PRA-W}_\mathrm{m}$ which accepts a language $L_2\subseteq V^{*,*}$ where $Accept\in \delta (q,([W_i'']^{2,k},$ $[W_{i+1}'']^{2,k},...,[W_f'']^{2,k}))$. Now, we can construct M which can accept $L_1\varPhi L_2$ by modifying the accepting state, that is, $Accept\in \delta (q,([W_i]^{2,k}\varPhi [W_i'']^{2,k}, [W_{i+1}]^{2,k}$ $\varPhi [W_{i+1}'']^{2,k} ,...,[W_f]^{2,k}\varPhi [W_f'']^{2,k}))$.

Lemma 5

The language class $\mathcal{{L}}(\text {2D-PRA-W}_\mathrm{m})$ with auxiliary special symbol is closed under intersection.

Proof

Let $\text {2D-PRA-W}_\mathrm{m}$ be a $M_1=(Q_1, V, \varGamma _1, \triangleleft , \triangleright , q_0',\delta _1)$ with auxiliary special symbols. Let $M_2=(Q_2, V, \varGamma _2, \triangleleft , \triangleright , q_0'',\delta _2)$ be another $\text {2D-PRA-W}_\mathrm{m}$ with special symbols where $\varGamma _1,\varGamma _2\supseteq V$. Now we can construct $M=(Q, V, \varGamma , \triangleleft , \triangleright , q_0,\delta )$ such that $L(M)=L_(M_1)\bigcap L_(M_2)$. Essentially, M will work as follows:

• M first simulates $M_1$, that is, it behaves exactly like $M_1$. If $M_1$ should get stuck on the given input, that is, $M_1$ does not accept, then neither does M. If, however, $M_1$ accepts, then instead of accepting, M marks the position (i, j) at which $M_1$ accepts, using a special symbol.

• Now only M should start simulating $M_2$. So, it is understood that we need to mark the last position by special symbol and because of that we introduced $\varGamma =V\cup T$ is the tape alphabet, $\varGamma \supseteq V$.

Lemma 6

The language class $\mathcal{{L}}(\text {2D-PRA-W}_\mathrm{m})$ is not closed under transposition.

Proof

Let $G =(V,A,C,\varphi )$ be a parallel internal column contextual array grammar where $V=\{a,b\}$,

where $B \in A$, $\varphi$ is a choice mapping,

We can construct $\text {2D-PRA-W}_\mathrm{m}$ such that $L(M)=L(G)$ where the configuration of acceptance , ACCEPT- $[W]^{3,7}=[\triangleleft ]^{3,1} B [\triangleright ]^{3,1}$. where $B\in A$. Now, if we consider the transposition of B, we obtain

Clearly, $B_T\notin L(M)$ because in this case we cannot construct $M_T$. If $B_T \in L(M)$ then the content of each sub-window $w_j$ in each cycle $c_i$ should be transposed to $w_{j_T}$ such that $\forall i\forall j \; Transpose(w_j,w_{j_T})$. In order to do that, the working procedure of our M for given G, needs to be changed.

4.3 Complexity of Membership Problem for PICCAL

In this section, we discuss the complexity of solving the membership problem for PICCAL. Let us start with internal contextual string languages with finite choice (ICSL(FIN)). ICSL(FIN) is contained in the family of languages generated by growing context-sensitive grammars (GCSG), and from this scenario we will comment on the time complexity of solving membership problem for PICCAL. So here, first we recall the definition of ICSL(FIN) and GCSG.

Definition 5

[17]. For an alphabet $\varSigma$, we denote by $\varSigma ^*$ the free monoid generated by $\varSigma$, by $\lambda$ its identity, and $\varSigma ^+ = \varSigma ^* - \{\lambda \}$. The family of finite languages is denoted by FIN. Contextual grammar is a construct, $G=(\varSigma , A, (sel_1,C_1), (sel_2, C_2),...,(sel_k,C_k))$, for some $k\ge 1$, where $\varSigma$ is an alphabet, $A\subset \varSigma ^*$ is a finite set, called the axiom set, $sel_i \subseteq \varSigma ^*, 1 \le i \le k,$ are the sets of selectors, and $C_i \subset \varSigma ^* \times \varSigma ^*$ where $1 \le i \le k$, and $C_i$ is a finite set of contexts. There are two basic modes of derivation, the internal mode of derivation as follows. For two words $x,y \in \varSigma ^*$, we have the internal mode of derivation:

$x\Longrightarrow _{in} y$ iff $x=x_1x_2x_3, y= x_1ux_2vx_3, x_2 \in sel_i, (u,v)\in C_i,$ for some $1 \le i \le k$.

The language generated by internal mode of derivation is: $L_{in}(G)= \{w \in \varSigma ^* \mid x\in A, x \Longrightarrow ^*_{in} w\}$, where $\Longrightarrow ^*_{in}$ denotes the reflexive - transitive closure of $\Longrightarrow _{in}$.

If the sets $sel_1, sel_2,..., sel_k$ are languages in a given family FIN, then G is said to be with FIN choice. The family of languages generated by contextual grammars with FIN choice in the internal mode of derivation is denoted by ICSL(FIN).

Now we recall the definition from [11].

Definition 6

A context-sensitive grammar (CSG) is a tuple $G=(V,T,P,S)$, where V is a set of alphabets, T is a finite set of terminal symbols, P is a finite set of production rules, and S is the starting symbol. We say that G is growing if S does not appear on the right and $|\alpha |<|\beta |$ for any $(\alpha \rightarrow \beta )$, with $\alpha \ne S$, from P.

Definition 7

A CSG $G=(V,T,P,S)$ is QGCSG if there exists a function $f : (V\cup T)^* \mapsto \mathbb {Z}^+$ such that, for all $p\in P$, $f(\alpha )>f(\beta )$.

Lemma 7

$ICSL(FIN)\subset GCSG$

Proof

$G=(\varSigma , A, (sel_1,C_1), (sel_2, C_2),...,(sel_k,C_k))$ be ICSL(FIN). We can assume that $(\lambda ,\lambda )\notin C_i$ for all $1\le i \le k$. The problem in developing a QGCSG, is to simulate an insertion step $x \Rightarrow _{in} y$ if $x=x_1x_3, \lambda \in S_i, y=x_1uvx_3$, and $(u,v)\in C_i$ for some $1\le i \le k$. In order to avoid this, we do as follows:

We define homomorphism $h : \varSigma ^* \rightarrow \varSigma '^*$ where $\varSigma '=\{a'\mid a\in \varSigma \}$ such that $\varSigma \cap \varSigma '=\phi$ and $h(a)=a'$ for $a\in \varSigma$. Now we are ready to construct QGCSG $G'=(\varSigma ' \cup S, \varSigma , P,S)$ where $S\notin \varSigma '$, the P is given below.

$P=\{S\rightarrow h(x) \mid x\in A\} \cup \{S\rightarrow h(u,v) \mid \lambda \in A\cap S_i, (u,v)\in C_i, 1\le i \le k\} \cup \{h(x)\rightarrow h(uxv) \mid x\in S_i \setminus \{\lambda \},(u,v)\in C_i, 1\le i \le k\} \cup \{h(a)\rightarrow h(uva), h(a) \rightarrow h(auv)\mid a\in \varSigma ,\lambda \in S_i,(u,v)\in C_i, 1\le i \le k\} \cup \{h(a)\rightarrow a \mid a\in \varSigma \}$ with the valuation $f(S)=1$ and $f(h(a))=2, f(a)=3$, if $a\in \varSigma$. So, here the constructed grammar is QGCSG and $L(G')=L_{in}(G)$.

Since $QGCSG=GCSG$, we can state that $ICSL(FIN)\subset GCSG$. Here the inclusion is strict because the cross-dependency language $L_{cross- dependency}=\{a^nb^mc^nd^m \mid n,m\ge 1\} \notin ICSL(FIN)$ but $L_{cross-dependency}\in GCSL$.

Lemma 8

[11]. The membership problem for internal contextual string languages with finite choice (ICSL(FIN)) is $LOG(CFL)-hard$.

Proof

From Lemma 7, we concluded that $ICSL(FIN)\subset GCSG$. In [5], it is shown that GCSL family of languages, is contained in LOG(CFL). This shows that the upper bound for membership problem for ICSL(FIN) is LOG(CFL).

Lemma 9

The membership problem for parallel internal column contextual array languages (PICCAL) is contained in NP.

Proof

Let VERIFIER(W, C) be a procedure where W, C are given inputs and denote a word and certificate respectively. Here C is a certificate, i.e., a derivation. The procedure VERIFIER(W, C) returns “YES” if the given certificate C is correct, otherwise “NO”. In other words, VERIFIER(W, C) verifies the correctness of C. Moreover the running time of VERIFIER(W, C) is bounded by a polynomial in |W| where |W| denotes the size of W. See Algorithm 1.

Corollary 2

The membership problem for PICCAL is at least $LOG(CFL)-hard$ and is contained in NP.

Proof

From Lemma 8 and Lemma 9, we can easily conclude this Corollary 2.

5 Conclusion and Future Work

In this paper, we have introduced a non-deterministic $\text {2D-PRA-W}_\mathrm{m}$ to solve the membership problem of PICCAL. Here we have introduced multiple windows in order to capture the parallel application of the parallel column contextual array rules. Also we discussed some of the important properties of $\text {2D-PRA-W}_\mathrm{m}$ and commented on the complexity of membership problem for PICCAL.

Here our focus was on column concatenation only. We can extend our work to take care of row concatenation too. In terms of future direction of work, it could be also interesting, if we can define a powerful subclass of PICCAG and solve the membership problem using deterministic $\text {2D-PRA-W}_\mathrm{m}$.